Extending the Local Convergence of a Seventh Convergence Order Method without Derivatives

Abstract

For the purpose of obtaining solutions to Banach-space-valued nonlinear models, we offer a new extended analysis of the local convergence result for a seventh-order iterative approach without derivatives. Existing studies have used assumptions up to the eighth derivative to demonstrate its convergence. However, in our convergence theory, we only use the first derivative. Thus, in contrast to previously derived results, we obtain conclusions on calculable error estimates, convergence radius, and uniqueness region for the solution. As a result, we are able to broaden the utility of this efficient method. In addition, the convergence regions of this scheme for solving polynomial equations with complex coefficients are illustrated using the attraction basin approach. This study is concluded with the validation of our convergence result on application problems.

1. Introduction

Numerous very complicated scientific and engineering phenomena may be treated using nonlinear equations of the kind:

$$\mathcal{G}\left(y\right)=0,$$

(1)

where $\mathcal{G}:\mathsf{\Omega }\subseteq {\mathcal{Y}}_1\to {\mathcal{Y}}_2$ is derivable, as suggested by Fréchet. ${\mathcal{Y}}_1$, ${\mathcal{Y}}_2$ are complete normed vector spaces, and $\mathsf{\Omega }\subseteq {\mathcal{Y}}_1$ is non-null, convex, and open. Confronting such nonlinearity has remained a major challenge in mathematics. Analytical solutions to these problems are incredibly difficult to come up with. As a result, scientists and researchers often utilize iterative procedures to obtain the desired answer. Among iterative approaches, Newton’s method is often employed to solve these nonlinear equations. Steffensen method [1,2] is well known among iterative schemes without derivatives. Sharma and Arora [3] deduced the following algorithm, which is a variant of the Steffensen method:

$$\begin{array}{cc}\hfill s_k& =y_k-B_k^{-1}\mathcal{G}\left(y_k\right),\hfill \\ \hfill y_{k+1}& =s_k-\left[3I-B_k^{-1}\left(\mathcal{G}[s_k,y_k]-\mathcal{G}[s_k,w_k]\right)\right]\times B_k^{-1}\mathcal{G}\left(s_k\right),\hfill \end{array}$$

(2)

where $B_k=\mathcal{G}[w_k,y_k]$ is the divided difference of order one, and $w_k=y_k+\mathcal{G}\left(y_k\right)$ and $y_0\in \mathsf{\Omega }$ is an initial point. This algorithm uses one matrix inversion. Furthermore, Wang and Zhang’s [4] extended method (3) to design a seventh convergence order method is as follows:

$$\begin{array}{cc}\hfill s_k& =y_k-B_k^{-1}\mathcal{G}\left(y_k\right),\hfill \\ \hfill z_k& =s_k-[\left[3I-B_k^{-1}\left(\mathcal{G}[s_k,y_k]-\mathcal{G}[s_k,w_k]\right)\right]\times B_k^{-1}\mathcal{G}\left(s_k\right),\hfill \\ \hfill y_{k+1}& =z_k-{\left(\mathcal{G}[z_k,y_k]+\mathcal{G}[z_k,s_k]-\mathcal{G}[y_k,s_k]\right)}^{-1}\mathcal{G}\left(z_k\right).\hfill \end{array}$$

(3)

In addition, numerous novel higher-order iterative strategies [3,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] have been developed and implemented during the past few years. The majority of these research papers provide convergence theorems for iterative schemes by imposing requirements on higher-order derivatives. Furthermore, these investigations make no judgments about the convergence radius, error distances, or existence-uniqueness area for the solution.

In the research of iterative schemes, it is essential to determine the domain of convergence. The convergence domain is often rather narrow in most circumstances. Thus, without making any additional assumptions, the convergence domain must be extended. Additionally, accurate error distances must be approximated in the convergence investigation of iterative methods. Focusing on these points, we consider a method without derivatives, which is as follows:

$$\begin{array}{cc}\hfill s_k& =y_k-A_k^{-1}\mathcal{G}\left(y_k\right),\hfill \\ \hfill z_k& =s_k-(3I-2A_n^{-1}\mathcal{G}[s_k,y_k])A_k^{-1}\mathcal{G}\left(s_k\right),\hfill \\ \hfill y_{k+1}& =z_k-\left(\frac{13}{4}I-A_k^{-1}\mathcal{G}[z_k,s_k]\left(\frac{7}{2}I-\frac{5}{4}{A}_k^{-1}\mathcal{G}[z_k,s_k]\right)\right)A_k^{-1}\mathcal{G}\left(z_k\right),\hfill \end{array}$$

(4)

where $\mathcal{G}[.,.]:\mathsf{\Omega }\times \mathsf{\Omega }\to B({\mathcal{Y}}_1,{\mathcal{Y}}_2)$, $A_k=\mathcal{G}[v_k,q_k]$, $v_k=y_k+\mathcal{G}\left(y_k\right)$ and $q_k=y_k-\mathcal{G}\left(y_k\right)$.

However, it is crucial to note that the seventh order convergence of (4) was achieved in [24] by the use of conditions on the derivative of order eight, while this scheme is derivative-free. Because the convergence of this scheme is reliant on derivatives of a higher order, its usefulness is reduced. Taking the function $\mathcal{G}$, defined on $\mathsf{\Omega }=[-\frac{1}{2},\frac{3}{2}]$ by:

$$\mathcal{G}\left(y\right)=\left\{\begin{array}{cc}{y}^{3}ln\left(y^2\right)+y^5-y^4,\hfill & \mathrm{if}y\ne 0\hfill \\ 0,\hfill & \mathrm{if}y=0\hfill \end{array}\right..$$

(5)

one can observe that the previous conclusion on the convergence of this method [24] fails to hold because of the unboundedness of ${\mathcal{G}}^{\prime \prime \prime }$. Aside from that, the analytical outcome in [24] is not sufficient for the calculation of error $\left|\right|y_k-y_{*}\left|\right|$ and convergence radius. There is no conclusion in [24] that can be drawn concerning the location and uniqueness of $y_{*}$. The local analysis results allow one to estimate the error $\left|\right|y_k-y_{*}\left|\right|$, convergence radius and uniqueness zone for $y_{*}$. The findings of local convergence, in particular, are very useful since they provide information on the critical problem of identifying starting points. For this reason, we propose a new extended local analysis of the derivative free method (4). In determining the convergence radius, error $\left|\right|y_k-y_{*}\left|\right|$, and uniqueness area of $y_{*}$, our work is beneficial. This technique can be used to extend the applicability of other methods and relevant topics along the same lines [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,25]. In addition, using the attraction basin approach, the areas where this method can find solutions to complex polynomial equations are shown.

The arrangement of this paper can be described by summarizing the remainder of the text into the following statements. Section 2 deduces the theoretical outcomes with respect to local convergence of method (4). In Section 3, attraction basins for this scheme are shown. The suggested local analysis is verified numerically in Section 4. Finally, several conclusions are offered.

2. Local Convergence

We introduce scalar parameters and functions to deal with the local convergence analysis of scheme (4). Let $c\ge 0,c_0\ge 0,d\ge 0$ and $M=[0,\infty )$.

Suppose function:

(1)

${\mathcal{P}}_0\left(t\right)-1$

• has a smallest zero $R_0\in M\setminus \left\{0\right\}$ for some function ${\mathcal{P}}_0:M\to M$, which is continuous and non-decreasing (function). Let $M_0=[0,R_0)$.

(2)

${\mathcal{Q}}_1\left(t\right)-1$

• has a smallest zero $r_1\in M_0\setminus \left\{0\right\}$ for some (function) $\mathcal{P}:M_0\to M$ and function ${\mathcal{Q}}_1:M_0\to M$ defined by:

  $${\mathcal{Q}}_1\left(t\right)=\frac{\mathcal{P}\left(t\right)}{1-{\mathcal{P}}_0\left(t\right)}.$$

(3)

${\mathcal{Q}}_2\left(t\right)-1$

• has a smallest zero $r_2\in M_0\setminus \left\{0\right\}$ for some (functions) ${\mathcal{P}}_1:M_0\to M$, ${\mathcal{P}}_2:M_0\to M$, ${\mathcal{P}}_3:M_0\to M$, ${\mathcal{P}}_4:M_0\to M$, and function ${\mathcal{Q}}_2:M_0\to M$ defined by:

  $${\mathcal{Q}}_2\left(t\right)=\frac{{\mathcal{P}}_1\left(t\right)}{1-{\mathcal{P}}_0\left(t\right)}+\frac{c{\mathcal{P}}_2\left(t\right)}{{(1-{\mathcal{P}}_0\left(t\right))}^2}.$$

(4)

${\mathcal{Q}}_3\left(t\right)-1$

• has a smallest zero $r_3\in M_0\setminus \left\{0\right\}$ for some function ${\mathcal{Q}}_3:M_0\to M$ defined by:

  $${\mathcal{Q}}_3\left(t\right)=\left[\frac{{\mathcal{P}}_3\left(t\right)}{1-{\mathcal{P}}_0\left(t\right)}+\frac{c\left(9+\frac{5d}{1-{\mathcal{P}}_0\left(t\right)}\right){\mathcal{P}}_4\left(t\right)}{4{(1-{\mathcal{P}}_0\left(t\right))}^2}\right]{\mathcal{Q}}_2\left(t\right).$$

The parameter $r_{*}$ defined by

$$\begin{array}{c}\hfill r_{*}=min\left\{r_j\right\},j=1,2,3\end{array}$$

(6)

is shown next to be a convergence radius for method (4).

Let $M_1=[0,r_{*})$. It follows from the definition of radius $r_{*}$ that for all $t\in M_1$:

$$\begin{array}{c}\hfill 0\le {\mathcal{P}}_0\left(t\right)<1\end{array}$$

(7)

and

$$\begin{array}{c}\hfill 0\le {\mathcal{Q}}_j\left(t\right)<1,j=1,2,3.\end{array}$$

(8)

By $U[y_{*},\delta ]$, we denote the closure of the open ball $U(y_{*},\delta )$ with center $y_{*}\in \mathsf{\Omega }$ and of radius $\delta >0$.

The conditions $\left(A\right)$ are needed provided that $y_{*}$ is a simple solution of equation $\mathcal{G}\left(y\right)=0$, and functions ${\mathcal{Q}}_j$ are used as previously defined.

Suppose the following:

(a₁)

$$\begin{array}{cc}\hfill \left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}(\mathcal{G}[y+\mathcal{G}\left(y\right),y-\mathcal{G}\left(y\right)]-{\mathcal{G}}^{\prime }\left(y_{*}\right))\left|\right|& \le {\mathcal{P}}_0\left(\right||y-y_{*}\left|\right|)\hfill \\ \hfill \left|\right|I+\mathcal{G}[y,y_{*}]\left|\right|& \le a\hfill \\ \hfill \left|\right|I-\mathcal{G}[y,y_{*}]\left|\right|& \le b\hfill \end{array}$$

• for all $y\in \mathsf{\Omega }$ and some $a\ge 0$, $b\ge 0$.
• Let ${\mathsf{\Omega }}_0=\mathsf{\Omega }\cap U(y_{*},R_0)$.

(a₂)

$$\begin{array}{cc}\hfill \left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}(\mathcal{G}[y+\mathcal{G}\left(y\right),y-\mathcal{G}\left(y\right)]-\mathcal{G}[y,y_{*}])\left|\right|& \le \mathcal{P}\left(\right||y-y_{*}|\left|\right),\hfill \\ \hfill \left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}(\mathcal{G}[s,y_{*}]-\mathcal{G}[y+\mathcal{G}\left(y\right),y-\mathcal{G}\left(y\right)])\left|\right|& \le {\mathcal{P}}_1\left(\right||y-y_{*}\left|\right|),\hfill \\ \hfill \left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}(\mathcal{G}[y+\mathcal{G}\left(y\right),y-\mathcal{G}\left(y\right)]-\mathcal{G}[s,y])\left|\right|& \le {\mathcal{P}}_2\left(\right||y-y_{*}\left|\right|),\hfill \\ \hfill \left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}(\mathcal{G}[y+\mathcal{G}\left(y\right),y-\mathcal{G}\left(y\right)]-\mathcal{G}[z,y_{*}])\left|\right|& \le {\mathcal{P}}_3\left(\right||y-y_{*}\left|\right|),\hfill \\ \hfill \left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}(\mathcal{G}[y+\mathcal{G}\left(y\right),y-\mathcal{G}\left(y\right)]-\mathcal{G}[z,s])\left|\right|& \le {\mathcal{P}}_4\left(\right||y-y_{*}\left|\right|),\hfill \\ \hfill \left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}\mathcal{G}[y,y_{*}]\left|\right|& \le c\hfill \end{array}$$

• and

  $$\begin{array}{c}\hfill \left|\right|\mathcal{G}[z,s]\left|\right|\le d\end{array}$$
• for all $y\in {\mathsf{\Omega }}_0$ some $c\ge 0$, $d\ge 0$, and s, z given by the first two substeps of method (4).

(a₃)

$U[y_{*},r]\subset \mathsf{\Omega }$, where $r=max\{r_{*},a{r}_{*},b{r}_{*}\}$.

Next, we show the following local convergence result for method (4) using the preceding notation and the conditions $\left(A\right)$.

Theorem 1.

Suppose that the conditions $\left(A\right)$ hold. Then, iteration $\left\{y_k\right\}$ generated by method (4) converges to $y_{*}$ provided that starter $y_0\in U(y_{*},r_{*})\setminus \left\{y_{*}\right\}$.

Proof. 

Mathematical induction shall be used to show items:

$$y_k\subset U(y_{*},r_{*})$$

(9)

$$\left|\right|s_k-y_{*}\left|\right|\le {\mathcal{Q}}_1\left(\right||y_k-y_{*}\left|\right|\left)\right||y_k-y_{*}\left|\right|\le \left|\right|y_k-y_{*}\left|\right|<r_{*}$$

(10)

$$\left|\right|z_k-y_{*}\left|\right|\le {\mathcal{Q}}_2\left(\right||y_k-y_{*}\left|\right|\left)\right||y_k-y_{*}\left|\right|\le \left|\right|y_k-y_{*}\left|\right|$$

(11)

and

$$\left|\right|y_{k+1}-y_{*}\left|\right|\le {\mathcal{Q}}_3\left(\right||y_k-y_{*}\left|\right|\left)\right||y_k-y_{*}\left|\right|\le \left|\right|y_k-y_{*}\left|\right|,$$

(12)

where the radius $r_{*}$ is defined by (6).

By hypothesis $y_0\in U(y_{*},r_{*})\setminus \left\{y_{*}\right\}\subset U(y_{*},r_{*})$, so (9) holds for $n=0$. Using (6), (7), and $\left(a_1\right)$, we obtain:

$$\left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}(A_0-{\mathcal{G}}^{\prime }\left(y_{*}\right))\left|\right|\le {\mathcal{P}}_0\left(\right||y_0-y_{*}\left|\right|)\le {\mathcal{P}}_0\left(r_{*}\right)<1.$$

(13)

Estimate (13) with the Banach perturbation lemma on linear invertible operators [5,25] and imply $A_0^{-1}\in B({\mathcal{Y}}_2,{\mathcal{Y}}_1)$ and:

$$\left|\right|A_0^{-1}{\mathcal{G}}^{\prime }\left(y_{*}\right)\left|\right|\le \frac{1}{1-{\mathcal{P}}_0\left(\right||y_0-y_{*}\left|\right|)}.$$

(14)

Hence, iterates $s_0,z_0$, and $y_1$ are well-defined by the three substeps of method (4), respectively. Moreover, we can write:

$$s_0-y_{*}=y_0-y_{*}-A_0^{-1}\mathcal{G}\left(y_0\right)=A_0^{-1}(A_0-\mathcal{G}[y_0,y_{*}])(y_0-y_{*}),$$

(15)

$$z_0-y_{*}=s_0-y_{*}-A_0^{-1}\mathcal{G}\left(s_0\right)+2A_0^{-1}(A_0-\mathcal{G}[s_0,y_0])A_0^{-1}\mathcal{G}\left(s_0\right)$$

(16)

and

$$\begin{array}{cc}\hfill y_1-y_{*}& =z_0-y_{*}-A_0^{-1}\mathcal{G}\left(z_0\right)\hfill \\ \hfill & -\left(\frac{9}{4}I-A_0^{-1}\mathcal{G}[z_0,s_0]\left(\frac{7}{2}I-\frac{5}{4}{A}_0^{-1}\mathcal{G}[z_0,s_0]\right)\right)A_0^{-1}\mathcal{G}\left(z_0\right)\hfill \\ \hfill & =A_0^{-1}(A_0-\mathcal{G}[z_0,y_{*}])(z_0-y_{*})\hfill \\ \hfill & -\frac{1}{4}{A}_0^{-1}\left[9(A_0-\mathcal{G}[z_0,s_0])+5\mathcal{G}[z_0,s_0](A_0-\mathcal{G}[z_0,s_0])A_0^{-1}\right]A_0^{-1}\mathcal{G}\left(z_0\right).\hfill \end{array}$$

(17)

Notice that $\left|\right|y_0+\mathcal{G}\left(y_0\right)-y_{*}\left|\right|=\left|\right|I+\mathcal{G}[y_0,y_{*}])(y_0-y_{*})\left|\right|\le \left|\right|I+\mathcal{G}[y_0,y_{*}]\left|\right|\left|\right|y_0-y_{*}\left|\right|\le a{r}_{*}$ and similarly $\left|\right|y_0-\mathcal{G}\left(y_0\right)-y_{*}\left|\right|\le b{r}_{*}$, so $y_0+\mathcal{G}\left(y_0\right),y_0-\mathcal{G}\left(y_0\right)\in U(y_{*},r)\subset \mathsf{\Omega }$.

Using (6), (8)(for $j=1$), (14), (15), and ($a_2$), we have:

$$\begin{array}{cc}\hfill \left|\right|s_0-y_{*}\left|\right|& \le \frac{\mathcal{P}\left(\right||y_0-y_{*}\left|\right|\left)\right||y_0-y_{*}\left|\right|}{1-{\mathcal{P}}_0\left(\right||y_0-y_{*}\left|\right|)}\le {\mathcal{Q}}_1\left(\right||y_0-y_{*}\left|\right|\left)\right||y_0-y_{*}\left|\right|\hfill \\ \hfill & \le \left|\right|y_0-y_{*}\left|\right|<r_{*},\hfill \end{array}$$

(18)

showing $s_0\in U(y_{*},r_{*})$ and (10) for $n=0$. Moreover, using (6), (8) (for $j=2$), (14), (16), ($a_2$), and (18), we obtain:

$$\begin{array}{cc}\hfill \left|\right|z_0-y_{*}\left|\right|& \le \left[\frac{{\mathcal{P}}_1\left(\right||y_0-y_{*}\left|\right|)}{1-{\mathcal{P}}_0\left(\right||y_0-y_{*}\left|\right|)}+\frac{c{\mathcal{P}}_2\left(\right||y_0-y_{*}\left|\right|)}{(1-{\mathcal{P}}_0\left(\right||y_0-y_{*}{\left|\right|\left)\right)}^2}\right]\left|\right|y_0-y_{*}\left|\right|\hfill \\ \hfill & \le {\mathcal{Q}}_2\left(\right||y_0-y_{*}\left|\right|\left)\right||y_0-y_{*}\left|\right|\le \left|\right|y_0-y_{*}\left|\right|,\hfill \end{array}$$

(19)

showing $z_0\in U(y_{*},r_{*})$ and (11) for $k=0$.

Furthermore, using (6), (8) (for $j=3$), (14), (17), ($a_2$), (18), and (19), we obtain:

$$\begin{array}{cc}\hfill \left|\right|y_1-y_{*}\left|\right|& \le \left[\frac{{\mathcal{P}}_3\left(\right||y_0-y_{*}\left|\right|)}{1-{\mathcal{P}}_0\left(\right||y_0-y_{*}\left|\right|)}+\frac{c\left(9{\mathcal{P}}_4\left(\right||y_0-y_{*}\left|\right|)+\frac{5d{\mathcal{P}}_4\left(\right||y_0-y_{*}\left|\right|)}{1-{\mathcal{P}}_0\left(\right||y_0-y_{*}\left|\right|)}\right)}{4(1-{\mathcal{P}}_0\left(\right||y_0-y_{*}{\left|\right|\left)\right)}^2}\right]\left|\right|z_0-y_{*}\left|\right|\hfill \\ \hfill & \le {\mathcal{Q}}_3\left(\right||y_0-y_{*}\left|\right|\left)\right||y_0-y_{*}\left|\right|\le \left|\right|y_0-y_{*}\left|\right|,\hfill \end{array}$$

(20)

showing (9) for $k=1$ and (12) for $k=0$.

So, items (9) for $k=0,1$ and (10)–(13) hold for $k=0$. Then, if we exchange $y_0,s_0,z_0,y_1$ by $y_m,s_m,z_m,y_{m+1}$ in the preceding calculations, we terminate the induction. It then follows from the estimation:

$$\left|\right|y_{m+1}-y_{*}\left|\right|\le \lambda \left|\right|y_m-y_{*}\left|\right|<r_{*},$$

(21)

where $\lambda ={\mathcal{Q}}_3\left(\right||y_0-y_{*}\left|\right|)\in [0,1)$ that $y_{m+1}\in U(y_{*},r_{*})$ and ${\displaystyle \underset{m\to \infty }{lim}{y}_m=y_{*}}$. □

Next, concerning the uniqueness of the solution $y_{*}$, we have:

Proposition 1.

Suppose the following: 

(i) 

Point$y_{*}\in \mathsf{\Omega }$is a simple solution of equation$\mathcal{G}\left(y\right)=0$.

(ii) 

${\mathcal{P}}_5\left(t\right)-1$has a smallest solution$\rho \in M\setminus \left\{0\right\}$.

Let $M_2=[0,\rho )$.

(iii) 

$\left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}(\mathcal{G}[y,y_{*}]-{\mathcal{G}}^{\prime }\left(y_{*}\right))\left|\right|\le {\mathcal{P}}_5\left(\right||y-y_{*}\left|\right|)$ for all $y\in \mathsf{\Omega }$ and some function ${\mathcal{P}}_5:M_2\to M$.

Let ${\mathsf{\Omega }}_1=\mathsf{\Omega }\cap U[y_{*},\rho ]$.

Then, the only solution of the equation $\mathcal{G}\left(y\right)=0$ in the set ${\mathsf{\Omega }}_1$ is $y_{*}$.

Proof. 

Let $T=\mathcal{G}[q,y_{*}]$ for some $q\in {\mathsf{\Omega }}_1$ with $\mathcal{G}\left(q\right)=0$. Then, using (ii) and (iii), we have:

$$\begin{array}{c}\hfill \left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}(T-{\mathcal{G}}^{\prime }\left(y_{*}\right))\left|\right|\le {\mathcal{P}}_5\left(\right||q-y_{*}\left|\right|)\le {\mathcal{P}}_5\left(\rho \right)<1,\end{array}$$

so, $T^{-1}\in B({\mathcal{Y}}_2,{\mathcal{Y}}_1)$. In view of the identity $T(q-y_{*})=\mathcal{G}\left(q\right)-\mathcal{G}\left(y_{*}\right)=0-0=0$, we conclude $q=y_{*}$. □

Remark 1. (a) Let us consider the choices $\mathcal{G}[y,s]=\frac{1}{2}({\mathcal{G}}^{\prime }\left(y\right)+{\mathcal{G}}^{\prime }\left(s\right))$ or $\mathcal{G}[y,s]={\int }_0^1{\mathcal{G}}^{\prime }(y+\theta (s-y))d\theta$ or the standard definition of the divided difference when ${\mathcal{Y}}_1={\mathbb{R}}^i$ [5,8,9,15,16,22]. Moreover, suppose:

$$\left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}({\mathcal{G}}^{\prime }\left(y\right)-{\mathcal{G}}^{\prime }\left(y_{*}\right))\left|\right|\le h_0\left(\right||y-y_{*}\left|\right|)$$

and

$$\left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}({\mathcal{G}}^{\prime }\left(y\right)-{\mathcal{G}}^{\prime }\left(s\right))\left|\right|\le h\left(\right||y-s\left|\right|),$$

where functions $h_0:M\to M$, $h:M\to M$ are continuous and nondecreasing. Then, under the first or second choice above, it can easily be seen that the hypotheses (A) require for $\left|\right|\mathcal{G}[y,y_{*}]\left|\right|\le c_0$, and the choices as given in Example 1.

(b) Hypotheses (A) can be condensed using instead the classical but strongest and less precise condition for studying methods with divided differences [22]:

$$\left|\right|{\mathcal{G}}^{\prime }{\left(y_{*}\right)}^{-1}(\mathcal{G}[u_1,u_2]-\mathcal{G}[u_3,u_4])\left|\right|\le {\mathcal{P}}_6\left(\right||u_1-u_3\left|\right|,\left|\right|u_2-u_4\left|\right|)$$

for all $u_1,u_2,u_3,u_4\in \mathsf{\Omega }$, where function ${\mathcal{P}}_6:M\times M\to M$ is continuous and nondecreasing. However this condition does not give the largest convergence conditions, and all the $“\mathcal{P}”$ functions are at least as small as ${\mathcal{P}}_6(t,t)$.

3. Attraction Basins

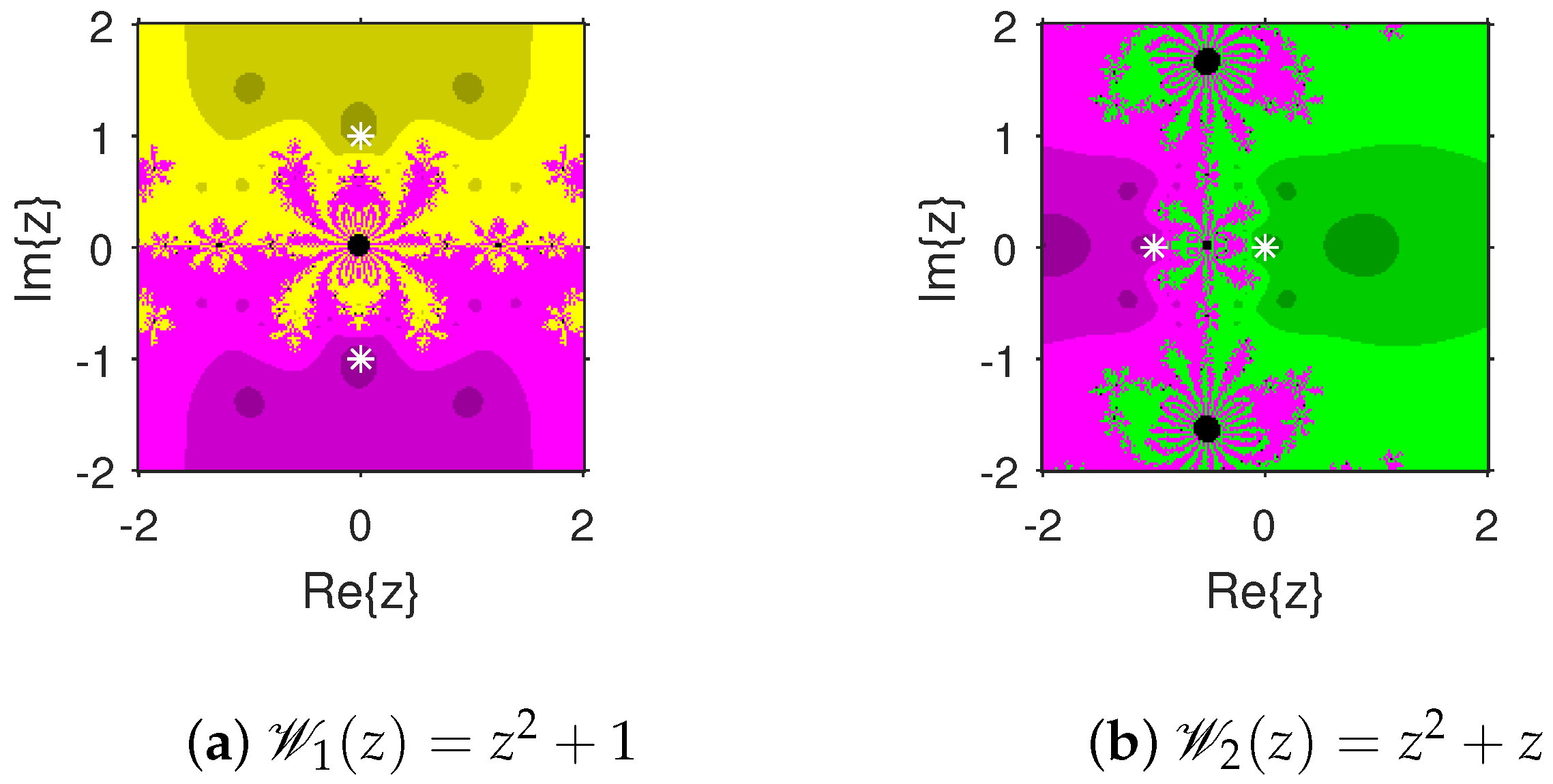
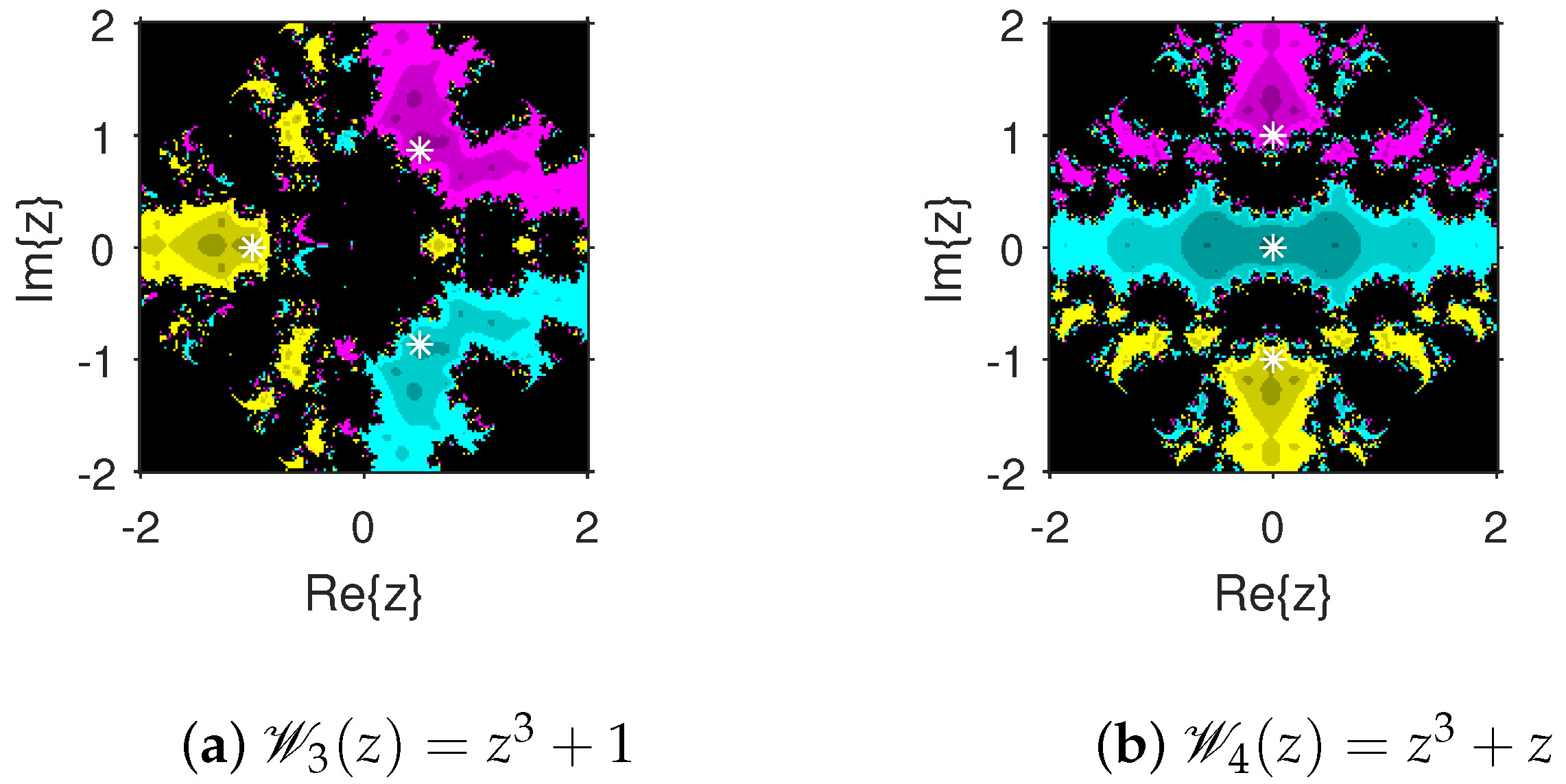
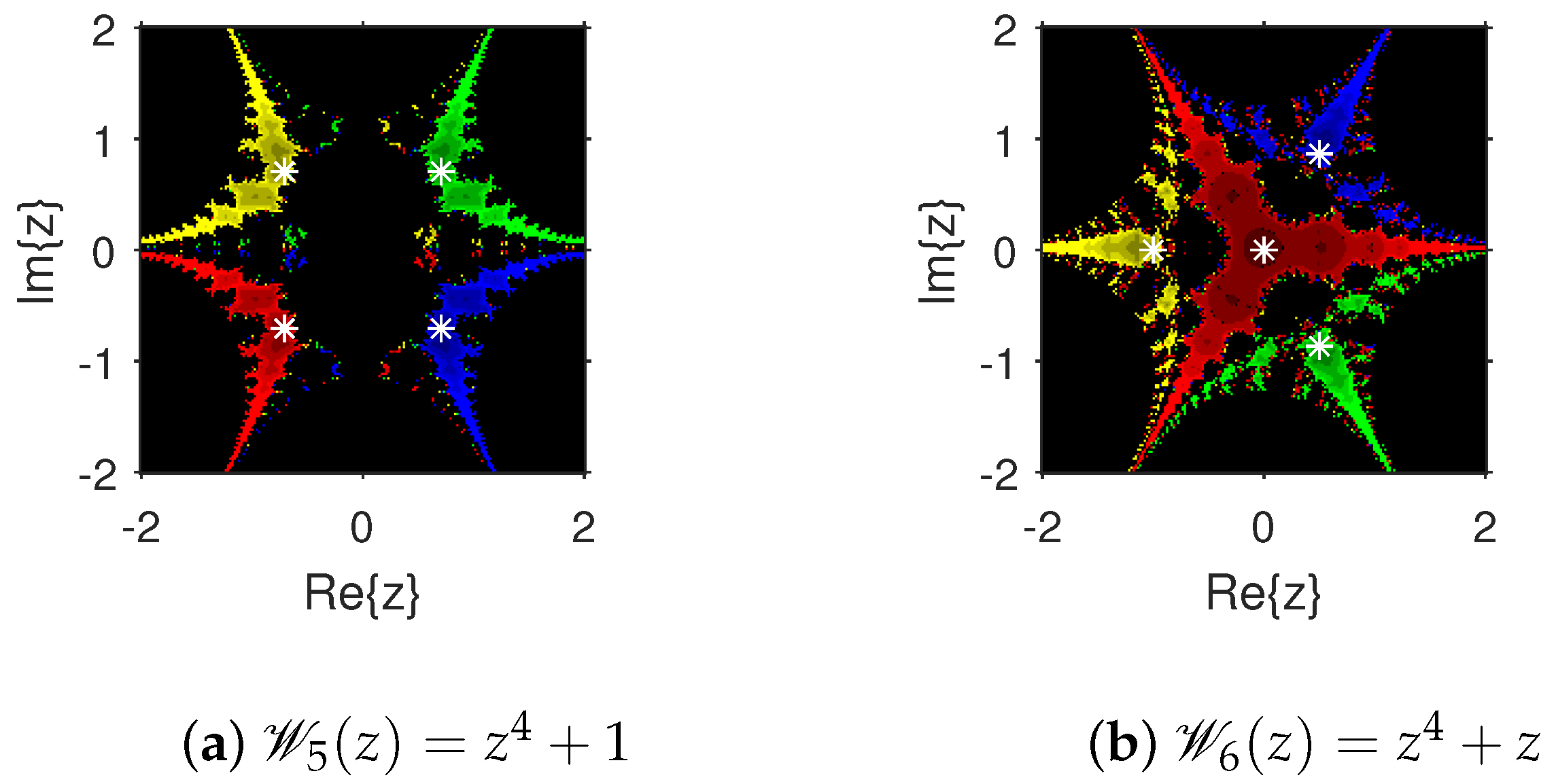
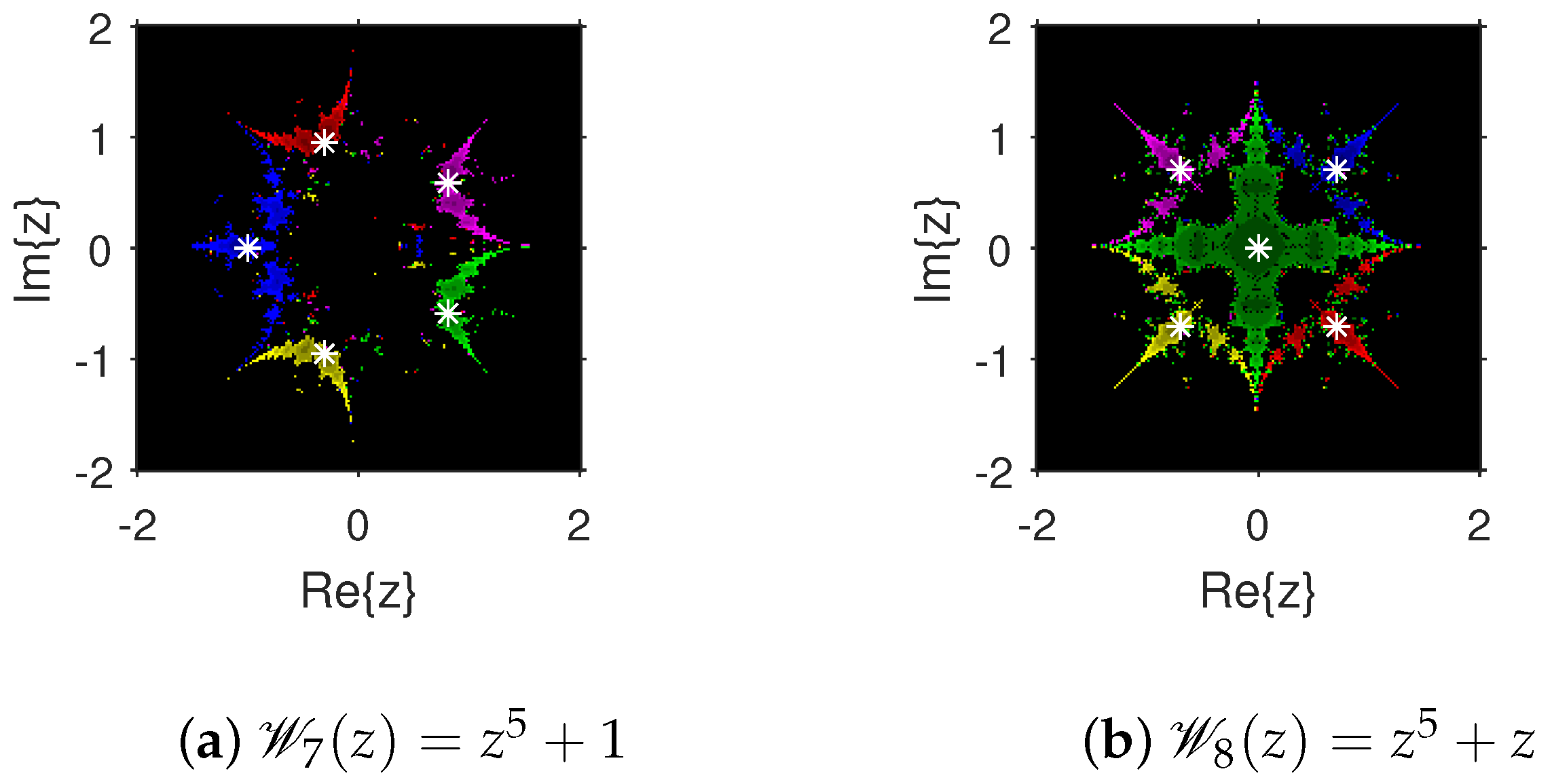
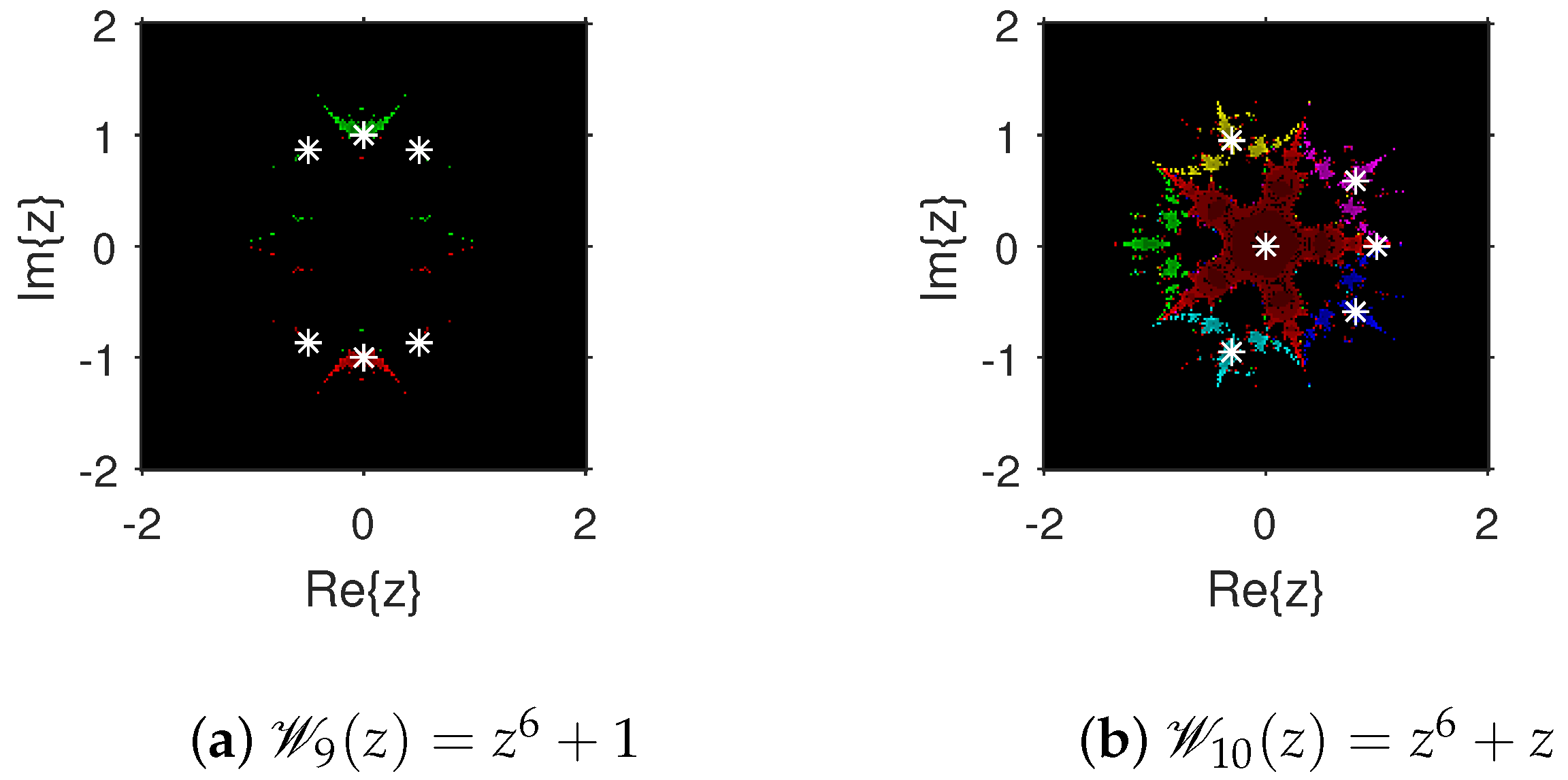
The attraction basins is an extremely valuable geometrical tool for measuring the convergence zones of various iteration schemes. Using this tool, we can see all of the beginning points that converge to any root when we use an iterative procedure. This allows us to identify in a visual fashion which locations are excellent selections as starting points and which ones are not. We select the starting point $z_0\in \mathcal{E}=[-2,2]$×$[-2,2]\subset \mathbb{C}$, and algorithm (4) is applied on 10 polynomials with complex coefficients. The point $z_0$ is a member of the basin of a zero $z_{*}$ of a test polynomial if ${\displaystyle \underset{n\to \infty }{lim}{z}_n=z_{*}}$, and then $z_0$ is displayed using a specific color associated with $z_{*}$. As per the number of iterations, we employ light to dark colors for each starting guess $z_0$. The point $z_0\in \mathcal{E}$ is denoted in black if it is not a member of the attraction basin of any zero of the test polynomial. The conditions $\left|\right|z_n-z_{*}\left|\right|<{10}^{-6}$ or maximum 100 iterations are set to end the iteration process. For constructing the fractal diagrams, MATLAB 2019a is employed.

In the first step, we take ${\mathcal{W}}_1\left(z\right)=z^2+1$ and ${\mathcal{W}}_2\left(z\right)=z^2+z$ to generate the basins related to their zeros. In Figure 1a, yellow and magenta colors indicate the attraction basins of the zeros i and $-i$, respectively, of ${\mathcal{W}}_1\left(z\right)$. Figure 1b displays the attraction basins related to the zeros $-1$ and 0 of ${\mathcal{W}}_2\left(z\right)$ in magenta and green colors, respectively. Next, we choose polynomials ${\mathcal{W}}_3\left(z\right)=z^3+1$ and ${\mathcal{W}}_4\left(z\right)=z^3+z$. Figure 2a shows the attraction basins associated to the zeros $\frac{1}{2}-\frac{\sqrt{3}}{2}i$, $-1$ and $\frac{1}{2}+\frac{\sqrt{3}}{2}i$ of ${\mathcal{W}}_3\left(z\right)$ in cyan, yellow, and magenta, respectively. In Figure 2b, the basins of the zeros 0, $-i$, and i of ${\mathcal{W}}_4\left(z\right)$ are illustrated in cyan, yellow, and magenta colors, respectively. Furthermore, the complex polynomials ${\mathcal{W}}_5\left(z\right)=z^4+1$ and ${\mathcal{W}}_6\left(z\right)=z^4+z$ of degree four are considered to demonstrate the attraction basins associated with their zeros. In Figure 3a, the basins of the solutions $0.707106+0.707106i$, $0.707106-0.707106i$, $-0.707106-0.707106i$ and $-0.707106+0.707106i$ of ${\mathcal{W}}_5\left(z\right)=0$ are respectively displayed in green, blue, red, and yellow zones. In Figure 3b, convergence to the zeros $-1$, $\frac{1}{2}+\frac{\sqrt{3}}{2}i$, $\frac{1}{2}-\frac{\sqrt{3}}{2}i$ and 0 of the polynomial ${\mathcal{W}}_6\left(z\right)$ is presented in yellow, blue, green, and red, respectively. Furthermore, ${\mathcal{W}}_7\left(z\right)=z^5+1$ and ${\mathcal{W}}_8\left(z\right)=z^5+z$ of degree five are selected. In Figure 4a, magenta, green, yellow, blue, and red colors stand for the attraction basins of the zeros $0.809016+0.587785i$, $0.809016-0.587785i$, $-0.309016-0.951056i$, $-1$, and $-0.309016+0.951056i$, respectively, of ${\mathcal{W}}_7\left(z\right)$. Figure 4b provides the basins related to the solutions $0.707106+0.707106i$, 0, $-0.707106+0.707106i$, $-0.707106-0.707106i$, and $0.707106-0.707106i$ of ${\mathcal{W}}_8\left(z\right)=0$ in blue, green, magenta, yellow, and red colors, respectively. Lastly, ${\mathcal{W}}_9\left(z\right)=z^6+1$ and ${\mathcal{W}}_{10}\left(z\right)=z^6+z$ degree six are considered. In Figure 5a, the basins of the solutions $0.500000-0.866025i$, $0.500000+0.866025i$, $1i$, $-0.500000-0.866025i$, $-0.500000+0.866025i$, and $-1i$ of ${\mathcal{W}}_9\left(z\right)=0$ are painted in yellow, blue, green, magenta, cyan, and red, respectively. Figure 5b gives the basins related to the roots $-1$, $-0.3090169+0.951056i$, 0, $-0.3090169-0.951056i$, $0.809016+0.587785i$, and $0.809016-0.587785i$ of ${\mathcal{W}}_{10}\left(z\right)=0$ in green, yellow, red, cyan, magenta, and blue colors, respectively.

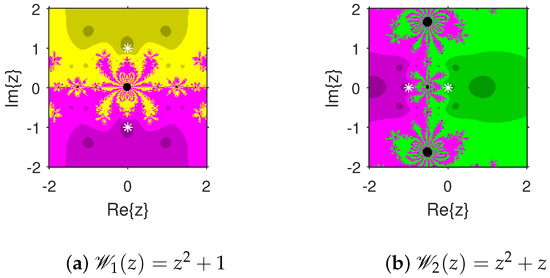
Figure 1. Attraction basins associated with polynomials ${\mathcal{W}}_1\left(z\right)$ and ${\mathcal{W}}_2\left(z\right)$.

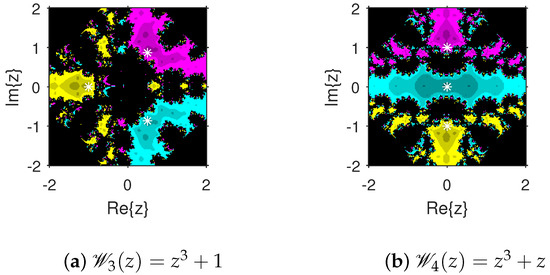
Figure 2. Attraction basins associated with polynomials ${\mathcal{W}}_3\left(z\right)$ and ${\mathcal{W}}_4\left(z\right)$.

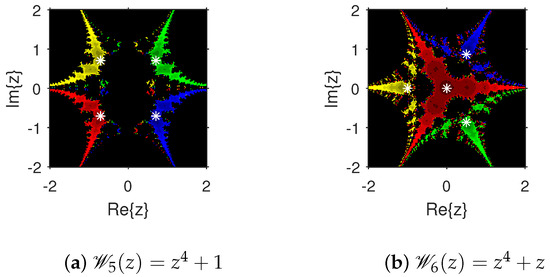
Figure 3. Attraction basins associated with polynomials ${\mathcal{W}}_5\left(z\right)$ and ${\mathcal{W}}_6\left(z\right)$.

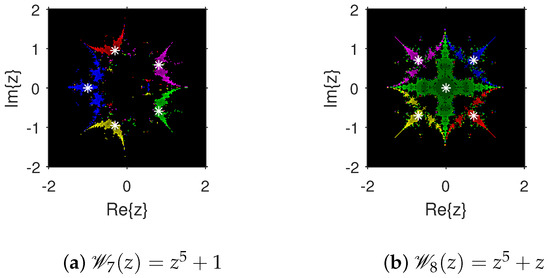
Figure 4. Attraction basins associated with polynomials ${\mathcal{W}}_7\left(z\right)$ and ${\mathcal{W}}_8\left(z\right)$.

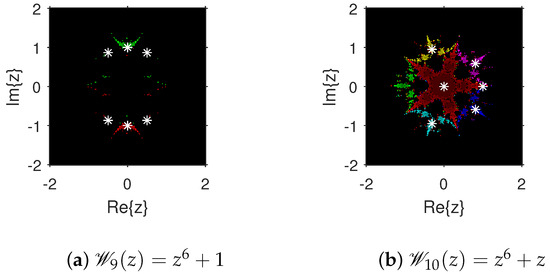
Figure 5. Attraction basins associated with polynomials ${\mathcal{W}}_9\left(z\right)$ and ${\mathcal{W}}_{10}\left(z\right)$.

4. Numerical Examples

The numerical verification of the new convergence result is conducted in this section. The following example is taken.

Example 1

([6]). Let ${\mathcal{Y}}_1={\mathcal{Y}}_2={\mathbb{R}}^3$ and $\mathsf{\Omega }=U[0,1]$. Consider $\mathcal{G}$ on Ω for $y={(y_1,y_2,y_3)}^t$ as:

$$\mathcal{G}\left(y\right)={(e^{y_1}-1,\frac{e-1}{2}{y}_2^2+y_2,y_3)}^t$$

We have: $y_{*}={(0,0,0)}^t$,

• $a=b=\frac{1}{2}(3+e^{\frac{1}{e-1}})$,
• $c=\frac{1}{2}(1+e^{\frac{1}{e-1}})=c_0$,
• $d=e^{\frac{1}{e-1}}$,
• $h_0\left(t\right)=(e-1)t$,
• $h\left(t\right)=e^{\frac{1}{e-1}}t$,
• ${\mathcal{P}}_0\left(t\right)=\frac{1}{2}(h_0\left(at\right)+h_0\left(bt\right))$,
• $\mathcal{P}\left(t\right)=\frac{1}{2}(h\left(c_{0}t\right)+h_0\left(bt\right))$,
• ${\mathcal{P}}_1\left(t\right)=\frac{1}{2}(h({\mathcal{Q}}_1\left(t\right)t+at)+h_0\left(bt\right))$,
• ${\mathcal{P}}_2\left(t\right)=\frac{1}{2}(h({\mathcal{Q}}_1\left(t\right)t+at)+h\left(c_{0}t\right))$,
• ${\mathcal{P}}_3\left(t\right)=\frac{1}{2}(h({\mathcal{Q}}_2\left(t\right)t+at)+h_0\left(bt\right))$
• and
• ${\mathcal{P}}_4\left(t\right)=\frac{1}{2}(h({\mathcal{Q}}_2\left(t\right)t+at)+h({\mathcal{Q}}_1\left(t\right)t+at))$. Using Equation (6), the value of $r_{*}$ is calculated and presented in Table 1.
  Table 1. Convergence radius for Example 1.

  ${\mathit{r}}_1$	${\mathit{r}}_2$	${\mathit{r}}_3$	${\mathit{r}}_{*}$
  $0.1347634094$	$0.0644916806$	$0.0393641483$	$0.0393641483$

Example 2.

Consider the following nonlinear system of equations:

$$\begin{array}{cc}\hfill 3y_1^2{y}_2+y_2^2-1+|y_1-1|& =0\hfill \\ \hfill y_1^4+y_1{y}_2^3-1+\left|y_2\right|& =0.\hfill \end{array}$$

Let $u=(u_1,u_2)$, $\mathcal{G}=G\left(u\right)+Q\left(u\right)$, $G=(G_1,G_2)$, $Q=(Q_1,Q_2)$, where $G_1\left(u\right)=3u_1^2{u}_2+u_2^2-1$, $G_2\left(u\right)=u_1^4+u_1{u}_2^3-1$, $Q_1\left(u\right)=|u_1-1|$ and $Q_2\left(u\right)=\left|u_2\right|$. The divided difference is a two-by-two real matrix defined for $v=(v_1,v_2)$ by ${[u,v;G]}_{j,1}=\frac{G_j(v_1,v_2)-G_j(u_1,v_2)}{v_1-u_1}$, ${[u,v;G]}_{j,2}=\frac{G_j(u_1,v_2)-G_j(u_1,u_2)}{v_2-u_2}$, if $v_1\ne u_1$ and $v_2\ne u_2$. However, if $v_1=u_1$ or $v_2=u_2$, then use $G^{\prime }$ for $[.,.;G]$. Similarly, replace $G_j$ by $Q_j$ above to define the divided difference $[.,.;Q]$ provided that $v_1\ne u_1$ and $v_2\ne u_2$. However, if $v_1=u_1$ or $v_2=u_2$, use the zero $2\times 2$ matrix for $[.,.;Q]$. Choose initial points $(5,5)$ and $(1,0)$. Then, after three iterations, the application of method (4) gives the solution $(y_1,y_2)=(0.894655373334687,0.327826521746298)$ for the given system of equations.

5. Conclusions

By eliminating the Taylor series tool from the existing convergence theorem, extended local convergence of a seventh order method without derivatives is developed. The first derivative is all that is required for our convergence result, unlike the preceding concept. In addition, the error estimates, convergence radius, and region of uniqueness for the solution are calculated. As a result, the usefulness of this effective algorithm is enhanced. The convergence zones of this algorithm for solving polynomial equations with complex coefficients are also shown. This aids in the selection of beginning points with the purpose of obtaining a certain root. Our convergence result is validated by numerical testing.