Enhanced Wireless Sensor Network Lifetime Using EGWO-Optimized Neural Network Approach
Abstract
1. Introduction
- RQ1: How effectively can Enhanced Grey Wolf Optimization (EGWO) dynamically optimize neural network parameters across operational rounds in WSNs to improve energy efficiency and network lifetime?
- RQ2: To what extent does the adaptive EGWO-NN approach outperform conventional hierarchical clustering methods (LEACH, PEGASIS, HEED, and EEHC) in terms of network lifetime and Packet Delivery Ratio (PDR)?
- RQ3: How does the convergence characteristic of EGWO influence stability and efficiency in neural network parameter optimization within WSN scenarios?
2. Materials and Methods
2.1. Benchmark Protocols
2.1.1. LEACH
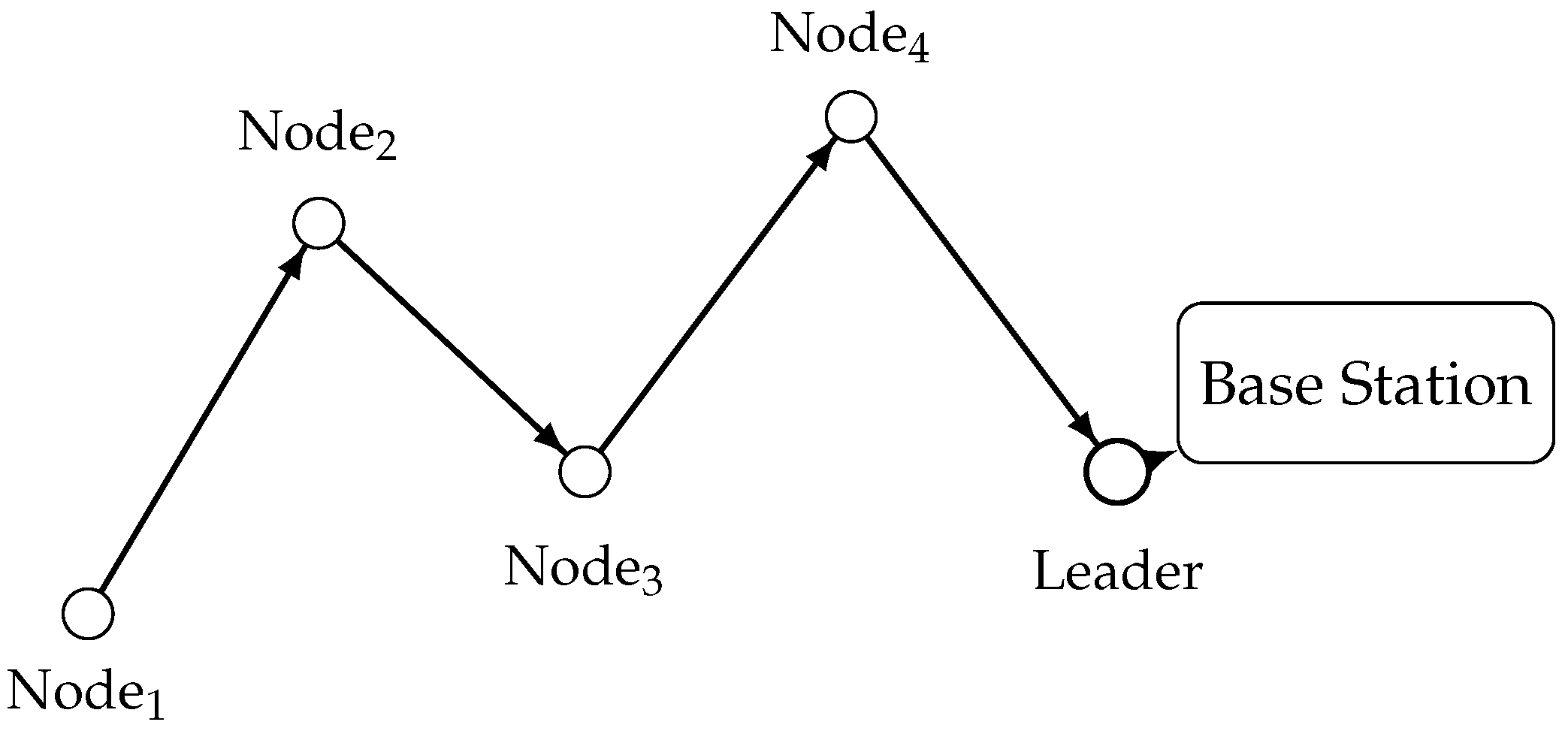
2.1.2. PEGASIS
2.1.3. HEED
2.1.4. EEHC
2.2. Proposed EGWO-NN Method
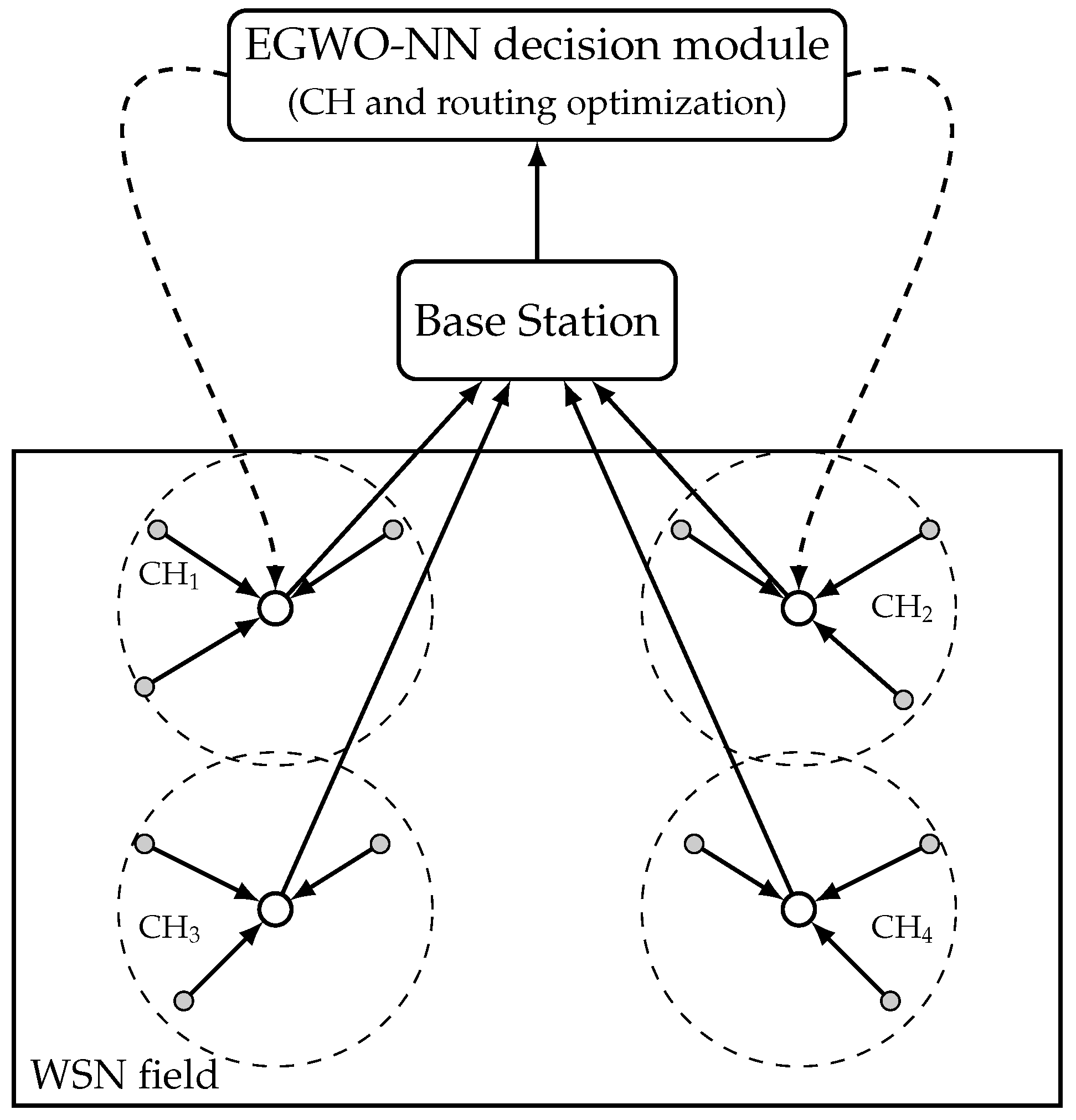
2.2.1. Overview of Proposed Framework
2.2.2. Enhanced Grey Wolf Optimization (EGWO)
- : best solution (leader);
- : second-best solution;
- : third-best solution;
- : remaining wolves (followers).
Notation
Distance Computation
Position Update Mechanism
Coefficient Vectors
Enhanced GWO (EGWO)
- Strengthen early exploration while avoiding premature convergence;
- Enhance late-stage exploitation for finer convergence;
- Weight the influence of based on their improvement rates.
2.2.3. Neural Network Model for CH Selection and Routing
2.2.4. Decision Making and Routing Actions
Input Normalization
Cluster-Head Decision
Routing Decision
2.2.5. Fitness Function and Objective
| Algorithm 1 Fitness Function |
|
- CH node energy consumption:
- Non-CH node energy consumption:
2.2.6. Flowchart
2.2.7. Parameter Optimization and Simulation Procedure
- Initialization of EGWO agents, where each agent encodes a candidate set of neural network parameters.
- Iterative optimization using EGWO to maximize the network lifetime, where fitness evaluation is performed based on the survival metric defined in Equation (20).
- During the optimization phase, fitness is estimated through partial simulations of limited duration (500 rounds) to reduce computational cost. The objective function used by EGWO is defined in Equation (23):
- The best-performing neural network parameters obtained from EGWO are subsequently validated using extended simulations over the full simulation horizon via the simulate_nn function to assess overall performance and robustness.
2.2.8. Simulation and Statistical Analysis
- Metrics such as alive nodes per round, total transmission energy, and CH count per round provide objective comparison.
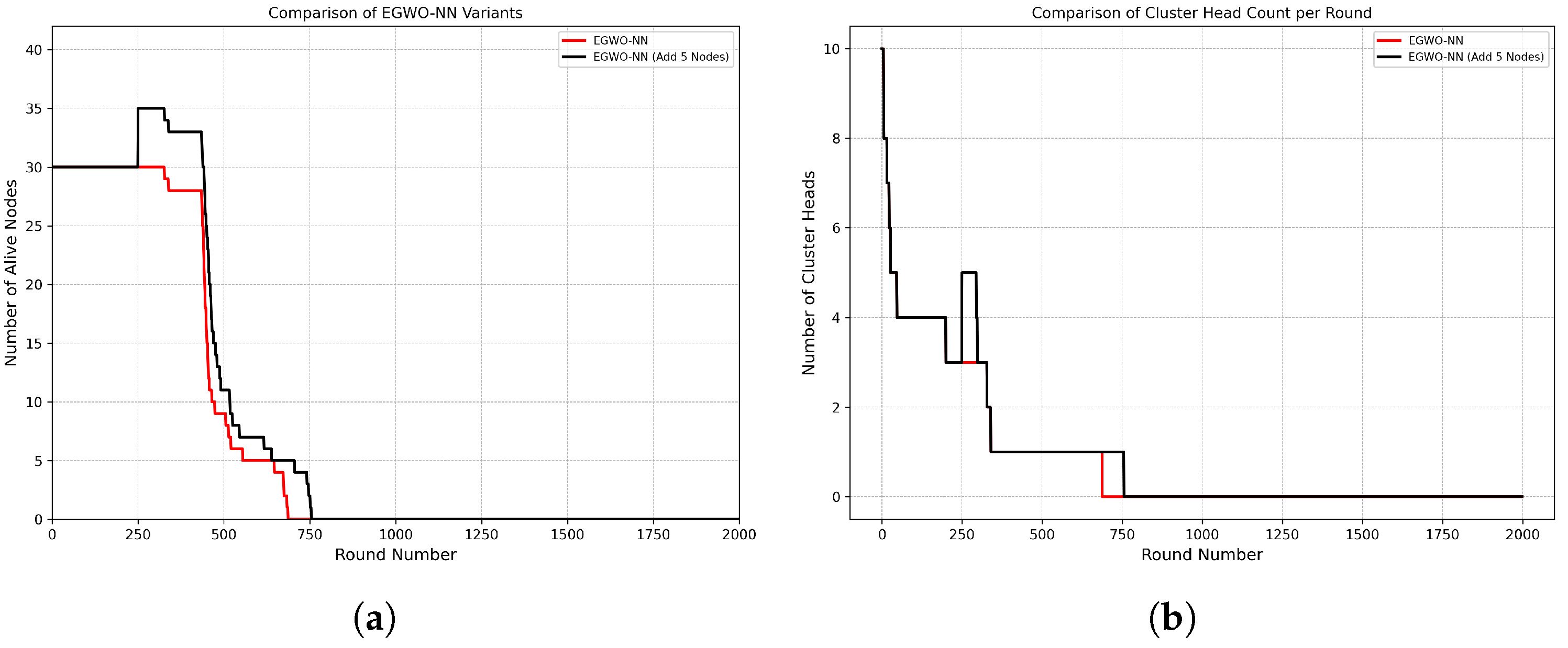
- Cross-scenario robustness evaluation: We generated 1000 WSN scenarios by randomly sampling the number of sensor nodes from , the sink position from , and the initial energy range from , with a fixed communication range of 40 m. For each scenario, node positions and initial energies were drawn at random and stored as a structured description (positions, , sink position, energy range, and communication radius). The same set of 1000 scenarios was then used to evaluate all compared algorithms (EGWO-NN, LEACH, PEGASIS, HEED, and EEHC), providing an assessment of robustness across heterogeneous WSN configurations.
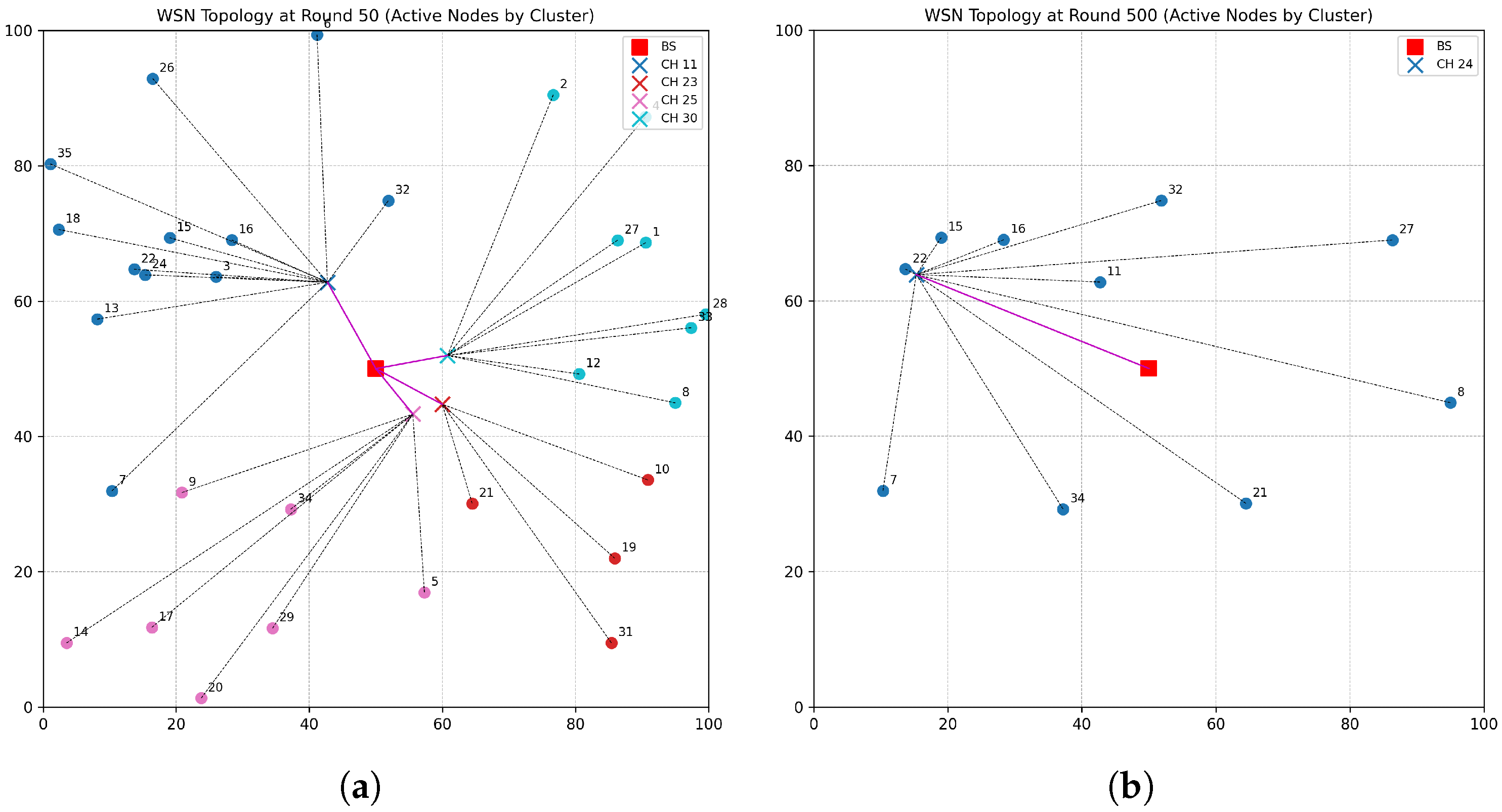
3. Results
3.1. Simulation Setup
3.2. Performance Metrics
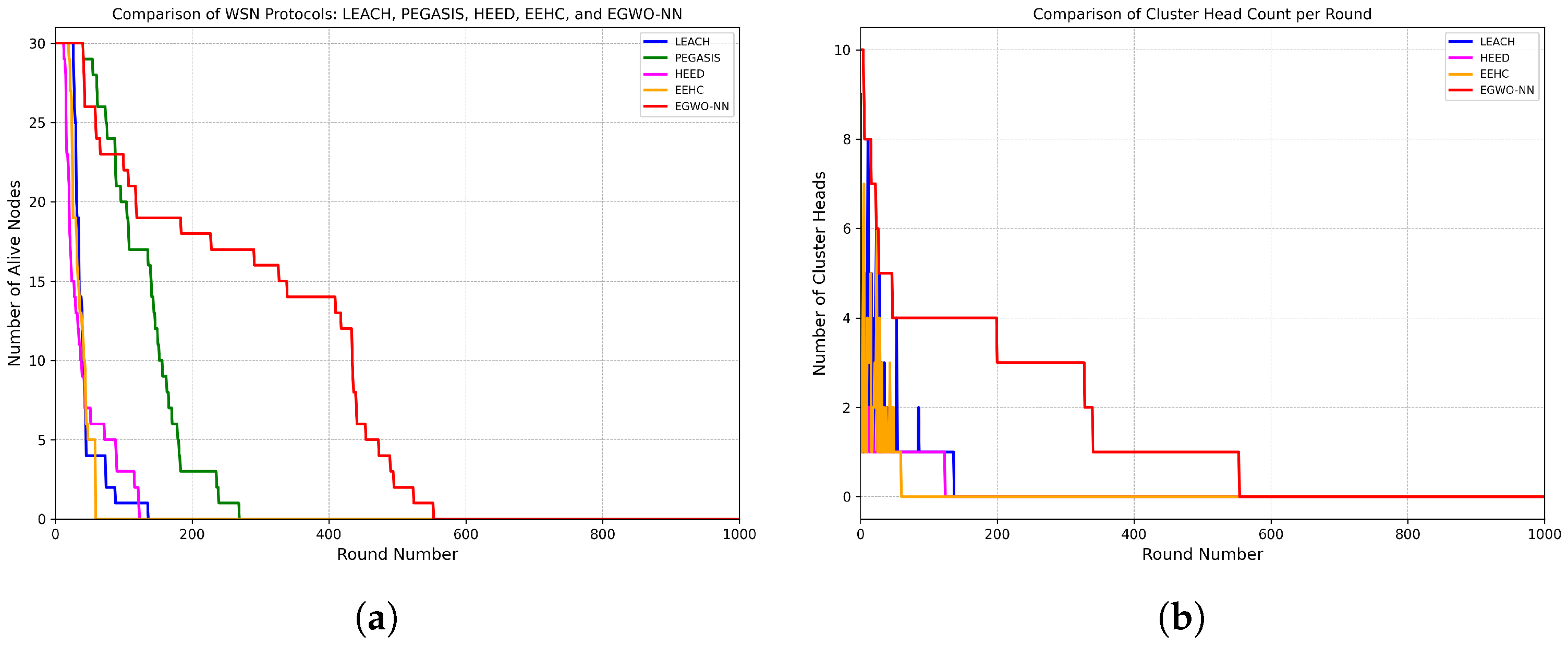
- Network Lifetime: Measured by counting the round in which the first node dies (first-dead-round) and the average number of alive nodes per round.
- Energy Efficiency: Evaluated by total transmission energy used during the simulation.
- Packet Delivery Ratio (PDR): Ratio of successfully received packets at the sink node to total transmitted packets.
Network Lifetime Analysis
3.3. Statistical Evaluation
3.4. Energy Efficiency
3.5. Packet Size Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gupta, A.; Gulati, T.; Bindal, A.K. WSN based IoT applications: A Review. In Proceedings of the 2022 10th International Conference on Emerging Trends in Engineering and Technology—Signal and Information Processing (ICETET-SIP-22), Nagpur, India, 29–30 April 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Jamshed, M.A.; Ali, K.; Abbasi, Q.H.; Imran, M.A.; Ur-Rehman, M. Challenges, Applications, and Future of Wireless Sensors in Internet of Things: A Review. IEEE Sens. J. 2022, 22, 5482–5494. [Google Scholar] [CrossRef]
- Houssein, E.H.; Saad, M.R.; Djenouri, Y.; Hu, G.; Ali, A.A.; Shaban, H. Metaheuristic algorithms and their applications in wireless sensor networks: Review, open issues, and challenges. Clust. Comput. 2024, 27, 13643–13673. [Google Scholar] [CrossRef]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An Application-Specific Protocol Architecture for Wireless Microsensor Networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
- Lindsey, S.; Raghavendra, C. PEGASIS: Power-efficient gathering in sensor information systems. In Proceedings of the Proceedings, IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002; Volume 3, p. 3. [Google Scholar] [CrossRef]
- Younis, O.; Fahmy, S. HEED: A hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks. IEEE Trans. Mob. Comput. 2004, 3, 366–379. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Coyle, E. An energy efficient hierarchical clustering algorithm for wireless sensor networks. In Proceedings of the IEEE INFOCOM 2003, Twenty-Second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No.03CH37428), San Francisco, CA, USA, 30 March–3 April 2003; Volume 3, pp. 1713–1723. [Google Scholar] [CrossRef]
- Neeha, S.; Charles, I.; Krishna, S.V.; Swarnakar, S. Performance Analysis of LEACH, LEACH-C, TS-LEACH, MOD-LEACH in WSN. Int. J. Comput. Intell. Commun. Technol. 2022, 11, 4–8. [Google Scholar] [CrossRef]
- Prakash, V.; Pandey, S. Metaheuristic algorithm for energy efficient clustering scheme in wireless sensor networks. Microprocess. Microsyst. 2023, 101, 104898. [Google Scholar] [CrossRef]
- Goudarzi, S.; Anisi, M.H.; Soleymani, S.A.; Ayob, M.; Zeadally, S. An IoT-Based Prediction Technique for Efficient Energy Consumption in Buildings. IEEE Trans. Green Commun. Netw. 2021, 5, 2076–2088. [Google Scholar] [CrossRef]
- Verma, D.; Gamad, R.S.; Nihalani, N. Optimizing Routing Efficiency in MANETs: Integrating PSO-Optimized Neural Network Model for Improved Data Transmission. In Proceedings of the 2024 Third International Conference on Artificial Intelligence, Computational Electronics and Communication System (AICECS), Manipal, India, 12–14 December 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Nuha, H.; Liu, B.; Mohandes, M.; Balghonaim, A.; Fekri, F. Seismic data modeling and compression using particle swarm optimization. Arab. J. Geosci. 2021, 14, 2542. [Google Scholar] [CrossRef]
- Rami Reddy, M.; Ravi Chandra, M.L.; Venkatramana, P.; Dilli, R. Energy-Efficient Cluster Head Selection in Wireless Sensor Networks Using an Improved Grey Wolf Optimization Algorithm. Computers 2023, 12, 35. [Google Scholar] [CrossRef]
- Jaiswal, K.; Anand, V. A Grey-Wolf based Optimized Clustering approach to improve QoS in wireless sensor networks for IoT applications. Peer-to-Peer Netw. Appl. 2021, 14, 1943–1962. [Google Scholar] [CrossRef]
- Kaddi, M.; Omari, M.; Salameh, K.; Alnoman, A. Energy-Efficient Clustering in Wireless Sensor Networks Using Grey Wolf Optimization and Enhanced CSMA/CA. Sensors 2024, 24, 5234. [Google Scholar] [CrossRef] [PubMed]
- Ajmi, N.; Helali, A.; Lorenz, P.; Mghaieth, R. MWCSGA—Multi Weight Chicken Swarm Based Genetic Algorithm for Energy Efficient Clustered Wireless Sensor Network. Sensors 2021, 21, 791. [Google Scholar] [CrossRef] [PubMed]
- Fauzan, M.N.; Munadi, R.; Sumaryo, S.; Nuha, H.H. Effect of p-value on LEACH Protocol Performance for Wireless Sensor Networks. In Proceedings of the 2022 International Conference on Data Science and Its Applications (ICoDSA), Bandung, Indonesia, 6–7 July 2022; pp. 166–170. [Google Scholar] [CrossRef]
- Fauzan, M.N.; Munadi, R.; Sumaryo, S.; Nuha, H.H. Enhanced Grey Wolf Optimization for Efficient Transmission Power Optimization in Wireless Sensor Network. Appl. Syst. Innov. 2025, 8, 36. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Miao, Z.; Yuan, X.; Zhou, F.; Qiu, X.; Song, Y.; Chen, K. Grey wolf optimizer with an enhanced hierarchy and its application to the wireless sensor network coverage optimization problem. Appl. Soft Comput. 2020, 96, 106602. [Google Scholar] [CrossRef]
- Ali, S.; Kumar, R. Hybrid energy efficient network using firefly algorithm, PR-PEGASIS and ADC-ANN in WSN. Sens. Int. 2022, 3, 100154. [Google Scholar] [CrossRef]
- Zheng, A.; Zhang, Z.; Liu, W.; Liu, J.; Xiao, Y.; Li, C. Dual Cluster Head Optimization of Wireless Sensor Networks Based on Multi-Objective Particle Swarm Optimization. Sensors 2022, 23, 231. [Google Scholar] [CrossRef]
- Pandey, H.M.; Chaudhary, A.; Mehrotra, D. A comparative review of approaches to prevent premature convergence in GA. Appl. Soft Comput. 2014, 24, 1047–1077. [Google Scholar] [CrossRef]
- Freitas, D.; Lopes, L.G.; Morgado-Dias, F. Particle Swarm Optimisation: A Historical Review Up to the Current Developments. Entropy 2020, 22, 362. [Google Scholar] [CrossRef]
- Zhang, T.; Huang, B.; Liu, X.; Fan, J.; Li, J.; Yue, Z.; Wang, Y. MCU Intelligent Upgrades: An Overview of AI-Enabled Low-Power Technologies. J. Low Power Electron. Appl. 2025, 15, 60. [Google Scholar] [CrossRef]
- Xi, M.; Dai, H.; He, J.; Li, W.; Wen, J.; Xiao, S.; Yang, J. A Lightweight Reinforcement-Learning-Based Real-Time Path-Planning Method for Unmanned Aerial Vehicles. IEEE Internet Things J. 2024, 11, 21061–21071. [Google Scholar] [CrossRef]
- Shirzadi, N.; Lau, D.; Stylianou, M. Surrogate Modeling for Building Design: Energy and Cost Prediction Compared to Simulation-Based Methods. Buildings 2025, 15, 2361. [Google Scholar] [CrossRef]












| Protocol | CH Selection | Routing | Key Characteristic |
|---|---|---|---|
| LEACH | Probabilistic | Single-hop | Probabilistic baseline |
| PEGASIS | Fixed leader | Chain-based | Chain energy efficiency |
| HEED | Energy-based | Single-hop | Residual energy aware |
| EEHC | Multi-level | Multi-hop | Hierarchical scalability |
| EGWO-NN | NN + EGWO | Single-hop (NN-driven) | Dynamic co-adaptation |
| Symbol | Description |
|---|---|
| Position vector of wolf i (candidate NN parameters) | |
| D | Dimensionality of solution (here, ) |
| Best three wolves (leaders) | |
| Positions of the leader wolves | |
| Current wolf position being updated | |
| Distance vectors toward leaders | |
| Attraction coefficients for each leader | |
| Random exploration coefficients | |
| t | Current iteration |
| T | Maximum number of iterations |
| a | Linearly decreasing control parameter |
| Uniform random vectors in |
| Component | Description |
|---|---|
| Input neurons | 2 inputs |
| Input features | Normalized residual energy Normalized distance to sink |
| Hidden layer | Single hidden layer |
| Hidden neurons | 2 neurons (ReLU activation) |
| Output neurons | 2 neurons |
| Output interpretation | Output 1: CH score (continuous) Output 2: Routing score (continuous) |
| Decision mechanism | Threshold-based CH activation Index-based neighbor selection for routing |
| Parameter initialization | Uniform random in |
| CH activation threshold | Fixed value: |
| Threshold adaptivity | Fixed (NN parameters are adaptive) |
| Parameter | Value |
|---|---|
| Field dimensions | 100 m × 100 m |
| Number of sensor nodes | 30 |
| Initial energy per node | 2 J |
| Data packet size | |
| Base station location | |
| Number of rounds | 2000 |
| Cluster Head/Leader Overhead | Value |
| LEACH CH overhead | |
| PEGASIS leader overhead | |
| HEED CH overhead | |
| EEHC CH overhead | |
| EGWO-NN (Proposed) CH overhead | |
| Radio Energy Model | Value |
| (Tx/Rx circuitry) | |
| (Tx amplifier) | |
| EGWO-NN Parameters | Value |
| Number of NN parameters | 12 |
| CH activation threshold |
| Comparison (Alive Nodes) | t-Statistic | p-Value | Significant |
|---|---|---|---|
| NN vs. LEACH | 18.2673 | 1.15 | Yes |
| NN vs. PEGASIS | 9.9360 | 5.35 | Yes |
| NN vs. HEED | 18.9110 | 1.84 | Yes |
| NN vs. EEHC | 18.9329 | 1.25 | Yes |
| Comparison | t-Statistic | p-Value | Significance |
|---|---|---|---|
| NN vs. LEACH | −5.1020 | Yes | |
| NN vs. PEGASIS | 46.3434 | Yes | |
| NN vs. HEED | −4.1236 | Yes | |
| NN vs. EEHC | −4.8182 | Yes | |
| Overall ANOVA Result | |||
| ANOVA F-statistic | 14.7432 | ||
| ANOVA p-value | |||
| Comparison | t-Statistic | p-Value | Significance |
|---|---|---|---|
| NN vs. LEACH | 17.6248 | Yes | |
| NN vs. PEGASIS | 17.8013 | Yes | |
| NN vs. HEED | 19.7492 | Yes | |
| NN vs. EEHC | 19.6191 | Yes |
| Comparison | t-Statistic | p-Value | Significance |
|---|---|---|---|
| NN vs. LEACH | 18.0664 | Yes | |
| NN vs. PEGASIS | 11.2524 | Yes | |
| NN vs. HEED | 18.7460 | Yes | |
| NN vs. EEHC | 22.8908 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Fauzan, M.N.; Munadi, R.; Sumaryo, S.; Nuha, H.H. Enhanced Wireless Sensor Network Lifetime Using EGWO-Optimized Neural Network Approach. Network 2026, 6, 5. https://doi.org/10.3390/network6010005
Fauzan MN, Munadi R, Sumaryo S, Nuha HH. Enhanced Wireless Sensor Network Lifetime Using EGWO-Optimized Neural Network Approach. Network. 2026; 6(1):5. https://doi.org/10.3390/network6010005
Chicago/Turabian StyleFauzan, Mohamad Nurkamal, Rendy Munadi, Sony Sumaryo, and Hilal Hudan Nuha. 2026. "Enhanced Wireless Sensor Network Lifetime Using EGWO-Optimized Neural Network Approach" Network 6, no. 1: 5. https://doi.org/10.3390/network6010005
APA StyleFauzan, M. N., Munadi, R., Sumaryo, S., & Nuha, H. H. (2026). Enhanced Wireless Sensor Network Lifetime Using EGWO-Optimized Neural Network Approach. Network, 6(1), 5. https://doi.org/10.3390/network6010005







