Abstract
Two neural networks were trained to predict, respectively, the Euler characteristic and the curvature of nuclear pastas in neutron star crust conditions generated by molecular dynamics simulations of neutron star matter with 0.1 < x < 0.5, 0.040 fm−3 < ρ < 0.085 fm−3 (0.68 × 1014 g/cm3 < ρ < 1.43 × 1014 g/cm3), and 0.2 MeV < T < 4.0 MeV, where x is proton content, the density is , and the temperature is T. The predictions of the two networks were combined to determine the nuclear pasta phase that is thermodynamically stable at a given x, , and T, and a three-dimensional phase diagram that extrapolated slightly the regions of existing molecular dynamics data was computed. The jungle gym and anti-jungle gym structures are prevalent at high temperature and low density, while the anti-jungle gym and anti-gnocchi structures dominate at high temperature and high density. A diversity of structures exist at low temperatures and intermediate density and proton content. The trained models used in this work are open access and available at a public repository to promote comparison to pastas obtained with other models.
Keywords:
neutron star matter; nuclear pasta; Minkowski functionals; molecular dynamics; nuclear phases; neural networks PACS:
26.60.+c; 26.60.−c; 02.70.Ns; 21.65.+f
1. Introduction
The structure of neutron star crusts is important for understanding neutrino flow [1] and the formation of nuclei in neutron star mergers [2]. Recent studies have shown that “pasta” structures can be formed both in nuclear matter (NM) [3] and neutron star matter (NSM) [4]. Those studies found that such structures are formed through dynamical processes, and vary depending on the proton content, density, and temperature. For a recent review see Ref. [5]. Here we continue a previous study [6,7] to relate the shape of the pasta structures to thermodynamic state variables. The hundreds of pastas analyzed were obtained through classical molecular dynamics (CMD) simulations in [4]. We use machine learning (ML) to learn the relationship between the Minkowski functionals of the different structure morphologies to the thermodynamics state variables of the CMD simulations that generated them.
1.1. Astrophysical Caveats
As this is not an article about astrophysics, but about a technique to categorize the nuclear pastas (that may exist in astrophysical objects), we believe it is convenient to state the range of applicability of the present work.
The composition of neutron star crusts is a complex and fascinating topic in astrophysics. The crust of a neutron star is a thin layer of matter that is about 1 kilometer thick, made up of a variety of elements, including iron, nickel, calcium, etc. forming a crystal lattice. The inner crust starts with , which has a proton fraction of Z/A = 26/56 = 0.46, and ends with , with a proton fraction of Z/A = 36/118 = 0.3 [8]. The drop of proton fraction with larger densities is due to the increase of electron capture by protons producing a large neutron excess and a correspondingly low proton fraction.
Thus, as it will be explained below and in Appendix A, the classical molecular dynamics model uses protons and neutrons and, as is, cannot be used to study the crust composed of a crystal lattice made of iron, nickel, calcium, etc.
At greater depths, that is, between the stellar core and the outer crust, there exists a transition region in which the density increases up to saturation density, and reaches higher values at the core. In this region, when the density is about half of the nuclear density, the nuclear system begins to undergo cluster formation, forming regions with nuclear density (clusters) and low-density regions (dilute neutron gas); such a system is known as the pasta. Since most field theories are unable to study clustering and other critical phenomena, the exact density of the crust-to-core transition has not been determined; Thomas-Fermi calculations place it at 0.067 fm−3 (or about 1.13 g/cm3) [9], while molecular dynamics simulations put it at about 0.08 fm−3 (or about 1.34 g/cm3) [5].
Similarly, the value of the proton fraction in this pasta region is also not well established; However, it is believed that the fraction of neutrons in the vapor and in the pastas is dictated by the nuclear symmetry energy [10]. Unfortunately, the symmetry energy is not firmly constrained by nuclear mass models (see the seriousness of this problem by a comparison of hundreds of models in Refs. [11,12]). The problem in this region is even more complicated for clustered systems, as the mean field results predict at low densities, whereas the experimental results [13] (and CMD calculations [5]) indicate to 10 MeV.
Thus, models that misestimate the value of at low densities predict proton ratios between and (e.g., Monte Carlo simulations [10]), or between at very low densities (e.g., Brueckner-Thomas-Fermi model within a energy density functional). Whereas CMD, which yields correct values for at low densities, predicts an unbound nuclear system at values of , with the possibility of finding pastas at higher values of [5].
In a different astrophysical scenario, the conditions inside a supernova are very similar to some of the conditions inside a neutron star, and nuclear pasta may also form inside supernovae. In this scenario, the pasta has to be warm and neutrinos that are trapped could play a role in setting the proton fraction [14]. Supernovae can be expected to have proton fractions of about 0.33 at high temperatures and at relatively low densities [15].
Another handicap of the CDM model is the impossibility of producing new particles through reactions, such as mesons and hyperons. Furthermore, when neutrons are spin-paired in neutron stars, they experience a decrease in energy due to the formation of Cooper pairs which leads to superfluidity; this phenomenon is not taken into account by CMD. However, it is expected that neutron pairing will not affect the pasta structures, as the energy change that occurs when neutrons pair is of the order of 1 MeV per neutron, much smaller than the binding energies of MeV per nucleon in the pasta structures.
In conclusion, in this work we study pastas with densities between fm−3 fm−3 (or 0.34 × 1014 g/cm3 g/cm3), temperatures MeV MeV, and between 0.5 and 0.3. [By extrapolation these ranges will be extended to fm−3 fm−3, MeV MeV, and ]. This hopefully covers the ranges of interest for both neutron star crusts and supernovae.
1.2. Terminology
“Nuclear matter” is composed of protons and neutrons. Likewise, “neutron star matter” is nuclear matter as it would be found on the crust of a neutron star, i.e., embedded in a gas of electrons. The “neutron star crust” is the outermost layer of a neutron star, with a thickness of about 1 km, where the density varies from zero to normal nuclear density. “Saturation density” is the density at which nuclear matter is at its most stable state, at zero temperature, = 0.16 fm−3 (2.74 × 1014 g/cm3). The “neutrino flow” in a neutron star is important for cooling and for transporting energy from the core to the crust. The “pasta” is a variety of exotic structures that can form in NM and NSM, and are called as such after their resemblance to pasta shapes, such as spaghetti, gnocchi, and lasagna. The “Minkowski functionals” of each structure are their respective values of the Euler characteristic, the volume and area occupied by the pastas, and the mean integral curvature. Finally, the “proton content” is the fraction of protons Z to the total number of nucleons A, which includes both neutrons and protons.
1.3. Nuclear Pasta
Neutron stars are the dense cadavers of large stars that have undergone a supernova explosion. Due to the intense gravitational pull of their compact mass, neutron stars overpower the electron degeneracy pressure, forcing electrons to fuse with protons, forming neutrons. This results in a tightly packed sphere of nearly pure neutron matter with protons and electrons scattered throughout, occupying a space several thousand times smaller than the original star.
At the neutron star surface, the pressure is relatively low, allowing nuclei from helium to iron to exist without being crushed together. However, in the crust, as the density increases, nuclear attraction and Coulomb repulsion forces become comparable in strength, and the interplay between them, and the pressure in the crust, leads to the formation of what has been dubbed “nuclear pasta” due to their resemblance to various types of pasta. If nuclear pasta does indeed exist, it would be the universe’s strongest material [16].
Formally, nuclear pasta is a theorized arrangement of protons and neutrons that may exist in the crusts of neutron stars [17]. The study of structures of nuclear pasta at zero temperature began in the 1980s through static methods like the liquid drop model [17,18], Thomas-Fermi models [19] and mean field theories [20]. At higher temperatures, the dynamics of nuclear pastas have been studied through quantum molecular dynamics simulations [21,22,23] and classical potential models [24,25]. Recently, classical molecular dynamics (CMD), which can find local minima by cooling, have studied non-traditional phases [26].
Various properties of clustered media, such as nuclear pastas, and their phase transitions into different pasta structures [26], have been calculated using CMD. In particular, recent studies have investigated the pasta-like structures and phase transitions of NM and NSM at sub-saturation densities, low temperatures, and proton content from 0.1 to 0.5 [1,2,3,4,5,6].
As an illustration, Figure 1 shows characteristic nuclear matter pastas obtained with CMD for 2000 nucleons at different values of density and temperatures, and for an equal number of protons and neutrons. The colors used represent protons (orange) and neutrons (purple), except at MeV, where some protons appear red and some neutrons blue.
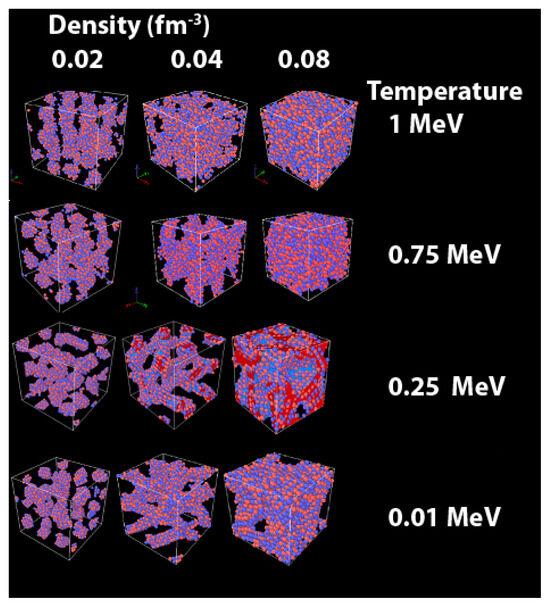
Figure 1.
Nuclei arrangements (pastas) stable at a given density and temperature when the proportion of protons is 0.5. See text for details. (color online).
The examples at 0.02 fm−3 (0.34 g/cm3) vary from “spaghetti” (tubes) at MeV to “gnocchi” (bundles) at MeV. At 0.04 fm−3 (0.68 g/cm3), the pastas go from “anti-gnocchi” (i.e., holes) at MeV to “jungle gym” (cross-linked structures similar to a lattice of rods) at MeV. These structures vary with the proton content and with the addition of the electron gas for NSM.
1.4. The Importance of This Study
The present work, although it is not an astrophysics study, it will develop a method to compare the structures obtained with various models at different temperatures, densities and proton content, that may apply to different astrophysical scenarios. The study will demonstrate the utility of the Minkowski functionals to characterize the nuclear pastas and determine phase changes among them. A public code based on machine learning technology will be available in a public repository.
2. Materials and Methods
2.1. Research Design
The goal of this project is to connect the structure of nuclear pastas to measurable quantities such as the Euler characteristic. This was achieved through the following steps:
- (i)
- Generate pastas.
- (ii)
- Compute the Minkowski functionals.
- (iii)
- Interpolate and extrapolate the values of the Minkowski functionals using neural networks.
- (iv)
- Plot the Minkowski functionals for the different types of pastas.
In this work we use the pastas obtained with CMD simulations in Refs. [6,7], compute the Minkowski functionals using cubic voxels, and use two neural networks to interpolate and extrapolate the value of the Euler characteristic and mean curvature for arbitrary values of proton content, temperature and density. Here we provide some details of the methods employed, more complete information can be found in Appendix A and Appendix B.
2.2. Classical Molecular Dynamics
CMD is a mature technique that has been applied to determine the pasta structures, both in NM and NSM [1,25,26]. In CMD, nucleons are treated as classical particles that interact through pair potentials. The dynamics of the nucleons are determined by their equations of motion. Other publications [25,26] describe the details and main advantages of CMD; the model optimized for NSM was introduced in Ref. [4]. The CMD model treats neutron star matter as a mixture of protons p, neutrons n, and electrons, with different potentials for the interactions between each pair of particles, , and . The electron gas is mimicked by a screening potential. Here, we use CMD to investigate pasta in NSM; the CMD model is presented in Appendix A.
To simulate neutron star matter, we used the LAMMPS code [27] with the potentials described in Appendix A. A = 4000 nucleons were prepared in a cubic cell under periodic boundary conditions with proton ratios of , 0.2, 0.3, 0.4, and 0.5, densities ranging between fm−3 fm−3 (0.68 g/cm3 g/cm3), and temperatures going from T = 4.0 MeV down to 0.2 MeV. Systems were prepared with nucleons placed at random with a minimum distance of 0.01 fm, and with speeds distributed according to a Maxwell-Boltzmann distribution at a given temperature. The evolution of the system at a given density was studied by solving the equations of motion. The position, momenta, and energy of the nuclei were stored at fixed time-steps. The pressure, temperature, and density were also recorded. At the end, the resulting pasta structures at the various combinations of values of x, and T were obtained.
2.3. Minkowski Functionals
The pasta, as any other geometrical figures, can be characterized by means of the Minkowski functionals [28]. The volume (V), surface area (S), Euler characteristic (), and integral mean curvature (B) can quantify the shape and connectivity of the nuclear structures. Previous studies [25,29,30,31] have used the Minkowski functionals to investigate the pasta. The Euler characteristic is a topological invariant that describes the shape of a geometric body with a topological invariant number, , that will not change if the body is stretched or bent. can be used to distinguish between different topological spaces. For example, a sphere has while a torus has = 0, so they cannot be topologically equivalent. A more thorough description can be found in Appendix B and in Refs. [3,25].
After the work of [25], it is known that the pasta structures can be classified in terms of the curvature and the Euler characteristic, as illustrated in Table 1. Notice that the term “anti” refers to the situation in which occupied regions are inverted into empty ones and vice versa. Likewise, the term “jungle gym” denotes a 3D trellis; the signs of these functionals are correlated with the different phases of the pasta [32]. In this work, pasta structures produced by CMD are “voxelized”, i.e., represented by “voxels”, or regular units of volume of fm per side. The V, S, and B are then computed, and is obtained according to Equation (A4). See the appendix of Ref. [3] for complete details.

Table 1.
Integral mean curvature (B) and Euler characteristic () of the pasta shapes.
2.4. Neural Network Interpolation
To interpolate the value of the two Minkowski functionals, the integral mean curvature and Euler characteristic, for arbitrary values of temperature and density, we trained fully-connected feed-forward neural networks of each functional using the package scikit-learn [33]. We used a network architecture of 4 hidden layers with 50 neurons per layer and with a rectified linear unit (ReLU) activation function. The weights of the network were determined by means of the method Adam of stochastic gradient-based optimization [34]. The data were partitioned 80% (randomly selected) for training the network, and 20% used to test the performance of the model. The normalized mean absolute error (NMAE) and the root-mean-square error (NRMSE) for the selected models on the test and the full data set are shown in Table 2. In the CMD data, the range of the integral mean curvature was and the range of the Euler characteristics was .

Table 2.
Normalized root-mean-square error (NRMSE) and normalized mean absolute error (NMAE) for the neural network models used in this work.
3. Results
In the study we use the 9600 pastas obtained with CMD simulations of the cooling of 4000 nucleons from an initial temperature of 4.0 MeV to different final temperatures, at different proton content and densities [6,7], compute the Minkowski functionals, and interpolate the value of the Minkowski functionals using neural networks for arbitrary values of T, x and . The end product of steps and is a dataset of values for the two Minkowski functionals in a dense data grid; these values are then used for training neural networks. This procedure is used to identify the structure of any pasta based on its proton content, density and temperature, without having to resort to the cumbersome voxeling. The methodology is independent of the method used to produce the pasta.
Phase Diagram
Sixteen constant-density cuts of the three-dimensional phase diagram of nuclear pastas in neutron star crusts predicted by our trained neural networks are shown in Figure 2. To generate the cuts, the predictions of each neural network were aligned with matplotlib [35] color maps: Greens, which is a sequential color map that starts with the color white and linearly moves towards green, was used for the mean curvature; seismic, which is a divergent color map with blue and red at the two extremes and white in the middle, was used for the Euler characteristic. Consequentially, blue is associated with the jungle-gym and anti-jungle gym structures (negative ); red with the gnocchi and anti-gnocchi structures (positive ); green with gnocchi, spaghetti, and jungle gym structures (positive B); and lighter colors are associated with anti-gnocchi, anti-spaghetti, and anti-jungle gym structures (negative B). Each cut was computed by making individual predictions at 500 points along the proton proportion axis, and 100 points along the temperature axis. Black squares show points at which either mean curvature or Euler characteristic change sign, and these changes were detected by scanning the data along both the proton proportion rows and temperature columns. The following predictions in the regions are extrapolations: fm−3 (0.68 g/cm3), fm−3, (1.43 g/cm3), , MeV, and MeV; are extrapolations.
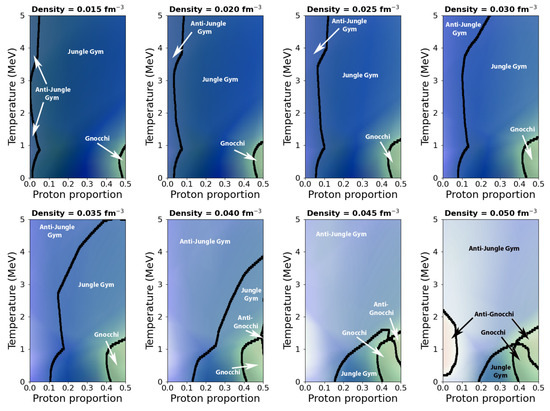
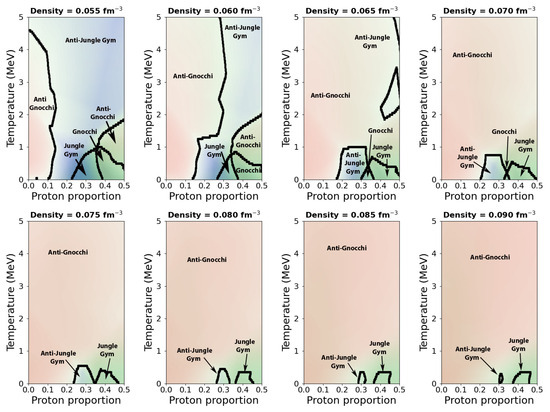
Figure 2.
Constant-density temperature vs. proton proportion cuts of the three-dimensional phase diagram of nuclear pasta structures of neutron star matter predicted by the current methodology. See text for details. (color online).
4. Discussion
It is easy to see that at MeV most structures are jungle gym, anti-jungle gym or anti-gnocchi. The rest of the other pasta structures exist only at lower temperatures, MeV, and higher proton proportions, . The lasagna is the least prominent of the structures, but it corresponds to the region near the boundary between any anti-structure and the corresponding structure; also notice that the lasagna is equivalent to its anti-lasagna. It is reassuring that the phase changes occur in the same temperature-density region where the caloric curve changes slopes, cf. Figures 48–50 in Ref. [5]; the change of slope could indicate the pasta structure changes are of first order. It must be mentioned that our results go beyond previous studies of the pasta diagram performed with static Hartree-Fock at fixed proton content and non-zero temperature [32], and for and [36], and with quantum molecular dynamics for and [37] for cold matter.
In Figure 3, we present a comparison of our (extrapolated) results for MeV with those of Ref. [36] for zero temperature obtained with static Hartree-Fock calculations. Using the labels and colors of Ref. [36] and assuming that () when their values are within percent ( percent) of their maximum values in our training set, we denote gnocchi as SPH (for sphere), spaghetti (cylinder-like) as ROD1, planar meshes of orthogonal rods as ROD2, jungle gym (three-dimensional grids of rods) as ROD3, lasagna as SLAB, anti-spaghetti (rod-bubble) as ROD1B, anti-planar meshes of orthogonal rods (ROD2 bubble) as ROD2B, and anti-gnocchi (sphere bubble) as SPHB. Notice that the slab and jungle gym are symmetric under the exchange of matter and voids. The uniform phase, i.e., without the pasta structure, is denoted as UNI. The difference between the results obtained by the two models underscores the advantage that CMD has in finding meta-stable minima by dynamical means. Other recent studies [38] show the same effect, obtaining large differences in pasta structures as a function of the generalized Skyrme effective interactions used. It is worth mentioning that the variety of pasta phases exists, say, in the density range of up to 0.08 fm−3 (1.43 × 1014 g/cm3), in agreement with [9].
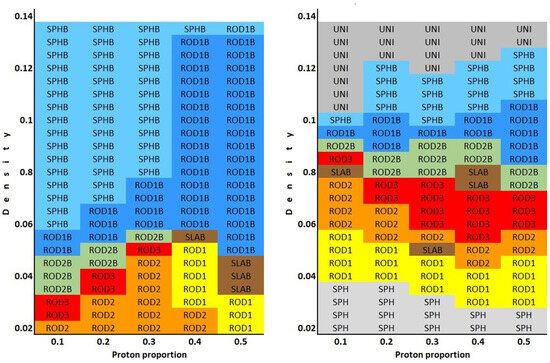
Figure 3.
Pasta phases at MeV for given densities (in fm−3) and proton proportion predicted by the current methodology (left), and static Hartree-Fock from Ref. [36] (right). (color online).
In passing, we remark that other classical dynamic models, c.f. [24,30,31] use different potentials, but produce the same type of pastas, although not necessarily in the same order in density and temperature. Likewise, it is worth mentioning that superfluidity, although relevant at MeV and [39] has not been shown to have any effect on the structure of the pastas.
To promote the comparison of the structures obtained with various models at different temperatures, densities and proton content, the code used and ML models used in this work are available in a public repository [40] under the name “Dangelo”, in honor of the Italian painter Sergio Dangelo, founder of the arte nucleare movement, and who could very well have painted the phase diagrams of Figure 2. The program produces phase diagrams of nuclear pastas using the neural network models trained on the classical molecular dynamics data presented in this work. The models are open access as well.
These findings are of interest to study the structure of the crust of neutron stars as a function of depth. In future work, we will combine these results with a Lane–Emden polytropic equation of state appropriate for a neutron star to determine the structure, i.e., the type of pasta, that exists at different depths, i.e., at different densities, temperatures and proton content, from the surface of the neutron star.
5. Conclusions
In this study we go beyond previous investigations of the structures attained by neutron star matter at varying conditions of T, and x [6,7]. Using molecular dynamics simulations, 9600 pastas were produced, analyzed with respect to their Minkowski functionals, and the Minkowski functionals used to train neural network models, which were then used to explore the pasta configuration of the 3D space . We found that the phase diagram of neutron star matter corresponds, in qualitative terms, to phase changes detected through the caloric curve in previous studies.
We conclude that machine learning techniques help estimate the Minkowski functionals for values of T, x, and . The evolution of the pasta structures as a function of x, T and is linked to the 3D representation of the functionals, that is, as goes from positive to negative, the structure goes from anti-pasta to pasta, etc. The linkage of the pasta structures to these functionals will be studied in a forthcoming article for neutron star matter and nuclear matter.
We encourage other investigators to compare the structures obtained with other models with those obtained with CMD by using the code “Dangelo” [40].
Author Contributions
Conceptualization, J.A.L. and J.A.M.; methodology, J.A.L. and J.A.M.; software, J.A.M.; validation, J.A.L. and J.A.M.; formal analysis, J.A.L. and J.A.M.; investigation, J.A.L. and J.A.M.; resources, J.A.L. and J.A.M.; data curation, J.A.L. and J.A.M.; writing—original draft preparation, J.A.L.; writing—review and editing, J.A.L. and J.A.M.; visualization, J.A.L. and J.A.M.; supervision, J.A.L. and J.A.M.; project administration, J.A.L. and J.A.M.; funding acquisition, J.A.L. and J.A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Reaching a New Energy Sciences Workforce (RENEW) program. J.A.M. was supported by RENEW Award Number DE-SC-0021994 and J.A.L. by RENEW Award Number CW46261 via Oak Ridge National Laboratory.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this article:
| CMD | Classical molecular dynamics |
| MD | Molecular dynamics |
| ML | Machine learning |
| NM | Nuclear matter |
| NSM | Neutron star matter |
| NMAE | Normalized mean absolute error |
| ReLU | Rectified linear unit |
| NRMSE | Normalized root mean square error |
Appendix A. Molecular Dynamics
Appendix A.1. Why Use Classical Molecular Dynamics
In nuclear physics theoretical models are indispensable tools for comprehending heavy-ion collisions at intermediate energies. The majority of researchers employ models where nucleons (or “test particles”) interact through an average mean field that allows them to incorporate some quantum and semi-quantum features. Unfortunately, such an approach sacrifices very important features of the reactions, such as clusterization, fragment formation, phase transitions, and other crucial phenomena.
Conversely, classical dynamics models, while failing to capture quantum effects, excel at preserving nucleon-nucleon correlations, statistical fluctuations, phase transitions, and other critical phenomena essential to understanding the later stages of fragmentation reactions.
In a paradoxical interplay, the quantum aspects of mean field models facilitate a realistic energy distribution in the early stages of the reaction but falter in fragmenting the system in the later stages. On the other hand, classical methods do not represent accurately the reaction dynamics in the early part, but excel in the latter phase of the collision.
Furthermore, after six decades of evolution of the independent mean field models, the community of practitioners has not agreed on a single model to use. Indeed, calculations from the two fundamental families, Quantum Molecular Dynamics (QMD) and Boltzmann-Uhling-Uhlenbeck (BUU), still exhibit grave inconsistencies in their predictions. A comparison of different models revealed variations in flow observables, such as the effectiveness of Pauli blocking in nucleon-nucleon collisions, the stability of initialized nuclei, and others, primarily attributed to differences in the initialization of the system, collision integral treatment, and other intertwined effects [41].
The latter discrepancies likely stem from the operator’s selection of “test particles” and the fluctuations manually introduced in both QMD and the BUU Langevin framework. While fragmentation was not examined in this comparison, it remains a critical challenge for all such models [42,43,44,45,46]. To compare model predictions to final yields, the resulting matter density distributions must be fed into “afterburner” computer programs such as the Statistical Multifragmentation Model [47] and similar tools.
In contrast, despite not respecting quantum principles, classical dynamics models (such as CMD) can capture both the equilibrium and non-equilibrium phases of a collision. CMD models can indeed describe hydrodynamic flow, non-equilibrium dynamics, and phase transitions with non-adjustable parameters. They can also simulate phase transitions (critical phenomena), neck fragmentation [48], obtain isoscaling and caloric curves in reactions, as well as nuclear pasta formation in infinite systems [4,5,49].
Thus, despite its failures in accounting for quantum effects (the limitations of which have been assessed in [50]), we believe we err less in studying nuclear systems using classical molecular dynamics than other models that do not include the many-body correlations necessary to study phase changes and a plethora of critical phenomena. Furthermore, it is clear that this study could have been performed with pastas produced by other methods; unfortunately, no other technique can generate the thousands of pastas needed to train a neural network at such a large range of T, x and , and without a large consumption of computer time. We understand that CMD is not the choice of most colleagues, and we ask them to have an open mind, and accept that other models can be used to explore nuclear phenomena.
Appendix A.2. The Classical Molecular Dynamics Model
In classical molecular dynamics (CMD) nucleons interact through a modified version of the Pandharipande Medium potential. The Pauli repulsion can be simulated in classical mechanics via a neutron-proton, attractive at large separations, and repulsive at small ones [51]. The potentials are phenomenological, constructed with combinations of Yukawa interactions, with parameters adjusted as to approximate the behavior of the Vlasov-Nordheim in the classical limit [52], and yield at saturation density, fm−3 (2.7 g/cm3), a binding energy MeV/nucleon, and a compressibility of about 250 MeV.
The corresponding mathematical expressions are
where, after the cutoff radius the potentials are set to zero. Notice that in this phenomenological approach, to have nuclear matter bound but purely neutron matter unbound, is attractive, and is purely repulsive. Furthermore, in studies of infinite systems, the proton-proton Coulomb interaction is ignored and ; the Coulomb interaction is only used in reactions.
The values of , , and , , were first determined by the Urbana-Champaign group of V.J. Pandharipande for cold nuclear matter [51,52,53], and were later improved to reproduce cold NM binding energies more accurately [2]; the values of the parameters are listed in Table A1.
The potentials developed by Pandharipande [51,52,53] were aimed at reproducing the experimental cross sections in nucleon–nucleon collisions. By design, these potentials did not contain the Coulomb potential of the proton–proton interactions, which is assumed to be embedded in the potentials. Furthermore, there is no momentum dependence in the potentials, and thus, one cannot extract the momentum dependence of the compressibility, saturation density, symmetry energy, etc.
In the neutron star crust, electrons fill the voids between protons and neutrons. This means that the effect of the Coulomb potential of the electron gas must be included in any model of the crust. The principal effect of the electron cloud is to screen the Coulomb potential of the protons. This screening effect reduces the strength of the Coulomb forces between the protons, which is important for understanding the structure and dynamics of the crust. The long range of the Coulomb interaction makes it difficult to simulate infinite systems. Some approximation is therefore needed when modeling the neutron star crust. One common approximation is to use the Thomas-Fermi approximation, which assumes that the electron gas is in a state of uniform density.
The Coulomb effect of the gas of electrons is implemented through the Thomas-Fermi screening potential [21,24], which takes the gas of electrons as a Fermi gas with the same density of the protons. The electron gas becomes polarized screening the protons. The corresponding Poisson equation yields the potential
with a cutoff distance for of 20 fm, and a screening length of fm, to have the properties of the resulting pasta essentially constant (see Ref. [54]).
The pasta configurations were obtained by cooling a system of 4000 nucleons of a given percentage of protons and neutrons and at a certain density, from MeV down to a final temperature of 0.2 MeV. The proportion of protons to neutrons used was of , and the densities were 0.04 fm−3 0.085 fm−3 (0.68 × 1014 g/cm3 g/cm3). The size of the cell is determined by the number of particles and the density; however, using it with periodic boundary conditions, it is large enough as to avoid finite size effects of smaller lengths than the cell size [54].
The pastas were extracted from a Markov chain produced by CMD. To avoid correlations between the positions of the nucleons, each of the pastas was separated from the previous one by 10,000 time steps. The total number of structures obtained was 9600.

Table A1.
Parameter set for the CMD computations.
Table A1.
Parameter set for the CMD computations.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 3097.0 MeV | 1.648 fm−1 | ||
| 2696.0 MeV | 1.528 fm−1 | ||
| 379.5 MeV | 1.628 fm−1 | ||
| 5.4/20 fm |
Appendix B. Minkowski Functionals
Geometries of complex structures can be decomposed into simple structures that are connected side by side. The simple structures used are the voxels. The connectivity across voxels can be quantified by the number of vertices, (), edges (), faces () and volume () of the external shape of the structure formed with voxels.
The Minkowski functionals, are defined in terms of , , and as follows [28]:
V is the volume of the intersection of the voxels, and S is the external surface area of the intersections of the voxels; these are two important properties that determine its shape. The mean breadth (B) functional is the mean external curvature of the collection of voxels, with positive values of B corresponding to smooth, round surfaces, such as spheres and cylinders, and negative values of B corresponding to bodies with spiky or irregular surfaces, such as bodies with inner bubbles or hollow cylinders [32,37]. A value of B = 0 (with ) corresponds to bodies with flat surfaces like slabs.
The Euler characteristic is the Euler number of the external shape of the voxels, which can be written as
Solid objects, including those with isolated voids, can have positive Euler characteristics. However, structures like sponges or large inner voids, like jungle gym structures, have negative Euler characteristics because the number of voids or tunnels is larger than the number of isolated regions.
The various values of corresponding to the different pastas associated are listed in Table 1 (see Ref. [25] for more information). As it was mentioned previously, slab-like structures (lasagnas) correspond to . Spherical-like (Gnocchi) or cylinder-like (spaghetti) structures, correspond to and . Likewise, sponge-like (Jungle-gym) structures attain . The structures with matter replaced by voids and vice versa use the prefix anti- in Table 1.
The calculation of the Minkowski functionals require that each nucleon is represented by a 3D structure. Here we bin space using “voxels”, each of which contains a single nucleon. The procedure to do this is explained in Ref. [5].
References
- Alcain, P.; Dorso, C. The neutrino opacity of neutron rich matter. Nucl. Phys. A 2017, 961, 183–199. [Google Scholar] [CrossRef]
- Alcain, P.N.; Dorso, C.O. Dynamics of fragment formation in neutron-rich matter. Phys. Rev. C 2018, 97, 015803. [Google Scholar] [CrossRef]
- Dorso, C.; Frank, G.; López, J. Phase transitions and symmetry energy in nuclear pasta. Nucl. Phys. A 2018, 978, 35–64. [Google Scholar] [CrossRef]
- Dorso, C.; Frank, G.; López, J. Symmetry energy in neutron star matter. Nucl. Phys. A 2019, 984, 77–98. [Google Scholar] [CrossRef]
- López, J.A.; Dorso, C.O.; Frank, G.A. Properties of nuclear pastas. Front. Phys. 2021, 16, 24301. [Google Scholar] [CrossRef]
- López, J.A.; Muñoz, J.A. Analytical expression and neural network study of the symmetry energy. CERN Proc. 2019, 1, 29–34. [Google Scholar]
- López, J.; Muñoz, J.; Dorso, C.; Frank, G. Machine learning Minkoswki functionals of neutron star crusts. J. Phys. Conf. Ser. 2020, 1643, 012054. [Google Scholar] [CrossRef]
- Utama, R.; Piekarewicz, J.; Prosper, H. Nuclear mass predictions for the crustal composition of neutron stars: A Bayesian neural network approach. Phys. Rev. C 2016, 93, 014311. [Google Scholar] [CrossRef]
- Sharma, B.K.; Centelles, M.; Viñas, X.; Baldo, M.; Burgio, G.F. Unified equation of state for neutron stars on a microscopic basis. Astron. Astrophys. 2015, 584, A103. [Google Scholar] [CrossRef]
- Piekarewicz, J.; Sánchez, G.T. Proton fraction in the inner neutron-star crust. Phys. Rev. C 2012, 85, 015807. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Sá Martins, J.S.; Delfino, A.; Stone, J.R.; Stevenson, P.D. Skyrme interaction and nuclear matter constraints. Phys. Rev. C 2012, 85, 035201. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Avancini, S.S.; Carlson, B.V.; Delfino, A.; Menezes, D.P.; Providência, C.; Typel, S.; Stone, J.R. Relativistic mean-field hadronic models under nuclear matter constraints. Phys. Rev. C 2014, 90, 055203. [Google Scholar] [CrossRef]
- Hagel, K.; Natowitz, J.B.; Röpke, G. The equation of state and symmetry energy of low-density nuclear matter. Eur. Phys. J. A 2014, 50, 1–16. [Google Scholar] [CrossRef]
- Horowitz, M.; Pérez García, M.; Piekarewicz, J. Neutrino-pasta scattering: The opacity of nonuniform neutron-rich matter. Phys. Rev. C 2004, 69, 045804. [Google Scholar] [CrossRef]
- Pi, M.; Barranco, M.; Perez-Canyellas, A.; Polls, A. Supernova matter: A semiclassical approach. Astron. Astrophys. Suppl. Ser. 1986, 64, 439–451. [Google Scholar]
- Caplan, M.E.; Schneider, A.S.; Horowitz, C.J. Elasticity of Nuclear Pasta. Phys. Rev. Lett. 2018, 121, 132701. [Google Scholar] [CrossRef]
- Ravenhall, D.G.; Pethick, C.J.; Wilson, J.R. Structure of Matter below Nuclear Saturation Density. Phys. Rev. Lett. 1983, 50, 2066–2069. [Google Scholar] [CrossRef]
- Hashimoto, M.A.; Seki, H.; Yamada, M. Shape of Nuclei in the Crust of Neutron Star. Prog. Theor. Phys. 1984, 71, 320–326. [Google Scholar] [CrossRef]
- Williams, R.; Koonin, S. Sub-saturation phases of nuclear matter. Nucl. Phys. A 1985, 435, 844–858. [Google Scholar] [CrossRef]
- Page, D.; Lattimer, J.M.; Prakash, M.; Steiner, A.W. Minimal Cooling of Neutron Stars: A New Paradigm. Astrophys. J. Suppl. Ser. 2004, 155, 623. [Google Scholar] [CrossRef]
- Maruyama, T.; Niita, K.; Oyamatsu, K.; Maruyama, T.; Chiba, S.; Iwamoto, A. Quantum molecular dynamics approach to the nuclear matter below the saturation density. Phys. Rev. C 1998, 57, 655–665. [Google Scholar] [CrossRef]
- Kido, T.; Maruyama, T.; Niita, K.; Chiba, S. MD simulation study for nuclear matter. Nucl. Phys. A 2000, 663, 877c–880c. [Google Scholar] [CrossRef]
- Watanabe, G.; Sato, K.; Yasuoka, K.; Ebisuzaki, T. Microscopic study of slablike and rodlike nuclei: Quantum molecular dynamics approach. Phys. Rev. C 2002, 66, 012801. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Pérez-García, M.A.; Carriere, J.; Berry, D.K.; Piekarewicz, J. Nonuniform neutron-rich matter and coherent neutrino scattering. Phys. Rev. C 2004, 70, 065806. [Google Scholar] [CrossRef]
- Dorso, C.O.; Giménez Molinelli, P.A.; López, J.A. Topological characterization of neutron star crusts. Phys. Rev. C 2012, 86, 055805. [Google Scholar] [CrossRef]
- Alcain, P.N.; Giménez Molinelli, P.A.; Dorso, C.O. Beyond nuclear “pasta”: Phase transitions and neutrino opacity of new “pasta” phases. Phys. Rev. C 2014, 90, 065803. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Michielsen, K.; De Raedt, H. Integral-geometry morphological image analysis. Phys. Rep. 2001, 347, 461–538. [Google Scholar] [CrossRef]
- Watanabe, G.; Sato, K.; Yasuoka, K.; Ebisuzaki, T. Structure of cold nuclear matter at subnuclear densities by quantum molecular dynamics. Phys. Rev. C 2003, 68, 035806. [Google Scholar] [CrossRef]
- Schneider, A.S.; Horowitz, C.J.; Hughto, J.; Berry, D.K. Nuclear “pasta” formation. Phys. Rev. C 2013, 88, 065807. [Google Scholar] [CrossRef]
- Caplan, M.E.; Horowitz, C.J. Colloquium: Astromaterial science and nuclear pasta. Rev. Mod. Phys. 2017, 89, 041002. [Google Scholar] [CrossRef]
- Schuetrumpf, B.; Klatt, M.A.; Iida, K.; Maruhn, J.A.; Mecke, K.; Reinhard, P.G. Time-dependent Hartree-Fock approach to nuclear “pasta” at finite temperature. Phys. Rev. C 2013, 87, 055805. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Schuetrumpf, B.; Iida, K.; Maruhn, J.A.; Reinhard, P.G. Nuclear “pasta matter” for different proton fractions. Phys. Rev. C 2014, 90, 055802. [Google Scholar] [CrossRef]
- Sonoda, H.; Watanabe, G.; Sato, K.; Yasuoka, K.; Ebisuzaki, T. Phase diagram of nuclear “pasta” and its uncertainties in supernova cores. Phys. Rev. C 2008, 77, 035806. [Google Scholar] [CrossRef]
- Shchechilin, N.N.; Pearson, J.; Chamel, N. Nuclear Pasta in Cold Non-Accreting Neutron Stars: Symmetry Energy Effects. Phys. Sci. Forum 2023, 7, 10. [Google Scholar] [CrossRef]
- Sedrakian, A.; Clark, J. Superfluidity in nuclear systems and neutron stars. Eur. Phys. J. A 2019, 55, 167. [Google Scholar] [CrossRef]
- Muñoz, J.A. Jamunozlab/Dangelo. 2023. Available online: https://zenodo.org/records/10032533 (accessed on 22 October 2023).
- Colonna, M.; Zhang, Y.; Wang, Y.; Cozma, D.; Danielewicz, P.; Ko, C.; Zhang, F. Comparison of Heavy-Ion Transport Simulations: Mean-field Dynamics in a Box. Phys. Rev. C 2021, 104, 024603. [Google Scholar] [CrossRef]
- Bertsch, G.; Das Gupta, S. A guide to microscopic models for intermediate energy heavy ion collisions. Phys. Rep. 1988, 160, 189–233. [Google Scholar] [CrossRef]
- Danielewicz, P. Determination of the mean-field momentum-dependence using elliptic flow. Nucl. Phys. A 2000, 673, 375–410. [Google Scholar] [CrossRef]
- Li, B.A. Neutron-Proton Differential Flow as a Probe of Isospin-Dependence of the Nuclear Equation of State. Phys. Rev. Lett. 2000, 85, 4221–4224. [Google Scholar] [CrossRef]
- Aichelin, J.; Stöcker, H. Quantum molecular dynamics—A novel approach to N-body correlations in heavy ion collisions. Phys. Lett. B 1986, 176, 14–19. [Google Scholar] [CrossRef]
- Ono, A.; Danielewicz, P.; Friedman, W.A.; Lynch, W.G.; Tsang, M.B. Isospin fractionation and isoscaling in dynamical simulations of nuclear collisions. Phys. Rev. C 2003, 68, 051601. [Google Scholar] [CrossRef]
- Bondorf, J.; Botvina, A.; Iljinov, A.; Mishustin, I.; Sneppen, K. Statistical multifragmentation of nuclei. Phys. Rep. 1995, 257, 133–221. [Google Scholar] [CrossRef]
- Chernomoretz, A.; Gingras, L.; Larochelle, Y.; Beaulieu, L.; Roy, R.; St-Pierre, C.; Dorso, C.O. Quasiclassical model of intermediate velocity particle production in asymmetric heavy ion reactions. Phys. Rev. C 2002, 65, 054613. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Pérez-García, M.A.; Berry, D.K.; Piekarewicz, J. Dynamical response of the nuclear “pasta” in neutron star crusts. Phys. Rev. C 2005, 72, 035801. [Google Scholar] [CrossRef]
- López, J.A.; Ramírez-Homs, E.; González, R.; Ravelo, R. Isospin-asymmetric nuclear matter. Phys. Rev. C 2014, 89, 024611. [Google Scholar] [CrossRef]
- Vicentini, A.; Jacucci, G.; Pandharipande, V.R. Fragmentation of hot classical drops. Phys. Rev. C 1985, 31, 1783–1793. [Google Scholar] [CrossRef]
- Lenk, R.J.; Schlagel, T.J.; Pandharipande, V.R. Accuracy of the Vlasov-Nordheim approximation in the classical limit. Phys. Rev. C 1990, 42, 372–385. [Google Scholar] [CrossRef]
- Lenk, R.J.; Pandharipande, V.R. Disassembly of hot classical charged drops. Phys. Rev. C 1986, 34, 177–184. [Google Scholar] [CrossRef] [PubMed]
- Alcain, P.N.; Giménez Molinelli, P.A.; Nichols, J.I.; Dorso, C.O. Effect of Coulomb screening length on nuclear “pasta” simulations. Phys. Rev. C 2014, 89, 055801. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).