Abstract
This paper presents an innovative entanglement-based protocol to address the Dining Cryptographers problem, utilizing maximally entangled tuples as its core. This protocol aims to provide scalability in terms of both the number of cryptographers n and the amount of anonymous information conveyed, represented by the number of qubits m within each quantum register. The protocol supports an arbitrary number of cryptographers n, enabling scalability in both participant count and the volume of anonymous information transmitted. While the original Dining Cryptographers problem focused on a single bit of information—whether a cryptographer paid for dinner—the proposed protocol allows m, the number of qubits in each register, to be any arbitrarily large positive integer. This flexibility allows the transmission of additional information, such as the cost of the dinner or the timing of the arrangement. Another noteworthy aspect of the introduced protocol is its versatility in accommodating both localized and distributed versions of the Dining Cryptographers problem. The localized scenario involves all cryptographers gathering physically at the same location, such as a local restaurant, simultaneously. In contrast, the distributed scenario accommodates cryptographers situated in different places, engaging in a virtual dinner at the same time. Finally, in terms of implementation, the protocol accomplishes uniformity by requiring that all cryptographers utilize identical private quantum circuits. This design establishes a completely modular quantum system where all modules are identical. Furthermore, each private quantum circuit exclusively employs the widely used Hadamard and CNOT quantum gates, facilitating straightforward implementation on contemporary quantum computers.
1. Introduction
In today’s rapidly evolving digital era, technology seamlessly integrates into every aspect of our lives, a fact that makes cybersecurity more crucial than ever. As we navigate the complexity of digital boundaries, we find ourselves immersed in a world where unforeseen threats coexist with the free exchange of knowledge. The concept of privacy has evolved, encompassing critical aspects of individual freedom and security in an era characterized by rapid technological discoveries and digitally interconnected realms. In such a time, privacy refers to an individual’s ability to manage personal information, choosing whether and how it is collected, used, and disclosed. The spectrum of issues where privacy is considered necessary has expanded significantly, ranging from personal communications and financial transactions to private health information. Privacy issues are more intricate as digital platforms and smart technologies have become more ingrained in our daily lives. Social media, internet services, and data-driven technologies have brought unprecedented convenience, triggering urgent concerns about individual privacy. The clash between the need for innovation and the demand for personal data protection has emerged as a central topic of discussion in recent years.
Cybersecurity is entrusted with safeguarding our data, privacy, and networked culture. It is responsible for protecting digital systems, networks, and devices from various threats in cyberspace. These risks, ranging from ransomware attacks and advanced espionage to computer viruses and data breaches, not only pose economic risks but also jeopardize the foundation of trust on the Internet. The development of the Internet and the widespread use of smart gadgets have transformed the way we work, communicate, shop, and spend our leisure time. However, the digital revolution has increased the attack possibilities that cybercriminals can exploit to their advantage. Consequently, cybersecurity is a constantly evolving field trying to stay ahead of these risks. Alongside the evolution of software and hardware, the security of these systems must also progress, fortifying each system against new threats. This is achieved by combining technological advancements, regulations, and human skills. As we traverse the realm of cybersecurity, it becomes evident that safeguarding our digital future involves more than simple data protection. Understanding and implementing robust cybersecurity measures are key to building a safer, more resilient digital society.
The cryptographic protocol known as the Dining Cryptographers problem explores the idea of anonymous communication in a social context. David Chaum first introduced it in 1988 [1] as a thought experiment to demonstrate the possibilities of private and secure communication among participants. Emphasis is placed on preserving the privacy and anonymity of each participant to achieve the goal of exchanging messages. To prevent the revelation of individual contributions, the protocol uses cryptographic techniques to ensure that the information exchanged between cryptographers reveals only the pre-agreed result (0/1). The scenario is based on real-life situations where people desire to share information with others while maintaining their privacy and the confidentiality of their messages. It is worth mentioning that techniques aimed at obfuscating the sender or receiver in a communication scheme have received considerable attention in classical cryptography in the context of numerous applications [2,3].
Anonymity, being a fundamental cryptographic primitive crucial for hiding the identity of the sender and/or receiver of a message, inevitably stimulated research within the emerging field of quantum cryptography. Boykin in 2002 proposed a quantum protocol, where participants distribute pairs of entangled qubits known as EPR pairs, which are subsequently utilized to generate cryptographic keys [4]. An EPR pair consists of two qubits entangled in a maximally entangled state, serving as a valuable resource for quantum communication and quantum computation, such as quantum teleportation. Boykin’s system enables the anonymous transmission of classical information based on quantum teleportation. Later, Christandl and Wehner introduced a new protocol for the anonymous distribution of qubits [5]. This protocol uses EPR pairs to transmit a quantum coin via teleportation. Unlike the classical protocol, it does not require all honest players to possess the same qubit at the end, avoiding conflicts with the non-cloning property of quantum states. Bouda and Sprojcar accomplished quantum communication without assuming that a trusted state is shared between the participants of the protocol [6]. Subsequently, Brassard and Tapp et al. presented information-theoretically secure protocols for anonymous quantum communication in [7,8], respectively. According to their proposal, the sender can transmit a quantum message with complete anonymity even if some participants are corrupted. They introduced the concept of fail-safe teleportation, ensuring that, in the case of quantum teleportation, the information reaches its destination with the highest possible precision and security, even in the presence of errors or disturbances. A quantum communication scheme based on nonmaximally entangled qubit pairs was proposed in [9], while [10] introduced anonymous entanglement using single photons and CNOT operations. Shi et al. presented a method for implementing quantum anonymous communication in a public receiver model using the anonymity features of DC-Nets and nonmaximally entangled quantum channels [11]. Wang and K Zhang analyzed the shortcomings of the above protocols and proposed some modifications, emphasizing the risk to the sender’s anonymity in the case of a malicious participant [12]. In 2015, Ramij Rahaman and Guruprasad Kar presented two quantum protocols addressing the Dining Cryptographers problem and the Anonymous Veto (AV) problem. These protocols are based on the GHZ paradox and the properties of GHZ correlations [13]. Later, Hameedi et al. proposed a new quantum solution to this problem using a one-way sequential protocol and extending it to the Anonymous Veto problem [14]. The protocol is characterized by relying on a single qubit, utilizing GHZ states due to their high symmetry. In 2021, Li et al. presented an anonymous transmission protocol using single-particle states with collective detection [15]. Finally, in 2022, Mishra et al. published a series of QAV protocols, quantum protocols for the Anonymous Veto [16].
In this work, we make the case for an innovative entanglement-based protocol for the Dining Cryptographers problem. The protocol is described as a quantum game, involving signature characters such as Alice, Bob, etc. The pedagogical nature of games is expected to enhance the comprehension of technical concepts. Quantum games, in particular, were initially introduced in 1999 [17,18] and have by now gained widespread acceptance because quantum strategies, at times, surpass classical ones [19]. Clearly, this is not the first time games have been used in quantum cryptography. Even the original groundbreaking article [20] presents the QKD protocol as a game. For some recent results regarding QKD the reader may consult [21] and references therein.
This study introduces an innovative entanglement-based protocol to solve the Dining Cryptographers problem, leveraging maximally entangled tuples as its foundation. The primary motivation behind this protocol is to provide scalability in terms of both the number of cryptographers n and the volume of anonymous information conveyed, represented by the number m of qubits within each quantum register.
The protocol accommodates an arbitrary number of cryptographers n, allowing scalability not only in participant count but also in the amount of anonymous information transmitted. While the original Dining Cryptographers problem dealt with a single bit of information—whether a cryptographer paid for dinner—the proposed protocol enables m, the number of qubits in each register, to be any arbitrarily large positive integer. This flexibility allows for the transmission of diverse information, such as the cost of the dinner or the timing of the arrangement.
A notable aspect of the introduced protocol is its adaptability to both localized and distributed versions of the Dining Cryptographers problem. The localized scenario involves all cryptographers physically gathering at the same spatial location, like a restaurant, simultaneously. In contrast, the distributed scenario accommodates cryptographers located in different places, engaging in a virtual dinner at the same time.
In terms of implementation, the protocol ensures uniformity as all cryptographers employ identical private quantum circuits. This design establishes a completely modular quantum system where all modules are identical. Additionally, each private quantum circuit exclusively employs the widely used Hadamard and CNOT quantum gates, facilitating straightforward implementation on contemporary quantum computers.
This article is organized as follows. Section 1 gives a comprehensive introduction to the subject and points to the most relevant works of the literature. Section 2 contains the necessary terminology that facilitates the exposition of the introduced protocol. Section 3 presents the rationale and the intuition behind the new protocol, while Section 4 provides an extensive and analytical presentation of the inner workings of the new quantum protocol. Section 5 summarizes and discusses the merits of this work.
2. Background Notions
Quantum physics reveals some astonishing and counterintuitive features that go beyond the limits of classical physics and common sense. One of these amazing phenomena is entanglement, which not only puzzles us but also offers great opportunities for achieving tasks that are hard or even impossible in the classical realm. Entanglement occurs in composite quantum systems, which have at least two subsystems, often located at different places. For more information, including mathematical formulation, we refer the interested reader to standard textbooks, such as [22,23,24]. Maximal entanglement can be easily and intuitively extended to the case of multipartite systems. Perhaps, the most well-known form of maximal entanglement found in composite systems of n qubits, where , is the state. In such a case, the composite quantum system is made of n separate qubits and each subsystem is just a single qubit. The astonishing fact is that the entangled qubits can very well be spatially separated, something that leads to intriguing possibilities, such as quantum teleportation and superdense coding [25,26]. The state is a maximally entangled state, meaning that the entanglement between the n qubits is as strong as it can be. For more details regarding multipartite entanglement measures of GHZ states, we refer to the recent works [27,28,29] and to [30] for multiplex multilayer networks. Mathematically, the situation can be expressed as follows:
where the subscript , denotes the ith qubit.
Contemporary quantum computers are powerful enough (see for instance the recent IBM quantum computers [31,32]) to be able to generate GHZ states utilizing standard quantum gates like the Hadamard and CNOT gates. Furthermore, the circuits responsible for producing these states exhibit high efficiency, requiring only steps for the state, as demonstrated in [33].
The full power of the introduced protocol requires a more complex and versatile quantum system where each subsystem is a quantum register , , containing m qubits. The distinguishing characteristic of this setting is that corresponding qubits across all n registers are entangled in the state. This concept is formally captured by the Symmetric Bitwise Entanglement Distribution Scheme. Definition 1 provides the details.
Definition 1.
The Symmetric Bitwise Entanglement Distribution Scheme, denoted by , specifies that
- There are n quantum registers ;
- Each register contains m qubits;
- The n qubits in the position of every register, , are entangled together in the state.
The n quantum registers can be either situated in the same locality or spatially distributed, depending on whether or not the registers are in the same or different geographical locations in space.
The global state of the composite system is given by the following equation.
In writing Formula (2), which is proved in [34], we take advantage of the standard notation explained below.
- is the binary set .
- To distinguish bit vectors from bits, we write bit vectors in boldface. A bit vector of length m corresponds to a sequence of m bits: . In the special case where all bits are zero, i.e., , we have the zero bit vector, denoted by .
- In this setting, a bit vector stands for the binary representation of one of the basis kets that form the computational basis of the Hilbert space at hand.
- To eliminate any source of ambiguity, we rely on the indices , to emphasize that is the state of the ith quantum register.
Figure 1 illustrates this setting, with the corresponding qubits belonging to the same n-tuple colored identically. This composite system is made of qubits as each of the n registers holds m qubits. We point out that it does not matter in the least whether the registers are all in the same place or are all in different spatial locations. The power of the entanglement effect, stemming from the mn-tuples, will instill the necessary correlation, irrespective of whether the composite system is localized or entirely distributed. It is precisely this unique effect of entanglement that allows us to envision the whole setting as a unified system.
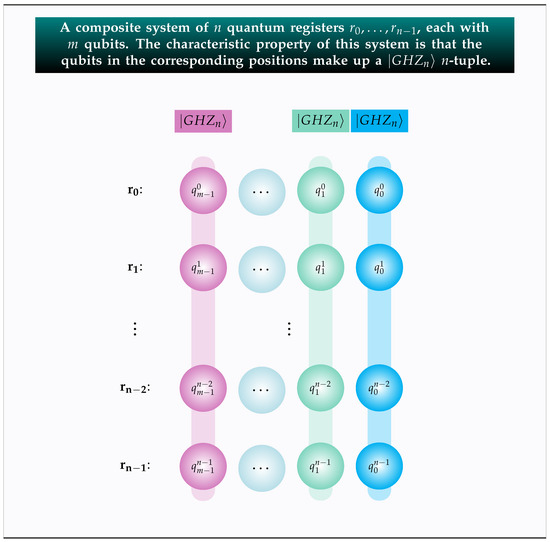
Figure 1.
This figure draws the n qubits that populate the same position in the registers with the same color so as to emphasize that they belong to the same n-tuple.
The forthcoming mathematical analysis will also use the important formula shown below that expresses the m-fold Hadamard transform of an arbitrary basis ket. Its proof is omitted because it can be easily found in most standard textbooks, e.g., [22,35].
The expression in (3) denotes the inner product modulo 2 operation. The inner product modulo 2 takes as inputs two bit vectors and outputs their inner product. Specifically, if and , then is computed as
where ⊕ is addition modulo 2. The inner product modulo 2 operation is characterized by a fundamental property whose application is central to many quantum algorithms. Consider any fixed element of ; if is different from , then, for half of , the outcome of the operation is 0 and, for the remaining half, the result of the operation is 1. The exception of is justified because, when , then, for all , . Following [36], we call this property the characteristic inner product (CIP) property.
For completeness, we also clarify that measurements are performed with respect to the computational basis .
3. The Scalable Quantum Protocol for the Dining Cryptographers Problem
In the current section, we introduce the novel entanglement-based scalable protocol that solves the Dining Cryptographers problem, SQDCP protocol for short. As is often carried out with most of the cryptographic protocols, to lighten up the presentation and make it more easy-going, we employ the format of a quantum game. This game is played by n cryptographers, one of whom is Alice, the star of the game. Alice has organized an official dinner for herself and her colleagues , …, . In the forthcoming small-scale examples, the roles of Alice’s colleagues will be assumed by other famous actors, namely, Bob, Charlie, and Dave. Nonetheless, in the formal presentation of the protocol and in order to stress its scalability for arbitrarily large values of n, the cryptographers will not be given particular names. Our n heroes, upon discovering that the dinner has been paid for, set out to discover whether it was one of them or their employer that paid the bill. The crucial thing here is that they must find out the truth in such a way so that the anonymity and privacy of all cryptographers are not compromised in any way whatsoever, and the identity of the cryptographer who paid remains unknown. In its essence, the Dining Cryptographers problem is a metaphor for anonymous and untraceable information transmission.
As we mentioned in the Introduction, the SQDCP protocol brings three main novelties to the table. So, before we begin its description in earnest, let us explain them in detail.
- (N1)
- Scalability. In the SQDCP protocol, the notion of scalability encompasses both parameters n and m. The number of cryptographers n can be any large positive integer. In addition to the scalability of players, our protocol can seamlessly scale in terms of the amount of anonymous information it conveys. Initially, the Dining Cryptographers problem was about just one bit of information, namely, whether or not one of the cryptographers paid for the dinner. In the SQDCP protocol, the number m of qubits in each register can also be any large positive integer. This number reflects the amount of information that can be transmitted. For instance, the cryptographer that actually paid the bill may also disclose how much it cost or when the arrangement was made, etc.
- (N2)
- Local and Distributed Mode. In its initial formulation in [1] and in the subsequent treatments, the cryptographers’ dinner was a localized event, in the sense that all cryptographers were together at the same spatial location at a specific point in time. The protocol introduced in this work can address not only this localized situation but also a distributed version of the Dining Cryptographers problem, in which the cryptographers are in different spatial locations.
- (N3)
- Uniformity and Ease of Implementation. All cryptographers employ identical quantum circuits, that is, the quantum implementation is completely modular, with all modules being the same. Furthermore, each quantum circuit can be easily implemented by a contemporary quantum computer because it only uses the ubiquitous Hadamard and CNOT quantum gates.
Given the above considerations, the following two definitions state formally the localized and the distributed versions of the Dining Cryptographers problem.
Definition 2
(Localized Setting). The localized setup is described below.
- Alice gathers together her cryptographer colleagues , …, for a friendly dinner in a nearby restaurant.
- For all n players, the dinner event takes place simultaneously and at the same location.
- Each player employs a quantum circuit where she secretly embeds the desired information, namely, whether or not she paid for the dinner.
- Upon measuring their quantum registers and publicly combining the obtained results, all the players know whether the dinner was paid for by one of them or by their employer, and, possibly, some additional information, e.g., the cost of the dinner or the date of the payment, etc.
- The identity of the one who paid the bill remains unknown to all other cryptographers.
One of the most useful traits of entanglement is that entangled subsystems are intertwined despite being spatially separated. This is the key that enables the effective operation of many distributed quantum protocols. The SQDCP protocol also takes advantage of entanglement in order to achieve the desired outcome in a completely distributed setting.
Definition 3
(Distributed Setting). Let us now envision a more general situation.
- Alice and her cryptographer colleagues , …, have made arrangement for dinner.
- There is a complication now compared to the previous case because all n agents reside at different geographical locations.
- Nevertheless, they are determined to dine at the same time, albeit in different restaurants, and be in constant audio and visual contact via teleconference.
- Each player employs a local quantum circuit where she secretly embeds the desired information, namely, whether or not she paid for the dinner.
- Upon measuring their quantum registers, they publicly exchange their measurements via classical channels. Subsequently, each player uses the received results to find out whether the dinner was paid for by one of them or by their employer, and, possibly, some additional information.
- The identity of the one who paid the bill remains unknown to all other cryptographers.
The task at hand is to devise a quantum protocol that can seamlessly operate in both localized and distributed modes, and reveal the required information while guaranteeing the privacy and anonymity of the generous cryptographer. Before we proceed with the detailed description of the protocol, it will be expedient to make some clarifications, to avoid any possible confusion.
- Although there is no theoretical limitation on the number n of cryptographers that can be an arbitrarily large integer, contemporary quantum apparatus may impose constraints to the generation of tuples, whenever n exceeds some threshold.
- We assume that, prior to the execution of the SQDCP protocol, certain arrangements have taken place among the cryptographers regarding the amount and nature of the desired information. This is necessary in order to fix the number of m, corresponding to the amount of information, and the proper interpretation of the outcome.
- In the distributed version, we also assume the existence of pairwise authenticated channels that enable the transmission of classical information.
Example 1.
This example features the four cryptographers Alice, Bob, Charlie, and Dave having dinner in both the localized and the distributed scenario. Common to both scenarios is the fact that their input quantum registers are entangled according to the Symmetric Bitwise Entanglement Distribution Scheme, explained in Definition 1. In this particular example, n = 4 and, if we assume that the desired information also includes the amount of money paid for the dinner, we may also take m equal to 4. Hence, the final outcome of the protocol will be m bits expressing the binary representation of the cost of the dinner, say in euros (EUR). This small-scale example requires four tuples evenly and uniformly distributed among the four players.
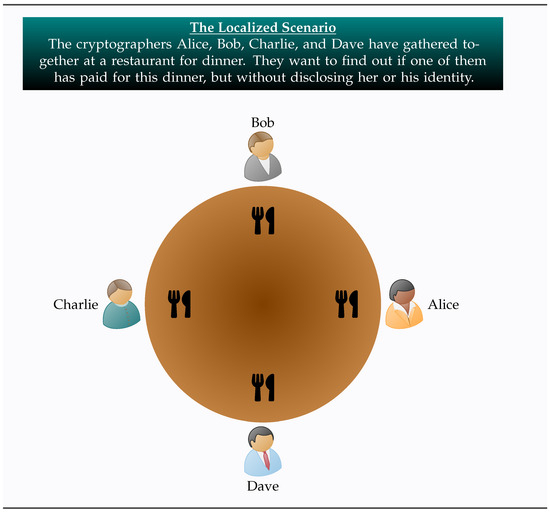
When the dinner event takes place at the same restaurant at the same time for all four cryptographers, we have the standard version of the Dining Cryptographers problem. This is what we refer to as the localized scenario, which is illustrated in Figure 2.

Figure 2.
This figure visualizes an example of the localized scenario. Four cryptographers, Alice, Bob, Charlie, and Dave, have gathered together at a restaurant for dinner. They want to find out if one of them has paid for this dinner, but without disclosing her or his identity.
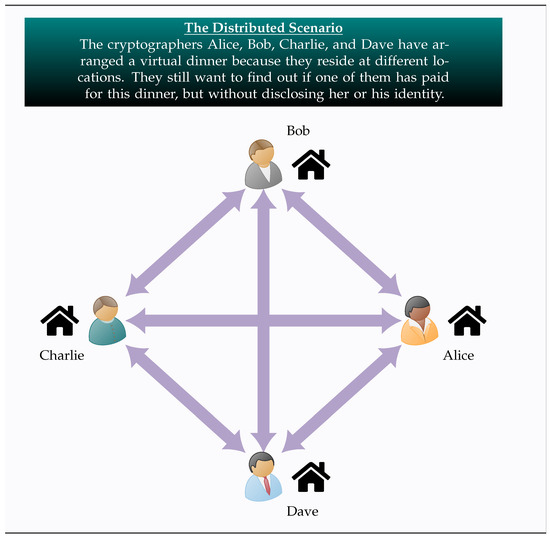
In addition to the standard approach, the fact that the quantum registers are entangled opens up the possibility of implementing the SQDCP protocol even in the case where the cryptographers are spatially separated. In such a scenario, they are having a virtual dinner at the same time, but now each of them resides at a different location, as depicted in Figure 3.

Figure 3.
The above figure illustrates an example of the distributed scenario. Four cryptographers, Alice, Bob, Charlie, and Dave, have arranged a virtual dinner using state-of-the-art technology because they are at different geographical locations. Of course, they still want to find out if one of them has paid for this dinner, but without disclosing her or his identity.
Having explained the general philosophy and intuition behind our protocol, we proceed to its detailed presentation in the next section.
4. Execution of the SQDCP Protocol in Three Phases
For pedagogical reasons, we may conceptually view the protocol as evolving in three phases. Before we begin in earnest, let us point out that our protocol does not violate the no-cloning theorem [37]. The state of the distributed tuples is known to all cryptographers participating in the protocol. At a subsequent phase, the cryptographers embed their private information into the distributed entangled state of the system.
4.1. Entanglement Distribution Phase
The first phase of the protocol is the entanglement distribution phase, during which the following actions take place. In the subsequent analysis, the number of qubits in every input quantum register is designated by m. This number is taken to be an appropriately chosen large positive integer, capable of conveying the amount of information desired. In the rest of this article, we mainly consider the case where this information is the amount of money paid for the dinner.
- (ED1)
- Alice or perhaps a third party, trusted by all cryptographers, generates a sequence of m tuples, qubits in total, which are necessary for the execution of the protocol and the private transmission of the required information. For the SQDCP protocol, the exact source responsible for the production of the tuples is not important; the only thing that matters is that they are faithfully created and uniformly distributed among the cryptographers.
- (ED2)
- Say for convenience that in every tuple the qubits are numbered from 0 to . Their distribution adheres to the following pattern, which guarantees the even and uniform distribution of entanglement among the cryptographers.
- Alice stores in her input register, denoted by in Figure 4, the qubit of each tuple.
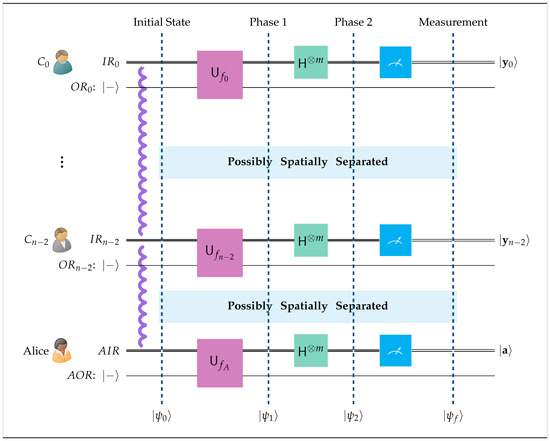 Figure 4. The above figure shows the composite quantum circuit used by the dining cryptographers, composed of the individual local circuits Alice and her colleagues possess. Even if these local circuits are spatially separated, they still constitute one composite system because they are linked due to entanglement. The state vectors , , , and describe the evolution of this composite system.
Figure 4. The above figure shows the composite quantum circuit used by the dining cryptographers, composed of the individual local circuits Alice and her colleagues possess. Even if these local circuits are spatially separated, they still constitute one composite system because they are linked due to entanglement. The state vectors , , , and describe the evolution of this composite system. - Cryptographer , , stores in her input register, symbolized by in Figure 4, the qubit of each tuple.
- (ED3)
- In addition to her input register, Alice utilizes a single-bit output register designated by in Figure 4, which is initialized at state . Likewise, all her cryptographer colleagues , , possess a similar single-bit output register denoted by in Figure 4. The output registers are crucial for the embedding of private information into the entangled state of the composite circuit.
All cryptographers operate privately and secretly on their own quantum circuits. The important remark in this respect is that all these circuits are identical. In closing this subsection, we point out that the entire algorithm hinges upon the existence of entanglement and, therefore, it is very important to verify that all the cryptographers’ quantum registers are appropriately entangled. Given its significance, this task has undergone thorough scrutiny in the existing literature. Our protocol adheres to the sophisticated methodologies outlined in prior works, including [38,39,40,41,42,43]. Hence, to preclude redundant exposition, we direct the reader to the previously mentioned bibliography for all the details essential for the successful validation of the entanglement.
4.2. Private Information Embedding Phase
During this phase, the cryptographer who actually paid for the dinner, assuming that this was indeed the case, is able to privately and secretly embed this information, perhaps along with any additional related information. In particular, the quantum circuit outlined in Figure 4 operates as described below.
- (PIE1)
- If it was Alice who secretly paid for the dinner and the binary representation of the amount she paid is in euros (EUR), then she will insert into the global entangled state of the circuit via her private unitary transform . Since is only known to her, the required information will be embedded secretly, privately, and none will be able to be trace it back to Alice.
- (PIE2)
- If Alice did not pay for the dinner, then she uses the zero bit vector in her private unitary transform , which in effect leaves the global state of the system unchanged.
- (PIE3)
- Entirely analogously, if it was cryptographer , , who secretly paid for the dinner and the binary representation of the amount paid is , then she will insert into the global entangled state of the circuit via her private unitary transform . Since is only known to cryptographer , this information will be embedded secretly, and privately, and none will be able to trace it back to . Obviously, if did not pay for the dinner, then she uses the zero bit vector in her private unitary transform .
- (PIE4)
- The quantum part of the protocol is completed when the cryptographers measure their input registers. The obtained measurements are added together using addition modulo 2, i.e., they are XOR-ed together. The final outcome gives the desired information in the following sense.
- ▸
- If is nonzero, this means that the dinner was paid by one of the cryptographers. We also find out how much the dinner cost, because is the binary representation of the cost in euros. The identity of the cryptographer who paid cannot be inferred from ; it remains unknown and untraceable.
- ▸
- If is the zero bit vector , this means that the dinner was paid for by their employer and not by one of the cryptographers.
- (PIE5)
- The SQDCP protocol will work even if all the players are in different geographical locations. This is because, even if the quantum input registers are spatially separated, they still constitute one composite distributed quantum system due to the strong correlations among their qubits originating from the entanglement. The only difference in the distributed case is that each cryptographer must communicate the obtained measurements to each other cryptographer using pairwise authenticated classical channels.
The whole setup is shown in Figure 4. For consistency, all quantum circuits in this work follow the Qiskit [44] convention in the ordering of their qubits, by placing the least significant qubit at the top of the figure and the most significant at the bottom.
In the graphical outline of the above quantum circuit, the notation employed is explained below.
- is Alice’s input register.
- is the input register of cryptographer , .
- In total, there are n input registers, each containing m qubits. The corresponding qubits in each of the n registers are entangled in the state.
- is Alice’s output register.
- is the output register of cryptographer , .
- All output registers contain just a single qubit in the state.
- is Alice’s unitary transform.
- is the unitary transform of cryptographer , .
- is the m-fold Hadamard transform.
The initial state of the distributed quantum circuit of Figure 4 is denoted by , which, using (2), can be written as
To eliminate any potential ambiguity, we rely on the subscripts A and , to indicate whether the kets refer to Alice or cryptographer i.
Alice and the other cryptographers start the execution of the SQDCP protocol by acting on their individual quantum circuits via their private unitary transforms and , . By doing so, each one of them can embed the required private information into the entangled state of the composite system. We stress this important fact: any one of them, by using her individual and local quantum circuit, can encode the private information that must be communicated to the other players into the entangled input registers of the composite, and potentially distributed, circuit. The unitary transforms and , , are based on the private and secret functions and , , which are known only to the corresponding cryptographer. Their formal definition is given below.
The unitary transforms follow the typical scheme →. Therefore, in view of (8) and (9), they can be explicitly written as
The combined effect of the unitary transforms results in the system getting into the state described below.
Therefore, at the end of Phase 1, the cryptographer who paid for the dinner has embedded the private information known only to her into the entangled state of the composite quantum circuit in a completely untraceable way. Now, it remains to decipher this information, so that it becomes known to all other cryptographers. This is explained in the following subsection.
4.3. Deciphering Phase
To decipher the embedded private information, Alice and the rest of the cryptographers apply the m-fold Hadamard transform to their input registers, as shown in Figure 4. Consequently, at the end of Phase 2, the state of the system has become :
By invoking relation (3), we may analyze , , …, further.
Via the above substitutions, can be cast in the alternative form shown below.
Although the above equation seems complicated, they can be greatly simplified if we apply the characteristic inner product property outlined in relations (5) and (6). Let us recall what the characteristic inner product property implies in this situation.
- If or, equivalently, ≠, the sum ⋯ appearing in (14) becomes just 0.
- If, on the other hand, or, equivalently, =, the sum ⋯ becomes ⋯.
The above explanation allows us to cast in the following reduced form.
where
Using the terminology introduced in [34,45], we refer to relation (16) as the Fundamental Correlation Property that intertwines the input registers of the dining cryptographers. This relation is the aftermath of the initial entanglement among all the input registers. At the end of Phase 2, the cryptographer who paid for the dinner has embedded all the relevant private information in the global state of the composite quantum circuit, which has appeared through this constraint on the contents of the input registers.
The quantum part of the SQDCP protocol is over when the cryptographers measure their input registers in the computational basis. By this action, the state of the composite system collapses to the final state that has the following form.
Let us emphasize that all the above equations hold true in both the localized and the distributed versions of the SQDCP protocol because their validity stems from the initial entanglement among all the input registers. As long as entanglement is present, the distance among the dining cryptographers plays no role. Furthermore, another profound consequence of entanglement is that the precise temporal sequence of measurements performed by Alice and her cryptographer colleagues is immaterial. The soundness of Equation (18) does not presuppose that all players measure their input registers at exactly the same moment. For instance, let us, momentarily, consider the simplest manifestation of maximal entanglement in the form of an EPR pair in the state. If Alice and Bob who are spatially separated possess one qubit of the pair each, and Alice measures her qubit first, she will know with probability the result of Bob’s subsequent measurement of his qubit. Symmetrically, if Bob measures his qubit first, he will know with probability the result of Alice’s subsequent measurement of her qubit. Obviously, the same situation is observed if both Alice and Bob measure their respective qubits simultaneously (ignoring relativistic considerations). The temporal ordering of the measurements does not change the constraint underlying this simple entanglement, namely, that upon measurement both qubits will collapse in the same state. Although, in our protocol, the entanglement assumes a much more complicated form and the resulting constraint, as expressed by (18), is more elaborate, the underlying physical principle is exactly the same. That is, the measurement of the players’ input registers may take place in any arbitrary order, sequentially, or even simultaneously. The resulting contents measured by Alice and cryptographers , …, , respectively, will satisfy the entanglement constraint (18).
The protocol completes the task of actually decrypting the embedded private information through the following steps.
- (D1)
- Every cryptographer communicates to every other cryptographer the measured contents of her input register. That is, Alice sends to her cryptographer colleagues, and each , , sends to Alice and every other cryptographer.
- (D2)
- In a localized setting, this step is quite trivial. In a distributed setting, it is also easily achievable, as it only requires the use of pairwise authenticated classical communication channels.
- (D3)
- At this point, every player knows all bit vectors . This allows each cryptographer to compute the modulo 2 sum , which, according to (18), produces the modulo 2 sum .
- (D4)
- The modulo 2 sum conveys the information the cryptographers wanted to uncover in the first place. Here is why.
- In case none of the cryptographers paid for the dinner, then, according to (PIE2) and (PIE3), . Consequently, their modulo 2 sum is , which means that the computed modulo 2 sum is also . Hence, the cryptographers infer that the dinner was paid for by their employer.
- In case , , paid for the dinner a certain amount of money, then, considering (PIE1) – (PIE3), , the binary representation of this amount, is nonzero, whereas and all other , , are zero. This implies that the computed modulo 2 sum is . Therefore, the cryptographers infer that it was one of them who paid for the dinner and, as an added bonus, they also get to know how much the dinner cost. Obviously, the same argument goes verbatim in case it was Alice who paid for the dinner.
- (D5)
- The above explanation also shows that the original source of the information remains unknown and untraceable. The private information, be it or some , , has been absorbed into the sum and there is no way that it can be retrieved.
Example 2.
The present example is a continuation of our previous Example 1. It does not matter whether they are physically together around the same table or if they are in different geographical locations dining virtually; the SQDCP Protocol will go through in both settings.
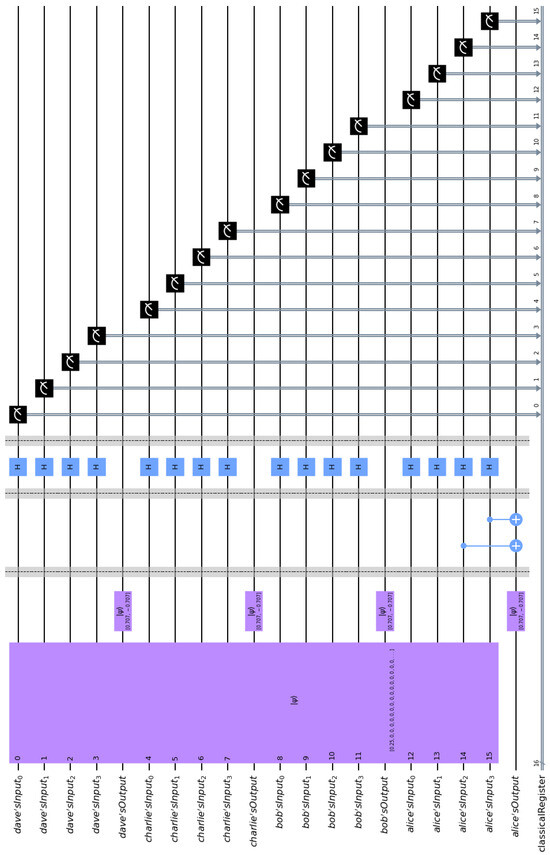
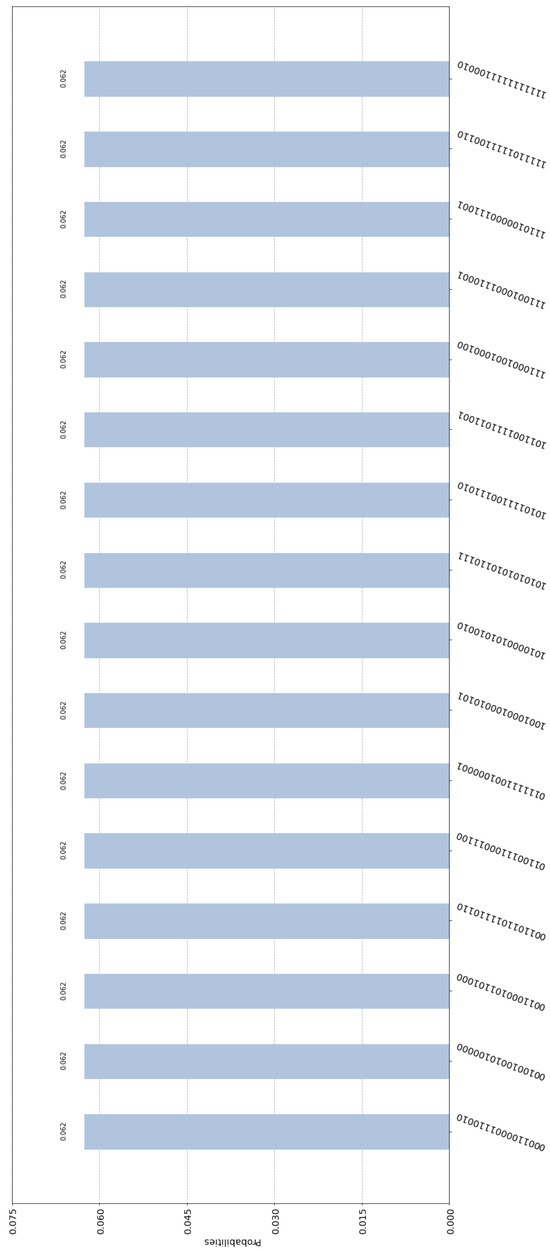
First, let us consider the case where one of the cryptographers, Alice, paid for the dinner. If Alice paid say EUR 12, then she embeds the binary representation of 12, namely, = 1100 in the entangled state of the composite circuit. This is easily achieved via CNOT gates. If we implement the general quantum circuit shown in Figure 4 in Qiskit, we end up with the specific implementation depicted in Figure 5. By measuring their input registers, Alice, Bob, Charlie, and Dave get one of the 216 = 65,536 equiprobable outcomes. For obvious technical limitations, we cannot show all these outcomes, since this would result in an unintelligible figure. Hence, we depict only 16 of them in Figure 6. It is straightforward to check that every possible outcome satisfies the Fundamental Correlation Property and verifies Equations (16) and (18). For example, we may examine the label of the first bar of the histogram contained in Figure 6, which is 0001 1000 0111 0010. This means that upon measurement the contents of Alice, Bob, Charlie, and Dave’s input registers are = 0001, = 1000, = 0111, and = 0010, respectively. These contents are shared among the four cryptographers, according to (D1) and (D2), and become common knowledge to all of them. Finally, they XOR them together to uncover the secret information, i.e., = 1100, which leads them to infer that one of them paid EUR 12 for the dinner. The crucial thing is that neither the measured contents , , , and of the input registers, nor the final private information can reveal the identity of the cryptographer who paid the bill.

Figure 5.
The above quantum circuit simulates the SQDCP protocol corresponding to the case where Alice paid for the dinner, as outlined in Example 2.

Figure 6.
Some of the possible measurements and their corresponding probabilities for the circuit in Figure 5.
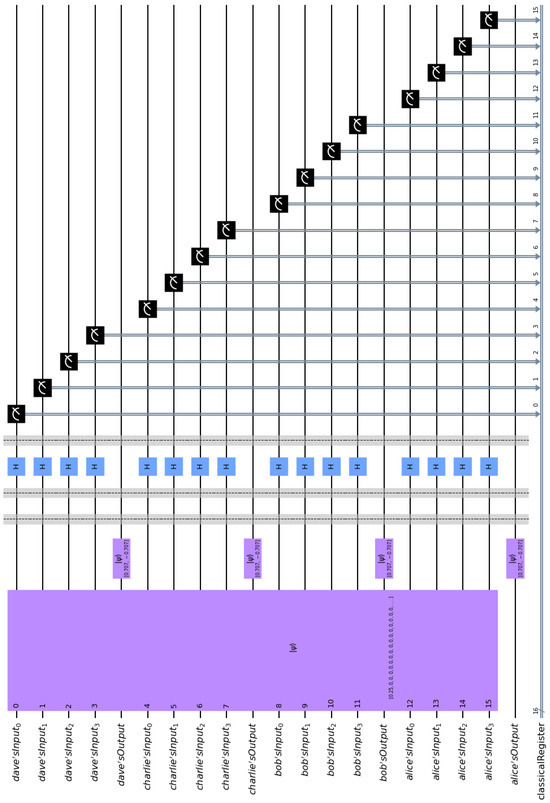
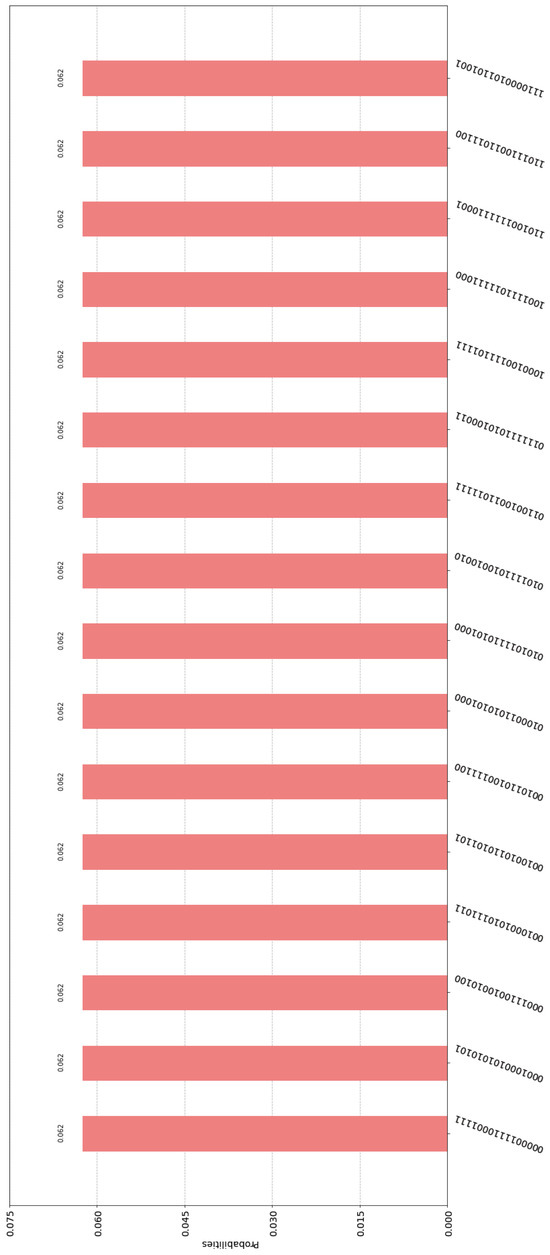
Let us also briefly examine the case where none of the cryptographers paid for the dinner. In such a situation all cryptographers embed the zero bit vector in the entangled state of the composite circuit, i.e., = 0000. The quantum circuit in this case is shown in Figure 7. Again, it is very easy to ascertain that every possible outcome satisfies the Fundamental Correlation Property and verifies Equations (16) and (18). For example, we may examine the label of the third bar of the histogram contained in Figure 8, which is 0001 1100 1001 0100. This means that the contents of Alice, Bob, Charlie, and Dave’s input registers are = 0001, = 1100, = 1001, and = 0100, respectively. These contents are shared among the four cryptographers, according to (D1) and (D2), and become common knowledge to all of them. Finally, they XOR them together to uncover the secret information, i.e., = 0000, from which they deduce that none of them paid for the dinner, so it must have been their employer.

Figure 7.
The above quantum circuit simulates the SQDCP protocol corresponding to the case where none of the four cryptographers paid for the dinner, as outlined in Example 2.

Figure 8.
Some of the possible outcomes and their corresponding probabilities for the circuit in Figure 7.
5. Discussion and Conclusions
This work introduces the novel entanglement-based SQDCP protocol for solving the Dining Cryptographers problem. The proposed protocol relies on maximally entangled tuples to achieve its goal. The main incentive was to offer scalability in terms of both the number of cryptographers n and the amount of anonymous information it conveys, measured by the number m of qubits contained in each quantum register. The number of cryptographers n can be any large positive integer. In addition to scalability in the number of participants, our protocol can seamlessly scale in terms of the amount of anonymous information it transmits. Originally, the Dining Cryptographers problem involved only one bit of information, namely, whether one of the cryptographers paid for the dinner. In the proposed SQDCP protocol, the number m of qubits in each register can also be any arbitrarily large positive integer. This number reflects the amount of information that can be transmitted. For instance, the cryptographer who actually paid the bill may also disclose how much it cost or when the arrangement was made, etc.
Another noteworthy feature of the protocol introduced in this work is its ability to address both a localized and distributed version of the Dining Cryptographers problem. The localized scenario involves all cryptographers being together at the same spatial location, i.e., at the same restaurant, at a specific point in time. The distributed scenario involves cryptographers being in different spatial locations but having dinner at the same time virtually.
We give a comparative assessment of the SQDCP protocol with respect to previous protocols designed to solve the same problem in Table 1. The comparison emphasizes some of the most important qualitative and quantitative traits of the protocols. The results contained in Table 1 corroborate the novelties incorporated in the SQDCP protocol.

Table 1.
Comparison between SQDCP and previous similar quantum protocols.
Finally, in terms of the actual implementation of the protocol, we point out that all cryptographers employ private quantum circuits that are identical. This achieves a completely modular quantum system, with all distinct modules being the same. Furthermore, each private quantum circuit utilizes only the ubiquitous Hadamard and CNOT quantum gates, making them easily implemented on contemporary quantum computers.
Author Contributions
Conceptualization, T.A. and P.K.; methodology, T.A.; validation, P.K.; formal analysis, T.A.; investigation, P.K.; writing—original draft preparation, T.A. and P.K.; writing—review and editing, T.A. and P.K.; visualization, P.K.; supervision, T.A.; project administration, T.A. and P.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chaum, D. The dining cryptographers problem: Unconditional sender and recipient untraceability. J. Cryptol. 1988, 1, 65–75. [Google Scholar] [CrossRef]
- Chaum, D.L. Untraceable electronic mail, return addresses, and digital pseudonyms. Commun. ACM 1981, 24, 84–90. [Google Scholar] [CrossRef]
- Von Ahn, L.; Bortz, A.; Hopper, N.J. k-anonymous message transmission. In Proceedings of the 10th ACM Conference on Computer and Communications Security, ACM 2003, Washington, DC, USA, 27–30 October 2003. [Google Scholar] [CrossRef]
- Boykin, P.O. Information Security and Quantum Mechanics: Security of Quantum Protocols. arXiv 2002, arXiv:quant-ph/0210194. [Google Scholar] [CrossRef]
- Christandl, M.; Wehner, S. Quantum Anonymous Transmissions. In Advances in Cryptology—ASIACRYPT 2005, Proceedings of the 11th International Conference on the Theory and Application of Cryptology and Information Security, Chennai, India, 4–8 December 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 217–235. [Google Scholar] [CrossRef]
- Bouda, J.; Sprojcar, J. Anonymous Transmission of Quantum Information. In Proceedings of the 2007 First International Conference on Quantum, Nano, and Micro Technologies (ICQNM’07), Guadeloupe, French Caribbean, 2–6 January 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Brassard, G.; Broadbent, A.; Fitzsimons, J.; Gambs, S.; Tapp, A. Anonymous Quantum Communication; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; pp. 460–473. [Google Scholar] [CrossRef]
- Broadbent, A.; Tapp, A. Information-Theoretic Security without an Honest Majority; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; pp. 410–426. [Google Scholar] [CrossRef]
- Shimizu, K.; Tamaki, K.; Fukasaka, H. Two-way protocols for quantum cryptography with a nonmaximally entangled qubit pair. Phys. Rev. A 2009, 80, 022323. [Google Scholar] [CrossRef]
- Wang, T.; Wen, Q.; Zhu, F. Quantum communications with an anonymous receiver. Sci. China Phys. Mech. Astron. 2010, 53, 2227–2231. [Google Scholar] [CrossRef]
- Shi, R.; Su, Q.; Guo, Y.; Lee, M.H. Quantum Secure Communication Based on Nonmaximally Entangled Qubit Pair and Dining Cryptographers Problem. In Proceedings of the 2011 IEEE 10th International Conference on Trust, Security and Privacy in Computing and Communications, Changsha, China, 16–18 November 2011; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Wang, Q.L.; Zhang, K.J. Security analysis and improvement of the dining cryptographer problem-based anonymous quantum communication via non-maximally entanglement state analysis. Int. J. Theor. Phys. 2014, 54, 106–115. [Google Scholar] [CrossRef]
- Rahaman, R.; Kar, G. GHZ correlation provides secure Anonymous Veto Protocol. arXiv 2015, arXiv:1507.00592. [Google Scholar] [CrossRef]
- Hameedi, A.; Marques, B.; Muhammad, S.; Wiesniak, M.; Bourennane, M. Experimental Quantum Solution to the Dining Cryptographers Problem. arXiv 2017, arXiv:1702.01984. [Google Scholar] [CrossRef]
- Li, Y.; Yu, C.; Wang, Q.; Liu, J. Quantum communication for sender anonymity based on single-particle with collective detection. Phys. Scr. 2021, 96, 125118. [Google Scholar] [CrossRef]
- Mishra, S.; Thapliyal, K.; Parakh, A.; Pathak, A. Quantum anonymous veto: A set of new protocols. EPJ Quantum Technol. 2022, 9, 14. [Google Scholar] [CrossRef]
- Meyer, D.A. Quantum strategies. Phys. Rev. Lett. 1999, 82, 1052. [Google Scholar] [CrossRef]
- Eisert, J.; Wilkens, M.; Lewenstein, M. Quantum games and quantum strategies. Phys. Rev. Lett. 1999, 83, 3077. [Google Scholar] [CrossRef]
- Andronikos, T.; Sirokofskich, A. The Connection between the PQ Penny Flip Game and the Dihedral Groups. Mathematics 2021, 9, 1115. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 10–12 December 1984; IEEE Computer Society Press: Washington, DC, USA, 1984; pp. 175–179. [Google Scholar]
- Aguiar, L.S.; Borelli, L.F.M.; Roversi, J.A.; Vidiella-Barranco, A. Performance analysis of continuous-variable quantum key distribution using non-Gaussian states. Quantum Inf. Process. 2022, 21, 304. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Yanofsky, N.S.; Mannucci, M.A. Quantum Computing for Computer Scientists; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Wong, T.G. Introduction to Classical and Quantum Computing; Rooted Grove: Omaha, NE, USA, 2022. [Google Scholar]
- Ghosh, S.; Kar, G.; Roy, A.; Sarkar, D.; Sen, U. Entanglement teleportation through GHZ-class states. New J. Phys. 2002, 4, 48. [Google Scholar] [CrossRef]
- Muralidharan, S.; Panigrahi, P.K. Perfect teleportation, quantum-state sharing, and superdense coding through a genuinely entangled five-qubit state. Phys. Rev. A 2008, 77, 032321. [Google Scholar] [CrossRef]
- Qiang, W.C.; Sun, G.H.; Dong, Q.; Dong, S.H. Genuine multipartite concurrence for entanglement of Dirac fields in noninertial frames. Phys. Rev. A 2018, 98, 022320. [Google Scholar] [CrossRef]
- Dong, Q.; Mercado Sanchez, M.A.; Sun, G.H.; Toutounji, M.; Dong, S.H. Tripartite Entanglement Measures of Generalized GHZ State in Uniform Acceleration. Chin. Phys. Lett. 2019, 36, 100301. [Google Scholar] [CrossRef]
- Dong, Q.; Manilla, A.A.S.; Yáñez, I.L.; Sun, G.H.; Dong, S.H. Tetrapartite entanglement measures of GHZ state with uniform acceleration. Phys. Scr. 2019, 94, 105101. [Google Scholar] [CrossRef]
- Frolov, N.S.; Maksimenko, V.A.; Makarov, V.V.; Kirsanov, D.V.; Hramov, A.E.; Kurths, J. Macroscopic chimeralike behavior in a multiplex network. Phys. Rev. E 2018, 98, 022320. [Google Scholar] [CrossRef]
- Newsroom, I. IBM Unveils 400 Qubit-Plus Quantum Processor. 2022. Available online: https://newsroom.ibm.com/2022-11-09-IBM-Unveils-400-Qubit-Plus-Quantum-Processor-and-Next-Generation-IBM-Quantum-System-Two (accessed on 3 February 2024).
- Gambetta, J. The Hardware and Software for the Era of Quantum Utility Is Here. 2023. Available online: https://www.ibm.com/quantum/blog/quantum-roadmap-2033 (accessed on 3 February 2024).
- Cruz, D.; Fournier, R.; Gremion, F.; Jeannerot, A.; Komagata, K.; Tosic, T.; Thiesbrummel, J.; Chan, C.L.; Macris, N.; Dupertuis, M.A.; et al. Efficient Quantum Algorithms for GHZ and W States, and Implementation on the IBM Quantum Computer. Adv. Quantum Technol. 2019, 2, 1900015. [Google Scholar] [CrossRef]
- Ampatzis, M.; Andronikos, T. Quantum Secret Aggregation Utilizing a Network of Agents. Cryptography 2023, 7, 5. [Google Scholar] [CrossRef]
- Mermin, N. Quantum Computer Science: An Introduction; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Andronikos, T.; Sirokofskich, A. One-to-Many Simultaneous Secure Quantum Information Transmission. Cryptography 2023, 7, 64. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Neigovzen, R.; Rodó, C.; Adesso, G.; Sanpera, A. Multipartite continuous-variable solution for the Byzantine agreement problem. Phys. Rev. A 2008, 77, 062307. [Google Scholar] [CrossRef]
- Feng, Y.; Shi, R.; Zhou, J.; Liao, Q.; Guo, Y. Quantum Byzantine Agreement with Tripartite Entangled States. Int. J. Theor. Phys. 2019, 58, 1482–1498. [Google Scholar] [CrossRef]
- Wang, W.; Yu, Y.; Du, L. Quantum blockchain based on asymmetric quantum encryption and a stake vote consensus algorithm. Sci. Rep. 2022, 12, 8606. [Google Scholar] [CrossRef]
- Yang, Z.; Salman, T.; Jain, R.; Pietro, R.D. Decentralization Using Quantum Blockchain: A Theoretical Analysis. IEEE Trans. Quantum Eng. 2022, 3, 4100716. [Google Scholar] [CrossRef]
- Qu, Z.; Zhang, Z.; Liu, B.; Tiwari, P.; Ning, X.; Muhammad, K. Quantum detectable Byzantine agreement for distributed data trust management in blockchain. Inf. Sci. 2023, 637, 118909. [Google Scholar] [CrossRef]
- Ikeda, K.; Lowe, A. Quantum protocol for decision making and verifying truthfulness among N-quantum parties: Solution and extension of the quantum coin flipping game. IET Quantum Commun. 2023, 4, 218–227. [Google Scholar] [CrossRef]
- Qiskit. Qiskit Open-Source Toolkit for Useful Quantum. Available online: https://www.ibm.com/quantum/qiskit (accessed on 3 February 2024).
- Andronikos, T.; Sirokofskich, A. An Entanglement-Based Protocol for Simultaneous Reciprocal Information Exchange between 2 Players. Electronics 2023, 12, 2506. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).