Abstract
Background/Objectives: This study aimed to examine how uncertainties in inertial properties and minimal sets of inertial parameters (MSIP) affect inverse-dynamics simulations of high-acceleration sport movements and to demonstrate that applying MSIP identified through the free vibration measurement method improves simulation accuracy. Methods: Monte Carlo simulations were performed for running, side-cutting, vertical jumping, arm swings, and leg swings by introducing uncertainties in inertial properties and MSIP. Results: These uncertainties significantly affect the joint torques and ground reaction forces and moments (GRFs&Ms), especially during large angular acceleration. The mass and longitudinal position of the center of gravity had strong effects. Subsequently, MSIP identified by our methods with free vibration measurement were applied to the same tasks, improving the accuracy of the predicted ground reaction forces compared with the standard regression-based estimates. The root mean square error decreased by up to 148 N. Conclusions: These results highlight that uncertainties in inertial properties and MSIP affected the calculated joint torques and GRFs&Ms, and combining experimentally identified MSIP with dynamics simulations enhances precision. These findings demonstrate that utilizing the MSIP from free vibration measurement in inverse dynamics simulations improves the accuracy of dynamic models in sports biomechanics, thereby providing a robust framework for precise biomechanical analyses.
1. Introduction
The inertial properties (mass, center of gravity, and inertia tensor) of objects are fundamental parameters used in motion control and simulation. In inverse dynamics simulations, the external and joint forces are calculated from the measured joint motions and the inertial properties of each link. In the forward dynamics simulations, the joint motions are derived from the external forces, joint forces, and inertial properties. Inertial properties are fundamental and critical input parameters in dynamic simulations and significantly influence the accuracy of the results [1,2,3,4]. In robotics and ergonomics, geometric parameters such as link lengths and the inertial properties of individual links are necessary when dealing with multibody dynamics models comprising multiple parts connected through joints. The demand for identifying the inertial properties of the links in the connected state has been increasing, owing to the constraint that the body segments cannot naturally be detached during measurement of the human body. The geometric parameters can easily be identified from static measurements. However, all inertial properties of individual links modeled with multiple links cannot be identified through link motions and interjoint torque or external force data because they are redundant to the multibody dynamics model. Therefore, the minimum dynamic parameters necessary to represent the multibody dynamics model have been defined and identified. These dynamic parameters are obtained by combining the geometric parameters and inertial properties of the counterpart elements, which are called the minimal set of inertial parameters (MSIP). Numerical and analytical methods for calculating the MSIP have been established [5,6,7,8], and various experimental identification methods have been developed.
Measuring representative body dimensions and estimating the inertial properties using regression equations are the simplest and most commonly used methods to obtain the inertial properties of human body segments. Regression equations are mainly derived from the direct inertial property measurements of corpse limbs [9,10]. Regression equations based on representative limb dimensions enable easy estimation; however, the databases lack comprehensive coverage of variations in height, weight, age, and ethnicity. This limitation reduces the accuracy of the estimations. Another method is to obtain both three-dimensional (3D) data and density using computed tomography [11,12] or magnetic resonance imaging [13,14,15,16]. However, owing to the high cost of equipment and examinations, it is unsuitable for frequent measurements or large-scale data collection.
The free vibration measurement method has been developed as a noninvasive approach to identify the MSIP of human body segments [17,18]. Compared with conventional identification methods that use motion and ground reaction forces and moments (GRFs&Ms), this method effectively uses prior identification of the whole body to identify MSIP in three dimensions with high accuracy without requiring complex movements. Nonetheless, the effect of this identification method on the dynamics simulations has not yet been demonstrated.
As described above, inertial properties and MSIP are fundamental and important parameters, and various identification methods have been developed. Because the inertial properties and MSIP of human limbs cannot be directly measured, direct evaluation is difficult. Therefore, the effect of the uncertainty of these inertial parameters on human dynamic simulations is a very important topic. Furthermore, as a method for verifying the identification results shown in Figure 1, it is common to measure the subject’s motion and GRFs&Ms, perform inverse dynamics simulations using the measured motion data and identified inertial properties or MSIP, and compare the GRFs&Ms obtained from the simulation with the measured values. Thus, dynamic simulations are also important in evaluating the identification results.
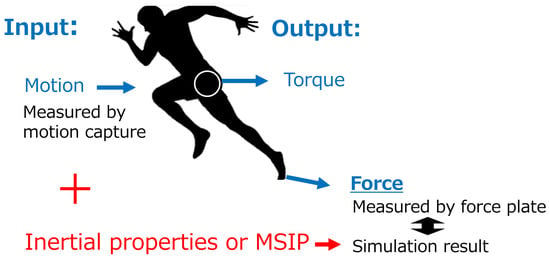
Figure 1.
Method for verifying the identification results.
Investigations into the effect of uncertainty in inertial properties on dynamic simulations have mainly been conducted for basic movements, such as walking [1,19,20,21,22,23,24,25,26]. Significant differences in the simulation results have been noted depending on the table data of the inertial properties used, highlighting the importance of accurately identifying inertial properties or the MSIP [1,4,19,22,25,27]. In high-acceleration motions that exceed the accelerations typically observed in daily activities such as normal walking, the effect of uncertainty in inertial properties becomes more pronounced as the acceleration increases. Therefore, investigations in high-acceleration motions are also important. However, research on high-acceleration motions primarily focuses on specific movements such as ski jumping [27] and arm flexion–extension movements [4]. In particular, how variations in inertial properties affect the simulation results of sports movements involving high acceleration remains unexplored. Therefore, elucidating the effect of the uncertainty in inertial properties or MSIP on the accuracy and reliability of inverse dynamics analysis in general sports movements is an important research issue.
This study clarifies the effect of uncertainty in inertial properties and MSIP on the results of inverse dynamic simulations in high-acceleration movements, such as those commonly seen in sports activities. After demonstrating the influence of these inertial parameters, the effect on the simulation accuracy of using MSIP identified using the free vibration measurement method is verified.
2. Materials and Methods
2.1. The Effect of Uncertainty in Inertial Properties and MSIP on Dynamic Simulation
2.1.1. Target Motions
Previous studies have shown that the maximum angular acceleration of the hip joint is approximately 40 and that of the knee joint is around 110 during normal walking. These values decrease even further when ascending or descending stairs or slopes [28]. The following movements were selected as high-acceleration motions that exceed these angular accelerations. Initially, running, side-cutting, and vertical jumping were chosen as common movements related to sports and recreational activities, which were addressed in a previous study [29]. In addition, arm swinging and leg swinging motions were selected as relatively simple yet high-acceleration movements. Furthermore, these five movements are also essential for evaluating the effectiveness of the MSIP identification method using the free vibration measurement approach. Conventional identification methods using ground reaction forces can estimate MSIP in the sagittal plane, such as during walking, but these parameters may not be valid when applied to movements outside this plane. However, the identification method using free vibration measurement enables the high-precision, three-dimensional identification of MSIP. The five selected movements were designed to represent different movement planes: running primarily involves forward motion in the sagittal plane, side-cutting involves lateral movements in the coronal plane, vertical jumping consists of upward and downward motions in the sagittal plane, arm swinging predominantly occurs in the transverse plane, and leg swinging includes both forward–backward and vertical motions in the sagittal plane. Since these movements engage different planes of motion, a three-dimensional identification approach is necessary to accurately capture the dynamics of these movements. Participant executed the selected movements, which were subsequently measured. These measurements then served as the basis for the analyses.
One healthy adult male (age 29 years, height 181.2 cm, weight 70.9 kg) participated in the experiments. The experimental procedures were approved by the Institute of Science Tokyo Human Subject Research Ethics Review Committee (Permit No. 2022104, 2024193), and the participant provided written informed consent. The participant performed the target movements while the motion and GRFs&Ms were measured using 8 Eagle EGL-500RT motion capture cameras from Motion Analysis Corporation (Rohnert Park, CA, USA) and 16 3D force plates from Kistler Group (Winterthur, Switzerland), as well as the markers shown in Figure 2. Markers were placed on the basis of anatomical landmarks recommended by the International Society of Biomechanics (ISB), and the coordinate system was established following its recommended guidelines [30,31]. The measured motions were used as the basis for the target movements. In this study, the human body was modeled as a set of 10 rigid bodies: torso, head, upper arms, forearms + hands, thighs, and lower legs + feet (Figure 3). The neck, shoulders, and hip joints are represented as spherical joints, whereas the elbows and knees are modeled as revolute joints, resulting in a 19-degree-of-freedom model. The revolute joints are assumed to rotate around the Z-axis. The relationship between each limb and the rigid body number is shown in Figure 3. To assess the uncertainty in inertial parameters, dividing the body into these 10 segments allows us to capture the major inertial parameters relevant to human movement without introducing excessive computational cost or measurement uncertainties. Further segmentation of smaller body parts would increase fidelity, but the influence of the inertial parameters of each segment would become smaller, and the phenomena would become harder to capture.

Figure 2.
Motion capture cameras, 3D force plates and markers.
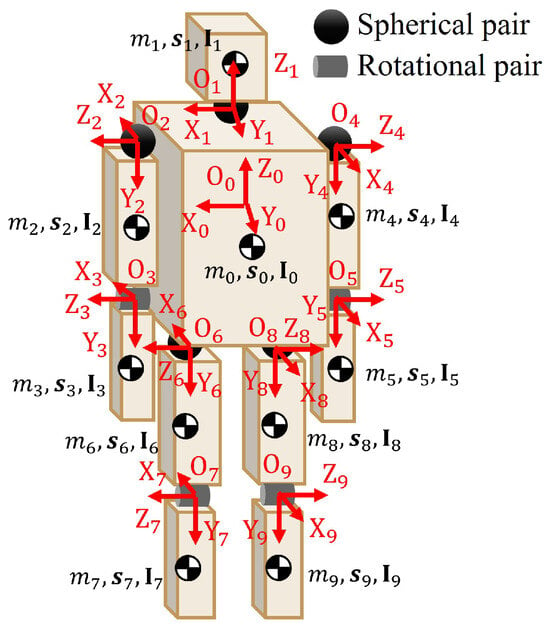
Figure 3.
Human model.
The motion capture was conducted at a sampling rate of 250 Hz. The time-series data of the marker positions were smoothed using a Gaussian weighted moving average filter. Then, the coordinate origins and axes of each segment were calculated from the 3D positions of the markers. The rotation matrices and translational displacements of each segment at each time point were determined from them. Velocities, accelerations, angular velocities, and angular acceleration were obtained by differentiating the rotation matrices and translational displacements using a zero-phase filter. The marker position data before and after interpolation, along with the calculated translational displacements, velocities, accelerations, rotational displacements, angular velocities, and angular accelerations for each motion, are presented herein. The rotational displacements were obtained by calculating the XYZ Euler angles from the rotation matrices.
The measured motion and calculated acceleration of running motion is illustrated in Figure 4. The interval shown is from the moment the left foot contacts the ground to when it leaves the ground. Then, for the side-cutting motion, the motion of repeatedly jumping sideways was adopted. The measured motion and calculated acceleration of side-cutting motion is displayed in Figure 5. The interval depicted begins from when the left foot makes contact with the ground for changing direction and continues until it leaves the ground. For the vertical jump motion, a movement of jumping vertically on one leg was executed. The measured motion and calculated acceleration of vertical jump motion is shown in Figure 6. The interval depicted ranges from crouching down by bending the left leg to the moment of pushing off, with the leg and the left foot leaving the ground. The measured motion and calculated acceleration of arm swing motion is presented in Figure 7, whereas those of leg swing motion is illustrated in Figure 8.
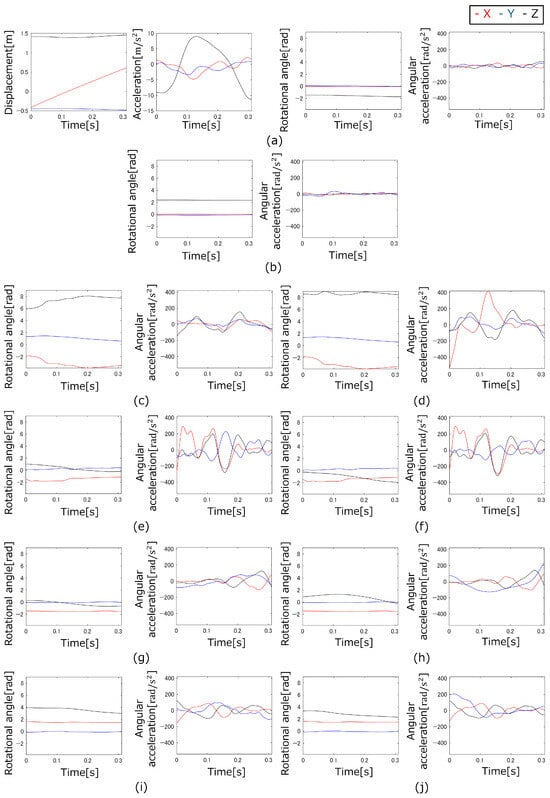
Figure 4.
Measured motion and calculated acceleration of running motion: (a) Trunk, (b) Head, (c) Right upper arm, (d) Right forearm + hand, (e) Left upper arm, (f) Left forearm + hand, (g) Right thigh, (h) Right lower leg + foot, (i) Left thigh, (j) Left lower leg + foot.
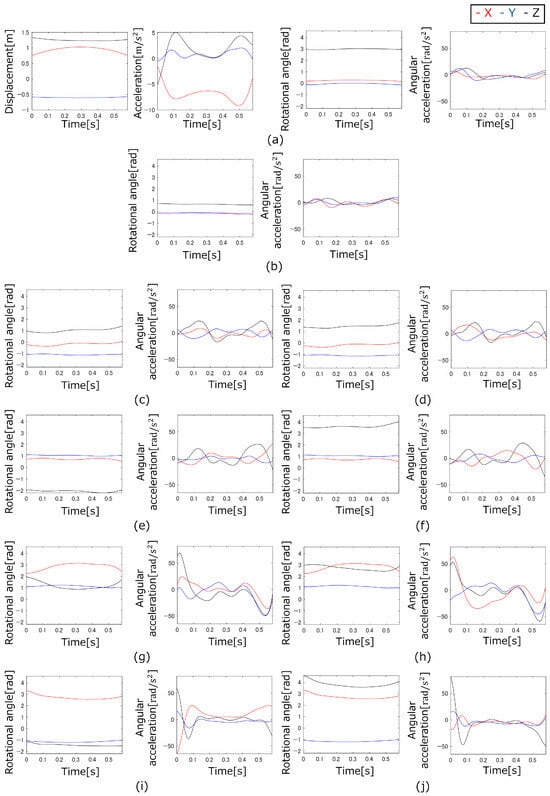
Figure 5.
Measured motion and calculated acceleration of side-cutting motion: (a) Trunk, (b) Head, (c) Right upper arm, (d) Right forearm + hand, (e) Left upper arm, (f) Left forearm + hand, (g) Right thigh, (h) Right lower leg + foot, (i) Left thigh, (j) Left lower leg + foot.
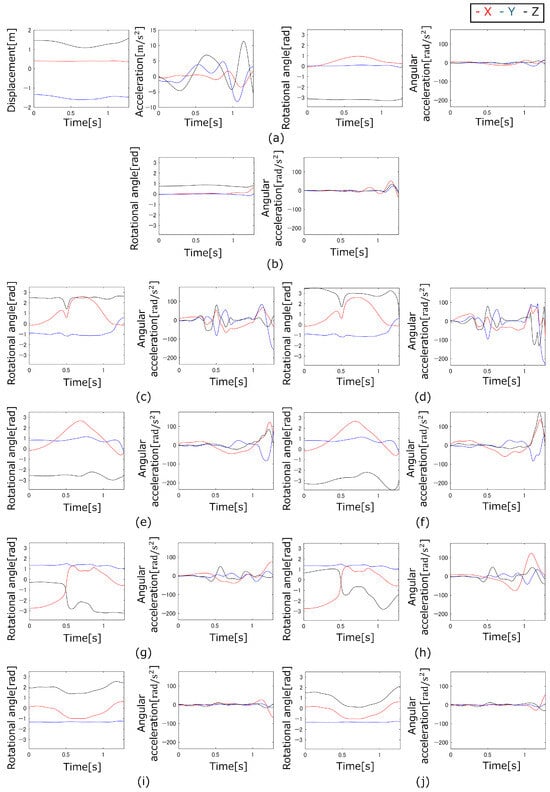
Figure 6.
Measured motion and calculated acceleration of vertical jump motion: (a) Trunk, (b) Head, (c) Right upper arm, (d) Right forearm + hand, (e) Left upper arm, (f) Left forearm + hand, (g) Right thigh, (h) Right lower leg + foot, (i) Left thigh, (j) Left lower leg + foot.
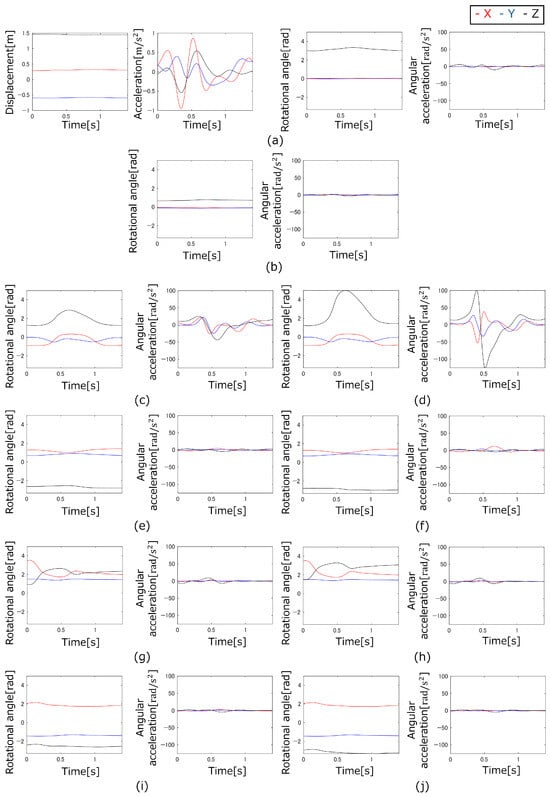
Figure 7.
Measured motion and calculated acceleration of arm swing motion: (a) Trunk, (b) Head, (c) Right upper arm, (d) Right forearm + hand, (e) Left upper arm, (f) Left forearm + hand, (g) Right thigh, (h) Right lower leg + foot, (i) Left thigh, (j) Left lower leg + foot.
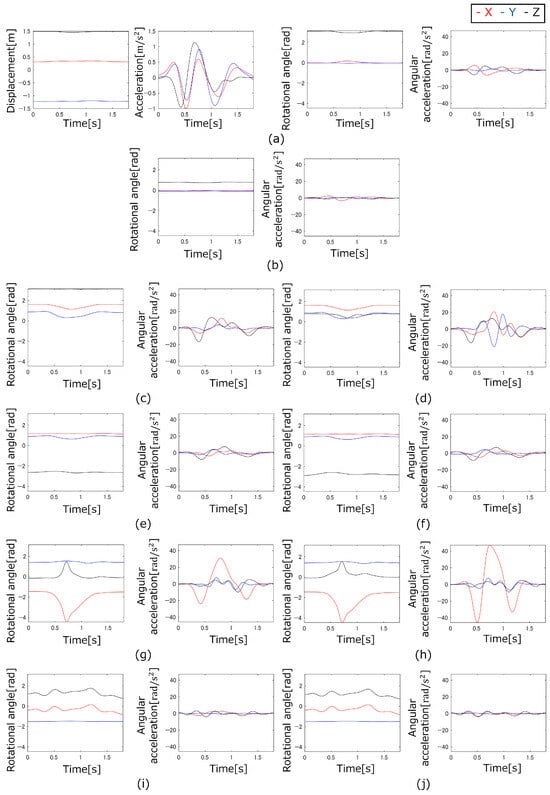
Figure 8.
Measured motion and calculated acceleration of leg swing motion: (a) Trunk, (b) Head, (c) Right upper arm, (d) Right forearm + hand, (e) Left upper arm, (f) Left forearm + hand, (g) Right thigh, (h) Right lower leg + foot, (i) Left thigh, (j) Left lower leg + foot.
2.1.2. Evaluation Methods
Using 10 rigid bodies and a 19-degree-of-freedom model, the joint torque and GRFs&Ms for arbitrary movements were calculated from the equations of motion. The equations of motion of the multibody system can be expressed in Equation (1) [32].
Here, the subscript O indicates the degree of freedom for a base link; subscript C represents the degree of freedom for the connected links; represents inertia matrix; is the sum of the Coriolis, centrifugal, and gravity forces; is the joint torque; is the the external force; is the generalized coordinates of the base link; and is the joint angle vector. Equation (1) can be transformed into Equation (2) using a vector of aligned MSIP [32].
Here, is a vector of MSIP, where MSIP is represented by mass, center of gravity, inertia tensors and vectors connecting the segment origins; represents the regressor matrix over , which is a function of , , , , , and .
As mentioned in the Introduction, inertial parameters are critical factors that can significantly influence the results of dynamic simulations. According to the equations of motion, as accelerations and angular velocities increase, even small inaccuracies in inertial parameters can lead to larger errors in simulation outcomes. Many studies have addressed the uncertainties related to body parameters such as mass, center of gravity, and inertia tensor. Therefore, uncertainties for mass, center of gravity, and inertia tensor were first established, and the uncertainties for the MSIP were then determined based on these. Normal distributions were used to model the uncertainties of each parameter. The means were the inertial properties obtained using the regression equations by Ae et al. [33] based on the lengths of each participant’s body segments.
According to D.J. Pearsall et al. [1], predictive equations from six different literature sources were used to estimate the inertial properties of the leg and thigh. Using data from 15 young adult men, the estimated values of the segment parameters were calculated for each predictive equation, and their differences were statistically compared. The results showed that even for the same individual, there can be a more than 40% difference in the estimated inertial properties depending on the literature. In addition, to investigate the influence of uncertainties in the inertial properties of the leg and thigh on inverse dynamics simulations during walking, simulations were conducted by varying the inertial properties within a range of up to ±40% from the reference values. Uncertainties were set as follows based on previous research:
- Mass: ±40% of each segment’s mass.
- Center of gravity: ±20% of the segment length in each axial direction considering that the center of gravity is approximately half of the segment length.
- Inertia tensor: ±20% of the maximum principal moment of inertia of the base inertia tensor.
Furthermore, to ensure that the total mass remained constant, the mass of the trunk was calculated by subtracting the masses (including their variations) of the other segments from the total mass. Figure 9 shows the means and standard deviations (SDs) of the inertial properties set in this way. The means and SDs of each MSIP under these settings are shown in Figure 10. Briefly, performing Monte Carlo simulations with the means and SDs of the inertial properties set as in Figure 9 is equivalent to performing Monte Carlo simulations with the means and SDs of each MSIP set as in Figure 10.
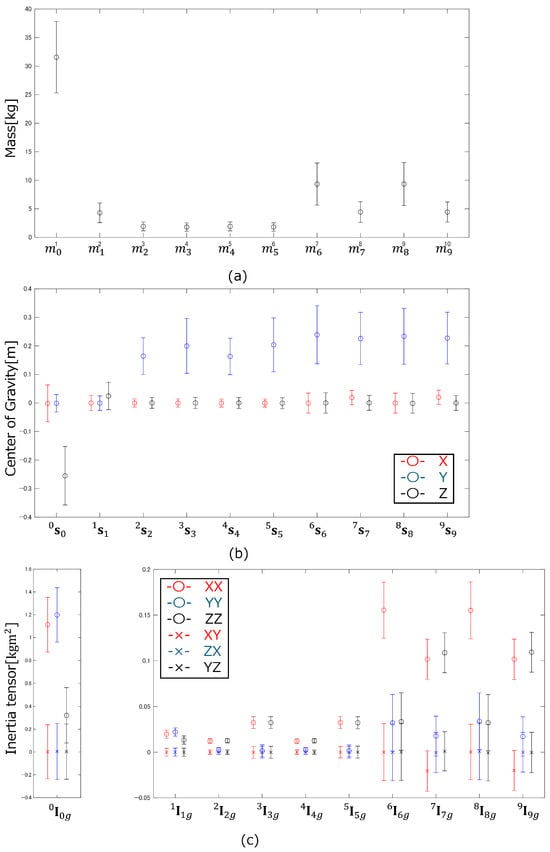
Figure 9.
Means and standard deviations of the (a) mass, (b) center of gravity and (c) inertia tensor.
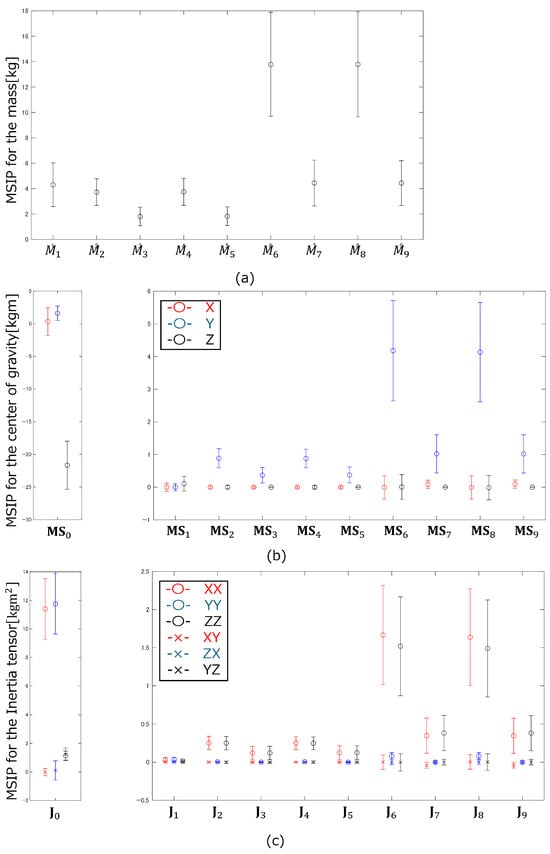
Figure 10.
Means and standard deviations of the MSIP for (a) mass, (b) center of gravity and (c) inertia tensor.
Monte Carlo simulations were performed for each measured motion. In each trial, the inertial parameters of each segment were randomly sampled from normal distributions whose means and standard deviations were defined based on the reference values and uncertainty ranges described above. Next, the participants’ measured motion data were used as inputs to the inverse dynamics equations. The joint torque and GRFs&Ms were then calculated for each sampled set of inertial parameters, and the results were recorded. The outputs of all 3000 trials were aggregated to derive the 5–95% confidence intervals at each time step. The mean, maximum, and minimum values at each time point within these intervals were computed. In addition, to determine which joint torques are more susceptible to the influence of uncertainties, the means and SDs of the widths of the 5–95% confidence intervals were calculated. The sensitivity of the input values was investigated by calculating Pearson’s correlation coefficients and p-values. Strengths of the correlations that were significant were categorized as weakly sensitive (r = 0.2–0.4), moderately sensitive (r = 0.4–0.6), or highly sensitive (r = 0.6–1.0) [19]. The Pearson’s correlation coefficients r and p-values were examined at characteristic points where the 5–95% confidence intervals reached their maximum values. Through this analysis, the uncertainties of the inertial properties and MSIP in inverse dynamics simulations involving high-acceleration movements were evaluated.
2.2. Evaluation of Inverse Dynamics Simulation Based on the Identification Results of MSIP Using Free Vibration Measurement
The accuracy of the inverse dynamics simulations using the experimentally identified MSIP was evaluated by comparing the GRFs. The participants’ MSIP was identified in advance using the identification method based on free vibration measurements [18]. The identified MSIP was compared with the MSIP calculated from the inertial properties obtained using the regression equations by Ae et al. [33], which were used as reference values in Section 2.2. The participants’ MSIP is shown in Table 1.

Table 1.
Identification results [18] and calculation results using the regression equations by Ae et al. [33] for all MSIP.
3. Results
The 5–95% confidence intervals and their means for the joint torques and GRFs&Ms obtained from the Monte Carlo simulations for each motion are presented. The time points where the widths of the 5–95% confidence intervals become largest are indicated with vertical black dotted lines.
For the running motion, the results for the GRFs&Ms and joint torques acting on the right and left shoulder, elbow, hip and knee joints are shown in Figure 11. In addition, the means and SDs of the widths of the 5–95% confidence intervals for the forces and moments acting on each joint are shown in Figure 12. Pearson’s correlation coefficients r and p-values were calculated to investigate the sensitivity of the input parameters. The correlation coefficients were calculated at the time points at which the joint torques reached their maximum values. The p-values for all correlation coefficients r presented below were confirmed to be less than 0.05. The input values of the inertial properties and MSIP that yielded the maximum correlation coefficients and their values are shown in Table 2, as well as the results of other motions in Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20 and Table 3, Table 4, Table 5 and Table 6.
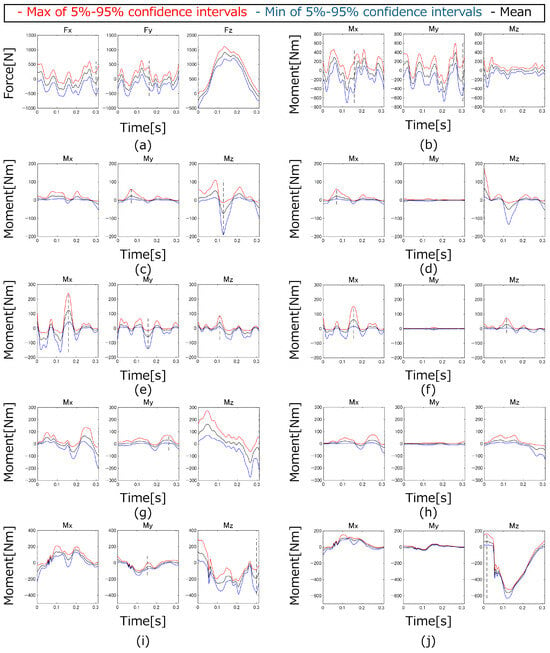
Figure 11.
The 5–95% confidence intervals of the GRFs&Ms and joint torques of the running motion: (a) GRFs, (b) GRMs, (c) Right shoulder joint, (d) Right elbow joint, (e) Left shoulder joint, (f) Left elbow joint, (g) Right hip joint, (h) Right knee joint, (i) Left hip joint, (j) Left knee joint.
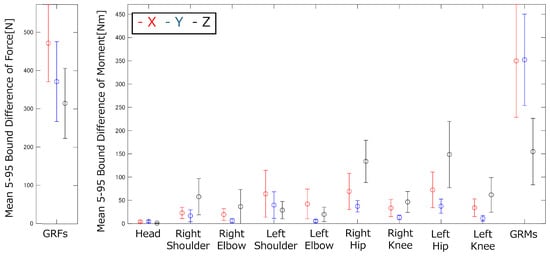
Figure 12.
Means and standard deviations of the widths of the 5–95% confidence intervals for the GRFs&Ms and joint torques of the running motion.

Table 2.
Maximum correlation coefficients and corresponding (a) inertial property and (b) MSIP of the running motion.
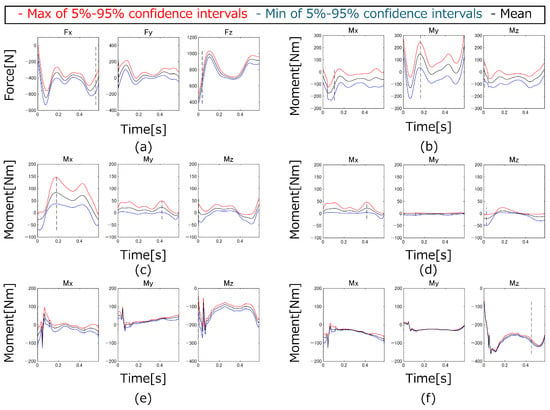
Figure 13.
The 5–95% confidence intervals of the GRFs&Ms and joint torques of the side-cutting motion: (a) GRFs, (b) GRMs, (c) Right hip joint, (d) Right knee joint, (e) Left hip joint, (f) Left knee joint.
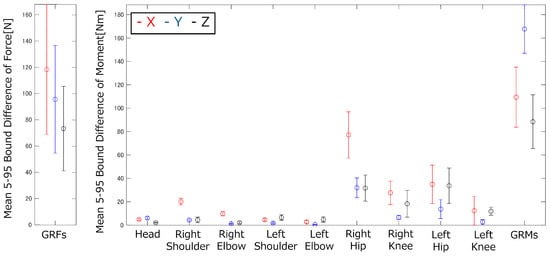
Figure 14.
Means and standard deviations of the widths of the 5–95% confidence intervals for the GRFs&Ms and joint torques of the side-cutting motion.
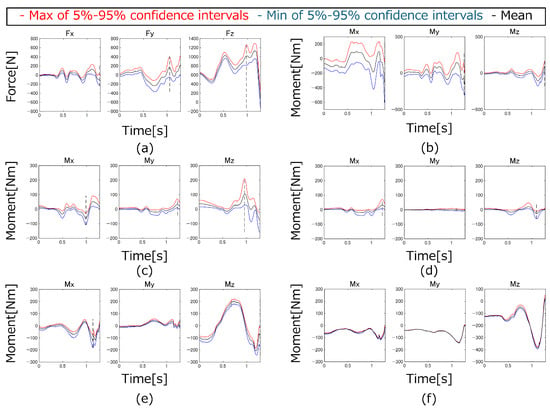
Figure 15.
The 5–95% confidence intervals of the GRFs&Ms and joint torques of the vertical jump motion: (a) GRFs, (b) GRMs, (c) Right hip joint, (d) Right knee joint, (e) Left hip joint, (f) Left knee joint.
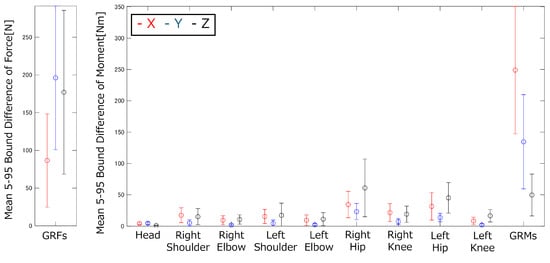
Figure 16.
Means and standard deviations of the widths of the 5–95% confidence intervals for the GRFs&Ms and joint torques of the vertical jump motion.
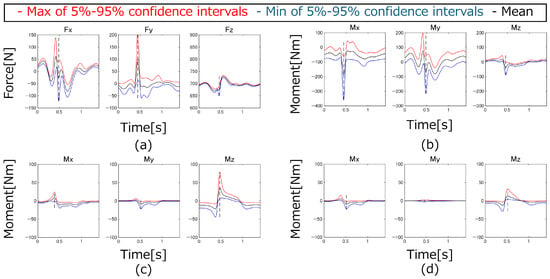
Figure 17.
The 5–95% confidence intervals of the GRFs&Ms and joint torques of the arm swing motion: (a) GRFs, (b) GRMs, (c) Right shoulder joint, (d) Right elbow joint.
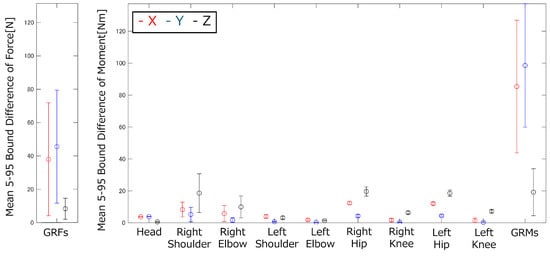
Figure 18.
Means and standard deviations of the widths of the 5–95% confidence intervals for the GRFs&Ms and joint torques of the arm swing motion.
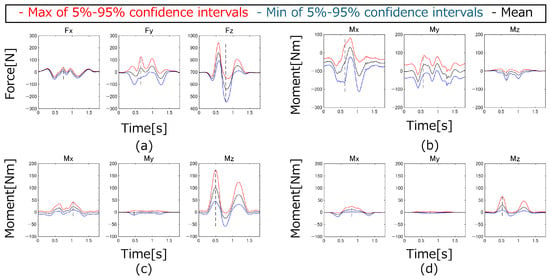
Figure 19.
The 5–95% confidence intervals of the GRFs&Ms and joint torques of the leg swing motion: (a) GRFs, (b) GRMs, (c) Right hip joint, (d) Right knee joint.
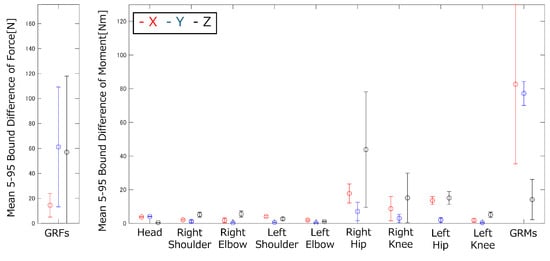
Figure 20.
Means and standard deviations of the widths of the 5–95% confidence intervals for the GRFs&Ms and joint torques of the leg swing motion.

Table 3.
Maximum correlation coefficients and corresponding (a) inertial property and (b) MSIP of the side-cutting motion.

Table 4.
Maximum correlation coefficients and corresponding (a) inertial properties and (b) MSIP of the vertical jump motion.

Table 5.
Maximum correlation coefficients and corresponding (a) inertial properties and (b) MSIP of the arm swing motion.

Table 6.
Maximum correlation coefficients and corresponding (a) inertial properties and (b) MSIP of the leg swing motion.
Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25 show the inverse dynamic analysis results using the MSIP identified using the free vibration measurement method, the inverse dynamics analysis results using table data, the 5–95% confidence intervals, and the measured GRFs.
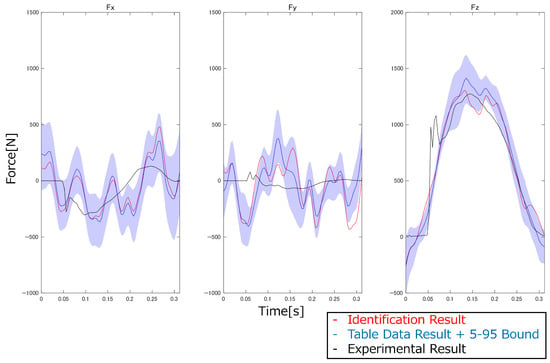
Figure 21.
Comparison of the estimated and experimental ground reaction forces (running).
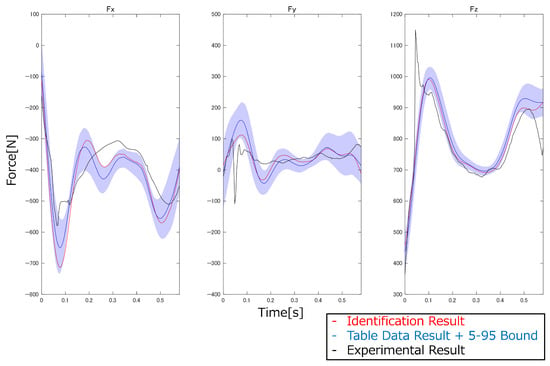
Figure 22.
Comparison of the estimated and experimental ground reaction forces (side-cutting).
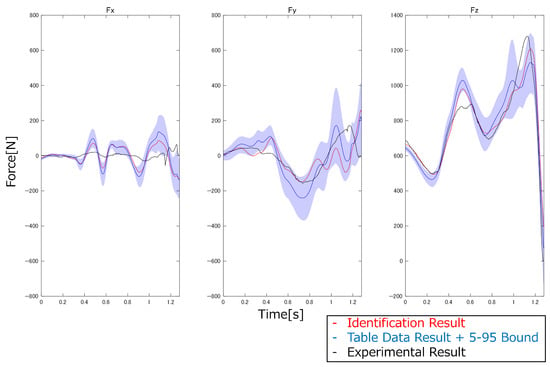
Figure 23.
Comparison of estimated and experimental ground reaction forces (vertical jump).
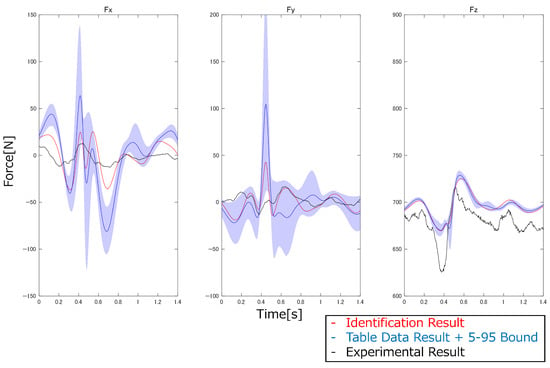
Figure 24.
Comparison of the estimated and experimental ground reaction forces (arm swing).
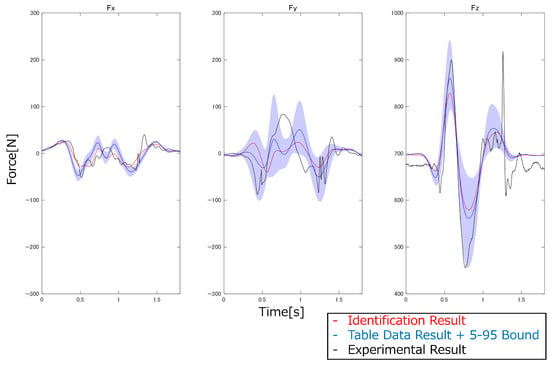
Figure 25.
Comparison of the estimated and experimental ground reaction forces (leg swing).
4. Discussion
When examining the means and SDs of the widths of the 5–95% confidence intervals for the forces and moments acting on each joint, two distinct patterns emerge. In some cases, the mean is large, whereas the SD is small. In other cases, both the mean and the SD are large.
When the mean is large but the SD is small, this is due to the influence of the gravitational term, particularly when the angular acceleration of the segment and subsequent segments are small. When both the means and SDs of the widths of the 5–95% confidence intervals are large, this is when the angular acceleration of the segments is large. The relationship between the angular acceleration of the segments and means and SDs of the widths of the 5–95% confidence intervals was examined. Table 7 shows the approximate ranges of angular acceleration for both arms and legs and the means and SDs of the widths of the 5–95% confidence intervals where they are maximized for each segment.

Table 7.
Relationship between angular acceleration and means and standard deviations of the widths of the 5–95% confidence intervals.
As the angular acceleration increases, the SDs of the widths of the 5–95% confidence intervals tend to increase (Table 7). The means do not fall below a certain threshold because of the influence of the gravitational term. However, as the angular acceleration exceeds a certain level, the means also tend to increase. This indicates that when angular acceleration is small, the gravitational term dominates. In contrast, as acceleration and angular acceleration become larger, the inertial terms become more significant, and the effect of the uncertainties in inertial properties increases.
In each motion, the points where the widths of the 5–95% confidence intervals for the joint torques are largest approximately coincide with the moments when the angular accelerations of each segment reach their maximum or minimum. This further indicates that as acceleration and angular acceleration increase, the influence of the uncertainties in inertial properties becomes more significant.
Then, examining the Pearson’s correlation coefficients at the points where the joint torques are maximized (Table 2, Table 3, Table 4, Table 5 and Table 6), the input values that yielded the maximum correlation coefficients were mainly the masses of each segment and the center of gravity in the longitudinal direction. The mass is used in all calculations when obtaining the MSIP. Therefore, the influence of mass arises in all inertial terms, and the influence of mass appears in the gravitational term, which likely leads to large correlation coefficients for mass. In addition, the center of gravity in the longitudinal direction has values larger than those in other directions because of the distance from the joint, resulting in a greater effect on the calculated results.
When comparing the correlation coefficients and their corresponding input values at the points where the joint torques reach their maximum values, a clear pattern emerges between cases using inertial properties and those using MSIP (Table 2, Table 3, Table 4, Table 5 and Table 6). The MSIP corresponding to the input values yielding the maximum correlation coefficients are the values derived from the inertial properties corresponding to the input values yielding the maximum correlation coefficients. Moreover, many MSIPs related to the inertia tensor appear in the results, indicating that uncertainties arising from angular acceleration also have significant effects. In addition, the correlation coefficients tend to be larger when using MSIP as the input values. This indicates that utilizing MSIP allows for a more accurate investigation of which terms have a stronger influence on the calculated joint torques.
From the results in Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25, the root mean square error (RMSE) and Pearson’s correlation coefficient between the analysis results and the experimental results for the vertical forces were calculated (Table 8).

Table 8.
RMSE and Pearson’s correlation coefficients between the analysis and experimental results.
From the results in Table 8, the use of the MSIP identified using the free vibration measurement method in the inverse dynamics analysis resulted in higher accuracy in estimating GRFs for the five high-acceleration motions than using the inverse dynamics analysis with the table data. In particular, the RMSE improved by as much as 148 N for vertical jumping. This result demonstrates that the free vibration measurement method, which enables high-precision, three-dimensional identification of MSIP, is highly useful for constructing three-dimensional dynamic simulations. Conversely, when comparing the Pearson’s correlation coefficients, the results using the identified MSIP tended to show slightly stronger correlations; however, no significant differences were observed. Looking at the comparisons of estimated and experimental GRFs in Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25, there are time points where the experimental results are not within the 5–95% confidence intervals. From this, the MSIP significantly affects the magnitudes of the forces and moments in the inverse dynamics analysis, whereas the shapes of the waveforms are largely influenced by factors other than the MSIP, such as the model degrees of freedom and the motion measurement results.
In fact, the model is simplified, with the lower legs and feet modeled as a single rigid body, the trunk modeled as a single rigid body, the shoulder and hip joints represented only by spherical joints, and the elbow and knee joints represented only by revolute joints (Figure 3). From these results, despite limitations in the calculation of the external forces because of the simplified model in this comparison, the MSIP identified by the proposed method can improve the estimation accuracy of the external forces for various motions within the simplified model.
This study was designed as an exploratory case study to evaluate the feasibility of our approach in a controlled setting. Focusing on a single participant enabled detailed measurements and analyses, establishing a baseline for future, more extensive research. However, only one participant was involved, and owing to factors such as model simplification and measurement errors, the generalization of the results is limited. Because the analysis was conducted based on data from a single individual, the effects of individual differences, including sex, age, and body size, could not be fully considered. Furthermore, because the focus was on the uncertainties of inertial properties and the MSIP, measurement errors such as inaccuracies in motion capture, force plate measurements, and marker placement errors were not accounted for.
Despite these limitations, this focused investigation provides a foundational framework that can be scaled up in subsequent studies. The findings highlight that uncertainties in inertial parameters exert a notably stronger influence under higher accelerations and angular velocities—conditions often found in sports and other dynamic activities. Importantly, using MSIP identified via the free vibration measurement method significantly improved the accuracy of the dynamic simulations. By illustrating both the heightened sensitivity to uncertainty and a practical way to mitigate its impact, this proof-of-concept research sets the stage for future studies involving larger, more diverse participant groups.
Therefore, future research should address several key areas. Increasing and diversifying the number of participants across sex, age, body size, skill level, and even psychological state would enhance the generalizability and reliability of the results. Developing a human body model with more detailed degrees of freedom would improve accuracy in replicating complex motions. Additionally, incorporating sources of measurement error—such as potential inaccuracies in motion capture and force plate data—into the verification process would provide a more comprehensive analysis. Addressing these challenges will deepen our understanding of human motion analysis and promote its application in various fields.
5. Conclusions
This study explored the effect of uncertainty in inertial properties and MSIP on the results of inverse dynamic simulations in high-acceleration movements, such as those commonly seen in sports activities. Uncertainty in MSIP was shown to cause substantial fluctuations in the results of inverse dynamics simulations for high-acceleration movements. This finding highlights the importance of precisely determining MSIP. The improvement in the accuracy of the inverse dynamics simulations by using MSIP identified using the free vibration measurement method was validated. These findings underscore both the necessity and importance of employing MSIP identified by the free vibration measurement method.
The Monte Carlo simulation results demonstrated that uncertainties in inertial properties, particularly mass and longitudinal position of the center of gravity, significantly affected the calculated joint torques. When the angular acceleration was small, the gravitational term dominated the variations, leading to larger means of the confidence interval widths but smaller SDs. Conversely, when the angular acceleration was large, the inertial terms became more influential, resulting in both larger means and SDs of the confidence interval widths. The use of MSIP allows for a more accurate investigation of which terms have a stronger influence on the calculated joint torques.
The MSIP identified using the free vibration measurement method were applied in inverse dynamic simulations of the same high-acceleration movements. The simulated GRFs were then compared with the measured forces obtained from the force plates. The findings indicated that the use of the identified MSIP improved the accuracy of the inverse dynamics simulations across all tested movements. The RMSE values were lower when the identified MSIP were used compared with using standard table data, decreasing by as much as 148 N. This result demonstrates that the free vibration measurement method, which enables the high-precision three-dimensional identification of MSIP, is highly useful for constructing three-dimensional dynamic simulations. Although Pearson’s correlation coefficients showed only slight improvements, the overall estimation of the GRFs was more precise with the identified MSIP. Errors falling outside the 5–95% confidence intervals, derived from the uncertainty evaluation, were observed. This suggests that factors other than the MSIP, such as model simplifications and measurement errors, also contribute to discrepancies in the simulation results.
This study has limitations, including the use of a single participant, model simplifications, and the exclusion of measurement errors from the motion capture and force plate data in the Monte Carlo simulation. These factors limit the generalizability of the results. Future research directions include increasing the participant pool to encompass diverse demographics, enhancing the human model’s complexity to better replicate actual human movement, and incorporating measurement errors into the analysis. Addressing these issues will enhance the applicability and accuracy of inverse dynamics simulations for high-acceleration movements.
Author Contributions
Conceptualization, T.H.; methodology, T.H.; software, T.H.; validation, T.H.; formal analysis, T.H.; investigation, T.H.; resources, T.H.; data curation, T.H.; writing—original draft preparation, T.H.; writing—review and editing, T.H. and H.Y.; visualization, T.H.; supervision, H.Y.; project administration, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki and was approved by the Institute of Science Tokyo Human Subject Research Ethics Review Committee (Permit No. 2022104, 2024193).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The original contributions of analyzed data in this study are included in the article. The raw data and other inquiries about data can be directed to the corresponding author.
Acknowledgments
The authors sincerely thank Resonic Japan Co., Ltd. for their help during the experiments. Moreover, the authors sincerely thank Emeritus Professor Masaaki Okuma of Tokyo Tech for his support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pearsall, D.J.; Costigan, P.A. The effect of segment parameter error on gait analysis results. Gait Posture 1999, 9, 173–183. [Google Scholar] [CrossRef] [PubMed]
- Hansen, C.; Venture, G.; Rezzoug, N.; Gorce, P.; Isableu, B. An individual and dynamic body segment inertial parameter validation method using ground reaction forces. J. Biomech. 2014, 47, 1577–1581. [Google Scholar] [CrossRef]
- Allen, R.W.; Klyde, D.H.; Rosenthal, T.J.; Smith, D.M. Estimation of passenger vehicle inertial properties and their effect on stability and handling. SAE Tech. Pap. 2003, 112, 1032–1050. [Google Scholar] [CrossRef]
- Piovesan, D.; Pierobon, A.; DiZio, P.; Lackner, J.R. Comparative analysis of methods for estimating arm segment parameters and joint torques from inverse dynamics. J. Biomech. Eng. 2011, 133, 031003. [Google Scholar] [CrossRef]
- Mayeda, H.; Yoshida, K.; Osuka, K. Base parameters of manipulator dynamic models. IEEE Trans. Robot. Automat. 1990, 6, 312–321. [Google Scholar] [CrossRef]
- Gautier, M. Numerical calculation of the base inertial parameters of robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinatti, OH, USA, 13–18 May 1990; IEEE Computer Society Press: Piscataway, NJ, USA, 1990; pp. 1020–1025. [Google Scholar] [CrossRef]
- Kawasaki, H.; Beniya, Y.; Kanzaki, K. Minimum dynamics parameters of tree structure robot models. Trans. Soc. Instrum. Control Eng. 1992, 28, 1444–1450. [Google Scholar] [CrossRef]
- Atkeson, C.G.; An, C.H.; Hollerbach, J.M. Estimation of inertial parameters of manipulator loads and links. Int. J. Robot. Res. 1986, 5, 101–119. [Google Scholar] [CrossRef]
- Hinrichs, R.N. Regression equations to predict segmental moments of inertia from anthropometric measurements: An extension of the data of Chandler et al. (1975). J. Biomech. 1985, 18, 621–624. [Google Scholar] [CrossRef] [PubMed]
- Clauser, C.E.; McConville, J.T.; Young, J.W. Weight, Volume, and Center of Mass of Segments of the Human Body, Technical Report AMRL-TR-69-70, Aerospace Medical Research Laboratory, Wright–Patterson Air Force Base, Dayton, Ohio. 1969. Available online: https://www.semanticscholar.org/paper/Weight%2C-volume%2C-and-center-of-mass-of-segments-of-Clauser-Mcconville/8eda33ffe8e628c2d058d880e011c3c76c10604b (accessed on 9 March 2025).
- Pearsall, D.J.; Reid, J.G.; Livingston, L.A. Segmental inertial parameters of the human trunk as determined from computed tomography. Ann. Biomed. Eng. 1996, 24, 198–210. [Google Scholar] [CrossRef]
- Liu, Y.; Antonijević, D.; Li, R.; Fan, Y.; Dukić, K.; Mićić, M.; Yu, G.; Li, Z.; Djurić, M.; Fan, Y. Study of sexual dimorphism in metatarsal bones: Geometric and inertial analysis of the three-dimensional reconstructed models. Front. Endocrinol. 2021, 12, 734362. [Google Scholar] [CrossRef]
- Cheng, C.K.; Chen, H.H.; Chen, C.S.; Chen, C.L.; Chen, C.Y. Segment inertial properties of Chinese adults determined from magnetic resonance imaging. Clin. Biomech. 2000, 15, 559–566. [Google Scholar] [CrossRef]
- Okada, H.; Yokozawa, T.; Takahashi, H. Estimation of body segment densities for Japanese athletes from magnetic resonance imaging. J. Soc. Biomech. 2020, 44, 162–170. [Google Scholar] [CrossRef] [PubMed]
- Martin, P.E.; Mungiole, M.; Marzke, M.W.; Longhill, J.M. The use of magnetic resonance imaging for measuring segment inertial properties. J. Biomech. 1989, 22, 367–376. [Google Scholar] [CrossRef] [PubMed]
- Mungiole, M.; Martin, P.E. Estimating segment inertial properties: Comparison of magnetic resonance imaging with existing methods. J. Biomech. 1990, 23, 1039–1046. [Google Scholar] [CrossRef] [PubMed]
- Homma, T.; Yamaura, H. Development of an identification method for the minimal set of inertial parameters of a multibody system. Multibody Syst. Dyn. 2024. [Google Scholar] [CrossRef]
- Homma, T.; Yamaura, H. Identification of the minimum set of inertial parameters of human body segments using a method applying free vibration measurements. J. Biomech. Sci. Eng. 2025, 24-00344. [Google Scholar] [CrossRef]
- Myers, C.A.; Laz, P.J.; Shelburne, K.B.; Davidson, B.S. A probabilistic approach to quantify the impact of uncertainty propagation in musculoskeletal simulations. Ann. Biomed. Eng. 2015, 43, 1098–1111. [Google Scholar] [CrossRef]
- Futamure, S.; Bonnet, V.; Dumas, R.; Venture, G. A sensitivity analysis method for the body segment inertial parameters based on ground reaction and joint moment regressor matrices. J. Biomech. 2017, 64, 85–92. [Google Scholar] [CrossRef]
- Pàmies-Vilà, R.; Font-Llagunes, J.M.; Cuadrado, J.; Alonso, F.J. Analysis of different uncertainties in the inverse dynamic analysis of human gait. Mech. Mach. Theor. 2012, 58, 153–164. [Google Scholar] [CrossRef]
- Rao, G.; Amarantini, D.; Berton, E.; Favier, D. Influence of body segments’ parameters estimation models on inverse dynamics solutions during gait. J. Biomech. 2006, 39, 1531–1536. [Google Scholar] [CrossRef]
- Andrews, J.G.; Mish, S.P. Methods for investigating the sensitivity of joint resultants to body segment parameter variations. J. Biomech. 1996, 29, 651–654. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.C.; Reynolds, K.J. The effect of variability in body segment parameters on joint moment using Monte Carlo simulations. Gait Posture 2014, 39, 346–353. [Google Scholar] [CrossRef] [PubMed]
- Riemer, R.; Hsiao-Wecksler, E.T.; Zhang, X. Uncertainties in inverse dynamics solutions: A comprehensive analysis and an application to gait. Gait Posture 2008, 27, 578–588. [Google Scholar] [CrossRef]
- Pàmies-Vilà, R.; Font-Llagunes, J.M.; Cuadrado, J.; Alonso, F.J. Influence of input data errors on the inverse dynamics analysis of human locomotion. In Proceedings of the 1st Joint International Conference on Multibody System Dynamics, Lappeenranta, Finland, 25–27 May 2010. [Google Scholar]
- Fritz, J.; Kröll, J.; Schwameder, H. Influence of body segment parameter estimation on calculated ground reaction forces in highly dynamic movements. J. Biomech. 2019, 84, 11–17. [Google Scholar] [CrossRef]
- Grimmer, M.; Elshamanhory, A.A.; Beckerle, P. Human lower limb joint biomechanics in daily life activities: A literature based requirement analysis for anthropomorphic robot design. Front. Robot. 2020, 7, 13. [Google Scholar] [CrossRef]
- Skals, S.; Jung, M.K.; Damsgaard, M.; Andersen, M.S. Prediction of ground reaction forces and moments during sports-related movements. Multibody Syst. Dyn. 2017, 39, 175–195. [Google Scholar] [CrossRef]
- Wu, G.; Siegler, S.; Allard, P.; Kirtley, C.; Leardini, A.; Rosenbaum, D.; Whittle, M.; D’Lima, D.D.; Cristofolini, L.; Witte, H.; et al. ISB recommendation on definitions of joint coordinate system of various joints for the reporting of human joint motion–part I: Ankle, hip, and spine. International Society of Biomechanics. J. Biomech. 2002, 35, 543–548. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; van der Helm, F.C.; DirkJan Veeger, H.E.J.; Makhsous, M.; Van Roy, P.; Anglin, C.; Nagels, J.; Karduna, A.R.; McQuade, K.; Wang, X.; et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion-Part II: Shoulder, elbow, wrist and hand. J. Biomech. 2005, 38, 981–992. [Google Scholar] [CrossRef]
- Ayusawa, K.; Venture, G.; Nakamura, Y. Identifiability and identification of inertial parameters using the underactuated base-link dynamics for legged multibody systems. Int. J. Robot. Res. 2014, 33, 446–468. [Google Scholar] [CrossRef]
- Ae, M.; Tang, H.; Yokoi, T. Estimation of inertia properties of the body segments in Japanese athletes. Biomechanisms 1992, 11, 23–33. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).