Abstract
Background: Sex estimation from skeletal remains is important for forensic identification, but many methodologies focus on complete elements despite high fragmentation rates in operational contexts. The aim of this study was to develop and validate discriminant function equations for sex estimation between complete and fragmented Thai femora. Materials and Methods: A total of 560 adult femora (280 males and 280 females) were used for measurements of eight osteometric variables. Then, discriminant function analysis was applied to complete femora and anatomically isolated segments, including proximal, diaphyseal, and distal, with leave-one-out cross-validation. Results: All measurements showed significant sexual dimorphism, with percentage differences ranging from 6.56% to 42.27%. Complete femur stepwise analysis achieved 90.47% accuracy by using four optimally selected variables, performing comparably to eight-variable models. Isolated segment accuracies varied substantially: proximal segments achieved 89.64% accuracy, differing by only 0.83 percentage points from complete performance; distal segments demonstrated 86.25% accuracy from bicondylar width alone; and diaphyseal segments achieved 80.88%. Combined segment approaches demonstrated synergistic effects approaching complete femur performance. Conclusions: These population-specific equations provided validated methodologies for sex estimation from complete and fragmentary Thai femora. Anatomical region selection still maintained high classification accuracy despite skeletal incompleteness, in line with the fragmentary conditions commonly encountered in forensic and archeological contexts.
1. Introduction
A biological profile provides basic information for the identification of unknown human skeletal remains in forensic anthropological practice, including estimations of sex, age at death, stature, and population affinity [1]. Among those parameters, sex estimation is paramount as it immediately reduces potential identities by approximately half and provides critical context for subsequent biological profile components. While the pelvis and cranium are commonly used as the primary indicators due to their noticeable sexual dimorphism, these elements are often absent or poorly preserved in forensic contexts [2]. Therefore, alternative skeletal elements are being elucidated. As demonstrated previously, the femur, combining considerable sexual dimorphism with robust preservation characteristics, can be a valuable alternative for sex estimation when primary indicators are unavailable [3,4].
Previous studies across diverse populations have revealed the reliability of femoral osteometric analysis for sex estimation, with high accuracies between 80% and 95% observed for complete elements [5,6,7]. It is known that the many anatomical parts of the femur can exhibit sexually dimorphic characteristics, including the proximal, midshaft, and distal regions [3,5,7]. Discriminant function analysis has remained the predominant analytical approach for developing sex classification equations, valued for producing explicit mathematical functions directly applicable to forensic casework [8,9]. However, despite consistent validation of femoral metrics across populations, published methodologies have overwhelmingly focused on the complete, intact specimens examined under controlled laboratory conditions [10,11]. While this study similarly employs complete femora to establish baseline standards, it extends analysis to isolated anatomical segments to address the fragmentary conditions commonly encountered in forensic practice.
In general, bone fragmentation can occur through perimortem trauma, postmortem carnivore activity, environmental degradation, and extended taphonomic processes, which are routinely encountered in forensic recovery contexts [12,13,14,15]. Although the complete femora demonstrate high classification accuracy, the performance of sex estimation methods applied to systematically isolated anatomical segments remains under characterized. Previously, Ranaweera and coworkers [16] examined multiple segments in a Sri Lankan population. In Thailand, such systematic evaluation with rigorous cross-validation across all femoral regions needs to be elucidated because population-specific morphological variations may influence discriminatory capacity.
This study attempted to address this gap by systematically evaluating sex classification performance across isolated femoral segments using discriminant function analysis. It was applied separately to proximal, diaphyseal, and distal measurements in comparisons with complete femur models.
2. Materials and Methods
2.1. Samples and Ethical Considerations
This cross-sectional study examined 560 adult human femora (280 male, 280 female) from the Unit of Human Bone Warehouse for Research (UHBWR), Department of Anatomy, Faculty of Medicine, Khon Kaen University, Thailand. All specimens were obtained from a documented body donation unit with confirmed sex, age, and population affinity information. Individuals ranged in age from 20 to 80 years at death. Inclusion criteria required complete skeletal maturity, known biological sex, and absence of pathological conditions or traumatic damage affecting the femur. Specimens with visible pathological alterations were excluded during visual inspection. Data collection and osteometric measurements were conducted between October 2024 and April 2025. This research received ethical approval from the Center for Ethics in Human Research, Khon Kaen University (approval number HE671557) 2 October 2024.
2.2. Measurements and Metric Analyses
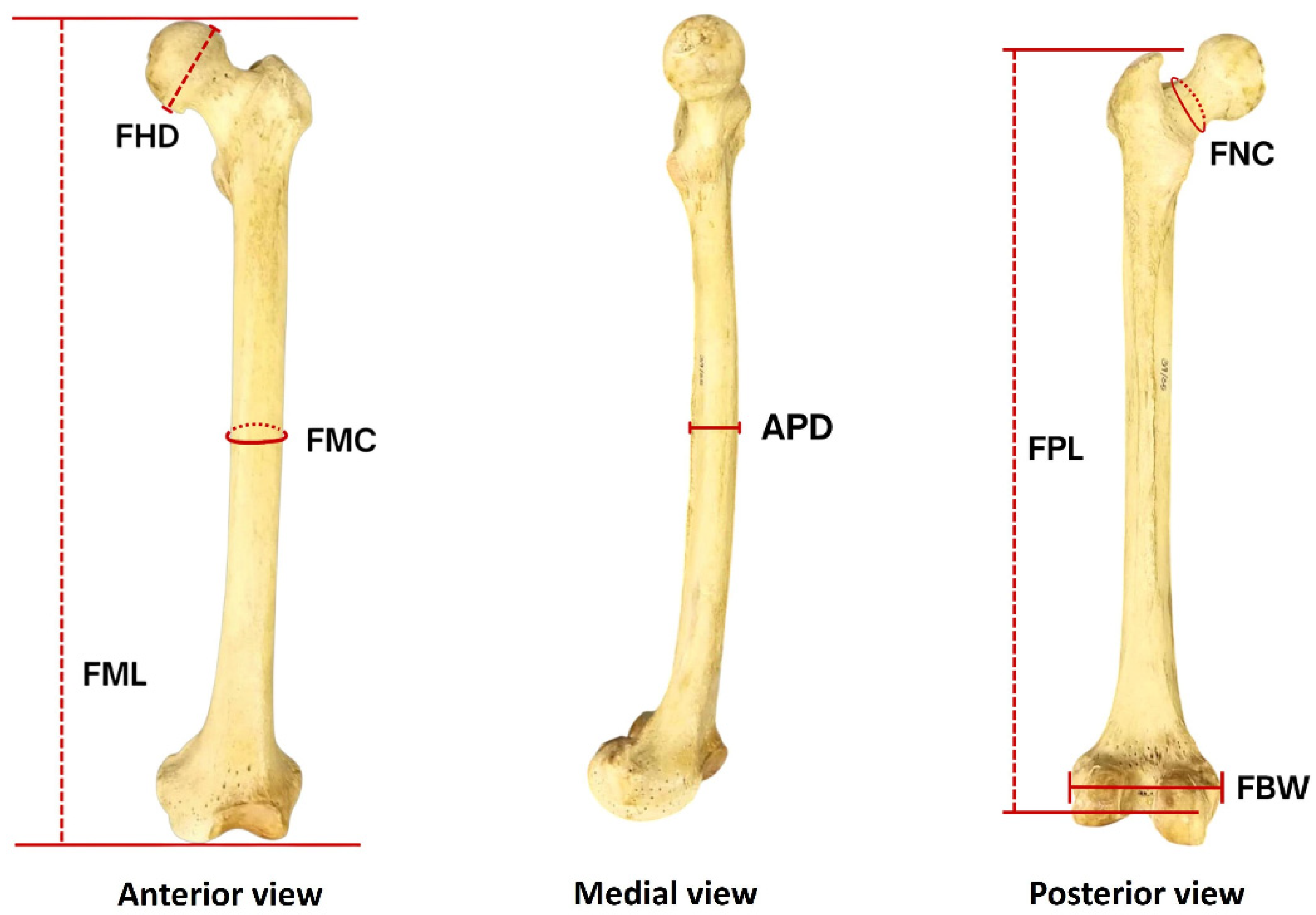
Seven standard osteometric variables (Figure 1) and the weights of femurs were recorded from each sample following established anatomical landmarks and measurement protocols.
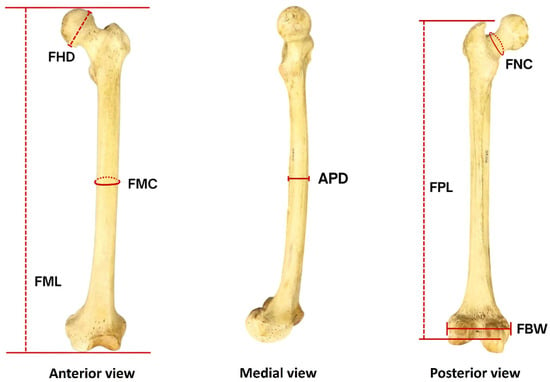
Figure 1.
Femoral osteometric measurements. FHD: femoral vertical head diameter, FMC: femoral midshaft circumference, FML: femur maximum length, APD: anteroposterior midshaft diameter, FNC: femoral neck circumference, FPL: femur physiological length, FBW: femoral bicondylar width.
- Femur maximum length (FML) was measured as the greatest distance from the most superior point of the femoral head to the most inferior point of the condyle.
- Femur physiological length (FPL) represented the distance from the most superior point of the femoral greater trochanter to the inferior margin of the intercondylar notch.
- Femur weight (FW) was measured using a digital precision scale.
- Anteroposterior midshaft diameter (APD) was recorded as the maximum anteroposterior diameter at the femoral midpoint.
- Femoral midshaft circumference (FMC) was obtained at the midpoint location using a flexible measuring tape.
- Femoral vertical head diameter (FHD) was defined as the maximum superior–inferior diameter of the femoral head measured with digital calipers.
- Femoral neck circumference (FNC) was measured at the narrowest point of the femoral neck using a flexible measuring tape.
- Femoral bicondylar width (FBW) represented the maximum mediolateral distance across both condyles measured with the posterior condylar surfaces.
All measurements were performed by two trained observers with prior experience in osteometric data collection. Each specimen was measured twice by each observer on separate occasions to assess both inter-observer and intra-observer measurement reliability. Linear dimensions were recorded to the nearest 0.01 mm using digital sliding calipers, while circumferences were measured to the nearest millimeter using a flexible measuring tape, and weight was recorded to the nearest gram.
2.3. Statistical Analyses
Measurement reliability was evaluated using the technical error of measurement (TEM), relative technical error of measurement (rTEM), and coefficient of reliability (R) for both inter-observer and intra-observer assessments. Acceptable reliability thresholds were set at rTEM < 5% and R > 0.95. Descriptive statistics (mean and standard deviation) were calculated for each variable by sex, and sexual dimorphism was assessed using independent samples t-tests. Discriminant function analysis (DFA) was performed to develop sex classification equations for seven models. For the complete femur model, two approaches were employed: the stepwise method using Wilks’ lambda and the direct entry method incorporating all eight variables simultaneously. DFA was also applied to proximal (femoral vertical head diameter and femoral neck circumference), diaphyseal (anteroposterior midshaft diameter and femoral midshaft circumference), and distal (femoral bicondylar width) segments, as well as combined segment models (proximal–diaphyseal, proximal–distal, and diaphyseal–distal). All analyses were performed in IBM SPSS Statistics version 26.0. Classification accuracy was assessed using leave-one-out cross-validation with equal prior probabilities. Statistical significance for t-tests and Wilks’ lambda was set at α = 0.05.
3. Results
3.1. Measurement Reliability
All osteometric variables demonstrated high measurement reliability (Table 1). Intra-observer assessment showed excellent consistency, with rTEM below 1% and R values exceeding 0.99 for all parameters. Inter-observer reliability remained acceptable, with rTEM ranging from 0.48% to 2.83% and R values above 0.88. Femoral head diameter exhibited the highest inter-observer variability (rTEM = 2.83%) but remained within acceptable thresholds. All variables met the predetermined reliability criteria (rTEM < 5%, R > 0.95 for intra-observer; R > 0.85 for inter-observer), confirming adequate measurement precision for discriminant function analysis. Femur weight was not included in reliability assessment as measurements were obtained using a calibrated digital precision scale with automated recording, eliminating observer-dependent variability.

Table 1.
Intra-observer and inter-observer measurement reliability.
3.2. Sexual Dimorphism
Descriptive statistics for all osteometric variables are presented in Table 2. Male femora consistently exhibited larger dimensions than female femora across all parameters, with all differences being statistically significant (p < 0.01). The sexual dimorphism magnitude, expressed as percentage difference, ranged from 6.56% to 42.27%. Femur weight demonstrated the highest dimorphism (42.27%), followed by femoral neck circumference, femoral vertical head diameter, and femoral bicondylar width. Linear length measurements showed lower dimorphism, and t-values ranged from 15.51 to 26.84, with femoral bicondylar width (t = 26.84), femoral vertical head diameter, and femoral neck circumference demonstrating high discriminatory capacity, indicating substantial potential for sex classification.

Table 2.
Descriptive statistics and sexual dimorphism of femoral measurements.
3.3. Discriminant Function Analysis for Sex Estimation
3.3.1. Discriminant Function Statistics
Discriminant function statistics revealed varying discriminatory capacity across analytical approaches (Table 3). Complete femur models demonstrated the strongest performance, with direct entry and stepwise methods achieving canonical correlations of 0.790 and 0.787, respectively. Among isolated segments, proximal and distal regions exhibited comparable discriminatory power (canonical correlations: 0.747 and 0.752), substantially exceeding that of the diaphyseal segment (0.590). Combined segment models showed intermediate performance, with the proximal–distal combination yielding the highest canonical correlation (0.771) among combined approaches. All discriminant functions demonstrated highly significant group separation (Wilks’ λ = 0.376–0.652, p < 0.01), with eigenvalues ranging from 0.534 to 1.657 reflecting varying degrees of sex differentiation capacity.

Table 3.
Discriminant function statistics for sex classification models.
3.3.2. Classification Accuracy Performance
Cross-validated classification accuracies varied considerably across models (Table 4). Complete femur approaches achieved the highest performance, demonstrating that four optimally selected variables perform comparably to all eight parameters. Among isolated segments, proximal segments achieved 89.64% accuracy, followed by distal and diaphyseal segments. Female specificity consistently exceeded male sensitivity across all approaches. Combined segment models demonstrated synergistic improvements, with proximal–diaphyseal and proximal–distal combinations approaching complete femur performance.

Table 4.
Discriminant function coefficients and classification accuracy for sex estimation models.
4. Discussion
This study has developed discriminant function equations for sex estimation from Thai femora. This approach is similar to previous reports demonstrating methodological robustness through high measurement reliability and rigorous cross-validation [5,6,17]. Complete femur stepwise analysis achieved 90.47% accuracy using four optimally selected variables, performing comparably to eight-variable models (91.25%), supporting parsimony in forensic applications [18]. This study addressed an important methodological area by systematically and comprehensively evaluating isolated femoral segments despite the high prevalence of fragmentary remains in forensic contexts [19,20,21]. Segment-specific accuracies ranged from 80.88% to 89.64%, with proximal and distal regions demonstrating superior discriminatory capacity consistent with established sexual dimorphism patterns in long bones. Combined segment models demonstrated synergistic effects, with proximal–diaphyseal and proximal–distal combinations approaching complete femur performance. Female specificity consistently exceeded male sensitivity, likely reflecting greater morphological homogeneity in female dimensions [22,23]. These findings validate the femur as a reliable element for sex estimation in Thai populations, providing population-specific equations applicable to both complete and fragmentary remains.
This study employed leave-one-out cross-validation (LOOCV), a rigorous internal validation approach that systematically tests each femur against a discriminant function developed from all other specimens [5,9]. LOOCV minimizes overfitting and produces unbiased accuracy estimates when independent datasets are unavailable. The cross-validated accuracies of 90.47% for complete femora and 89.64% for proximal segments demonstrate robust classification performance within the studied population characteristics. The negligible reduction from original accuracies (less than 1 percentage point) demonstrates that the equations maintain consistent performance and are not overfitted to the training data, confirming the stability and predictive reliability of the developed discriminant functions. While external validation using independent Thai samples represents a necessary validation benchmark [11] and would further strengthen generalizability, the current LOOCV results provide strong evidence of equation reliability for forensic applications.
Sexual dimorphism analysis revealed that Thai male femora consistently exceeded female dimensions across all parameters, with percentage differences ranging from 6.56 to 42.27%. The magnitude of dimorphism directly influenced segment-specific discriminatory capacity, with proximal and distal measurements demonstrating substantially higher dimorphism than diaphyseal dimensions. Femoral vertical head diameter exhibited the highest discriminatory power. Such a result might reflect its biomechanical role in transmitting hip joint reaction forces of 2–5× body weight, which scale with body mass and sex-specific loading patterns [24,25,26]. Femoral neck circumference similarly revealed high dimorphism through integration of structural reinforcement against habitual mechanical stresses as previously described [27]. These highly dimorphic measurements contributed to the superior accuracy of the proximal segments. The distal bicondylar width achieved discriminatory capacity through sensitivity to pelvic morphology and lower limb biomechanics. The distal segment’s high performance could have resulted from a single measurement [28]. Conversely, diaphyseal measurements showed lower dimorphism, as midshaft dimensions respond primarily to mechanical loading rather than sex-specific developmental patterns [27], producing high within-sex variability that diminished segment accuracy to 80.88%. Femur weight demonstrated exceptionally pronounced dimorphism, substantially exceeding dimensional differences and likely amplified by age-related bone loss. This is reflected in the sample’s mean age (64.83 years), which encompasses postmenopausal females who experience cumulative bone mineral density decline of 15–30%, while males exhibit gradual and substantially slower decline [29,30,31]. However, preservation requirements and taphonomic alterations severely limit weight-based applications in fragmentary remains. Taphonomic processes, including soil infiltration and weathering, substantially alter bone mass, obscuring sex differences. Incomplete recovery and postmortem modifications such as burning or aquatic submersion create unpredictable mass changes, while weight requires complete structural integrity rarely achieved in forensic contexts. Therefore, femur weight should only be used with complete intact femora showing minimal taphonomic alteration, whereas linear and circumferential measurements should be prioritized for most forensic cases.
Fragmentary bone analysis represents an essential consideration in forensic anthropology, as skeletal fragmentation is commonly encountered with differential preservation favoring denser regions [32,33,34]. Proximal segments achieved 89.64% accuracy, differing by only 0.83 percentage points from complete femur performance despite utilizing two measurements; this indicates that these fragments are effective complete specimen substitutes [35,36]. Distal segments demonstrated remarkable efficiency, achieving 86.25% accuracy from the bicondylar width alone by integrating multiple biomechanical factors into a single dimension [28,37]. Diaphyseal segments yielded lower accuracy (80.88%) due to reduced sexual dimorphism in midshaft dimensions. This lower dimorphism results from midshaft dimensions responding primarily to mechanical loading [27], which produces high variability within each sex rather than between sexes [16]. While this study used systematic segmentation, the equations remain applicable when fragments preserve sufficient anatomical landmarks. For practical implementation, practitioners should identify preserved regions and select appropriate equations: for complete femora use the four-variable equation, for proximal fragments use the two-variable equation, for distal fragments use bicondylar width, and use diaphyseal segments when alternatives are unavailable. Combined segment equations should be prioritized when multiple fragments are available. This extends sex estimation capability beyond complete-bone-only methods, though validation with naturally fragmented cases represents an important next step.
Previous Thai studies have demonstrated high sex discrimination accuracies from complete femora, with Monum et al. [4] and Boonthai et al. [7] achieving 81.7–91.0% sex classification rates using intact specimens. However, systematic evaluation of fragmentary femora for sex discrimination has not been conducted in Thai populations despite the prevalence of skeletal fragmentation in forensic contexts. Comparative evaluation of fragmentary femur performance with international studies demonstrates population-specific variation in segment-specific sex estimation accuracies. (Table 5). European [35,38,39,40,41] and American [42] populations have been shown to achieve high accuracies, with Chilean samples [36] reaching exceptional performance at 95.7%—the highest reported accuracy—while Asian populations exhibit greater variability, as evidenced by lower Sri Lankan [16] accuracies observed across segments. The current study conducted in a Thai population has similar results within this context, substantially exceeding Sri Lankan performance across all segments. This superior performance likely reflected methodological advantages, including larger sample size, enhanced measurement precision, and population-specific characteristics. Notably, Thai distal segment accuracy substantially exceeds Sri Lankan distal performance by 15.8 percentage points and approaches European proximal segment accuracies, demonstrating that bicondylar width maintains robust discriminatory capacity comparable to traditionally favored proximal measurements.

Table 5.
Comparative accuracy of femoral segment-specific sex estimation methods across populations.
5. Conclusions
This study has developed population-specific discriminant function equations for sex estimation from Thai femora with high measurement reliability and validation, achieving 80.88–91.25% accuracy across complete and fragmented femora. Systematic segment evaluation provided utility (80.88%) despite limitations. Combined approaches demonstrated synergistic effects approaching complete femur accuracy. These validated methodologies for forensic and archeological contexts contribute to Thai osteometric data, demonstrating that strategic region selection maintains high accuracy despite skeletal incompleteness.
Limitation of Study
The femur weight is only applicable to intact specimens unaffected by taphonomic alteration or soil infiltration, making it unreliable in environmentally compromised contexts. Substantial elderly representation (mean age: 64.83 years) may amplify sexual dimorphism in weight-related parameters through age-related bone loss. Caution is advised when applying equations incorporating femur weight to younger populations. Diaphyseal measurements require midshaft identification, which is only feasible when terminal ends exhibit minor damage, limiting their utility in severely fragmented remains. In addition, the systematic segmentation approach establishes population-specific equations that remain applicable when fragmentary remains preserve identifiable anatomical landmarks, providing forensic practitioners with validated tools despite skeletal incompleteness. Future validation with naturally fragmented specimens would further enhance real-world applicability.
Author Contributions
Conceptualization, C.P., N.C., W.B. and S.D.; methodology, S.D., N.C., W.B. and C.P.; formal analysis, N.C., W.B., S.D. and C.P.; resources, N.T., S.A. and S.I.; data curation, J.C., S.L., S.I. and K.S.; visualization, J.C. and S.L.; writing—original draft preparation, S.D. and S.I.; writing—review and editing, all authors; project administration, C.P.; funding acquisition, S.D. and C.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by an undergraduate student thesis grant from the Faculty of Medical Science, Naresuan University, Thailand.
Institutional Review Board Statement
This investigation received ethical approval from the Center for Ethics in Human Research, Khon Kaen University (HE671557) 2 October 2024.
Informed Consent Statement
According to KKUEC's Exemption Determination Regulation 6.7.3, which specifically covers “Research studying bones, skeletons, extracted teeth, and cadavers.” As our study involves skeletal remains (cadaveric bones) and falls under the exemption category, informed consent was not required.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors express their sincere gratitude for the femoral specimens provided for use in this study. We are profoundly grateful to the body donors whose selfless contributions made this research possible and will contribute to advancing forensic identification practices. During the preparation of this work, the authors used Claude Sonnet 4.5 for sentence refinement, grammatical verification, and minor translation. All conceptual frameworks, analytical approaches, research interpretations, scholarly discussions, and conclusions presented in this study remain the exclusive intellectual contribution of the authors. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the published article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Austin, D.; King, R.E. The Biological Profile of Unidentified Human Remains in a Forensic Context. Acad. Forensic Pathol. 2016, 6, 370–390. [Google Scholar] [CrossRef]
- Garoufi, N.; Bertsatos, A.; Chovalopoulou, M.E.; Villa, C. Forensic sex estimation using the vertebrae: An evaluation on two European populations. Int. J. Legal Med. 2020, 134, 2307–2318. [Google Scholar] [CrossRef]
- Bakici, R.S.; Ayvat Ocal, Z.; Meral, O.; Oner, Z.; Oner, S. Estimation of sex from femoral bone using radiological imaging methods in Turkish population. Anthropol. Anz. 2024, 81, 361–371. [Google Scholar] [CrossRef]
- Monum, T.; Prasitwattanseree, S.; Das, S.; Siriphimolwat, P.; Mahakkanukrauh, P. Sex estimation by femur in modern Thai population. Clin. Ter. 2017, 168, e203–e207. [Google Scholar] [PubMed]
- Curate, F.; Umbelino, C.; Perinha, A.; Nogueira, C.; Silva, A.M.; Cunha, E. Sex determination from the femur in Portuguese populations with classical and machine-learning classifiers. J. Forensic Leg. Med. 2017, 52, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Ujaddughe, O.M.; Haberfeld, J.; Bidmos, M.A.; Olateju, O.I. Evaluation of standards for sex estimation using measurements obtained from reconstructed computed tomography images of the femur of contemporary Black South Africans. Int. J. Legal Med. 2025, 139, 1409–1422. [Google Scholar] [CrossRef] [PubMed]
- Boonthai, W.; Poodendaen, C.; Kamwong, J.; Sangchang, P.; Duangchit, S.; Iamsaard, S. Sex and stature estimations from dry femurs of Northeastern Thais: Using a logistic and linear regression approach. Transl. Res. Anat. 2025, 38, 100376. [Google Scholar] [CrossRef]
- Nhoem, S.; Domett, K. Sex estimation by discriminant function analysis of long bones in prehistoric Southeast Asian populations. Int. J. Osteoarchaeol. 2024, 35, e3365. [Google Scholar] [CrossRef]
- Rani, D.; Krishan, K.; Kanchan, T. A methodological comparison of discriminant function analysis and binary logistic regression for estimating sex in forensic research and case-work. Med. Sci. Law. 2022, 63, 227–236. [Google Scholar] [CrossRef]
- Cuzzullin, M.C.; Curate, F.; Freire, A.R.; Costa, S.T.; Prado, F.B.; Júnior, E.D.; Cunha, E.; Rossi, A.C. Validation of anthropological measures of the human femur for sex estimation in Brazilians. Aust. J. Forensic Sci. 2020, 54, 61–74. [Google Scholar]
- Poodendaen, C.; Choompoo, N.; Namvongsakool, P.; Linlad, S.; Chalermrerm, J.; Duangchit, S.; Boonthai, W.; Iamsaard, S.; Aorachon, P.; Putiwat, P. External validation of femoral sex estimation equations: Evidence supporting population-specific standards in forensic anthropology. Transl. Res. Anat. 2025, 41, 100445. [Google Scholar] [CrossRef]
- Flavel, A.; Franklin, D. Counting human bone fragments using landmarks: Camposanto case study. Aust. J. Forensic Sci. 2024, 56, 187–190. [Google Scholar] [CrossRef]
- Christensen, A.M.; Hefner, J.T.; Smith, M.A.; Webb, J.B.; Bottrell, M.C.; Fenton, T.W. Forensic Fractography of Bone: A New Approach to Skeletal Trauma Analysis. Forensic Anthropol. 2018, 1, 32–51. [Google Scholar] [CrossRef]
- Indra, L.; Errickson, D.; Young, A.N.; Lösch, S. Uncovering Forensic Taphonomic Agents: Animal Scavenging in the European Context. Biology 2022, 11, 601. [Google Scholar] [CrossRef] [PubMed]
- Moraitis, K.; Eliopoulos, C.; Spiliopoulou, C. Fracture Characteristics of Perimortem Trauma in Skeletal Material. Internet J. Biol. Anthropol. 2008, 3, 1–8. [Google Scholar]
- Ranaweera, L.; Cabral, E.; Dissanayake, D.M.R.M.; Lakshan, W.S.V. Estimation of Sex from the Osteometric Measurements of the Femur in a Contemporary Sri Lankan Population. Int. J. Morphol. 2022, 40, 1009–1017. [Google Scholar] [CrossRef]
- Albanese, J. A method for estimating sex using the clavicle, humerus, radius, and ulna. J. Forensic Sci. 2013, 58, 1413–1419. [Google Scholar] [CrossRef]
- Morrison, G.S. In the context of forensic casework, are there meaningful metrics of the degree of calibration? Forensic Sci. Int. Synerg. 2021, 3, 100157. [Google Scholar] [CrossRef]
- Das, A.; Hembram, P.; Roy, K.; Mukherjee, S.; Bhandari, R.; Kundu, S. Reconstructions of Length of Radius From its Fragments- A Pilot Study in Eastern Indian Population. J. Indian Acad. Forensic Med. 2023, 45, 153–158. [Google Scholar] [CrossRef]
- Alfsdotter, C. Forensic archaeology and forensic anthropology within Swedish law enforcement: Current state and suggestions for future developments. Forensic Sci. Int. Rep. 2021, 3, 100178. [Google Scholar] [CrossRef]
- Ubelaker, D.H.; Wu, Y. Fragment analysis in forensic anthropology. Forensic Sci. Res. 2020, 5, 260–265. [Google Scholar] [CrossRef]
- Candelas González, N.; Rascón Pérez, J.; Chamero, B.; Cambra-Moo, O.; González Martín, A. Geometric morphometrics reveals restrictions on the shape of the female os coxae. J. Anat. 2017, 230, 66–74. [Google Scholar] [CrossRef] [PubMed]
- Caiaffo, V.; Feitosa de Albuquerque, P.P.; Virginio de Albuquerque, P.; Duarte Ribeiro de Oliveira, B. Sexual Diagnosis Through Morphometric Evaluation of the Proximal Femur. Int. J. Morphol. 2019, 37, 391–396. [Google Scholar] [CrossRef]
- Banerjee, S.; Pivec, R.; Issa, K.; Kapadia, B.H.; Khanuja, H.S.; Mont, M.A. Large-diameter femoral heads in total hip arthroplasty: An evidence-based review. Am. J. Orthop. 2014, 43, 506–512. [Google Scholar]
- Cridlin, S. Piecewise Regression Analysis of Secular Change in the Maximum Femoral Vertical Head Diameter of American White Males and Females. Hum. Biol. 2016, 88, 47–55. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Pomeroy, E.; Mushrif-Tripathy, V.; Kulkarni, B.; Kinra, S.; Stock, J.T.; Cole, T.J.; Shirley, M.K.; Wells, J.C.K. Estimating body mass and composition from proximal femur dimensions using dual energy x-ray absorptiometry. Archaeol. Anthropol. Sci. 2019, 11, 2167–2179. [Google Scholar] [CrossRef]
- Ruff, C.; Holt, B.; Trinkaus, E. Who’s afraid of the big bad Wolff?: “Wolff’s law” and bone functional adaptation. Am. J. Phys. Anthropol. 2006, 129, 484–498. [Google Scholar] [CrossRef]
- Singh, P.K.; Karki, R.K.; Palikhe, A.K.; Menezes, R.G. Sex Determination From the Bicondylar Width of the Femur: A Nepalese Study Using Digital X-ray Images. Kathmandu Univ. Med. J. 2016, 55, 198–201. [Google Scholar]
- Cheng, X.-G.; Yang, D.-Z.; Zhou, Q.; Zhuo, T.-J.; Zhang, H.-C.; Xiang, J.; Wang, H.-F.; Ou, P.-Z.; Liu, J.-L.; Xu, L.; et al. Age-Related Bone Mineral Density, Bone Loss Rate, Prevalence of Osteoporosis, and Reference Database of Women at Multiple Centers in China. J. Clin. Densitom. 2007, 10, 276–284. [Google Scholar] [CrossRef]
- Khosla, S.; Monroe, D.G. Regulation of Bone Metabolism by Sex Steroids. Cold Spring Harb. Perspect. Med. 2018, 8, a031211. [Google Scholar] [CrossRef]
- Almeida, M.; Laurent, M.R.; Dubois, V.; Claessens, F.; O’Brien, C.A.; Bouillon, R.; Vanderschueren, D.; Manolagas, S.C. Estrogens and Androgens in Skeletal Physiology and Pathophysiology. Physiol. Rev. 2017, 97, 135–187. [Google Scholar] [CrossRef]
- Ubelaker, D.H.; Khosrowshahi, H. Estimation of age in forensic anthropology: Historical perspective and recent methodological advances. Forensic Sci. Res. 2019, 4, 1–9. [Google Scholar] [CrossRef]
- Kolpan, K.E.; Vadala, J.; Dhanaliwala, A.; Chao, T. Utilizing augmented reality for reconstruction of fractured, fragmented and damaged craniofacial remains in forensic anthropology. Forensic Sci. Int. 2024, 357, 111995. [Google Scholar] [CrossRef]
- Jankova, R. Anthropological analysis of human skeletal remains in forensic cases. J. Morphol. Sci. 2024, 7, 77–83. [Google Scholar] [CrossRef]
- Colman, K.L.; Janssen, M.C.L.; Stull, K.E.; van Rijn, R.R.; Oostra, R.J.; de Boer, H.H.; van der Merwe, A.E. Dutch population specific sex estimation formulae using the proximal femur. Forensic Sci. Int. 2018, 286, 268.e1–268.e8. [Google Scholar] [CrossRef] [PubMed]
- Carvallo, D.; Retamal, R. Sex estimation using the proximal end of the femur on a modern Chilean sample. Forensic Sci. Int. Rep. 2020, 2, 100077. [Google Scholar] [CrossRef]
- Alunni-Perret, V.; Staccini, P.; Quatrehomme, G. Sex determination from the distal part of the femur in a French contemporary population. Forensic Sci. Int. 2008, 175, 113–117. [Google Scholar] [CrossRef] [PubMed]
- Curate, F.; Coelho, J.; Gonçalves, D.; Coelho, C.; Ferreira, M.T.; Navega, D.; Cunha, E. A method for sex estimation using the proximal femur. Forensic Sci. Int. 2016, 266, 579.e1–579.e7. [Google Scholar] [CrossRef]
- Wysocka, J.; Cieślik, A.I.; Danel, D.P. Sex estimation using measurements of the proximal femur in a historical population from Poland. Anthropol. Rev. 2023, 86, 37–49. [Google Scholar] [CrossRef]
- Clavero, A.; Salicrú, M.; Turbón, D. Sex prediction from the femur and hip bone using a sample of CT images from a Spanish population. Int. J. Leg. Med. 2015, 129, 373–383. [Google Scholar] [CrossRef]
- du Jardin, P.; Ponsaillé, J.; Alunni-Perret, V.; Quatrehomme, G. A comparison between neural network and other metric methods to determine sex from the upper femur in a modern French population. Forensic Sci. Int. 2009, 192, 127.e1–127.e6. [Google Scholar] [CrossRef]
- Albanese, J.; Eklics, G.; Tuck, A. A metric method for sex determination using the proximal femur and fragmentary hipbone. J. Forensic Sci. 2008, 53, 1283–1288. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).