Geomechanical Modeling of the Northern Katpar Deposit (Kazakhstan): Assessing the Impact of Rock Mass Disturbance on Stability Safety Factor

Abstract

The development of a geomechanical model is aimed at enhancing the safety of mining operations through the determination of optimal slope angles and the probabilistic assessment of pit wall stability. For the conditions of open-pit mining, three-dimensional geomechanical models were constructed based on the calculation of the slope stability factor using the Rocscience Slide2/Slide3 (v.9.027, 2023) software package. The stress–strain state of the rock mass at the final stage of extraction was evaluated using the finite element method. Strength reduction factors (SRF) were determined considering the physico-mechanical properties of the rocks forming the near-contour zone of the massif. The stability of the pit slopes was assessed along individual geological cross-sections in accordance with the design contours of the Northern Katpar open pit. Calculations performed using several methods confirmed the overall stability of the pit walls. The final design parameters of the projected open pit were determined. For the first time, it was established that in the southern and southwestern sectors of the Northern Katpar pit, within the elevation range of +700 to +400 m, a reduction in the SFR (from 1.18 to 1.41) occurs due to the predominance of siltstones and the presence of tectonic disturbances. The generalized results of numerical slope stability analyses for the design pit contour, together with the developed geological–structural model of the deposit, provide a basis for ensuring the safe conduct of mining operations at the site.

1. Introduction

One of the key challenges of modern open-pit mining remains to ensure slope stability while simultaneously improving the efficiency of mining operations [1,2,3]. As reserves in deposits with simple geological structures and high grades are depleted, the industry inevitably shifts to deeper horizons and to areas with complex block fault structures, variable hydrogeological regimes, and anisotropic rock properties [4,5,6]. This shift increases extraction costs, necessitates a revision of initial design decisions, and raises the bar for justifying overall slope angles and bench parameters in deep pits [7,8,9].

With increasing mining depth, slope stability issues acquire not only technical but also pronounced economic significance: rational slope configurations reduce overburden volumes, optimize haul distances, and extend the service life of operating enterprises [10,11,12]. Practice shows that even a moderate increase in admissible slope angles can yield a substantial cumulative effect over a pit’s life cycle [13,14]. At the same time, any increase in slope angle is permissible only when reliable information on the geomechanical state of the rock mass is available and risk scenarios are controlled [15,16].

A fundamental prerequisite for adjusting design parameters is obtaining representative data on the stress–strain state, structural–geological features, lithology, jointing, and physico-mechanical characteristics of the host rocks and ore bodies, as well as on their water saturation and possible degradation of properties over time [17,18,19,20]. Under these conditions, classical limit equilibrium methods often prove insufficient because of simplifying assumptions regarding geometry and properties; numerical approaches (finite element/finite difference methods and hybrid schemes) are required to account for nonlinearity and spatial heterogeneity of parameters [21,22,23].

Current studies emphasize the value of an integrated cycle—“field observations–laboratory testing–geomechanical modeling–inverse calibration”—in which results of instrumental monitoring (geodetic surveys, inclinometry, strain and pore pressure measurements) are used to refine model parameters and verify computational slope stability scenarios [24,25]. This approach is especially important in the presence of tectonic disturbances, weathered zones, local inflows, and layer–joint anisotropy, where stability is governed by the weakest links in the rock mass structure [26,27].

Against this background, the scientific novelty of the present work lies in a comprehensive justification of open-pit design parameters considering the combined influence of: (I) lithology and block–joint structure; (II) the range of physico-mechanical properties upscaled to rock mass scale via the Geological Strength Index (GSI); (III) water saturation and pore pressure as factors reducing effective strength; and (IV) bench geometry and the overall configuration of pit walls. For the case study, three-dimensional block modeling of the rock mass stress–strain state was performed with variation in GSI and shear strength parameters under Mohr–Coulomb/Hoek–Brown criteria; the dependence of the on GSI levels (in particular, at GSI 40, 50 and higher) was established and linked to rational choices of overall slope angle and parameters of newly designed benches at deeper horizons [28,29,30,31]. Additionally, scenarios of changing filtration conditions (flooding/drainage), including the influence of captured horizons and local pressure relief, were examined to incorporate realistic hydro-geomechanical coupling and assess solution sensitivity to water saturation [32,33].

The practical significance of the work is the formation of a reproducible design methodology: from acquiring source data and their statistical normalization to parametric computational ranges and ranking of safe slope configurations under operational constraints and target risk levels. The proposed approach provides defensible decisions, readiness to assimilate monitoring results for on-the-fly model updates, and a foundation for critically important optimization of capital and operating expenditures without compromising industrial safety [34,35,36]. Taken together, this creates prerequisites for the safe development of deeper and structurally complex areas—especially relevant for operating enterprises exploiting deposits at late life-cycle stages.

2. Materials and Methods

The Northern Katpar deposit is located within a gently undulating intermountain depression, characterized by relative elevation differences ranging from 5 to 10 m and a general slope of the surface from the south and west towards the northeast and east. The absolute surface elevations vary between 698 and 707.8 m. Mineralization occurs at depths ranging from 2 to 520 m. The ore bodies are predominantly steeply dipping, although horizontal and gently dipping forms of occurrence are also present. The thickness of the ore bodies varies significantly, from 10 to 370 m. Morphologically, they are represented by tabular, ellipsoidal, sinuous, lenticular, crescent-shaped, and swollen forms. Within the deposit, three genetic types of ores are distinguished: oxidized ores, associated with clayey and clay–rubble weathering crusts; skarn–greisen ores, confined to recrystallized limestones and marbles; and quartz–greisen ores, developed in granites. Structurally, the deposit is situated in the central part of the Uspensky synclinorium, within the Akamay–Katpar ore zone.

The tungsten-bearing Northern Kappar deposit (Kazakhstan) is predominantly characterized by a two-tiered structure. The upper tier is composed of unconsolidated and semi-consolidated soils, while the lower tier consists of dislocated bedrock, including recrystallized limestones, marbles, skarns, siltstones, sandstones, metasomatites, granites, diorites, and diabase porphyrites. The deposit is classified as being of medium complexity, as it is confined to fractured and dislocated rock masses with zones of crushing and weathering, overlain by both cohesive and non-cohesive soils. Tungsten ores contain between 0.2 and 1% tungsten, and therefore, the extraction of an industrially significant quantity of metal requires the processing of large volumes of ore.

Open-pit mining of tungsten-bearing ores using a complex of drilling and blasting operations, even when conducted in accordance with project documentation, does not always guarantee the absence of deformations of pit slopes, local slope sections, or benches, particularly during the formation of the final pit contour. The causes of slope instability vary depending on geological, engineering–geological, hydrogeological conditions, and the design parameters of the slope in a specific section of the pit field.

The open-pit extraction of ore reserves leads to changes in the stress–strain state of the rock mass, which increases the risk of landslides or collapses. Excessively steep slope angles may cause slope failures, while overly gentle angles significantly increase the volume of overburden removal. Therefore, ensuring the safety of open-pit mining operations by substantiating the optimal design parameters of the pit, including slope angles under various complicating factors and orebody discontinuities, is a highly relevant task. Such substantiation must be based on the lithology and physico-mechanical properties of the near-slope rock mass, employing geomechanical modeling methods.

Analytical studies of the structural and geomechanical conditions of the deposit have made it possible to identify the main factors contributing to the reduction in slope stability.

Administratively, the deposit is located in the Shet District of the Karaganda Region, 35 km from the Zharik railway station (Figure 1).

Figure 1. Overview map of the study area.

The geological structure of the deposit has a two-tiered character: the upper tier is composed of unconsolidated and semi-consolidated sediments, whereas the lower tier consists of disturbed hard rocks, including marbleized limestones, marbles, skarns, siltstones, sandstones, metasomatites, granites, diorites, diabases, and porphyrites. The thickness of the loose overburden varies from 0 to 220 m, with an average of about 36 m. The region is considered seismically stable, with no significant landslide hazards. The system of tectonic faults within the deposit has been studied in detail and is illustrated in Figure 2.

Figure 2. Tectonic disturbances of the North Katpar deposit.

According to the engineering–geological classification of the VSERINGEO Institute [37], the deposit, based on its geological–structural position, engineering–geological, and hydrogeological conditions, belongs to Type V (in massifs of rhythmically interbedded latitudinally layered rocks of marginal troughs). In terms of the complexity of its study, it is classified as a medium–complexity deposit, confined to fractured and dislocated hard rocks (yellow color), with the presence of crushed zones (light green color), weathered zones (orange color), overlain by cohesive (dark green color) and non–cohesive (blue color) soils.

The Severny Katpar deposit is classified as moderately complex and is associated with fractured and disjunctively disturbed hard rocks that include zones of crushing and weathering, overlain by both cohesive and non-cohesive soils. According to the geological–structural features of the deposit and the physico-mechanical properties of the rocks, the pit wall materials are subdivided by stability conditions as follows: very unstable conditions are characteristic of Neogene clays and clay–detrital soils within the weathering crust, where the overall thickness of unconsolidated overburden exceeds 20 m; unstable conditions are associated with highly fractured rocks in zones of crushing and weathering, where the increased fracturing significantly reduces cohesion and the overall stability of the rock mass; moderately stable conditions correspond to transition zones with moderately fractured rocks between strongly weathered and nearly monolithic formations; stable conditions are observed in weakly fractured or almost monolithic rocks located outside structurally weakened zones.

Several key factors influence the reduction in slope stability under open-pit mining conditions. Among them are the presence of faults, loose overburden, and fracturing in the rocks; the high susceptibility of rocks to weathering, with the weathering crust being widely developed across the deposit and reaching a thickness of up to 220 m, particularly near the intersections of tectonic faults, and composed predominantly of clayey materials; and the structural heterogeneity of the rock mass, whereby pit walls often contain zones of increased fracturing coinciding with tectonic disturbance zones. Major fault systems and their associated fracture networks lead to a reduction in structural strength and a significant decrease in cohesion values, which directly affects the slope stability factor. Once such zones are exposed, weathering processes intensify, further diminishing slope stability. In addition, the presence of groundwater within the study area reduces the available stability margin.

The tectonic framework of the deposit is formed by two main fault systems: the northeast sublatitudinal faults of the Uspensky type, which include deep-seated dislocations such as thrusts, reverse faults, normal faults, and overlaps that pose significant risks to slope stability; and the northwest regional faults, characterized by steeply dipping normal faults, reverse faults, and strike–slip dislocations. Other identified faults are of secondary nature and originate from these two principal systems.

One of the primary tasks in open-pit mining is to ensure operational safety while achieving effective and rational extraction of mineral resources. As mining operations progress to greater depths, the expansion of pit slopes and the increase in overburden removal volumes become inevitable. An alternative approach to involving deeper horizons in exploitation without a substantial rise in production costs is to revise the initial design and increase the slope angle of the final pit contour. However, this approach raises serious concerns regarding slope stability and the selection of geomechanically justified parameters for newly designed benches at greater depths.

A fundamental requirement for revising the initial plans is the availability of comprehensive information on the geomechanical state of the rock mass, including stress–strain conditions, structural and geological features, and the physico-mechanical properties of the host rocks and ores. Existing industrial methods often do not allow for a full consideration of the complexity of conditions encountered in deep open pits.

The mathematical framework of the experiment based on the finite element method (FEM) was implemented through three stages: discretization (the studied domain of the problem is divided into subdomains—finite elements), approximation (using discrete functions, each defined on a finite element), and algebraization (substitution of the approximating functions into the governing equations to obtain a system with respect to the studied parameters).

The size of each finite element ranges from 0.4 to 0.5 m, resulting in a total of more than 100,000 finite elements, each assigned specific physico-mechanical and strength parameters.

A geomechanical model of the deposit was developed to visualize and compute the spatial distribution of lithological units and to delineate stability categories of the rock mass, which serve as the basis for determining optimal pit slope parameters at the stages of mine design, construction, and subsequent extraction of tungsten-bearing ores. The study requires analyzing processes that are mathematically described by partial differential equations. The variational formulation of the finite element method (FEM) adopted herein, together with the model of the stress–strain distribution, follows the classical foundations of FEM. The behavior of the sought function in a bounded domain with its boundary is governed by a differential equation involving a parameter that characterizes the properties of a continuous medium under external actions, a differential operator of partial derivatives, the unknown field itself, and the spatial coordinates. The solution is a function that minimizes a suitable functional whose argument is the unknown field. Substituting the grid (discrete) representation of the field into the governing expression enables evaluation of the function at any point of the solution domain; subsequent differentiation and integration yield additional problem parameters of interest. The methodological framework rests on geomechanical modeling of the geomechanical state of the rock mass, analysis of the mining and geological conditions of the deposit, and evaluation of the physico-mechanical and strength properties of the rocks to substantiate pit slope stability parameters. For the Northern Katpar deposit (Karaganda region), the geomechanical justification of slope parameters was carried out on the basis of numerical simulation. In accordance with national standards, slope and bench parameters are commonly determined via the SFR using classical limit equilibrium methods; however, such methods do not capture structural discontinuities in the rock mass, which can markedly reduce slope stability. Most conventional models consider only the self-weight of the potentially sliding mass. In hard rock settings, where horizontal stresses may exceed vertical stresses, neglecting unloading-induced deformations can lead to hazardous situations in pits deeper than 200–250 m. Unloading produces significant deformation, including subparallel cracking along slopes (near the toe), partitioning the mass into steeply dipping blocks prone to toppling or flexural failure. The baseline procedure for assessing slope stability in heterogeneous masses includes constructing a cross-section normal to the pit wall, superposing the design outline and groundwater level, identifying lithological contacts, aquifers, potential slip surfaces, and design profiles. These elements are described mathematically using locally interpolated low-order polynomials or splines. A Cartesian system is defined with the origin at the slope toe (X directed into the massif, Y vertically upward). Characteristic (nodal) points are specified on each boundary together with the interpolation scheme (linear or quadratic). Boundaries are numbered from bottom to top, and nodal points are ordered by increasing X. An approximate slip surface is then defined, average input parameters are computed by a weighted-average procedure, and the SFR is evaluated. Numerical simulations were performed in Rocscience software for the full design depth of the pit. Both circular–cylindrical and cylindrical slip surfaces were modeled to assess stability for cylindrical and non-cylindrical failure mechanisms in rocks and soils.

3. Discussion

An analysis of the stability of the near-slope rock mass was carried out using geomechanical modeling methods based on the finite element method (FEM) to assess the stress–strain state under the influence of controlling factors. The methodology for the development and study of a geomechanical model of the deposit under open-pit mining conditions includes the following objectives: substantiating mining parameters; ensuring safe mining operations; fulfilling the production plan while reducing extraction costs; assessing predicted geological and geomechanical conditions; maintaining the stability of pit slopes throughout the mine’s operational period under all possible conditions; and forecasting the degree of rock mass fracturing.

In the study, the finite element method was applied as a numerical approach for solving differential equations arising in mathematical modeling. The method involves discretizing the problem domain into a finite number of elements, approximating the solution within each element, and then combining these to obtain a solution for the entire region. This allowed for the identification of inelastic deformation zones along pit slopes, based on three-dimensional geomechanical modeling and FEM analysis to account for factors affecting the state of the rock mass.

The stability criterion used was the Geological Strength Index (GSI), which, through deformation modulus and structural conditions, enables the assessment of maximum strength parameters of structural rock zones based on the residual strength of the rock mass. To determine the range of values of the safety factor depending on the degree of fracturing, modeling of the stress–strain state was performed at different GSI values.

The relationship between the safety factor (SRF) and the Geological Strength Index (GSI) was investigated, and a kinematic analysis of probable slope failure mechanisms along pit walls was conducted. Previous studies [38] have shown that with increasing depth of operating open pits, slope stability issues acquire significant economic importance when substantiating stable slope and bench parameters for deep pits. This, in turn, provides opportunities for the exploitation of deeper ore bodies at existing enterprises.

Earlier studies of pit slope stability were carried out along cross, longitudinal, and diagonal engineering–geological sections in the near-slope zone, considering deepening, with the use of numerical mathematical modeling and the identification of potentially hazardous areas. Various slope stability assessment methods (Spencer, E.A., Fellenius, W.K.A., Hoek, E., Sdvyzhkova, O.) [39,40,41] were applied and tested in practice when substantiating slope parameters for other open pits in Kazakhstan and neighboring countries [42].

Comparative validation. The obtained relationships between rock mass quality (GSI) and slope stability parameters (SRF/FoS) were cross-checked against independent sources. First, the linear increase in SRF with GSI reported here (see the regression equation and R² in the Results) is consistent with empirical understanding of how structural integrity governs the stability of fractured rock slopes used for design stage assessment of slope angles (see reviews and applied studies on pit wall stability [11,28,29]). Second, our FoS values for GSI = 40–60 fall within the range commonly reported for deep benches in moderately to highly jointed rock under controlled hydrogeological conditions in the cited case studies [11,28,29]. Finally, a qualitative comparison with the Northern Katpar bench stability investigation [43] shows that the recommended slope configurations and achieved safety factors are of the same order and follow the same sensitivity trend with respect to structural weakening.

Taken together, these comparisons support the conclusion that the target FoS ≈ 1.5 is exceeded for GSI ≥ 40 and corroborate the applicability of the proposed methodology— geomechanical modeling parameterized by GSI—for justifying pit slope stability in complex geomechanical settings. To further strengthen external validity, we plan to broaden the field monitoring dataset and include direct comparisons with inclinometer/geodetic measurements across several operational sections.

Possible kinematic mechanisms of planar, wedge-shaped, and toppling failures are shown in Figure 3.

Figure 3. Kinematic mechanisms of planar, wedge, and toppling failures.

The considered integration of a deterministic block theoretical assessment into the existing FEM-based methodology appears promising for accounting for the structural control of slope stability. Block theory allows for the identification of potentially removable blocks, their orientations, and dimensions at the preliminary stage, which can serve as a basis for refining boundary conditions and weakening parameters in subsequent geomechanical modeling. Such a combined approach—“block analysis + FEM calibration”—will enable a more realistic representation of the interaction between fractured structures and stress distribution within the rock mass [44].

The study was conducted to identify the relationship between the SFR and the degree of disturbance in the rock mass. The deposit contains rocks with varying stability characteristics. GSI = 40 corresponds to rocks with weakened strength properties and the presence of tectonic dislocations, whereas GSI = 50 and GSI = 60 exhibit progressively higher stability levels within the deposit under consideration.

To determine the range of SFR values corresponding to different levels of disturbance, the stress–strain state of the rock mass was modeled using the finite element method for GSI values of 40, 50, and 60. These values, respectively, represent the worst-case scenario (GSI = 40), the expected scenario (GSI = 50), and the optimistic scenario (GSI = 60). The results of stress–strain state modeling of the slope-forming rock mass at different levels of disturbance, in terms of slope displacements, are presented in Figure 4.

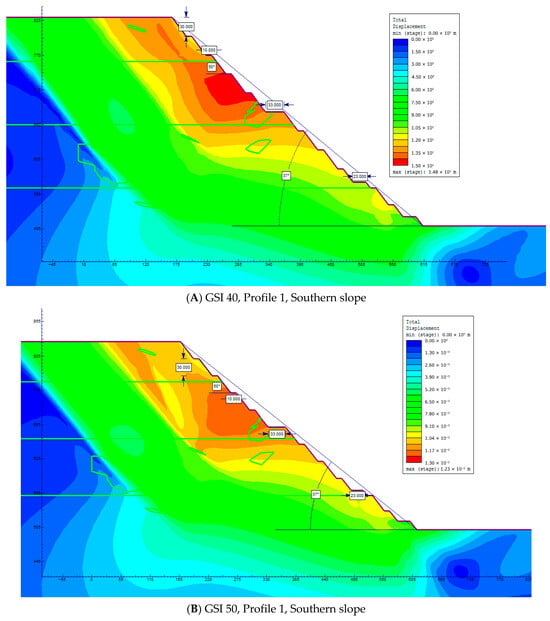
Figure 4. Finite element modeling of the stress–strain state of the slope-forming rock mass depending on the degree of fracturing.

In Figure 4, the values represent absolute displacements in meters. The color scale illustrates the distribution of the total displacement vector magnitude, ranging from 0 m (dark blue—stable zones) to 1.46 × 10⁻² m ≈ 15 mm (red—the area of maximum deformation at GSI = 50). Thus, the scale reflects the gradient of the stress–strain state of the rock mass and indicates the localization of potential plastic shear zones.

The results of finite element modeling of the stress–strain state of the slope-forming rock mass (using the southern slope as an example) are presented in Figure 5. According to the modeling results, a correlation between the SFR and the GSI value was established. The modeling showed that for GSI values of 40 and above, the SFR exceeds 1.5.

Figure 5. Relationship between the SFR and the Geological Strength Index (GSI). The correlation follows a linear trend described by the regression equation. SRF = 0.046 × GSI − 0.23 (R² = 0.98), indicating a strong positive relationship between the rock mass quality and slope stability parameters. The inclusion of the linear regression equation and the determination coefficient (R² = 0.98) confirms a high degree of correlation between the GSI value and the strength reduction factor (SRF). The linear nature of the dependence reflects the gradual increase in slope stability with the improvement of the structural integrity of the rock mass.

Analysis of the possible types of failures showed the following—Figure 6.

Figure 6. Analysis of the possible types of slope failures for different pit walls.

Recommendations regarding deformations with potential risk of slope failures are as follows: for the northern wall, there is a likelihood of local sliding within individual benches; the eastern wall also has the potential for sliding at the bench level; the southern wall is similarly prone to sliding at bench level, with an additional probability of wedge-type failures occurring on the benches. The western wall is characterized by the risk of toppling failures at the bench level, with possible wedge-type failures within certain benches.

The stability assessment of benches and pit walls was also carried out using the finite element method based on the layout of calculation lines shown in Figure 6. To determine the range of SFR values depending on the degree of rock mass disturbance, stress–strain state modeling was performed at GSI values of 40, 50, and 60.

For a detailed analysis of the pit slope stability, vertical sections of the southern, western, northern, and eastern slopes were constructed. These sections were developed within the framework of geomechanical modeling using the finite element method and make it possible to assess the stress–strain state of the rock mass under different degrees of disturbance (Figure 7).

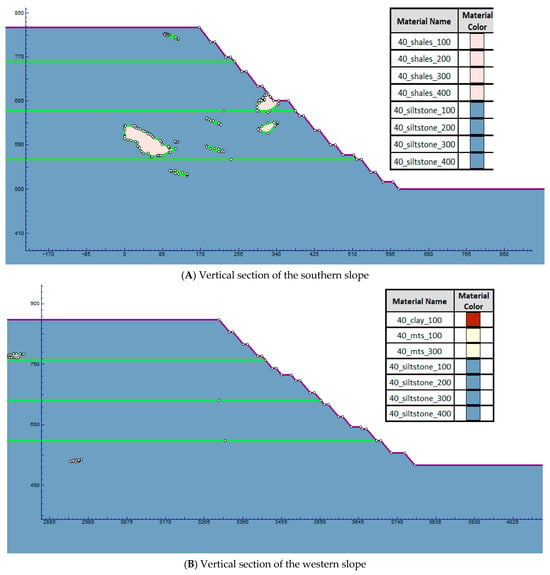
Figure 7. Stability assessment of benches and pit slopes using numerical modeling with the finite element method.

For the modeling, the following physical and mechanical properties of the rock mass and clayey materials were used, as presented in Table 1 and Table 2. The main indicators of the strength properties of the rocks (both hard and clayey) include density (γ), uniaxial compressive strength (σₛ), tensile strength (σₜ), cohesion (C), and internal friction angle (ϕ).

Table 1. Physico-mechanical properties of the hard rock mass.

Rock Type	Strength Properties						Stiffness		Failure Range
	Compressive Strength	GSI			Mi	D	Poisson’s Ratio	Young’s Modulus, MPa	Unit Weight, MN/m3
Shale	35	40	50	6	60	0.7	0.23	7600	0.026
Aleurolite	95.8	40	50	7	60	0.7	0.23	87,470	0.027
Sandstone	107.4	40	50	17	60	0.7	0.24	71,590	0.027
Metasomatite	67.8	40	50	20	60	0.7	0.24	68,080	0.028

Table 2. Physical and mechanical properties of clays.

Lab Sample Number from Geological Wells	VKR 4-21			VKR 5-21			VKR 11-21			Average Value
Lateral pressure, MPa	0.1	0.2	0.3	0.	0.2	0.3	0.1	0.2	0.3
Poisson’s ratio	0	0.4	0.29	0.07	0.51	0.36	0	0.17	0.17	0.22
Internal friction angle	22	22	22	3	3	3	1	1	1	8.67
Cohesion, MPa	0.02	0.02	0.02	0.06	0.06	0.06	0.03	0.03	0.03	0.04
Deformation modulus under load, E, MPa	1.27	2.28	4.65	0.86	1.36	1.63	0.65	1.58	0.65	1.66

A relationship has been established between the Safety Factor (SRF) and the Geological Strength Index (GSI), as shown in Figure 8.

Figure 8. Relationship between the Safety Factor (SRF) and the Geological Strength Index (GSI).

According to the simulation results, when the Geological Strength Index (GSI) reaches values of 50 or higher, the Safety Factor (SRF) exceeds 2.0, which confirms that the rock mass remains in a stable state under such conditions.

Figure 9 shows the linear relationship between the Safety Reduction Factor (SRF) and the Geological Strength Index (GSI), demonstrating the increase in slope stability with growing structural integrity of the rock mass. The regression equation SRF = 0.046 × GSI − 0.23 (R² = 0.98) confirms a strong positive correlation between rock mass quality and slope stability parameters, consistent with empirical models commonly used in geomechanical design.

Figure 9. Linear relationship between the Safety Reduction Factor (SRF) and the Geological Strength Index (GSI).

4. Conclusions

The study presents the results of slope stability assessment of open pit walls along cross-sectional, longitudinal, and diagonal engineering–geological profiles corresponding to the final geometry of the pit boundaries. Numerical modeling was performed to identify potentially hazardous zones and to quantify the relationship between the Safety Reduction Factor (SRF) and the Geological Strength Index (GSI). Kinematic analysis confirmed the prevalence of planar, wedge, and toppling failure modes along structurally controlled discontinuities.

Modeling using the Finite Element Method (FEM) demonstrated that for GSI values of 40 and above, the SRF exceeds 1.5, while at GSI = 50 and higher it surpasses 2.0, indicating stable conditions of the slope-forming rock mass. These findings can be directly applied in optimizing slope design parameters for deep open pits, allowing engineers to refine bench geometry and overall slope angles while maintaining safety margins.

The developed approach can be implemented during the design and operational stages of mining projects to update pit wall configurations in response to changes in geotechnical or hydrogeological conditions. The proposed methodology also supports real-time stability monitoring by integrating back-calculated GSI values from field surveys.

However, the study has certain limitations. The current model assumes isotropic mechanical properties within each lithological unit and does not explicitly account for time-dependent creep or dynamic effects from blasting and seismicity.