Abstract
Computer vision applications require high-quality reproductions of original images, typically demanding complex models with many trainable parameters and floating-point operations. This increases computational load and restricts deployment on resource-constrained devices. Therefore, we designed a new dilation depthwise super-resolution (DDSR) model that is composed of dilation convolution, depthwise separable convolution, and residual connection, to overcome the predicaments. Compared with the well-known model, fast super-resolution convolutional neural network (FSRCNN), the developed DDSR shows better performance in evaluations and You Only Look Once (YOLO v8) confidence scores. Most importantly, the architecture of the developed DDSR has 55% trainable parameters, 19% floating-point operations per second (FLOPs) of one-channel FSRCNN, 27% of the trainable parameters, and 8% of the FLOPs of three-channel FSRCNN.
1. Introduction
Super-resolution (SR) in image processing improves the resolution of an image and the pixel density and enables a higher-quality image from a lower-resolution input. It involves reconstructing or predicting details not present in the original low-resolution image. For simplicity, SR is used to recover a high-resolution (HR) image from a given low-resolution (LR) image [1,2]. Therefore, in the machine learning (ML) approach, LR images are used as the training data, HR images as the labels, and SR images as the predictions.
Computer vision applications, such as medical imaging, satellite imaging, security and surveillance, and consumer photography, demand high-quality reproductions of original images. In non-real-time scenarios, superior SR images rely on complex and powerful models without the need for immediate results. These applications can afford the longer computation times. However, real-time applications require usable SR images instantly, as they cannot afford the delays associated with extended computation times. On the other hand, the peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) are traditional metrics to evaluate the quality of SR images [3,4]. They are used to quantify how close the SR image is to the HR image. However, since ML algorithms process the images obtained from the SR technique, the evaluation criterion of the ML algorithm is incorporated with the conventional criteria for comprehensive assessment.
For example, SR images are processed in autonomous driving by You Only Look Once (YOLO) [5] to classify objects in the driving view in various control strategies. YOLO is a popular real-time object detection method where confidence refers to how many objects a specific bounding box contains in classification. Hence, in this study, the confidence level in YOLO is incorporated with the conventional criteria in assessing the SR images and designing a novel architecture that benefits all requirements. We adopt a fast super-resolution convolutional neural network (FSRCNN) [2] to design a real-time SR model with efficient training and testing. The number of trainable parameters and floating-point operations (FLOPs) is determined using two critical criteria [6,7,8]. The trainable parameters refer to the elements of a neural network that are updated in training. The number of trainable parameters in a neural network depends on the architecture, including the number of layers, the types of layers, and the number of units in each layer. FLOPs are used to measure the computational complexity of a model. They represent the number of operations that the model performs to process a single input. Hence, the developed architecture in this study has an order of magnitude equal to or lower than FSRCNN to guarantee real-time efficiency.
Based on the above methods, we designed a new model with better evaluation criteria (confidence levels of PSNR, SSIM, and YOLO) and a smaller number of trainable parameters of FLOPs than those of FSRCNN. The developed dilation depthwise super-resolution (DDSR) model is composed of dilation convolution, depthwise separable convolution, and residual connection. These components satisfy all requirements.
The rest of this article is organized as follows. Section 2 provides the necessary background knowledge. Section 3 and Section 4 detail the designs and present an analysis and discussion of the experimental results supporting our hypothesis. Finally, Section 5 concludes the study and presents potential directions for future work.
2. Background Knowledge
2.1. Traditional SR Algorithms
Traditional SR algorithms have disadvantages compared with deep learning-based algorithms, including nearest-neighbor interpolation, bilinear interpolation, and bicubic interpolation. They also have limited detail recovery, edge artifact, an assumption of smoothness, an inability to generate new information, a fixed interpolation kernel, no learning capability, and so forth. For instance, traditional methods apply the same operation to all image parts using a fixed interpolation kernel. This identical approach applies to different image regions, especially in complex or textured areas. No learning capability is required for traditional methods as they are rule-based and do not improve with data. This contrasts with current deep learning-based algorithms that learn more from datasets to reconstruct SR images better.
2.2. FSRCNN
FSRCNN eliminates bicubic interpolation in preprocessing by directly learning the mapping from LR to HR images. It incorporates a deconvolution layer to upscale efficiently and utilizes smaller filter sizes with more layers to improve performance. These changes make FSRCNN much faster than its previous version, SRCNN [2]. Also, it achieves superior image restoration quality. Recently, FSRCNN has become the most popular real-time SR algorithm.
2.3. Critical Components in Deep Learning
There are three critical components in the developed model.
2.3.1. Dilation Convolution
This is a type of convolutional operation for exponentially expanding receptive fields without losing resolution or coverage. Dilation convolution is conducted by inserting spaces between the filter elements based on a dilation factor to enable the network to capture multi-scale contextual information efficiently [9].
2.3.2. Depthwise Separable Convolution
This is a convolutional operation that significantly reduces the computational complexity of standard convolutional operations by breaking them into two separate steps, i.e., depthwise convolution and pointwise convolution. This is particularly effective for mobile and embedded applications with limited computational efficiency [10].
2.3.3. Residual Connection
This technique is utilized in deep neural networks to mitigate the vanishing gradient problem. It allows deep neural networks to be trained effectively with higher accuracy. This is achieved by adding a shortcut connection that bypasses one or more layers, directly connecting the input of a layer to its output [11].
3. Designs of DDSR
Based on the three critical components, we established two DDSR models for two different inputs, i.e., one-channel input Y from the color space YCbCr and three-channel input RGB from the color space RGB. Since FSRCNN has these two designs for different inputs, we provide two different versions to evaluate the corresponding performance.
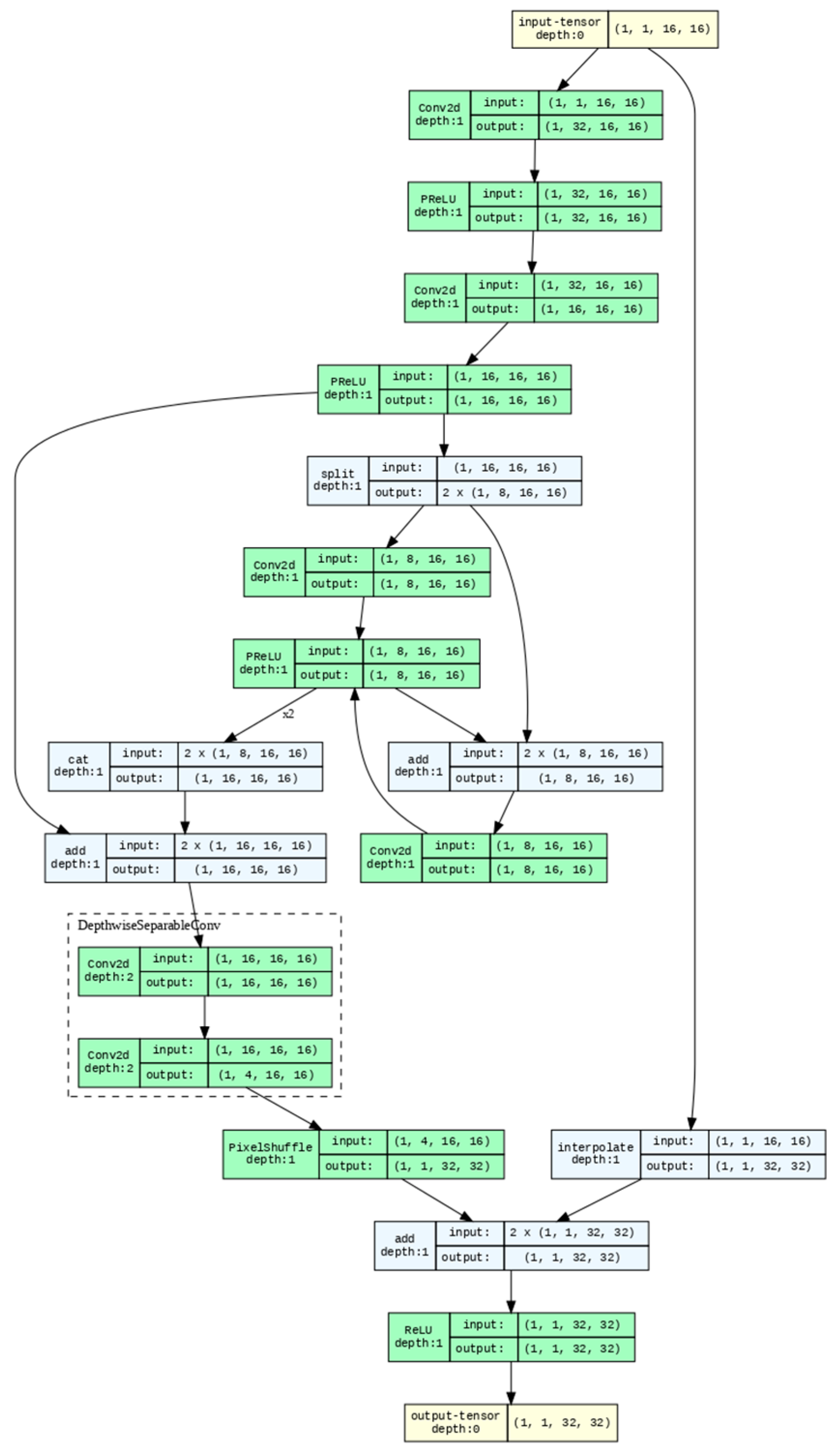
Figure 1 shows the developed DDSR with one-channel input. The network starts with an input size (1, 1, 16, and 16) and ends with an output size (1, 1, 32, and 32). Since convolution kernels with different sizes improve feature transmission, we apply this method after splitting layers with features. However, the number of trainable parameters increases. Therefore, we introduced dilated convolutions to enlarge the receptive field while keeping the parameter count to achieve the same effect. The depthwise separable convolution block is highlighted in the dashed box. The architecture has several residual connections to combine different levels of features. The design with three-channel input is similar to that in Figure 1, with the tensor sizes of each layer being different. For simplicity, a similar figure was not used repeatedly.
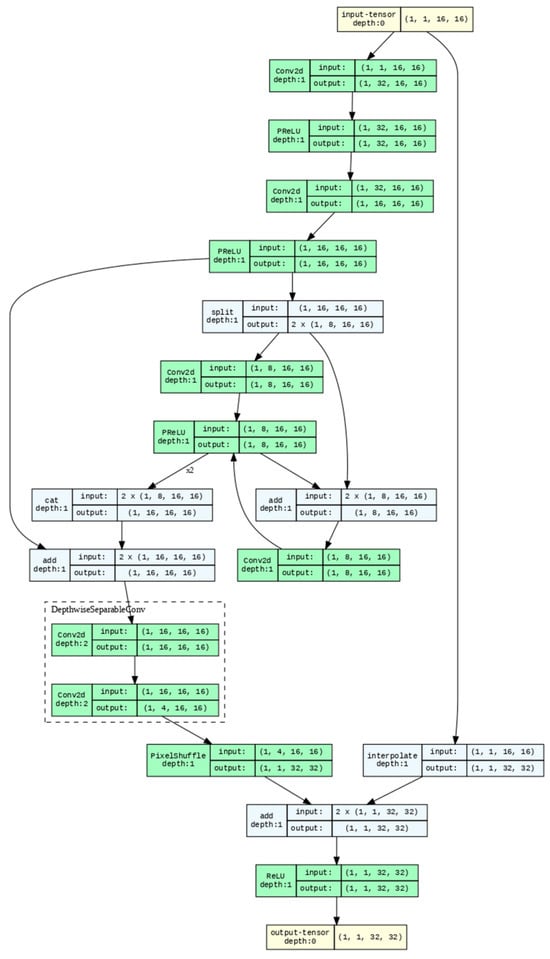
Figure 1.
DDSR with one-channel input.
The number of trainable parameters and FLOPs among two FSRCNNs and two DDSRs is shown in Table 1. The architecture of the developed DDSR has 55% of all trainable parameters, 19% of FLOPs of one-channel FSRCNN, 27% of all trainable parameters, and 8% of FLOPs of three-channel FSRCNN, which indicates the superiority of the developed DDSR in computation.

Table 1.
Comparison among FSRCNNs and DDSRs in the number of trainable parameters and FLOPs.
4. Results and Discussions
The settings of the developed DDSR are as follows.
- Training data: T91 [12].
- Data augmentation: the resize, rotate, crop, and sliding window techniques are adopted to augment the original T91.
- The parameters of the training procedure: the batch size is 256, the learning rate is 10−4, and the Adam optimizer is used.
- Testing data: Set5 and Set14 [13].
- The training and testing data are not mutually exclusive. They do not overlap or contain the same examples. This ensures that the model is evaluated to reflect its true performance.
- Evaluation criteria: the confidence levels of PSNR, SSIM, and YOLO.
- YOLOv8 [5] is adopted and trained by MSCOCO 2017 [14]. More specifically, we find the same bounding box containing the same object in each testing figure and then gather the statistics of these results to obtain the average YOLO confidence.
- The specification of the experimental computer includes the Apple M2 Ultra processor, a memory of 192 GB, and an SSD of 1 TB.
The experimental results are presented in Table 2. The performance metrics of two SR models are compared across different input types and datasets, where the results are categorized based on one-channel input and three-channel input. DDSR performed better than PSNR, SSIM, and YOLO across different datasets and input types. It also surpasses FSRCNN, especially when dealing with three-channel input. According to the comparison in Table 1, DDSR showed superiority in computation. Hence, DDSR is appropriate for mobile and limited computational devices.

Table 2.
Comparison of FSRCNN and DDSR in PSNR, SSIM, and YOLO confidence.
The SR value was lower than the LR value for FSRCNN with three-channel input in the confidence level of YOLO. YOLOv8, on the contrary, could not effectively recognize objects after SR processing. Consequently, traditional SR deep learning is not appropriate for ML applications.
5. Conclusions and Future Works
We propose the DDSR model by incorporating dilation convolution, depthwise separable convolution, and residual connections to address the real-time SR challenges. The results indicate that DDSR offers superior performance in PSNR and SSIM, as well as in YOLO confidence scores. DDSR has significantly fewer trainable parameters and FLOPs, making it more efficient and appropriate for mobile and computationally limited devices. It is still necessary to further optimize DDSR by experimenting with various deep learning components and identifying appropriate applications. The DDSR model can be incorporated into machine learning systems to evaluate its versatility.
Author Contributions
Methodology, C.-C.C.; software, W.-P.C., Y.-W.L., Y.-J.L. and P.-J.P.; validation, C.-C.C., W.-P.C. and Y.-W.L.; formal analysis, C.-C.C., W.-P.C. and Y.-W.L.; writing—original draft preparation, C.-C.C.; writing—review and editing, C.-C.C.; funding acquisition, C.-C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Science and Technology Council, Taiwan, under grant 112-2221-E-035-062-MY3.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European Conference on Computer Vision 2014, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the European Conference on Computer Vision 2016, Amsterdam, The Netherlands, 11–14 October 2016; pp. 391–407. [Google Scholar]
- Sethi, D.; Bharti, S.; Prakash, C. A comprehensive survey on gait analysis: History, parameters, approaches, pose estimation, and future work. Artif. Intell. Med. 2022, 129, 102314. [Google Scholar] [CrossRef] [PubMed]
- Rouse, D.M.; Hemami, S.S. Understanding and simplifying the structural similarity metric. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008. [Google Scholar]
- Terven, J.; Cordova-Esparza, D. A comprehensive review of YOLO architectures in computer vision: From YOLOv1 to YOLOv8 and YOLO-NAS. arXiv 2024, arXiv:2304.00501v7. [Google Scholar] [CrossRef]
- Hwang, K. Cloud Computing for Machine Learning and Cognitive Applications; The MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Hwang, K.; Chen, M. Big-Data Analytics for Cloud, IoT and Cognitive Computing; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Azadbakht, A.; Kheradpisheh, S.R.; Khalfaoui-Hassani, I.; Masquelier, T. Drastically reducing the number of trainable parameters in deep CNNs by inter-layer kernel-sharing. arXiv 2022, arXiv:2210.14151v1. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2016, arXiv:1511.07122v3. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861v1. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385v1. [Google Scholar]
- T91 Image Dataset [Online]. Available online: https://www.kaggle.com/datasets/ll01dm/t91-image-dataset (accessed on 1 January 2025).
- Set 5 & 14 Super Resolution Dataset [Online]. Available online: https://www.kaggle.com/datasets/ll01dm/set-5-14-super-resolution-dataset (accessed on 1 January 2025).
- Lin, T.-Y.; Maire, M.; Belongie, S.; Bourdev, L.; Girshick, R.; Hays, J.; Perona, P.; Ramanan, D.; Zitnick, C.L.; Dollár, P. Microsoft COCO: Common Objects in Context. arXiv 2015, arXiv:1405.0312v3. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).