Modelling, Analysis and Sensory Metrication Towards a Quantitative Understanding of Complexity in Systems ^†

Abstract

Modelling and metrication of the complexity of systems have occupied a growing and largely underdeveloped problem space in the literature of complex systems. In this research, preliminary results depicting the complexity of a service system premised on a tertiary institution of learning is presented. The concept deployed focused on modelling the trio core entities viz: functional elements, physical elements and the intricacy of connectivity associated with the flow of signals in the normal systemic operations. The numerous activities depicting diversity and multiplicity were holistically enumerated prior to sensing and metrication. The outcome of this research underscores effectiveness in the proposed model.

1. Introduction

Modern day engineering, enterprises and socio-cultural systems are becoming increasingly complex. Systems are more integrated due to modern technologies, such as cyber-physical systems that allow for a greater degree of communication and interconnectedness than previously possible [1,2]. The increase in system complexity has been observed within many social systems and enterprises, but modelling and metrication of complexity in such systems has remained underdeveloped within the available literature. There is currently no widely accepted model to analyse and metricate the complexity of service systems, such as education systems. The development of such models is significant in improving knowledge and decision-making capabilities within education systems [3].

A complex system is a system which exhibits non-linear and emergent behaviour in which the total system complexity is not easily predicted based on the constituent system elements [4]. Complexity in systems increases when the system acquires additional functional and physical elements, hence resulting in additional hardware. The intricacy of interconnectivity between elements also increases overall system complexity [5]. The behaviour and outcomes of a complex system cannot be easily and reliably predicted without counting or understanding the system parts or sub-systems [2].

The need to model systems’ complexity by first gaining insight into their structure is quite important for effectiveness in quantification. System elements are the building blocks from which all systems are made. System elements refer to functions and physical components [6] including the overall interactions that take place within the integrated network of elements.

Functional elements can be identified as system units which can purposefully alter information, material elements or energy elements in the system. The functional elements relate to the system capabilities, activities and functional attributes [7]. System functions are performed when system elements interact, and activities take place in a sequence. The functions are made up of processes that take place within the system architecture. The processes, interactions and functional relationships that take place within the physical system must be identified to understand the functional system architecture [8].

Physical elements refer to the physical components that are necessary for the functional system elements to operate [7], i.e., the hardware and software components required for the system to function. Electronic, electro-optical, electromechanical, mechanical, thermomechanical and software elements are the six most recognised categories of physical system elements [7]. In the context of social service systems, such as a tertiary educational institution, human participants are included as an important part of the physical system structure.

The system architecture can be represented using network diagrams to visualise the system and interactions between different system elements [8,9]. Complexity metrication is generally derived based on easily quantifiable system properties that connect the system’s form, function, structure and quantifiable aspects of system behaviour [6]. Multiplicity, diversity and interconnectedness are frequently used in the creation of quantitative complexity metrics. Multiplicity refers to the number of system elements, e.g., system components, agents, features, etc., while diversity refers to the number of unique elements within the system and how dissimilar the different elements are from each other. Interconnectedness refers to the number of connections between interacting system elements [6]. The physical and functional complexity of a system both contribute to the overall system complexity, and a system may be highly complex in either/both the functional and physical domain [6]. The intricacy of connectivity, i.e., the relationships between system elements, is another defining feature of system complexity [10]. In this paper, complexity is holistically examined from both a functional and a physical point of view. A system element count approach was applied to physical and functional system elements. The inter-relationships between interacting elements were also identified by using contextual questioning. The system has been modelled to gain a more complete understanding of the examined part of a generic tertiary educational institution.

2. Methods

The complexity model and metrication are based on a system element count approach using the Hybrid Structural Interaction Matrix (HSIM) method to create a Binary Interaction Matrix. The unique functional and physical elements are used in the BIM to identify the functional interactions within the presented system. The functional interactions are used to quantify the intricacy of the interconnectivity of the system. The complexity score (CS) is then calculated relative to the peak count (PC) of system elements that are applicable to the given system.

2.1. Systems Engineering Modelling Approach

The Systems Engineering Method, as described by [7], consists of four basic activities, namely requirements analysis, functional definition, physical definition and design validation. The requirements analysis phase consists of the identification of the system objectives and capabilities. The functional system capabilities are then used to identify the individual tasks and activities that take place within the system. System activities are broken down to the constituent functional elements and are mapped to an appropriately identified sub-system. The system functions may intra-interact within a system function or inter-interact with functions from different sub-systems. The physical components required for the system to perform the identified functions are identified and allotted to the corresponding function on the component, sub-component and part level. The system design can be validated using suitable models and tests, but this step is beyond the scope of the current research.

2.2. Structure of Systems

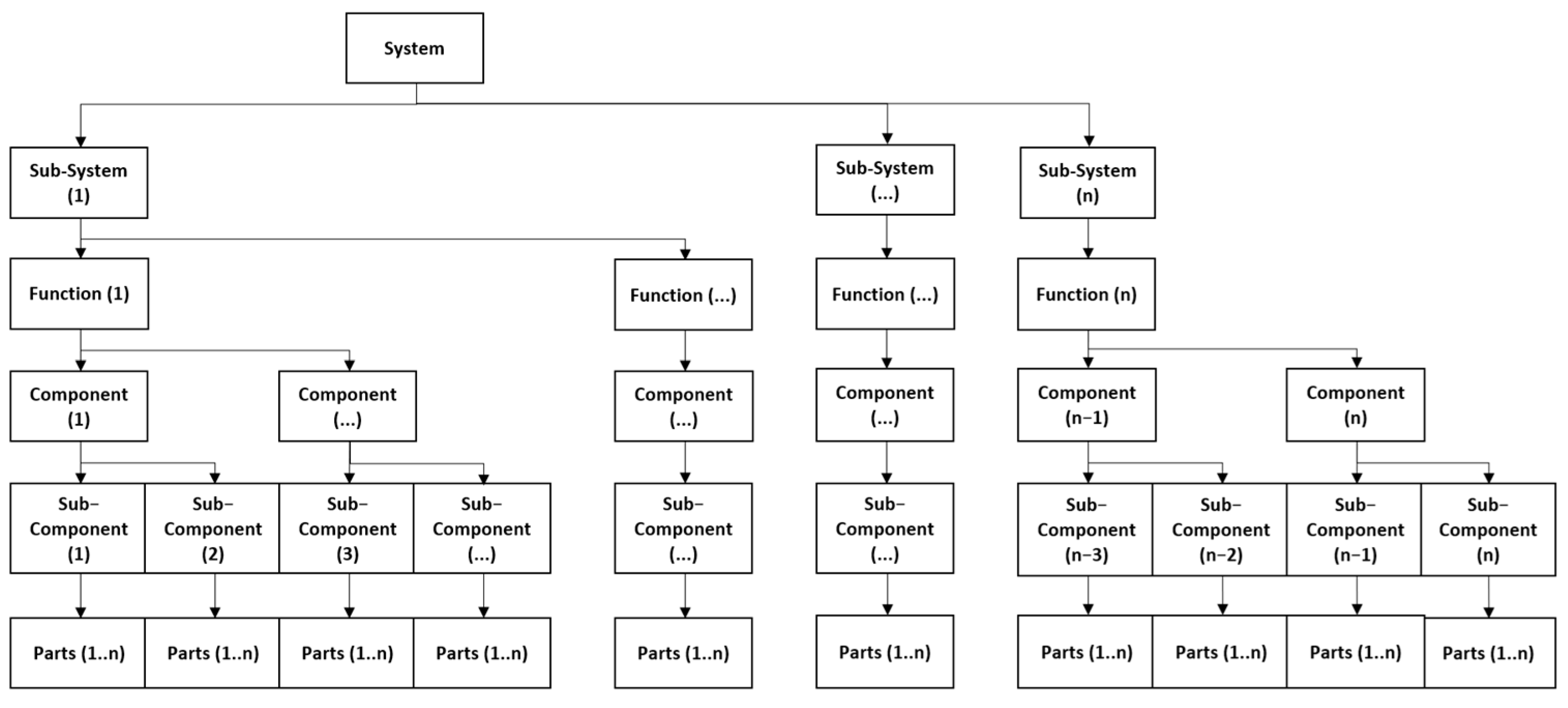
System architecture refers to the organization of functional and physical elements in relation to each other and the environment which can be visually represented as a network of interconnected sub-systems, components, sub-components and parts [11]. Sub-systems and functions are identified at the functional level based on the requisite system activities. The physical embodiments of system functions are represented at the sub-ordinate level of the system hierarchy. A general system representation is illustrated in Figure 1.

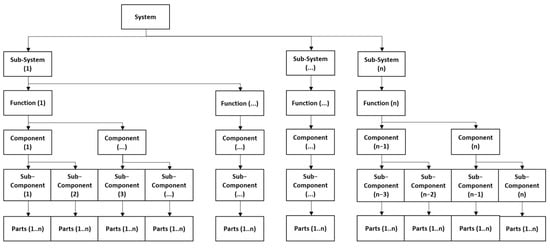
Figure 1. Generalised system structure.

The structural system complexity increases with the diversity, multiplicity and interconnectivity of system elements [6]. These three factors are identifiable and measurable based on a system structure diagram. The number of similar elements (multiplicity), dissimilar elements (diversity) and existing interactions between physical and functional elements are noted for use in the complexity metrication.

2.3. Hybrid Structural Interaction Matrix (HSIM)

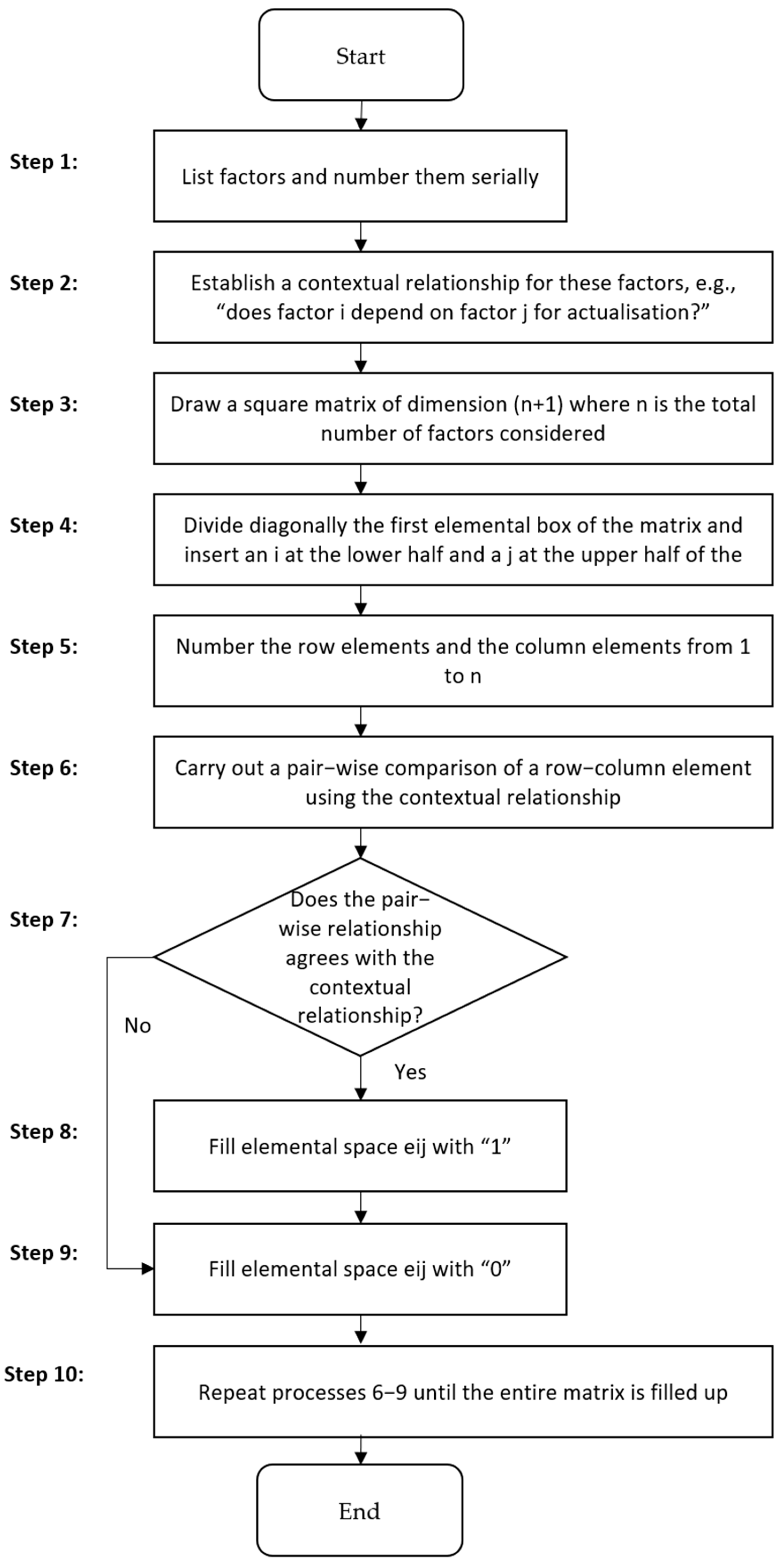
HSIM is a matrix-based methodology, developed by [12] and further expanded on in [13,14]. System elements are mapped into a matrix as per the method shown in Figure 2. The elements are subjected to pairwise comparisons to determine the relationships between system elements. The relationship between factors is established via the use of an appropriate contextual question, e.g., does factor (i) have a direct effect on factor (j)?

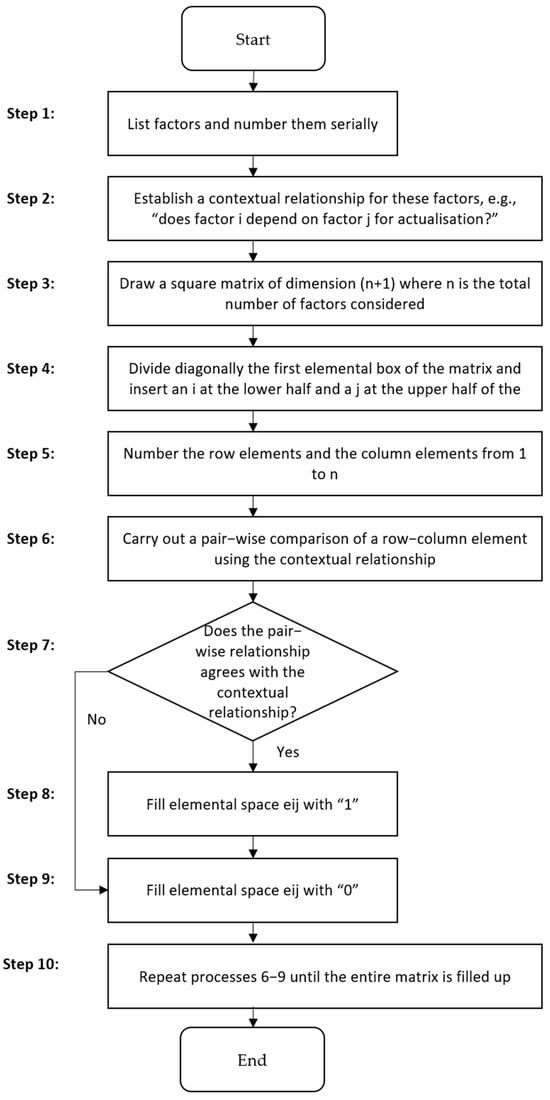
Figure 2. HSIM methodology as described in [12,13,14].

Here, this methodology is adapted to establish the intricacy of connectivity of system functional and physical elements for a service system. First, all physical and functional elements are holistically identified and enumerated. A BIM is drawn with functional elements (i) on the vertical axis and physical elements (j) on the horizontal axis. The relationship between the functional element (i) and the physical element (j) is established via the use of an appropriate contextual question, e.g., does functional element (i) have a direct effect on physical element (j)? A pairwise comparison is done by applying the contextual question to determine the relationship between the system elements. If functional element (i) has a direct effect on physical element (j), then the assigned value is 1; otherwise, it is 0. The identified intricacy of connectivity can then be used to calculate a complexity score as per the complexity model presented in Section 2.4.

2.4. Complexity Model

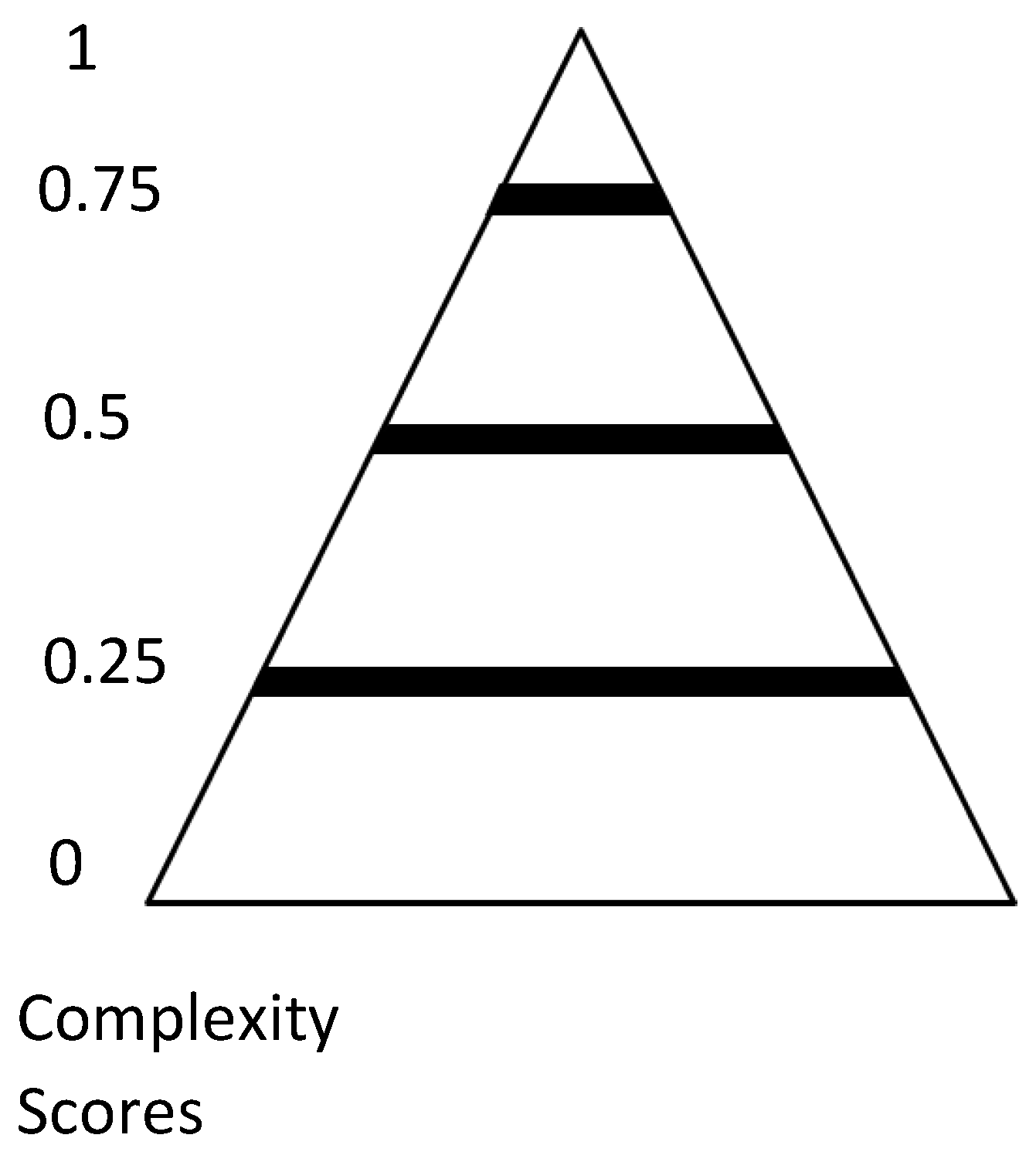
The system complexity model makes use of a pyramid allocation scheme for the complexity score (CS), premised on the three cardinal quartiles where

• Top benchmark—1;
• Upper quartile—0.75;
• Average—0.50;
• Lower quartile—0.25;
• Base—0.

The categorisation of complexity is based on the peak count (PC) of system elements as shown in Table 1. The system element count method is derived from the part count method of predicting system failures. The complexity of a system is scored relative to the described complexity scale. The PC is used to identify the level of complexity in which the system operates based on the maximum number of elements that could be found in the system. The CS is thus measured within an identified complexity domain.

Table 1. Complexity categorisation based on Peak Count (PC) of system elements.

Peak Count (PC)	Description	Complexity Category
10	a peak count of ten for early tens	Simple Complexity
100	a peak count of hundred for late tens	Moderate Complexity
1000	a peak count of a thousand for the late hundreds	Moderately Intricate Complexity
10,000	a peak count of ten thousand for the early thousands	Intricate Complexity
100,000	a peak count of hundred thousand for the extended early thousands	Extended-Intricate Complexity
1,000,000	a peak count of one million for the late thousands	Ultra Complexity
10,000,000	a peak count of ten million for early millions	Ultra-Super Complexity
100,000,000	a peak count of hundred million for extended early millions	Super Complexity
1,000,000,000	a peak count of one billion for late millions	Hyper Complexity
10,000,000,000	a peak count of ten billion for early billions	Hyper Super Complexity
100,000,000,000	a peak count of hundred billion for extended early billions	Apex Complexity
1,000,000,000,000	a peak count in the trillions for the late billions	Hyper Apex Complexity

By deploying the pyramid modelling approach and incorporating the quartiles in a sequenced ratio composition, the following Figure 3 is obtained:

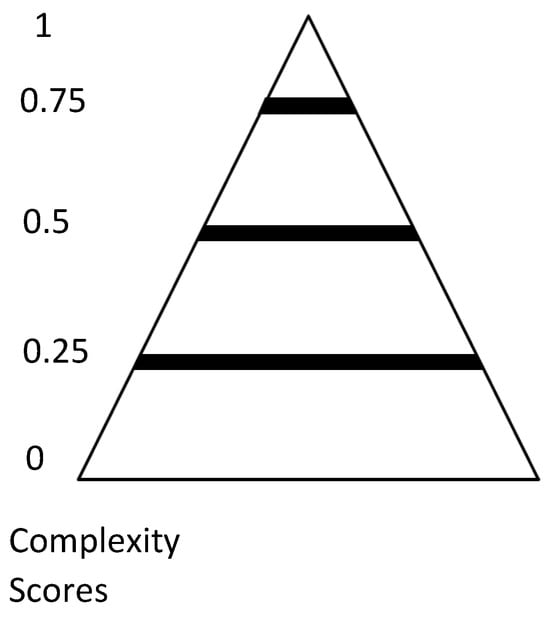
Figure 3. Complexity pyramid allocation.

The CS is the level of complexity per the PC number of system elements. The following equation, derived from the part count method, is presented for calculating the CS:

$$CS={\displaystyle \frac{\mathrm{A}\mathrm{C}}{pc}}$$

(1)

where

• CS = Complexity score;
• AC = Actual count;
• pc = corresponding peak count.

The actual count (AC) is calculated as follows:

$$\begin{array}{c}{AC=[\mathit{p}\mathit{h}\mathit{y}.(\alpha d}_{c\left(p_{\left(i\right)}\right)}+{\beta d}_{sc\left(p_{\left(i\right)}\right)}+{\gamma d}_{p\left(p_{\left(i\right)}\right)}\left)\right]\\ +\left[\mathit{f}\mathit{u}\mathit{n}.\left({\alpha d}_{c\left(\left(f_{\left(i\right)}\right)\right)}+{\beta d}_{sc\left(\left(f_{\left(i\right)}\right)\right)}\right)\right]+[\mathit{i}\mathit{n}{\mathit{t}}_{\mathit{c}\mathit{o}\mathit{n}}.\left(f_{ij}\right)]\end{array}$$

(2)

where

• $\mathrm{P}\mathrm{h}\mathrm{y}.$ = Physical elements;
• $\mathrm{f}\mathrm{u}\mathrm{n}.$ = Functional elements;
• $\mathrm{i}\mathrm{n}{\mathrm{t}}_{\mathrm{c}\mathrm{o}\mathrm{n}.}$ = Functional Interconnectivity;
• $\mathrm{i}$ = counter from 1 to n;
• $\mathrm{j}$ = (i + 1); counter from 1 to m;
• $\mathsf{\alpha }$ = Multiplier factor for components;
• $\mathsf{\beta }$ = Multiplier factor for sub-components;
• $\mathsf{\gamma }$ = Multiplier factor for parts;
• ${\mathrm{d}}_{\mathrm{c}\left({\mathrm{p}}_{\left(\mathrm{i}\right)}\right)}$ = Diversity of physical components;
• ${\mathrm{d}}_{\mathrm{s}\mathrm{c}\left({\mathrm{p}}_{\left(\mathrm{i}\right)}\right)}$ = Diversity of physical sub-components;
• ${\mathrm{d}}_{\mathrm{p}\left({\mathrm{p}}_{\left(\mathrm{i}\right)}\right)}$ = Diversity of physical parts;
• ${\mathrm{d}}_{\mathrm{c}\left({\mathrm{f}}_{\left(\mathrm{i}\right)}\right)}$ = Diversity of components’ functions;
• ${\mathrm{d}}_{\mathrm{s}\mathrm{c}\left({\mathrm{f}}_{\left(\mathrm{i}\right)}\right)}$ = Diversity of sub-components’ functions;
• ${\mathrm{f}}_{\mathrm{i}\mathrm{j}}$ = Interconnectivity between functional elements (i) and (j).

3. Results and Discussion

A tertiary institution of learning was selected as the service system that was modelled and quantified. The case comprises of 17 holistically identified systems, 56 functions, 227 components, 306 sub-components and numerous parts. The first three functions of the “Teaching and Learning” system were selected as an example of the system modelling and metrication procedure and categorised as applicable, resulting in a total of 5 identified sub-functions.

3.1. Identification of System Elements

The system elements of the “Teaching and Learning” system at a generic tertiary institution of learning were holistically identified. First, system tasks and activities were listed and assigned to functions (F1…F3) and sub-functions (SF1…SF5). The most prominent physical embodiments were identified and listed alongside the functions in Table 2.

Table 2. Functions and primary physical embodiments.

Functions	Sub-Functions	Physical Embodiments
F1—Assessment	SF1—Assessment Creation SF2—Assessment Submission SF3—Assessment Grading	Lecturers Students
F2—Lectures	SF4—Lecture Preparation	Lecturers
	SF5—Class Delivery	Students Lecture Hall
F3—Tutorials	-	Lecturers Students

The physical system elements are then expanded on in Table 3 with the listed components (C1…C9), sub-components (SC1…18), sub-sub-components (SSC1…SSC7) and parts (P1…P28).

Table 3. Physical system elements.

Physical Components	Sub-Components	Parts
C1—Lecturers	SC1—Assistant Lecturers	-
	SC2—Moderators SC3—Examiners SC4—Invigilators SC5—Guest Lecturers
C2—Text Books	SC6—Book Chapters	P1—Book Cover
	SSC1—Chapter Sections	P2—Pages
C3—Students	-	-
C4—Software	SC7—Word Processor	P3—User Interface
	SC8—Electronic Submission Platform SC9—Prescribed Software	P4—Files P5—Codebase
C5—Computers	SC10—Monitor SC11—Mouse SC 12—Keyboard	P6—Central Processing Unit (CPU) P7—Motherboard P8—Random Access Memory (RAM)
		P9—Power Supply
		P10—Cooling Fan P11—Storage Drive
C6—Printers	-	P12—Paper Support P13—Sheet Feeder P14—Output Tray P15—Print Head P16—Ink Cartridge P17—Power Supply P18—Control Circuit
C7—Course Content	SC13—Lecture Notes SC14—Class Notes SSC2—Presentation Slides SSC3—Sections	P19—Paper P20—Files
C8—Lecture Hall	SC15—Furniture SC16—Teaching Tools SSC4—Whiteboard SSC5—Projector	P21—Lens P22—Light Source P23—Screen P24—Condenser P25—Mirror P26—Power Circuit
C9—Documents	SC17—Assessment Instructions SC18—Assessment Rubric SSC6—Assessment Sections SSC7—Rubric Sections	P27—Paper P28—Files

3.2. Constructed System Architecture

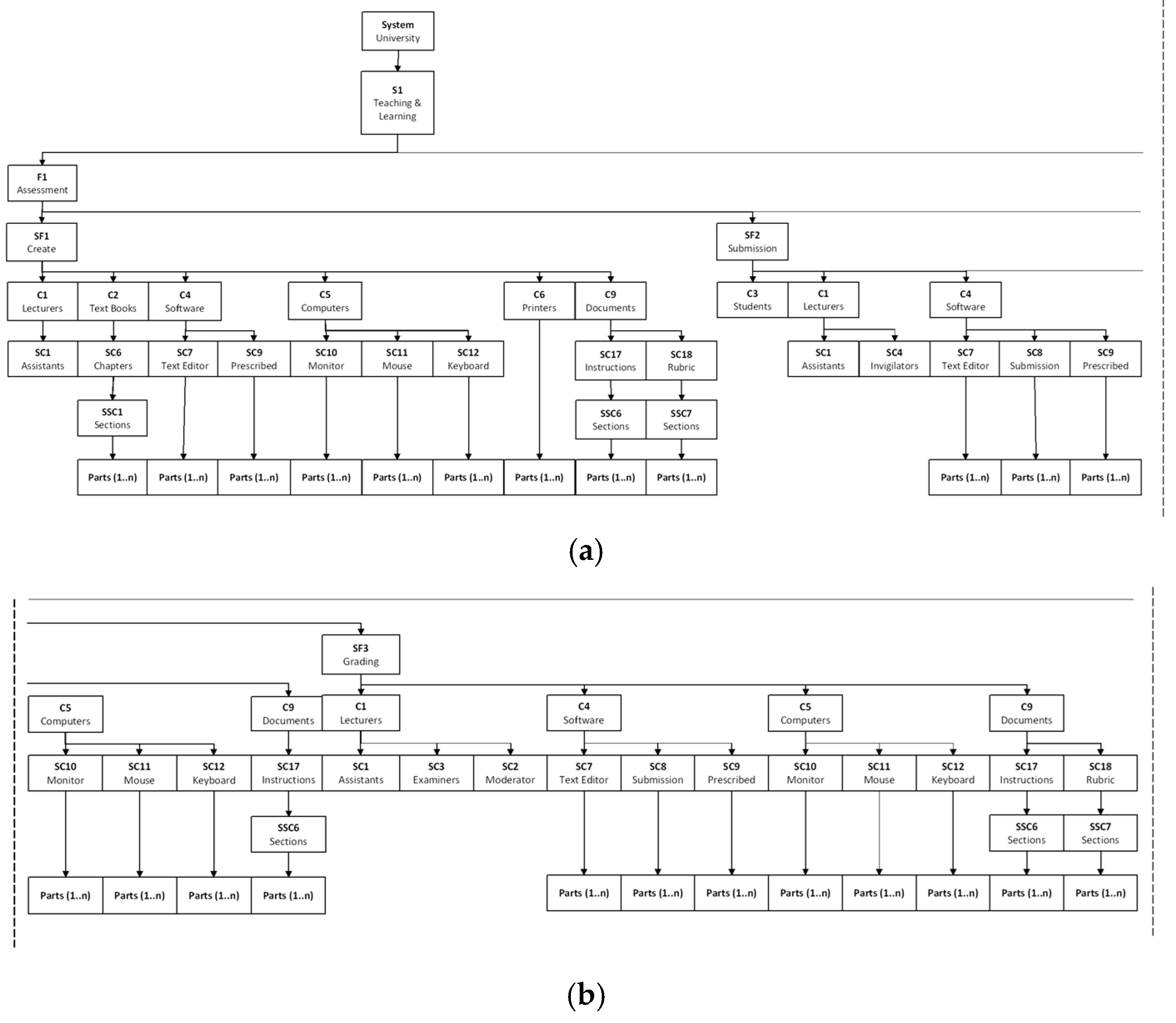
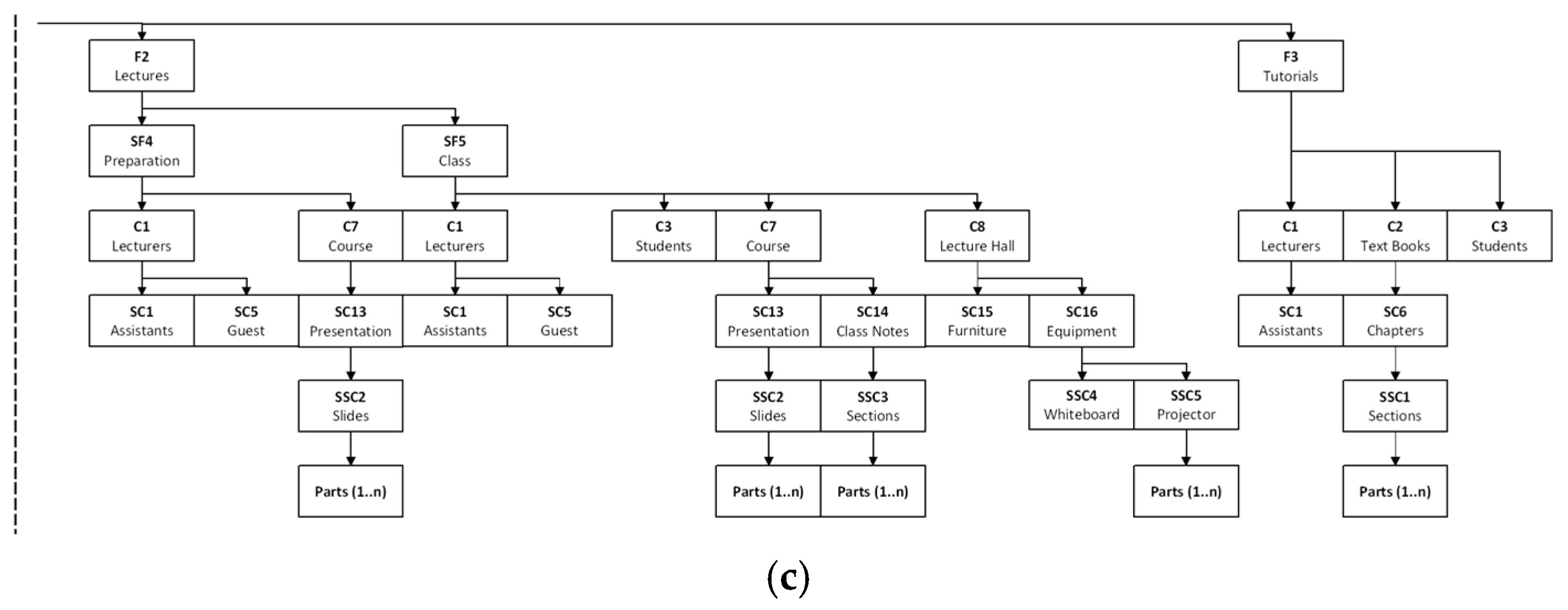
The system structure for the generalised “Teaching and Learning” system was constructed based on the listed, sensed and metricated system components. The system structure is shown in Figure 4.

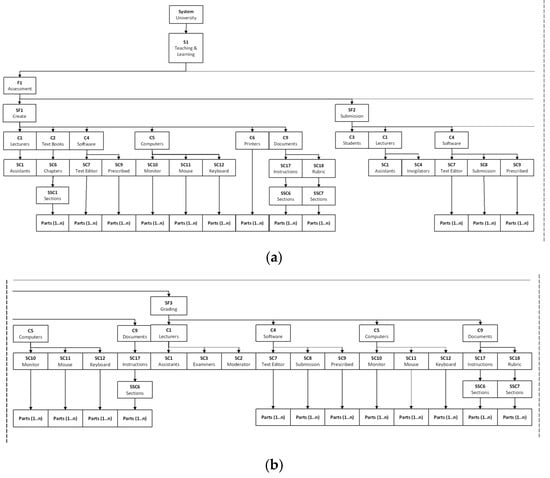
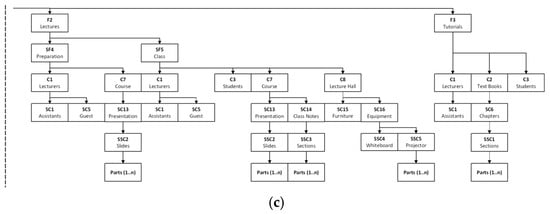
Figure 4. Construct system architecture: (a) create assessment sub-function; submit assessment sub-function; (b) submit assessment sub-function continued; assess grading sub-function; (c) lectures function; tutorials function.

3.3. Model Formulation

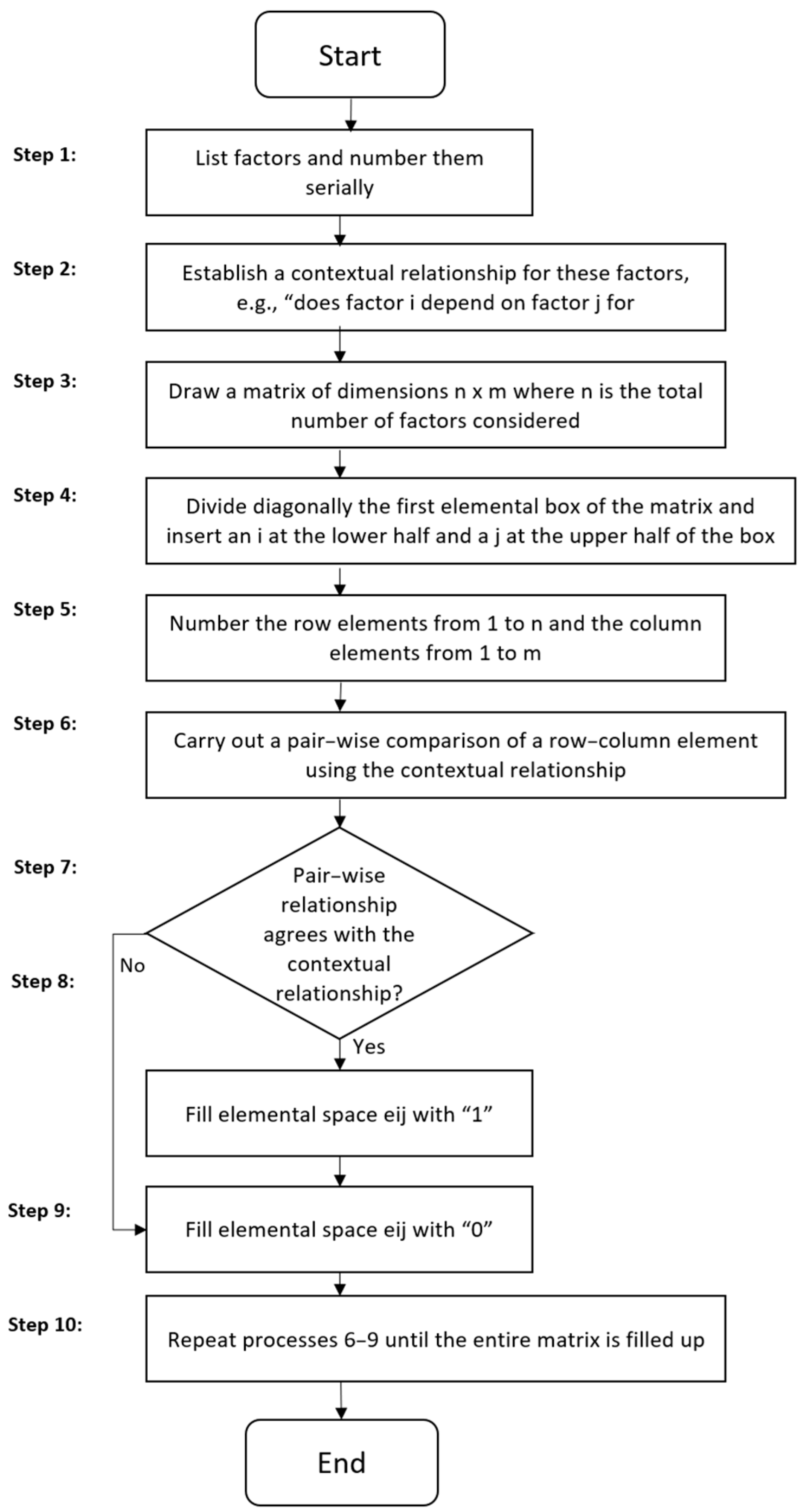
The functional and physical elements were identified and modelled as a BIM according to the HSIM approach. The adapted HSIM method used is shown in the form of a flowchart in Figure 5. The BIM is shown in Table 4.

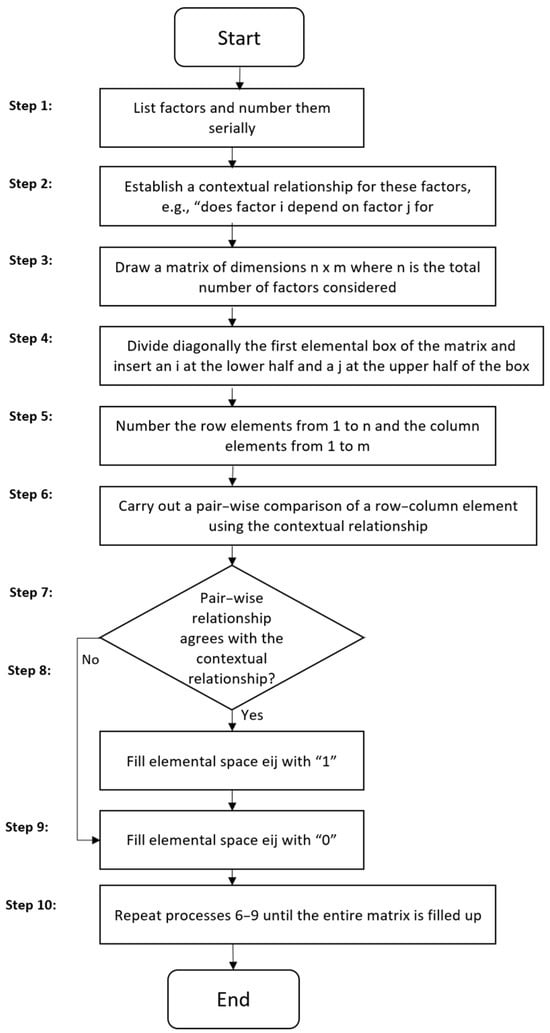
Figure 5. HSIM method, adapted from [12,13,14].

Table 4. Binary interaction matrix.

i\j	C1	C2	C3	C4	C5	C6	C7	C8	C9	SC1	SC2	…	P28
F1	1	0	1	1	0	1	0	0	1	1	1	…	1
F2	1	0	0	0	1	0	1	1	0	1	0	…	0
F3	1	0	0	0	0	0	0	0	0	1	0	…	0
SF1	1	0	0	0	0	1	0	0	1	1	0	…	0
SF2	1	0	0	1	0	0	0	0	1	1	0	…	1
SF3	1	0	1	0	0	0	0	0	1	1	1	…	1
SF4	1	0	0	0	1	1	1	0	0	1	0	…	0
SF5	1	0	0	0	1	0	1	1	0	1	0	…	0

Contextual question: does functional element (i) have a direct effect on physical element (j)? If “yes”, then assign 1, but if “no”, then assign 0.

Mathematically

$$eij=\left\{\begin{array}{c}1\mathrm{i}\mathrm{f}i\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{n}j\\ 0\mathrm{i}\mathrm{f}i\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{n}j\end{array}\right.$$

(3)

The BIM is used to determine the number of functional interactions between system elements and thus determine the intricacy of connectivity of the system. The presented “Teaching and Learning” system consists of 8 functional elements, 62 unique physical elements and 169 functional interactions. The total system count is in the 100s, thus the system PC is 1000. The system is characterised as being at the level of moderately intricate complexity. The ratio between the counted system elements and the peak count is 0.346, which places this system in the second quartile of this complexity domain. The conclusion is that the level of complexity knowledge required to manage this system is relatively low. However, the level of complexity management and decision-making skills will increase as the system acquires additional physical elements and functions.

4. Conclusions

The presented complexity metric is an effective heuristic for identifying the complexity domain of a system based on the novel complexity scale presented in the paper. The complexity of the system can be scored relative to systems of a similar size and can thus be used to estimate the difficulty of complexity management and decision-making within the system. The method is intended to be suitable for heterogenous systems, i.e., other educational systems.

Future research includes the expansion of the studied system to include a whole tertiary educational institution. The isolated “Teaching and Learning” sub-system is on its own not very complex as per the complexity scale presented here, but a model which includes all of the sub-systems within a generic educational institution will have many more functions and physical elements and thus a higher level of complexity. Future research should expand on the exact complexity management and decision-making approaches that should be followed within each identified complexity domain on the presented complexity scale.