Hybrid Chemical and Data-Driven Model for Stiff Chemical Kinetics Using a Physics-Informed Neural Network ^†

Abstract

Models of chemical kinetic processes, comprising systems of stiff ordinary differential equations (ODEs), are essential for modeling important chemical reactions relevant to drinking water chemistry, such as disinfectant decay and disinfection byproduct formation. However, the accuracy of these models can be inhibited by (1) the challenge of fully describing the chemical reaction system, and (2) additional chemical reactions occurring in actual environmental settings that were not accounted for in the laboratory conditions used to develop and calibrate the models. This study proposes the use of a Physics-Informed Neural Network framework, utilizing the eXtreme Theory of Functional Connections (X-TFC) technique to create a hybrid chemical- and data-driven model that incorporates data and the underlying system of ODEs into the trained model in order to increase the accuracy of the predicted chemical concentrations.

1. Introduction

Key characteristics of water quality paramount for the protection of public health, such as decay of free chlorine, monochloramine, and formation of disinfection byproducts, can be modeled using a system of stiff ordinary differential equations (ODEs). Despite the widespread adoption of stiff chemical models, these may yield inaccurate results for two key reasons. First, some of the underlying chemical mechanisms occurring in the actual reaction scheme may not be discovered or fully described in the description of the chemical model [1]. Second, additional reactions that occur in actual environmental systems may not have been accounted for in the laboratory conditions in which the model was developed [2].

Therefore, we propose a Physics-Informed Neural Network (PINN) framework based on the eXtreme Theory of Functional Connections (X-TFC), which has been demonstrated to effectively model stiff systems of chemical equations [3,4]. Previous implementations for solving stiff ODEs use X-TFC as an equation-solving method rather than a predictive modeling tool [4]. Therefore, the purpose of this work is to (1) expand the capabilities of the X-TFC framework by including pH, a key parameter that affects the rate of many aquatic chemical reactions, as a second input variable in order to predict chemical concentrations over a range of water quality conditions; and (2) incorporate data into the model training process. The outcome is a model that relies on the underlying system of chemical equations and data in order to increase prediction accuracy. We demonstrate the proposed method using a subset of the chemical model used to simulate the decay of monochloramine, a disinfectant used by approximately 25% of water utilities in the United States [5].

2. Methods

2.1. X-TFC Overview

PINNs have been shown to have difficulty solving stiff systems of chemical equations with initial conditions due to competition between loss functions representing the initial conditions and gradient loss components [4]. Therefore, we employ the X-TFC framework, which has been shown to effectively solve stiff systems of chemical equations with high accuracy and speed. The key feature of the X-TFC framework is the use of a constrained expression to analytically satisfy the initial conditions, thus eliminating the competition between different components in the loss function.

Consider a system of constrained ODEs for different species and pH values with initial conditions:

$$\left\{\begin{array}{cc}{\displaystyle \frac{d{y}_i(t;ph)}{dt}}=f_i\left(t,y_i,\dots ,y_m;ph\right)& \forall t\in \left[t_0,t_f\right]\\ \begin{array}{c}\\ y\left(t_0;ph\right)=y_{i,0}\end{array}& \end{array}\right.$$

(1)

where $i=1,\dots ,m$ is the species, $y_i\left(t\right)$ is the concentration of a chemical species $i$ at time $t$, $t_0$ is the initial time, $t_f$ is the final time, and $y_{i,0}$ and $f_i\left(t,y_i,\dots ,y_m;ph\right)$ are the initial condition and rate expression of a chemical species $i$, respectively. In the X-TFC framework, the concentration of a species $y_i$ is represented with a constrained expression where $y_i\cong y_{ce}=g\left(t;ph\right)+y\left(t_0;ph\right)-g\left(t_0;ph\right)$. Hence, when $t=t_0$, the constrained expression is guaranteed to satisfy the initial conditions. The constrained expression is substituted back into the ODEs, resulting in a simplified unconstrained system of ODEs. The function $g\left(t;ph\right)$ is defined as the free function, which in the X-TFC framework is approximated using a single-layer neural network (NN).

2.2. Neural Network Architecture

The single-layer NN, $g\left(t;ph\right)$, has two inputs: time and pH. The number of outputs is equal to the number of chemical species included in the chemical system. The number of nodes in the hidden layer is a tunable hyperparameter. The $\tanh$ activation function, which was shown to be effective, is used [4]. The values of $t$ and $ph$ are scaled to a domain of [0, 1] or [−1, 1] to coincide with the domain of the $\tanh$ activation function.

2.3. Neural Network Loss Functions

The loss function used to train the NN includes the gradient loss and, if partial data are available, the data loss components. The gradient loss incorporates information about the chemical kinetics by minimizing the mismatch between the time derivates, ${\displaystyle \frac{d{y}_i(t;ph)}{dt}}$, and rate of change, $f_i\left(t,y_{ce,i},\dots ,y_{ce,m};ph\right)$. An additional data loss component is added for each species that has data available that minimizes the difference between the data, ${\tilde{y}}_i\left(t;ph\right),$ and NN prediction, $y_{ce,i}\left(t;ph\right)$.

2.4. Neural Network Optimization

The NN is trained via the extreme learning machine technique, in which the values of input weights and biases at each hidden node are randomly sampled from a uniform distribution between [−1,1] and held constant [6]. The values of the output weights are tuned during model training. The NN is linear with respect to the output weights, enabling the use of iterative least squares regression to optimize the NN output weights extremely quickly.

3. Results

We demonstrate our proposed methodology using the first three reactions of the unified model of monochloramine decay [7]. The reaction scheme contains four chemical species, monochloramine (NH₂Cl), dichloramine, (NHCl₂), hypochlorous acid (HOCl), and ammonia (NH₃) [7]. We train the proposed X-TFC model using the chemical equations for in-sample pH values and training data for a subset of species. Then, we evaluate the performance of the trained model using out-of-sample pH values not used in training and compare the performance to hold-out species for which data were not included in the model training. In the X-TFC model, and in the figures below, the concentrations of the acid and base species (HOCl and NH₃) are represented by the total amount of conjugate acid and base for each species. The initial concentration of monochloramine was set as ${4.22·10}^{-5}$ mol/L, corresponding to 3.0 mg/L as Cl₂, which is a typical monochloramine concentration for treatment plant effluent entering a water distribution system [8]. To generate data, we solved the system of equations with increased rate constants, which we consider to be the ground truth in this scenario. If implemented on a system with measured data, the measured data would be used instead.

Figure 1 shows the results of the trained X-TFC model, using data for TOTNH and TOTCl. In this figure, chemical model refers to the result of the chemical model with the original rate constants solved using ode15s, training data refers to data that were used to train the model for in-sample pH values, hold-out data refers to data for out-of-sample pH values, and hold-out species refers to species for which data were not included during training. Thus, the X-TFC model relies on the chemical model and data for a subset of chemical species to predict concentrations of species for which no data were incorporated into the training of the X-TFC model. The key finding is that the X-TFC model is able to accurately predict the concentrations of hold-out species NH₂Cl for in-sample and out-of-sample pH values (solid lines align closely with dotted lines), even though no data were supplied for this species was included during model training.

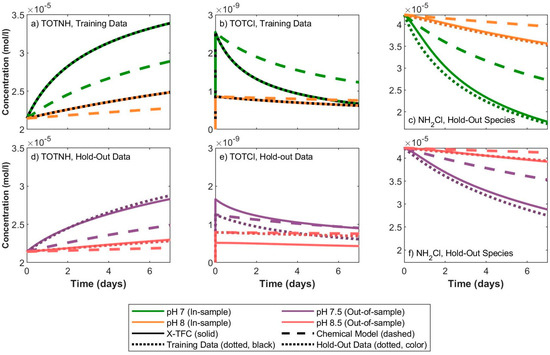
Figure 1. X-TFC model results using training data for TOTNH and TOTCl.

4. Discussion and Conclusions

This work proposes a PINN-based modeling framework that improves the accuracy of chemical predictions for chemical systems, with multiple implications and opportunities for future work. We observed that the modeling framework is able to accurately predict the concentrations of hold-out species, as shown in Figure 1. However, the ability to predict hold-out species is dependent on the dynamics of the chemical system and which species are used for training data. The proposed modeling framework could be expanded in many different directions, for example, coupling X-TFC with hydraulic models of a water distribution system to approximate chemical concentrations at a particular location within the system. In addition, because the X-TFC model trains extremely quickly (the training time for the X-TFC model shown in Figure 1 was under 5 s), there is potential to use the X-TFC model as a data assimilation technique for real-time predictions of water quality at unmeasured locations within a water distribution system. Opportunities for future work include developing optimized X-TFC model hyperparameters, utilizing different optimization methods, and implementing additional chemical reaction schemes.

In the face of rising water quantity and quality concerns and the continuous development of chemical kinetic process models, the impact of the proposed X-TFC model framework is far-reaching [9]. In addition, systems of stiff differential equations are used in a variety of disciplines, such as atmospheric chemistry, biology, and epidemiology, showing promise for many use cases of a hybrid modeling framework in multiple domains.