Differential Evolution Optimized Non-Orthogonal Multiple Access for Sum Rate Maximization ^†

Abstract

Non-orthogonal multiple access (NOMA) is a potential technology to support high network density, while satisfying the quality of service (QoS) demands. To maximize the attainable sum rate of individual users and minimize outage, the power allocation (PA) factors must be optimized. In the proposed work, a differential evolution (DE) algorithm is implemented to optimize the power factors assigned to users. The proposed optimization maximizes the sum rate by $\approx 5.87\mathrm{\%}$ to $\approx 12.65\mathrm{\%}$ compared to random PA. The near user requires $\approx 8.24\mathrm{d}\mathrm{B}\mathrm{m}$ to $\approx 14.13\mathrm{d}\mathrm{B}\mathrm{m}$ less transmit power, whereas the cell-edge user requires $\approx 6.56\mathrm{d}\mathrm{B}\mathrm{m}$ to $\approx 9.18\mathrm{d}\mathrm{B}\mathrm{m}$ less transmit power compared to random PA to attain an outage probability of ${10}^{-3}$.

1. Introduction

In comparison to previous mobile generation upgrades, the capabilities of the next-generation network are intended to grow by a factor of 10–100 [1]. Since the advent of smart gadgets, the internet of everything (IoE), and device-to-device communication, mobile users’ data demands have boosted tremendously. Additionally, machine-to-machine connection utilization will grow drastically which leads to an increase in congestion for every mobile node. In 2010, around 5 GB of mobile device traffic was generated in a month. In the forthcoming decade, this volume will have enormous growth. Future communication networks are predicted to find widespread use in applications such as holographical interactions, unmanned aircraft (UA), mixed reality, Industry 5.0, extra-terrestrial and underwater communication [2]. Achieving substantially higher wireless data speeds, efficient spectrum utility, massive connectivity, and maximizing connected area are the goals of next-generation networks.

Classical orthogonal multiple access (OMA) techniques provide orthogonal resources for various users according to time, frequency, or code. Massive connectivity and improved spectral efficiency are two prerequisites for the growing demand for mobile internet and IoE devices. The bandwidth, time slots, and codes in orthogonal resources determine the maximum number of supported users in standard OMA methods [3]. It is well known that OMA sometimes fails to meet the sum rate specifications needed for multiuser environment. In NOMA, various users utilize the common bandwidth and time slot while being distinguishable by different power levels [4]. In the NOMA downlink scenario, superimposing is used for the transmission, and successive interference cancellation (SIC) is used for the reception. The next-generation networks’ total rate requirements may be met with the help of NOMA. More power is given to cell-edge users by NOMA to support the data rate demands [5]. Maximizing the data rate in the NOMA scheme is supported by the optimization framework for power allocation (PA) schemes [6].

Our paper is arranged accordingly: Section 2 describes the related works. The system model is presented in Section 3. Section 4 presents power factor optimization framework using a DE algorithm for the proposed system. Section 5 describes and discusses the simulation results. Section 6 concludes the manuscript.

2. Related Work

The authors of [7] compare the fixed PA, fractional transmit PA, and full search PA in the NOMA system. The authors of [7] take into account simulated scenarios including spectral and energy efficiencies (EEs) and sum rates. Techniques for user matching are investigated, including irregular user grouping and user grouping based on channel gains. The findings demonstrate that, although more complex than fixed transmit PA, full search PA has the highest performance when compared to the other PA techniques. The authors of [8] focus on an efficient user grouping method and the PA design of downlink NOMA. This work considers an NP-hard problem under extreme and least transmission data and SIC utilization. The Lagrangian multiplier model is employed with the KKT optimization algorithm, and PA factors are estimated. In the scheme, the maximum EE is observed, and it is verified via the simulations.

To minimize the power consumption problem, the authors of [9] discuss the MISO-NOMA technique. By combining methods of joint user grouping and beamforming, the PA in a non-convex problem is considered with repetitive distribution. The user grouping is based on two methods, namely channel-gain-based user grouping, which is less complex, and energy-based user grouping, which considers both channel condition and information on intrusions between the cells. The method has EE, better outage performance than the conventional non-grouped MISO-NOMA system, and it is validated through simulations.

The cooperative UA path (UAP) and PA optimization for NOMA in a cognitive network (CN) is investigated in [10]. The PA is converged using a consecutive convex development tool for the given UAP and total transmit power. Then, with optimal PA, the UAP is amended by a Taylor series estimation. The tightness and effectiveness of the algorithm is verified using simulations. To further improve the stability and exactness of the algorithm [10], it is suggested to combine massive MIMO (mMIMO) and reconfigurable intelligent surface with CN. To support the optimal sum rate with minimal intrusion between the antennas, NOMA-based spatial modulation (S-NOMA) techniques are investigated in [11] for UA-assisted services. The simulation results prove that S-NOMA surpasses classical NOMA under the strikes of the altitude of the UA and velocity of users’ mobility and concludes that S-NOMA has more EE than classical NOMA. The enhancement in the throughput of a cell-free system with NOMA-based mMIMO systems for next-generation wireless systems under an uncertain network node and user positions is investigated in [12]. The user positions are derived using the Poisson point method. In [12], the authors consider an uplink scenario by employing the time division duplexing mode for channel estimation with uplink pilots. They perform precoding in downlink transmission using the reciprocity principle with the matched filter. The consolidated received signal is determined by a moment generating function and matching the moments systematically. From the numerical results, NOMA-based mMIMO boosts the data rate considerably compared to OMA-based mMIMO in cell-free systems.

The authors of [13] provide the finding for the non-convex problem resulting from the enhancement of the proportionate offset objective. A dynamic methodology is utilized to obtain the optimal PA according to the irrational proportionate offset condition, without any constraint on the number of users. The simulation result validates the methodology by remaining stable for any number of users which has very large values. Outage probability is one of the parameters used to estimate and compare the performance of different algorithms in most of the works. An optimization scheme for EE improvement in the NOMA-supported downlink system is investigated in the work by [14]. The focus is to optimize the coefficients generated to control the allocated power for different users in a power-based NOMA scheme. The primary objective is to reduce the energy utilization with constraints of minimum fairness and maximum throughput, and to have the performance verified by outage comparison. A non-convex kind of objective is derived for optimization, which is simplified by deriving it in to sub problems. The quadratic method in sequential format is used as the algorithm, and the results validates the theoretical study. A comparison of different heuristic models for optimization in case of PA is covered in [15]. The ant colony mode, which is a nature-inspired method outperforms all other methods. The complexity is compared in terms of convergence rate, peak detection, and implementation difficulty.

The goal is to attain a favorable outage scenario with maximum sum rate, through which the network meets the quality of service (QoS) demands. It can be achieved by using the optimized values of the PA factors. In this work, we have employed a DE algorithm [16], a metaheuristic approach, to optimize PA coefficients, and the main contribution of this work is summarized as follows:

• A DE algorithm is developed to maximize the sum rate for a two-user NOMA system and to obtain converged values of the PA factors;
• The performance is validated by comparing the DE optimized system with random PA schemes;
• The sum rate and outage analysis is carried out for comparison.

3. System Model

The system consists of a base station (BS) and two users, as shown in Figure 1. It is considered that the BS and each user are equipped with a single antenna. The user with the shortest distance from the BS, i.e., the near user (user-1), experiences stronger channel conditions. The user with maximum distance from BS, i.e., the far user (user-2), experiences weaker channel conditions. Due to stronger channel conditions, lower power is allocated to user-1 $\left(a_1\right)$. To maintain fairness, higher power is allocated to user-2 $\left(a_2\right)$, i.e., $a_2>a_1$, $a_2+a_1=1$. The PA for user-$i$ decides the QoS. Hence, $a_i,i=1,2,$ should be optimized to maximize the sum rate and minimize outages.

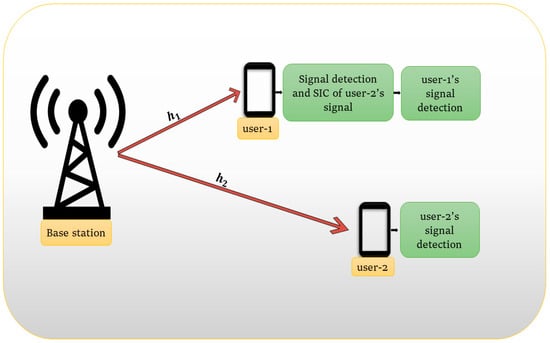
Figure 1. Downlink transmission model for two-user NOMA system.

The expression for the transmitted signal from the BS is [17,18]

$$\mathit{S}={\mathit{x}}_{\mathbf{1}}\sqrt{{\mathit{P}}_{\mathbf{1}}}+{\mathit{x}}_{\mathbf{2}}\sqrt{{\mathit{P}}_{\mathbf{2}}},{\mathit{P}}_{\mathbf{2}}>{\mathit{P}}_{\mathbf{1}}$$

(1)

where $x_i$ and $P_i$ are the data and power allocated to user-i, $i=1,2$. The PA for user-i is given by

$${\mathit{P}}_{\mathit{i}}={\mathit{a}}_{\mathit{i}}{\mathit{P}}_{\mathit{t}},\mathit{i}=\mathbf{1},\mathbf{2}$$

(2)

where $P_t$ represents the total transmit power. The signal received by the $i^{th}$ user is given by

$${\mathit{y}}_{\mathit{i}}={\mathit{h}}_{\mathit{i}}\mathit{S}+{\mathit{Z}}_{\mathit{i}},\mathit{i}=\mathbf{1},\mathbf{2}$$

(3)

where $h_i$ is the complex fading coefficient, $h_iϵ\mathcal{C}\mathcal{N}\left(0,d_i^{-\eta }\right)$. Here, $d_i$ is the distance of the $i^{th}$ user from BS, and $\eta$ is the path loss exponent. $Z_i$ is the noise added to user-i, $Z_iϵ\mathcal{C}\mathcal{N}\left(0,n_0\right)$. Here, $n_0$ is the noise variance. Due to a higher $a_2$, user-2 decodes its signal directly at the receiver. The signal-to-interference-noise ratio (SINR) for user-2 is represented as

$${\mathit{\gamma }}_{\mathit{u}\mathbf{2}}=\frac{{\left|{\mathit{h}}_{\mathbf{2}}\right|}^{\mathbf{2}}{\mathit{a}}_{\mathbf{2}}{\mathit{P}}_{\mathit{t}}}{{\left|{\mathit{h}}_{\mathbf{2}}\right|}^{\mathbf{2}}{\mathit{a}}_{\mathbf{1}}{\mathit{P}}_{\mathit{t}}+{\mathit{n}}_{\mathbf{0}}}$$

(4)

User-1 decodes user-2’s data first and employs SIC. From here, the residual signal user-2’s data are decoded, and the corresponding signal-to-noise ratio (SNR) is given by

$${\mathit{\gamma }}_{\mathit{u}\mathbf{1}}=\frac{{\left|{\mathit{h}}_{\mathbf{1}}\right|}^{\mathbf{2}}{\mathit{a}}_{\mathbf{1}}{\mathit{P}}_{\mathit{t}}}{{\mathit{n}}_{\mathbf{0}}}$$

(5)

The achievable rate of user-2 is given by,

$${\mathit{R}}_{\mathit{u}\mathbf{2}}={\mathit{log}}_{\mathbf{2}}\left(\mathbf{1}+\frac{{\left|{\mathit{h}}_{\mathbf{2}}\right|}^{\mathbf{2}}{\mathit{a}}_{\mathbf{2}}{\mathit{P}}_{\mathit{t}}}{{\left|{\mathit{h}}_{\mathbf{2}}\right|}^{\mathbf{2}}{\mathit{a}}_{\mathbf{1}}{\mathit{P}}_{\mathit{t}}+{\mathit{n}}_{\mathbf{0}}}\right)$$

(6)

The achievable rate of user-1 is given by,

$${\mathit{R}}_{\mathit{u}\mathbf{1}}={\mathit{log}}_{\mathbf{2}}\left(\mathbf{1}+\frac{{\left|{\mathit{h}}_{\mathbf{1}}\right|}^{\mathbf{2}}{\mathit{a}}_{\mathbf{1}}{\mathit{P}}_{\mathit{t}}}{{\mathit{n}}_{\mathbf{0}}}\right)$$

(7)

The sum rate ($R_{sum})$ of the two-user NOMA system is given by [19,20]

$${\mathit{R}}_{\mathit{s}\mathit{u}\mathit{m}}={\mathit{R}}_{\mathit{u}\mathbf{2}}+{\mathit{R}}_{\mathit{u}\mathbf{1}}={\mathit{log}}_{\mathbf{2}}\left(\mathbf{1}+\frac{{\left|{\mathit{h}}_{\mathbf{2}}\right|}^{\mathbf{2}}{\mathit{a}}_{\mathbf{2}}{\mathit{\rho }}_{\mathit{t}}}{{\left|{\mathit{h}}_{\mathbf{2}}\right|}^{\mathbf{2}}{\mathit{a}}_{\mathbf{1}}{\mathit{\rho }}_{\mathit{t}}+\mathbf{1}}\right)+{\mathit{log}}_{\mathbf{2}}\left(\mathbf{1}+\left|{{\mathit{h}}_{\mathbf{1}}}^{\mathbf{2}}\right|{\mathit{a}}_{\mathbf{1}}{\mathit{\rho }}_{\mathit{t}}\right)$$

(8)

where ${\rho }_t=\frac{P_t}{n_0}$ is the received SNR.

An outage occurs when the data rate does not meet the minimum requirement condition, which is expressed as follows:

$$\mathrm{Outage}\mathrm{condition}:({\mathit{R}}_{\mathit{u}\mathbf{1}}<{\tilde{\mathit{R}}}_{\mathit{u}\mathbf{1}})\cap ({\mathit{R}}_{\mathit{u}\mathbf{2}}<{\tilde{\mathit{R}}}_{\mathit{u}\mathbf{2}})$$

(9)

where ${\tilde{R}}_{u1}$ and ${\tilde{R}}_{u2}$ are the minimum data rate demand for user-1 and user-2, respectively.

4. Power Factor Optimization Using DE Algorithm

The optimized values of $a_i$ are essential to maximize the sum rate given in (8). The optimization problem is formulated as

$$\left.\begin{array}{c}\begin{array}{c}\begin{array}{c}\underset{{\mathit{a}}_{\mathit{i}}}{\mathit{max}}{\mathit{R}}_{\mathit{s}\mathit{u}\mathit{m}}\\ \mathit{s}\mathit{u}\mathit{b}\mathit{j}\mathit{e}\mathit{c}\mathit{t}\mathit{t}\mathit{o}\\ {\mathit{a}}_{\mathbf{1}}+{\mathit{a}}_{\mathbf{2}}=\mathbf{1}\\ {\mathit{a}}_{\mathbf{2}}>{\mathit{a}}_{\mathbf{1}}>\mathbf{0}\\ {\mathit{R}}_{\mathit{u}\mathbf{1}}>{\tilde{\mathit{R}}}_{\mathit{u}\mathbf{1}}\\ {\mathit{R}}_{\mathit{u}\mathbf{2}}>{\tilde{\mathit{R}}}_{\mathit{u}\mathbf{2}}\end{array}\end{array}\end{array}\right\}$$

(10)

In this work, the DE algorithm is adapted to optimize the PA factors. It is built on the ideas of genetic algorithms and natural selection [16]. The detailed description of the DE algorithm’s operation is elaborated in this section. A population of randomly generated candidate solutions is the starting point for the DE algorithm. An individual in the solution is represented as a vector of real-valued parameters. Based on the existing population, the algorithm iteratively generates new candidate solutions. The steps for the DE algorithm include initialization, mutation, crossover, and selection. The pseudo code of the DE algorithm is illustrated in Algorithm 1.

Initialization: In the initialization step, the objective function $\left(f\right)$ used for optimization, i.e., (10) is determined. The population size $\left(N_P\right)$, which indicates the quantity of candidate solutions, is defined. $N_P$, number of set of PA factors, and $\mathit{A}=\left\{a_i,i=1,2.\}\right.$ are randomly generated as the initial population. The number of generations $\left(T\right)$is decided, which is used for the total iteration. The population $A\left(t\right)$ is set, where $t=1,2,\dots .T$, is the generation counter, with $N_P$ randomly generated individuals.

Mutation: For each individual in the population, three distinct individuals are randomly selected from $\mathit{A}$, which are denoted by $A_{k1}$, $A_{k2}$, and $A_{k3}$. A mutation operation is applied to the chosen individuals to produce a trial vector, designated as $v\left(j,t\right)$. It will be performed using

$$\mathit{v}\left(\mathit{j},\mathit{t}\right)={\mathit{A}}_{\mathit{k}\mathbf{1}}+\mathit{F}\left({\mathit{A}}_{\mathit{k}\mathbf{2}}-{\mathit{A}}_{\mathit{k}\mathbf{3}}\right)$$

(11)

where $F$ is the mutation factor. It is ensured that the newly formed vector satisfies the required constrains in (10).

Crossover: This operation is performed between the trial vector and the current individual. For each individual in the population, a crossover operation between the trial vector $v\left(j,t\right)$ and the current individual $A\left(j,t\right)$ is performed. The algorithm replaces the current individual with new trial vector, depending on the crossover probability $\left(P_c\right)$and a random number $\left(m_{rand}\right)$, and the component is denoted as$u\left(j,t+1\right)$.

Algorithm 1: The DE algorithm for maximization of sum rate.

Inputs: $N_P,T,F,P_c,l_b,u_b,m_{rand},D,f,$ Rayleigh fading channel coefficients $\left\{h_i,i=1,2\right\}$ of size $N_s$.

Initialization: Random population $\mathit{A}=\left\{a_i,i=1,2\}\right.$ of size $N_P\times 2$ with constraints in $\left(10\right)$.

Steps: 1:   Form $f\left(a_i\right)$ of size $N_P$ by evaluating the sum rate for all individuals. 2:   for $t=1toT$ 3:      for $j={1toN}_P$ do 4:          Randomly select three position index of $\mathit{A}$, $k_1\ne k_2\ne k_3\ne j$ 5:          Generate a donor vector $v\left(j,t\right)$ using $\left(11\right)$ 6:          $m_{rand}=randi(1,D)$ 7:          for $m=1toD$ do 8:              if rand <$P_c$ or $m=m_{rand}$ then 9:                 $u\left(j,t+1\right)=v\left(j,t\right)$ 10:              else 11:                $u\left(j,t+1\right)=A\left(j,t\right)$ 12:              end if 13:          end for 14:      end for 15:      for $n=1toNp$ do 16:          Evaluate the fitness for $u(j,t+1)$ 17:          if $f\left(u\left(j,t+1\right)\right)$ is greater or equal to $f\left(A\left(j,t\right)\right)$ then 18:              Replace $A\left(j,t\right)$ with $u\left(j,t\right)$ 19:          end if 20:      end for 21:   end for 22:   Repeat the process for $Ns$ number of channel coefficients and find the average of sum rate.

Selection: The algorithm evaluates the fitness of $u\left(j,t+1\right)$and $A\left(j,t\right)$ using an objective function, and a greedy selection is performed. If $u\left(j,t+1\right)$ performs better, then it replaces $A\left(j,t\right)$. Otherwise, $A\left(j,t\right)$is retained in the population.

The mutation, crossover, and selection steps are repeated for all individuals in the population. The algorithm terminates, when it reaches the maximum iterations or generations. $\mathrm{H}\mathrm{e}\mathrm{r}\mathrm{e},l_b$ and $u_b$are the maximum and minimum values of $a_i$, and $D$ is the length of $l_b$.

5. Simulations and Discussions

In this section, the numerical results are compared for the DE-optimized NOMA and NOMA with different random PA factors $\left({a_1,a}_2\right)$. The DE-algorithm-optimized NOMA is referred to as NOMA-DE. For NOMA with random PA, three different PA values are considered: case-1 ($a_1=0.35,a_2=0.65$), case-2 ($a_1=0.25,a_2=0.75$), and case-3 ($a_1=0.15,a_2=0.85$). Table 1 introduces the numerous parameters utilized for simulation.

Table 1. Simulation parameters.

Parameters	Values
Distance of user-1 from BS, $d_1$	300 m
Distance of user-2 from BS, $d_2$	600 m
Bandwidth, B	${10}^6\mathrm{H}\mathrm{z}$
Initial population size, $N_p$	50
Number of iterations, $T$	100
Scaling factor for mutation, $F$	0.85
Crossover probability, $P_c$	0.8
Lower bound for individual vectors, $l_b$	0
Upper bound for individual vectors, $u_b$	1
Path loss exponent, $\eta$	4
Number of channel coefficients, $N_s$	${10}^4$
Minimum data rate demand for user-1, ${\tilde{R}}_{u1}$	1 bps/Hz
Minimum data rate demand for user-2, ${\tilde{R}}_{u2}$	1 bps/Hz

Figure 2 compares the sum rate of NOMA-DE with random PA. The sum rate improves as the transmit power increases. For the analysis, a transmit power of $10\mathrm{dBm}$ is considered, and the corresponding sum rate values are given in Table 2. At $10\mathrm{dBm}$, transmit power, NOMA-DE achieves a sum rate of $\approx 7.57\mathrm{b}\mathrm{p}\mathrm{s}/\mathrm{H}\mathrm{z}$, and using random PA, case-1 achieves $\approx 7.15\mathrm{b}\mathrm{p}\mathrm{s}/\mathrm{H}\mathrm{z}$, case-2 achieves $\approx 6.93\mathrm{b}\mathrm{p}\mathrm{s}/\mathrm{H}\mathrm{z}$, and case-3 achieves $\approx 6.72\mathrm{b}\mathrm{p}\mathrm{s}/\mathrm{H}\mathrm{z}$. NOMA-DE surpasses random PA for the demands of sum rate. The sum rates of NOMA-DE,$\approx 5.87\%,\approx 9.24\%$, and $\approx 12.65\%$, are higher than random PA in case 1, 2, and 3, respectively.

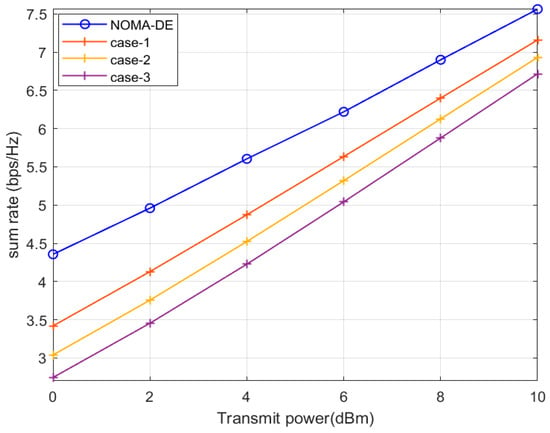
Figure 2. Sum rate comparison of NOMA-DE with random PA.

Table 2. Sum rate comparison of NOMA-DE and random PA.

Scheme	Sum Rate at 10 dBm Transmit Power	% of Sum Rate Improvement of NOMA-DE over Random PA
NOMA-DE	$\approx$7.57 bps/Hz	-
case-1	$\approx$7.15 bps/Hz	$\approx$5.87%
case-2	$\approx$6.93 bps/Hz	$\approx$9.24%
case-3	$\approx$6.72 bps/Hz	$\approx$12.65%

An outage probability comparison of NOMA-DE with random PA for user-1 is shown in Figure 3. The probability of outage reduces as the transmit power improves. User-1 achieves a desired outage probability of ${10}^{-3}$ at $\approx 20\mathrm{d}\mathrm{B}\mathrm{m}$transmit power under NOMA-DE, whereas under random PA with case-1 achieved the same value at $\approx 28.24\mathrm{d}\mathrm{B}\mathrm{m}$, case-2 at $\approx 31.50\mathrm{d}\mathrm{B}\mathrm{m}$, and case 3 at $\approx 34.13\mathrm{d}\mathrm{B}\mathrm{m}$. NOMA-DE requires $\approx 8.24\mathrm{d}\mathrm{B}\mathrm{m},\approx 11.50\mathrm{d}\mathrm{B}\mathrm{m}$, and $\approx 14.13\mathrm{d}\mathrm{B}\mathrm{m}$ less power than random PA in case 1, 2, and 3, respectively.

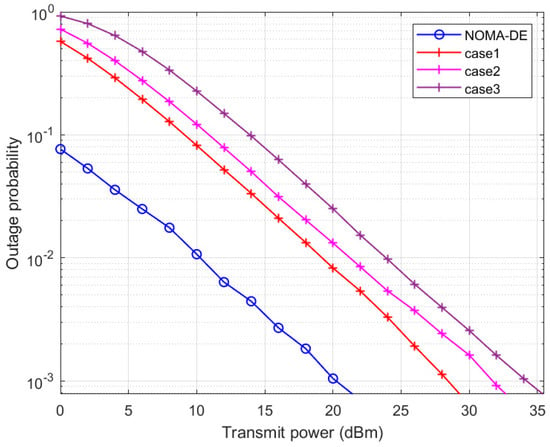
Figure 3. User-1’s outage comparison of NOMA-DE with random PA.

The outage probability comparison of NOMA-DE with random PA for user-2 is shown in Figure 4. The outage probability can be minimized by increasing the transmit power. User-2 achieves a desired outage probability of ${10}^{-3}$ at $\approx 16.82\mathrm{d}\mathrm{B}\mathrm{m}$ transmit power under NOMA-DE, whereas under random PA with case-1 achieved the same value at $\approx 26\mathrm{d}\mathrm{B}\mathrm{m}$, with case-2 at $\approx 24.90\mathrm{d}\mathrm{B}\mathrm{m}$, and with case 3 at $\approx 23.38\mathrm{d}\mathrm{B}\mathrm{m}$. NOMA-DE requires $\approx 9.18\mathrm{d}\mathrm{B}\mathrm{m}$,$\approx 8.08\mathrm{d}\mathrm{B}\mathrm{m}$, and $\approx 6.56\mathrm{d}\mathrm{B}\mathrm{m}$ less power than random PA in case 1, 2, and 3, respectively. The transmit power values to achieve the desired outage and the corresponding difference between the different cases are given in Table 3.

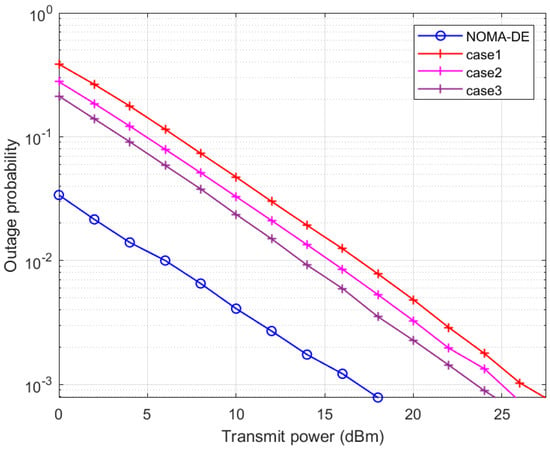
Figure 4. User-2’s outage comparison of NOMA-DE with random PA.

Table 3. Outage comparison of NOMA-DE with random PA.

Scheme	User-1		User-2
	Transmit power (dBm) to achieve a target outage of ${10}^{-3}$	Improvement of DE over other cases.	Transmit power (dBm) to achieve a target outage of ${10}^{-3}$	Improvement of DE over other cases
NOMA-DE	$\approx$20 dBm	-	$\approx$16.82 dBm	-
case-1	$\approx$28.24 dBm	$\approx$8.24 dBm	$\approx$26 dBm	$\approx$9.18 dBm
case-2	$\approx$31.50 dBm	$\approx$11.50 dBm	$\approx$24.90 dBm	$\approx$8.08 dBm
case-3	$\approx$34.13 dBm	$\approx$14.13 dBm	$\approx$23.38 dBm	$\approx$6.56 dBm

6. Conclusions

This paper proposes an optimization framework for PA in NOMA using DE to maximize the sum rate. NOMA-DE provides a minimum of $\approx 6\%$ improvement in the sum rate over the random PA scheme. NOMA-DE performs better in terms of outage when compared with random PA. For user-1, NOMA-DE requires a minimum of $\approx 8.24\mathrm{d}\mathrm{B}\mathrm{m}$ less transmit power than random PA to achieve the targeted outage. Similarly for user-2, NOMA-DE requires a minimum of $\approx 6.56\mathrm{d}\mathrm{B}\mathrm{m}$ less transmit power than random PA to achieve the targeted outage. Hence, DE-optimization-algorithm-generated PA factors outperform random PA in every case. NOMA-DE can perform better for a greater number of users. To accommodate multiple users, NOMA can be combined with user pairing schemes, like near–far pairing, near–near pairing, random user pairing, channel aware pairing, etc. To reduce the complexity of the optimization, machine learning algorithms can be employed to decide the PA factors of users.