Finite Physical Dimensions Thermodynamic Analysis for Gamma Stirling Engine ^†

Abstract

In the foreseeable future, the depletion of finite fossil fuel reserves is a growing concern due to the increasing consumption of these resources by humans. Moreover, the emission of greenhouse gases from fossil fuel consumption contributes to global warming, resulting in significant harm to the Earth’s ecosystem. The Stirling engine (SE) offers an outstanding solution for harnessing various heat sources, including solar, nuclear, and fossil fuels, among others. It provides numerous advantages, such as high efficiency, a long lifespan, low noise levels, and minimal or no emissions. This study conducts a finite physical dimensions thermodynamic analysis (FPDT) on a gamma-type double-piston cylinder engine and compares the results with other isothermal models and experimental data. The current model’s results align closely with those of other thermodynamic models.

1. Introduction

In the coming years, the depletion of fossil fuel reserves poses a critical concern, primarily due to the ever-increasing human consumption of these non-renewable resources. Notably, the heightened usage of fossil fuels contributes significantly to the emission of greenhouse gases, exacerbating global warming and causing substantial damage to the delicate balance of the Earth’s ecosystem [1,2]. Consequently, there is an urgent need for alternative energy sources to address this pressing issue. Among potential solutions, solar energy stands out as a safe, environmentally friendly, and cost-free option, presenting a viable competition to conventional fossil fuels. With the escalating demand for sustainable energy, solar power emerges as a promising choice to alleviate the strain on fossil fuel resources and mitigate their adverse impact on the planet.

In this context, the Stirling engine (SE) comes into focus as a promising mechanism for harnessing solar power effectively. The Stirling engine boasts a range of advantageous features, including high efficiency, a long operational lifespan, low noise levels, and minimal or virtually no emissions [3,4]. By leveraging these benefits, the Stirling engine provides a sustainable and reliable means of converting every form of energy into usable power, offering a pathway to reduce our reliance on fossil fuels and curbing their detrimental effects on the environment. With the pressing need to address climate change and preserve the planet’s ecological balance, the adoption of solar energy, particularly through the utilization of Stirling engines, becomes a crucial step toward a more sustainable and greener future.

Within this research paper, an investigation delves into the performance of a gamma-type Stirling engine through the implementation of a finite physical dimensions thermodynamic (FPDT) model. The outcomes produced by the FPDT model are subjected to a comparative analysis against another established thermodynamic model. The findings exhibit that the power output and efficiency yielded by the FPDT model reach 154.89 W and 34.1%, respectively. These values surpass the outcomes obtained from experimental estimates, as well as those documented in the existing literature. This particular model proves instrumental in uncovering insights regarding diverse losses present within the Stirling engine. Notably, a meticulous examination highlights that hysteresis losses within the Stirling engine supersede other forms of losses. This phenomenon can be attributed to the unique operational characteristics of the closed-cycle system in consideration.

2. Engine Data and Mathematical Equation

The engine under study is a gamma-type double-piston Stirling engine. In this engine, the exhaust gas of the diesel engine is used as the heat source [5]. To heat the heater tubes of the Stirling engine, a cap is specially made for the Stirling engine. Further details of the engine are given below.

In this finite physical dimensional thermodynamic analysis, the important equations are described below, and for further information about the equations, readers are referred to this [6]. In the finite physical dimensions thermodynamic (FPDT) approach, finite physical dimensions are taken into account, including factors like the heat transfer area and the speed of the working piston. These considerations align better with an engineering perspective. The losses within the engine can be represented as functions of the gas speed or rotational speed. These losses encompass elements such as mechanical friction, hysteresis loss, pressure reduction from the finite-speed movement of the piston, and the dissipation of energy through viscosity within the heat exchanger channels.

A Stirling engine is an important machine. The volumes of the expansion and compression spaces of a gamma-type Stirling machine can be expressed as [6]

$$V_e=\frac{V_{e0}}{2}\left[1-\cos \left(\omega t\right)\right]$$

(1)

$$V_c=\frac{V_{e0}}{2}\left[1+\kappa +\cos \left(wt\right)-\kappa \cos \left(\omega t-\varphi \right)\right]$$

(2)

$$\kappa =\frac{V_{c0}}{V_{e0}}$$

(3)

The total volume of the engine is calculated as

$$V_t=V_e+V_c+V_t=\frac{V_{e0}}{2}\left[2+\kappa -\kappa \cos \left(\omega t-\varphi \right)+2\chi \right]$$

(4)

$$\chi =\frac{V_r}{V_{e0}}$$

(5)

$$P=\frac{m{r}_g{T}_e}{V_{e0}}{\left[\frac{2\chi }{1+\tau }+\frac{1+\tau +\kappa }{2\tau }+\frac{\left(1-\tau \right)\cos \left(\omega t\right)}{2\tau }+\frac{\cos \left(\omega t-\varphi \right)}{2\tau }\right]}^{-1}$$

(6)

where $\tau =T_c/T_e$, and the indicated mechanical power of a Stirling engine is calculated as

$$\dot{W}=\frac{1}{2\pi /\omega }{\displaystyle \oint Pd{V}_t}$$

(7)

After the integration, the indicated mechanical power of the engine is denoted as

$$\dot{W}=\omega m{r}_g\frac{\tau \left(1-\tau \right)\kappa \sin \left(\varphi \right)}{a^2+b^2}\left[\frac{\beta }{\sqrt{{\beta }^2-\left(a^2+b^2\right)}}-1\right]$$

(8)

where $a=1-\tau -\kappa \cos \left(\varphi \right),b=\kappa \sin \left(\varphi \right),\beta =\frac{4\tau \chi }{1+\tau }+1+\kappa$; the heater transfer flow in the heater, which is rejected from the cooler and stored in the regenerator, can be calculated.

$${\dot{Q}}_h=\omega m{r}_g{T}_e\frac{\tau \kappa \sin \left(\varphi \right)}{a^2+b^2}\left[\frac{\beta }{\sqrt{{\beta }^2-\left(a^2+b^2\right)}}-1\right]$$

(9)

$${\dot{Q}}_k=-\omega m{r}_g{T}_e\frac{{\tau }^2\kappa \sin \left(\varphi \right)}{a^2+b^2}\left[\frac{\beta }{\sqrt{{\beta }^2-\left(a^2+b^2\right)}}-1\right]$$

(10)

$${\dot{Q}}_r={\dot{m}}_{av}{c}_p\left(1-{\epsilon }_r\right)\left(T_e-T_c\right)$$

(11)

where m_av is the average mass flow rate, and ε_r is the efficiency of the regenerator. For detailed information about losses in a Stirling engine, readers are referred to [6].

3. Results and Discussion

Model Validation

For model validation and a detailed analysis of the FPDT model, a p-V diagram is shown below which describes the performance of the Stirling engine. Furthermore, Table 1 shows a summary of thermodynamic model in which the work, power, and efficiency of the FPDT model are compared with a simple model, an adiabatic model, and experimental data. The Figure 1 shows the comparison of FPDT thermal model with other thermodynamic model. The indicated work of the FPDT model is 10.7 J, while the experimental value determined by Abdul Rab et al. [5] is 7.50 J, which is 41% more than the experimental estimated value. The average pressure of the engine is 3.58 bar, but the value estimated using this method is 4.75 bar, and the peaks value of the p-V diagram curve are also greater than the estimated values.

Table 1. Engine data of gamma-type double-piston Stirling engine [5].

Engine Data	Values	Engine Data	Values
Cooler temperature	294	Pressure (bar)	3.58
Heater temperature	424	Rotational speed (rpm)	882
Cooler volume	223 × 10−6	Phase angle (degree)	88°
Heater volume	87.28 × 10−6	Regenerator volume (m3)	308.93
Expansion swept volume (m3)	221 × 10−6	Compression swept volume (m3)	194 × 10−6
Expansion clearance volume (m3)	24 × 10−6	Compression clearance volume (m3)	35 × 10−6

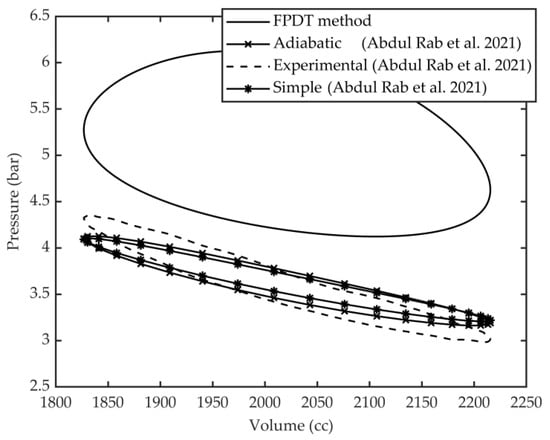
Figure 1. Comparison of FPDT model with other isothermal models and experimental data [5].

Table 2 shows the summary of comparison FPDT thermal model with other thermodynamic model. There are various losses also estimated in this research work, i.e., the average power losses, shuttle losses, hysteresis losses, and average fluid friction losses. Table 3 shows the projected values of these losses. The working gas undergoes a closed cycle; therefore, hysteresis losses in the Stirling engine are more than other losses and are estimated to be 27.53 W.

Table 2. Summary of thermodynamic models.

Parameters	Simple [5]	Adiabatic [5]	Experimental [5]	FPDT Model
Work (J)	6.30	9.70	7.50	10.7
Power (W)	93.2	143.75	111.43	154.89
Efficiency (%)	21.2	30.90	24.70	34.1

Table 3. Different types of losses estimated for a gamma Stirling engine.

Different Losses (W)	Values
Power Losses	7.8
Shuttle Losses	9.7
Hysteresis Losses	27.53
Fluid friction Losses	24.73

Upon closer examination, it becomes evident that hysteresis losses within the Stirling engine hold precedence over other forms of energy dissipation. This intriguing phenomenon can be attributed to the distinctive operational dynamics characterizing the enclosed cyclic system under scrutiny.

4. Conclusions

In this research paper, the performance of a gamma-type Stirling engine is analyzed using a finite physical dimensions thermodynamic (FPDT) model. The results of the FPDT model are compared with other thermodynamic models. The results show that the power and efficiency obtained by FPDT model are 154.89 W and 34.1%, which is more than the experimental estimated values when comparing this model’s results with the literature. By using this model, various losses in the Stirling engine are also analyzed. It is found that hysteresis losses in the Stirling engine are greater than other losses due to the working condition of the closed cycle.