Train Pulses with a Random Spatial Distribution to Measure In-Plane Thermal Diffusivity ^†

Abstract

A thermal diffusivity measurement approach is proposed in which the sample is thermally excited by a periodic train of pulsed, spatially random laser light. The temperature field on the surface is observed by IR camera and the diffusion is recorded by a sequence of IR images. The analysis of the diffusion in time and space is followed by suitable models. Fitting of the spatiotemporal evolution of the surface temperature allows to determine the thermal diffusivity of clay brick with an accuracy of 5%.

1. Introduction

In this work, we explored the use of infrared (IR) thermography for the thermal characterization of building materials. This approach has the potential to determine both the heat transportation and the heat storage properties via the thermal diffusivity. The most classical IR thermography configuration is the flash method, in which one side of the sample is illuminated with a pulse, and the temperature is measured (via the IR radiation) on the back side [1]. While this method is well established, it has the disadvantage that the sample thickness should be in a suitable range; moreover, it requires the access to both sides of the material. Other approaches have been developed in which the lateral thermal diffusion is monitored, resulting from heating the sample with a non-uniform light pattern. Up to now, the investigated patterns were: Gaussian spot [2], Gaussian line [3], 1D periodic grid [4], step [5], and random [6]. This approach allows us to measure thermal diffusivity in a one-sided (reflection) configuration and, therefore, on thermally thick (eventually semi-infinite) samples. The idea in this work is that of projecting a random pattern of light on the surface of a sample, pulsed in time, like in laser-flash technique. The modeling of the thermal problem is based on the work of Philippi [7], which gave the solution for a spatial pattern of a generic shape. Moreover, we take advantage of averaging the thermographic images over many pulses to increase the SNR [8].

2. Modeling

The heat conduction Equation (1), where $T\equiv T(x,y,z,t)$ is temperature, t is time, $x,y,z$ spatial coordinates, $\alpha$ thermal diffusivity, by means of the Fourier integral transform in space ($x,y$) and time (t), is as follows:

$${\nabla }^{2}T-\frac{1}{\alpha }\frac{\partial T}{\partial t}=0$$

(1)

which can be transformed as follows:

$$\left(\frac{{\partial }^2}{\partial z^2}-{\sigma }^2\right)\theta (k_x,k_y,z,\omega )=0$$

(2)

where $\sigma =\sqrt{k_x^2+k_y^2+\frac{ı\omega }{\alpha }}$, and $\omega =2\pi f$, f is the frequency.

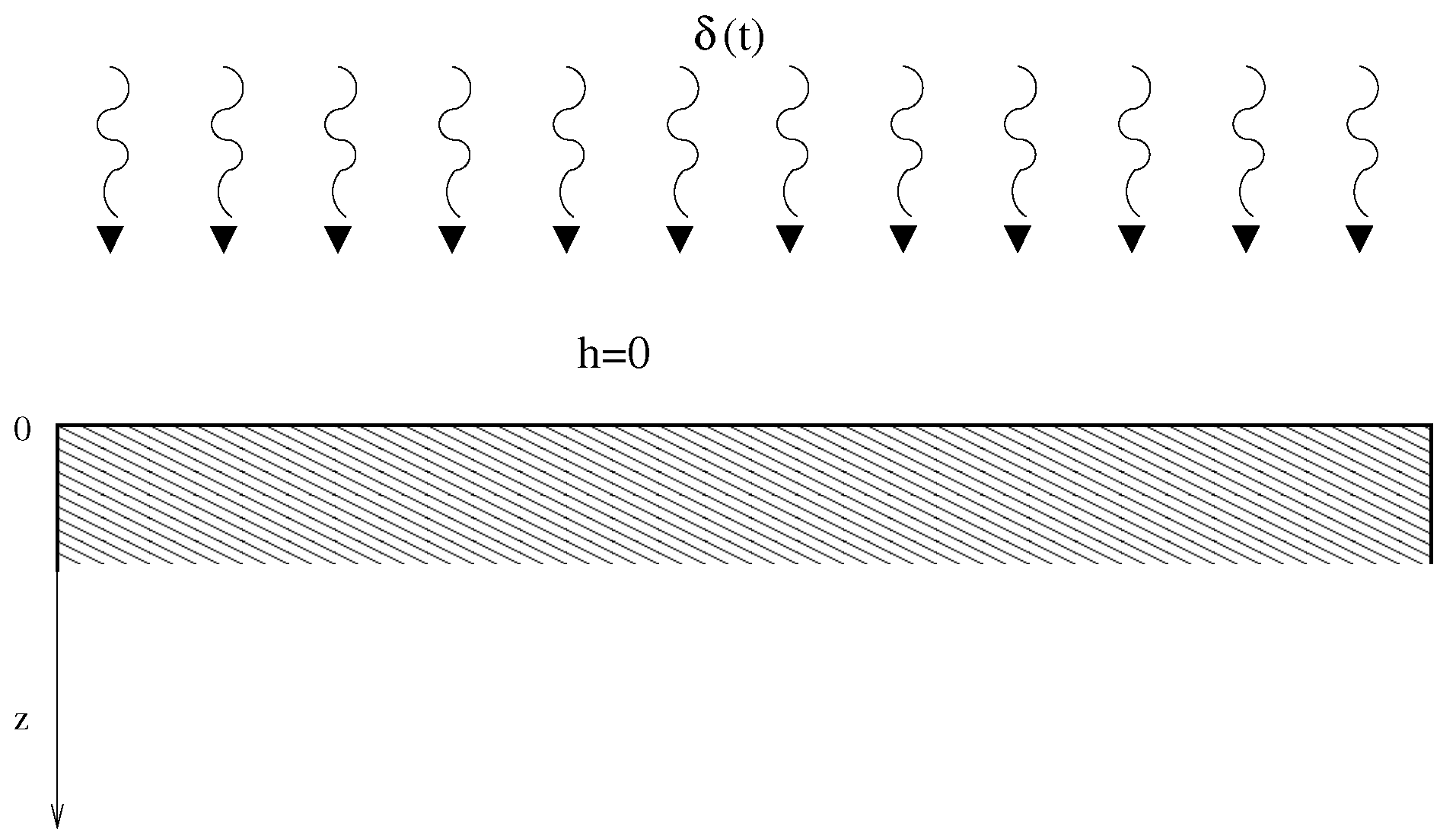
The boundary condition for the semi-infinite body (no heat exchange with the environment, heated on the surface by a generic spatial function and by a Dirac delta in time) is sketched in Figure 1, and is defined in Equation (3):

$$-\lambda \frac{\partial \theta (k_x,k_y,z,p)}{\partial z}{|}_{z=0}=Q·g(k_x,k_y)·\frac{\sqrt{2\pi }}{\tau }\sum _{n=-\infty }^{\infty }\delta \left(\omega -\frac{2\pi n}{\tau }\right)$$

(3)

where $\mathcal{F}\left[f(x,y)\right]\equiv g(k_x,k_y)$, $\mathcal{F}\left[{\sum }_{m=-\infty }^{\infty }\delta \left(t-m\tau \right)\right]\equiv \frac{\sqrt{2\pi }}{\tau }{\sum }_{n=-\infty }^{\infty }\delta \left(\omega -\frac{2\pi n}{\tau }\right)$, Q is the energy absorbed by the surface, $\lambda$ is the thermal conductivity, and $\tau$ is the period of the pulse.

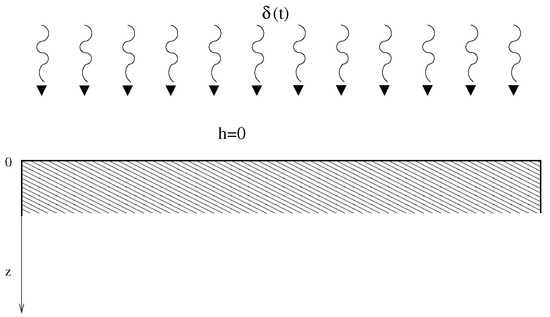
Figure 1. The semi-infinite body with no heat exchange with the environment, and prescribed heating function $f(x,y)$ on the surface and Dirac delta $\delta \left(t\right)$ in time.

In case of just one pulse, the spatial Fourier transform as a function of time and spatial coordinate z is obtained:

$$\Theta (k_x,k_y,z,t)=g(k_x,k_y)·e^{-(k_x^2+k_y^2)\alpha t}·\frac{Q}{ϵ\sqrt{\pi t}}{e}^{-z^2/4\alpha t}$$

(4)

where the effusivity $ϵ=\frac{\sqrt{\alpha }}{\lambda }$ is introduced. Normalizing by the DC component of the Fourier Transform and taking the logarithm of the ratio, it is possible to estimate the thermal diffusivity that appears in the slope of the straight line:

$$log\frac{\Theta (k_x,k_y,z=0,t)}{\Theta (k_x=0,k_y=0,z=0,t)}=const-(k_x^2+k_y^2)\alpha t$$

(5)

3. Materials and Methods

An experiment was performed on a piece of clay brick with thermal diffusivity $\alpha =4.91\times {10}^{-7}$ [m${}^2$ s${}^{-1}$] ± $2.7\%$, as obtained by measurement of thermal conductivity by a Hot Disk ($\lambda =0.56$ [W m${}^{-1}$ K${}^{-1}$] ±$1.9\%$), specific heat by a DSC ($c_p=783$ [J kg${}^{-1}$ K${}^{-1}$] ± $1.9\%$), and density by weight and volume ratio ($\rho =1466.5$ [kg m${}^{-3}$] ± $0.6\%$). The laser is shot at the sample in a random pattern, similar to a QR-code. The single pulse duration is 2 ms with an energy of 1 Joule. The repetition rate is 30 Hz. The laser beam passing through the pattern has a diameter of 0.5. The IR camera collects a sequence of images, 80 × 320 pixels, at a frame rate of 150 Hz. The Field of View corresponding to a pixel is 108 μm. Those pieces of the experimental set-up are shown in Figure 2. Eight different random pattern were produced in the facilities of the Tokyo Institute of Technology and Tsukuba AIST by sputter deposition of gold on glass substrate, 14 × 20 × 0.7 mm. The area covered by the pattern is 10 × 10 mm. The eight patterns with different spatial resolutions are depicted in Figure 3.

Figure 2. (a) Clay brick sample; (b) sample mounted in holder; (c) random pattern mounted in front of the exit of the laser; (d) experimental layout: the yellow dashed line indicates the field of view of the IR camera, the green arrow indicates the incident laser beam.

Figure 3. Eight random patterns were prepared in the facilities of the Tokyo Tech and Tsukuba AIST. A 100 nm layer of gold was sputtered on a glass substrate.

4. Results

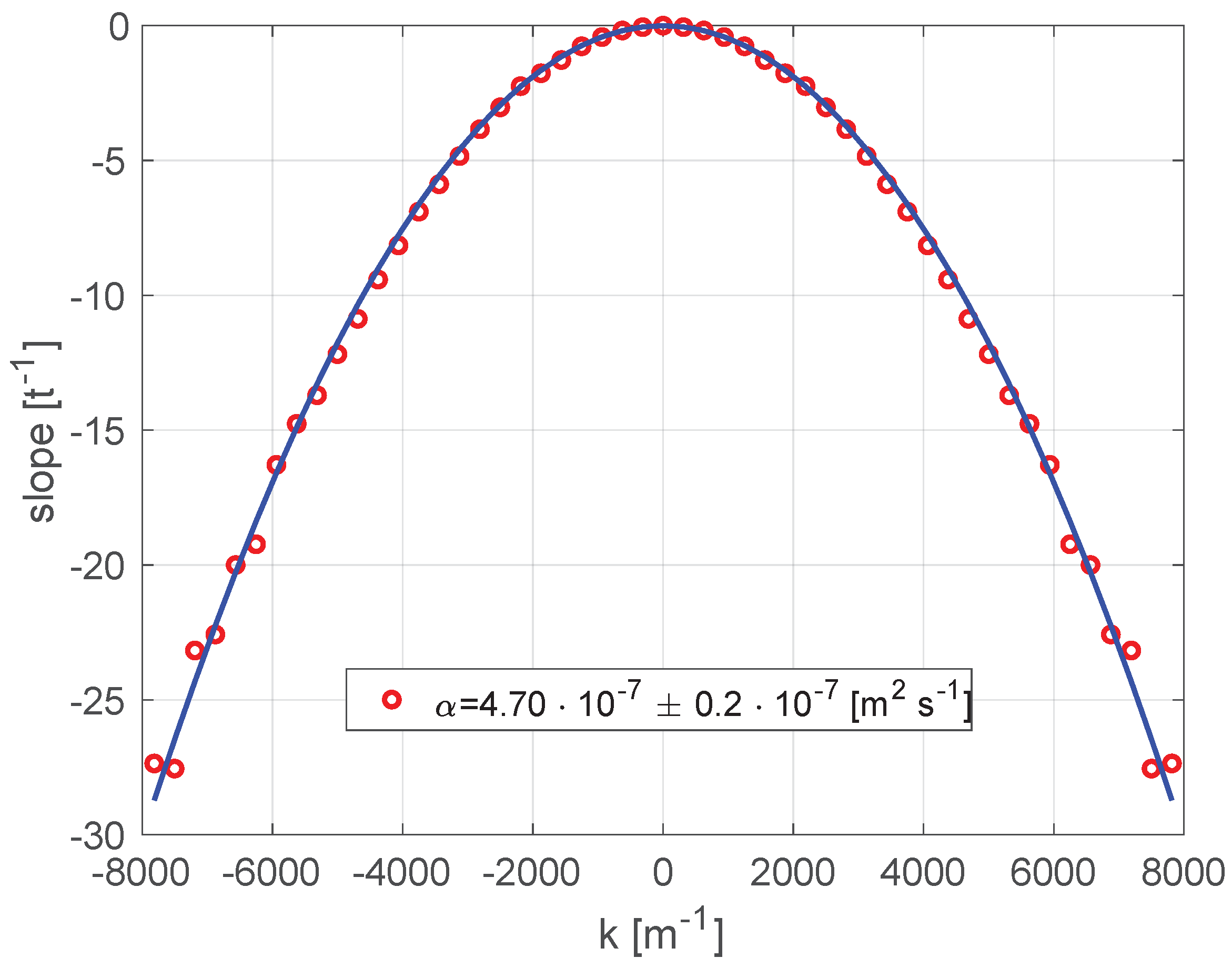
Figure 4 shows the IR image immediately after illumination by a laser pulse. By analyzing in time the spatial frequencies of the Fourier Transform of the IR images, a plot of the slopes vs. the spatial frequencies (k) is obtained as in Figure 5. Each point is the slope of the straight line fitting the amplitude of the spatial Fourier Transform at a certain spatial frequency. According to Equation (5), the slope depends quadratically on the spatial frequency k. The coefficient of the quadratic term gives the thermal diffusivity. The obtained preliminary value of thermal diffusivity is $\alpha =4.7$· 10${}^{-7}$ [m${}^2$ s${}^{-1}$] $\pm 4.3\%$.

Figure 4. IR image immediately after the shot of the laser. The camera was running in windowing mode with images of 80 × 320 pixels at 150 Hz frame rate.

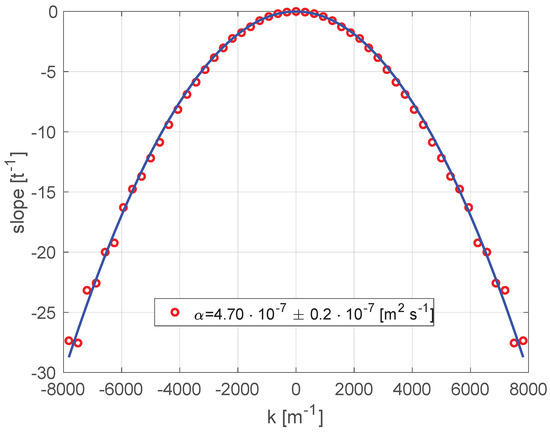
Figure 5. Each point in the plot is the slope of the straight line that fits the amplitude of the spatial Fourier Transform of the IR image at a certain spatial frequency. The slopes depend quadratically on the spatial frequency k and the coefficient of the quadratic term in the parabola is the thermal diffusivity.