Abstract
This paper presents a practical guideline to implement and evaluate time and frequency diversity techniques in Orthogonal Frequency Division Multiplexing (OFDM) systems under Rician fading using MATLAB R2024a. The MATLAB framework allows flexible configuration for several parameters, such as modulation schemes, cyclic prefix lengths, and channel parameters. We present the results in terms of Bit Error Rate (BER) versus Signal-to-Noise Ratio (SNR) and Power Spectral Density (PSD). Our software aims to facilitate the study of different diversity techniques in OFDM systems for both academics and students.
1. Introduction
In recent decades, wireless communications have transformed the way people instantly exchange information through devices with wireless connections [1,2]. This has driven the development of technologies that optimize the use of the radio spectrum, increase spectral efficiency, and maintain quality of service in increasingly challenging environments [3,4].
In wireless communications, one of the main challenges is multipath fading. This phenomenon degrades the signal due to the superposition of several versions of the transmitted signal, which arrive at the receiver with different delays, amplitudes, and phases [5,6,7]. To mitigate its effects, several diversity techniques have been proposed, which transmit information over different channel domains—time, frequency, space, or polarization—so that the probability of all signal replicas experiencing a deep fade simultaneously is minimized [8,9,10].
Orthogonal Frequency Division Multiplexing (OFDM) has become one of the key technologies in modern wireless communication systems (5G, LTE, Wi-Fi), due to its high spectral efficiency and robustness against channel time dispersion [11,12,13,14]. However, the presence of multipath fading can significantly degrade system performance. One way to mitigate these adverse effects is through time and frequency diversity techniques [15,16].
Although the literature describes in detail the theoretical foundations of these diversity techniques, their understanding and practical implementation can be challenging for students and professionals in training. For this reason, this paper proposes a practical guideline for implementing and evaluating the time and frequency diversity techniques in OFDM systems under Rician fading using MATLAB. The framework allows flexible configuration of different parameters such as modulation schemes, cyclic prefix lengths, and channel conditions. The results are presented in terms of Bit Error Rate (BER) versus Signal-to-Noise Ratio (SNR), and Power Spectral Density (PSD).
The remainder of this paper is organized as follows: Section 2 describes the theoretical foundations about the main topics of the paper. Section 3 details the design of the system. Section 4 describes the MATLAB implementation. Section 5 discusses the simulation results. Finally, Section 6 summarizes the main conclusions and outlines recommendations for future research and practical applications.
2. Theoretical Foundations
In wireless communication systems, multipath fading is a major drawback, which results in the superposition of multiple copies of the transmitted signal, each arriving with different delays, phases, and attenuations [5,6,7]. This phenomenon causes fluctuations in amplitude and phase, especially in mobile and Non-Line-Of-Sight (NLOS) environments [11,12,13,14,15].
One of the most representative statistical models for the fading channel is Rician fading model, which is applicable when a dominant Line-Of-Sight (LOS) path coexists with multiple scattered components [11,14,15]. The Rician impulse response is expressed as Equation (1):
where is the LOS component and the sum represents the scattered paths.
The severity of Rician fading is characterized by the -factor, defined as Equation (2):
where is the amplitude of the LOS component, and is the variance of the scattered components. As , the model approximates Rayleigh fading; as , it tends toward an AWGN channel [14,15]. In practical terms, higher values indicate stronger LOS dominance and thus more stable received signal amplitudes, leading to smoother BER performance and reduced outage probability in wireless links [14,15].
Another important parameter is the coherence bandwidth , which relates to the channel’s rms delay spread . It defines the frequency range over which the channel remains approximately constant and is given by (Equation (3)):
When the system bandwidth exceeds , the channel exhibits frequency-selective fading [7,8,9,10,11,12,13]. Although OFDM has strong immunity to multipath fading, deep fading can affect individual subcarriers or temporal signal degradation [4,9,11].
Diversity techniques are fundamental strategies to combat multipath fading, due to the possibility of transmitting redundant information across independent domains (time, frequency, or space). This redundancy ensures that even if some replicas are severely degraded by fading, others can be correctly received, thereby improving system reliability [6].
The main forms of diversity include:
- Time diversity, which exploits the temporal variation in the channel by transmitting symbol replicas across different OFDM symbols, exploiting time-varying channel characteristics [6,12,14].
- Frequency diversity, which spreads replicas over non-adjacent subcarriers to mitigate frequency-selective fading [6,12,14].
- Spatial diversity, which relies on multiple transmit or receive antennas to obtain independently faded copies of the signal [6,13,14].
- Polarization diversity, which uses orthogonal polarizations to exploit differences in the fading characteristics of electromagnetic waves [13,14].
At the receiver, the independently faded signal replicas obtained through these diversity mechanisms are coherently combined to maximize the post-combining Signal-to-Noise Ratio (SNR). Among several combining methods, the most effective is Maximum Ratio Combining (MRC), which weights each received branch according to the conjugate of its estimated channel coefficient. Mathematically, this process can be expressed as Equation (4):
where and denote the received symbol and the channel response for the -th branch in time and/or frequency, respectively.
Among these, time and frequency diversity are the most extensively studied and widely implemented due to their effectiveness and relative simplicity of integration within multicarrier systems such as OFDM. Time diversity takes advantage of the channel’s time-varying nature, while frequency diversity leverages the spectral selectivity of multipath channels, both contributing significantly to improving system robustness and reliability [6,9,12,14].
3. OFDM System Design
3.1. General System Overview
Orthogonal Frequency Division Multiplexing (OFDM) is a multicarrier transmission technique in which the available bandwidth is divided into multiple orthogonal subcarriers, each modulated with a low-rate data stream. This orthogonality allows efficient spectral utilization and provides strong immunity to Inter-Symbol Interference (ISI) caused by multipath propagation, since each subcarrier experiences a nearly flat channel response. The use of a Cyclic Prefix (CP) further simplifies equalization at the receiver by converting the linear convolution of the channel into a circular one, enabling simple frequency-domain processing. Due to these advantages, OFDM constitutes the physical layer foundation of most contemporary wireless systems, including Wi-Fi, LTE, and 5G New Radio.
In this work, the modular simulation framework models each of these functional stages—in the transmitter: data generation, mapping, IFFT/FFT processing, cyclic prefix, channel modeling, and receiver—as individual blocks, as depicted in Figure 1, to facilitate performance evaluation under different fading and diversity conditions.

Figure 1.
General block diagram of the OFDM transmitter simulator.
- TX Data Generator: Random binary sequences are generated to represent the transmitted information and then the data are mapped using a digital modulation scheme such as BPSK, QPSK, 16-QAM, or 64-QAM, depending on the selected system configuration.
- OFDM Modulator: The mapped symbols are placed across orthogonal subcarrier, which are converted into the time-domain by applying an Inverse Fast Fourier Transform (IFFT). A Cyclic Prefix (CP) of configurable length is appended to each OFDM symbol to preserve orthogonality under multipath propagation.
- Channel: The signal is transmitted through either an Additive White Gaussian Noise (AWGN) channel or a Rician fading channel. For multipath environments, a configurable delay vector defines the taps and amplitudes of the channel.
- OFDM Demodulator: After CP removal and FFT processing, the received symbols are demodulated based on the chosen modulation order. When diversity techniques are enabled, the received signal replicas are combined using Maximum Ratio Combining (MRC) [6,14].
- Results Presentation (BER/PSD): This block is implemented to generate and analyze the simulation results, which are presented in terms of Bit Error Rate (BER) versus Signal-to-Noise Ratio (SNR) and Power Spectral Density (PSD). Both metrics are obtained through Monte Carlo simulations, transmitting a defined number of OFDM symbols, , at each SNR level. For every point in the SNR sweep, the expected BER is estimated as the ratio of erroneously detected bits to the total number of transmitted bits, providing a statistical measure of system performance. The accuracy of this estimate depends directly on the number of simulated bits, as the total error count affects the confidence and reliability of the BER curve [12].
The SNR range was limited to 0–20 dB with increments of 2 dB, as this interval encompasses the practically relevant performance region: from high error rates at low SNR values, through the steep BER transition region where performance improves rapidly, to high-SNR conditions where BER becomes negligible and further improvements yield diminishing returns. The selected 2 dB step size provides an appropriate balance between resolution and simulation time, while allowing the identification of key characteristics such as slope and operating thresholds. If higher granularity is required, the sweep can be refined locally around the transition region without significantly increasing computational burden.
3.2. Configurable Parameters
The simulation framework was designed to support multiple OFDM configurations. Its key adjustable parameters include the modulation order , with } corresponding to BPSK (), QPSK (), 16-QAM (), and 64-QAM (). The number of subcarriers , which defines the FFT size and spectral resolution, with . The cyclic prefix length is configurable to mitigate Inter-Symbol Interference (ISI).
The framework also supports two channel models: AWGN and Rician channels, the latter including a configurable delay profile to represent LOS and multipath components [11,15]. Moreover, both time diversity (symbol repetition with MRC) and frequency diversity (subcarrier interleaving with MRC) can be activated independently or in combination.
3.3. Diversity Activation
The simulator enables the implementation of time and frequency diversity through configurable parameters, allowing direct performance comparisons without modifying the core code. In the case of time diversity, OFDM symbols are repeated across different time slots and coherently combined at the receiver using MRC, thereby exploiting temporal variations in the channel [12,14]. On the other hand, frequency diversity distributes symbol replicas over non-adjacent subcarriers to mitigate deep fades caused by frequency-selective fading, with MRC applied in the frequency domain [14,15,16]. Both techniques can be activated independently or jointly via the time_diversity and freq_diversity flags, and their modular integration enables an isolated and systematic analysis of their impact on BER and PSD.
4. MATLAB Implementation
A modular OFDM simulation framework was implemented in MATLAB to evaluate the impact of diversity techniques in wireless channels. The system allows dynamic configuration of modulation schemes, channel models (AWGN or Rician), cyclic prefix length, and optional activation of time and/or frequency diversity. The performance is evaluated in terms of BER vs. SNR and PSD.
4.1. Architecture and Configuration
The simulator is structured according to the description of Section 3. We implement a centralized configuration script (configurar_parametros.m), which contains the main parameters through a structure (cfg) passed to the simulation routine. This includes:
- Waveform parameters: Number of subcarriers , cyclic prefix length , and modulation order {BPSK, QPSK, 16-QAM, 64-QAM}.
- Channel configuration: AWGN, Rician, or combined models, with path delays, tap gains, -factor, and optional Doppler spread. The Rician model supports manual convolution or MATLAB’s comm.RicianChannel object.
- SNR range: Defined as dB, evaluated across 10,000 Monte Carlo iterations per point.
- Diversity control: Flags ‘diversidad_activa’ and ‘diversidad_frecuencia’ activate time and frequency diversity, respectively.
- Validation: Ensures ≥ maximum delay spread to avoid ISI.
4.2. Processing Blocks
Each block in the transmission and reception chain was implemented as an independent function, ensuring clarity and modularity. The key components are:
- Bit Generator (generate_bits.m) Produces random binary sequences per frame.
- Modulator (modulator.m): Maps bits to constellation symbols.
- Diversity Mapper (map_freq_diversity.m):
- Time diversity: Repeats symbols across independent OFDM time slots.
- Frequency diversity: Interleaves replicas across distant subcarriers.
- IFFT (apply_ifft.m): Converts symbols to the time domain.
- Cyclic Prefix (add_cp.m, remove_cp.m): Manages insertion and removal of .
- Channel (channel_tx.m): Adds Rician multipath fading and AWGN.
- FFT (apply_fft.m): Recovers symbols in the frequency domain.
- Combiner (combine_mrc.m): Applies Maximum Ratio Combining (MRC) using ideal channel knowledge.
- Demodulator (demodulator.m): Estimates the bitstream from received symbols.
- BER Computation (compute_BER.m): Compares transmitted and received bits across all trials.
- PSD Estimation (plot_psd.m): Evaluates the power spectral density before the channel.
To support beginners and facilitate reproducibility, a simplified step-by-step workflow is included (Figure 2). This workflow shows the execution order of the main simulation scripts:
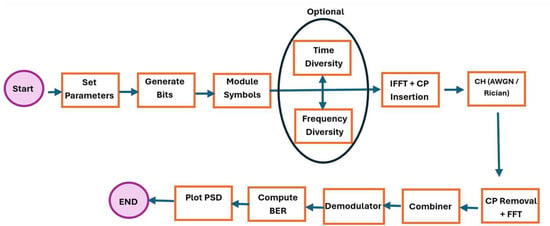
Figure 2.
Illustrates this workflow in flowchart form for clarity.
4.3. Diversity Implementation
In the MATLAB simulation framework, time and frequency diversity were implemented through dedicated mapping stages inserted between the modulation and the IFFT blocks.
For time diversity, the simulator duplicates each OFDM frame at the transmitter and transmits it over subsequent time slots separated by at least the channel coherence time. This ensures that replicas encounter decorrelated channel realizations. At the receiver, both copies are aligned in time after CP removal and processed by the FFT. The Maximum Ratio Combining (MRC) algorithm is then applied across replicas, using ideal channel estimates to weigh each branch before reconstruction. This functionality was implemented through the function map_time_diversity.m.
For frequency diversity, redundancy is introduced prior to the IFFT by assigning symbol replicas to non-adjacent subcarriers within the same OFDM frame. A dedicated function (map_freq_diversity.m) performs this interleaving, ensuring that each data symbol is distributed over widely spaced subcarriers. At the receiver, after FFT demodulation, the distributed replicas are reassembled and coherently combined with MRC in the frequency domain, effectively mitigating deep fades concentrated in certain spectral regions.
For joint diversity, both processes are activated simultaneously: the OFDM frame is first replicated in time, and within each replica, symbols are interleaved across non-adjacent subcarriers. At the receiver, the system performs two levels of combining: first across subcarriers (frequency domain) and then across time slots (temporal domain). This hierarchical MRC ensures that the maximum available energy is extracted from all diversity branches, significantly improving BER performance under severe multipath fading.
5. Results and Discussion
The performance was evaluated based on Bit Error Rate (BER) and Power Spectral Density (PSD) under various scenarios, including with and without diversity. The results highlight the effectiveness of diversity techniques in combating multipath fading in wireless channels.
5.1. BER Analysis: Frequency Diversity
In Figure 3, the BER curves demonstrate that both time diversity and frequency diversity significantly reduce the error probability compared to the baseline system without diversity. Time diversity provides substantial improvements in scenarios characterized by rapid temporal variations, where the channel coherence time is short. In contrast, frequency diversity proves particularly effective in frequency-selective fading environments, where the coherence bandwidth is narrower than the OFDM signal bandwidth. Furthermore, the joint application of both techniques achieves the lowest BER values across all tested SNR ranges, thereby confirming the complementary benefits of their combined use
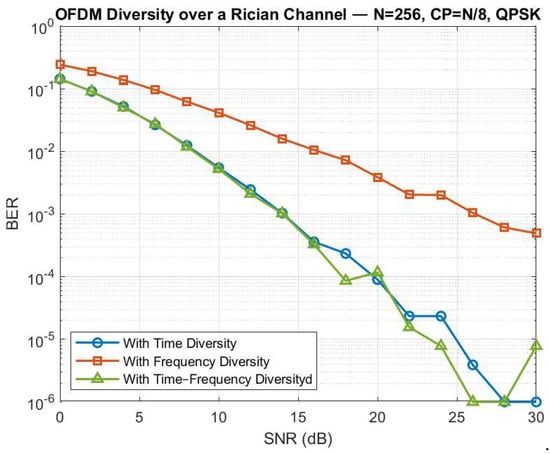
Figure 3.
BER vs. SNR with Time and Frequency Diversity in Rician Channel.
5.2. Power Spectral Density (PSD) Analysis
We examine the PSD of the transmitted signals before channel distortion, which provides insight into the spectral occupancy and signal distribution, allowing us to evaluate the impact of redundancy and diversity on bandwidth usage and spectral shaping.
Figure 4 presents the PSD of the OFDM system transmitted through a Rician fading channel using different FFT sizes without applying any diversity techniques. The spectral shape corresponds to the typical behavior of OFDM signals, showing a main lobe centered at zero frequency with decaying side lobes, indicative of subcarrier orthogonality. As the number of subcarriers increases, the spectrum becomes smoother and more compact. Specifically, the case exhibits a flatter spectral envelope with steeper roll-off at the band edges, which is desirable for limiting out-of-band emissions. In contrast, smaller FFT sizes such as produce broader and less regular spectrum. Without diversity, the signal energy remains confined within its assigned spectral range, maximizing spectral efficiency. However, this configuration lacks robustness against fading, as no symbol replication in time or frequency is present. Consequently, symbols affected by severe fading may be entirely lost.
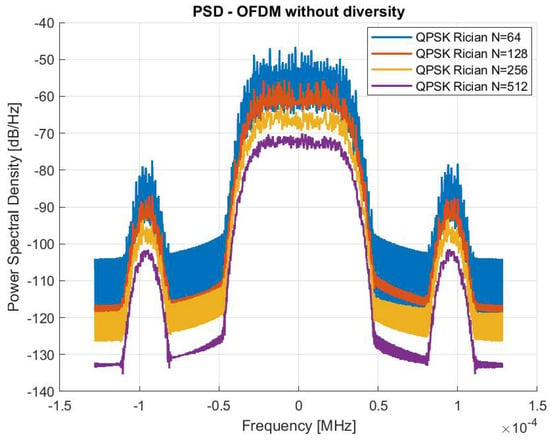
Figure 4.
PSD without Diversity over Rician Channel.
Figure 5 illustrates the PSD of OFDM signals over a Rician fading channel when time diversity is applied. The comparison includes four FFT sizes: N = {64,128,256}. As shown, the spectral shape is notably different from the non-diverse case.
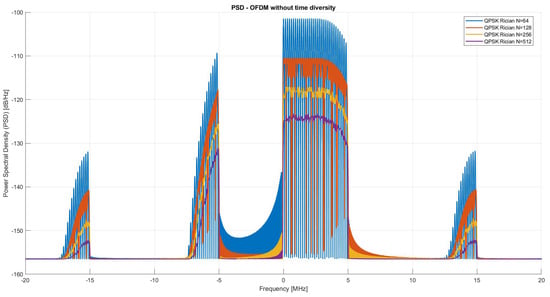
Figure 5.
PSD of OFDM with Time Diversity under Rician Channel.
The use of time diversity involves replicating OFDM symbols across different time slots, which introduces temporal redundancy. While this technique improves robustness against time-selective fading, it causes spectral spreading due to the loss of perfect orthogonality between subcarriers. This effect is particularly visible in the outer subcarriers, where sidelobe levels fluctuate irregularly.
In general, larger FFT sizes still produce more confined spectra, but the influence of symbol repetition is evident across all cases. Compared to the baseline in Figure 3, time diversity introduces a broader and more distorted spectrum, which is the expected trade-off for improved performance under fading.
In Figure 6, the PSD of OFDM signals with frequency diversity is illustrated for different FFT sizes (), transmitted over a Rician channel. The purpose of this configuration is to evaluate how the replication of symbols across non-adjacent subcarriers affects the spectral distribution and overall signal shaping.
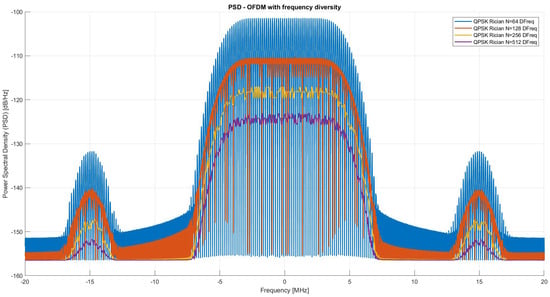
Figure 6.
PSD with Frequency Diversity over a Rician Channel.
Unlike time diversity, frequency diversity introduces redundancy across the frequency domain before the IFFT operation. This results in a redistribution of spectral components, which can be observed in the widening and smoothing of the PSD curves, particularly at the transitions and edges of the spectrum.
Key observations include:
- For , the PSD shows more spectral leakage and sharper transitions, indicating lower frequency resolution [10].
- As N increases, the PSD becomes progressively narrower and smoother, evidencing improved spectral confinement and resolution.
- The symmetry around the center frequency is preserved, and the energy remains concentrated in the main lobe, confirming that the spectral efficiency is not severely affected.
These results validate that frequency diversity can be applied without compromising the spectral integrity of the OFDM signal. Furthermore, the spectral shaping remains consistent across increasing FFT sizes, making this technique suitable for multipath mitigation in practical wireless systems.
6. Conclusions
This paper presents a technical guideline, developed in MATLAB, for understanding, implementing, and evaluating time and frequency diversity techniques in OFDM systems operating over Rician fading channels. This paper proposes a theoretical foundation with a modular simulation framework, which aims to bridge the gap between conceptual knowledge and practical application. Simulation results show that the diversity techniques achieve a significant Bit Error Rate (BER) reduction. We show that time diversity achieved significant performance improvements in severe multipath environments with limited coherence time, while frequency diversity enhanced robustness in frequency-selective scenarios. Power Spectral Density (PSD) results showed that, although diversity introduces minor spectral spreading, the signal remains confined within the allocated bandwidth, preserving spectral efficiency. Overall, these findings validate diversity techniques as effective, low-complexity strategies for enhancing the resilience of OFDM-based wireless systems against multipath fading. At the same time, the proposed guideline provides a reproducible and structured approach for both academic learning and practical system design.
Future research may focus on extending the framework to MIMO-OFDM systems, considering imperfect channel estimation, and validating the approach through software-defined radio (SDR) platforms. These improvements would strengthen the applicability of the framework to 5G/6G scenarios such as URLLC and vehicular communications.
Author Contributions
C.C.-C. and M.C.P.-P. contributed to the conceptualization of the study and the definition of the research objectives. The methodology, including the design of the modular OFDM simulation framework, was collaboratively developed by M.O.-F. and C.C.-C. The software implementation in MATLAB, covering the development of independent functions for modulation, channel modeling, and diversity activation, was carried out by C.C.-C. Validation through Monte Carlo simulations and consistency checks of BER and PSD metrics were performed by M.C.P.-P. and M.O.-F. Formal analysis of the results, particularly the evaluation of time and frequency diversity under Rician fading, was conducted by C.C.-C. and M.O.-F. Data curation and figure preparation (BER vs. SNR curves and PSD plots) were managed by C.C.-C. The original draft was prepared by M.O.-F., while review and editing were undertaken by M.C.P.-P., M.O.-F. and C.C.-C. Supervision and project administration were provided by M.C.P.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Escuela Politécnica Nacional.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All relevant data are presented in the main text.
Acknowledgments
The authors would like to thank the administrative and academic staff of the Department of Electronics, Telecommunications, and Information Networks (EPN) for their support during the development of this work, which was carried out as part of the final project of the Wireless Communications course.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| AWGN | Additive White Gaussian Noise |
| BER | Bit Error Rate |
| CP | Cyclic Prefix |
| FFT | Fast Fourier Transform |
| IFFT | Inverse Fast Fourier Transform |
| LOS | Line of Sight |
| MRC | Maximum Ratio Combining |
| NLOS | Non Line of Sight |
| OFDM | Orthogonal Frequency Division Multiplexing |
| PSD | Power Spectral Density |
| QAM | Quadrature Amplitude Modulation |
| QPSK | Quadrature Phase Shift Keying |
| SNR | Signal-to-Noise Ratio |
References
- Jiménez, V.M. Performance of IEEE 802.11a Physical Layer in Multipath Fading Channels; University of Sevilla: Sevilla, Spain, 2004. [Google Scholar]
- Carrillo, S. Simulación de Sistemas de Comunicaciones Móviles E Inalámbricas. Master’s Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2001. [Google Scholar]
- Ahmed, A.; Siddqui, A.; Khan, R.; Nabi, G.; Ali, M. Comparative analysis of OFDM in AWGN & Local Acoustic Channel. In Proceedings of the 2024 IEEE 1st Karachi Section Humanitarian Technology Conference (KHI-HTC), Tandojam, Pakistan, 8–9 January 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Van Nee, R.; Prasad, R. OFDM for Wireless Multimedia Communications; Artech House: Boston, MA, USA, 2000. [Google Scholar]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Chaudhari, Q. Diversity in Wireless Communication Systems. Wireless Pi, 2020. Available online: https://wirelesspi.com/diversity-in-wireless-communication-systems/ (accessed on 9 August 2025).
- Barcelona, U.P. Modelado de Canal—Características de Canales Inalámbricos; Apuntes: Mexico City, Mexico, 2018. [Google Scholar]
- Prasad, R. OFDM for Wireless Communication Systems, Volume 2, Artech House Universal Personal Communications Series; Artech House: Boston, MA, USA, 2004; pp. 1–272. ISBN 978-1-58053-799-5. [Google Scholar]
- Hanzo, L.; Münster, M.; Choi, B.J.; Keller, T. OFDM and MC-CDMA for Broadband Multi-User Communications, WLANs and Broadcasting. John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Li, Y.; Stüber, G.L. Orthogonal Frequency Division Multiplexing for Wireless Communications; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Rappaport, T.S. Wireless Communications: Principles and Practice, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Proakis, J.G.; Salehi, M. Digital Communications, 5th ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Haykin, S.; Moher, M. Modern Wireless Communications; Pearson Education: London, UK, 2005. [Google Scholar]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Sklar, B. Rayleigh fading channels in mobile digital communication systems. I. Characterization. IEEE Commun. Mag. 1997, 35, 90–100. [Google Scholar] [CrossRef]
- Rohling, H. OFDM: Concepts for Future Communication Systems; Rohling, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).