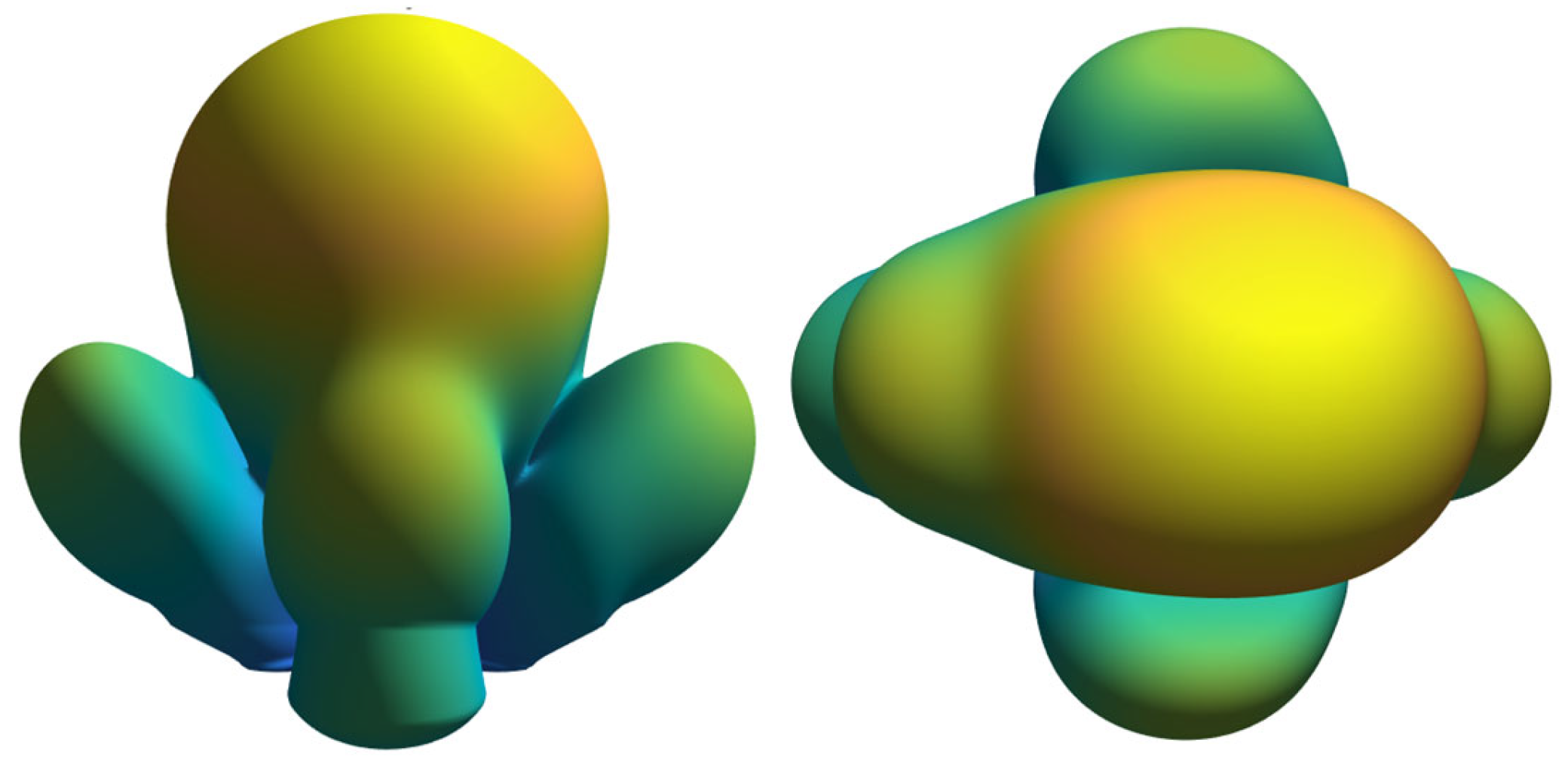Full-Coverage Radar Antenna ^†

Abstract

In the work at hand, we contribute a system study of a full-coverage antenna array for applications ranging from wireless communication base station transceivers to aerospace applications. There are two main objectives in the road toward achieving active, electronically scanned array antennas: the passage from mechanical to electronic steering and the subsequent accommodation of a large number of simultaneously active, independent beams and respective Tx-Rx chains. The first objective comes with the unwanted introduction of scanning losses, which degrade the system’s performance. This problem is solved in the current work by employing a toroidal array antenna and scanning the beam by exploiting the double curvature of the host surface. Furthermore, the second issue, of signal path routing complexity, is also resolved by the contributed 2D, hierarchical (exhibiting both horizontal and vertical organization) beam-forming network. The stated results successfully validate our contribution.

1. Introduction

Effortless, wide solid-angle coverage is one of the key performance indicators of radar antennas. Here we, contribute a potent design based on conformal array theory.

Conformal antenna arrays provide high-performance solutions for various application areas [1].

We can mention applications ranging from radar [2,3,4,5,6] and wireless communications base stations [7,8,9] to automotive applications [10].

Based on this framework, in the work at hand, we contribute an antenna phased array that is conformal (in other words, embedded in a specific surface area) to a toroidal host. There are critical characteristics to the designed device. In general, each sub-array (in fact, each elementary radiator of a conformal antenna array) is embedded into a different electromagnetic environment, which renders the element pattern multiplication principle invalid. This complicates the analysis and design of such structures significantly. On the other hand, beam-focusing processes may benefit from the fact that a broadside radiating sub-array on a conformal surface emits electromagnetic power in the direction of the surface’s normal. In this way, one can cover a significant angular domain by placing and subsequently enabling sub-arrays on areas of the conformal surface that present surface-normal that covers the specific angular domain. In other words, if the surface is covered by sub-arrays and a beam towards (φ_o, θ_o) is desired, then one can feed the sub-array that is placed on the surface patch which exhibits a surface- normal towards (φ_o, θ_o).

This paper is organized as follows. In Section 2, we first provide the mathematical background and then a full detailed description of the contributed full-coverage radar antenna. In the results section, we provide our evaluation of the full Toroidal Phased Array. This paper ends with the discussion and conclusion section.

2. System Description

The contributed design is based on the theory of the cylindrical Phased Array (CPA).

A CPA is a phased array that forms a loop around a cylindrical host surface. The element-to-element spacing is nearly half the wavelength, a characteristic that is common and has become the usual choice for planar phased-array antennas.

2.1. Mathematical Background

The radiation pattern of a CPA, with a radius equal to R and N elements placed on the normal circle of a cylinder at (${\phi }_n=n\cdot \mathrm{\Delta }\phi$, $z_n=0$), obeys the following:

$$E\left(\theta ,\phi \right)={\displaystyle \sum _{n=1}^N{A}_{n}F\left(\theta ,\phi -n\cdot \mathrm{\Delta }\phi \right)e^{jkR(\sin (\theta )\cos (\phi -n\cdot \mathrm{\Delta }\phi ))}}$$

(1)

where $A_n$ and $F\left(\theta ,\phi -n\cdot \mathrm{\Delta }\phi \right)$ are the excitation and element pattern of the n-th radiating element, respectively.

Note that, if a specific excitation $A_n$ produces a main lobe beam at φ_ο, then by shifting the excitation by v places ($\overline{n}=n+v$), we attain a new pattern

$$\begin{array}{l}{E}_{v-shifted}\left(\theta ,\phi \right)={\displaystyle \sum _{n=1}^N{A}_{\overline{n}}F\left(\theta ,\phi -n\cdot \mathrm{\Delta }\phi \right)e^{jkR(\sin (\theta )\cos (\phi -n\cdot \mathrm{\Delta }\phi ))}}=\\ {\displaystyle \sum _{n=1}^N{A}_{\overline{n}}F\left(\theta ,(\stackrel{\overline{\phi }}{\overbrace{\phi +v\cdot \mathrm{\Delta }\phi }})-\overline{n}\cdot \mathrm{\Delta }\phi \right)e^{jkR(\sin (\theta )\cos ((\stackrel{\overline{\phi }}{\overbrace{\phi +v\cdot \mathrm{\Delta }\phi }})-n\cdot \mathrm{\Delta }\phi )}}=\\ {\displaystyle \sum _{n=1}^N{A}_{\overline{n}}F\left(\theta ,\overline{\phi }-\overline{n}\cdot \mathrm{\Delta }\phi \right)e^{jkR(\sin (\theta )\cos (\overline{\phi }-n\cdot \mathrm{\Delta }\phi )}}=E\left(\theta ,\overline{\phi }\right)\end{array}$$

(2)

at

$${\overline{\phi }}_o={\phi }_o+v\cdot \mathrm{\Delta }\phi$$

(3)

Thus, shifting the excitation by v places also shifts the resulting pattern by the same angle in azimuth.

Analogous properties hold for the Toroidal Phased Array (TPA), both for the azimuth and for the elevation angle.

While cylindrical arrays have been used extensively [11,12], to the best of our knowledge, this is the first time such an array has been contributed. Indeed, one can find numerous uses of the CPA for radar applications [13,14,15,16,17,18,19], but the employment of the toroidal host surface appears to be new.

2.2. System Description

Taking advantage of the characteristics of the uniform, circular, cylindrical array, here, we describe the contributed system. The array host surface, being a torus, is defined by two angular parameters: the azimuthal and the elevation position angles of the nearly uniformly placed element antenna radiators. Here, first, we will present the structure of the element radiator block, the basic building block of the whole array; then, we proceed to the circular sub-array that populates the azimuthal angle; and last, we will include the elevation sub-array.

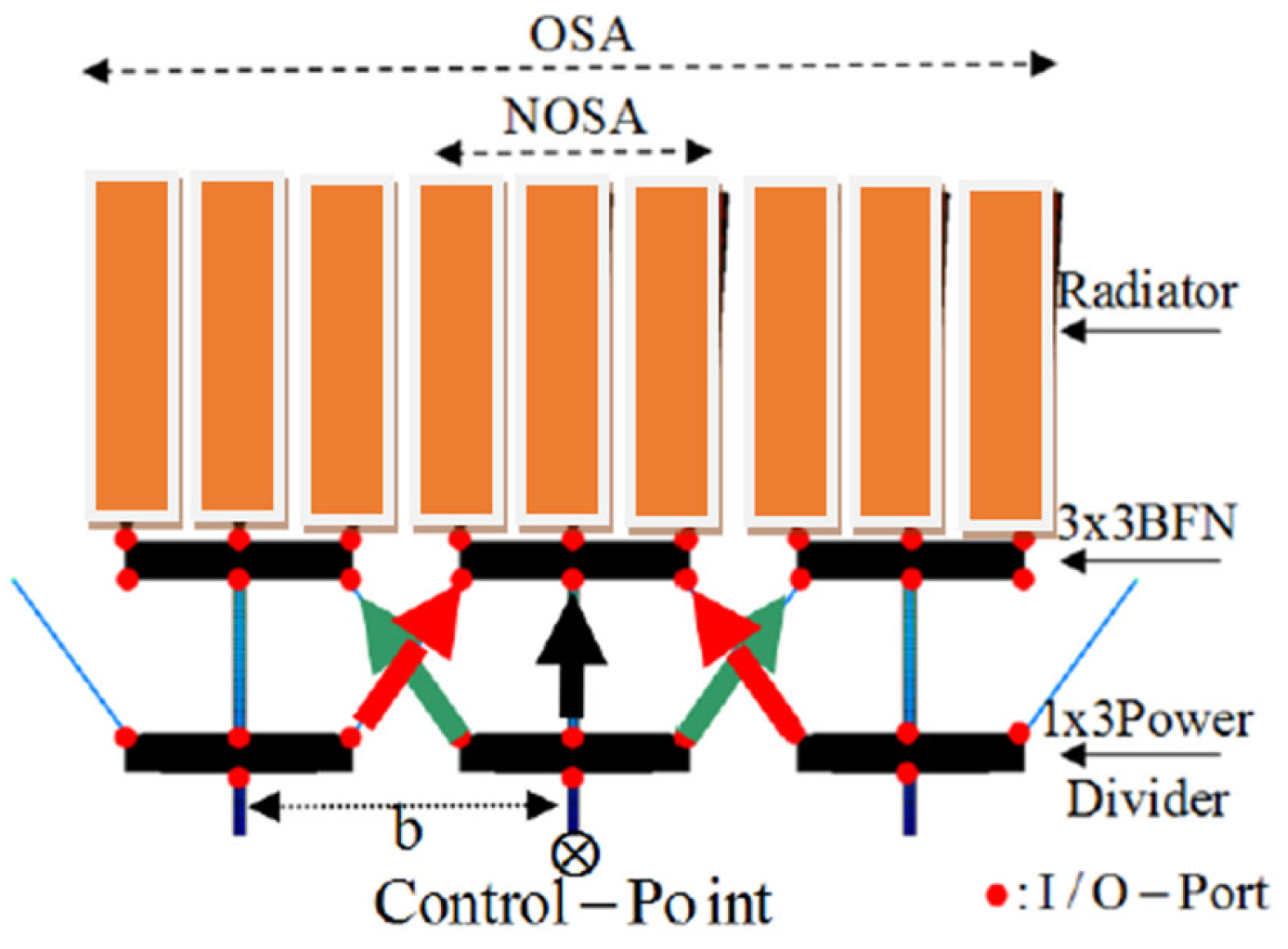
The basic block of the array is presented in Figure 1 [20,21]. There, a three-radiating-element basic sub-array is depicted, which is the so-called Non-Overlapped Sub-Array (NOSA) [22].

In the NOSA, there are the Beam-Forming Network (BFN) and the power divider (PD). The central path of the PD feeds the BFN and the central path of the BFN feeds the radiators. The non-central paths of the PD feed the neighboring BFNs and thus the neighboring NOSAs.

Let us now present the way the azimuthal sub-array is formed. The examined NOSA along with neighboring ones forms an overlapping sub-array (OSA) (see Figure 2).

From Figure 2, it can be understood that the signal from the feeding control point propagates via the PD and the BFNs not only to the NOSA in question but also to the neighboring ones. Then, a linear overlapped element array is presented. In this array, a number of NOSAs are embedded. The side paths of each PD of the NOSAs feed the side ports of the neighboring BFNs, thus providing the overlapping function. A set of NOSAs that are fed by the same control point creates an overlapping sub-array (OSA). The overlap between two OSAs (the blue and the yellow) is shown in Figure 3.

If the NOSAs and OSAs shown in Figure 3 are repeated in a circle, then a 1D, circular, overlapping antenna sub-array is formed. This is the uniform, cylindrical, azimuthal sub-array. Here, scanning in the azimuth is achieved by simply choosing a different port/control point either in transmit or in the receiving case.

3. Results

In the current section, we evaluate the proposed design in order to assess the merit of the contributed antenna array configuration. We must note that the same ‘logic’ that was presented in Figure 3 for the formation of the azimuth array is also followed for the elevation angle, shaping the whole system shown in Figure 4.

In detail, in Figure 4, the contributed toroidal array antenna (with the azimuthal and elevation defining radii denoted by R and r, respectively) is presented. Each rectangle represents a radiating element. For illustration purposes, on the toroidal antenna, we depict the 3 × 3 NOSA that is fed by the self port/control point. For an assumed element pattern of cos()^2 form, the produced far-field pattern is included in Figure 5. The far-field’s main lobe points in the NOSA’s normal direction. Also, the HPBW in the azimuth is smaller than the HPBW in the elevation because we used fewer elements to populate the elevation compared to the azimuth. Nevertheless, the contributed design is scalable and can easily provide a response complying with design prescriptions.

In detail, we place the elementary radiators—which are assumed to be probe-fed, square microstrip patches resonant to the operating frequency—at λ/2 distances from each other, both on the azimuth and the elevation planes. The big radius of the torus surface is equal to 12/pi, which means that 48 patches are used for a circular array to fill an entire azimuth circle. Also, the small radius of the toroidal surface is taken to be equal to 6/pi, so that 12 element radiators are used to fill a semi-circle in the elevation plane. Thus, in the current example, we use 48 × 12 = 576 radiators, to cover the full, solid angular space.

The shape of the produced pattern of the sub-array, when the cos^2 element pattern is used, is shown in Figure 5.

Last, in Figure 6, we present the results when scanning on the elevation plane.

Those results prove that apart from the azimuth, the contributed system can also effortlessly (and without exhibiting scan loss) scan the elevation angle.

4. Discussion and Conclusions

Currently, applications for array antennas range from wireless communication base station transceivers to aerospace applications. Different off-course applications place different constraints and prescriptions on the desired system, and in the respective evaluation phase, one has to enforce different key performance indicators. Nevertheless, there are objectives that always are desirable, and various performance problems emerge when they are not properly addressed. The issues of scanning losses and signal-processing complexity are key ones, and scan across all the relative application areas. In the work at hand, we successfully address those challenges by employing for the first time an advantageous conformal host surface and a dense, 2D (horizontal and vertical), hierarchical beam-forming network. The provided results prove our contributed antenna array and place confidence on employing the system in various application sectors of wireless and aerospace use cases.