Parallel Finite Element Algorithm for Large Elastic Deformations: Program Development and Validation
Abstract
1. Introduction
2. Methods and Models
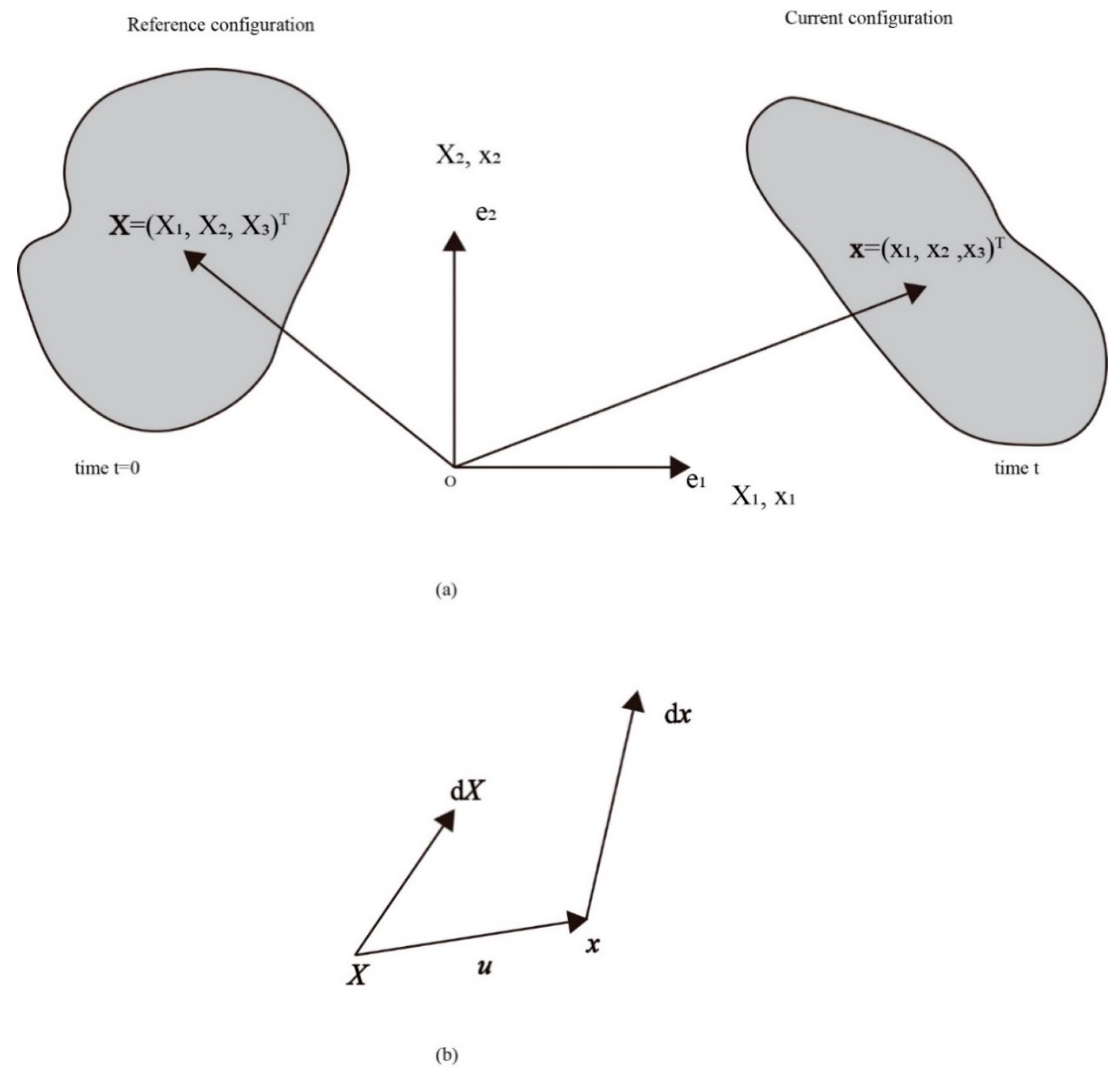
2.1. Reference Coordinate System for Large Deformations
2.2. Green Strain Tensor and Cauchy Stress Tensor
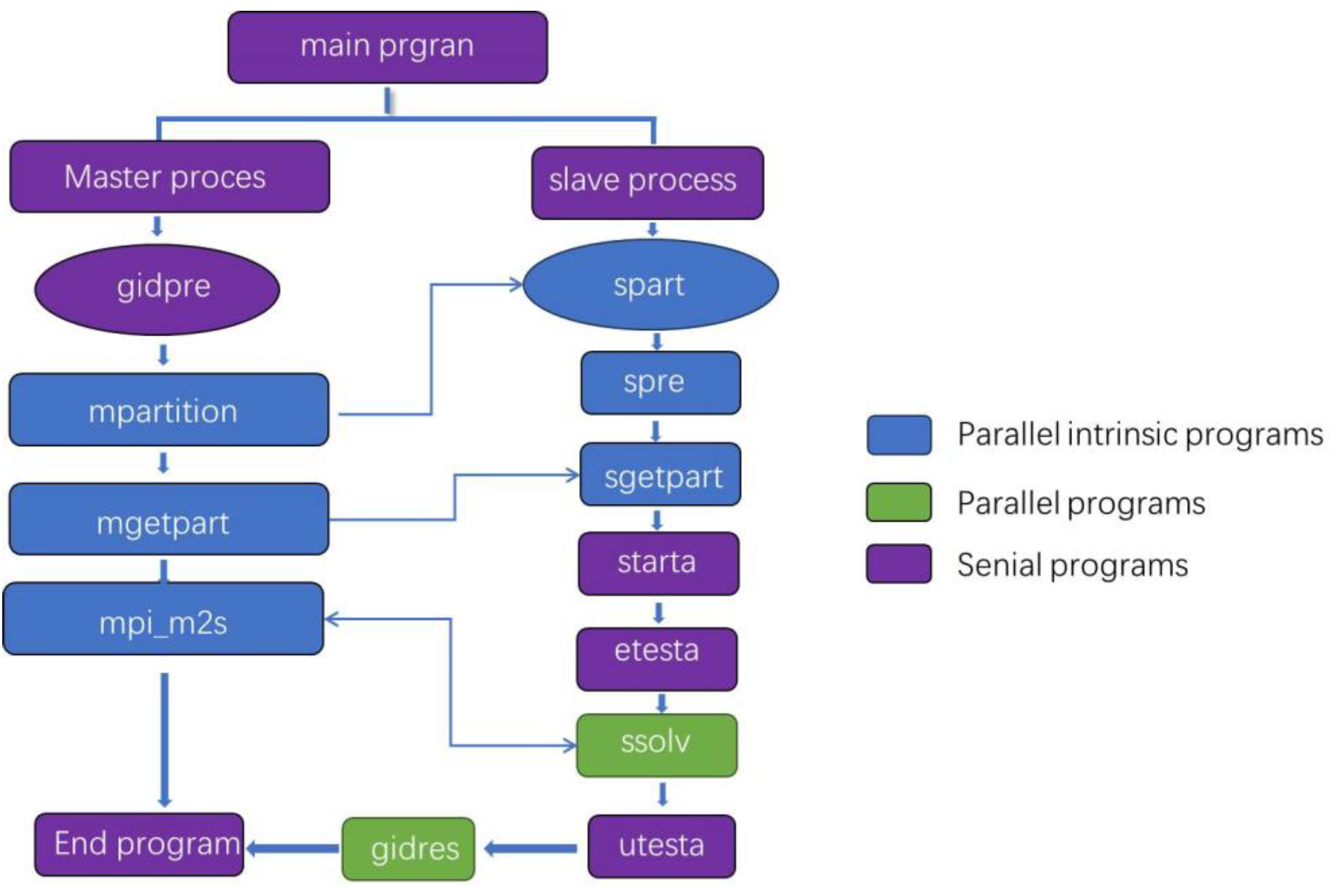
2.3. Parallel Finite Element Implementation of Elastic Large Deformation Theory
- test1.post.msh, test2.post.msh, test3.post.msh…
- test1.post.res, test2.post.res, test3.post.res…
- (1)
- It offers a better stability and maintainability with C language compared to Fortran.
- (2)
- The main program flow is simpler, requiring automatic generation only for different problems.
- (3)
- PFELAC includes features for controlling nonlinear problems, providing more flexibility than FEPG’s communication methods.
- (4)
- Point-to-point communication in PFELAC is more efficient than FEPG’s master–slave approach.
- (5)
- PFELAC reduces computation time by eliminating the need to send result data back to the main process.
- (6)
- The results are partition-specific, with no need to consolidate them in the main process.
- (7)
- The parallel computing workflow is streamlined, removing the need for data conversion and additional pre/post-processing steps. After uploading the source code to the server, it simply needs to be compiled and executed.
3. Parallel Finite Element Program Verification: Two Ideal Cases of Elastic Large Deformation
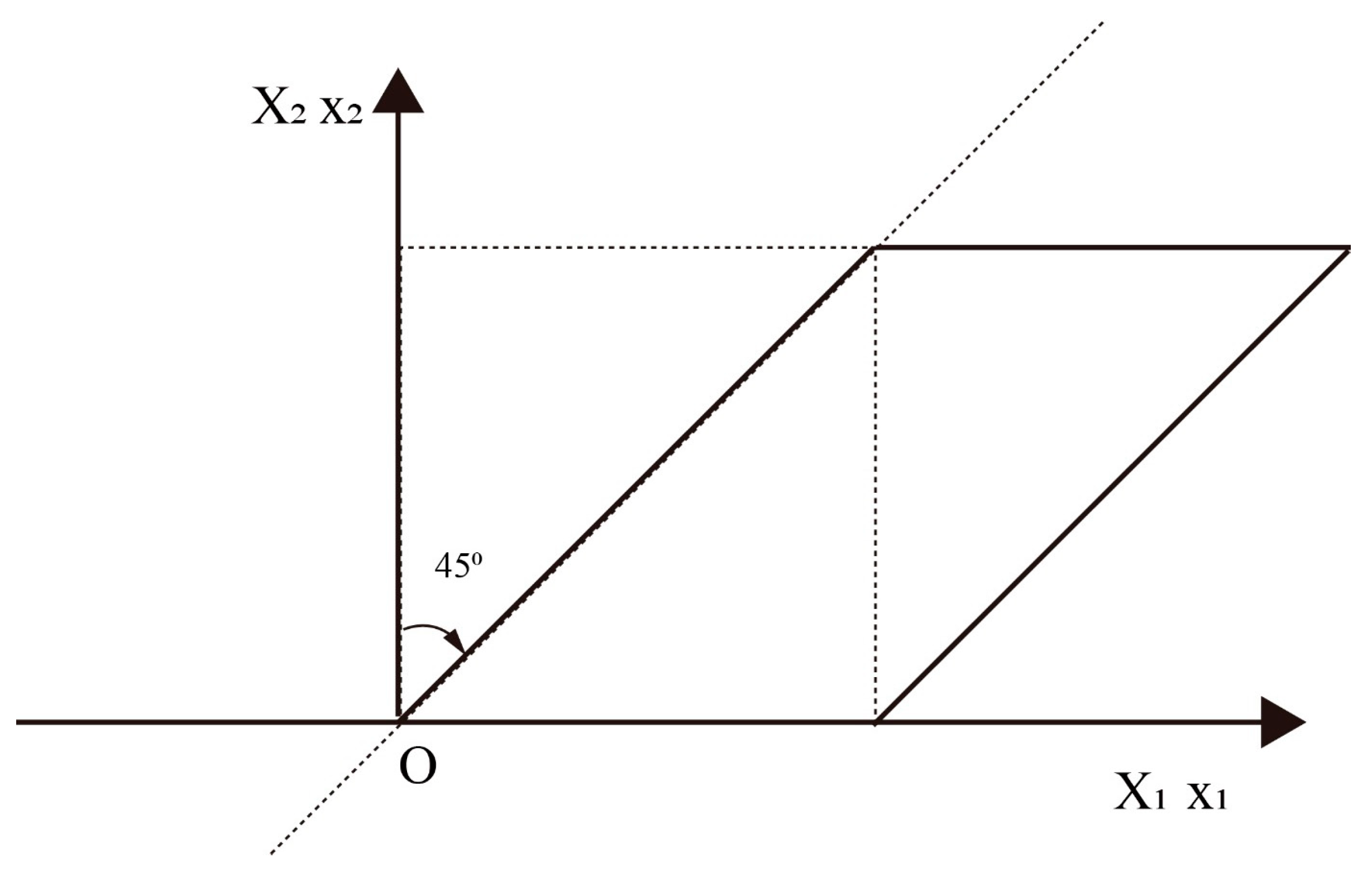
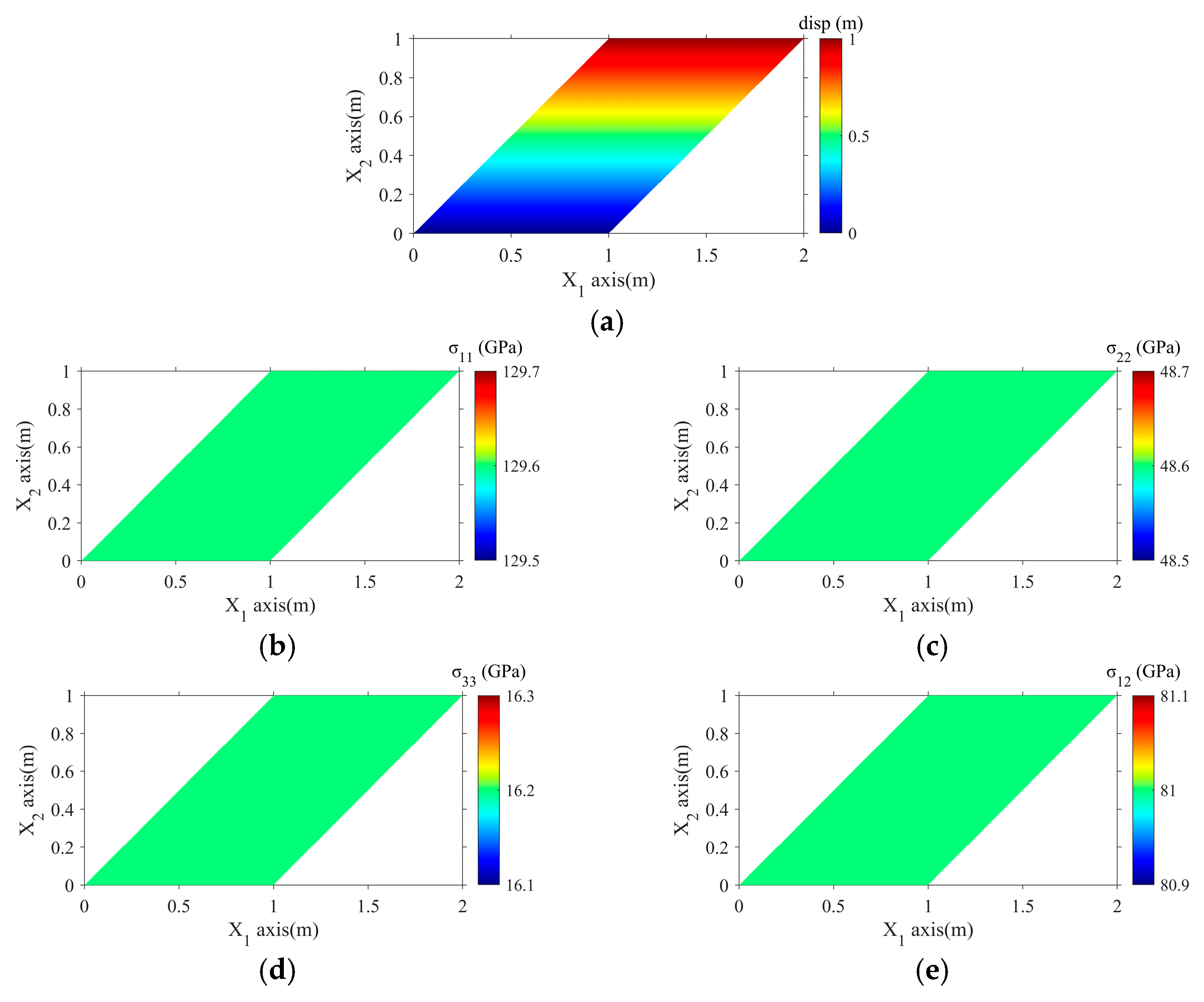
3.1. Case 1: Elastic Large Deformation with 45° Stretching and Rotation
3.2. Case 2: Elastic Large Deformation Under Simple Shear
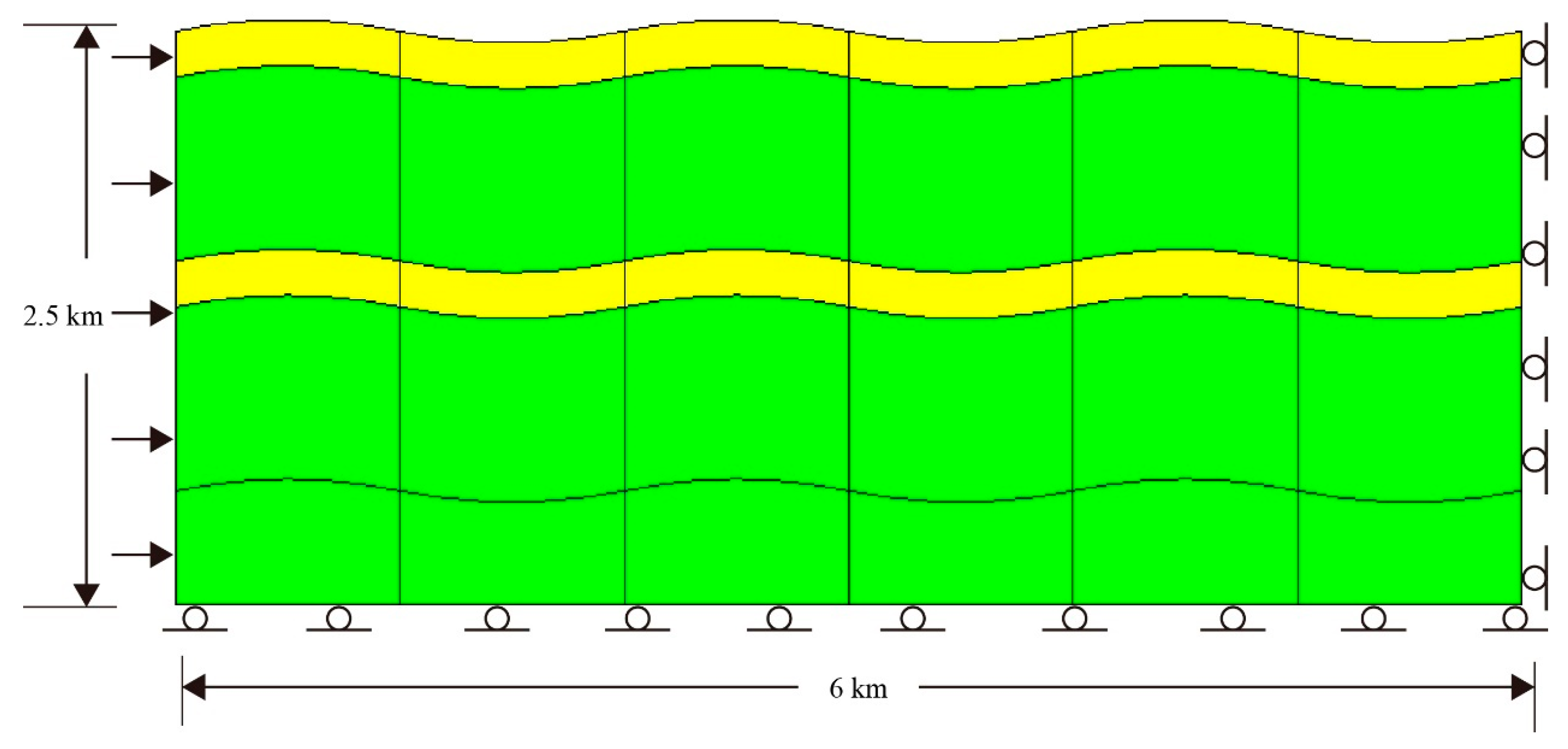
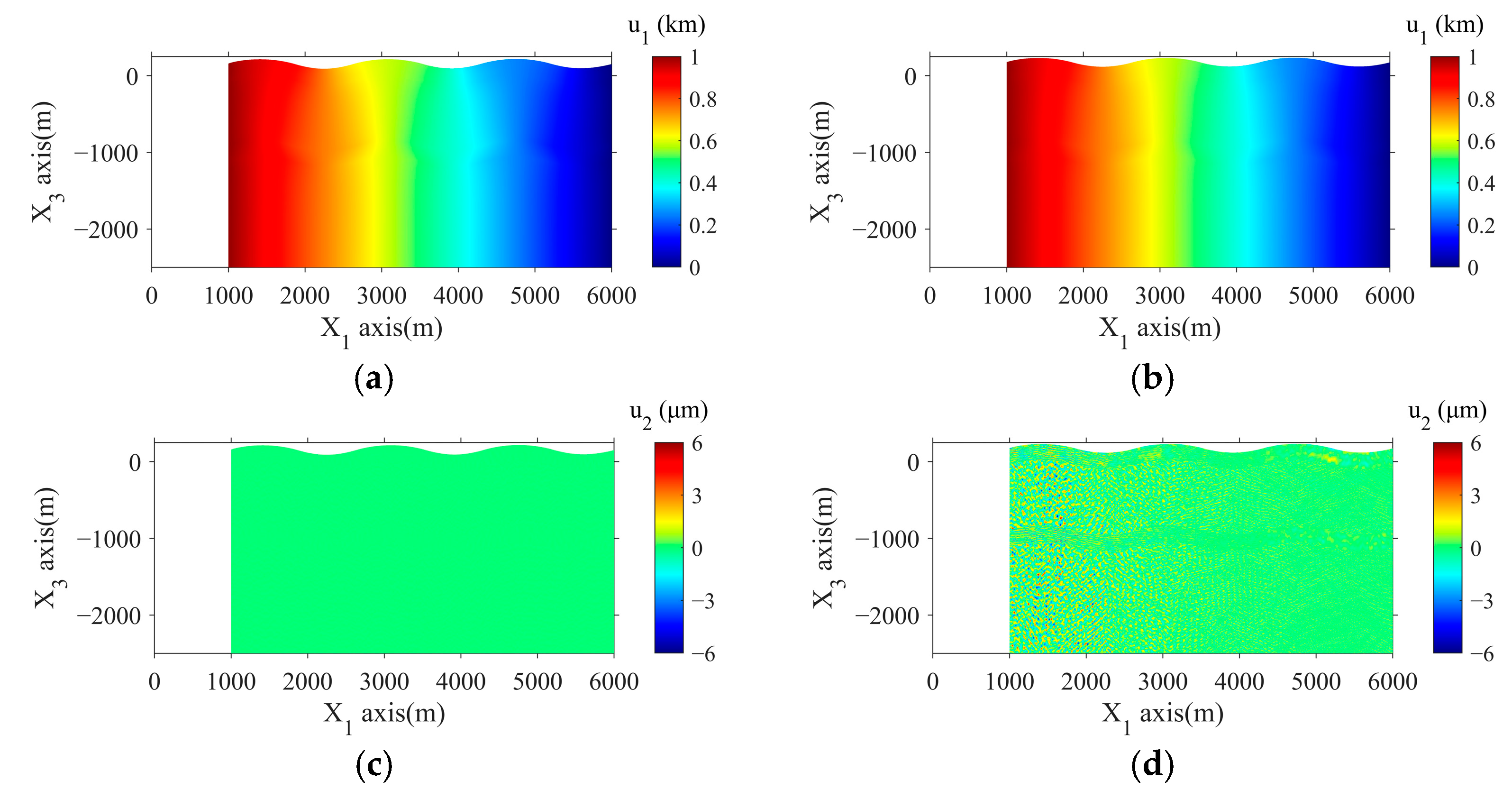
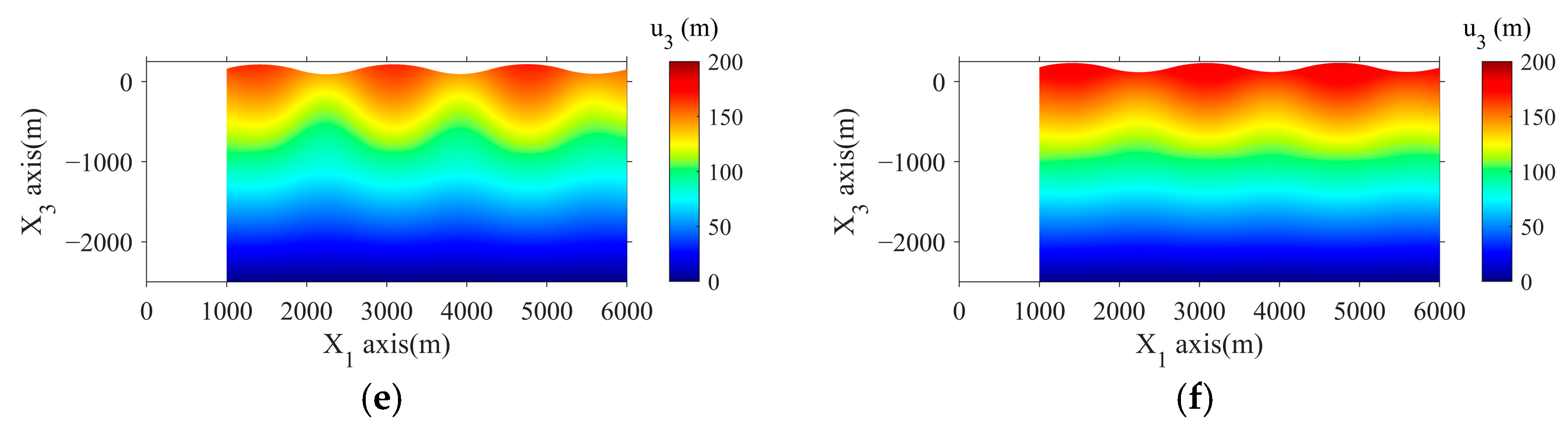
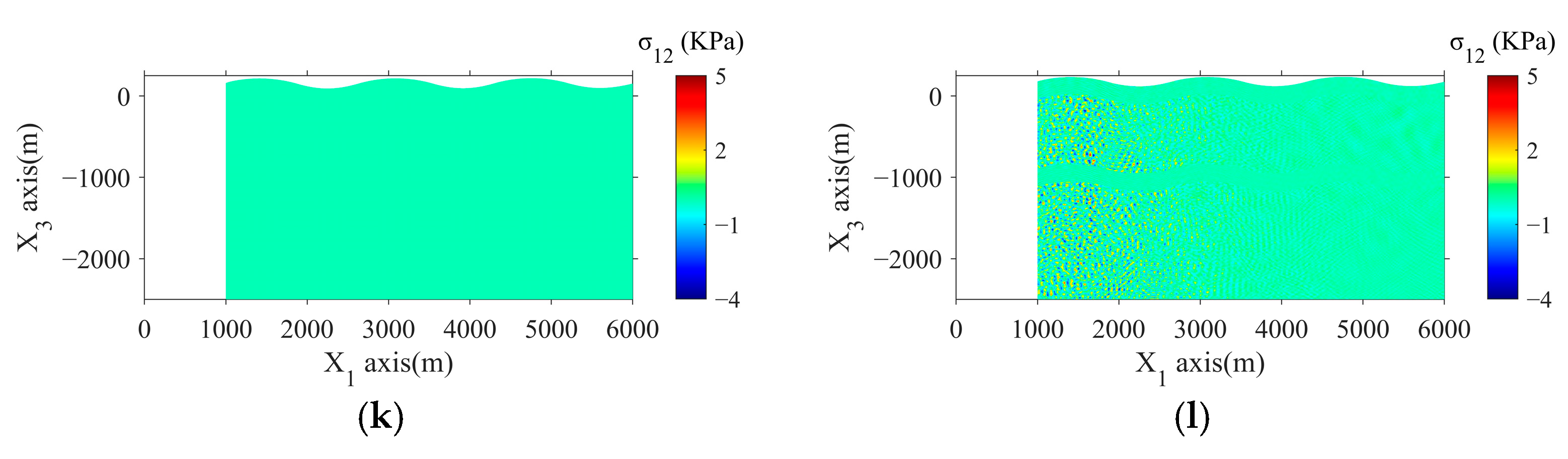
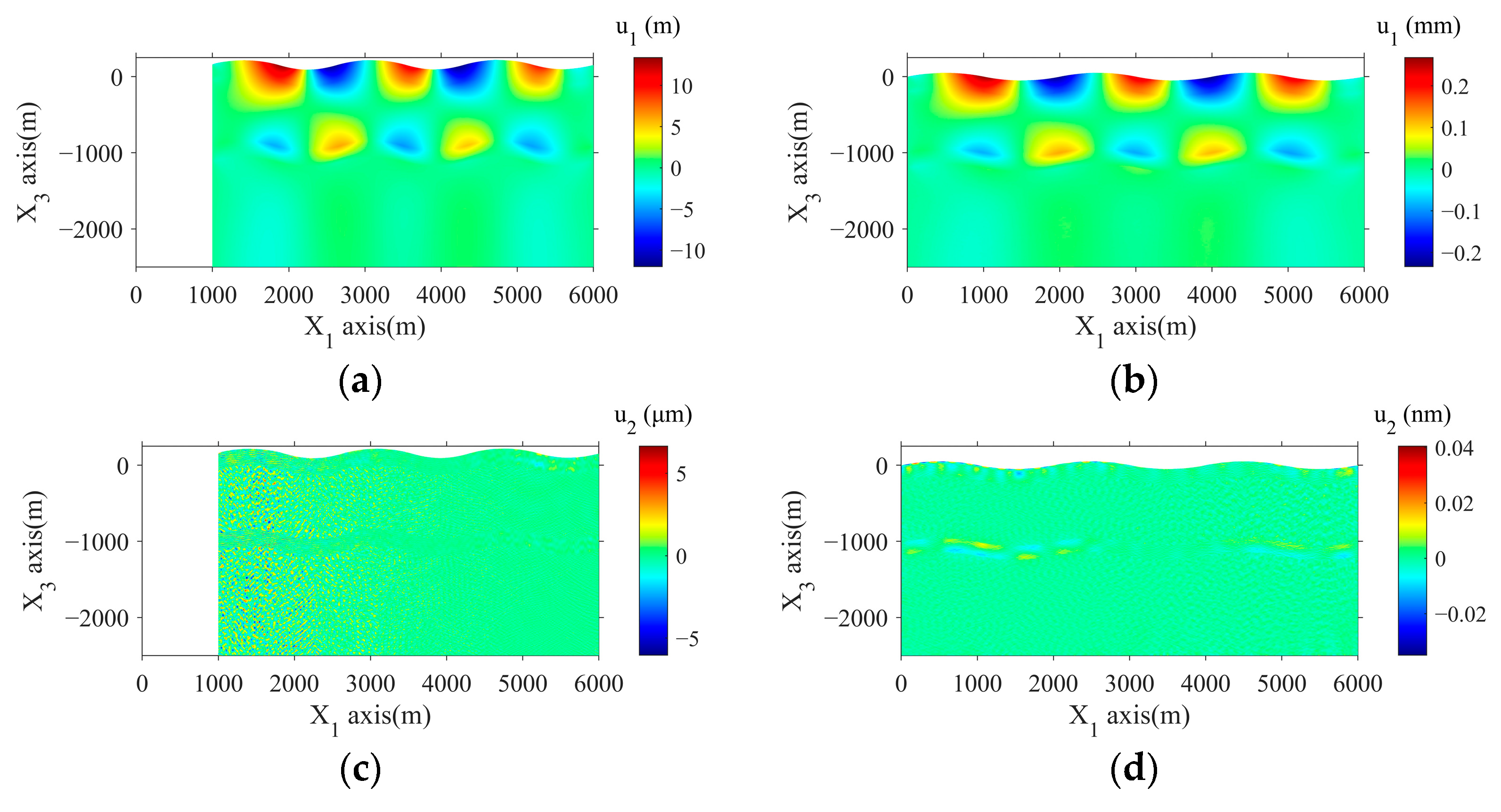
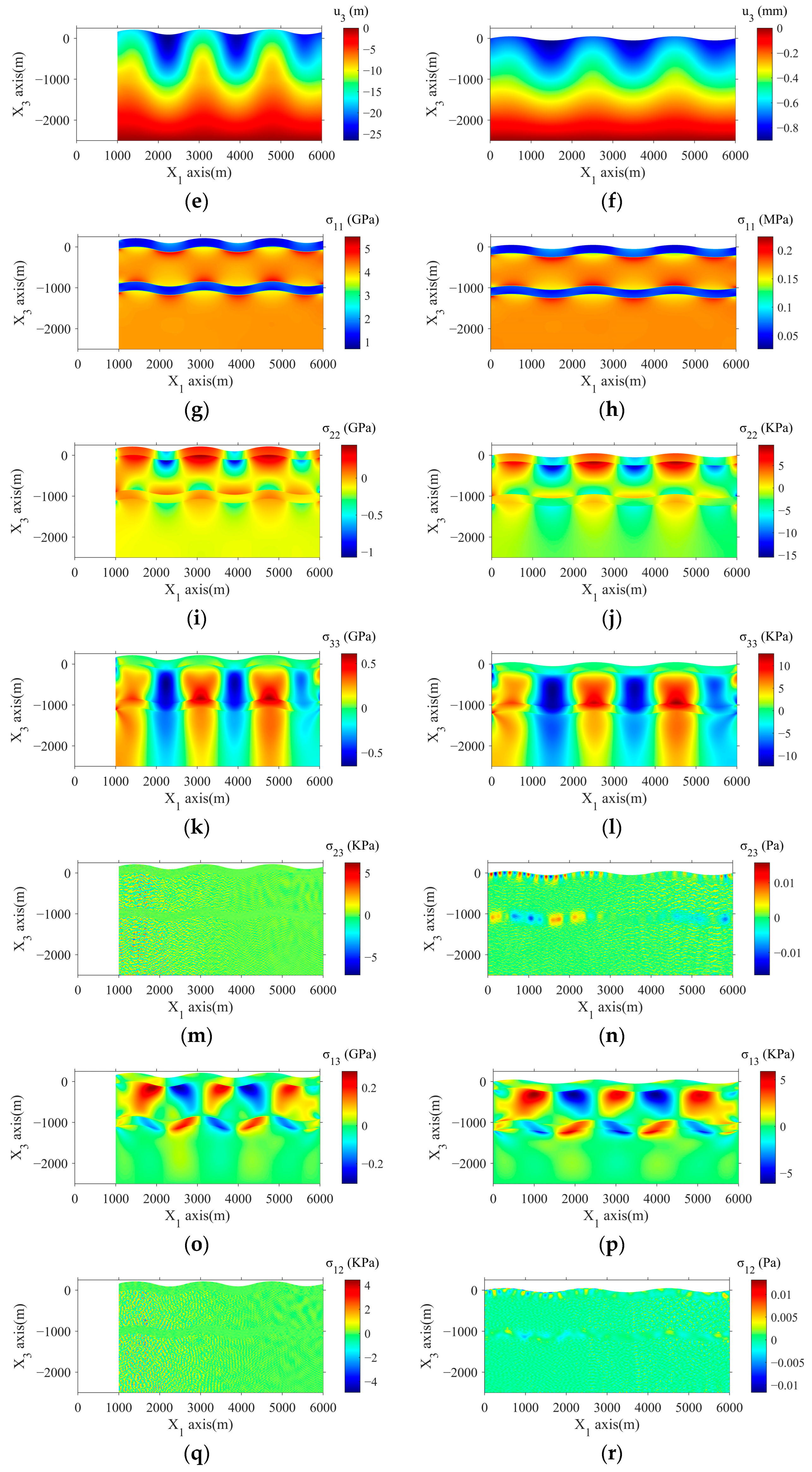
4. Real-World Application
5. Discussion and Conclusions
- In this study, we developed a parallel finite element program for elastic large deformation using the PFELAC software platform. We validated this program by comparing its results with analytical solutions from the following two conceptual models: a 45-degree rotated tensile large deformation model and a simple shear large deformation model.
- The comparison with results from the small deformation theory, exemplified by a fold-large deformation case, demonstrated the necessity of accounting for geometric nonlinearity in real crustal deformation studies. The Green strain tensor’s nonlinear relation to displacements highlighted its significance when paired with the Cauchy stress tensor.
- The higher the number of cores, the greater the parallel acceleration ratio, but the lower the parallel efficiency. For 16 cores, the acceleration ratio was 11.36–12.24 and the parallel efficiency was 0.71–0.77, and for 64 cores, the acceleration ratio was 24.70–34.78 and the parallel efficiency was 0.39–0.43. The parallel acceleration ratios and parallel efficiencies of our parallel resilient large model program were excellent.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, D.; Jiang, Y.; Sun, X.; Luan, H.; Zhang, H. Nonlinear Large Deformation Mechanism and Stability Control of Deep Soft Rock Roadway: A Case Study in China. Sustainability 2019, 11, 6243. [Google Scholar] [CrossRef]
- Liu, W.; Chen, J.; Chen, L.; Luo, Y.; Shi, Z.; Wu, Y. Nonlinear Deformation Behaviors and a New Approach for the Classification and Prediction of Large Deformation in Tunnel Construction Stage: A Case Study. Eur. J. Environ. Civ. Eng. 2020, 26, 1–29. [Google Scholar] [CrossRef]
- Sui, Q.; He, M.; He, P.; Xia, M.; Tao, Z. State of the Art Review of the Large Deformation Rock Bolts. Undergr. Space 2022, 7, 465–482. [Google Scholar] [CrossRef]
- Ma, D.; Tan, Z.; Bian, L.; Zhang, B.; Zhao, J. Research on Deformation and Loose Zone Characteristics of Large Cross Section Tunnel in High Geo-Stress Soft Rock. Appl. Sci. 2023, 13, 9009. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, Z. Prediction and Classification of Large Deformations in Deep Tunnels Based on Stress Inversion Method. Geotech. Geol. Eng. 2023, 41, 2343–2358. [Google Scholar]
- Malvern, L.E. Introduction to the Mechanics of a Continuous Medium; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1969; p. 713. [Google Scholar]
- Jeremic, B.; Runesson, K.; Sture, S. Finite Deformation Analysis of Geomaterials. Int. J. Numer. Anal. Meth. Geomech. 2001, 25, 809–840. [Google Scholar] [CrossRef]
- Hashiguchi, K.; Yamakawa, Y. Introduction to Finite Strain Theory for Continuum Elasto-Plasticity; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Shabana, A.A. Computational Continuum Mechanics, 3rd ed.; Wiley: Hoboken, NJ, USA, 2018; pp. 1–350. [Google Scholar]
- Soga, K.; Alonso, E.; Kumar, K.; Bandara, S. Trends in Large-deformation Analysis of Landslide Mass Movements with Particular Emphasis on the Material Point Method. Géotechnique 2016, 3, 248–273. [Google Scholar] [CrossRef]
- Zhang, X.; Sheng, D.; Sloan, S.W.; Bleyer, J. Lagrangian Modelling of Large Deformation Induced by Progressive Failure of Sensitive Clays with Elastoviscoplasticity. Int. J. Numer. Meth. Eng. 2017, 112, 963–989. [Google Scholar] [CrossRef]
- Liu, B.; Wang, W.; Liu, Z.; Ouyang, N.; Mao, K.; Zhou, F. Study on Large Deformation of Soil–rock Mixed Slope Based on GPU Accelerated Material Point Method. Sci. Rep. 2024, 14, 6983. [Google Scholar] [CrossRef]
- Milliner, C.; Donnellan, A.; Aati, S.; Avouac, J.P.; Zinke, R.; Dolan, J.F.; Wang, K.; Burgmann, R. Bookshelf Kinematics and the Effect of Dilatation on Fault Zone Inelastic Deformation: Examples from Optical Image Correlation Measurements of the 2019 Ridgecrest Earthquake Sequence. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020551. [Google Scholar] [CrossRef]
- He, M.C.; Xie, H.P.; Peng, S.P.; Jiang, Y.D. Study of Rock Mechanics in Deep Mining Engineering. Chin. J. Rock Mech. Eng. 2005, 16, 2803–2813. (In Chinese) [Google Scholar] [CrossRef]
- Mcivor, M.; Anderson, W.J.; Buak-Zochowski, M. An Experimental Study of the Large Deformation of Plastic Hinges. Int. J. Solids Struct. 1977, 13, 53–61. [Google Scholar] [CrossRef][Green Version]
- Lubliner, J. Normality Rules in Large-deformation Plasticity. Mech. Mater. 1986, 5, 29–34. [Google Scholar] [CrossRef]
- Sakai, Y.; Yamasita, A. Elastic-plastic Large Deformation Analysis Using SPH. In Computational Methods; Liu, G.R., Tan, V.B.C., Han, X., Eds.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 1515–1519. [Google Scholar]
- Guo, Z.; Watanabe, O. Study on Accuracy of Finite-Element Solutions in Elastoplastic Large Deformation. JSME Int. J. Ser. A 1996, 39, 99–107. [Google Scholar]
- Levin, V.A.; Taras’ev, G.S. One Variant of the Model of a Viscoelastic Body at Large Deformations. Sov. Appl. Mech. 1983, 19, 615–618. [Google Scholar] [CrossRef]
- Chandra, A.; Mukherjee, S. Boundary Element Formulations for Large Strain-large Deformation Problems of Viscoplasticity. Int. J. Solids Struct. 1984, 20, 41–53. [Google Scholar] [CrossRef]
- Pai, P.F.; Palazotto, A.N. Large-deformation Analysis of Flexible Beams. Int. J. Solids Struct. 1996, 33, 1335–1353. [Google Scholar] [CrossRef]
- Takanoa, N.; Ohnishia, Y.; Zakoa, M.; Nishiyabu, K. The Formulation of Homogenization Method Applied to Large Deformation Problem for Composite Materials. Int. J. Solids Struct. 2000, 37, 6517–6535. [Google Scholar] [CrossRef]
- Akhundov, V.M. A 4D Composite Reinforced along Cube Diagonals with a Small Content of Yarns under Large Tensile Deformations. Mech. Compos. Mater. 2002, 38, 197–210. [Google Scholar]
- Akhundov, V.M. A 4D Composite Reinforced along Cube Diagonals with a Small Content of Yarns under Large Shear Deformations. Mech. Compos. Mater. 2002, 38, 215–222. [Google Scholar] [CrossRef]
- Gu, Y.T. An Adaptive Local Meshfree Updated Lagrangian Approach for Large Deformation Analysis of Metal Forming. Adv. Mater. Res. 2010, 97–101, 2664–2667. [Google Scholar] [CrossRef]
- Chekhov, V.V. Matrix FEM Equation Describing the Large-strain Deformation of an Incompressible Material. Int. Appl. Mech. 2011, 46, 1147–1153. [Google Scholar] [CrossRef]
- Wu, Y.Z.; Zhu, Y.P.; Dui, G.S. Influence of Small-strain and Large-strain Methods on Mechanical Behaviors in Shape Memory Alloys. Adv. Mater. Res. 2011, 328–330, 1556–1559. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, I.V.; Mishra, B.K.; Singh, A. Numerical Simulation of Large Deformation Problems by Element Free Galerkin Method. Key Eng. Mater. 2013, 535–536, 85–88. [Google Scholar] [CrossRef]
- Davydov, R.L.; Sultanov, L.U. Numerical Algorithm for Investigating Large Elasto-plastic Deformations. J. Eng. Phys. Thermophys. 2015, 88, 1280–1288. [Google Scholar] [CrossRef]
- Ma, Y.; Zhou, Y. Hybrid Natural Element Method for Large Deformation Elastoplasticity Problems. Chin. Phys. B 2015, 24, 030204. [Google Scholar] [CrossRef]
- Iai, S. Developments in Earthquake Geotechnics. Geotech. Geol. Earthq. Eng. 2018, 43, 367–409. [Google Scholar] [CrossRef]
- He, M. High Slope Engineering of Open Pit Mine; China Coal Industry Publishing House: Beijing, China, 1991. (In Chinese) [Google Scholar]
- He, M. General Theory of Soft Rock Tunnel Engineering; China University of Mining and Technology Press: Xuzhou, China, 1993. (In Chinese) [Google Scholar]
- He, M.; Chen, X.; Liang, G.; Qian, H.; Zhou, Y.; Zhuang, X. Software System for Large Deformation Mechanical Analysis of Soft Rock Engineering at Great Depth. Chin. J. Rock Mech. Eng. 2007, 26, 934–943. (In Chinese) [Google Scholar]
- He, M.; Sui, Q.; Tao, Z. Excavation Compensation Theory and Supplementary Technology System for Large Deformation Disasters. Deep Undergr. Sci. Eng. 2023, 2, 105–128. [Google Scholar] [CrossRef]
- Yin, Y. Introduction to Nonlinear Finite Elements in Solid Mechanics; Peking University Press: Beijing, China, 2007. [Google Scholar]
- Hu, C. A New Method to Study Earthquake Triggering and Continuous Evolution of Stress Field. Ph.D. Thesis, Peking University, Beijing, China, 2009. [Google Scholar]
- Hu, C.; Zhou, Y.; Cai, Y.; Wang, C. Study of Earthquake Triggering in a Heterogeneous Crust Using a New Finite Element Model. Seismol. Res. Lett. 2009, 80, 799–807. [Google Scholar] [CrossRef]
- Hu, C.; Cai, Y.; Wang, Z. Effects of Large Historical Earthquakes, Viscous Relaxation, and Tectonic Loading on the 2008 Wenchuan Earthquake. J. Geophys. Res. Solid Earth 2012, 117, B06410. [Google Scholar] [CrossRef]
- Liang, G.P.; Zhou, Y.F. Finite Element Language and Its Application I; Science Press: Beijing, China, 2015. [Google Scholar]
- Liang, G.P.; Zhou, Y.F. Finite Element Language and its Application II; Science Press: Beijing, China, 2015. [Google Scholar]
- Shi, M.; Meng, S.; Hu, C.; Shi, Y. Crustal Heterogeneity Effects on Coseismic Deformation: Numerical Simulation of the 2008 MW 7.9 Wenchuan Earthquake. Front. Earth Sci. 2023, 11, 1245677. [Google Scholar] [CrossRef]
- Xu, M.; Li, H.; Song, Z.; Xu, Q.; Zhang, X.; Fu, P. An Electric-thermal-solid Physical Fields Coupling Calculation based on FELAC Platform, 2022. In Proceedings of the IEEE 5th International Conference on Electronics Technology, Chengdu, China, 13–16 May 2022; pp. 532–536. [Google Scholar] [CrossRef]
- Element Computing Technology Co., Ltd. Fundamentals and Applications of Finite Element Analysis of FELAC; Element Computing Technology Co., Ltd.: Tianjin, China, 2018; pp. 48–59. (In Chinese) [Google Scholar]
- Element Computing Technology Co., Ltd. Parallel Architecture of FELAC; Element Computing Technology Co., Ltd.: Tianjin, China, 2018; pp. 8–14. (In Chinese) [Google Scholar]
- Amdahl, G.M. Validity of the Single Processor Approach to Achieving Large Scale Computing Capabilities. AFIPS Conf. Proc. 1967, 30, 483–485. [Google Scholar]
- Grama, A.; Gupta, A.; Karypi, G.; Kumar, V. Introduction to Parallel Computing, 2nd ed.; Addison Wesley: Boston, MA, USA, 2003; pp. 1–664. [Google Scholar]

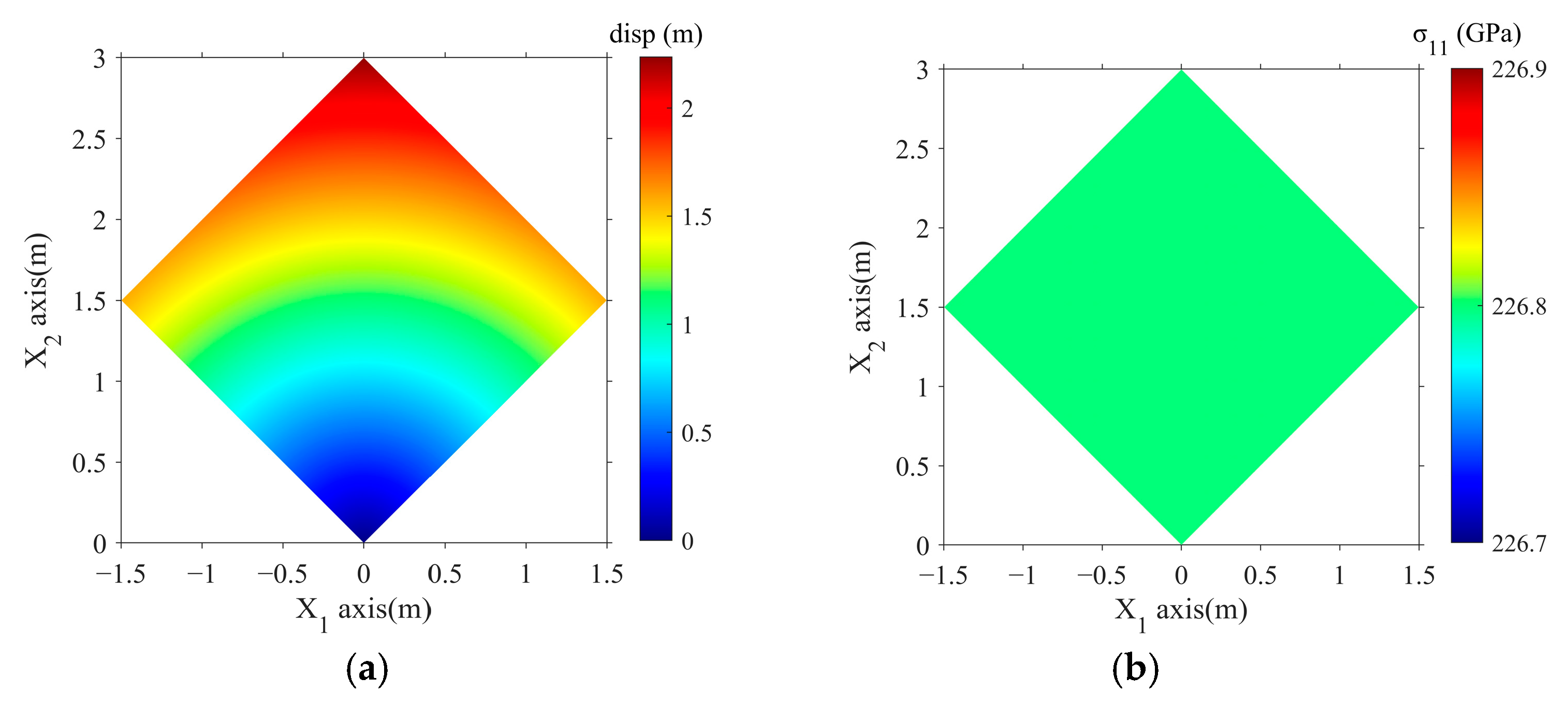


| Model | 1 | 2 | 3 | 4 | Analytic Solution |
|---|---|---|---|---|---|
| /m | −0.5 | ||||
| /m | 1.0000000 | 1 | |||
| /m | 0 | ||||
| /Pa | |||||
| /Pa | |||||
| /Pa | |||||
| /Pa | 1.3011090 | 0 | |||
| /Pa | 1.0016021 | 0 | |||
| /Pa | 0 | ||||
| t/s(parallel) | 7.67 | 773 | 3160 | 739 |
| Model | 5 | 6 | 7 | 8 | Analytic Solution |
|---|---|---|---|---|---|
| (m) | 0.5 | ||||
| (m) | 0.0000000 | 0 | |||
| (m) | 0.0000000 | 0 | |||
| (Pa) | |||||
| (Pa) | |||||
| (Pa) | |||||
| (Pa) | 0 | ||||
| (Pa) | 0 | ||||
| (Pa) | |||||
| t/s(parallel) | 7.66 | 776 | 3210 | 755 |
| Models | 1 | 2 | 3 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 1 core | 28.4 s/1/1 | 2920 s/1/1 | 11,900 s/1/1 | 28.5 s/1/1 | 2950 s/1/1 | 12,100 s/1/1 |
| 4 cores | 7.67 s/3.70/0.93 | 773 s/3.78/0.94 | 3160 s/3.77/0.94 | 7.66 s/3.72/0.93 | 776 s/3.80/0.95 | 3210 s/3.77/0.94 |
| 16 cores | 2.5 s/11.36/0.71 | 237 s/12.32/0.77 | 990 s/12.02/0.75 | 2.5 s/11.40/0.71 | 241 s/12.24/0.77 | 1000 s/12.10/0.76 |
| 64 cores | 1.15 s/24.70/0.39 | 107 s/27.29/0.43 | 450 s/26.44/0.41 | 1.15 s/34.78/0.39 | 108 s/27.31/0.43 | 463 s/26.13/0.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Hu, C.; Zhang, H. Parallel Finite Element Algorithm for Large Elastic Deformations: Program Development and Validation. Eng 2025, 6, 48. https://doi.org/10.3390/eng6030048
Chen Y, Hu C, Zhang H. Parallel Finite Element Algorithm for Large Elastic Deformations: Program Development and Validation. Eng. 2025; 6(3):48. https://doi.org/10.3390/eng6030048
Chicago/Turabian StyleChen, Yuhang, Caibo Hu, and Huai Zhang. 2025. "Parallel Finite Element Algorithm for Large Elastic Deformations: Program Development and Validation" Eng 6, no. 3: 48. https://doi.org/10.3390/eng6030048
APA StyleChen, Y., Hu, C., & Zhang, H. (2025). Parallel Finite Element Algorithm for Large Elastic Deformations: Program Development and Validation. Eng, 6(3), 48. https://doi.org/10.3390/eng6030048