Comprehensive Investigation of Relative Permittivity Effects on Perovskite Solar Cell Performance Using SCAPS-1D and Impedance Spectroscopy

Abstract

Perovskite solar cells (PSCs) are promising photovoltaic technologies, yet their performance is critically influenced by the relative permittivity (ε_r) of the active layer, which governs charge carrier dynamics. This study employs SCAPS-1D simulations coupled with complex impedance and modulus spectroscopy to systematically investigate the impact of varying the ε_r of the MAPbI₃ layer from 4 to 12. We find that while the open-circuit voltage (V_oc~1.05 V) and short-circuit current density (J_sc~25 mA cm⁻²) remain stable, the FF and efficiency η (%) decline from 78% to 70% and 20% to 17%, respectively, with increasing εr. Impedance analysis deconvoluted this trend, revealing a decrease in recombination time (τ₁) and a peak in ionic transport time (τ₂) at ε_r = 7. The optimal performance of 18.86% was achieved at a lower ε_r, demonstrating that minimizing recombination losses through permittivity engineering is crucial for advancing PSC efficiency.

1. Introduction

In recent years, perovskite-based materials have generated considerable interest. Perovskite refers to a group of minerals with a specific crystal structure, which can also describe synthetic materials engineered to possess the same structure. This structure is typically represented as ABX3, where ‘A’ and ‘B’ are metal cations, and ‘X’ is a non-metal anion. Perovskite materials exhibit high ionic conductivity, making them valuable for various energy-related applications, including fuel cells and solid electrolytes. Additionally, they display intriguing optical properties, such as strong light absorption and effective photoluminescence, making them promising candidates for applications in photovoltaics and optoelectronics [1,2,3].

PSCs, particularly those based on Methylammonium lead iodide (CH₃NH₃PbI₃), have shown remarkable progress, with certified power conversion efficiencies (PCEs) now exceeding 27% [4,5,6,7,8,9]. While this rivals traditional silicon technologies [6], a critical barrier to their commercial viability is operational stability, which is intrinsically linked to ionic motion and recombination losses within the perovskite layer. Optimizing fundamental material properties, such as relative permittivity (ε_r), is essential to mitigate these losses and unlock the full potential of PSCs.

Numerical simulation tools like SCAPS-1D are vital for probing the internal physics of PSCs. While numerous studies have employed SCAPS-1D to optimize device architecture, including the selection of electron and hole transport layers [10,11,12,13,14], a critical and underexplored parameter is the relative permittivity (ε_r) of the perovskite absorber itself [15,16]. The permittivity governs the Coulombic interaction between charge carriers, directly influencing recombination rates and ionic transport dynamics, key factors limiting efficiency and stability. Most SCAPS-1D studies focus on typical J-V output, lacking a detailed analysis linking ε_r to these underlying electrochemical processes.

This work addresses this gap by employing SCAPS-1D simulations to systematically investigate the impact of the CH₃NH₃PbI₃ layer’s relative permittivity (varying from 4 to 12) on device performance. Crucially, we move beyond standard current–voltage (J-V) analysis by integrating a novel simulation and analysis of complex impedance and electric modulus spectra. This dual approach allows us to deconvolute the distinct influences of ε_r on electronic recombination and ionic transport, providing deeper mechanistic insight that is rarely captured in conventional simulation studies. Our goal is to identify the optimal permittivity range that minimizes detrimental processes and to establish a more comprehensive framework for the electrochemical design of high-performance, stable PSCs. Relative permittivity, also known as dielectric constant, is a critical property that significantly influences the performance of solar cells. Although the dielectric constant of CH₃NH₃PbI₃ has been widely reported in experimental studies, its fundamental and isolated impact on the internal charge dynamics of a solar cell remains less explored through simulation. In this work, we systematically vary the permittivity not to replicate a single experimental value, but to isolate its fundamental role in screening Coulomb interactions within the active layer. The primary novelty of this approach lies in using permittivity variation as a tool to trigger and deconvolve the hidden ionic and electronic dynamics via impedance and modulus analysis, a significant step beyond the standard J-V characterization prevalent in many simulation studies. This methodology provides unique insight into how permittivity governs the critical trade-off between recombination and ionic transport, which is essential for designing high-performance devices [17,18,19,20]. The study begins by detailing the fundamental principles behind solar cell operation and the role of relative permittivity in influencing the efficiency of these cells. By employing advanced simulation techniques, we successfully modeled the behavior of PSCs under a range of environmental and operational conditions, including variations in temperature, illumination intensity, and electrical load, allowing us to gain in-depth insights into their efficiency, degradation mechanisms, and overall stability, thereby gaining insights into the optimal relative permittivity values. Through these simulations, we can predict how changes in relative permittivity affect key performance metrics, such as V_oc, J_SC, and overall power conversion efficiency. These predictions are crucial for designing solar cells that are more efficient and for identifying potential improvements in cell materials and structures. Furthermore, our analysis includes a thorough examination of the electronic properties of perovskite materials, focusing on their dielectric constant and how it interacts with the cell’s architecture. This analysis not only helps in fine-tuning the solar cell performance but also in elucidating the physical processes that govern the conversion of solar energy into electrical energy. By optimizing the relative permittivity, we aim to enhance the operational stability and efficiency of PSCs, making them more viable for large-scale applications. This research contributes to the ongoing efforts in the field of renewable energy to develop more effective and sustainable solutions for energy production.

2. Method

2.1. Simulation Parameters Using SCAPS-1D

The simulations were performed using SCAPS-1D version 3.3.10; the simulation parameters were set to closely mimic standard test conditions (STC). The incident light power is standardized at 1000 W/m² under the AM1.5G spectrum, with the operating point voltage at 0 V and a controlled temperature of 300 K. These conditions are crucial for ensuring the reproducibility and relevance of the simulation outcomes to real-world solar cell performance.

2.2. Device Structure Modeled

The device structure modeled in SCAPS-1D includes a complex layering of materials; each component plays a vital role in contributing to the overall functionality of the PSCs. The structure comprises an n-type hole transport layer (HTL) of NiOx and a p-type electron transport layer (ETL) of ZnO, which are used as the metal electrode, with CH₃NH₃PbI₃ serving as the perovskite material sandwiched between them, ranging in relative permittivity from 4 to 12. (Ag/Al). FTO/ITO is used as the back contact (Figure 1). This configuration is essential for studying the interactions within the PSC, particularly the movement of electrons and holes, which are crucial for the device’s energy conversion efficiency. In addition, it is essential to provide a typical structure with an appropriate band diagram; the latter illustrates the energy levels of the materials involved. In the diagram, the Fermi level of the ETL is aligned with the conduction band of the perovskite, facilitating efficient electron transfer. The valence band of the perovskite aligns with the HTL, allowing for effective hole transfer. The conduction band of the ETL is higher in energy compared to the perovskite conduction band, while the valence band of the HTL is lower in energy than the perovskite valence band. This energy alignment is crucial for minimizing energy losses and enhancing the efficiency of the cell [21,22].

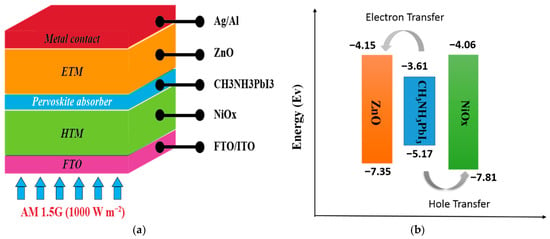
Figure 1. Device structure model: (a) PSCs and (b) energy band diagram.

2.3. Simulation Steps

The SCAPS-1D simulation involves several steps tailored to optimize the PSC design. Initially, layer thicknesses are set as follows: FTO at 500 nm, ZnO at 80 nm, CH₃NH₃PbI₃ at 700 nm, and NiOx at 80 nm. The material properties, such as bandgap and electron affinity, are precisely defined for each layer, ensuring accurate simulation of the photovoltaic behavior (Table 1) [23]. The simulation also incorporates advanced models for radiative and Auger recombination processes, with specific coefficients set for the perovskite absorption layer (PAL), enhancing the understanding of carrier dynamics within the cell (Table 2) [23].

Table 1. Optical and electrical properties of the various layers employed in SCAPS-1D.

S.L.	Properties	NiOx	CH3NH3PbI3	ZnO
1	Thickness (nm)	80	700	80
2	Bandgap (ev)	3.75	1.56	3.2
3	Affinity (ev)	2.1	3.90	4.10
4	Dielectric perm	10.7	10	8.1
5	DOSCB (cm−3)	2.8 × 1019	2.76 × 1018	4.5 × 1018
6	DOSVB (cm−3)	1.8 × 1019	3.9 × 1018	1 × 1018
7	µe (cm2/VS)	12	15	300
8	µh (cm2/VS)	25	15	1
9	Acceptor concentration (cm−3)	1 × 1015	1 × 1011	0
10	Donnor concentration (cm−3)	0	0	1 × 1019

Table 2. Different defect properties of different layers.

S.L.	Defect Properties	NiOx	CH3NH3PbI3	ZnO
1	Defect type	acceptor	neutral	donor
2	Total defect density (cm−3)	1 × 1017	1.5 × 1016	1 × 1017
3	Electron Diffusion length, Ln (nm)	180	510	280
4	Hole Diffusion length, Lp (nm)	800	510	51

2.4. Impedance Spectroscopy Analysis of CH₃NH₃PbI₃

Impedance spectroscopy (IS) is a powerful, non-destructive technique used to probe the electrochemical dynamics at interfaces and within the bulk of materials exhibiting mixed electronic and ionic behavior. In this study, IS were performed using SCAPS-1D to analyze the device’s frequency response. To ensure reproducibility and a valid interpretation of the impedance data, a standard methodology was applied: a small alternating current (AC) potential perturbation of weak amplitude was used across a frequency range of 0.01 Hz to 10 MHz. The impedance spectra were specifically simulated under operational conditions at a constant bias voltage equivalent to the maximum power point (MPP) of the J-V characteristic under standard AM1.5G illumination (1000 W/m²) [24,25].

3. Results and Discussion

3.1. J-V Characteristics

In order to investigate the influence of relative permittivity on PSCs, we have performed simulations on the structure depicted in Figure 1. The form of the heterojunction characteristics (Figure 2), measured under illumination, is closely associated with the dielectric constant of the CH₃NH₃PbI₃ layer; i.e., the higher the relative permittivity, the more both the FF (%) and efficiency η (%) were improved.

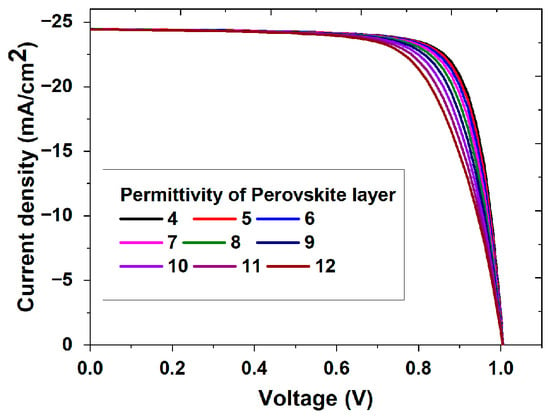
Figure 2. J-V curves for a stack FTO/ITO/NiOx/CH₃NH₃PbI₃/ZnO/Ag/Al with different relative permittivity of CH₃NH₃PbI₃ under illumination (1000 W/m²).

The parameters deduced from Figure 2, including J_SC, open-circuit potential V_OC, FF (%), and η (%), at different relative permittivity levels of CH₃NH₃PbI₃ under illumination are reported in Figure 3. We observe that the efficiency and FF (%) decrease with increasing relative permittivity due to the increase in recombination electron–hole. On the other side, V_oc and J_sc become constant along the range of relative permittivity.

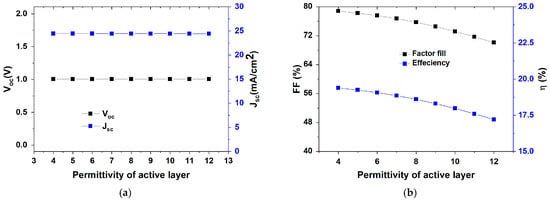
Figure 3. Effect of relative permittivity of CH₃NH₃PbI₃ on PSCs (a) Voc, Jsc, and (b) FF (%) and η (%).

The analysis of Figure 3 reveals the impact of relative permittivity on CH₃NH₃PbI₃ PSCs, specifically focusing on V_oc, J_sc, FF (%), and η (%). The results indicate that both V_oc and J_sc remain constant at approximately 1.05 V and 25 mA cm⁻², respectively, across a permittivity range of 4 to 12, suggesting that these parameters are not significantly affected by changes in permittivity (Figure 3a). In contrast, the FF and η exhibit a noticeable decline with increasing permittivity. The FF decreases from around 78% to 70%, while efficiency drops from about 20% to 17%, implying that higher permittivity adversely impacts these aspects of the PSCs’ performance (Figure 3b). This trend aligns with literature findings: Wang et al. [26] reported that increased permittivity can enhance charge carrier recombination, thereby reducing FF and efficiency. Jarwal et al. [27] studied the impact of several device parameters, such as the density and thickness of defects in the perovskite layer, on solar cell performance. They simulated a PSC architecture (FTO/TiO₂/CH₃NH₃PbI₃/HTLs/Au) to optimize absorber layer thickness and defect density, achieving an η of 10.01% for MEH-PPV, 13.94% for PEDOT:PSS, 14.75% for P3HT, 15.42% for PQT, 15.74% for NPB, 17.08% for PTAA, and 17.11% for spiro-OMeTAD. The study shows that spiro-OMeTAD is the most promising HTL, with an η of 17.11%, a V_OC of 1.10 V, a J_SC of 20.772 mA cm⁻², and an FF of 0.74%.

Strong recombination and trap-assisted recombination pathways result from a strong Coulomb attraction force between the electron and hole pairs. Therefore, it is favored in PSCs to lessen the attractiveness between mobile carriers. Reduced FF and η have been directly tied to the carrier loss brought on by recombination. In summary, the diminution of FF and η implies that a reduction in recombination strength could be afforded by using higher ε_r perovskite materials.

3.2. Complex Impedance Simulations

It has been noted that the device mechanisms are still unclear for OILH materials with mixed electronic–ionic conductivity compared with conventional all-inorganic materials [28,29]. Furthermore, the ionic conductivity gating the electronic motion generally obscures the explanation of the operation mechanism of PSCs. Thus, the ionic movement or ion/defect migration and resultant influence on device mechanism in PSCs should be fully elucidated for stable and highly efficient PSCs development.

Figure 4 shows the simulation electrical impedance for various relative permittivity values ranging from 4 to 12. In the Nyquist diagram (Figure 4a), it is clear that the impedance spectra consist of a sizable semicircle, which is highly influenced by the permittivity of the active layer of CH₃NH₃PbI₃. This shape of impedance spectra in the Nyquist diagram belongs to the responses usually encountered in solar systems, in which carrier transport is determined by diffusion–recombination. With an increase in the dielectric permittivity of the active layer, the semicircle’s diameter shrank.

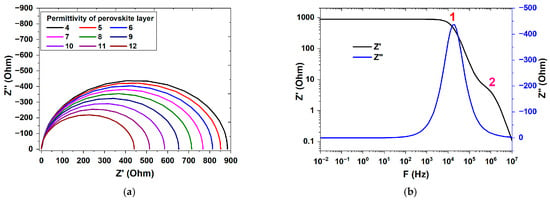
Figure 4. Impedance spectra with different relative permittivity of perovskite layer: (a) Nyquist diagram and (b) Bode diagram.

In the Bode diagram (Figure 4b), the variation in the real part showed two slope changes. This variance suggests the presence of two processes, and the modulus function will be examined as a result.

3.2.1. Complex Modulus Simulations

Figure 5 exhibits modulus spectra at various relative permittivity of perovskite layer, where Figure 5a shows M”–M’ to the variation in the real part and imaginary part in relative permittivity ranges of 4–12. The real axis intersection displays at the intercept the capacitance caused by recombination or ionic transport. Semicircular arcs at low and high frequencies (two relaxation processes) were detected for each sample. The small semicircular arcs at high frequencies are due to the effect of the recombination process. At low frequencies, the huge semicircular arcs correspond to the electrode processes’ effects on the ionic transport. Figure 5b depicts the imaginary part of electrical modulus, M” against the frequency in the relative permittivity order perovskite layer range from 4 to 12. It is clearly seen that similar behavior was observed. It is clearly observed from (Figure 5b) that M” versus frequency curves have two peaks at each value of relative permittivity; one of the peaks is in a low-frequency region and the other in a high-frequency region. It can be noticed that those peaks observed at low frequency move to the higher-frequency regions, and the peaks observed at higher frequencies move to the low-frequency region with increasing relative permittivity. We also noticed that at higher values of relative permittivity, both peaks overlapped.

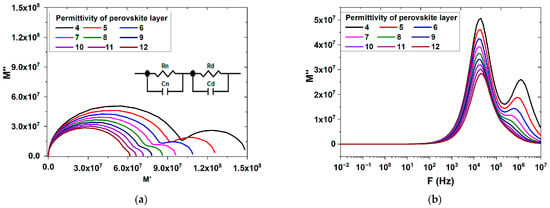
Figure 5. Modulus spectra with different relative permittivity of perovskite layer: (a) Nyquist diagram and (b) Bode diagram.

Impedance modeling of spectra with equivalent circuits is the best method to extract different electric and electronic parameters related to the performance of solar cells. Several authors [30,31,32,33] have studied the performance of solar cells using impedance spectroscopy, but they are limited to the analysis of impedance spectra, and consequently, a semicircle was observed in the impedance spectra; thus, they have used one block (R//C) to model this semicircle.

As we have shown in the modulus spectra (Figure 5), two processes exist, so for this reason, we have developed an equivalent circuit composed of two blocks (R₂//C₂) + (R₁//C₁).

The total complex impedance of the circuit described above can be expressed as follows:

$$Z^{*}\left(\omega \right)={\displaystyle \frac{R_1}{1+j\omega {\tau }_1}}+{\displaystyle \frac{R_2}{1+j\omega {\tau }_2}}$$

(1)

where τ₁ and τ₂ are the relaxation times, ω is the angular frequency, R₁ and R₂ are the resistors, and C₁ and C₂ are the capacitors.

It is very usual to have the imaginary part (Z″) be at a maximum during the relaxation process; this can be explained with the equation below:

$${\omega }_{1max}={\displaystyle \frac{1}{{\tau }_1}}={\displaystyle \frac{1}{{R_{1}C}_1}} \mathrm{a}\mathrm{n}\mathrm{d} {\omega }_{2max}={\displaystyle \frac{1}{{\tau }_2}}={\displaystyle \frac{1}{{R_{2}C}_2}}$$

(2)

These expressions are obtainable from the derivative of the imaginary part (Z″) versus angular frequency (ω). The complex impedance (Z*) and the modulus (M*) are related by Equation (3):

$$Z^{*}\left(\omega \right)=j\omega M^{*}\left(\omega \right)$$

(3)

Then, the real and imaginary parts of the electric modulus can be expressed as follows:

$$M^{\prime }\left(\omega \right)={\displaystyle \frac{C_0}{C_1}}\left[{\displaystyle \frac{{\left(\omega {\tau }_1\right)}^2}{1+{\left(\omega {\tau }_1\right)}^2}}\right]+{\displaystyle \frac{C_0}{C_2}}\left[{\displaystyle \frac{{\left(\omega {\tau }_2\right)}^2}{1+{\left(\omega {\tau }_2\right)}^2}}\right]$$

(4)

$$M^{″}\left(\omega \right)={\displaystyle \frac{C_0}{C_1}}\left[{\displaystyle \frac{\omega {\tau }_1}{1+{\left(\omega {\tau }_1\right)}^2}}\right]+{\displaystyle \frac{C_0}{C_2}}\left[{\displaystyle \frac{\omega {\tau }_2}{1+{\left(\omega {\tau }_2\right)}^2}}\right]$$

(5)

where C₀, C₁, and C₂ are Capacitor; ω is the angular frequency; and R₁ and R₂ are resistors.

Similarly, the angular frequency (ω₁ max) and (ω₂ max) values can be calculated by differentiating the imaginary part (M″) in terms of angular frequency (ω). This allows us to obtain the very same value corresponding to real part (ω max) for every maximum found in the imaginary part M″.

Therefore, the previous equations give some explanation on why each maximum observed in the real-part evolution for both (Z″) and (M″) at low-frequency and high-frequency can be at the special frequency value (F max).

Consequently, important parameters that can be extracted after fitting with an equivalent circuit model include capacitances (C), resistances (R), and time constants (τ), corresponding to various contributions at both low and high frequencies.

To show the validity of the equivalent circuit, the fit of the modulus function in the Nyquist diagram for relative permittivity was 4 and was selected as a typical sample to show the fit. Figure 6 shows the best fit using an equivalent electrical circuit.

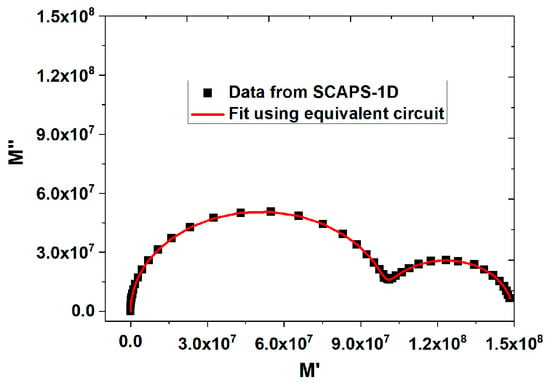
Figure 6. Fit of modulus spectra at different relative permittivity of the perovskite layer.

3.2.2. Analysis of Extracted Parameters from the Equivalent Electrical Circuit

In a PSC, the characterization and identification of the recombination and ionic transport mechanisms in thin-film solar cells have been an important challenge for the community [34,35,36]. The equivalent circuit model described contains two characteristic times related to the recombination τ₁ (recombination time) and the ionic transport τ₂ [33,37]. Figure 7 shows the dependence of both relation times deduced from the equivalent circuit on an increasing relative permittivity. We have observed that the recombination time, τ₁, decreases with an increase in ε_r, indicating that the recombination rate increases. This enhanced recombination directly leads to the degradation of the solar cell’s performance, as observed in the reduction in FF and η. For the ionic transport time τ₂, their evolution shows a peak at 7 of the relative permittivity value. Above this value, the ionic transport process is more dominant compared with the recombination process; this phenomenon generates a cell with low efficiency, as shown in Figure 3b.

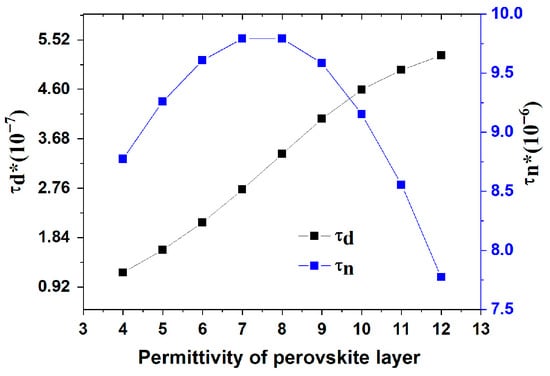
Figure 7. Recombination time and ionic transport time versus relative permittivity.

The optimal relative permittivity was observed, which led to obtaining an efficiency of 18.86%, J_sc of 24.44 mA cm⁻², open-circuit potential Voc 1.005 V, and an FF of 76.75%. These values have been improved compared with the values obtained in the work of Sazzadur Rahman et al. [7].

To translate the optimal relative permittivity identified in this simulation into a practical engineering strategy, the dielectric environment of the perovskite layer can be tailored through material design. A primary approach is cation engineering, where alloying the A-site (e.g., incorporating formamidinium (FA⁺) or cesium (Cs⁺) alongside methylammonium (MA⁺)) systematically tunes the material’s polarizability and effective permittivity. Alternatively, composite engineering, such as forming low-dimensional perovskite phases or incorporating dielectric additives into the bulk or at interfaces, can locally enhance charge screening and passivate defects. By targeting these synthesis routes, experimental efforts can rationally approach the optimal permittivity window, thereby mitigating recombination losses and advancing the development of high-performance PSCs.

4. Conclusions

This study used SCAPS-1D simulation to analyze the role of the perovskite layer’s relative permittivity (ε_r) in planar CH₃NH₃PbI₃ solar cells. The results show a clear trade-off: while V_OC and J_SC remain stable, the FF and power conversion efficiency decrease as ε_r increases from 4 to 12. An optimal efficiency of 18.86% was identified for a specific permittivity value. More importantly, by integrating impedance spectroscopy analysis, we provided a novel mechanistic explanation for this trend. The deconvolution of the impedance spectra revealed that increasing ε_r simultaneously extends recombination time but also promotes unfavorable ionic transport dynamics beyond a critical point (ε_r = 7). This dual effect clarifies why simply maximizing permittivity is detrimental and establishes ε_r as a key parameter for balancing electronic and ionic processes in the perovskite absorber.

The primary scope of this work is to provide a theoretical and simulation-based framework linking a fundamental material property (ε_r) to the electrochemical performance of PSCs. To translate these findings into higher experimental device performance, future work must focus on material synthesis guided by this optimal ε_r target. This can be achieved through compositional engineering, such as A-site cation mixing or the incorporation of specific additives designed to precisely tune the dielectric constant of the perovskite film. Subsequent experimental validation should fabricate devices with these tailored materials and employ impedance spectroscopy to confirm the predicted suppression of ionic losses and recombination. This targeted approach, moving from simulation to controlled synthesis and characterization, offers a direct pathway to fabricating more efficient and stable PSCs.