Abstract
Multi-criteria methods are highly attractive tools to address the inherent complexity of evaluating problems in various scientific areas. The combination of methods such as Delphi/AHP is emerging as a robust alternative to evaluate the sustainability of renewable energy sources. In this theoretical-descriptive research, the use of the Delphi method is proposed to select criteria and sub-criteria to obtain a high level of reliability, while the AHP method is used to establish an order of preference among the alternatives analyzed. This process requires the support of a committee of experts, whose role is to identify the various biomass alternatives that can be used in the sugar industry, considering aspects related to sustainability. The selected experts have identified energy, exergy, and emergetic indicators, in which economic, environmental, and social aspects are integrated. The multi-criteria analysis shows that the V1 variant was the most satisfactory in terms of biomass sustainability, representing 45% and 53% of the overall priorities in the evaluated case studies. In addition, the sensitivity analysis under an equal-weighted scenario for both study cases evidenced that variant V1 acquired the highest score (38.17%) among all alternatives. Variant V4 achieved the second highest score (31.79%), while alternative V2 achieved only 29.04%, respectively. The integration of Delphi/AHP methods emerges as a novel tool to assess sustainability in different industries of the energy sector.
1. Introduction
In recent years, the interest in using renewable energy sources (RES) as an energy policy has experienced a remarkable increase worldwide. This increase is attributed to growing environmental awareness, motivated by the adverse impacts of fossil fuels on the environment and the finiteness of their reserves.
Fossil fuels dominate global energy supply. The total primary energy supply has an 80% share of fossil fuels in its matrix (27% coal, 29% oil, and 24% gas). Renewable energy technologies (solar, wind, hydro, biomass, geothermal, etc.) accounted for 15% of the primary energy supply in 2020. Agriculture is a key sector for increasing the potential for bioenergy use in the future. Although the sector accounts for about 10% of the global biomass supply, there is significant potential to increase its contribution. In 2020, 69% of all bioenergy generated came from solid biomass sources, followed by 17% from municipal and industrial waste. In the case of Cuba, the use of renewable energy sources is currently low, as only 4.3% of the country’s electricity is produced from such sources, and biomass contributes 3.5% of this amount. However, based on a diagnosis of the current situation and the need to gradually reverse the situation that the country is experiencing today by 2020, there is a new policy proposal for energy transition with a view to 2050 [1]. According to this context, it is planned to increase the share of RES in electricity generation to 31%, producing 9960 GWh/year with RES. In the case of biomass as a fuel, this policy proposes an investment opportunity mainly in the sugar industry, where biomass as an energy source is expected to comprise 9% of the country’s energy matrix. It should also be noted that this energy penetration intended to be achieved with the use of RES should guarantee environmental sustainability in line with the sustainable development goals of the 2030 agenda.
Additionally, the vulnerability associated with reliance on imports of these fuels and the enactment of laws restricting the use of non-renewable energy sources has led many countries, particularly the more developed ones, to explore alternatives that promote the use of renewable energy sources (RES). This strategy aims to strengthen the security of energy supply options. However, the shift from fossil fuel-based energy supplies to renewable sources involves expanding green energy generation capacity and adopting more efficient and appropriate practices in its use.
One of the main drawbacks today is the difficulty of measuring sustainability. This abundance of measures is a major drawback, as the various synthetic indicators convey different messages. This causes great confusion among statisticians and policymakers. A wide variety of indicators is available, but there are reasons why a comprehensive assessment of sustainability is difficult to establish fully and consensually. Sustainability assessment requires many assumptions and policy choices and is further complicated by the existence of interactions between the socioeconomic and environmental models that different countries develop. The problem is indeed complex, more complex than the already complicated issue of measuring well-being or current performance [2].
There are sustainability assessment studies such as [3,4,5,6,7,8,9,10,11], along with those related to the environmental impacts associated with biomass use in general terms [12,13,14,15]. Each of them provides a unique assessment perspective.
One of the approaches for measuring sustainability is based on physical costs, which relies mainly on the first and second principles of thermodynamics and systems ecology. It takes into consideration the analysis of embodied energy, exergetic analysis, and the emergy synthesis from the ecology of systems, providing the energetic memory of processes and systems. It also studies the industrial ecology, the material flow analysis, and the energy costs invested in a certain process, making the embodied energy analysis the most known method. It also analyzes the replacement energy cost (costs in usable or undissipated energy) involved in the use of natural capital. Finally, it is based on systems ecology, and its main difference from other energy analysis studies lies in its ability to discern between different energy qualities and to make explicit the relationships between the economic system and the biogeophysical system.
At present, multicriteria decision methods are widely studied for the evaluation of alternatives that include several indicators, providing a reliable evaluation of the results.
Another approach in the multi-criteria decision-making process (MCDM) aligned with government policies has, as a fundamental purpose, the replacement of energy generated from fossil fuels by RES [16,17,18]. These methods are a valuable decision-making tool for energy planning projects [19,20,21,22].
The MCDMs currently consider technological, social, economic, and environmental factors [23,24], with development and energy sustainability-based decision making predominating in the analyses [25,26,27,28,29,30].
Multi-criteria decision analysis (MCDA) methods tackle the decision-making process when confronted with multiple objectives [31,32,33]. These approaches necessitate the involvement of a decision maker to evaluate and select among various criteria, both quantifiable and non-quantifiable, which often have conflicting objectives.
Therefore, the solution is heavily influenced by the decision maker’s preferences [34]. Often, multiple groups of decision-makers participate in this process, each contributing diverse criteria and viewpoints. It is essential to address these differences within a framework of mutual understanding and compromise [35].
In the study conducted by [36], the usage prevalence of various MCDM methods was investigated. The research highlighted that the Analytic Hierarchical Process (AHP), the Analytic Network Process (ANP), ELimination Et Choix Traduisant la REalité (ELECTRE), and the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) are the most frequently utilized methods in academic literature.
To analyze projects and investments in the field of RES utilization, methods such as ELECTRE and Preference Ranking Organization Methods for Enrichment Evaluations (PROMETHEE) are still insufficient, and the use of biomass as a renewable source for energy generation has not been evaluated in depth. Among the applications of MCDMs is the planning of microgrids. The study proposed by [37] presents a stochastic planning algorithm considering the unification of renewable energy resources, determining the error prediction from the optimal operation.
According to [38], the Combinative Distance Assessment (CODAS) method aims to conduct multi-criteria selection by considering both Euclidean distance and Taxicab distance relative to negative ideal solutions. This study proposes alternative strategies to manage uncertainty in MCDM.
In the context of imprecise decision-making with multiple conflicting goals, ref. [39] introduces a novel weighted additive fuzzy multiple choice goal programming model (WA-FMCGP). Each goal within this model has multiple-choice aspiration levels. The primary contribution of this model is its objective function, which aims to minimize the weighted additive sum of the normalized variances.
According to [25], the uncertainty in performance ratings is represented as lower and upper goals, which are adjusted to the model’s segregation thresholds. This study introduces a modified version of the ELimination and Choice Translating Reality (ELECTRE) III model.
Utilizing a neural network and variance approach, ref. [40] assessed technical, economic, social, and environmental variables for the optimal and efficient management of renewable energy sources (RES). This approach aims to ensure the sustainability of energy systems that do not depend on fossil fuels.
The integration of economic, technical, and environmental aspects in strategic decision-making for autonomous off-grid energy supply systems presents challenges, as highlighted by [41]. This study introduces a novel method that combines multi-criteria analysis with the Analytic Hierarchy Process (AHP) and system optimization. The goal is to identify universal priority criteria and determine the optimal system configuration, taking into account expert opinions.
The research conducted by [42] suggested a combined utilization of GISMCDA and the Fuzzy Decision-Making Trial and Evaluation Laboratory (F-DEMATEL) technique to pinpoint optimal sites for biomass facilities, with a focus on long-term sustainability. Their approach entails the establishment, evaluation, weighting, and categorization of primary criteria into three groups: environmental, geophysical, and socioeconomic.
Ref. [43] investigated an integrated multi-criteria decision-making (MCDM) approach employing Shannon entropy to evaluate and assess different energy sources. This method takes into account economic, technical, social, environmental, political, and adaptable criteria, encompassing options such as thermal, gas, nuclear, solar, wind, biomass, and hydroelectric.
On the contrary, the study by [44] illustrates that an integrated methodological framework, combining life cycle analysis (LCA) and multi-criteria decision-making (MCDM), proves effective in evaluating the sustainability of renewable energy systems. This approach offers a range of sustainable indicators and assessment methodologies, adaptable to various contexts such as energy policy, power supply, and project evaluation. Among several hybrid frameworks, the combination of LCA and Hierarchical Analytical Process (HAP) emerges as the preferred choice due to its simplicity and efficacy in sustainable assessment within energy systems.
As per [45], the Delphi method is employed to select an initial set of renewable energy alternatives for electricity generation, accompanied by initial criteria encompassing economic, environmental, social, and additional factors. Subsequently, the Fuzzy Analytic Hierarchy Process (FAHP) may be utilized to prioritize these criteria, accounting for uncertainties in the experts’ judgments.
Ultimately, global categorization is conducted utilizing FPROMETHEE (Fuzzy Preference Ranking Organization Method for Enrichment Evaluation) to formulate an assessment of the renewable energy alternatives while considering uncertainties.
The research by [46] underscores the significance of MCDM/A methods in attaining the sustainable development goals outlined by the United Nations for 2030. This study emphasizes the application of MCDM/A in evaluating renewable energies using efficiency indicators as a crucial aspect. Additionally, it provides recommendations for long-term research based on MCDM/A to advance sustainability efforts.
There are studies where energy and exergy assessments have been carried out, in addition to considering environmental criteria in the evaluation of biomass utilization processes for energy purposes [47,48,49,50,51]. Each of these studies, with their scopes and limitations, provide indicators to quantify the efficiency and effectiveness of the process.
Generally, energy and exergy evaluation methods are focused on the determination of efficiencies in steam generators (G.V.), auxiliary equipment, and combined heat and power cycles. They are carried out by determining irreversibilities from exergy balances. They value several fuels within the G.V., such as Bagasse and agricultural harvest residues (AHR); however, they do not include, in any case, marabu as fuel, nor combinations of mixtures of these.
One of the approaches that for some time has been of special interest in the evaluation of environmental impacts associated with the use of resources is the emergy method. This method is little used in the sugar industry, nor applied to different fuels other than sugarcane bagasse [52,53]. It is a method based on the third and fourth principles of thermodynamics, evaluating the sustainability of the system by determining a wide range of indicators.
In the research by [54], the combined development of the TOPSIS and AHP MCDMs is presented. In this study, as base criteria, balances from the perspectives of energy, exergy and emergy were taken, applied fundamentally to the combustion process present in the sugar industry.
However, it does not consider evaluating the importance of various indicators in achieving sustainability in biomass utilization using the Delphi method. Neither does it consider more than one utilization technology, nor fuel mixes.
This article presents several contributions, such as:
- •
- Considering the combined application of the Delphi-AHP method in the assessment of biomass sustainability for the sugar industry.
- •
- Incorporating biomass blends and evaluating them from economic, environmental and social perspectives.
- •
- Evaluating sustainability for five variants applied in two types of energy conversion technology.
This article is structured as follows: Section 1, the Introduction, presents the importance of the MCDM in renewable energy planning, where it is a valuable tool in decision making when multiple criteria exist. Section 2, Materials and Methods, presents the method for the selection of experts and their level of competence, as well as the Delphi method for the evaluation of criteria and sub-criteria. The AHP method for the multi-criteria decision of alternatives is also described. Section 3, Results and Discussion, presents the evaluation of the 12 sub-criteria by the experts according to their importance, the hierarchical structure for the selection of alternatives, and the AHP technique for the determination of the final priorities. A sensitivity analysis is also applied for the study variants. Section 4, Conclusions, shows the most sustainable variant for the evaluated case studies.
2. Materials and Methods
For the evaluation of sustainability based on physical costs in the use of biomass for energy purposes, methods of analysis have been developed mainly from the energetic, exergetic, and emergetic perspective. Each of these methods has its scope and limitations. The proposed study aims to integrate these methods as a solution and contribute to the analysis of sustainability for different types biomass to be used as fuel in the sugar industry. To this end, we start from the energetic and exergetic methods, and using balances, the determination of yields or efficiencies. The indicators obtained are used for the hierarchization of the level of importance by using the emerging method as a tool for environmental analysis, where from indicators it is possible to obtain a global vision of the process through the sustainability of the alternatives considered.
The first stage starts with the selection of an expert advisory system to identify/modify biomass-to-energy options and the factors affecting their selection. Such a consultation process should involve different sectors, including decision-making departments, industries, and research institutes, and should be formed on the basis of background knowledge of the problem. The next stage involves the selection of the criteria and/or sub-criteria to be used in the evaluation through the application of the Delphi Criteria Evaluation Method. With this method, it is possible to carry out the screening to select the criteria and/or subcriteria necessary to achieve the research objective, depending on the considerations of the decision-makers (committee of experts). Once the criteria and/or sub-criteria to be used in the evaluation have been obtained, the AHP method is applied to establish the ranking of alternatives.
This study provides criteria for decision making within the current sugar industry, allowing, with the integration of the methods, a clear and robust vision of which variants may be the best for fuel utilization within the sugar sector. The indicators used in the research, determined by means of the energy, exergy, and emergence balances, were proposed by [8].
The analysis is focused on the determination of energetic–exergetic and emergic indicators that allow the formation of a basis for general evaluation through the application of the combined Delphi–AHP method. The technologies selected as a case study for which it was considered to apply the proposed balances are the high pressure G.VU-40 and the Retal type G.V., both technologies present in the Cuban sugar industry, whose technical characteristics are shown by [8].
Thermodynamics analyzes the conversion of energy in systems, evaluating performance and efficiency. In combustion, the energy balance measures the energy produced and consumed. The amount of energy released is determined by the heat of combustion of the fuel. This balance is crucial for designing efficient and safe systems such as engines and steam generators [55].
The exergy balance in biomass fuel utilization compares the useful exergy (thermal energy utilized) with the total exergy (available energy). The objective is to maximize the useful exergy and minimize the lost exergy to improve the efficiency of the process [47].
In addition, the emergy method evaluates environmental impacts by comparing natural energy with that produced by humans. The emergy is the total energy required to produce an energy flow over a period of time, helping to assess the sustainability of resources [52].
According to the literature, there are two main methods for calculating energy efficiency: the direct method and the indirect method. The latter takes into account a greater amount of losses in combustion. These methods have been developed by different authors such as [8,55,56]. On the other hand, exergy analysis within an exergy balance allows evaluation of the exergy efficiency, the same defined as the ratio between the exergy used in the product or process and the exergy supplied to the process [57,58,59,60].
The selection of experts and the level of competence of the candidates must be defined by drawing up a list of candidates who meet the predetermined requirements of experience, years of service, and knowledge of the subject matter [61,62].
Competence is determined by a coefficient K, which is calculated as the semisum (Equation (1)) of a coefficient (Kc) that assesses the level of knowledge on the subject under investigation and another (Ka) that establishes a measure of the sources of information [63,64].
To estimate the Kc and Ka coefficients, a survey is prepared in which the candidates carry out a self-evaluation. Before this, each candidate must be informed of the context and importance of the study to obtain their commitment.
Once the self-evaluations have been obtained, the Kc coefficient is calculated as the average of the values (Vc) that the candidates give to the aspects of the survey (nc) multiplied by the factor 0.1 as shown in Equation (2).
The argumentation coefficient (Ka) is calculated as the sum of the values of the degree of influence of each of the candidates’ sources of knowledge (Va), as shown in Equation (3). To determine the argumentation coefficients according to experience, knowledge, or lack of knowledge of the subject, among others, values must be assigned according to the answer to be obtained. These scales in function of the argumentation coefficients are described by [61].
Equation (4) is used to select the number of experts to participate in the decision process.
where m represents the number of experts, p is the proportion of the error made in making estimates of the problem with the number of experts, i is the precision of the experiment, and k is a constant that depends on the statistical significance level (1 −
).
It should be noted that p ∈ (0.1), and to achieve reliable results it is recommended that i ≤ 0.12. The m experts whose K coefficients are higher will then be selected for the study; it is recommended that all have high competence.
2.1. Delphi Method for the Evaluation of Criteria and/or Sub-Criterian
The Delphi method is applied to evaluate criteria, submitted to a group of experts, who give evaluation categories to the previously selected criteria. In case these criteria are not previously determined, the experience and knowledge of the experts can be used to shape the criteria to be evaluated. This process consists of two rounds.
Round 1: The experts are given the objective to be achieved and are asked to give their thoughts on the criteria needed to achieve this objective.
Round 2: The results of the experts are received, and those criteria that are not represented by the majority of the experts (less than 20%) should be evaluated in an additional round for the minority group only, in order to know whether their proportion is raised to 20% or remains below, in which case the criteria will be eliminated. In general, this round can facilitate the decantation of the minority criteria; if there are problems with this, then an additional round should be completed to clarify the eliminated criteria. Table 1 presents the linguistic variables to identify the degree of importance of the criteria evaluated.

Table 1.
Linguistic variables used for criteria evaluation.
Once the surveys have been carried out and the criteria have been evaluated by the panel of experts, the table of observed frequencies and accumulated frequencies of the n criteria is constructed. The number of experts who selected each evaluation range is shown.
To obtain the relative cumulative frequency table, the value of each cumulative frequency is divided by the number of experts. The last valuation range should be eliminated since only k−1 cut-off points (CP) are sought Table 2.

Table 2.
Normal distribution of expert evaluation for criteria screening with N unspecified.
For the development of this specific research, the criteria that will be considered are those that present an evaluation of Important and Very Important by the experts.
Once the final propositions of the experts about the evaluation have been obtained, it is necessary to analyze the degree or level of agreement that exists among the experts, to give greater authenticity to the study. For this purpose, the degree of coincidence of the assessments made by the experts is checked using Kendall’s Coefficient of Concordance (Equation (4)).
2.2. MCDM Analytic Hierarchy Process (AHP)
The AHP method serves as a robust and versatile tool for multi-criteria decision-making in intricate scenarios [65]. This approach breaks down the decision problem into more manageable sub-problems, organized hierarchically across multiple levels. It enables the comparison of variables at each level and the assessment of alternatives at the lowest level to facilitate optimal decision-making [66].
Group discussions and adjustments may be required in AHP to reach a final consensus. There are steps described by [67] to apply this method, which are described in Figure 1.
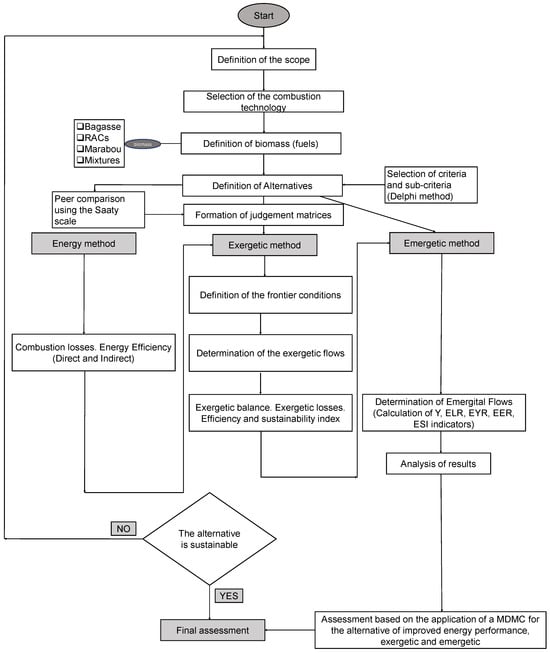
Figure 1.
Proposed method to assess the sustainability of biomass as fuel in the sugar industry.
The judgments are based on a standardized comparison of the nine-level Saaty scale [68]. These comparisons are carried out by a committee of experts with competence in the addressed topic.
Furthermore, to determine the priorities of the alternatives, the AHP methodology is employed, which entails solving judgment matrices [52]. The local priority vector (PVE) is derived by normalizing and subsequently averaging the vectors in each column of the judgment matrix. However, the global priorities for each alternative are established by synthesizing the local priorities across the hierarchy.
To ensure consistency in pairwise comparison judgments and calculate the consistency ratio (CR) [52], first, we calculate the principal eigenvalue (max) for each matrix using Equation (5):
Subsequently, the consistency index (CI) is computed for each “n” dimensional matrix using Equation (6):
The random index (RI) value is chosen based on the comparison matrix (n) order. According to [69], this presents the different RI values for matrices with orders ranging from 1 to 10. The acceptable threshold for RI values varies depending on the matrix size. For instance, the acceptable RI value for a 3 × 3 matrix is 0.05, for a 4 × 4 matrix it is 0.08, and for matrices of size ≥ 5 × 5 or larger, it is 1.12 [52,70].
3. Results
For this study, the results obtained by [8] for the five variants proposed in both cases of study for both the energetic and exergetic methods were used. These results are presented in Figure 2 and Figure 3, and validated by the authors of [50,51,56,71,72,73,74,75], where similar results were obtained under similar evaluation conditions.
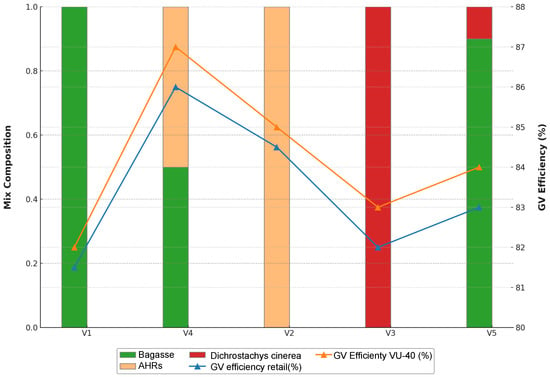
Figure 2.
Mix composition and GV energy efficiency.
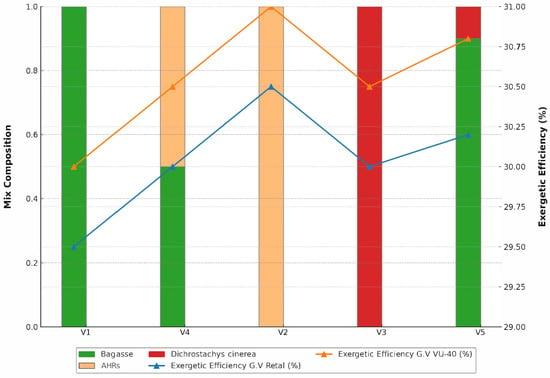
Figure 3.
Mix composition and GV exergetic efficiency.
The results of the energy efficiency indicators calculated for fuels and fuel blends, as well as for energy recovery technologies, are presented in Figure 2. In the case of the energy balance, it is shown that considering fuel blends leads to higher efficiency values, mainly related to the caloric power of biomass.
The behavior of the exergy efficiency represented in Figure 3 follows the same behavior patterns as in the case of energy efficiency. The highest efficiencies in this case were related to the use of AHRs and the mixture of bagasse and Dichrostachys cinerea.
A multiple regression analysis was also carried out to determine the influence of the different biomasses (Bagasse, AHR, Dichrostachys cinerea) on the G.V. Retal (%) and G.V. VU-40 (%) efficiencies. The analysis is based on the experimental data provided. The corresponding mathematical models, their correlation level
, and mean absolute percentage error (MAPE) were obtained (Table 3).

Table 3.
Multiple linear regression model considering different fuels and technologies.
X1, X2, and X3 correspond to the biomass types Bagasse AHR and Dichrostachys cinerea.
For the case of the Retal technology, the interpretation of the models suggests that a 1% increase in the proportion of Bagasse and AHRs in the mixture is associated with a decrease and increase of approximately 0.66% and 2.04% in efficiency, respectively. For the case of Dichrostachys cinerea, a 1% increase in the proportion of this biomass in the mixture is associated with a decrease of approximately 1.37% in efficiency.
The interepretation for the case of VU-40 technology also depends on each coefficient of the proposed model. Mixtures with higher proportions of AHRs tend to improve G.V. Retal and G.V. VU-40 efficiencies, while higher proportions of Bagasse and Dichrostachys cinerea tend to decrease efficiencies.
The coefficient of determination
for G.V. Retal is 0.54, meaning that approximately 54.89% of the variability in the efficiency of this technology can be explained by the model, indicating a moderate predictive ability based on the proportions of Bagasse, AHRs, and Dichrostachys cinerea. For the G.V. VU-40, the
is 0.41, which implies that the model explains 41.92% of the variability, suggesting a moderate to low predictive ability. As for the MAPE, for the G.V. Retal it is 1.06%, reflecting a relatively low prediction error, while for the G.V. VU-40 it is 1.27%, a slightly higher value, but still acceptable. These results suggest that the model is fairly accurate in both cases, with low prediction error and moderate predictive ability, especially in G.V. Retal. These results show that the models have good accuracy, although the
indicates that there are other factors or variability that are not being accounted for by the independent variables (Bagasse, AHRs, and Dichrostachys cinerea).
The calculation of the number of experts to participate in the decision process was determined using Equation (3), assuming an error proportion p = 0.01, a precision of the experiment i = 0.05, and a statistical significance level (1 −
) = 95%. This showed that approximately 15 experts were needed to carry out the group decision process. For this purpose, a total of 20 candidates with experience in the sugar industry were proposed. Of the 20 proposed candidates, the 15 best ones were selected according to the determination of the concordance level W Equation (4) equal to 0.79.
The experts selected a total of 12 sub-criteria, grouped into energy, exergy, and emergetic methods. These corresponded to the different aspects of sustainability (economic, environmental, and social) (Table 4).

Table 4.
Sub-criteria to be used in the evaluation [8].
Once the sub-criteria for the research had been selected, the surveys were carried out, submitting them to the judgment of the experts. Once the information was collected, the Delphi evaluation method was applied to screen the sub-criteria, using the Expert Consultation Method.v1.0 software.
Table 5 shows the level of importance given by each expert to the sub-criteria analyzed to achieve the objective proposed in the research.

Table 5.
Expert evaluation of the level of importance of the sub-criteria.
From the results obtained in the screening process, the sub-criteria that reached an evaluation (level of importance) of Important or Very Important were PE, En1, En2, Ex1, Ex2, Em1, Em2, Em3, Em4, S1, E1 and E2.
However, there exists a relationship between sub-criteria Em2 and Em3, because the environmental load ratio is a parameter to be taken into account when determining the sustainability index, and has an inversely proportional influence on its magnitude. Subcriterion Em2 is considered in the literature as a more comprehensive indicator compared to Em3 since it provides more economic-environmental information on the systems evaluated.
According to the AHP method, the modified alternatives, sub-criteria, and criteria were grouped at different levels, which is shown in Figure 4.
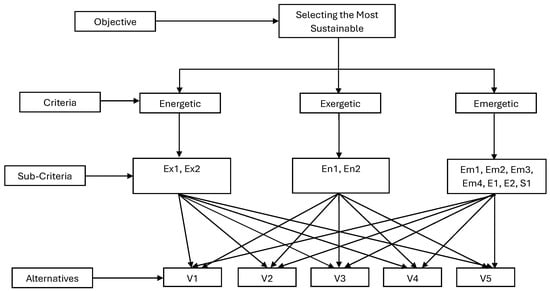
Figure 4.
Hierarchical structure for the selection of alternatives.
The fundamental factors head the hierarchical structure of the problem. These, considered as a group, in turn include the sub-factors with the corresponding alternatives, as shown in Figure 1.
The hierarchical structure is distributed as follows: a first primary group that includes the three methods proposed by [42], En, Ex, and Em, as well as a secondary group that includes the fundamental sub-criteria of En1, En2, Ex1, Ex2, Em1, Em2, Em3, Em4, E1, E2, and S1.
The five fuel variants or mixtures were discussed by [8] and evaluated in two case studies or technologies. The first one was a Retal type steam generator (G.V.) and the second one a G.V. model VU-40. The evaluation of the effect of each of the alternatives on the criteria and sub-criteria formed a fundamental output, generating feedback. As a starting point, the AHP method was also applied in the study of sustainability assessment [52], considering only sugarcane bagasse and agricultural crop residues applied to a case study of sugarcane technology.
The matrix presented in Table 6 was organized based on the identified factors related to energy, exergy, and emergy balances [52]. Each element of the matrix was assigned a numerical rating using Saaty’s nine-point scale. Using Saaty’s nine-point scale, a numerical rating was assigned to each element of the matrix. This matrix reflects the values corresponding to the relevant criteria, since when a criterion is compared to itself, all elements of the main diagonal take a value of 1.

Table 6.
Pairwise comparison matrix of the criteria related to the target [52].
The reciprocal values of the entries above the main diagonal of the matrix were taken as the input elements below it, while when compared to other values of the matrix, values other than 1 were assigned according to the Saaty scale.
The preferences located above the main diagonal of the matrix were taken into account. Table 7 shows how the criteria with the highest weighting were those belonging to the emergy method, followed by the exergetic and energetic methods. From the normalization of the vectors of each column and the determination of the mean value of each row of the resulting matrix, the local priority vectors (PVE) were normalized. The calculated PVEs were 0.164, 0.297, and 0.539, respectively.

Table 7.
Local priority vector computation [52].
To verify the consistency of the judgments provided by the experts, for this purpose the eigenvalue principle (max) was calculated according to [52]. Consequently, using Equation (8), the consistency index (CI) was calculated as:
Finally, the CR was calculated using Equation (8):
Considering a matrix size n = 3, the random coefficient RI is obtained from [52,70] at 0.58. The value CR = 0.00794 lower than 0.05 indicates that the ratings are considered consistent. The PVE vector calculated for the case of the sub-criteria is shown in (Table 8).

Table 8.
Expert evaluation of the level of importance of the sub-criteria.
In the final stage, an assessment of individual criteria and sub-criteria is conducted to establish preferences among the alternatives. This process involves simplifying all matrices.
Streamlining entails multiplying the local priority vector of the alternatives by the local priority vector of each criterion and then aggregating them to determine the overall weight of each alternative. This process involves multiplying the assessment of each alternative by the weights of the sub-criteria and then summing these values to obtain the local priority vector for the alternatives with respect to that criterion. This vector is then multiplied by the local priority vector of each criterion and summed to calculate the overall weight of each alternative. The overall results for the variants studied are presented in Table 9.

Table 9.
Final outcomes presented as overall priorities [8].
From the development of the AHP method and using the experts’ weightings, the experts took into consideration that the emergy sub-criteria have the greatest weight in sustainability with the local priority vector PVE of 0.539, followed by the exergy and energy criteria, respectively (PVE = 0.297, PVE = 0.164).
The weight distribution for the evaluation was taken according to the experts as follows: energy efficiency by the direct method En1, with 66% importance within the energy criterion, the exergy sustainability index Ex2, with 75% importance within the exergy criterion, and as the emergy sustainability index, with 41% importance.
However, it was demonstrated that complementary fuels such as agriculture harvest residues (AHR) and Dichrostachys cinerea presented even better performances in terms of energy-exergy efficiency than bagasse, as well as mixtures of these fuels.
According to the general priorities calculated by applying the AHP method, for both case studies the most sustainable alternative corresponded to variant V1, which the experts took as the most influential indicator for those related to energy as explained above due to the weight they hold within the sustainability of the systems and processes. Nevertheless, such results represent that using bagasse as a base fuel in the generation mixed with other additional fuels incorporates an opportunity for the expansion of the current sugar industry.
In decision-making problems, the assessments provided by decision-makers can sometimes be imprecise due to the difficulty in accurately assigning values to the criteria. Therefore, it is common practice to conclude with a sensitivity analysis of the options [76,77,78].
Sensitivity analysis is crucial for observing how the overall rankings of biomass utilization options change with variations in the priorities of the criteria or sub-criteria. This analysis is extensively employed in studies incorporating subjective evaluations to validate the robustness of the results [79,80,81].
Considering a scenario of equal weight for both study cases (33.3% for each criterion or method), the results show that for both technologies the V1 variant had the highest score (38.17%) among all the alternatives. Variant V4 had the second highest score (31.79%), while alternative V2 reached only 29.04%, as shown in Figure 5.
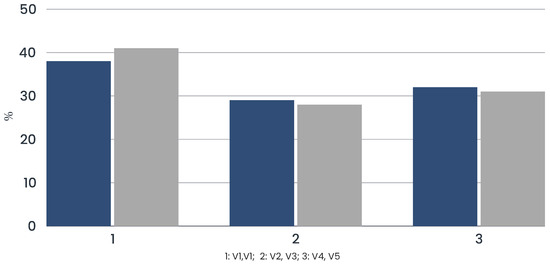
Figure 5.
Sensitivity analysis for the studied variants considering both study cases.
The results obtained from the case studies evaluated can complement the decisions made in new investment processes that are being made in the sugar industry and others that involve the use of biomass, as well as in the pre, during, and post evaluations, allowing the comparison of different biomass types and technologies. In addition, they can be used as indicators of sustainable development in the exploitation processes of these biomass and other FRE.
Table 10 presents a comparison of the different applications of MCDMs for biomass in particular, highlighting the key contributions and techniques applied.

Table 10.
MCDM application studies in the biomass field, methods, and fuels considered.
The studies shown above include the application of the MCDM; however, there have still been insufficient studies applied to the sugar industry, which do not include mixtures of these fuels. Most authors have applied the analytical hierarchy process (AHP) as a multi-criteria method combined mainly with the TOPSIS method to evaluate sustainability in some cases, but no combined applications including the Delphi method have been found. On the other hand, no studies have been reported that integrate the simultaneous application of the energetic, exergetic, and emergetic methods to evaluate the sustainability of biomass and mixtures of these as fuel in the generation of energy for the sugar industry from the Delphi–AHP combination.
4. Conclusions
For the case studies evaluated, the selected experts considered two energy indicators, two exergy indicators, and seven energy indicators as significant, which corresponded to three economic indicators, five environmental indicators, and three social indicators.
In effect, the V1 variant emanated from multi-criteria analysis assessing that it was the most sustainable variant, with 45% and 53% grades in general priority assessment, exposing superiority in the integration of economic, environmental, and social criteria.
The sustainability assessment conducted in the study showed that the emergy sub-criteria had the highest impact with a local priority vector of 0.539, followed by exergy and energy with values of 0.297 and 0.164, respectively. This research considered the importance of emergy in assessing the sustainability of biomass in different agricultural industries.
The analysis examined a situation where all criteria were given equal value, yet the V1 variant managed to stand out from other options with a score of 38.17%. This consistency in the face of equal weighting highlights the full sustainability of V1 across different evaluation metrics.
This article presents several contributions, such as:
- •
- Considering the combined application of the Delphi–AHP method in the assessment of biomass sustainability for the sugar industry.
- •
- Incorporating biomass blends and evaluating them from economic, environmental, and social perspectives.
- •
- Evaluating sustainability for five variants applied in two types of energy conversion technology.
Author Contributions
Conceptualization, R.J.B. and A.L.A.-G.; methodology, R.J.B., L.A.I.C. and Y.C.A.; software, R.J.B. and A.L.A.-G.; validation, J.M.Á.-A. and J.R.-R.; formal analysis, L.A.I.C., E.B.A., Y.C.A. and B.R.P.; investigation, R.J.B. and A.L.A.-G.; data curation, L.A.I.C., J.M.Á.-A. and J.R.-R.; writing—original draft preparation, R.J.B. and A.L.A.-G.; writing—review and editing, J.M.Á.-A. and J.R.-R.; visualization, E.B.A., Y.C.A. and B.R.P.; supervision, E.B.A. and B.R.P. All authors have read and agreed to the published version of the manuscript.
Funding
The authors reported there is no funding associated with the work featured in this article.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available upon reasonable request.
Conflicts of Interest
No potential conflicts of interest were reported by the authors.
Abbreviations
The following abbreviations are used in this manuscript:
| Principal eigenvalue | |
| AHP | Analytic Hierarchical Process |
| ANP | Analytic Network Process |
| C | Overall rating |
| CI | Consistency index |
| CODAS | Combinative Distance Assessment |
| CP | Cut-off Points |
| CR | Consistency Ratio |
| ELECTRE | ELimination Et Choix Traduisant la Realité |
| FAHP | Fuzzy Analytic Hierarchy Process |
| G.V. | Steam generator |
| i | Precision of the experiment |
| K | Competence level |
| Ka | Argumentation coefficient |
| Kc | Level of knowledge on the subject under |
| LCA | Life Cycle Analysis |
| m | Number of experts |
| MAPE | Mean Absolute Percentage Error |
| MCDA | Multi-criteria decision analysis |
| MCDM | Multi-criteria decision-making |
| n | Dimensional matrix |
| P | Proportion of the error made in making |
| PROMETHEE | Preference Ranking Organization Methods for Enrichment Evaluations |
| PVE | Local priority vector |
| Correlation level | |
| AHR or AHRs | Agricultural Harvest Residues |
| RES | Renewable Energy Sources |
| RI | Random index |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| V1 | Bagasse 100% |
| V2 | AHRs 100% |
| V3 | Dichrostachys cinerea 100% |
| V4 | Bagasse 50%-AHRs 50% |
| V5 | Bagasse 90%-Dichrostachys cinerea 10% |
| Vc | Self-evaluations of experts |
| W | Kendall’s Coefficient of Concordance |
| WA-FMCGP | Weighted additive fuzzy multiple choice goal programming |
References
- Guevara-Luna, M.A.; Madrazo, J.; Meneses, E.; Mora, H.; Clappier, A. Strategies toward an effective and sustainable energy transition for Cuba. Renew. Sustain. Energy Rev. 2024, 197, 114387. [Google Scholar] [CrossRef]
- Sen, A. Sustainable development and our responsibilities. Notizie Polit. 2010, 26, 129–137. [Google Scholar]
- de Jesus, K.R.E.; Torquato, S.A.; Machado, P.G.; Zorzo, C.R.B.; Cardoso, B.O.; Leal, M.R.L.V.; Picoli, M.C.A.; Ramos, R.C.; Dalmago, G.A.; Capitani, D.H.D.; et al. Sustainability assessment of sugarcane production systems: SustenAgro Decision Support System. Environ. Dev. 2019, 32, 100444. [Google Scholar] [CrossRef]
- Balcioglu, G.; Jeswani, H.K.; Azapagic, A. A sustainability assessment of utilising energy crops for heat and electricity generation in Turkey. Sustain. Prod. Consum. 2023, 41, 134–155. [Google Scholar] [CrossRef]
- Kumari, S.; Chintamani, B.G.; Gurpur, S. Antecedents for Circular Economy in Sugar Industrial Ecology in Emerging Economy. Int. J. Sustain. Dev. Plan. 2024, 19. [Google Scholar] [CrossRef]
- Aguilar-Rivera, N. Bioindicators for the sustainability of sugar agro-industry. Sugar Tech 2022, 24, 651–661. [Google Scholar] [CrossRef]
- López Bastida, E.J.; García Martínez, Y.; Valdés López, A. Evaluación de la sostenibilidad de la producción de azúcar crudo mediante el análisis emergético. Cent. Azúcar 2018, 45, 59–67. [Google Scholar]
- Borges, R.J.; Iturralde Carrera, L.A.; Bastida, E.J.L.; García-Martínez, J.R.; Carrillo-Serrano, R.V.; Rodríguez-Reséndiz, J. Energy Sustainability Indicators for the Use of Biomass as Fuel for the Sugar Industry. Technologies 2024, 12, 36. [Google Scholar] [CrossRef]
- Machín-Armas, F.O.; Fernández-Santiesteban, E. Sostenibilidad de la agroindustria azucarera cubana Y bioenergía. Cienc. PC 2015, 85–101. [Google Scholar]
- Joglekar, S.N.; Dalwankar, G.; Qureshi, N.; Mandavgane, S.A. Sugarcane valorization: Selection of process routes based on sustainability index. Environ. Sci. Pollut. Res. 2022, 29, 10812–10825. [Google Scholar] [CrossRef]
- Meghana, M.; Shastri, Y. Sustainable valorization of sugar industry waste: Status, opportunities, and challenges. Bioresour. Technol. 2020, 303, 122929. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Deng, Y.; Wang, X.; Zhang, W.; Shi, X.; Chen, X.; Lakshmanan, P.; Zhang, F. Global direct nitrous oxide emissions from the bioenergy crop sugarcane (Saccharum spp. inter-specific hybrids). Sci. Total Environ. 2021, 752, 141795. [Google Scholar] [CrossRef] [PubMed]
- Cardozo, N.P.; de Oliveira Bordonal, R.; La Scala, N., Jr. Greenhouse gas emission estimate in sugarcane irrigation in Brazil: Is it possible to reduce it, and still increase crop yield? J. Clean. Prod. 2016, 112, 3988–3997. [Google Scholar] [CrossRef]
- Ilari, A.; Duca, D.; Boakye-Yiadom, K.A.; Gasperini, T.; Toscano, G. Carbon footprint and feedstock quality of a real biomass power plant fed with forestry and agricultural residues. Resources 2022, 11, 7. [Google Scholar] [CrossRef]
- Nejad, M.S.; Almassi, M.; Ghahderijani, M. Life cycle energy and environmental impacts in sugarcane production: A case study of Amirkabir Sugarcane Agro-Industrial Company in Khuzestan province. Results Eng. 2023, 20, 101545. [Google Scholar] [CrossRef]
- Mourmouris, J.C.; Potolias, C. A multi-criteria methodology for energy planning and developing renewable energy sources at a regional level: A case study Thassos, Greece. Energy Policy 2013, 52, 522–530. [Google Scholar] [CrossRef]
- Bakhtavar, E.; Prabatha, T.; Karunathilake, H.; Sadiq, R.; Hewage, K. Assessment of renewable energy-based strategies for net-zero energy communities: A planning model using multi-objective goal programming. J. Clean. Prod. 2020, 272, 122886. [Google Scholar] [CrossRef]
- Hartmann, B.; Börcsök, E.; Groma, V.O.; Osán, J.; Talamon, A.; Török, S.; Alföldy-Boruss, M. Multi-criteria revision of the Hungarian Renewable Energy Utilization Action Plan–Review of the aspect of economy. Renew. Sustain. Energy Rev. 2017, 80, 1187–1200. [Google Scholar] [CrossRef]
- Michailos, S.; Parker, D.; Webb, C. A multicriteria comparison of utilizing sugar cane bagasse for methanol to gasoline and butanol production. Biomass Bioenergy 2016, 95, 436–448. [Google Scholar] [CrossRef]
- Ahmed, A.; Sutrisno, S.W.; You, S. A two-stage multi-criteria analysis method for planning renewable energy use and carbon saving. Energy 2020, 199, 117475. [Google Scholar] [CrossRef]
- Karunathilake, H.; Hewage, K.; Prabatha, T.; Ruparathna, R.; Sadiq, R. Project deployment strategies for community renewable energy: A dynamic multi-period planning approach. Renew. Energy 2020, 152, 237–258. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Safder, U.; Nguyen, X.N.; Yoo, C. Multi-objective decision-making and optimal sizing of a hybrid renewable energy system to meet the dynamic energy demands of a wastewater treatment plant. Energy 2020, 191, 116570. [Google Scholar] [CrossRef]
- Koponen, K.; Le Net, E. Towards robust renewable energy investment decisions at the territorial level. Appl. Energy 2021, 287, 116552. [Google Scholar] [CrossRef]
- Mrówczyńska, M.; Skiba, M.; Sztubecka, M.; Bazan-Krzywoszańska, A.; Kazak, J.; Gajownik, P. Scenarios as a tool supporting decisions in urban energy policy: The analysis using fuzzy logic, multi-criteria analysis and GIS tools. Renew. Sustain. Energy Rev. 2021, 137, 110598. [Google Scholar] [CrossRef]
- Ezbakhe, F.; Pérez-Foguet, A. Decision analysis for sustainable development: The case of renewable energy planning under uncertainty. Eur. J. Oper. Res. 2021, 291, 601–613. [Google Scholar] [CrossRef]
- Çelikbilek, Y.; Tüysüz, F. An integrated grey based multi-criteria decision making approach for the evaluation of renewable energy sources. Energy 2016, 115, 1246–1258. [Google Scholar] [CrossRef]
- Witt, T.; Dumeier, M.; Geldermann, J. Combining scenario planning, energy system analysis, and multi-criteria analysis to develop and evaluate energy scenarios. J. Clean. Prod. 2020, 242, 118414. [Google Scholar] [CrossRef]
- San Cristóbal, J.R. Multi-criteria decision-making in the selection of a renewable energy project in spain: The Vikor method. Renew. Energy 2011, 36, 498–502. [Google Scholar] [CrossRef]
- Kwak, Y.; Deal, B.; Heavisides, T. A large scale multi criteria suitability analysis for identifying solar development potential: A decision support approach for the state of Illinois, USA. Renew. Energy 2021, 177, 554–567. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R.C. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Shorabeh, S.N.; Argany, M.; Rabiei, J.; Firozjaei, H.K.; Nematollahi, O. Potential assessment of multi-renewable energy farms establishment using spatial multi-criteria decision analysis: A case study and mapping in Iran. J. Clean. Prod. 2021, 295, 126318. [Google Scholar] [CrossRef]
- Balezentis, T.; Siksnelyte-Butkiene, I.; Streimikiene, D. Stakeholder involvement for sustainable energy development based on uncertain group decision making: Prioritizing the renewable energy heating technologies and the BWM-WASPAS-IN approach. Sustain. Cities Soc. 2021, 73, 103114. [Google Scholar] [CrossRef]
- Soltaniyan, S.; Salehizadeh, M.R.; Taşcıkaraoğlu, A.; Erdinç, O.; Catalão, J.P. An interactive multi-criteria decision-making framework between a renewable power plant planner and the independent system operator. Sustain. Energy Grids Netw. 2021, 26, 100447. [Google Scholar] [CrossRef]
- Mastrocinque, E.; Ramírez, F.J.; Honrubia-Escribano, A.; Pham, D.T. An AHP-based multi-criteria model for sustainable supply chain development in the renewable energy sector. Expert Syst. Appl. 2020, 150, 113321. [Google Scholar] [CrossRef]
- Pohekar, S.D.; Ramachandran, M. Application of multi-criteria decision making to sustainable energy planning—A review. Renew. Sustain. Energy Rev. 2004, 8, 365–381. [Google Scholar] [CrossRef]
- Ilbahar, E.; Cebi, S.; Kahraman, C. A state-of-the-art review on multi-attribute renewable energy decision making. Energy Strategy Rev. 2019, 25, 18–33. [Google Scholar] [CrossRef]
- Hakimi, S.M.; Hasankhani, A.; Shafie-khah, M.; Catalão, J.P. Stochastic planning of a multi-microgrid considering integration of renewable energy resources and real-time electricity market. Appl. Energy 2021, 298, 117215. [Google Scholar] [CrossRef]
- Deveci, K.; Cin, R.; Kağızman, A. A modified interval valued intuitionistic fuzzy CODAS method and its application to multi-criteria selection among renewable energy alternatives in Turkey. Appl. Soft Comput. 2020, 96, 106660. [Google Scholar] [CrossRef]
- Hocine, A.; Zhuang, Z.Y.; Kouaissah, N.; Li, D.C. Weighted-additive fuzzy multi-choice goal programming (WA-FMCGP) for supporting renewable energy site selection decisions. Eur. J. Oper. Res. 2020, 285, 642–654. [Google Scholar] [CrossRef]
- Ifaei, P.; Farid, A.; Yoo, C. An optimal renewable energy management strategy with and without hydropower using a factor weighted multi-criteria decision making analysis and nation-wide big data-Case study in Iran. Energy 2018, 158, 357–372. [Google Scholar] [CrossRef]
- Jamal, T.; Urmee, T.; Shafiullah, G. Planning of off-grid power supply systems in remote areas using multi-criteria decision analysis. Energy 2020, 201, 117580. [Google Scholar] [CrossRef]
- Jeong, J.S.; Ramírez-Gómez, Á. Optimizing the location of a biomass plant with a fuzzy-DEcision-MAking Trial and Evaluation Laboratory (F-DEMATEL) and multi-criteria spatial decision assessment for renewable energy management and long-term sustainability. J. Clean. Prod. 2018, 182, 509–520. [Google Scholar] [CrossRef]
- Saraswat, S.; Digalwar, A.K. Evaluation of energy alternatives for sustainable development of energy sector in India: An integrated Shannon’s entropy fuzzy multi-criteria decision approach. Renew. Energy 2021, 171, 58–74. [Google Scholar] [CrossRef]
- Campos-Guzmán, V.; García-Cáscales, M.S.; Espinosa, N.; Urbina, A. Life Cycle Analysis with Multi-Criteria Decision Making: A review of approaches for the sustainability evaluation of renewable energy technologies. Renew. Sustain. Energy Rev. 2019, 104, 343–366. [Google Scholar] [CrossRef]
- Seddiki, M.; Bennadji, A. Multi-criteria evaluation of renewable energy alternatives for electricity generation in a residential building. Renew. Sustain. Energy Rev. 2019, 110, 101–117. [Google Scholar] [CrossRef]
- Bortoluzzi, M.; de Souza, C.C.; Furlan, M. Bibliometric analysis of renewable energy types using key performance indicators and multicriteria decision models. Renew. Sustain. Energy Rev. 2021, 143, 110958. [Google Scholar] [CrossRef]
- Terzi, R. Application of Exergy Analysis to Energy Systems; IntechOpen: London, UK, 2018; Volume 109. [Google Scholar]
- Golato, M.A.; Franck Colombres, F.J.; Aso, G.; Correa, C.A.; Paz, D. Metodología de cálculo de la eficiencia térmica de generadores de vapor. Rev. Ind. Agríc. Tucumán 2008, 85, 17–31. [Google Scholar]
- Cavalcanti, E.J.; Carvalho, M.; da Silva, D.R. Energy, exergy and exergoenvironmental analyses of a sugarcane bagasse power cogeneration system. Energy Conv. Manag. 2020, 222, 113232. [Google Scholar] [CrossRef]
- Barrosoa, J.; Barrerasb, F.; Amavedac, H.; Lozanob, A. On the optimization of boiler efficiency using bagasse as fuel. Fuel 2003, 82, 1451–1463. [Google Scholar] [CrossRef]
- Rodríguez Arias, A.D.; Carrasco García, S.Y.; López Bastida, E.J.; Jiménez Borges, R. Metodología para la evaluación del proceso de co/combustión de biomasas a partir de diferentes tecnologías en una caldera retal. Rev. Univ. Soc. 2019, 11, 295–302. [Google Scholar]
- Jiménez Borges, R.; López Bastida, E.J.; Bravo Amarante, E.; Álvarez González, A.L.; Hernández Nodarse, M.T. Evaluación de la sostenibilidad para la biomasa cañera a partir del método AHP. Rev. Univ. Soc. 2020, 12, 73–79. [Google Scholar]
- Álvarez, S.; Lomas, P.L.; Martín, B.; Rodríguez, M.; Montes, C. La Síntesis Emergética (“Emergy Synthesis”): Integrando Energía, Ecología y Economía; Publicaciones de la Fundación Interuniversitaria Fernando González Bernáldez para los Espacios Naturales: Madrid, Spain, 2006; Volume 2. [Google Scholar]
- Borges, R.J.; Alvarez, Y.C.; Bastida, E.J.L.; Amarante, E.B. Application of the AHP and TOPSIS Method in the Combustion Process of a Steam Generator. In Proceedings of the 2023 IEEE Seventh Ecuador Technical Chapters Meeting (ECTM), Ambato, Ecuador, 10–13 October 2023; IEEE: New York, NY, USA, 2023; pp. 1–7. [Google Scholar]
- Rubio-González, A. Generadores de Vapor. Funcionamiento y Explotación; Versión Electrónica. 2015. Available online: https://www.researchgate.net/profile/Angel-Rubio-Gonzalez/publication/333903174_Generadores_de_vapor_Funcionamiento_y_Explotacion_Angel_Rubio-Gonzalez/links/5d0b95d0a6fdcc117822254d/Generadores-de-vapor-Funcionamiento-y-Explotacion-Angel-Rubio-Gonzalez.pdf (accessed on 4 April 2024).
- Rubio González, A.; Clara, V. Estudio de la pérdida de calor por incombustión mecánica volátil en calderas RETAL, mediante simulación aerodinámica. Int. Sugar J. 2019, 100, 32–34. [Google Scholar]
- Dincer, I. Thermodynamics, exergy and environmental impact. Energy Sources 2000, 22, 723–732. [Google Scholar] [CrossRef]
- Inoussah, M.M.; Adolphe, M.I.; Daniel, L. Assessment of sustainability indicators of thermoelectric power generation in cameroon using exergetic analysis tools. Energy Power Eng. 2017, 9, 22–39. [Google Scholar] [CrossRef]
- Tolga Balta, M.; Hepbasli, A.; Dincer, I. Thermodynamic performance comparison of some renewable and non-renewable hydrogen production processes. In Proceedings of the WHEC 2010, Essen, Germany, 16–21 May 2010. [Google Scholar]
- Song, G.; Shen, L.; Xiao, J. Estimating specific chemical exergy of biomass from basic analysis data. Ind. Eng. Chem. Res. 2011, 50, 9758–9766. [Google Scholar] [CrossRef]
- Herrera Masó, J.R.; Calero Ricardo, J.L.; González Rangel, M.Á.; Collazo Ramos, M.I.; Travieso González, Y. El método de consulta a expertos en tres niveles de validación. Rev. Habanera Cienc. Méd. 2022, 21. [Google Scholar]
- Hernández, R.A.M.; Fernández, A.S. Diseño del grupo de expertos para contribuir a la gestión de la planificación del mantenimiento. Univ. Soc. 2022, 14, 97–109. [Google Scholar]
- Sossa, J.W.Z.; Hincapié, J.M.M.; Jaramillo, I.D.T.; VILLADA, H.S. Método Delphi-Propuesta para el cálculo del número de expertos en un estudio Delphi sobre empaques biodegradables al 2032. Revista ESPACIOS 2014, 35, 10. [Google Scholar]
- Rodríguez Perón, J.M.; Aldana Vilas, L.; Villalobos Hevia, N. Método Delphi para la identificación de prioridades de ciencia e innovación tecnológica. Rev. Cubana Med. Mil. 2010, 39, 214–226. [Google Scholar]
- Daniel, J.; Vishal, N.V.; Albert, B.; Selvarsan, I. Evaluation of the significant renewable energy resources in India using Analytical Hierarchy Process. In Proceedings of the Multiple Criteria Decision Making for Sustainable Energy and Transportation Systems: Proceedings of the 19th International Conference on Multiple Criteria Decision Making, Auckland, New Zealand, 7–12 January 2008; Springer: Berlin/Heidelberg, Germany, 2010; pp. 13–26. [Google Scholar]
- Qazi, W.A.; Abushammala, M.F.; Azam, M.H. Multi-criteria decision analysis of waste-to-energy technologies for municipal solid waste management in Sultanate of Oman. Waste Manag. Res. 2018, 36, 594–605. [Google Scholar] [CrossRef]
- Saaty, T.L. Fundamentals of the analytic hierarchy process. In The Analytic Hierarchy Process in Natural Resource and Environmental Decision Making; Kluwer Academic Publishers: New York, NY, USA, 2001; pp. 15–35. [Google Scholar]
- Saaty, T.L.; Vargas, L.G.; Saaty, T.L.; Vargas, L.G. The seven pillars of the analytic hierarchy process. In Models, Methods, Concepts & Applications of the Analytic Hierarchy Process; Springer: Boston, MA, USA, 2012; pp. 23–40. [Google Scholar]
- Aghajani Bazzazi, A.; Osanloo, M.; Karimi, B. A new fuzzy multi criteria decision making model for open pit mines equipment selection. Asia-Pac. J. Oper. Res. 2011, 28, 279–300. [Google Scholar] [CrossRef]
- Sindhu, S.P.; Nehra, V.; Luthra, S. Recognition and prioritization of challenges in growth of solar energy using analytical hierarchy process: Indian outlook. Energy 2016, 100, 332–348. [Google Scholar]
- Rodríguez, A.; Rosabal, L.; Martínez, P. Teoría y Práctica de los Procesos de Combustión. In Combus. Sólidos; Editorial Academia: La Habana, Cuba, 2000. [Google Scholar]
- Golato, M.A.; Feijóo, E.A.; Franck Colombres, F.J.; Paz, D.; Cárdenas, G.J. Estudio preliminar del aprovechamiento de los residuos agrícolas de cosecha de la caña de azúcar como combustible adicional para calderas bagaceras de Tucumán (Argentina). Rev. Ind. Agríc. Tucumán 2017, 94, 21–31. [Google Scholar]
- Khattak, S.; Greenough, R.; Sardeshpande, V.; Brown, N. Exergy analysis of a four pan jaggery making process. Energy Rep. 2018, 4, 470–477. [Google Scholar] [CrossRef]
- Ameri, M.; Ahmadi, P.; Khanmohammadi, S. Exergy analysis of a 420 MW combined cycle power plant. Int. J. Energy Res. 2008, 32, 175–183. [Google Scholar] [CrossRef]
- Singh, O.K. Exergy analysis of a grid-connected bagasse-based cogeneration plant of sugar factory and exhaust heat utilization for running a cold storage. Renew. Energy 2019, 143, 149–163. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Z. A combined interval TOPSIS with multiple sensitivity strategies decision-making framework. J. Clean. Prod. 2023, 422, 138611. [Google Scholar] [CrossRef]
- Więckowski, J.; Wątróbski, J.; Kizielewicz, B.; Sałabun, W. Complex sensitivity analysis in Multi-Criteria Decision Analysis: An application to the selection of an electric car. J. Clean. Prod. 2023, 390, 136051. [Google Scholar] [CrossRef]
- Yang, M.; Liu, F.; Lin, L.; Zeng, G.; Lang, Y. Comprehensive performance evaluation and sensitivity analysis method of a cutter-changing robot for a large-diameter shield machine. Expert Syst. Appl. 2024, 238, 122282. [Google Scholar] [CrossRef]
- Al Garni, H.; Kassem, A.; Awasthi, A.; Komljenovic, D.; Al-Haddad, K. A multicriteria decision making approach for evaluating renewable power generation sources in Saudi Arabia. Sustain. Energy Technol. Assess. 2016, 16, 137–150. [Google Scholar] [CrossRef]
- Pan, C.; Farouk, N.; Wei, H.; Shawabkeh, A.; Elboughdiri, N.; Bouzgarrou, S.M.; Alturise, F.; Alkhalaf, S.; Islam, S. A multi-criteria decision study with sensitivity analysis on a tri-generation system based on gas turbine fueled by wheat straw biomass. Therm. Sci. Eng. Prog. 2024, 47, 102271. [Google Scholar] [CrossRef]
- Sultana, M.N.; Dhar, N.R. Comparative evaluation and sensitivity analysis of multi-modelling and optimization of milling Ti–6Al–4V alloy with high-pressure coolant jets. Heliyon 2023, 9. [Google Scholar] [CrossRef] [PubMed]
- Sahabuddin, M.; Khan, I. Multi-criteria decision analysis methods for energy sector’s sustainability assessment: Robustness analysis through criteria weight change. Sustain. Energy Technol. Assess. 2021, 47, 101380. [Google Scholar] [CrossRef]
- Firouzi, S.; Allahyari, M.S.; Isazadeh, M.; Nikkhah, A.; Van Haute, S. Hybrid multi-criteria decision-making approach to select appropriate biomass resources for biofuel production. Sci. Total Environ. 2021, 770, 144449. [Google Scholar] [CrossRef]
- Xu, Y.P.; Lin, Z.H.; Ma, T.X.; She, C.; Xing, S.M.; Qi, L.Y.; Farkoush, S.G.; Pan, J. Optimization of a biomass-driven Rankine cycle integrated with multi-effect desalination, and solid oxide electrolyzer for power, hydrogen, and freshwater production. Desalination 2022, 525, 115486. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, H.; Huang, Z.; Sun, Q. Location mapping for constructing biomass power plant using multi-criteria decision-making method. Sustaina. Energy Technol. Assess. 2022, 49, 101707. [Google Scholar] [CrossRef]
- Mojaver, M.; Hasanzadeh, R.; Azdast, T.; Park, C.B. Comparative study on air gasification of plastic waste and conventional biomass based on coupling of AHP/TOPSIS multi-criteria decision analysis. Chemosphere 2022, 286, 131867. [Google Scholar] [CrossRef]
- Vaid, S.K.; Vaid, G.; Kaur, S.; Kumar, R.; Sidhu, M.S. Application of multi-criteria decision-making theory with VIKOR-WASPAS-Entropy methods: A case study of silent Genset. Mater. Today Proc. 2022, 50, 2416–2423. [Google Scholar] [CrossRef]
- Manirambona, E.; Talai, S.M.; Kimutai, S.K. Sustainability evaluation of power generation technologies using Multi-Criteria Decision Making: The Kenyan case. Energy Rep. 2022, 8, 14901–14914. [Google Scholar] [CrossRef]
- Ji, L.; Zheng, Z.; Huang, Y.; Xie, Y.; Sun, L.; Huang, G. An integrated decision support method for strategic planning and tactical management of regional biomass power plants under uncertainties. J. Clean. Prod. 2023, 388, 135968. [Google Scholar] [CrossRef]
- Ogorure, O.J.; Heberle, F.; Brüggemann, D. Thermo-economic analysis and multi-criteria optimization of an integrated biomass-to-energy power plant. Renew. Energy 2024, 224, 120112. [Google Scholar] [CrossRef]
- Roy, D.; Bhowmik, M.; Roskilly, A.P. Technoeconomic, environmental and multi criteria decision making investigations for optimisation of off-grid hybrid renewable energy system with green hydrogen production. J. Clean. Prod. 2024, 443, 141033. [Google Scholar] [CrossRef]
- Agar, D.A.; Hansen, P.; Rudolfsson, M.; Blagojević, B. Combining behavioural TOPSIS and six multi-criteria weighting methods to rank biomass fuel pellets for energy use in Sweden. Energy Rep. 2023, 10, 706–718. [Google Scholar] [CrossRef]
- Mola-Yudego, B.; Dimitriou, I.; Gagnon, B.; Schweinle, J.; Kulišić, B. Priorities for the sustainability criteria of biomass supply chains for energy. J. Clean. Prod. 2024, 434, 140075. [Google Scholar] [CrossRef]
- Alves, A.S.; Nunes, L.J.; Matias, J.C.; Espadinha-Cruz, P.; Godina, R. An integrated PROMETHEE II-Roadmap model: Application to the recovery of residual agroforestry biomass in Portugal. J. Clean. Prod. 2024, 445, 141307. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).