Abstract
This article addresses the phenomenon of the decreased absorption of γ-radiation when the thickness of the absorber equals a multiple of the mean free path, as observed in relevant laboratory experiments with various absorbing materials. This phenomenon can be compared with the periodic peaks in intensity in an open-ended sound tube that appear at multiples of half wavelength. This could suggest that there is analogy between the two physical systems that are the γ-ray absorber and the sound wave resonance tube. More similarities between the two systems are also presented.
1. Introduction
In experiments regarding the attenuation of γ (gamma) rays in matter, it has been observed that the buildup effect can be seriously underestimated, especially if the gamma ray beam is uncollimated [1]. It is equally interesting that while the detected radiation intensity I past the absorber decreases with the absorber thickness, there is also a sudden rise, a bump, if the thickness equals a multiple of the mean free path (mfp) of the material. In this work, we also try to provide an explanation for the later systematic variation.
In order for such variations from the expected absorption behavior to be detected, one has to progressively increase the thickness only slightly, thus taking a lot of measurements within each mfp. However, in many undergraduate laboratory experiments, the supporting theory is the well-known Beer–Lambert law
, where I0 is the radiation intensity reaching the absorber, μ is the attenuation coefficient and x is the thickness of the absorber. This law does not account for the aforementioned variations; however, these can remain undetected due to the common practice whereby the measurements must be taken at thickness values of the order of the mfp or more [2,3,4,5]. A more precise law does exist, that is
, where B is the buildup factor and Eγ is the energy of each photon [6,7]; however, this law is rarely used. Yet, this law can better support research and development on the radioprotection and safe shielding field, where great thickness of absorbers is demanded of the order of tens or even hundreds of mfps [8,9,10,11,12,13].
Commonly, in measurements of the γ-ray absorption, the distances inside the absorber where a measurement is conducted are widely spaced (typically every one, two or even five mfps). Such measurements only provide the average intensity I per mfp and they cannot provide any further details, which means that possible variations in the intensity I(x) of the passing through γ-radiation in between the measurement points may not be observed.
In our experiment, detailed measurements were conducted regarding the traversing 60Co γ-radiation through various absorbers with a broad range of (effective) atomic number Z values (more specifically Hg, Pb, Cu, Fe, Al, glycerin and water) using uncollimated or collimated beams and taking 10–12 almost equally spaced points per mfp. Our initial aim was also to check the validity of a usual undergraduate laboratory experiment regarding the absorption of γ-radiation and the measurement of the absorption coefficient based on the exponential Beer–Lambert law. All our experiments were conducted with a 60Co source that emits γ-radiation of an average energy of 1.25 MeV. At that energy, the radiation interacts with matter mainly through Compton scattering, with the photoelectric and pair production effects being negligible [14]. The experiments showed that the buildup effect is quite strong and not to be ignored [7,9,15]. Moreover, regular bumps at the end of mfps were observed for all the γ-absorber systems studied, which, to the best of our knowledge, has not been presented before. The periodic appearance of those bumps suggests an analogy between γ-ray attenuation through an absorbing material created by piling up individual absorber pieces and the well-known sound wave resonance tube.
The article is structured as follows: Section 2 presents a brief description of the experimental procedures and some relevant results; Section 3 attempts an explanation of those results (focusing on the local peaks in the intensity of the detected local radiation) and describes the analogies between the γ-ray absorption and the creation of standing waves in a sound wave resonance tube; and Section 4 provides some concluding remarks.
2. Experiments and Results
2.1. Experiments
The experiments were conducted at the Physics Laboratory of the University of West Attica, Athens, Greece. The general experimental parameters are provided below, while more detailed descriptions of the experiments, including photographs, tables of measurements and some details on the Monte Carlo (MC) simulations based on a well-established numerical code [16] can be found in our previously published works (e.g., [1,17]).
- (a)
- The γ-ray source: A 60Co γ-ray source was used with a strength of 5 μCi. 60Co emits two γ-rays of energies 1.173 MeV and 1.325 MeV that, being very close and of the same intensity, allow for 60Co to be treated as a monoenergetic source of 1.25 MeV. Its radioactive constant is λ = 0.1315 year−1. The 60Co γ-ray source, on the other hand, consisted of a cylindrical stick of length 5.0 cm and diameter 5.0 mm with the 60Co radioactive substance being placed on one edge of the stick. Due to the distance between the γ-ray source and the detector being much larger compared to the source’s dimensions, the γ-ray source can be considered as a point-like one [18,19].
- (b)
- The γ-ray detector: A Geiger–Müller detector was used with an active volume of cylindrical geometry with a length of 4.0 cm and diameter of 1.44 cm. The detector was also considered as a point-like one. The detector had a thin plastic mask to stop electrons and only allow γ-rays to pass through, thus solely detecting γ-rays. The relative efficiency of the detector was almost constant (with a variation of about 1%) for all the detected γ-rays.
- (c)
- The γ-ray absorbers: A large number of absorbers was used from high to lower values of effective Z, specifically Hg (ρ = 13.56 g/cm3), Pb (ρ = 11.35 g/cm3), Cu (ρ = 8.96 g/cm3), Fe (ρ = 7.895 g/cm3), Al (ρ = 2.702 g/cm3), glycerin (ρ = 1.261 g/cm3) and water (ρ = 1.0 g/cm3). For 60Co γ-rays, the mass attenuation coefficient μm had a roughly constant value of about 0.05 cm2/g. This is due to the fact that the main interaction mechanism was Compton scattering. Z was approximately inversely proportional to the mfp.
- (d)
- The solid absorbers were piled up in thin pieces, the thickness of which was accurately measured with the use of a micrometer. A broad set of absorbers was considered necessary in order to pin out systematic variations in the way matter attenuates γ-radiation. For the liquid absorbers, that is mercury, glycerin and water, thin-glass and plastic cylindrical tubes with a diameter of 7.5 and 2.5 cm were used. In those cases, a small increase in the absorber’s thickness during the experiments was achieved by either accurate weighing of the absorber material placed in the tubes or optically by marking the tubes.The experimental set-up geometries: Both broad and narrow beam geometries were used, that is uncollimated and collimated beams. In the broad beam, two kinds of absorber sheets were used, one of rectangular shape with a side of 7.0 cm and the other in the form of thin discs with a diameter of 2.5 cm. In the case of liquid absorbers, the tubes described above in (c) were used. In the narrow beam measurements, the ‘buildup minimizing assembly’ (BMA) apparatus was used, developed by our group in order to minimize the buildup effect [16,17]. BMA is a simple device that acts as a beam collimator. In Figure 1a, a schematic diagram of an uncollimated beam experiment is illustrated (including the conceptual trajectories of some photons), while in Figure 1b the beam collimator is depicted. Some small absorber (lead) disks are piled up between the source and the detector.
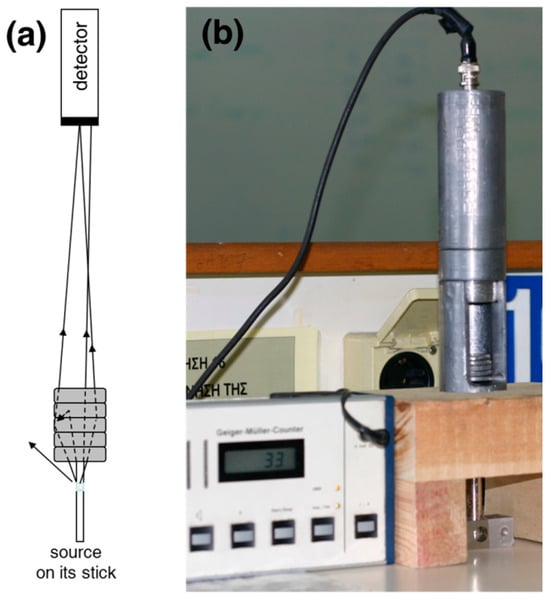 Figure 1. Experimental set-up. (a) Schematic diagram of uncollimated source. It includes absorber disks and the detector. The reason for the build-up effect is also depicted. Note that some photons are scattered away while others that are not initially emitted towards the detector can be scattered towards it. (b) A photograph of a collimated beam experiment. The white counter of the Geiger–Müller can be seen to the left of the picture.
Figure 1. Experimental set-up. (a) Schematic diagram of uncollimated source. It includes absorber disks and the detector. The reason for the build-up effect is also depicted. Note that some photons are scattered away while others that are not initially emitted towards the detector can be scattered towards it. (b) A photograph of a collimated beam experiment. The white counter of the Geiger–Müller can be seen to the left of the picture. - (e)
- The measurements: The duration and repetitions (in some cases, up to 30) of each measurement aimed at adequately reducing statistical errors, while the measurements for a specific absorber could last for several days. The background radiation was measured and subtracted. The thickness of the absorbers covered 2–3 mfps and was increased in very small steps. With the aid of the Geiger–Müller counter, the intensity I of γ-radiation passing through the absorber was indirectly measured versus the absorber’s thickness x presented in mfps.
2.2. Results
Some characteristic results of the experiments are presented in the plots of Figure 2 that depict the intensity I of γ-radiation (in the form of lnI) as a function of the absorber’s thickness x (expressed in mfp units) for Fe, Hg and Cu. The mfp for Fe, Hg and Cu for the specific γ-rays used is around 23.8 mm, 12.7 mm and 21.21 mm respectively; however, the use of mfp units enables the normalization of the absorbers’ thickness x and facilitates comparisons between the plots. Similar results for different absorbers can be found in previous publications [1,17].
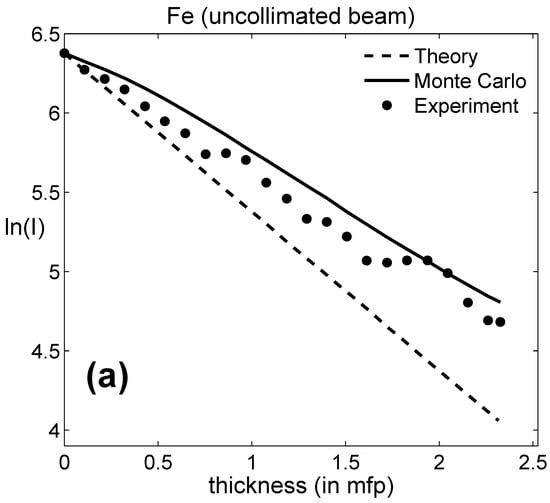
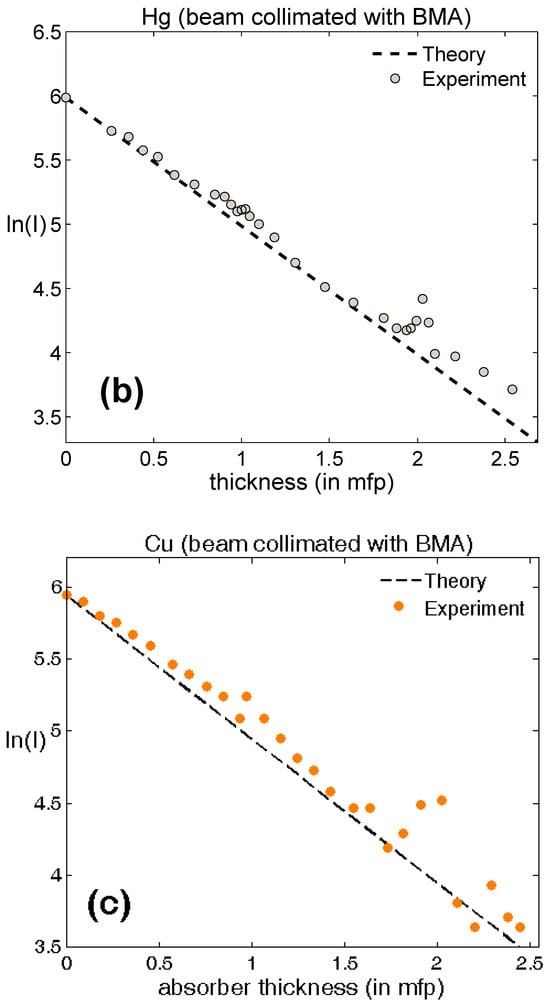
Figure 2.
lnI = f(x) describes the attenuation of 60Co γ-rays in (a) Fe (small discs, broad beam), (b) Hg and (c) Cu (narrow beam, BMA method) absorbers. Points denote experimental measurements; the full line is the Monte Carlo (MC) simulations and broken line is the Lambert–Beer theory. The absorber thickness axis x was divided in units of mfp.
At this point, a difference between the measurements regarding plot 2a and plots 2(b), 2(c) has to be mentioned. While all experiments were conducted with the absorber added in the form of small disks with a diameter of 2.5 cm (in the case of the liquid Hg a cylindrical testing tube was used), for the experiment with Fe the beam was kept uncollimated, while for the experiments with Hg and Cu, a collimator was used. It can be seen that the buildup effect is stronger for the uncollimated beams as compared with the collimated one, as in the former case the experimental points deviate further form the theoretical prediction.
The deviation from the Beer–Lambert law appears more profound for the Fe absorber than that for the Hg and the Cu ones. This has to be attributed to the fact that the experiment with Fe was conducted with an uncollimated beam (where the build-up effect is stronger) unlike the measurements with Hg and Cu that were performed with uncollimated beams (for which the build-up effect is weaker). However, in all three cases, the results are similar in that the maxima appear at, or rather around, those certain values of thickness. Moreover, they are similar to the previous results, such as the ones published in references [1,17] of the current manuscript.
3. Discussion
3.1. Explanation of the Bumps in the Detected γ-ray Intensity at the Mean Free Path Absorber Thickness
As stated above, the γ-photon of 60Co entering into the absorber interacts with its matter mainly through Compton scattering, during which the γ photon does not disappear, but simply scatters, in contradiction to the Lambert–Beer theory, which requires the γ-photon to be lost through the photoelectric absorption.
One explanation we could offer is the following: The 60Co γ-photon traveling through the absorber has the maximum probability of interaction with the building blocks of the absorber at a thickness equal to the mfp. It is actually the value of interaction depth x where its probability function f(x) =
has a maximum, which means that the number of photons colliding to and deflected by the atoms of the material is greater around the mfp than at other thickness values [20]. Additionally, due to Compton scattering that dominates, some of the scattered photons are not absorbed, but redirected. The wider the beam is and the wider the absorber is, the more prominent this phenomenon appears. Since some of the scattered photons can always be redirected towards the detector, even though they were initially heading away, the maximization of scattering events around the specific thickness could be the explanation for the fact that the intensity of the detected γ-radiation shows local peaks at positions that are integer multiples of the mfp that is there is a “resonance” in the detected γ-photons at those positions within the absorber.
An explanation for the inconsistency between the experiment and simulations could be the following: The γ-photons traveling inside the absorber ionize the absorber’s material, creating a cloud of ions, electrons and positive ions that increases the photoelectric absorption and hinders the γ-photons from passing through. This mainly regards the scattered photons (that can contribute to buildup) which are of lower energy [21,22]. More specifically, the attenuation varies as
. Moreover, the plasma of the ions slightly increases the effective charge of the positive ions, again increasing the photoelectric cross section which varies as Z5.
The above process takes place throughout the length of the mfp reducing the buildup effect (which we could call “noise”) that would otherwise cover the bump at the mfp (continuous line in Figure 2a). If the MC simulations do not include the mechanism mentioned above (which increases absorption), then the buildup is calculated to be stronger than the one experimentally found. Moreover, at the end of the mfp, another phenomenon takes place: the production of Compton γ-photons is maximized; hence, at the end of each mfp one would expect a sudden increase (bump) in the intensity of the γ-photons counted by the Geiger–Müller detector [14].
3.2. Comparison of γ-ray Absorption with the Sound Wave Resonance Tube
In a sound wave resonance tube, the vibrating structure could be an open-ended hollow tube of length L containing the vibrating medium (most probably, a column of air). The disturbance, that is a harmonic sound wave of frequency f, enters the tube, ‘recognizes’ the tube’s shape and can create a standing sound wave (such as the one depicted in Figure 3), also depending on the state (open or closed) of the tube’s edges [23].
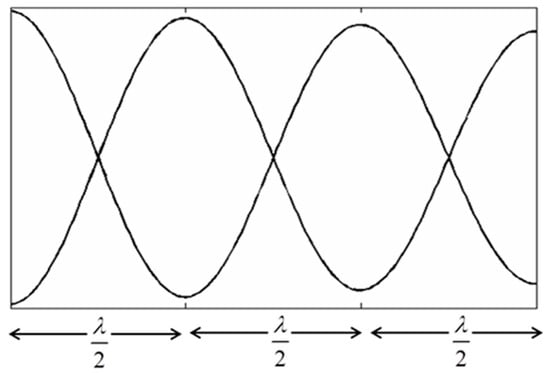
Figure 3.
An example of a standing sound wave formed in an open-ended sound tube of length equal to 3λ/2 (λ being the wavelength of the sound wave). The amplitude of the wave is presented as diminished due to losses.
As mentioned in Section 2.1.e, regarding the attenuation of the γ-ray, the absorber was piled up in a cylindrical configuration with increasing thickness. This will be characterized as the ‘γ-ray absorber tube’ in analogy with the sound tube. In this system, the parameter which corresponds to the basic resonance length λ/2 of the sound tube is the mean free path
of the γ ray/absorber system (see Figure 4), where n is the density of atoms of the absorber (number of atoms/cm3) and
is the cross section for the interaction of a γ photon with an atom of the absorber.

Figure 4.
A conceptual picture of the ‘γ-ray absorber tube’. The absorber’s thickness is measured in mfps. In front of the ‘tube’ there is the 60Co radioactive source. The ‘+’ signs represent the positive ions remaining after Compton scattering of γ and δ-rays. The dark gray color represents the cloud of electrons diffused after Compton scattering. The light gray color represents the bulk material of the absorber.
In Figure 4, the first maximum, at the surface of the absorber, is due to the fact that the intensity of the γ-rays, and hence the number of interactions, is at its highest at the absorber surface or at a very short thickness inside it [24,25].
A key observation regarding the γ-ray attenuation regards the ‘bumps’ that clearly appear at every mfp of absorber thickness (see Figure 2), a fact that, in typical MC simulations, is usually hidden under an overestimated build-up effect which shows a smooth, exponentially decaying variation. This forms an analogy with a sound wave emerging from the resonant tube which shows better defined discrete frequencies if the noise is added out of phase and/or attenuated.
By extending the analogy between a sound tube (or musical instrument) and the observations of detailed measurements of gamma ray absorption and transmission through matter, we could propose two more points of similarity. One would be the timbre and the other the musical tone of the instrument. The former could be seen to correspond to the spectrum of photons emerging form the material after Compton scattering, while the later could correspond to the dominant photon frequency.
4. Conclusions
In this work, we have highlighted certain analogies between γ-ray absorption and the open-ended sound wave resonance tube. The basic analogy is that the mfp of the first system acts like the resonance length λ/2 in the second one. At the mfp, the γ-ray intensity, that is transmitted through the absorber to the detector, presents a bump. Correspondingly, at λ/2, the sound wave intensity inside the sound tube is maximized. Regarding the ‘bumps’ in the intensity of the outgoing γ-rays that appear at thicknesses, within the absorber, equal to a multiple of the mfp and the overestimation of the buildup effect by possible MC simulations, we have proposed that the cloud of electrons and the positive ions created by the Compton collisions increase the photoelectric absorption, ‘clearing out’ much of the buildup-created photons.
A reason for choosing the sound wave tube for the comparison made (despite the obvious difference with the photon–matter interaction) is that the tube is a rather simple system that (together with the set-up for the γ-ray attenuation measurement) can be found in several undergraduate Physics labs allowing for the proposed comparison to be also used for educational reasons.
The equivalence principle between two different physical systems is very important, because one can transform phenomena and laws from the simpler system (source) to obtain better insights into the more complicated one (target). The analogy discussed here might seem peculiar, given that the compared systems are physically different. The detected intensity of γ-radiation through matter should be the result of a vast number of uncorrelated absorption and scattering events, without any periodicity, while the resonance in a sound tube is the result of the interference of waves. In our view, this makes the comparison all the more interesting. It has to be noted that the comparison made mainly regards the maxima appearing in the two phenomena (the photon–matter interaction and the standing waves) and not the phenomena themselves, as well as that the observed similarity occurs regardless of the measurement type and the absorber used.
Author Contributions
Conceptualization, E.A., A.K., P.S.K. and N.M.; Methodology, E.A., A.K., P.S.K. and N.M.; Validation, E.A., A.K., P.S.K., N.M. and G.P.; Investigation, N.M.; Data curation, E.A., A.K. and P.S.K.; Writing–original draft, E.A., A.K., P.S.K. and N.M.; Writing–review & editing, G.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to thank the students of the Physics Laboratory of the University of West Attica for their remarks. This paper is dedicated to the memory of Stylianos Koutroubas, emeritus professor of the University of West Attica, who passed away before the submission of the paper. Stylianos Koutroubas was involved in the experimental study and the conception of the ideas expressed in the submitted paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Adamides, E.; Kavadjiklis, A.; Koutroubas, S.K.; Moshonas, N.; Yiasemides, K. Gamma ray attenuation measurements as a laboratory experiment: Some remarks. Phys. Ed. 2011, 46, 398–402. [Google Scholar] [CrossRef]
- Ahmed, G.S.M.; Mahmoud, A.S.; Salem, S.M.; Abou-Elnasr, T.Z. Study of Gamma-Ray Attenuation Coefficients of Some Glasses Containing CdO. Am. J. Phys. Appl. 2015, 3, 112–120. [Google Scholar]
- Aguilar, R.; Powers, P.; Abramzon, N.; Siegel, P.B. Soil analysis using a 2-inch NaI gamma detector. Am. J. Phys. 2021, 89, 647–654. [Google Scholar] [CrossRef]
- Lab Experiment 3: Gamma-ray Absorption in Matter (Basic). Available online: https://www.mirion.com/learning-center/lab-experiments/gamma-ray-absorption-in-matter-basic (accessed on 25 July 2024).
- Pires, L.F.; Cássaro, F.A.M.; Tech, L.; Pereira, L.A.A.; De Oliveira, J.A.T. Gamma ray attenuation for determining soil density: Laboratory experiments for Environmental Physics and Engineering courses. Rev. Bras. Ensino Fís. 2020, 42, e20190340. [Google Scholar] [CrossRef]
- Singh, P.S.; Singh, T.; Kaur, P. Variations of energy absorption buildup factors with incident photon energy and penetration depth for some commonly used solvents. Ann. Nucl. Energy 2008, 35, 1093–1097. [Google Scholar] [CrossRef]
- White, G.R. The Penetrations and Diffusion of Co60 Gamma-Rays in Water using Spherical Geometry. Phys. Rev. 1950, 80, 154–156. [Google Scholar] [CrossRef]
- Koutroubas, S.K. New Shielding materials for photons and neutrons produced by radiotherapy units. J. Radiol. Prot. 1992, 12, 37–40. [Google Scholar] [CrossRef]
- Attix, F.H.; Roesch, W.C.; Tochilin, F. Radiation Dosimetry; Academic Press: New York, NY, USA; London, UK, 1968. [Google Scholar]
- Mann, K.S.; Singla, J.; Kumar, V.; Sidhu, G.S. Investigations of mass attenuation coefficients and exposure buildup factors of some low-Z building materials. Ann. Nucl. Energy 2012, 43, 157–166. [Google Scholar] [CrossRef]
- Jubair, S.I. Calculation of Buildup Factors for Ceramic Materials. Iraqi J. App. Phys. 2011, 7, 23–26. [Google Scholar]
- Oberer, R.B.; Gunn, C.A.; Chiang, L.G.; Valiga, R.E.; Cantrell, J.A. Small-Angle Compton Scattering to Determine the Depth of a Radioactive Source in Matter. 2011. Available online: https://www.osti.gov/servlets/purl/1016162 (accessed on 25 July 2024).
- Mukherjee, B.; Negodin, E.; Hott, T.; Simrock, S. Efficacy Testing of Shielding Materials for XFEL Using the Radiation Fields Produced at FLASH. 2008. Available online: https://bib-pubdb1.desy.de/record/85037/files/TESLA-FEL2008-06.pdf (accessed on 25 July 2024).
- Choppin, G.; Liljenzin, J.-O.; Rydberg, J.; Ekberg, C. Radiochemistry and Nuclear Chemistry; Academic Press: Oxford, UK; Amsterdam, The Netherlands, 2013. [Google Scholar]
- Lamarsh, J.R.; Baratta, A.J. Introduction to Nuclear Engineering; Prentice-Hall: Hoboken, NJ, USA, 2001. [Google Scholar]
- Briesmeister, J.F. (Ed.) MCNP A General Monte Carlo N-Particle Transport Code; Version 4C, LA 13709 Manual. 8 December 2000. Available online: https://permalink.lanl.gov/object/tr?what=info:lanl-repo/lareport/LA-13709-M (accessed on 25 July 2024).
- Adamides, E.; Kavadjiklis, A.; Koutroubas, S.K.; Moshonas, N.; Tzedakis, A. Buildup Minimizing Assembly’ a system to minimize the buildup effect in γ-ray attenuation measurements as a laboratory experiment. Eur. J. Phys. 2016, 37, 045706. [Google Scholar] [CrossRef]
- Johansen, G.A. Gamma-ray tomography. In Industrial Tomography, Systems and Applications; Elsevier: Cambridge, UK, 2015; p. 197. [Google Scholar]
- Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/9783527626809.app2 (accessed on 25 July 2024).
- Available online: http://ftp.astro.wisc.edu/~townsend/resource/teaching/astro-310-F08/10-radiation-matter.pdf (accessed on 25 July 2024).
- Deshmukh, P.C.; Banik, A.; Angom, D. Atomic photoionization in the Born Approximation and Angular Distribution of Photoelectrons. In Collection of Articles from DST-SERC School on Theoretical Techniques in Atomic and Molecular Collision Physics at the Birla Institute of Technology, Pilani, 9–28 January 2011; DST-SERC-School Publication; Narosa: Delhi, India, 2011. [Google Scholar]
- Hussein, E.M. Handbook on Radiation Probing, Gauging, Imaging and Analysis: Basics and Techniques; DordrechtKluwer Academic Pub: Dordrecht, The Netherlands, 2003; Volume I. [Google Scholar]
- Serway, R.A.; Jewett, J.W. Physics for Scientists and Engineers, 6th ed.; Thomson-Brooks/Cole: Belmont, CA, USA, 2004; pp. 559–562. [Google Scholar]
- Alenezi, M.; Stinson, K.; Maqbool, M.; Bolus, N. Klein-Nishina electronic-cross section, Compton-cross section, and buildup factor of wax for radiation shielding and protection. J. Radiol. Prot. 2018, 38, 372–381. [Google Scholar] [CrossRef] [PubMed]
- Johns, H.E.; Cunningham, J.R. The Physics of Radiology; Chapter 10; Charles C Thomas: Springfield, IL, USA, 1983. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).