Physics, Tuning, and Performance of the TMD-Inerter for Harmonic Vibrations
Abstract
1. Introduction
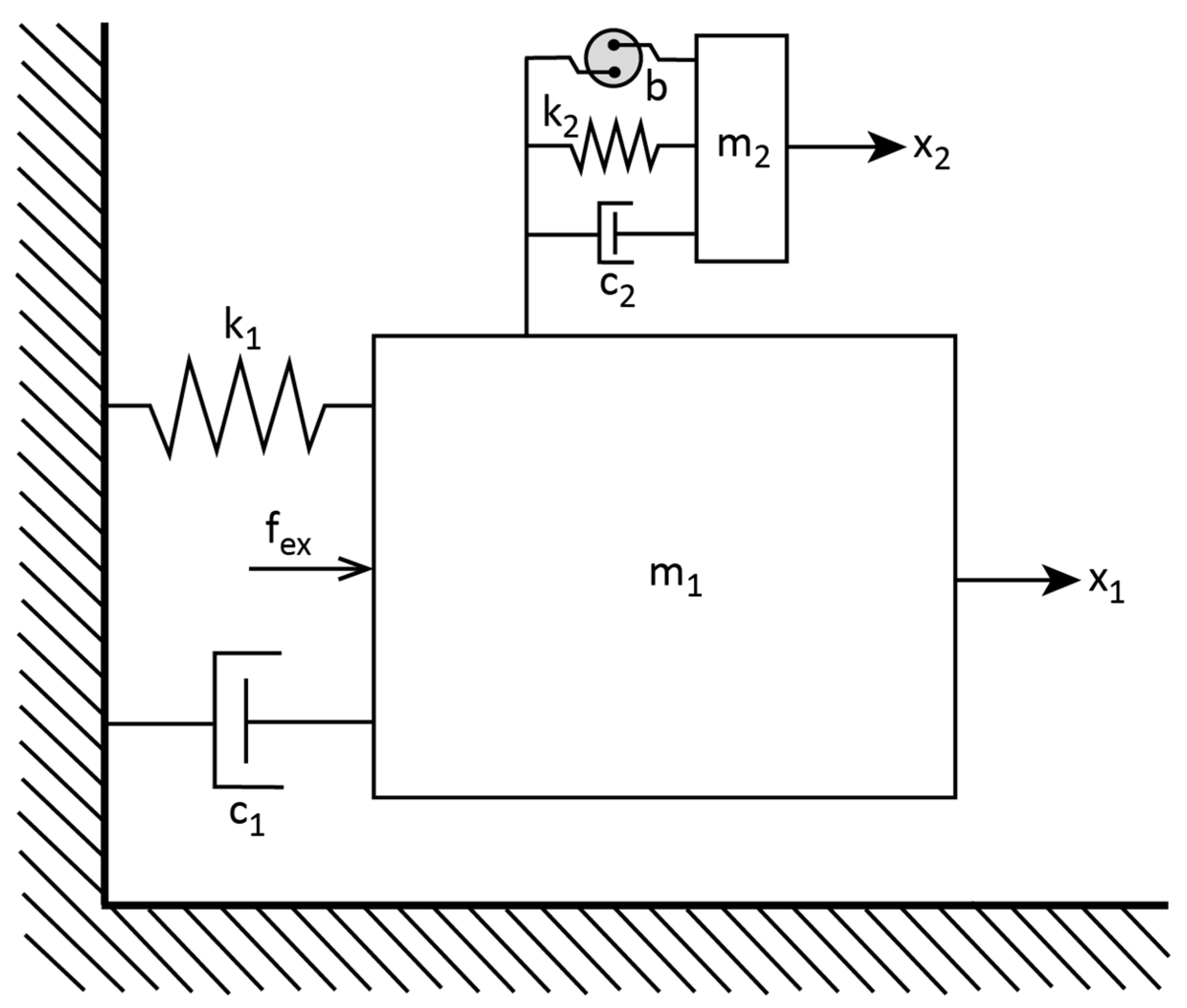
2. Modeling of the Primary Structure with TMD-Inerter
2.1. Equations of Motion for Harmonic Vibrations
2.2. Inerter Force Equation
2.3. Excitation Force and Assessment Method
2.4. Classical TMD as Benchmark
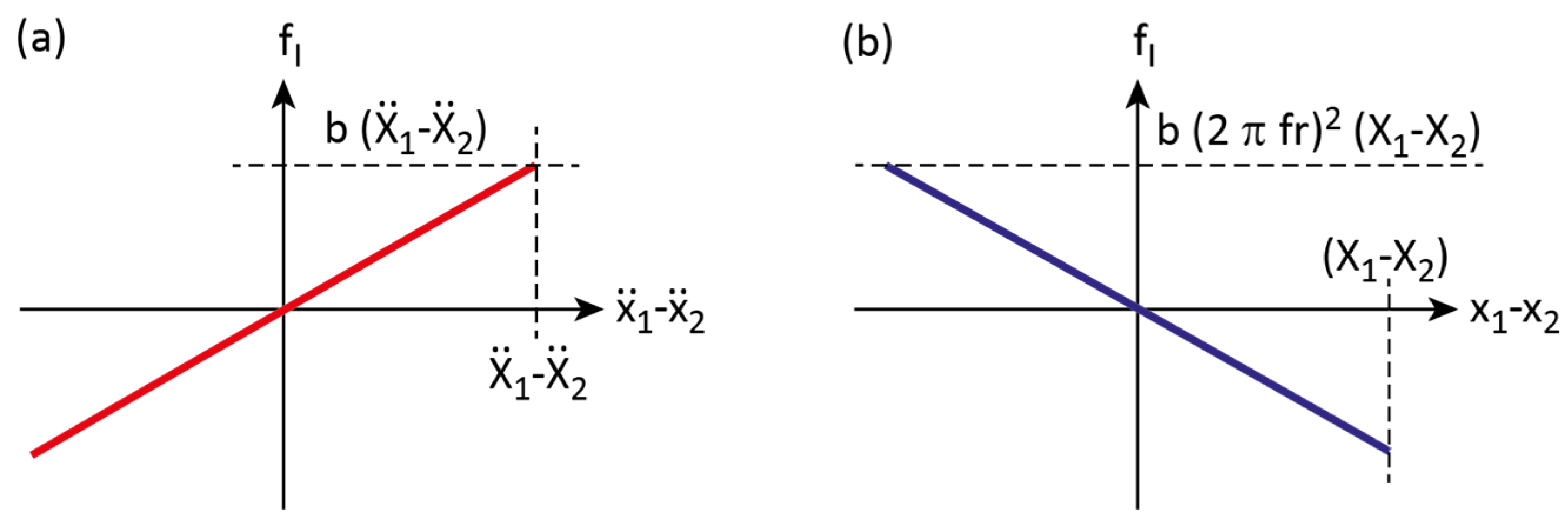
3. Inerter Force for Harmonic Vibrations
3.1. Inerter Force Characteristics
3.2. Strategies to Compensate for Inerter Negative Stiffness
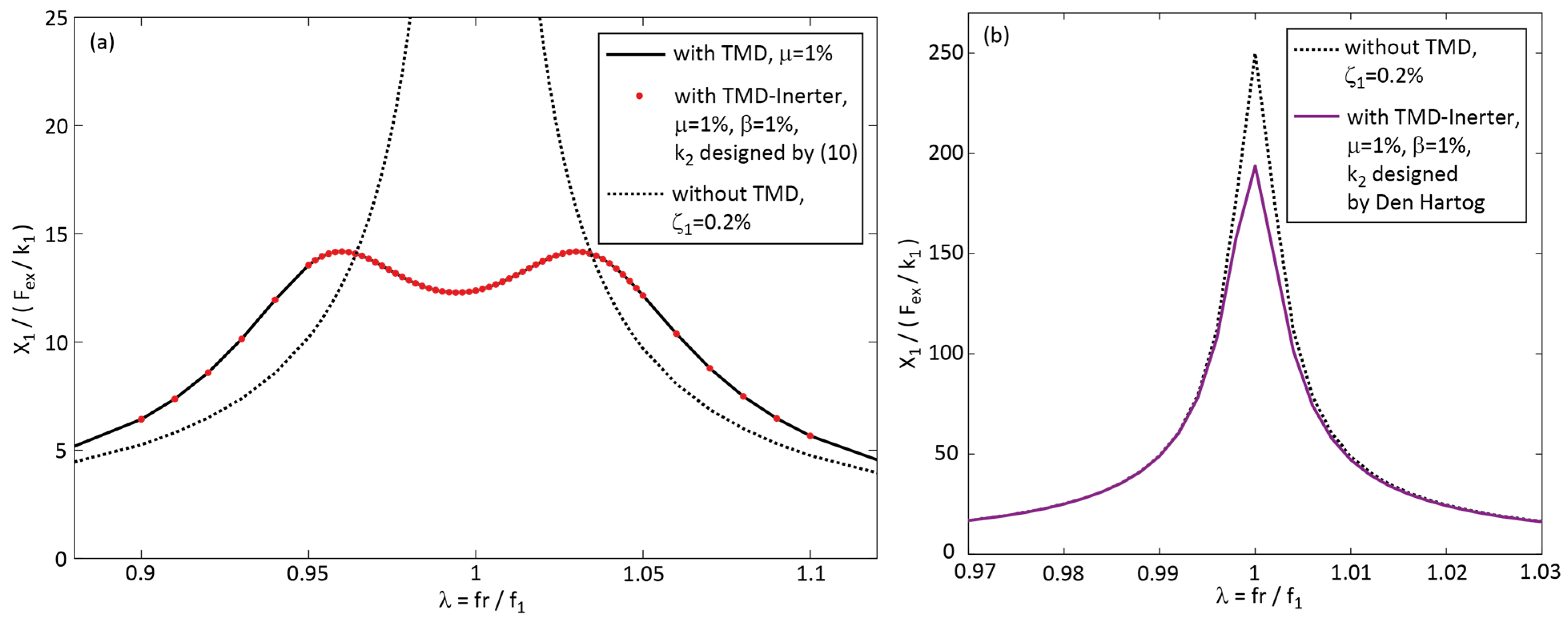
4. Optimization of the TMD-Inerter
4.1. Compensation of Frequency-Dependent Negative Stiffness Force of the Inerter
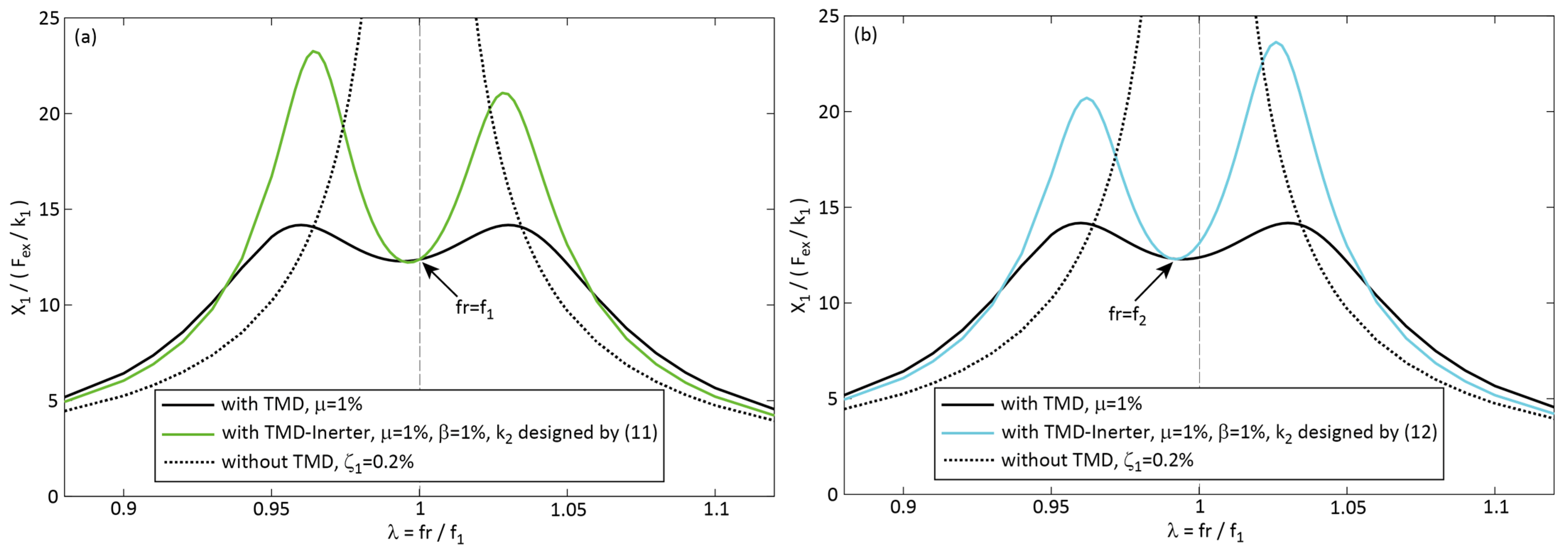
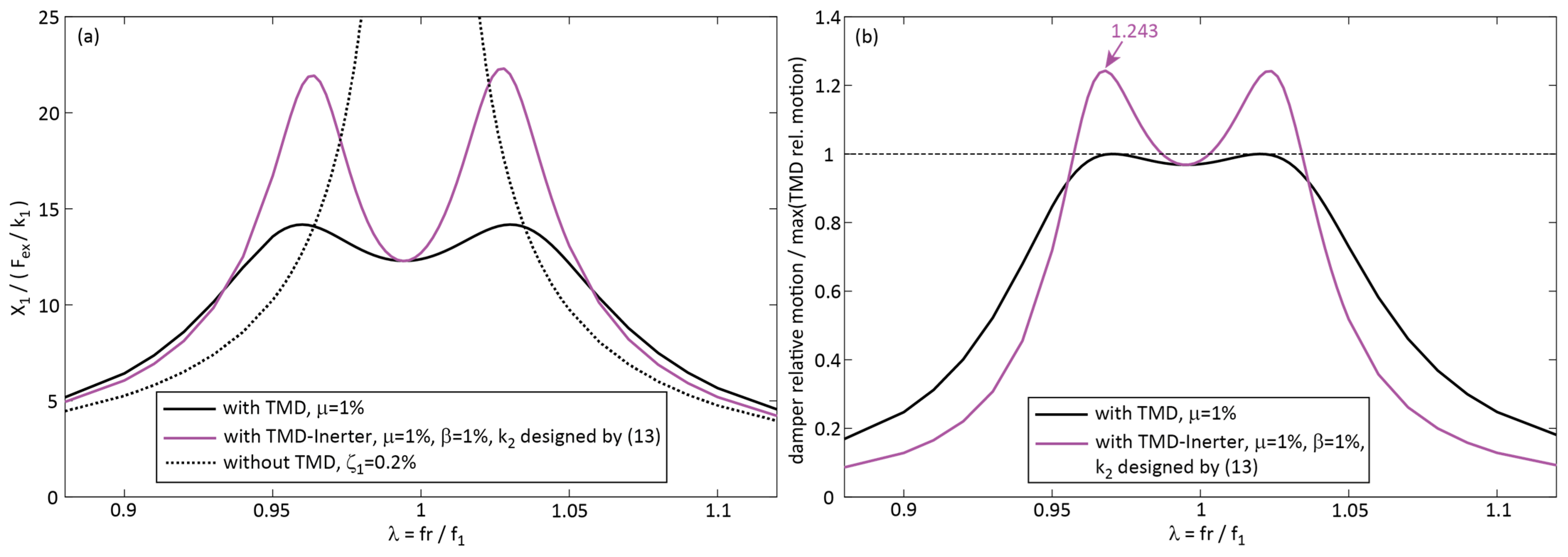
4.2. Compensation of Inerter Negative Stiffness by a Passive Spring
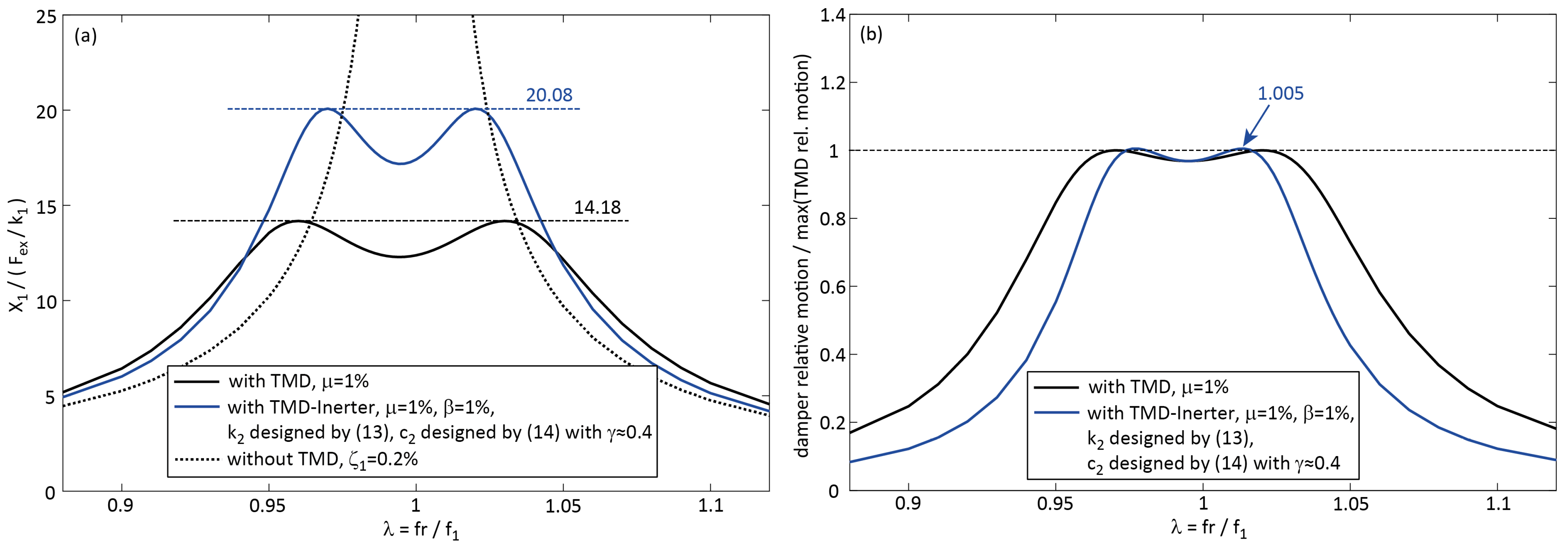
4.3. Passive Inerter Stiffness Compensation Combined with Numerically Optimized Damping
5. Summary and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Den Hartog, J.P. Mechanical Vibrations, 4th ed.; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Zucca, M.; Longarini, N.; Simoncelli, M.; Aly, A.M. Tuned Mass Damper Design for Slender Masonry Structures: A Framework for Linear and Nonlinear Analysis. Appl. Sci. 2021, 11, 3425. [Google Scholar] [CrossRef]
- ISO 10137; Bases for Design of Structures—Serviceability of Buildings and Walkways against Vibrations. International Organization for Standardization, ISO Central Secretariat, Chemin de Blandonnet 8, CP 401-1214 Vernier: Geneva, Switzerland, 2007.
- Smith, M.C. The Inerter: A Retrospective. Annu. Rev. Control Robot. Auton. Syst. 2020, 3, 361–391. [Google Scholar] [CrossRef]
- Giaralis, A.; Petrini, F. Wind-induced vibration mitigation in tall buildings using the tuned mass-damper-inerter. J. Struct. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Pietrosanti, D.; De Angelis, M.; Basili, M. Optimal design and performance evaluation of systems with Tuned Mass Damper Inerter (TMDI). Earthq. Eng. Struct. Dyn. 2017, 46, 1367–1388. [Google Scholar] [CrossRef]
- Weber, F. TMD-Inerter for Tall Building Damping: Approximate Closed-Form Solution, Performance and Conclusions. Buildings 2025, 15, 1829. [Google Scholar] [CrossRef]
- Dai, J.; Xu, Z.D.; Gai, P.P. Tuned mass-damper-inerter control of wind-induced vibration of flexible structures based on inerter location. Eng. Struct. 2019, 199, 109585. [Google Scholar] [CrossRef]
- Petrini, F.; Giaralis, A.; Wang, Z. Optimal tuned mass-damper-inerter (TMDI) design in wind-excited tall buildings for occupants’ comfort serviceability performance and energy harvesting. Eng. Struct. 2020, 204, 109904. [Google Scholar] [CrossRef]
- Wang, Q.; Qiao, H.; Li, W.; You, Y.; Fan, Z.; Tiwari, N. Parametric optimization of an inerter-based vibration absorber for wind induced vibration mitigation of a tall building. Wind Struct. 2020, 31, 241–253. [Google Scholar]
- Weber, F.; Huber, P.; Borchsenius, F.; Braun, C. Performance of TMDI for Tall Building Damping. Actuators 2020, 9, 139. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, B.; Hua, X. Closed-form optimization of tuned mass-damper-inerter (TMDI) in flexible structures. J. Build. Eng. 2023, 72, 106554. [Google Scholar] [CrossRef]
- Barredo, E.; Larios, M.; Mayén, J.; Flores-Hernández, A.A.; Colín, J.; Arias-Montiel, M. Optimal design for high-performance passive dynamic vibration absorbers under random excitation. Eng. Struct. 2019, 195, 469–489. [Google Scholar] [CrossRef]
- Barredo, E.; Larios, M.; Colín, J.; Mayén, J.; Flores-Hernández, A.A.; Arias-Montiel, M. A novel high-performance passive non-traditional inerter-based dynamic vibration absorber. J. Sound Vib. 2020, 485, 115583. [Google Scholar] [CrossRef]
- Alotta, G.; Failla, G. Improved inerter-based vibration absorbers. Int. J. Mech. Sci. 2021, 192, 106087. [Google Scholar] [CrossRef]
- Weber, F.; Borchsenius, F.; Distl, J.; Braun, C. Performance of numerically optimized Tuned Mass Damper with Inerter (TMDI). Appl. Sci. 2022, 12, 6204. [Google Scholar] [CrossRef]
- Konar, T.; Ghosh, A. Tuned mass damper inerter for seismic control of multi-story buildings: Ten years since inception. Structures 2024, 63, 106459. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weber, F. Physics, Tuning, and Performance of the TMD-Inerter for Harmonic Vibrations. CivilEng 2025, 6, 61. https://doi.org/10.3390/civileng6040061
Weber F. Physics, Tuning, and Performance of the TMD-Inerter for Harmonic Vibrations. CivilEng. 2025; 6(4):61. https://doi.org/10.3390/civileng6040061
Chicago/Turabian StyleWeber, Felix. 2025. "Physics, Tuning, and Performance of the TMD-Inerter for Harmonic Vibrations" CivilEng 6, no. 4: 61. https://doi.org/10.3390/civileng6040061
APA StyleWeber, F. (2025). Physics, Tuning, and Performance of the TMD-Inerter for Harmonic Vibrations. CivilEng, 6(4), 61. https://doi.org/10.3390/civileng6040061





