Fault Diagnosis Method Using CNN-Attention-LSTM for AC/DC Microgrid
Abstract
1. Introduction
- (1)
- Conventional machine learning methods for fault diagnosis of AC/DC microgrid rely on manual feature extraction algorithms, which not only increases the amount of computation but also complicates the fault identification process.
- (2)
- Existing fault identification methods do not possess sufficient capability to extract the time series features of the data, which have difficulty in dealing with the power data collected by the sensors.
- (3)
- Influenced by the current-limiting control of power electronic devices in AC/DC microgrids, some faults present weak characteristics, which have not been considered seriously by the existing strategy.
- (1)
- Unlike model-based approaches that rely on accurate system modeling and struggle with parameter uncertainties, CAL directly learns from operational data, enhancing robustness under nonlinear and dynamic conditions.
- (2)
- (3)
- In the field of fault diagnosis of the AC/DC microgrid, the input data, including voltage and current collected by sensors, possesses temporal characteristics, which cannot be mined using the existing CNN [17,45]. In this paper, we introduce the LSTM layer combined into the CNN, which can capture long-term dependencies and automatically learn time-related features.
- (4)
- Due to the fact that the current limiting control of power electronic devices in the AC/DC microgrid weakens fault features, there is an urgent need to improve the existing technology to increase the accuracy of recognizing tiny fault features. Different with the CNN in [46], a hybrid attention mechanism is integrated to focus subtle changes in these features so that the fault diagnosis performance can be enhanced for the AC/DC microgrid.
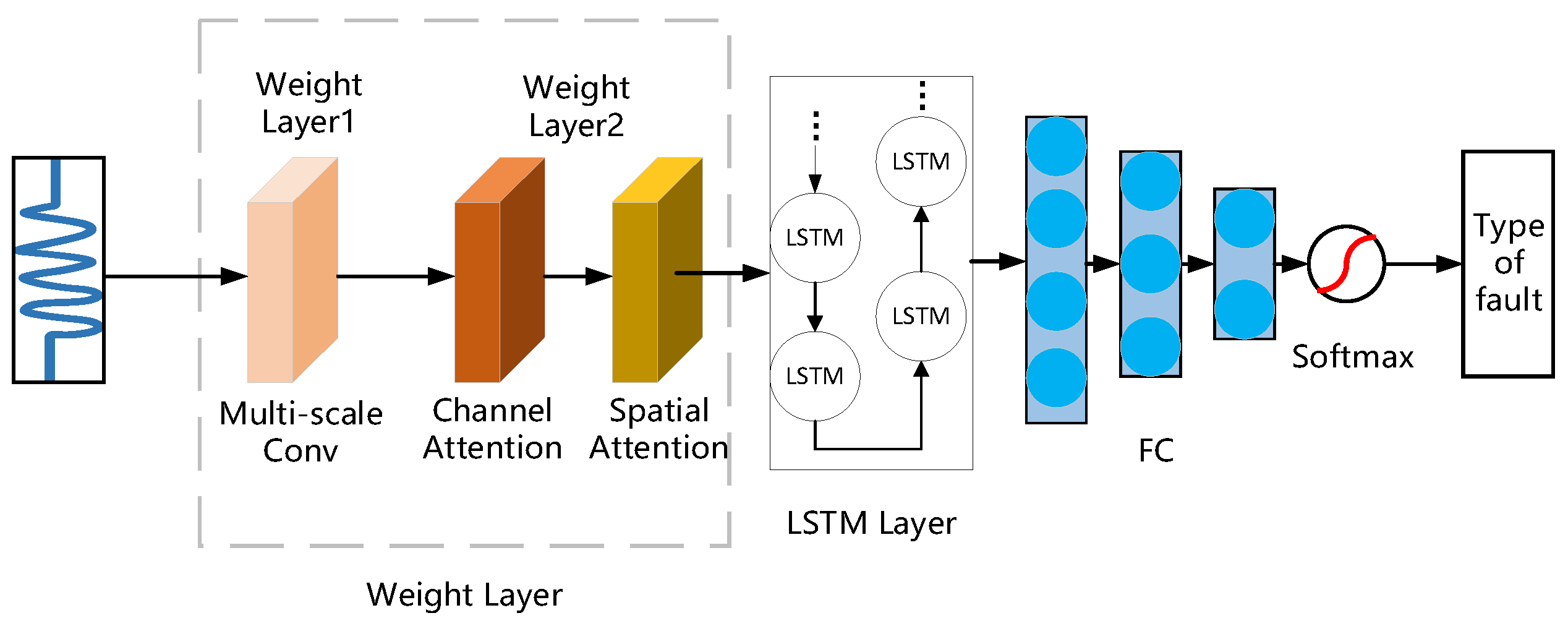
2. CNN-Attention-LSTM Modeling
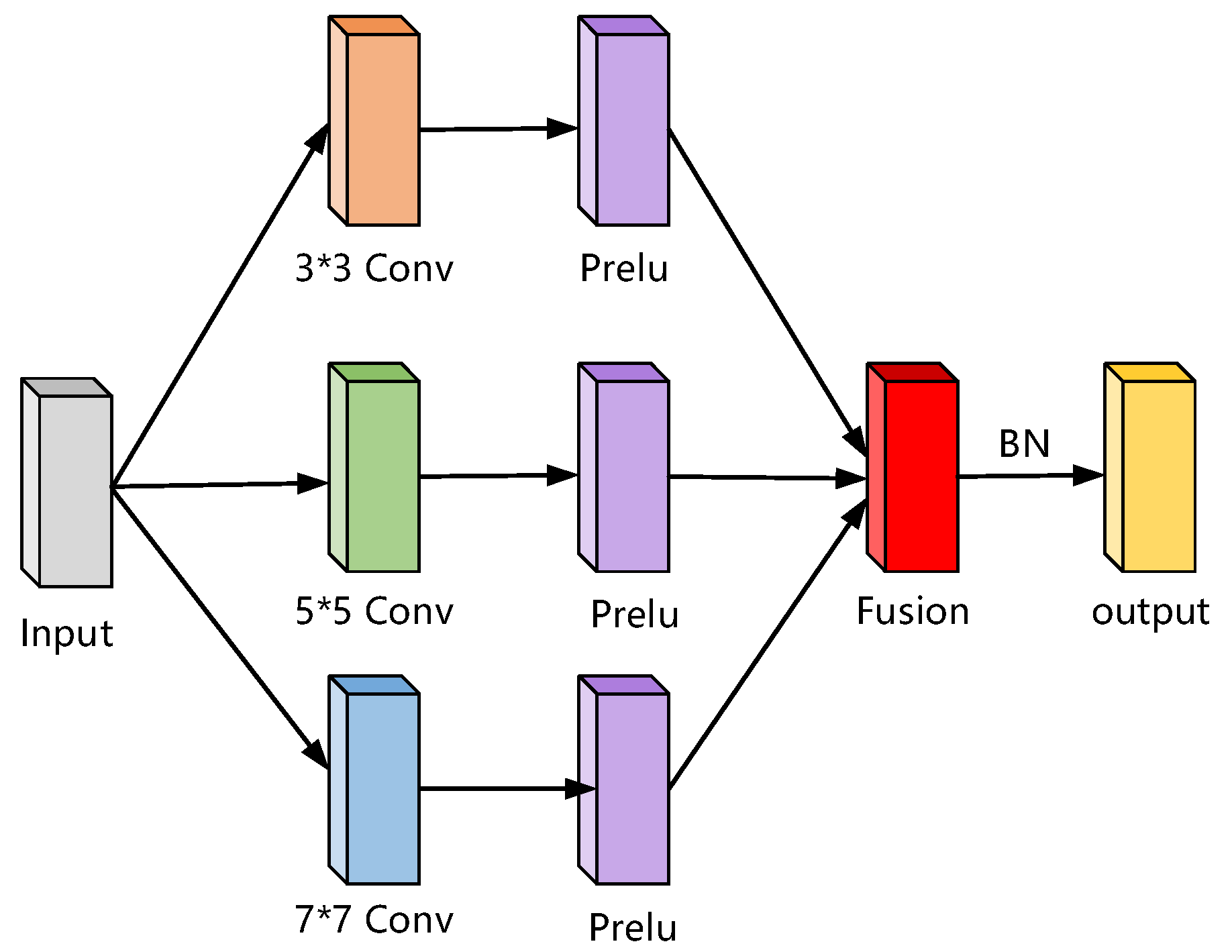
2.1. Multi-Scale Parallel Convolutional Networks
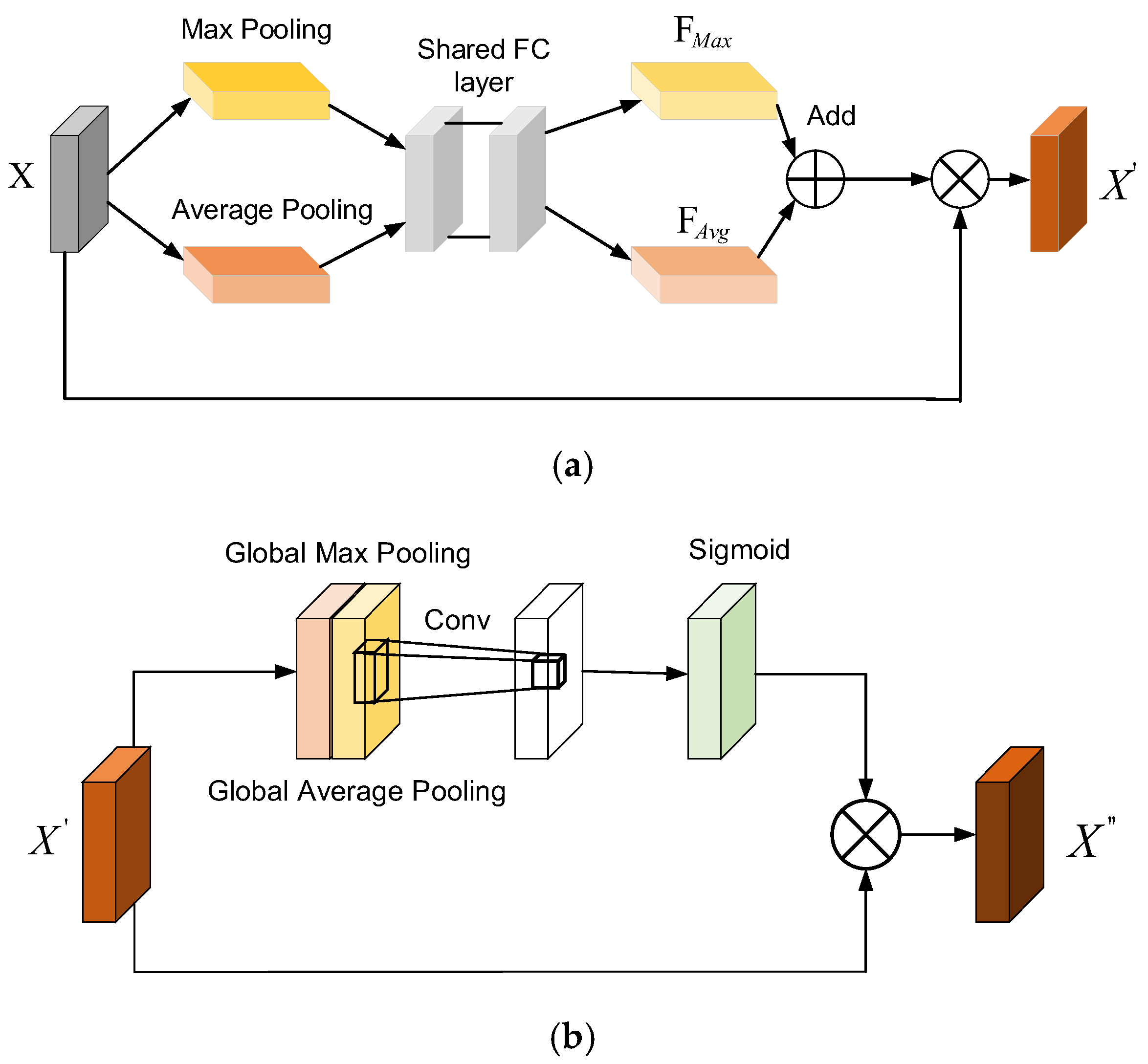
2.2. Convolutional Block Attention Module (CBAM)
2.3. LSTM Layer
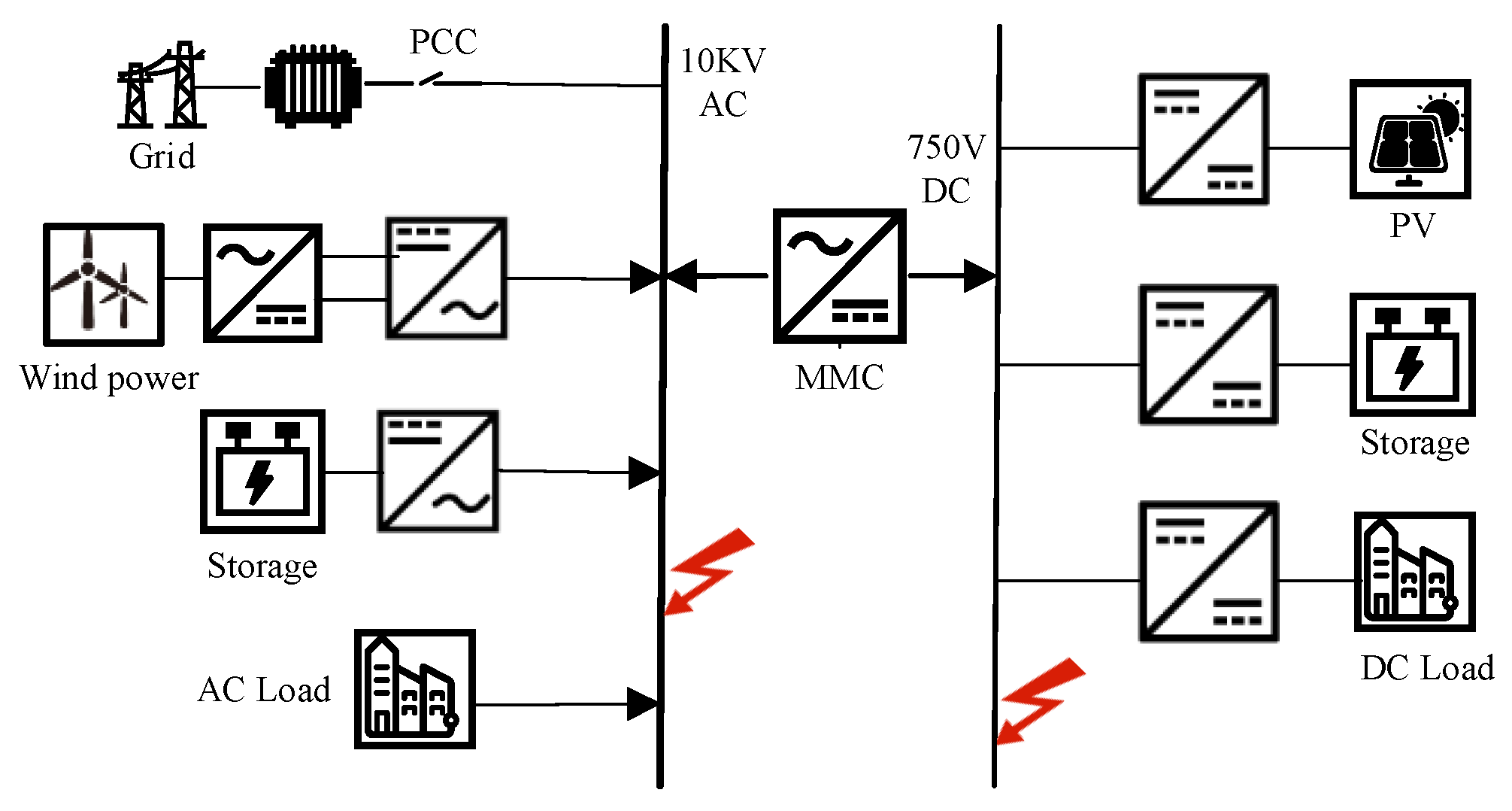
3. Fault Feature Extraction and Data Processing
3.1. Fault Dataset Construction
3.2. Fault Data Processing
4. Simulation Validation
4.1. Fault Diagnosis with Clean Data
4.2. Comparison Analysis
4.3. Anti-Interference Analysis
4.4. Applicability Analysis Against New Topology
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pradhan, R.; Jena, P. An innovative fault direction estimation technique for AC microgrid. Electr. Power Syst. Res. 2023, 215, 108997. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, L.; Wang, P. Microgrid Fault Detection Method Based on Lightweight Gradient Boosting Machine–Neural Network Combined Modeling. Energies 2024, 17, 2699. [Google Scholar] [CrossRef]
- Montoya, R.; Poudel, B.P.; Bidram, A.; Reno, M.J. DC microgrid fault detection using multiresolution analysis of traveling waves. Int. J. Electr. Power Energy Syst. 2022, 135, 107590. [Google Scholar] [CrossRef]
- Pola, S.; Azzouz, M.A.; Mirhassani, M. Synchronverters with fault ride-through capabilities for reliable microgrid protection during balanced and unbalanced faults. IEEE Trans. Sustain. Energy 2024, 15, 1663–1676. [Google Scholar] [CrossRef]
- Vinayagam, A.; Suganthi, S.; Venkatramanan, C.; Alateeq, A.; Alassaf, A.; Ab Aziz, N.F.; Mansor, M.H.; Mekhilef, S. Discrimination of high impedance fault in microgrid power network using semi-supervised machine learning algorithm. Ain Shams Eng. J. 2025, 16, 103187. [Google Scholar] [CrossRef]
- Mohan, F.; Sasidharan, N. Protection of low voltage DC microgrids: A review. Electr. Power Syst. Res. 2023, 225, 109822. [Google Scholar] [CrossRef]
- Ghzaiel, W.; Ghorbal, M.J.-B.; Slama-Belkhodja, I.; Guerrero, J.M. Grid impedance estimation based hybrid islanding detection method for AC microgrids. Math. Comput. Simul. 2017, 131, 142–156. [Google Scholar] [CrossRef]
- Fang, M.; Zhang, D.; Qi, X. Real-Time Voltage Drop Compensation Method With Cable Impedance Detection Capability for Remote Power Supply Systems. IEEE Trans. Power Electron. 2023, 38, 9322–9328. [Google Scholar] [CrossRef]
- Yadegar, M.; Zarei, S.F.; Meskin, N.; Blaabjerg, F. A distributed high-impedance fault detection and protection scheme in DC microgrids. IEEE Trans. Power Deliv. 2023, 39, 141–154. [Google Scholar] [CrossRef]
- Hamatwi, E.; Imoru, O.; Kanime, M.M.; Kanelombe, H.S.A. Comparative analysis of high impedance fault detection techniques on distribution networks. IEEE Access 2023, 11, 25817–25834. [Google Scholar] [CrossRef]
- Alaei, S.A.; Damchi, Y. A new method based on the discrete time energy separation algorithm for high and low impedance faults detection in distribution systems. Electr. Power Syst. Res. 2023, 218, 109200. [Google Scholar] [CrossRef]
- Dubey, K.; Jena, P. Impedance angle-based differential protection scheme for microgrid feeders. IEEE Syst. J. 2020, 15, 3291–3300. [Google Scholar] [CrossRef]
- Saleh, K.; Hooshyar, A.; El-Saadany, E.F. Fault detection and location in medium-voltage DC microgrids using travelling-wave reflections. IET Renew. Power Gener. 2020, 14, 571–579. [Google Scholar] [CrossRef]
- Chen, H.; Li, J.; Chen, P. Design of fault location algorithm based on online distributed travelling wave for HV power cable. PLoS ONE 2024, 19, e0296513. [Google Scholar]
- Sahoo, B.; Samantaray, S.R. An enhanced travelling wave-based fault detection and location estimation technique for series compensated transmission network. In Proceedings of the 2017 7th International Conference on Power Systems (ICPS), Pune, India, 21–23 December 2017. [Google Scholar]
- Kumar, R.; Tripathy, M. A novel impedance based fault locator algorithm for transmission line. Electr. Power Syst. Res. 2023, 224, 109731. [Google Scholar] [CrossRef]
- Bhargav, R.; Gupta, C.P.; Bhalja, B.R. Unified impedance-based relaying scheme for the protection of hybrid AC/DC microgrid. IEEE Trans. Smart Grid 2021, 13, 913–927. [Google Scholar] [CrossRef]
- Zhang, G.; Shi, M.; Zhang, C.; Sha, H.; She, C. Harmonic impedance detection based on capacitor switching and wavelet packet analysis. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Suzhou, China, 29 July–2 August 2019. [Google Scholar]
- Couto, V.F.; Moreto, M. High impedance fault detection on microgrids considering the impact of VSC based generation. IEEE Access 2023, 11, 89550–89560. [Google Scholar] [CrossRef]
- Saleh, K.A.; Hooshyar, A.; El-Saadany, E.F. Ultra-high-speed traveling-wave-based protection scheme for medium-voltage DC microgrids. IEEE Trans. Smart Grid 2017, 10, 1440–1451. [Google Scholar] [CrossRef]
- Kiaei, I.; Lotfifard, S. Fault section identification in smart distribution systems using multi-source data based on fuzzy Petri nets. IEEE Trans. Smart Grid 2019, 11, 74–83. [Google Scholar] [CrossRef]
- Zhou, J.; Xiao, M.; Niu, Y.; Ji, G. Rolling Bearing Fault Diagnosis Based on WGWOA-VMD-SVM. Sensors 2022, 22, 6281–6308. [Google Scholar] [CrossRef]
- Chauhan, V.K.; Dahiya, K.; Sharma, A. Problem formulations and solvers in linear SVM: A review. Artif. Intell. Rev. 2019, 52, 803–855. [Google Scholar] [CrossRef]
- Nie, F.; Zhu, W.; Li, X. Decision Tree SVM: An extension of linear SVM for non-linear classification. Neurocomputing 2020, 401, 153–159. [Google Scholar] [CrossRef]
- Zidan, A.; Khairalla, M.; Abdrabou, A.M.; Khalifa, T.; Shaban, K.; Abdrabou, A.; El Shatshat, R.; Gaouda, A.M. Fault detection, isolation, and service restoration in distribution systems: State-of-the-art and future trends. IEEE Trans. Smart Grid 2016, 8, 2170–2185. [Google Scholar] [CrossRef]
- Yan, J.; Li, Q.; Duan, S. A simplified current feature extraction and deployment method for DC series arc fault detection. IEEE Trans. Ind. Electron. 2023, 71, 625–634. [Google Scholar] [CrossRef]
- Li, B.; Cheng, T.; Jiang, Q.; Su, X.; Zhang, J.; Zhang, H. Faulty Feeders Identification for Single-phase-to-ground Fault Based on Multi-features and Machine Learning. IEEE Trans. Ind. Appl. 2023, 59, 7259–7270. [Google Scholar] [CrossRef]
- Mamuya, Y.D.; Lee, Y.-D.; Shen, J.-W.; Shafiullah, M.; Kuo, C.-C. Application of machine learning for fault classification and location in a radial distribution grid. Appl. Sci. 2020, 10, 4965. [Google Scholar] [CrossRef]
- Sapountzoglou, N.; Lago, J.; De Schutter, B.; Raison, B. A generalizable and sensor-independent deep learning method for fault detection and location in low-voltage distribution grids. Appl. Energy 2020, 276, 115299. [Google Scholar] [CrossRef]
- Arévalo, P.; Cano, A.; Benavides, D.; Jurado, F. Fault analysis in clustered microgrids utilizing SVM-CNN and differential protection. Appl. Soft Comput. 2024, 164, 112031. [Google Scholar] [CrossRef]
- Rizeakos, V.; Bachoumis, A.; Andriopoulos, N.; Birbas, M.; Birbas, A. Deep learning-based application for fault location identification and type classification in active distribution grids. Appl. Energy 2023, 338, 120932. [Google Scholar] [CrossRef]
- Korkmaz, D.; Acikgoz, H. An efficient fault classification method in solar photovoltaic modules using transfer learning and multi-scale convolutional neural network. Eng. Appl. Artif. Intell. 2022, 113, 104959. [Google Scholar] [CrossRef]
- Liu, H.; Liu, S.; Zhao, J.; Bi, T.; Yu, X. Dual-channel convolutional network-based fault cause identification for active distribution system using realistic waveform measurements. IEEE Trans. Smart Grid 2022, 13, 4899–4908. [Google Scholar] [CrossRef]
- Swaminathan, R.; Mishra, S.; Routray, A.; Swain, S.C. A CNN-LSTM-based fault classifier and locator for underground cables. Neural Comput. Appl. 2021, 33, 15293–15304. [Google Scholar] [CrossRef]
- Kok, C.L.; Ho, C.K.; Aung, T.H.; Koh, Y.Y.; Teo, T.H. Transfer learning and deep neural networks for robust intersubject hand movement detection from EEG signals. Appl. Sci. 2024, 14, 8091. [Google Scholar] [CrossRef]
- Aviña-Corral, V.; Rangel-Magdaleno, J.d.J.; Barron-Zambrano, J.H.; Rosales-Nuñez, S. Review of fault detection techniques in power converters: Fault analysis and diagnostic methodologies. Measurement 2024, 234, 114864. [Google Scholar] [CrossRef]
- Bhatnagar, M.; Yadav, A.; Swetapadma, A.; Abdelaziz, A.Y. LSTM-based low-impedance fault and high-impedance fault detection and classification. Electr. Eng. 2024, 106, 6589–6613. [Google Scholar]
- Vaswani, A. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- de Santana Correia, A.; Colombini, E.L. Attention, please! A survey of neural attention models in deep learning. Artif. Intell. Rev. 2022, 55, 6037–6124. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, P.; Liang, P. SAKD: Sparse attention knowledge distillation. Image Vis. Comput. 2024, 146, 105020. [Google Scholar] [CrossRef]
- Su, E.; Cai, S.; Xie, L.; Li, H.; Schultz, T. STAnet: A spatiotemporal attention network for decoding auditory spatial attention from EEG. IEEE Trans. Biomed. Eng. 2022, 69, 2233–2242. [Google Scholar] [CrossRef]
- Jiang, B.; Lu, Y.; Chen, X.; Lu, X.; Lu, G. Graph attention in attention network for image denoising. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 7077–7088. [Google Scholar] [CrossRef]
- Ukwuoma, C.C.; Cai, D.; Bamisile, O.; Chukwuebuka, E.J.; Favour, E.; Emmanuel, G.S.; Caroline, A.; Abdi, S.F. Power transmission system’s fault location, detection, and classification: Pay close attention to transmission nodes. Int. J. Electr. Power Energy Syst. 2024, 156, 109771. [Google Scholar] [CrossRef]
- Karthick, R.; Saravanan, R.; Arulkumar, P. Fault Detection and Fault Location in a Grid-Connected Microgrid Using Optimized Deep Learning Neural Network. Optim. Control Appl. Methods 2024, 46, 896–911. [Google Scholar] [CrossRef]
- Bukhari, S.B.A.; Kim, C.-H.; Mehmood, K.K.; Haider, R.; Zaman, M.S.U. Convolutional neural network-based intelligent protection strategy for microgrids. IET Gener. Transm. Distrib. 2020, 14, 1177–1185. [Google Scholar] [CrossRef]
- Siddique, M.N.I.; Shafiullah; Mekhilef, S.; Pota, H.; Abido, M.A. Fault classification and location of a PMU-equipped active distribution network using deep convolution neural network (CNN). Electr. Power Syst. Res. 2024, 229, 110178. [Google Scholar] [CrossRef]
- Ma, J.; Tang, Q.; He, M.; Peretto, L.; Teng, Z. Complex PQD Classification Using Time–Frequency Analysis and Multiscale Parallel Attention Residual Network. IEEE Trans. Ind. Electron. 2024, 71, 9658–9667. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Hochreiter, S. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
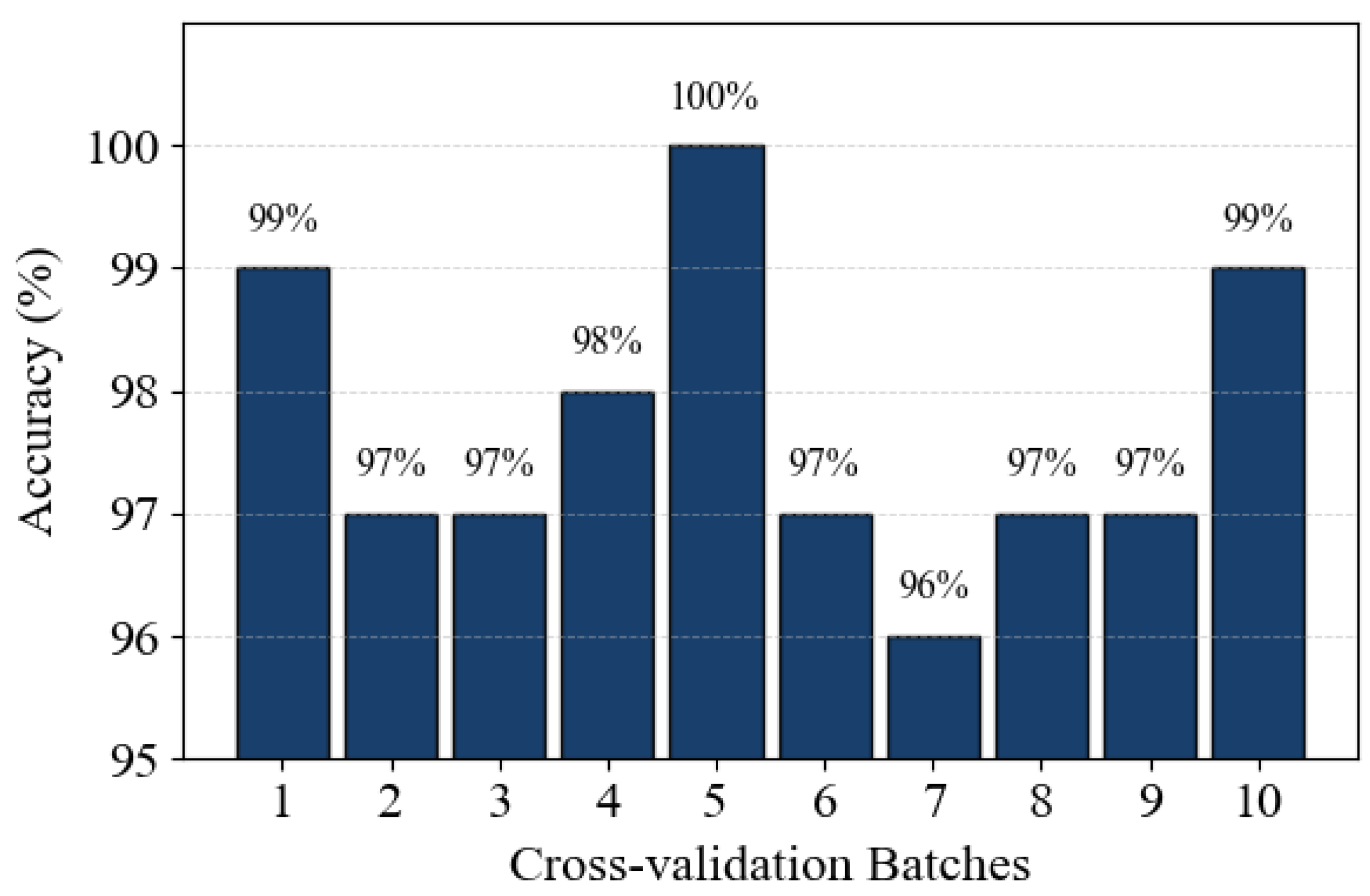
- Fu, W.J.; Carroll, R.J.; Wang, S. Estimating misclassification error with small samples via bootstrap cross-validation. Bioinformatics 2005, 21, 1979–1986. [Google Scholar] [CrossRef] [PubMed]
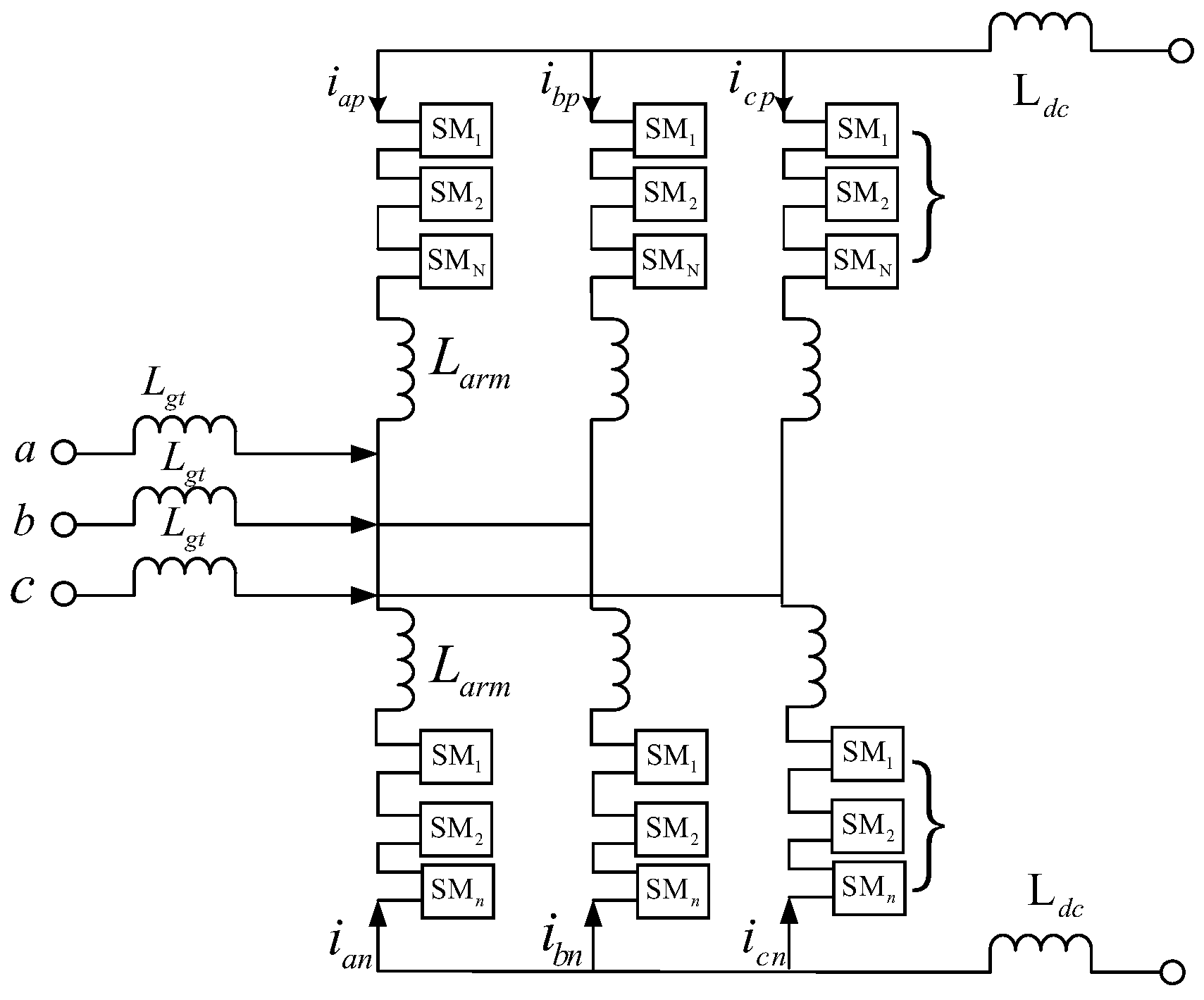




| Parameter | Value |
|---|---|
| Transformation ratio | 10/0.38 kV |
| Transformer power | 20 MVA |
| DC voltage | 750 V |
| Photovoltaic power | 0.2 MW |
| Turbine power | 0.2 MW |
| capacity | 10 MVA |
| AC voltage | 10 kV |
| Submodule capacitance | 20 mF |
| Bridge Arm inductors | 1 mH |
| Number of submodules | 100 |
| Fault Label | Sample Size |
|---|---|
| A-G | 100 |
| B-G | 100 |
| C-G | 100 |
| AB-G | 100 |
| AC-G | 100 |
| BC-G | 100 |
| ABC-G | 100 |
| P-N | 100 |
| P-P | 100 |
| Normal | 100 |
| Model Name | Accuracy (%) | Time (s/Sample) |
|---|---|---|
| CAL | 99.5 | 1.9 × 10−3 |
| CNN | 96.5 | 1.44 × 10−3 |
| SVM | 96 | 7.8 × 10−4 |
| Parameter | Value |
|---|---|
| Transformation ratio | 10/0.38 kV |
| Transformer power | 10 MVA |
| DC voltage | 1 kV |
| Photovoltaic power | 0.2 MW |
| Frequency | 50 Hz |
| Model | Accuracy (%) | |||
|---|---|---|---|---|
| Clean | 40 dB | 20 dB | 10 dB | |
| CAL | 98.85 | 98.46 | 98.46 | 97.69 |
| CNN | 96 | 95 | 94.62 | 92.69 |
| SVM | 95 | 94.23 | 93.46 | 89.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, Q.; Lyu, P.; Sun, R.; Jing, J.; Lyu, Z.; Hou, S. Fault Diagnosis Method Using CNN-Attention-LSTM for AC/DC Microgrid. Modelling 2025, 6, 107. https://doi.org/10.3390/modelling6030107
Bu Q, Lyu P, Sun R, Jing J, Lyu Z, Hou S. Fault Diagnosis Method Using CNN-Attention-LSTM for AC/DC Microgrid. Modelling. 2025; 6(3):107. https://doi.org/10.3390/modelling6030107
Chicago/Turabian StyleBu, Qiangsheng, Pengpeng Lyu, Ruihai Sun, Jiangping Jing, Zhan Lyu, and Shixi Hou. 2025. "Fault Diagnosis Method Using CNN-Attention-LSTM for AC/DC Microgrid" Modelling 6, no. 3: 107. https://doi.org/10.3390/modelling6030107
APA StyleBu, Q., Lyu, P., Sun, R., Jing, J., Lyu, Z., & Hou, S. (2025). Fault Diagnosis Method Using CNN-Attention-LSTM for AC/DC Microgrid. Modelling, 6(3), 107. https://doi.org/10.3390/modelling6030107





