2.1. Dataset Generation
To address the inherent challenges in obtaining extensive real-world carbonation progression data within feasible timeframes, this study developed a synthetic dataset containing 20,000 instances. The dataset was generated using the Possan equation [
20] (Equation (1)), a widely validated deterministic model that takes into consideration key factors influencing carbonation depth in concrete structures. Six input features were incorporated into the dataset: CO
2 concentration, concrete compressive strength, relative humidity, type of cement, exposure conditions, and time of exposure. These variables were randomly sampled within realistic ranges observed in reinforced concrete applications and environmental scenarios, ensuring a comprehensive and diversified parameter space. By enabling a controlled and systematic evaluation of ML models, the synthetic dataset overcomes limitations commonly associated with experimental data, such as restricted variability, small sample sizes, and non-random distributions. It is important to emphasize that the purpose of this dataset is not to explore new physical phenomena, but rather to provide a robust and unbiased platform for assessing the predictive performance of ML techniques in replicating known deterministic behaviors.
In Equation (1),
ec represents the average carbonation depth (mm);
fc is the compressive strength of concrete (MPa);
kc is a factor related to the type of cement;
kfc is a factor associated with compressive strength, also dependent on cement type;
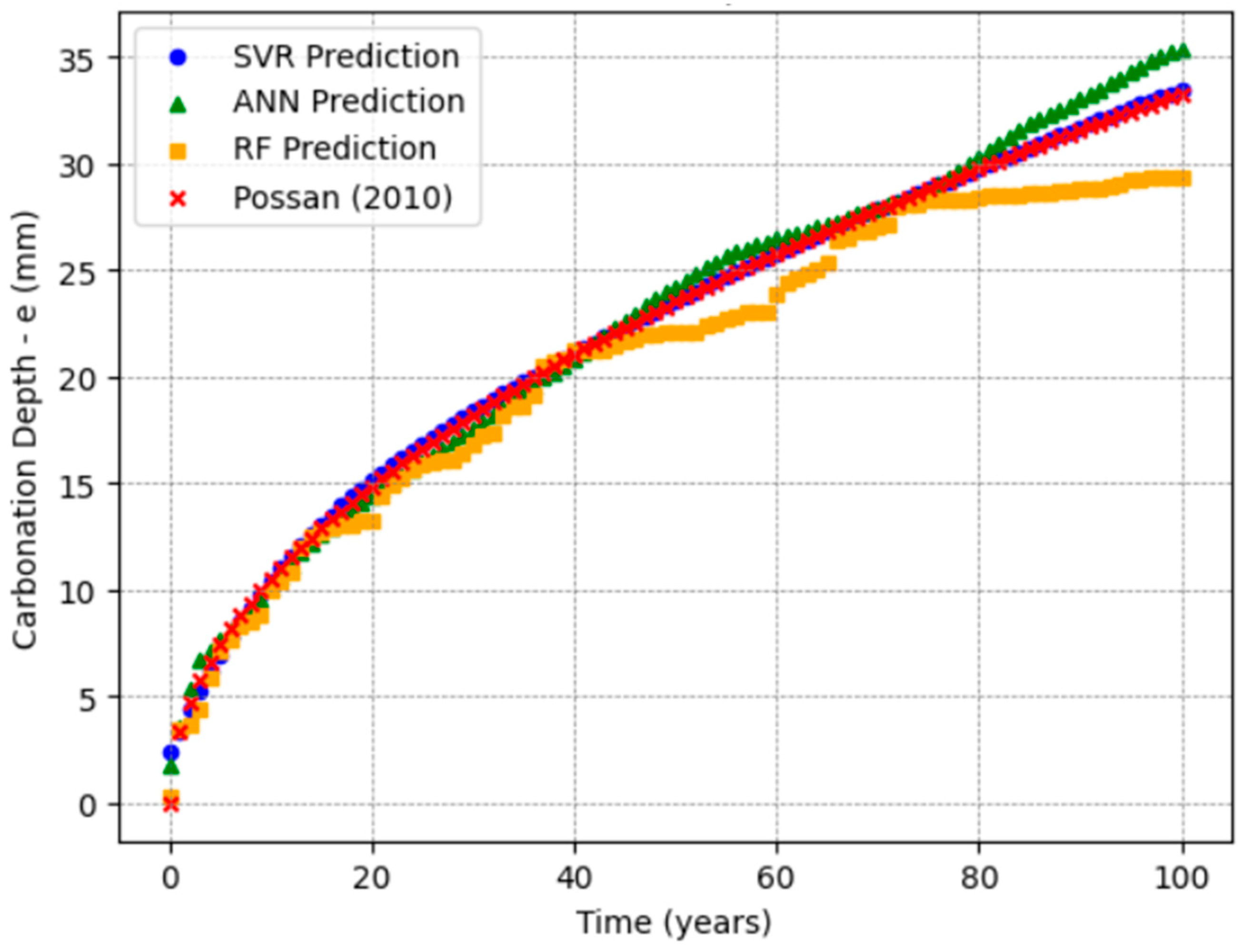
t is the age of the concrete (years);
ad is the percentage of pozzolanic addition relative to the cement mass;
kad is a factor related to pozzolanic additions;
UR is the average relative humidity (expressed as a fraction);
kUR is a factor linked to relative humidity, influenced by the type of cement; CO
2 is the atmospheric CO
2 concentration (%);
kCO2 is a factor accounting for CO
2 effects depending on cement; and
kce is a factor related to rain exposure and the environmental conditions. The values of the coefficients (
kc,
kfc,
kad,
kUR,
kCO2, and
kce) are listed in
Table 2 and
Table 3 [
20]. Additional information regarding the types of cement and environmental conditions related to the coefficients presented in these tables is discussed in the subsequent paragraphs of this section.
The dataset was generated in Python v. 3.10 using the
numpy library, specifically the
numpy.random.uniform function to create random values within defined ranges.
Table 4 summarizes the range for each variable considered, ensuring diversity and realism while minimizing potential biases. It is important to emphasize that the objective of this dataset is not to discover new physical phenomena but to evaluate the ML models’ ability to replicate known deterministic behaviors with high accuracy.
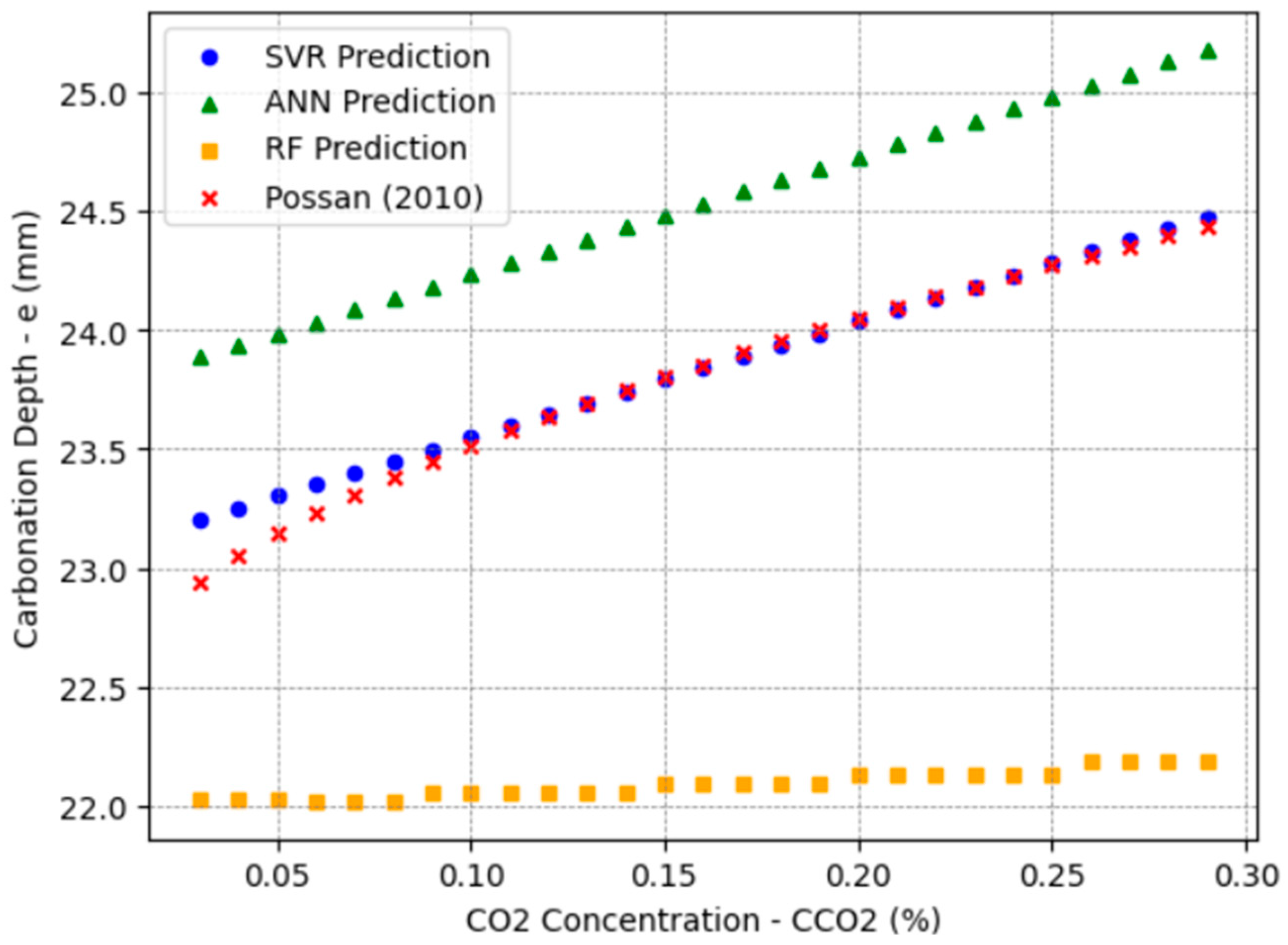
The CO
2 concentration range, from 0.03% to 0.30%, was selected based on values observed in various environments. Rural areas typically exhibit concentrations around 300 ppm (0.03%), whereas urban outdoor areas vary between 400 ppm (0.04%) and 500 ppm (0.05%) [
44,
45,
46,
47,
48,
49]. In enclosed environments within large cities, concentrations can reach 0.3% (3000 ppm), justifying the upper limit chosen. Although even higher concentrations can occur in poorly ventilated spaces such as garages, reaching up to 1% [
46], the Possan equation mainly applies to typical urban conditions.
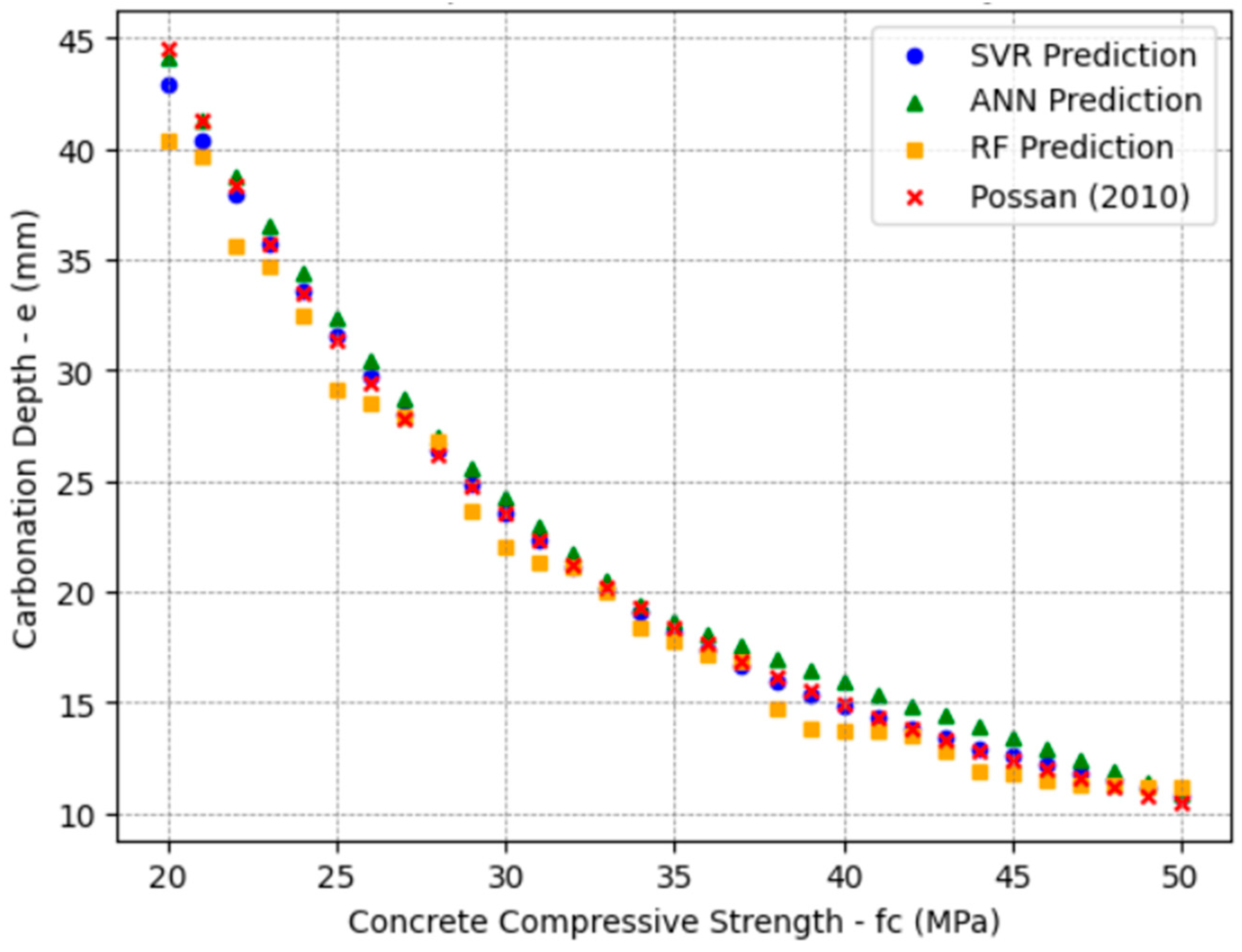
The adopted range (20–50 MPa) for concrete strength corresponds to Strength Class Group I concretes, as established by the Brazilian standard NBR 8953 [
50]. The dataset was appropriately restricted because most existing RC structures fall within this group.
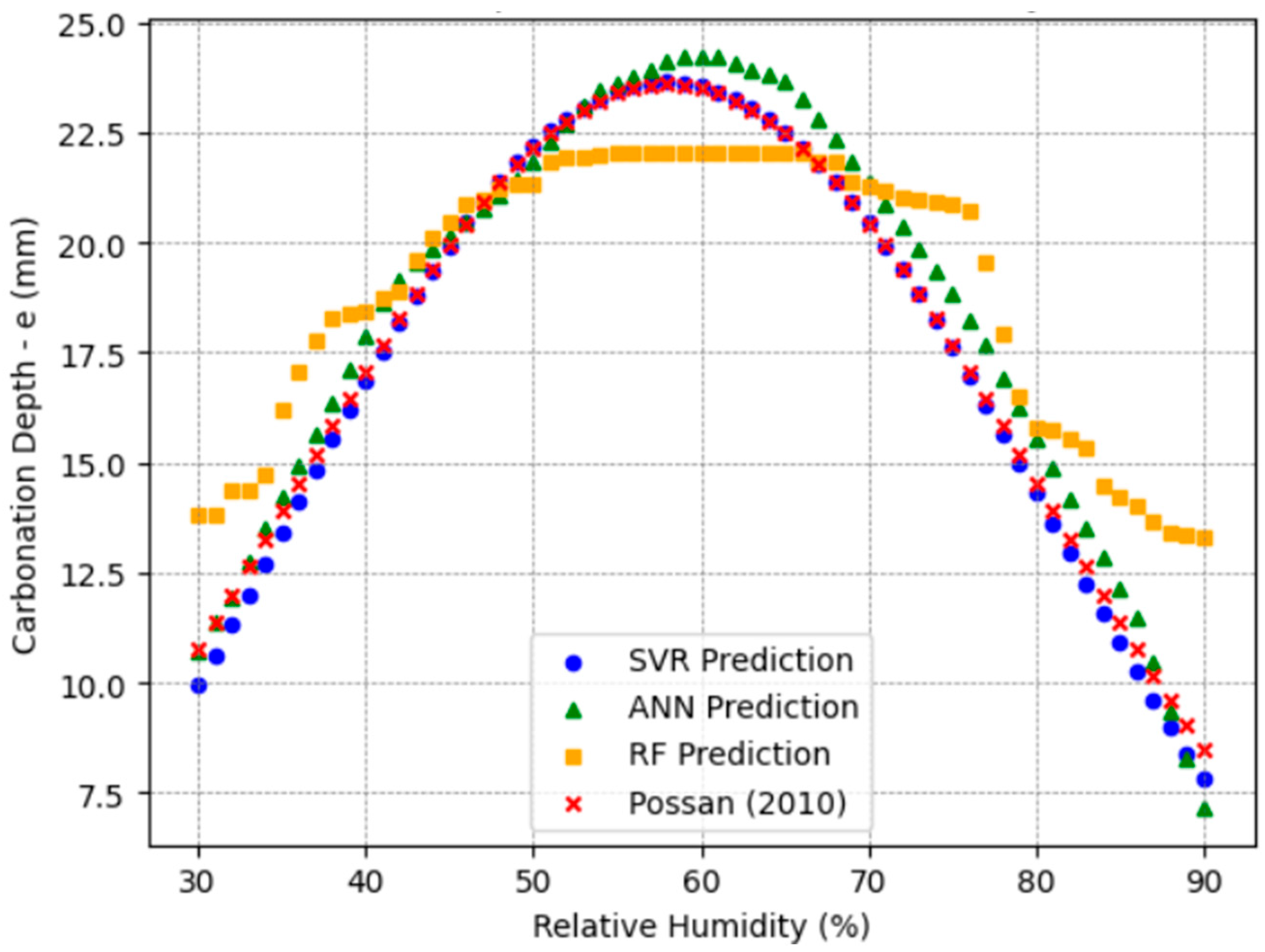
Regarding relative humidity, carbonation rapidly advances within the 50–70% range [
20,
46]. Thus, variations between 30% and 90% were considered to capture accelerated carbonation and protective effects caused by very low or very high humidity, reflecting global conditions.
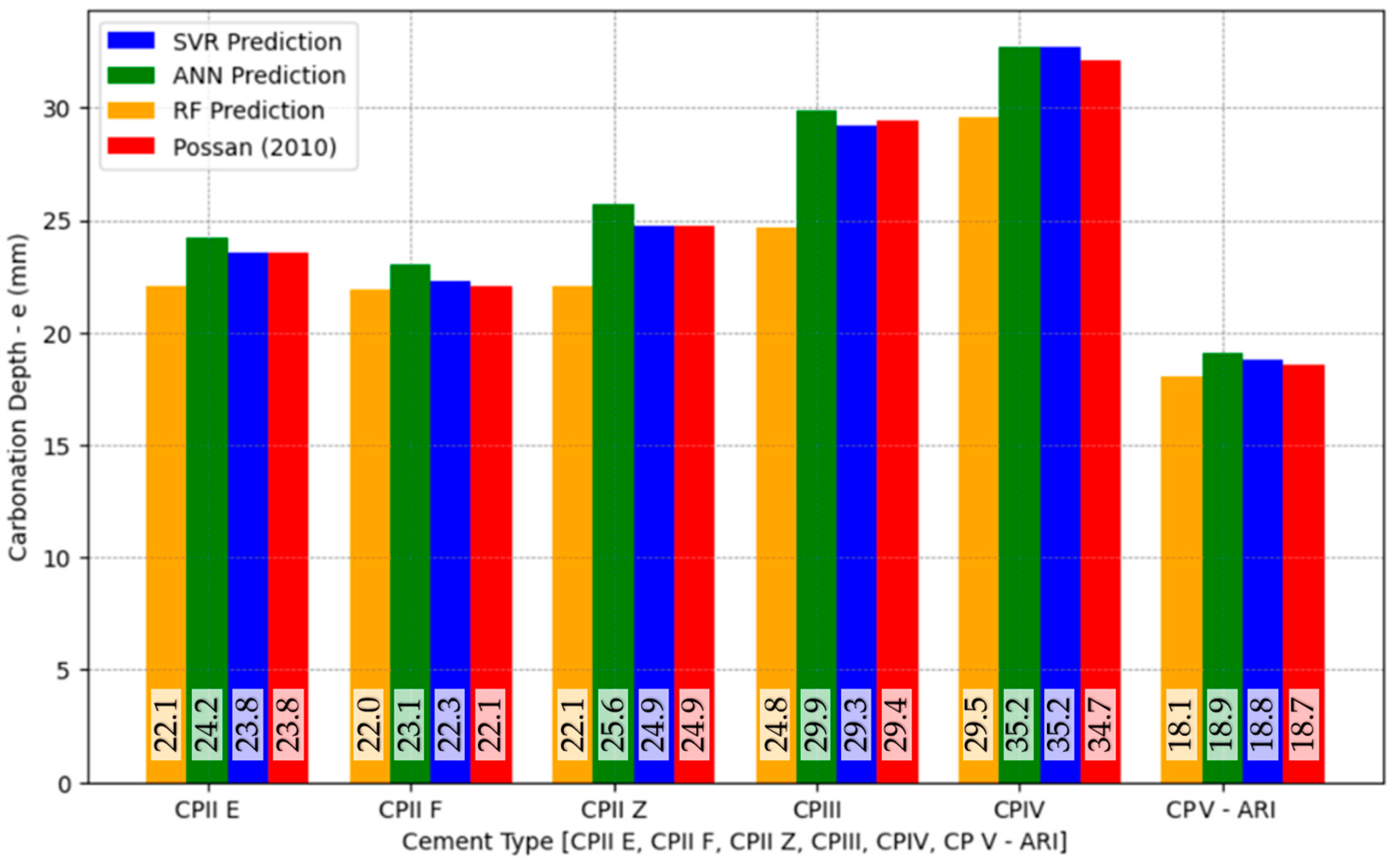
The approximate chemical compositions of the cement, based on typical formulations available in the Brazilian market and according to NBR 16697 [
51], are as follows: CPII E contains about 70–80% clinker and 15–25% blast furnace slag; CPII F has approximately 70–80% clinker and 10–20% limestone filler; CPII Z comprises around 70–80% clinker and 15–25% pozzolanic materials; CPIII typically contains only 25–35% clinker and a high proportion of slag (60–70%); CPIV includes about 55–65% clinker and 25–40% pozzolans; and CPV-ARI is characterized by more than 90% clinker with minimal additions. These differences in clinker content are critical because carbonation resistance tends to decrease with lower clinker levels, as pozzolans and fillers generally provide less alkalinity buffering capacity. It is important to note that CPI (pure Portland cement) and RS (sulfate-resistant cement) were deliberately omitted from the analysis. Although CPI has a high clinker content similar to CPV-ARI, it offers no significant differentiation in carbonation resistance compared to CPV-ARI. It is rarely used in Brazilian conventional construction. Likewise, RS cement, which is designed explicitly for sulfate resistance with a chemical composition optimized for that exposure condition, was excluded due to its limited applicability in typical carbonation-prone environments [
52]. Therefore, the cements analyzed in this study represent the most commonly used types in Brazilian practice and offer wide variability in clinker factors, ensuring a meaningful investigation into their influence on carbonation behavior and ML model predictions.
Exposure conditions were categorized as Protected Indoor (AIP), Protected Outdoor (AEP), and Unprotected Outdoor (AED) environments, aligned with the classifications embedded in the Possan equation. This classification takes into consideration air circulation, CO2 concentration retention, and the effect of rain exposure on carbonation rates.
The preprocessing of the dataset is an important step in preparing the data for ML models. For this, a BaseEstimator class was implemented in Python and designed to handle various ML models (SVR, ANN, and RF). This class manages the preprocessing of input data, applies necessary transformations, and returns the trained model, which is then used for carbonation depth prediction. The preprocessing step explicitly addresses converting categorical features into a numerical format suitable for ML algorithms. In this case, the One-Hot Encoding (OHE) technique was employed to process the type of cement and features of exposure conditions, as these are categorical variables. OHE creates a separate binary column for each category within these features, assigning numerical values (1 or 0) to represent each category. This approach showed superior performance in early predictive evaluations. All models were trained using cross-validation to ensure generalization and robustness. The extensive dataset, containing 20,000 instances, enabled a comprehensive evaluation of the carbonation depth prediction models, resulting in reliable and consistent outcomes.
At this stage, no experimental datasets were incorporated for model benchmarking. As a future direction, incorporating small-scale experimental datasets is recommended to benchmark and verify the robustness of the trained models, particularly for carbonation depths within the typical service life range.
2.2. Design and Evaluation of the Performance of ML Methods
This study applied three ML approaches—RF, SVR, and ANNs—to predict the carbonation depth in RC structures. These three models were selected based on the literature (
Section 1), which identified RF, SVR, and ANNs as the most commonly applied and effective ML techniques in carbonation depth prediction studies. Their use in this research allows for consistency with existing works while providing a robust comparative assessment of their performance using the synthetic dataset.
ML models require an appropriate configuration of hyperparameters to ensure optimal performance. Hyperparameters are parameters set prior to the learning process, which influence how the model is trained and how well it generalizes. For instance, in ANNs, defining the number of neurons in the hidden layers is essential according to the specific application. To avoid overfitting during hyperparameter optimization, the dataset was randomly divided into two subsets: a validation set comprising 8000 instances and an evaluation set with 12,000 instances. The validation set was used exclusively for hyperparameter tuning, while the evaluation set was reserved for assessing model performance after optimization.
Hyperparameter tuning uses the Grid Search with Cross-Validation (Grid Search CV) technique. This method exhaustively explores all possible combinations of selected hyperparameters and identifies the set that provides the best performance based on a chosen metric. The performance of the models during hyperparameter optimization was evaluated through the coefficient of determination (
R2), defined by Equation (2).
where
ei is the carbonation depth value calculated by the deterministic equation,
is the mean of the deterministic carbonation depths,
pi is the carbonation depth value predicted by the ML model, and
is the mean of the predicted values.
For the RF model, the hyperparameters investigated were
min_samples_split, tested with values of 0.01, 0.005, and 0.0025, and
max_features, tested with values of 10, 8, 6, and 4. The
min_samples_split parameter defines the minimum number of instances required to split a node, while
max_features specifies the number of features considered at each split [
36]. Additionally, the number of estimators (
n_estimators)—representing the number of trees in the forest—was tested with values of [1, 5, 10, 20, 30, 50, 100, 150, 200, 300, 400, and 500], with the best performance achieved using 500 estimators. The optimal configuration for RF was obtained with
min_samples_split = 0.0025 and
max_features = 10.
For the SVR model, the parameters evaluated included the
kernel function, which was fixed as ‘
rbf’, the penalty parameter
C, with tested values of 1, 1024, 2048, 4096, and 10,000, and the margin of tolerance
epsilon, with values of 0.30, 0.25, 0.20, 0.15, 0.10, and 0.05. The kernel function enables the model to handle nonlinear relationships; the penalty parameter
C controls the trade-off between achieving a low error on the training data and maintaining a simplified decision boundary; and
epsilon defines the width of the margin within which no penalty is applied to errors [
36]. The best performance for SVR was achieved with
kernel = rbf,
C = 10,000, and
epsilon = 0.30.
Regarding the ANN, the hyperparameters tested were the initial learning rate (
learning_rate_init), evaluated with values of 1, 0.1, 0.01, and 0.001, the number of neurons in the hidden layer (
hidden_layer_sizes), tested with configurations of (100), (50), (25), and (10), and the maximum number of training iterations (
max_iter), tested with values of 500, 200, 100, 50, 25, and 10. The
learning_rate_init controls the magnitude of updates to the model’s weights during training; the
hidden_layer_sizes parameter defines the model’s capacity to capture complex patterns; and the
max_iter parameter sets the limit for the number of training epochs [
53]. The ANN model performed best with
learning_rate_init = 0.001,
hidden_layer_sizes = (100), and
max_iter = 500.
A fixed random state was employed to ensure the reproducibility of the results and facilitate the future replication of the study by other researchers. For the RF model, random_state was set to 10, and for the ANN model, random_state was set to 1. The random_state parameter controls the internal randomization processes of each model, such as the initial split of samples in RF or the initial weights in the ANN, ensuring consistent results across multiple runs. This practice is particularly recommended in ML applications involving stochastic components.
After identifying the best hyperparameter configuration for each model, the evaluation set containing 12,000 instances was used to validate model performance. To ensure a robust assessment, a five-fold cross-validation procedure was adopted. This approach divided the evaluation set into five parts, which were alternately used as the validation set. In contrast, the remaining parts were used for training, thus ensuring that each instance contributed to the training and validation phases.
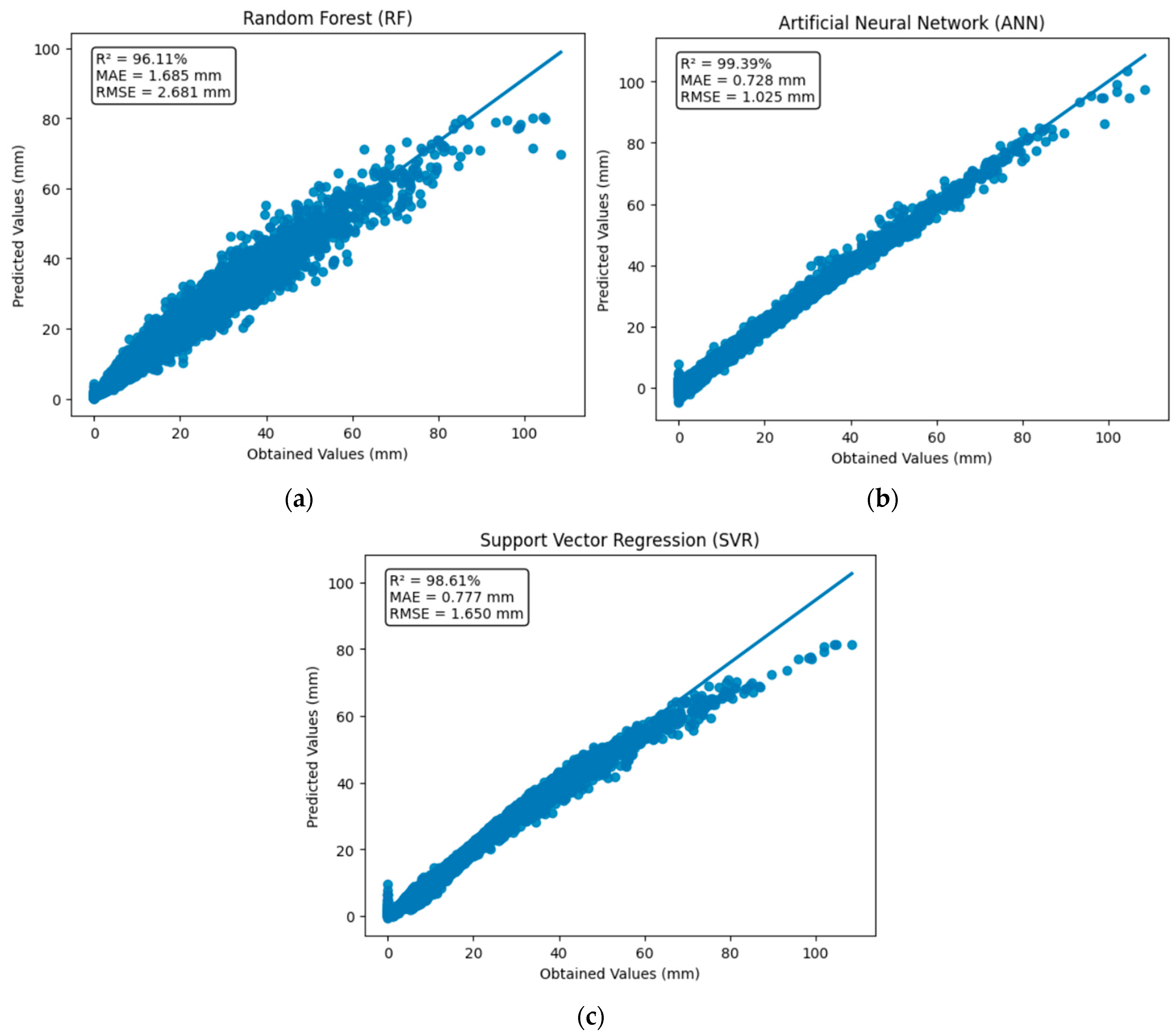
For the final performance evaluation of the models, besides the coefficient of determination (R
2), the mean absolute error (MAE) and the root mean square error (RMSE) were also calculated, according to Equations (3) and (4).
where
ei is the carbonation depth value obtained by the deterministic equation,
pi is the carbonation depth predicted by the ML model, and n is the total number of instances.
The evaluation metrics obtained allowed for a complete comparison of the predictive capacity of each ML method in forecasting carbonation depth in RC, thus ensuring the reliability of the adopted models for different scenarios.