Abstract
This study introduces a comprehensive physical modeling framework for phototransistors based on quasi-two-dimensional transition metal dichalcogenides, with a particular emphasis on MoS2. By integrating electromagnetic simulations of optical absorption with semiconductor transport calculations, the model captures both dark and photocurrent behaviors across diverse operating conditions. For 20 nm MoS2 films, the model reproduces the experimental transfer characteristics with a threshold voltage accuracy better than 0.1 V and achieves quantitative agreement with photocurrent and dark current values across the full range of gate voltages, with the worst-case deviation not exceeding a factor of seven. Additionally, the model captures a three-order-of-magnitude increase in the photocurrent as the MoS2 thickness varies from 4 nm to 40 nm, reflecting the strong thickness dependence observed experimentally. A key insight from the study is the critical role of defect states, including traps, impurities, and interfacial imperfections, in governing the dark current and photocurrent under channel pinch-off conditions (Vg < −1.0 V). The model successfully replicates the qualitative trends observed in experimental devices, highlighting how small variations in film thickness, doping levels, and contact geometries can significantly influence device performance, in agreement with published experimental data. These findings underscore the importance of precise defect characterization and optimization of material and structural parameters for 2D-material-based phototransistors. The proposed modeling framework serves as a powerful tool for the design and optimization of next-generation phototransistors, facilitating the integration of 2D materials into practical electronic and optoelectronic applications.
1. Introduction
Two-dimensional (2D) graphene-like materials are among the most actively studied materials due to their unique electronic, optical, and mechanical properties [1]. Since the discovery of graphene, a multitude of other 2D materials have been explored, including transition metal dichalcogenides (TMDCs) such as MoS2, WS2, and MoSe2 [2]. These materials exhibit properties such as high carrier mobility, strong light–matter interactions, and mechanical flexibility, making them promising for a broad range of applications in micro- and nanoelectronics, optoelectronics, sensing, and energy storage [3,4,5,6].
Among the various TMDC-based device concepts, phototransistors have garnered special attention for their potential to achieve high sensitivity and rapid response times across a broad range of wavelengths [7,8]. Their performance arises from the direct bandgap of monolayer TMDCs, which simplifies the light absorption process and leads to efficient electron–hole pair generation. While these materials hold great promise for enabling a wide range of innovative devices, significant challenges remain in terms of material quality, scalability, and device integration [9].
However, despite the promising laboratory demonstrations, commercially viable 2D-material-based electronic and optoelectronic devices remain scarce. One of the primary obstacles is the difficulty in synthesizing large-area 2D films with high crystalline quality, uniform thickness, and controllable defect densities. Although chemical vapor deposition, molecular beam epitaxy, and mechanical exfoliation have achieved substantial progress in producing such films [10], variations in synthesis routes lead to significant discrepancies in defect concentration, layer thickness, and interface properties. Consequently, device-to-device variability is high, complicating the reliability and reproducibility needed for market adoption.
This issue is particularly critical in photodetectors—especially phototransistors—where the photocurrent and key performance metrics, such as responsivity, detectivity, and spectral selectivity, can vary by orders of magnitude between nominally identical devices. Several experimental works report high responsivities for specific designs from mA/W to GA/W [11], underscoring that synthesis routes, contact geometries, and device architectures critically impact the final performance. A further complication is the poor spectral selectivity often observed in 2D photodetectors, attributed to suboptimal light–semiconductor interactions and interference effects that are highly sensitive to layer thickness and interface quality.
From a theoretical perspective, modeling phototransistor structures is notably more challenging than modeling simpler transistor configurations. Phototransistors require the coupling of optical and electrical phenomena, including carrier generation, transport, and recombination in the presence of defect states and Schottky contacts. These phenomena must be captured in three-dimensional (3D) or at least quasi-3D computational domains to accurately account for lateral contacts, depletion regions beneath the electrodes, and complex interface effects. While simplified two-dimensional approximations can be used in certain cases, they may fail to reproduce the localized field distributions or edge effects that are critical for device performance.
An even greater challenge arises in modeling advanced phototransistors that incorporate plasmonic ordered structures [12,13], metasurfaces [14], or optical microcavities [15] to enhance photocurrent. In such devices, spatial inhomogeneities in the electromagnetic and electric fields become significant, making comprehensive three-dimensional modeling indispensable. Thus, the combined demand for 3D simulations and sophisticated experimental verification adds a layer of complexity rarely encountered in conventional transistor studies.
Despite these difficulties, some theoretical works have attempted to describe the electronic and optoelectronic behavior of 2D phototransistors [16,17]. However, many of these studies focus on simpler transistor-type structures, neglecting full phototransistor operation in the presence of variable illumination, spectral selectivity, and pronounced contact effects. For instance, certain articles concentrate primarily on Schottky barrier formation [18], providing valuable insights into the ways thermionic emission and tunneling govern dark current and contact resistance. Other studies address phototransistor simulations but assume idealized one-dimensional optical models [19]. Consequently, direct comparisons between theory and experiment often remain inconclusive, particularly for quasi-2D or thicker MoS2 films.
In fact, a number of studies report partial correlation between simulated and measured characteristics; however, a comprehensive coupled model that bridges the gap between optical absorption and detailed semiconductor transport (including defect states, interfacial effects, and realistic contact geometries) is still lacking. Moreover, most reported theoretical works do not offer side-by-side comparisons to experiments across multiple wavelengths and device thicknesses. Hence, it is clear that more advanced physical modeling—carried out in tandem with carefully characterized experimental structures—remains a pressing need in the field of 2D photonics and nanoelectronics.
This study seeks to address these gaps by developing and validating a multiphysics model for phototransistors based on MoS2 and quasi-2D thicker films. We integrate optical absorption simulations with detailed semiconductor transport calculations that account for thermionic emission, tunneling, and defect-mediated carrier dynamics. A particularly strong emphasis is placed on capturing the role of defect states, thickness effects, and interfacial phenomena in determining photocurrent and dark current. By comparing our simulations to experimental data from [20]—covering multiple film thicknesses, photon wavelengths, and gate biases—we demonstrate a robust correlation between measured and simulated device behavior. Our work thus provides a direct comparison of theory and experiment for quasi-2D phototransistors, aiding the rational design and optimization of such devices for future technologies.
2. Materials and Methods
To perform reliable physical modeling, it is essential to base the simulation on the geometry of a real device. This approach not only confirms the validity of the modeling results but also ensures their relevance to practical applications by aligning closely with experimentally obtained operational characteristics. It is equally critical to use a two-dimensional material with well-documented optical and electronic properties, as relying on poorly characterized materials could reduce modeling efforts to mere parameter fitting, undermining the physical insight provided.
MoS2 has traditionally been favored for such applications due to its exceptional properties. As a monolayer material, MoS2 exhibits a direct bandgap (~1.8 eV), making it highly efficient for light absorption and electron–hole pair generation in the visible spectrum. Additionally, it demonstrates strong photoconductive responses, high chemical stability, and compatibility with established fabrication techniques. These characteristics position MoS2 as the most studied and widely adopted material for 2D phototransistors [21].
Also important is the method of creating two-dimensional films. Mechanical exfoliation is the preferred approach as it ensures minimal defect density in the material. This simplifies the modeling process by reducing the complexities associated with non-uniform defects, thereby enhancing the accuracy and reliability of simulations when compared to experimental data [22].
For this study, the work [20] was chosen as an ideal reference. This selection is particularly advantageous because the authors provided not only experimental results on the optical properties and operational characteristics of the devices created but also other critical experimentally derived data on the material properties. While the referenced study employed quasi-two-dimensional MoS2 films, this does not pose a significant limitation as long as all optical and electronic parameters for the material are well-documented. Furthermore, the availability of experimental data for films with varying thicknesses and geometries enables a more thorough validation of the proposed model, ensuring its accuracy and applicability across a range of device configurations.
The schematic representation of the selected phototransistor design is shown in Figure 1. It features a quasi-two-dimensional MoS2 layer positioned on a dielectric film—50 nm of Al2O3, which in turn, is supported by a Si substrate. Al2O3 was chosen for its higher absorption coefficient compared to SiO2, which not only reduces the device’s energy consumption but also aids in visualizing the quasi-2D material layers.
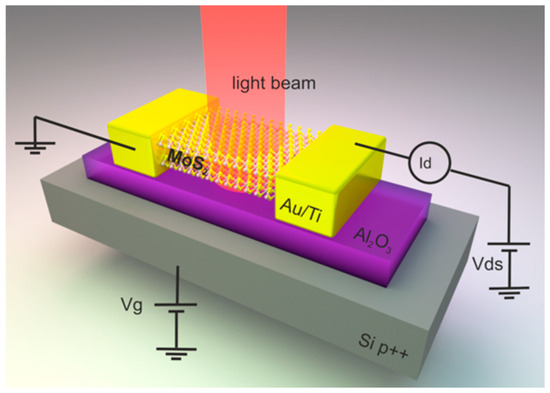
Figure 1.
Schematic representation of the phototransistor based on quasi-two-dimensional transition metal dichalcogenide film.
In this study, transitioning to a 2D model geometry was deemed optimal due to the system’s inherent depth symmetry. Unlike in the actual experimental setup, the electrodes in the model are connected laterally to the quasi-2D layer rather than being deposited on top. This simplification serves two purposes: first, it significantly reduces computational resource requirements; second, it ensures an accurate representation of the Schottky barrier, whose thickness substantially exceeds that of the monolayer [18].
In the model, the thickness of the gold electrodes is set to be greater than that of the quasi-2D film. However, as will be demonstrated later, this parameter has negligible influence on the simulation outcomes. Apart from these modifications, the configuration follows a conventional design paradigm.
All simulations were conducted using the Comsol Multiphysics 5.2, which provides a robust framework for modeling complex multi-physics phenomena. The software’s capabilities were essential for accurately simulating the coupled optical and electronic processes in quasi-2D phototransistors. Specifically, the Wave Optics Module was employed to model the interaction of electromagnetic radiation with the photodetector, enabling precise calculation of the electric field distribution, energy flux, and optical absorption within the thin MoS2 layer. For semiconductor properties, the Semiconductor Module facilitated the simulation of charge carrier dynamics, including the calculation of potential distribution and charge carrier concentrations under various operating conditions.
The overall workflow can be divided into three main stages:
- Optical Modeling. First, we simulated how electromagnetic radiation interacts with the photodetector and its photosensitive layers—namely the quasi-2D MoS2. This step generated essential data on the electric field distribution, energy flux, and optical absorption within the semiconductor film, forming the foundation for the subsequent phases.
- Dark Current Analysis. Next, we modeled the intrinsic semiconductor properties in the absence of illumination, effectively treating the device as a conventional transistor. This involved calculating the potential distribution and charge carrier concentrations, which served as the initial conditions for the final stage.
- Photocurrent Evaluation. In the final step, we combined the outcomes of the optical and semiconductor simulations to assess the phototransistor’s optical sensitivity. This integrated approach provided a comprehensive evaluation of the device’s performance under realistic operating conditions.
All the parameters used in this work are summarized in Table 1. A detailed description of the physical models and the primary equations can be found in Supplementary S1.

Table 1.
Main parameters used in the model.
3. Results
3.1. Optical Radiation Modeling
Modeling optical absorption was the most straightforward task in terms of both computational resources and interpretation of the results. To simplify the model, we excluded the interaction of incident electromagnetic waves with the gold electrodes. This simplification is justified because the electrodes are completely opaque to the incident optical radiation, effectively shielding the quasi-2D semiconductor beneath them. Consequently, the semiconductor regions under the electrodes do not contribute to the photocurrent.
While the edges of the electrodes can cause localized scattering of light, potentially altering the power distribution in their immediate vicinity, this effect has a negligible impact (<1%) on absorption in the quasi-2D layer at wavelength of 400 nm. This conclusion derives from electromagnetic simulations of our reference geometry [20], which assumes smooth, planar gold electrodes with a 100 nm thickness—parameters chosen to match the experimental configuration. Under these conditions, the electrodes’ opacity creates optical shadowing that suppresses plasmonic enhancement effects and limits edge-related absorption contributions to sub-1% levels, as quantified in Supplementary S2.
Additionally, the illumination of the metallic electrode structures may affect the photoconductive properties of the 2D films via the photothermoelectric effect [26]. In our model, we intentionally restrict illumination to the inter-electrode channel region, excluding metallic contact areas entirely. This design choice eliminates the potential for localized heating gradients near contacts—a prerequisite for measurable photothermoelectric contributions—while ensuring that optical losses from metal reflection and absorption do not compromise the effective photon flux reaching the active semiconductor region. Under these conditions of symmetric lateral electrodes and uniform channel illumination, any opposing thermoelectric voltages generated at the contacts would cancel each other out, rendering the photothermoelectric component negligible compared to the dominant photoconductive mechanisms [27].
Considering these factors, we excluded the metallic electrodes from the initial simulation stage. Instead, a simplified two-dimensional configuration was used, consisting of the following layers: air/MoS2/Al2O3/Si. This assumption was made under the condition that the light was restricted to the inter-electrode gap, ensuring that the simulation remained accurate while avoiding unnecessary complexity.
All optical coefficients for the materials used in the simulations were sourced from experimentally obtained data reported in the literature. Specifically, for MoS2, the data from [23] were utilized. This reference is particularly valuable as it provides not only spectral dependencies but also absorption characteristics as a function of MoS2 thickness, which is critical for the accuracy of the modeling.
When constructing the computational mesh, special attention was given to the unique requirements of thin quasi-2D structures. The mesh size needed to be on the same order of magnitude as the subwavelength features of the material, not only within the MoS2 layer itself but also in the surrounding domains. This level of detail ensures accurate resolution of the electromagnetic field distribution.
It is important to note that in addition to the electromagnetic field distribution, the key output for the simulations is the optical absorption within the quasi-2D layer. This is because absorbed photons in the semiconductor are directly converted into electron–hole pairs, which ultimately determine the photocurrent generated by the device.
The wavelength-dependent absorption in the MoS2 film was calculated for various MoS2 film thicknesses, and the results are shown in Figure 2 as solid lines. These calculated dependencies qualitatively correlate with experimental data presented as discrete points in [20]. Notably, there is strong agreement in the positions of the absorption peaks.
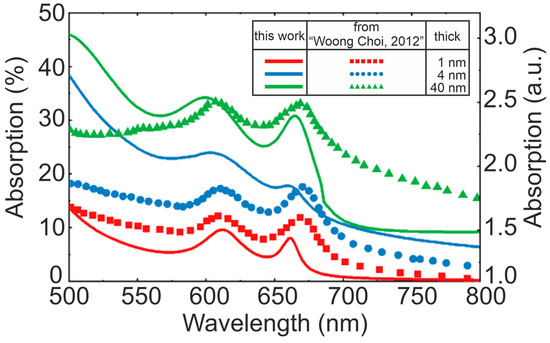
Figure 2.
Absorption spectra of MoS2 layers with varying thicknesses. The solid lines represent the calculated dependencies, while the points correspond to reference data from [20].
Some discrepancies between the simulated and experimental results can be attributed to the inherent challenges in obtaining precise absorption measurements in thin films. This is why the referenced study appropriately presents its results in relative units. It is also important to note that, for such systems, absorption is influenced by both conventional Beer–Lambert absorption and multi-beam interference effects [28], which slightly distort the observed dependencies. These contributions are discussed in greater detail in Supplementary S3. It also presents the results of modeling the dependence of optical absorption in the MoS2 film on its thickness and wavelength of incident light, which is important for determining the highest efficiency of photosensors.
To further validate the optical model proposed in this study, a series of parametric simulations were conducted, focusing on the classical problem of contrast enhancement for a 2D MoS2 film on a substrate with varying oxide thickness. The results of these simulations, detailed in Supplementary S4, exhibit full numerical agreement with the benchmark data reported in [29]. This consistency underscores the accuracy and reliability of the optical model used in this study.
It is important to note that the number of electron–hole pairs generated is proportional to photon absorption. However, this does not directly correspond to the photocurrent measured at the electrodes. As such, these absorption dependencies are intermediate results and can only be used for a rough estimation of the device’s efficiency.
3.2. Dark Current Modeling
The next stage involved modeling the processes responsible for the dark current in the studied structures. Given that the contribution of air to current formation is negligible, the air region was excluded from the calculations. However, it became necessary to account for the electrodes on the surface of the 2D semiconductor and the region beneath these electrodes.
If the silicon substrate is heavily doped and can be considered equipotential (with low resistance), its role in shaping the potential distribution in the upper part of the structure is minimal. Therefore, in a simplified approach, silicon does not need to be modeled as a full-fledged semiconductor. Instead, it can be replaced entirely with a boundary condition of fixed potential, or only a small portion of the substrate can be constructed in the model.
A key feature in this context is the formation of a depletion region in the 2D material beneath the electrodes, as detailed in [18]. To accurately account for this zone in the model, an additional thin domain was introduced, with a thickness no less than the Debye length (approximately 20 nm for MoS2). The mesh in this region was refined to a high density, as this is where the Schottky barrier forms and the charge carrier distribution undergoes the sharpest changes. Moreover, the proper tuning of the operation of this metal-semiconductor junction can play a crucial role for the studied two-dimensional materials, as demonstrated in Supplementary S5.
At the metal–semiconductor interface, charge transport occurs via thermionic emission (described by the Richardson–Schottky equation) and tunneling, either direct or Fowler–Nordheim. At sufficiently high temperatures, carriers overcome the barrier thermally, while at lower temperatures or under high electric fields, tunneling becomes the dominant mechanism. Both processes must be incorporated into the model to avoid underestimating the dark current.
During the modeling process, several parameters of the MoS2 film were identified as critical variables requiring careful optimization. Charge carrier mobility exhibits a well-documented thickness dependence in exfoliated MoS2 films, showing a non-monotonic relationship with maximum values (~90 cm2V−1s−1) occurring at ~7 monolayers (≈4 nm) [30]. For our 20 nm thick quasi-2D films—substantially thicker than the optimal monolayer count—literature reports indicate mobility reduction due to interlayer scattering and defect accumulation. Through systematic parameter sweeps across the reported experimental range (0.01–100 cm2V−1s−1), we identified 65 cm2V−1s−1 as providing optimal agreement with experimental transfer characteristics while remaining consistent with thickness-dependent mobility trends. This differs from effective mobility, which depends on transistor operating conditions and additional scattering mechanisms.
Similarly, the donor concentration (5 × 1017 cm−3) was selected from the established literature range (1016–1018 cm−3). This value accounts for intrinsic doping levels in mechanically exfoliated MoS2 while compensating for defect-induced carrier compensation effects observed in thicker films.
The resulting transfer characteristics for several source voltage values are shown in Figure 3 for a MoS2 film with a thickness of 20 nm. The data demonstrate good agreement across the simulations, confirming the model’s validity, at least under the operating conditions of a standard transistor. The obtained curves exhibit the expected behavior for semiconductor films, showing that the channel is effectively blocked at negative effective gate voltages (Veff = Vg − Vth).
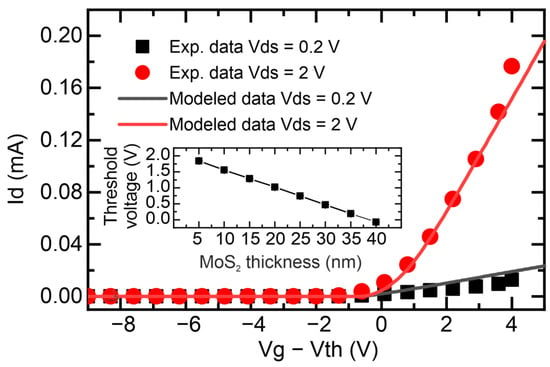
Figure 3.
Transfer characteristics for a quasi-2D MoS2 film with a thickness of 20 nm. Solid lines represent the calculated dependencies, while points correspond to reference data from [20].
To further confirm the reliability of the simulation results, additional plots illustrating the dark current dependencies were constructed and are presented in Supplementary S6. These supplementary graphs include the dependence of current on output characteristics. These additional results provide further validation of the modeled behavior and highlight key performance parameters of the device.
To further validate the channel blocking effect and analyze its dependence on the thickness of the MoS2 film, carrier concentration maps were generated. These are presented in Supplementary S7.
The MoS2 film effectively acts as an integrated channel. As a result, the film thickness has a significant impact on the effective gate voltage. Simulations revealed that the threshold voltage (Vth) exhibits a linear dependence on the thickness of the MoS2 film, as shown in the inset of Figure 3. This thickness-dependent behavior is attributed to the redistribution of the electric field in the “gate-channel” system, where a thicker channel screens the gate’s influence on charge carriers. A more detailed explanation of this relationship, along with the transfer characteristics from which it was derived, can be found in Supplementary S8.
The depletion region depth in the semiconductor, which forms under an applied bias across the Schottky barrier, was also evaluated. The results indicate that this depth varies with the thickness of the MoS2 layer and can reach up to 50 nm (see Supplementary S9).
This stage of the modeling is essential for assessing the photocurrent, as it ensures the accuracy of the geometric parameters and material properties used in the simulations. Additionally, it provides the necessary “dark state” initial conditions for the final stage, where the structure is subjected to optical excitation.
3.3. Photocurrent Modeling
In the final stage, the models developed in the previous steps were combined into a unified framework. Since the initial conditions for the “dark state” had already been established and the optical field distribution was pre-calculated, this stage required fewer computational resources compared to earlier steps. The main distinction in this phase was the inclusion of a module to simulate charge carrier generation resulting from photon absorption.
It is also important to note that in this configuration, achieving the maximum ratio of photocurrent to dark current requires operating in the pinch-off regime. Under strongly negative gate voltages (Vg − Vth), where the channel “pinches off” and the structure’s conductivity decreases, leakage currents in the absence of illumination (dark current) are minimized. While this operating mode reduces the overall current level (including both dark and photocurrent), the signal-to-noise ratio improves, leading to enhanced photosensitivity. This approach is standard practice for phototransistor structures, whether based on two-dimensional films or more traditional semiconductor channels.
A major challenge in modeling the pinch-off regime is accurately capturing the dark current, which often appears significantly lower in simulations than in experiments. The discrepancy arises primarily from the incomplete representation of defect-driven processes: in two-dimensional materials such as MoS2, even a minimal number of localized traps or impurities can significantly affect carrier generation and recombination under strongly negative gate voltages. As the channel current becomes extremely low in this regime, small defect-induced currents can dominate. Consequently, if the model does not comprehensively account for distributed trap states and other defect-related phenomena—ranging from surface to interlayer and volumetric gradients—the resulting dark current values will inevitably be underestimated. Indeed, Supplementary S10 shows that both mobility and defect concentration critically influence the simulated dark current.
Under illumination, these same defects can either enhance or suppress the photocurrent, depending on their specific capture and recombination mechanisms. As a result, any mismatch between simulated and experimental data should be attributed primarily to the dominant influence of defects in determining both dark and photocurrents in the pinch-off regime.
Despite accounting for various factors, including trap density, donor impurities, Shockley–Read–Hall recombination, and surface traps, discrepancies with experimental data persist (Figure 4a–c). Notably, the model aligns closely with measured data at Vg − Vth > 0 due to carefully selected parameters. However, as soon as the induced channel is fully depleted, noticeable deviations arise, with errors reaching up to a factor of seven. Such discrepancies are not unexpected and may be attributed not only to inherent limitations in the modeling approach but also to variations in the fabricated films and electrode structures that affect the reliability of experimental measurements.
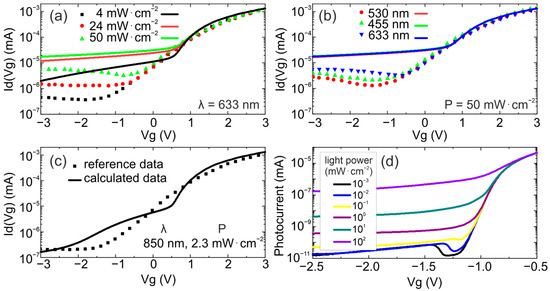
Figure 4.
Photocurrent dependence on gate voltage at a fixed wavelength of incident light (a) and at a fixed power of incident radiation (b). Solid lines represent the calculated dependencies, while points correspond to reference data from [20]. Photocurrent dependence (c) for 850 nm and 2.3 mWcm2 incident light radiation. Vds = 1V. Transfer characteristics (d) exhibiting negative differential resistance (NDR) behavior in the gate voltage range Vg = −1.5 to −1.0 V, with the effect diminishing at higher incident optical powers.
Furthermore, temperature variations significantly influence photocurrent through thermally activated carrier detrapping mechanisms beyond simple thermionic emission and tunneling effects. Experimental studies demonstrate that photocurrent exhibits a pronounced linear increase with temperature, attributed primarily to thermally assisted photobolometric electron detrapping from shallow intragap states such as sulfur vacancies. This process operates with a characteristic time constant τ1 ~ 10 s, corresponding to electrons being released from shallow trap states under the combined effect of thermal and optical energies [31]. At elevated temperatures, enhanced thermal energy facilitates the photoinduced detrapping process, where trapped electrons in defect states gain sufficient energy to overcome the shallow potential barriers and contribute to conduction. Our temperature-dependent modeling captures these thermally activated detrapping mechanisms and reproduces the experimentally observed enhancement of photocurrent with increasing temperature, validating our approach to defect characterization and trap state modeling. The detailed temperature-dependent photocurrent calculations and their comparison with experimental trends are presented in Supplementary S11, demonstrating quantitative agreement between our model predictions and the measured temperature coefficients of photoresponse.
Additionally, uncertainties in optical absorption due to surface imperfections in quasi-two-dimensional layers and at the MoS2–dielectric interface can significantly affect the results. Nevertheless, the simulated transfer characteristics still exhibit good qualitative agreement with experimental observations, particularly when varying optical power or illumination wavelength.
The transfer characteristics also exhibit negative differential resistance (NDR) behavior (Figure 4d), which manifests as a decrease in current with increasing voltage, resulting in an unconventional current–voltage characteristic. This phenomenon has been increasingly observed in phototransistors based on two-dimensional and quasi-two-dimensional materials, particularly such as MoS2 and WSe2 [32]. The NDR effect in such structures presents significant opportunities for implementing logic devices, oscillators, and highly sensitive photodetectors with controllable electrical characteristics. As evident from the transfer characteristics, the device investigated in this work exhibits an NDR region in the gate voltage range of Vg = −1.5 to −1.0 V. Notably, this effect diminishes with increasing incident optical power and disappears at approximately P = 0.1 mW/cm2.
The physical origin of NDR in these phototransistors arises from a complex interplay of charge accumulation, trap states, space charge effects, thermionic emission, and contact barrier phenomena. Localized trap states, originating from defects within the material bulk or at substrate interfaces, can capture charge carriers and form space charge regions, leading to reduced conductivity as voltage increases. Poole–Frenkel thermionic emission plays a crucial role in this process, as electrons overcome energy barriers and are released from traps under elevated electric fields; however, simultaneously, other trap states begin to capture carriers intensively, resulting in current reduction [33]. Additionally, Schottky contact barrier effects significantly influence the NDR behavior by modifying the effective barrier height as a function of applied voltage [34].
Material parameters including layer thickness, doping concentration, contact type, and defect density critically determine the magnitude and characteristics of the NDR effect. Layer thickness variations can promote the formation of additional interlayer tunneling channels, doping modifications alter the Fermi level position and tunneling current probability, while contact materials determine the interfacial barrier characteristics [35]. The comprehensive modeling framework developed in this study incorporates all these effects, enabling qualitative assessment of device operating characteristics and providing insights into the underlying physical mechanisms governing NDR behavior in quasi-2D phototransistors. It should be noted that at lower gate voltages, the photodetector exhibits a strong sensitivity to the incident light, confirming that operating in the pinch-off region indeed optimizes the photo-detector’s response. More details on the theoretical power dependencies are given in Supplementary S12.
The spectral dependence on the different thicknesses of MoS2 was subsequently modeled. The graphs presented in Figure 5a,b reveal a relationship between the shape of the optical absorption curve and photocurrent, although the dependence on thickness is more straightforward. For example, at a wavelength of 700 nm, the absorption for thicknesses of 4 nm and 40 nm coincides (the lines in Figure 5a intersect). However, the photocurrent at this point differs by three orders of magnitude, which cannot be explained solely in terms of absorption.
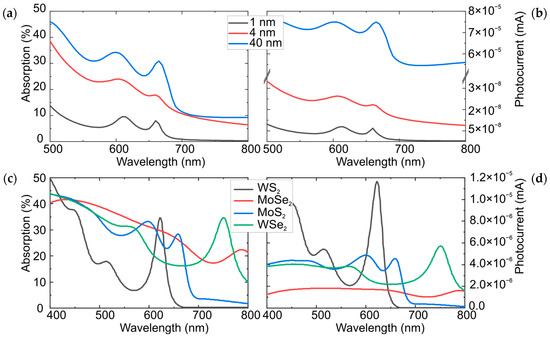
Figure 5.
(a) Spectral dependences of absorption and (b) photocurrent on optical wavelength for different MoS2 thicknesses. Dependence of (c) absorption and (d) photocurrent for different types of TMDCs.
This discrepancy arises from changes in the specific conductivity of the integrated channel. As the channel becomes wider with increasing thickness, the carrier concentration within it also increases. This phenomenon is consistent with the results presented in Supplementary S7, which provide further confirmation.
The presented modeling methodology can be adapted to analyze similar structures by modifying electrode materials, semiconductor composition, layer thickness, electrode structure, and other relevant parameters. To ensure the reliability of these simulations, accurate material parameters are essential, and it is important to account for additional physical processes, such as variations in contact resistance and interface trap dynamics, which can influence device behavior. To demonstrate this adaptability, we conducted further simulations using other common TMDC materials (WS2, WSe2, and MoSe2) with varied thicknesses and electrode configurations. For these simulations, we utilized experimentally determined physical constants for each material, sourced from reputable studies in the literature [36,37,38]. This ensured that our simulations accurately reflected the material-specific characteristics of each 2D film. The key parameters considered included bandgap, electron–hole effective masses, dielectric constant, and optical absorption spectra.
The analysis of current characteristics (Figure 5c,d) in field-effect transistors based on thin films reveals a correlation between the relative dielectric permittivity (εr) and the drain current (Id). Specifically, there is a trend indicating increased current levels in transistors utilizing channel materials with higher εr values. This phenomenon arises from the synergistic influence of electrostatic and quantum-mechanical effects, which govern both the efficiency of channel control and the resulting charge carrier concentration. The relative dielectric permittivity of the channel material directly modulates the extent of Coulomb interaction screening within the system. The magnitude of εr dictates the material’s polarizability under an external electric field, thereby affecting the efficiency with which charge carriers are induced in the channel by the applied gate voltage. Elevating εr diminishes the screening of the gate electric field, thus promoting enhanced charge modulation within the channel and augmenting the concentration of free carriers. Conversely, at diminished εr values, the heightened Coulomb interactions between charged impurity centers and mobile charge carriers lead to intensified scattering and a concomitant reduction in carrier mobility. In contrast, elevated εr values mitigate Coulomb interactions, thereby fostering increased mobility and a corresponding augmentation of drift current.
We also explicitly modeled different electrode materials to assess their impact. The results demonstrate that electrode material selection primarily influences threshold voltage positioning (±0.3 V variation), while exhibiting a negligible impact on device performance in the critical pinch-off regime, where all configurations converge to similar current–voltage characteristics (Supplementary S13). This finding is particularly relevant for optimizing device sensitivity while minimizing the impact of electrode material variations.
4. Conclusions
In this study, we developed and validated a fully three-dimensional (3D) modeling framework for phototransistors based on quasi-two-dimensional (quasi-2D) transition metal dichalcogenides, marking one of the first direct comparisons between 3D simulations and experimental devices in this field. By integrating electromagnetic simulations of optical absorption with detailed semiconductor transport calculations, our model accurately reproduces both dark and photocurrents, particularly in the pinch-off regime, where defect states (including traps, impurities, and interfacial imperfections) critically influence carrier dynamics. Although the dark current can be underestimated by up to a factor of seven in certain bias regimes, the overall agreement with experimental data confirms the validity of our approach.
Importantly, our results show that even minor changes in film thickness, doping concentration, or contact geometry can lead to substantial differences in device performance, highlighting the necessity of robust 3D modeling. Simple Fresnel-based or purely 2D approximations often fail to capture the complex field distributions and plasmonic effects that arise in more advanced phototransistor structures. By accurately reflecting these complexities, the proposed 3D methodology provides a powerful tool for designing and optimizing next-generation 2D phototransistors, paving the way for higher sensitivity, improved reliability, and more sophisticated architectures in practical nanoelectronic and optoelectronic applications.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/modelling6020047/s1: Supplementary S1—Description of the physical models; Supplementary S2—Edge effects of electrode structures; Supplementary S3—Spectral dependence of optical absorption in a DPM film on its thickness; Supplementary S4—Contrast modeling of a two-dimensional MoS2 film; Supplementary S5—Parameters of metal-semiconductor transition; Supplementary S6—Id characteristics; Supplementary S7—Charge carrier concentration in the MoS2 Film; Supplementary S8—Influence of MoS2 thickness on current; Supplementary S9—Assessment of the depletion region in MoS2; Supplementary S10—Dependence of dark current on MoS2 Characteristics; Supplementary S11—The impact of temperature on photocurrent behavior; Supplementary S12—The impact of optical power on photocurrent behavior; Supplementary S13—The impact of electrode materials.
Author Contributions
Conceptualization, S.D.L.; validation, S.D.L.; writing—original draft preparation, S.D.L. and A.A.G.; writing—review and editing, S.D.L. and A.A.G.; visualization, A.A.G.; formal analysis, A.A.G. and S.D.L.; supervision, S.D.L.; data curation, S.D.L. All authors have read and agreed to the published version of the manuscript.
Funding
The study was supported by the Russian Science Foundation [project number 24-79-10304] in the part of the semiconductor modeling of phototransistor characteristics and the Ministry of Science and Higher Education of the Russian Federation [project number FSFZ-2024-0047] in the part of the theoretical calculations of the optical components.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cao, L. Two-dimensional transition-metal dichalcogenide materials: Toward an age of atomic-scale photonics. MRS Bull. 2015, 40, 592–599. [Google Scholar] [CrossRef]
- Upadhyay, S.N.; Satrughna, J.A.K.; Pakhira, S. Recent advancements of two-dimensional transition metal dichalcogenides and their applications in electrocatalysis and energy storage. Emergent Mater. 2021, 4, 951–970. [Google Scholar] [CrossRef]
- Mir, S.H.; Yadav, V.K.; Singh, J.K. Recent advances in the carrier mobility of two-dimensional materials: A theoretical perspective. ACS Omega 2020, 5, 14203–14211. [Google Scholar] [CrossRef]
- Zhang, S.-R.; Batool, S.; Han, S.-T.; Zhou, Y.; Idrees, M. Novel charm of 2D materials engineering in memristor: When electronics encounter layered morphology. Nanoscale Horiz. 2022, 7, 480–507. [Google Scholar] [CrossRef]
- Papadakis, R.; Liu, J.; Jafri, S.H.M.; Zheng, X.; Zhao, M.; Hao, Y.; Zhang, C.; Zhai, R.; Liu, B.; Liu, W.; et al. Advances in two-dimensional materials for optoelectronics applications. Crystals 2022, 12, 1087. [Google Scholar] [CrossRef]
- Qumar, U.; Kaner, N.T.; Cassinese, A.; Babar, Z.U.D.; Hassan, J.Z.; Raza, A. 2D material-based sensing devices: An update. J. Mater. Chem. A 2023, 11, 6016–6063. [Google Scholar] [CrossRef]
- Kuc, A.; Heine, T.; Kis, A. Electronic properties of transition-metal dichalcogenides. MRS Bull. 2015, 40, 577–584. [Google Scholar] [CrossRef]
- Dias, A.C.; Fu, J.; Qu, F.; Azevedo, D.L. Band structure of monolayer transition-metal dichalcogenides and topological properties of their nanoribbons: Next-nearest-neighbor hopping. Phys. Rev. B 2018, 98, 075202. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Peng, X.; Qiu, Y.; Liu, A.; Jiang, H.; Deng, T.; Guo, H.; Qin, Y.; Li, Y.; et al. The roadmap of 2D materials and devices toward chips. Nano-Micro Lett. 2024, 16, 119. [Google Scholar] [CrossRef]
- Yao, Z.; Jannat, A.; Zhong, L.; Ou, J.Z.; Haidry, A.A.; Zavabeti, A. Two-dimensional materials in large-areas: Synthesis, properties and applications. Nano-Micro Lett. 2020, 12, 66. [Google Scholar] [CrossRef]
- Nalwa, H.S. A review of molybdenum disulfide (MoS2) based photodetectors: From ultra-broadband, self-powered to flexible devices. RSC Adv. 2020, 10, 30529–30602. [Google Scholar] [CrossRef]
- Liu, J.; Guo, Z.; Chang, Z.; Li, J.; Guo, Y. Engineering plasmonic environments for 2D materials and 2D-based photodetectors. Molecules 2022, 27, 2807. [Google Scholar] [CrossRef]
- Stepanov, M.A.; Mishina, E.D.; Abdullaev, D.A.; Lavrov, S.D.; Guskov, A.A.; Galiev, R.R.; Shahurin, E.S. MoS2-based polarization-sensitive photodetectors with asymmetric plasmonic structures and decreased detection time. Opt. Mater. 2024, 152, 115452. [Google Scholar] [CrossRef]
- Chen, D.; Takahara, J. Absorption Enhancement of Excitons in WS2 by Silicon Huygens’ Metasurface. In JSAP-Optica Joint Symposia; Optica Publishing Group: Washington, DC, USA, 2024. [Google Scholar] [CrossRef]
- Xu, X.; Li, Z.; Wang, J.; Tao, L.; Xu, J.; Chen, Z. Enhancing light-matter interaction in 2D materials by optical micro/nano architectures for high-performance optoelectronic devices. InfoMat 2021, 3, 36–60. [Google Scholar] [CrossRef]
- Zhao, Z.; Rakheja, S.; Zhu, W.; Shukla, A.; Tunga, A. Physics-based modeling and validation of 2-D Schottky barrier field-effect transistors. IEEE Trans. Electron Devices 2023, 70, 2034–2041. [Google Scholar] [CrossRef]
- Stradi, D.; Stokbro, K.; Jacobsen, K.W.; Jelver, L. Schottky barrier lowering due to interface states in 2D heterophase devices. Nanoscale Adv. 2021, 3, 567–574. [Google Scholar] [CrossRef]
- Kim, N.Y.; Yang, H.; He, Z. Device simulation study of multilayer MoS2 Schottky barrier field-effect transistors. Nanotechnology 2024, 36, 035701. [Google Scholar] [CrossRef]
- Menyuk, C.R.; Islam, R.; Anjum, I.M.; Simsek, E. Study of an MoS2 phototransistor using a compact numerical method enabling detailed analysis of 2D material phototransistors. Sci. Rep. 2024, 14, 15269. [Google Scholar] [CrossRef]
- Kim, S.; Joo, J.; Choi, W.; Hong, S.C.; Cho, M.Y.; Kim, J.; Lee, J.H.; Jena, D.; Konar, A.; Cha, G.; et al. High-detectivity multilayer MoS2 phototransistors with spectral response from ultraviolet to infrared. Adv. Mater. 2012, 24, 5832–5836. [Google Scholar] [CrossRef]
- Dirè, S.; Pancheri, L.; Taffelli, A.; Quaranta, A. MoS2 based photodetectors: A review. Sensors 2021, 21, 2758. [Google Scholar] [CrossRef] [PubMed]
- Le, C.T.; Ky, D.L.C.; Khac, B.-C.T.; Kim, Y.S.; Chung, K.-H. Friction characteristics of mechanically exfoliated and CVD-grown single-layer MoS2. Friction 2018, 6, 395–406. [Google Scholar] [CrossRef]
- Chen, X.; Wang, R.; Song, B.; Jiang, H.; Zhai, T.; Gu, H.; Fang, M.; Ho, Y.; Liu, S. Layer-dependent dielectric function of wafer-scale 2D MoS2. Adv. Opt. Mater. 2019, 7, 1801250. [Google Scholar] [CrossRef]
- Handbook Series on Semiconductor Parameters; Levinshtein, M.S.Y.P.M., Ed.; World Scientific: Singapore, 1997; Volume 1. [Google Scholar]
- Brendel, R.; Bothe, K.; Schirmacher, A.; Kröger, I.; Lim, S.; Schinke, C.; Winter, S.; Nguyen, H.T.; Schmidt, J.; Vogt, M.R.; et al. Uncertainty analysis for the coefficient of band-to-band absorption of crystalline silicon. AIP Adv. 2015, 5, 067168. [Google Scholar] [CrossRef]
- Zwiller, V.; Steele, G.A.; Barkelid, M.; Buscema, M.; van der Zant, H.S.J.; Castellanos-Gomez, A. Large and tunable photothermoelectric effect in single-layer MoS2. Nano Lett. 2013, 13, 358–363. [Google Scholar] [CrossRef]
- Pospischil, A.; Furchi, M.M.; Mueller, T.; Polyushkin, D.K. Mechanisms of photoconductivity in atomically thin MoS2. Nano Lett. 2014, 14, 6165–6170. [Google Scholar] [CrossRef]
- Guskov, A.A.; Lavrov, S.D.; Bezvikonnyi, N.V. Kretschmann configuration as a method to enhance optical absorption in two-dimensional graphene-like semiconductors. Russ. Technol. J. 2024, 12, 96–105. [Google Scholar] [CrossRef]
- Wan, Y.; Dai, L.; Ma, Y.; Xie, Z.; Wang, W.; Rong, X.; Zhang, H. Measuring the refractive index of highly crystalline monolayer MoS2 with high confidence. Sci. Rep. 2015, 5, 8440. [Google Scholar] [CrossRef]
- Lin, M.-W.; Kravchenko, I.; Fowlkes, J.; Li, X.; Puretzky, A.A.; Rouleau, C.M.; Geohegan, D.; Xiao, K. Thickness-dependent charge transport in few-layer MoS2 field-effect transistors. Nanotechnology 2016, 27, 165203. [Google Scholar] [CrossRef]
- Romano, P.; Sessa, A.; Durante, O.; Sleziona, S.; Di Bartolomeo, A.; Giubileo, F.; Schleberger, M.; Martucciello, N.; Kumar, A.; Faella, E.; et al. Temperature-dependent photoconductivity in two-dimensional MoS2 transistors. Mater. Today Nano 2023, 24, 100382. [Google Scholar] [CrossRef]
- Chang, W.-H.; Hsieh, S.-H.; Li, K.-S.; Yang, S.-T.; Hou, T.-H.; Lu, C.-I.; Lin, C.-P.; Lu, T.-H.; Chen, J.-H.; Chen, C.-H.; et al. Defect-engineered room temperature negative differential resistance in monolayer MoS2 transistors. Nanoscale Horiz. 2022, 7, 1533–1539. [Google Scholar] [CrossRef]
- Sreelakshmi, B.; Thamankar, R. Investigation of the transient photo-response and switching window of an Al/indigo/Al device: Unveiling negative photoconductivity and the photo-enhanced memory window. Mater. Adv. 2024, 5, 5912–5921. [Google Scholar] [CrossRef]
- Terabe, K.; Takagi, S.; Toprasertpong, K.; Takenaka, M.; Tsuchiya, T.; Nur, R. A floating gate negative capacitance MoS2 phototransistor with high photosensitivity. Nanoscale 2022, 14, 2013–2022. [Google Scholar] [CrossRef]
- Zubair, A.; Nourbakhsh, A.; Dresselhaus, M.S.; Palacios, T. Transport Properties of a MoS2/WSe2 Heterojunction Transistor and Its Potential for Application. Nano Lett. 2016, 16, 1359–1366. [Google Scholar] [CrossRef]
- Laturia, A.; Van De Put, M.L.; Vandenberghe, W. Dielectric properties of hexagonal boron nitride and transition metal dichalcogenides: From monolayer to bulk. Npj 2D Mater. Appl. 2018, 2, 6. [Google Scholar] [CrossRef]
- Chernozatonskii, L.A.; Artyukh, A.A. Quasi-two-dimensional transition metal dichalcogenides: Structure, synthesis, properties, and applications. Phys.-Uspekhi 2018, 61, 2–28. [Google Scholar] [CrossRef]
- Gerardot, B.D.; Krauss, T.F.; Sapienza, R.; Tartakovskii, A.I.; Vezzoli, S.; Huq, T.; Louca, C.; Hu, X.; Sortino, L.; Randerson, S.; et al. Van der Waals Materials for Applications in Nanophotonics. Laser Photon Rev. 2023, 17, 2200957. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).