1. Introduction
Nowadays, environmental pollution has become increasingly severe, and the development of clean energy is an important way to alleviate environmental pollution. Natural gas is widely used in clean energy due to its good economy and reliable safety [
1]. Liquefied natural gas (LNG) is mainly used for long-distance natural gas transportation. Natural gas is compressed and cooled to become LNG for loading and transportation [
2]. During transportation, it is necessary to pressurize and liquefy natural gas at low temperatures to reduce its volume and store more natural gas. In the process of use, it needs to be re-gasified and transported to the user end [
3]. In the re-gasification process, a heat source is required to exchange heat with natural gas to turn it from a liquid to a gas state. However, most of the re-gasification processes use seawater as a heat source for heat exchange, which not only results in a large amount of waste of thermal energy but also has a certain impact on the ocean [
4].
Some technologies that use the cold energy of LNG have been proposed, including low-temperature power generation, seawater desalination, cold energy storage, and food processing [
5]. Among them, the organic Rankine cycle (ORC) has received extensive attention due to its safety, reliability, high efficiency, energy saving, and environmental friendliness, becoming an energy utilization technology with broad application prospects and high technical advantages [
6]. The ORC is a more promising LNG re-gasification cold energy utilization technology than others [
7]. Several methods have been proposed by scholars for LNG cold energy utilization in power generation. Ma et al. [
8] used parallel and series configurations of the ORC, Brayton Cycle, and Supercritical Carbon Dioxide Power Cycle to utilize the cold energy of LNG. The results showed that the best combination cycle was a two-stage continuous ORC, with the highest net power output ratio of 202.15 kJ/kg and the lowest leveling cost of electricity at 0.11 USD/kWh. Joy et al. [
9] compared the performance of a multi-stage, cascaded ORC using seawater as the heat source and LNG as the cold source. They found that only the two-stage system cascaded with the first stage could reduce the electricity generation by 8.6% compared with the three-stage system. However, the simplicity of the two-stage system cascaded with the first stage greatly improved, and the surface area of the heat exchanger correspondingly decreased by 20%. Huang et al. [
10] designed a novel cold–electricity cogeneration system based on refrigeration warehouses, which used the waste heat generated by natural gas power plants as a heat source and LNG as a cold source. They investigated the changes in design performance at different re-gasification rates. The main results showed that compared with traditional systems, the peak-to-valley ratio of the cold–electricity cogeneration system can be significantly increased from 0.4 to 1. The investment payback period of the system can be reduced by half, to 0.67 years.
The working fluid is crucial and directly impacts the performance of the ORC system. Yang et al. [
11] utilized a multi-objective genetic algorithm to optimize three combined heat and power systems based on organic Rankine cycles, the outcomes of which can offer guidance for the selection of working fluids. Mohan et al. [
12] screened 11 candidate working fluid mixtures based on the output power and thermodynamic efficiency. They found that R600a was the optimal working fluid when taking the maximum output power into account. Hu et al. [
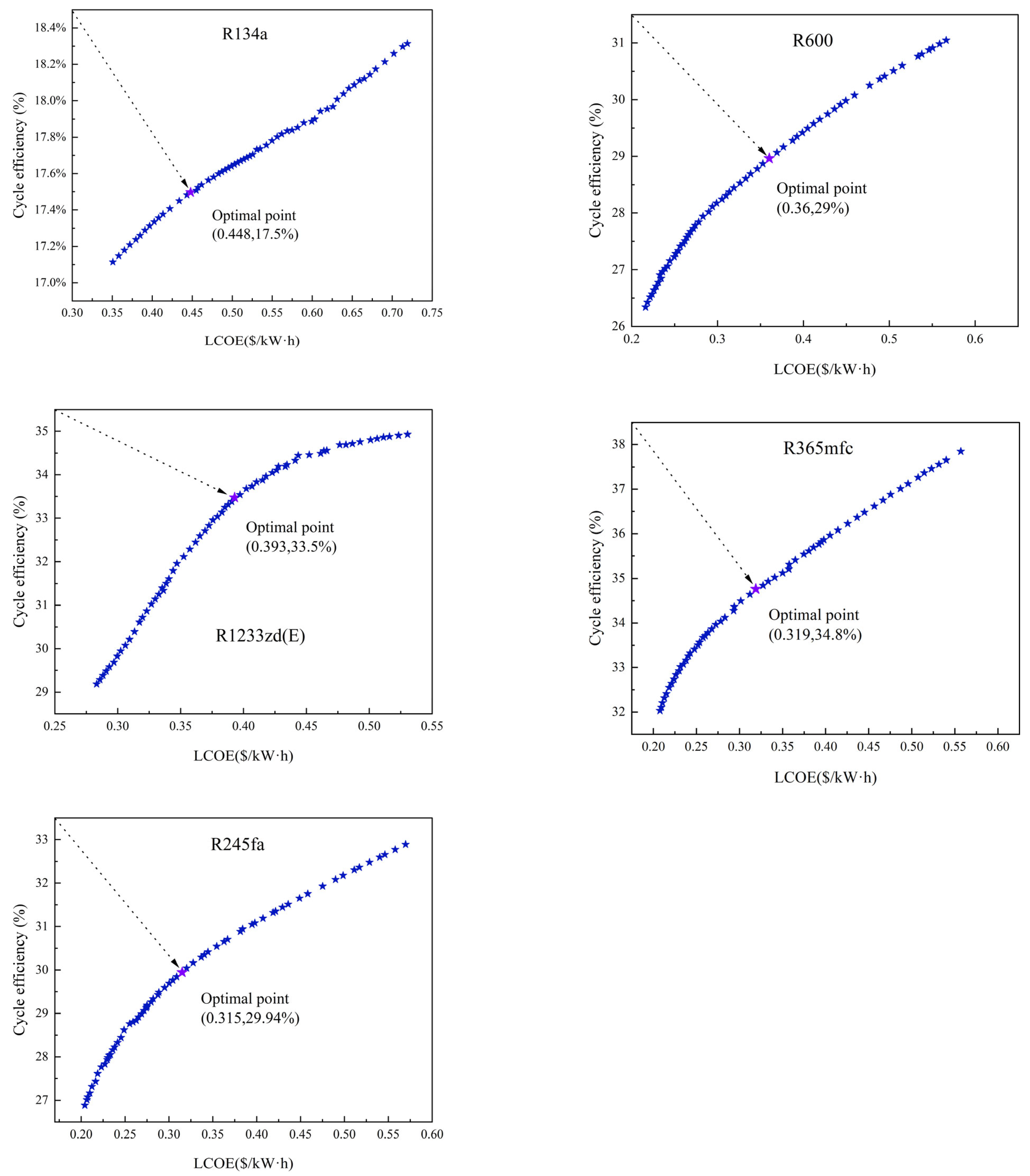
13] established mathematical and physical models for the thermal process of the ORC system. They optimized the process using 245 organic working fluids with unit mass net electricity generation from hot water as the optimization objective. R245fa was selected as the optimal working fluid. In the research focusing on the selection of working fluids, it is imperative not only to consider the thermodynamic and economic performance of the system, but also to engage in a critical discussion regarding the environmental implications.
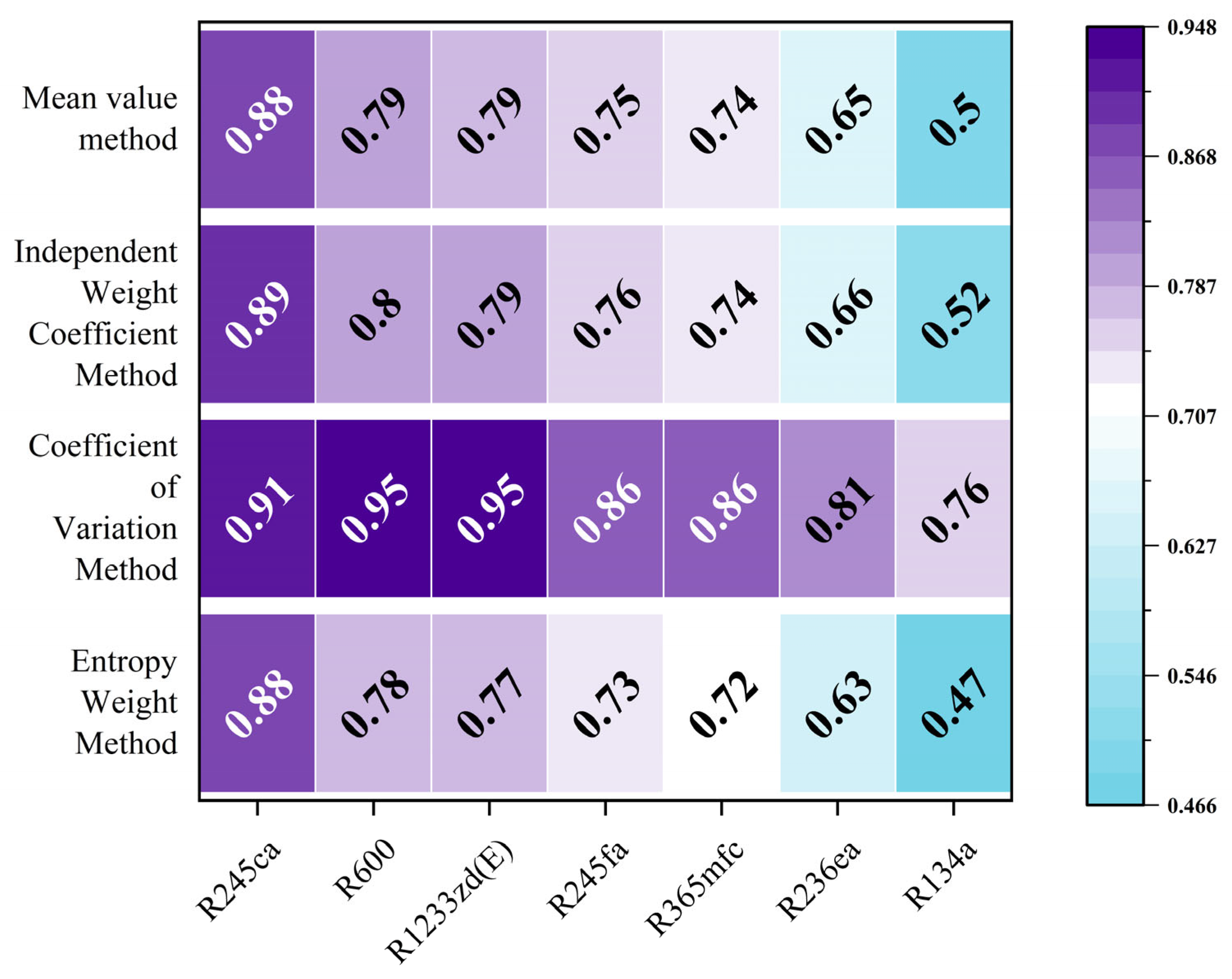
The comprehensive evaluation and optimization decision-making for thermal systems necessitate the consideration of multiple assessment criteria, which are interrelated with the ultimate optimal outcome. The Gray Relational Analysis (GRA) method is based on the gray system theory and can analyze the correlation between each indicator, obtain the influence weightings of each indicator on the comprehensive evaluation results, and make optimization decisions. Mausam et al. [
14] used GRA to verify the optimized experimental results of a flat-plate-collector solar energy collection system. They evaluated the performance using the flow rate, intensity, and tilt angle as targets. It was found that the maximum instantaneous efficiency was 2.25% at the flow rate of 68.7 lpm, intensity of 1 W/m
2, and tilt angle of 400°. Bademlioglu et al. [
15] studied the cycle characteristics of the ORC system and used GRA to optimize and evaluate the main process parameters, including evaporator temperature, turbine efficiency, heat exchanger efficiency, and condenser temperature, to determine the system operating conditions. The findings indicate the first and second law efficiencies of the system were 18.1% and 65.52%, respectively. Wu et al. [
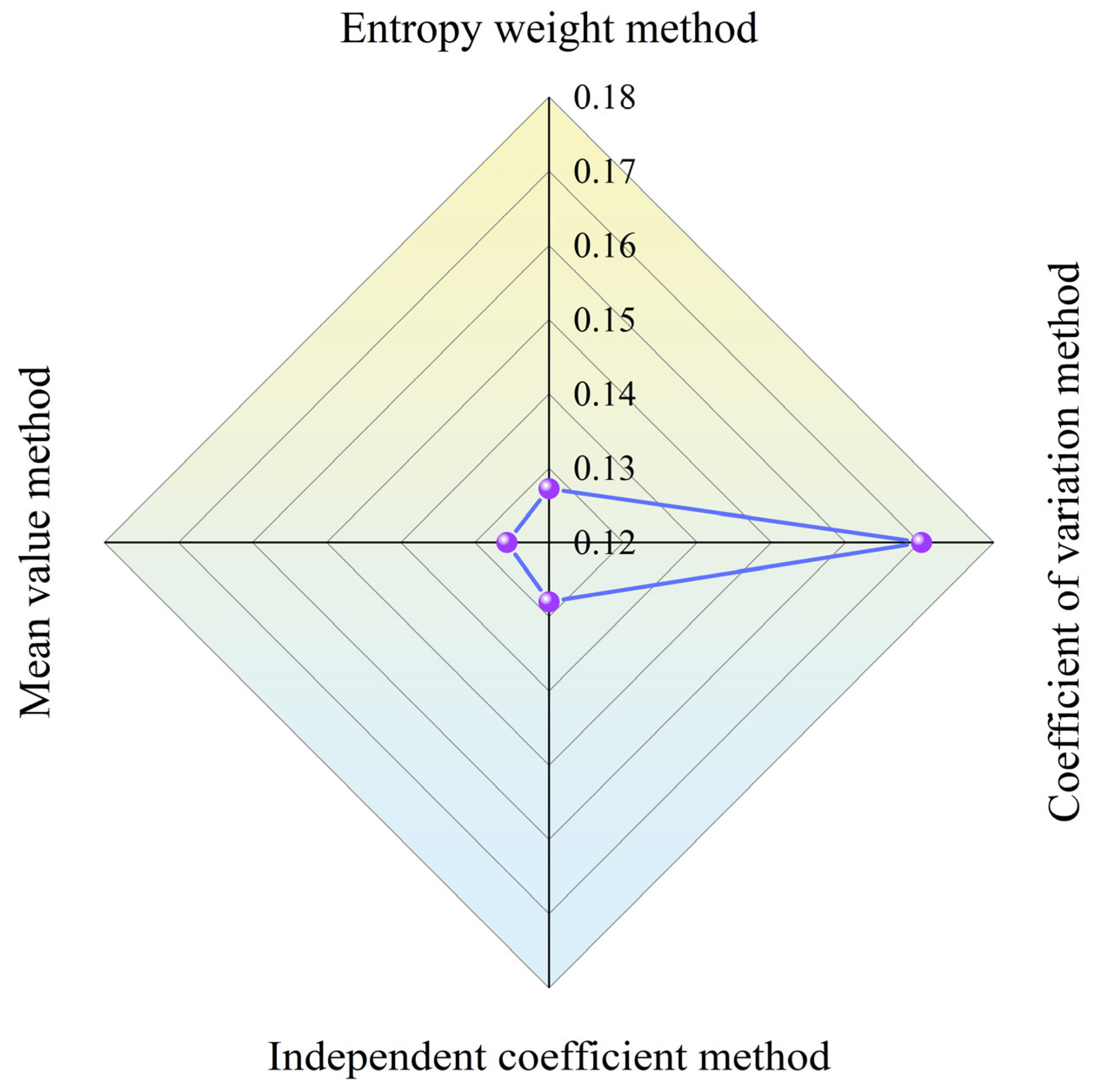
16] studied the performance of the ORC system under different load powers based on a built low-temperature waste heat power generation test platform. The analysis showed that there the closest correlation was between the power and load power, with a gray correlation degree of 0.632. In the GRA evaluation, the weighting of each indicator directly affects the accuracy and credibility of the comprehensive evaluation results, with a higher weighting indicating a greater contribution to the comprehensive evaluation results. In the GRA, the assignment of weightings has a direct effect on the final optimization results; however, to date, no publications have isolated the impact of disparate weighting methodologies on the GRA outcomes.
Previous research has shown that cascading or multi-stage ORCs can improve heat-source matching, yet most published schemes still operate with a single evaporator, rely on fixed fluid selections, and neglect the synergistic use of waste heat and LNG cold energy. Moreover, the studies that apply Gray Relational Analysis (GRA) to working fluid screening seldom examine how alternative weighting strategies influence the final decision, leaving important sources of evaluation bias unaddressed.
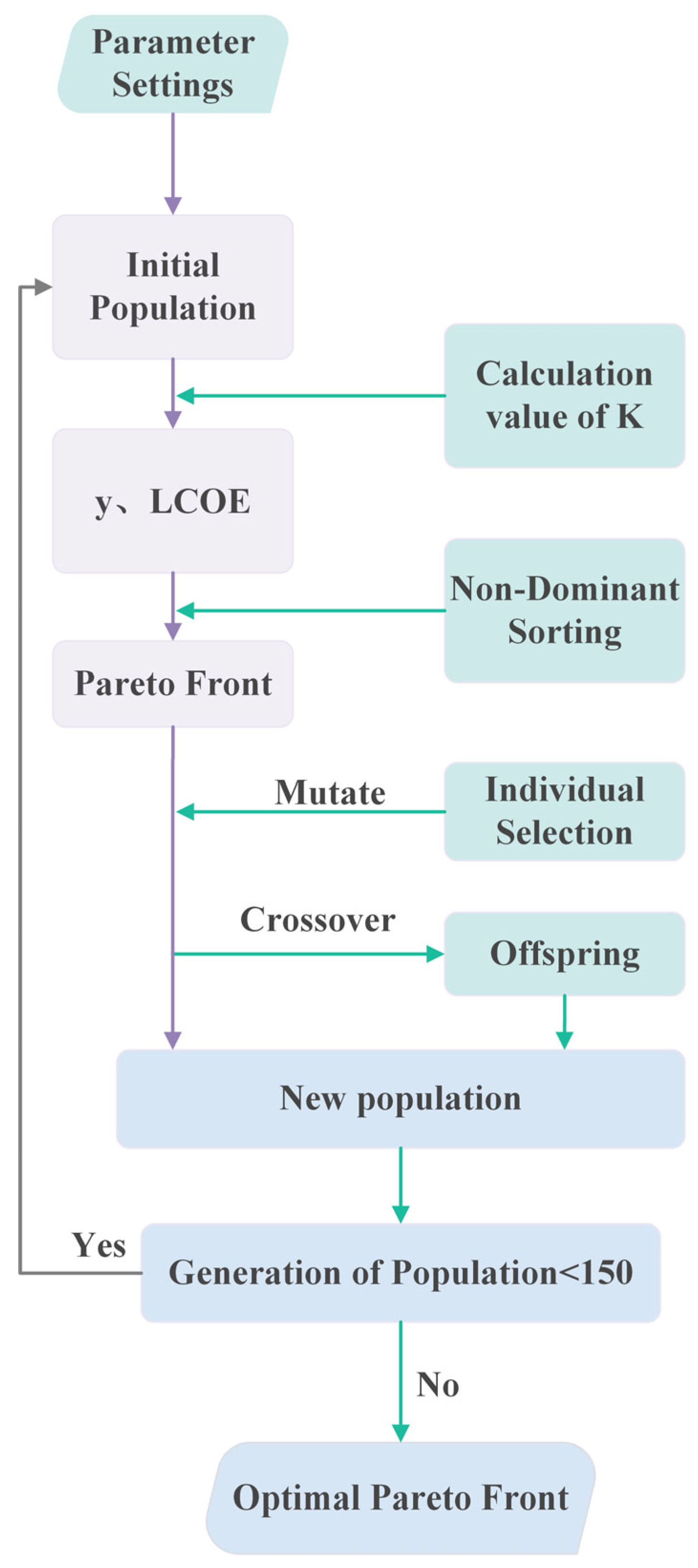
Against this backdrop, the present work introduces a multi-stage Rankine system driven by waste heat and LNG cold energy (MSR-LNG). The system couples a dual-stage ORC with an LNG expansion module and embeds an internal preheater/recuperator to recover sensible heat between the stages. A comprehensive optimization framework links thermodynamic, economic, and environmental objectives through non-dominated sorting genetic algorithm II (NSGA-II) and TOPSIS, while four distinct GRA weighting schemes are compared to clarify their impact on fluid ranking. By integrating these elements, this study advances the state of the art in three ways: (1) realizes a tighter temperature-glide match between the heat source and sink through a dual-stage topology, reducing irreversibility across the entire temperature span; (2) embeds internal heat recovery, lowering external heat exchange area demand and simplifying pipework; (3) delivers a unified thermo-economic–environmental optimization routine that shows how the weighting method affects fluid selection, providing a transparent basis for material choice; and (4) presents a comparison table later in the paper, which benchmarks these contributions against the representative LNG–ORC studies published in recent years, evidencing the superior conversion performance and lower levelized cost achieved by the proposed configuration.
2. System Description
The flow diagram of the MHUS-MSR-LNG is illustrated in
Figure 1.
Figure 2 shows the overall process flow diagram for the MSR-LNG cycle.
The MSR-LNG proposed in this article consists of two modules, an ORC module and an LNG module, which are connected by pipes for heat exchange. The red piping represents the waste heat, the purple piping denotes the working fluid circuit, and the blue piping symbolizes the natural gas sub-process.
In
Figure 2, the blue line indicates the natural gas treatment process, the pink line is the ground source hot water treatment process, and the purple line indicates the working fluid change process.
The ORC module in the MSR-LNG operates as follows: Exogenous high-temperature waste heat H1 undergoes a dual heat exchange within evaporators 1 and 2 of the waste heat circuit, transforming into low-temperature waste heat H3. Throughout this process, the thermal energy generated from the waste heat can be thoroughly exploited. The liquid working medium F1 absorbs heat within evaporator 1, transmuting into a high-temperature superheated gas F2, which propels the rotation of the expander, consequently driving the coaxial generator to produce electricity. Post-expansion, it becomes a low-temperature gaseous working medium, F3. F3 conveys heat to the liquid working medium F6 within the condenser through the preheater. Subsequently, the temperature of the gaseous working medium F4 decreases. F4 absorbs the cold energy of natural gas and becomes a saturated liquid, F5, in the condenser. After being pressurized by the pump, F5 becomes saturated liquid working fluid F7 after absorbing heat from F6. In this module, the preheater is located after the pumps and heats the spent gas after it passes through the expander by means of the work mass from the condenser. Its main function is to recover the waste heat from the work mass and increase the efficiency.
In the LNG module, LNG L1 needs to be maintained at a suitable temperature and pressure (0.1 MPa, −162 °C) during storage and transportation. It is pressurized by water pump 3 to become L2, which absorbs heat in the condenser and becomes a saturated liquid (L3). L3 exchanges heat with waste heat H2 and becomes a high-temperature gas working fluid (L4), which then cools and depressurizes through expander 2 to become gaseous natural gas that can be directly used.
LNG is considered a multi-component mixture with the molar composition CH4 90.1%, C2H6 5.8%, C3H8 3.0%, n-C4H10 0.6%, i-C4H10 0.3%, N2 0.2%. Thermophysical properties were evaluated with REFPROP 10.0, which accounts for the non-ideal phase behavior of cryogenic mixtures.
By splitting the evaporation process into two temperature-matched stages, the dual-stage Rankine configuration markedly narrows the average temperature difference between each evaporator and its heat source, which in turn suppresses irreversibilities on the heat-addition side. Combined with an internal recuperator, the layout yields a clear improvement in the overall second-law efficiency. Compared with a conventional single-stage ORC, this architecture achieves a pronounced enhancement in thermoelectric conversion performance, yet it preserves the compactness and modularity that make ORC systems attractive, since both stages share a single generator shaft and control loop and therefore require no extra major equipment.
The paper is aimed at (i) academic researchers working on thermodynamic cycle modeling and (ii) process engineers of LNG re-gasification and low-temperature waste-heat recovery.