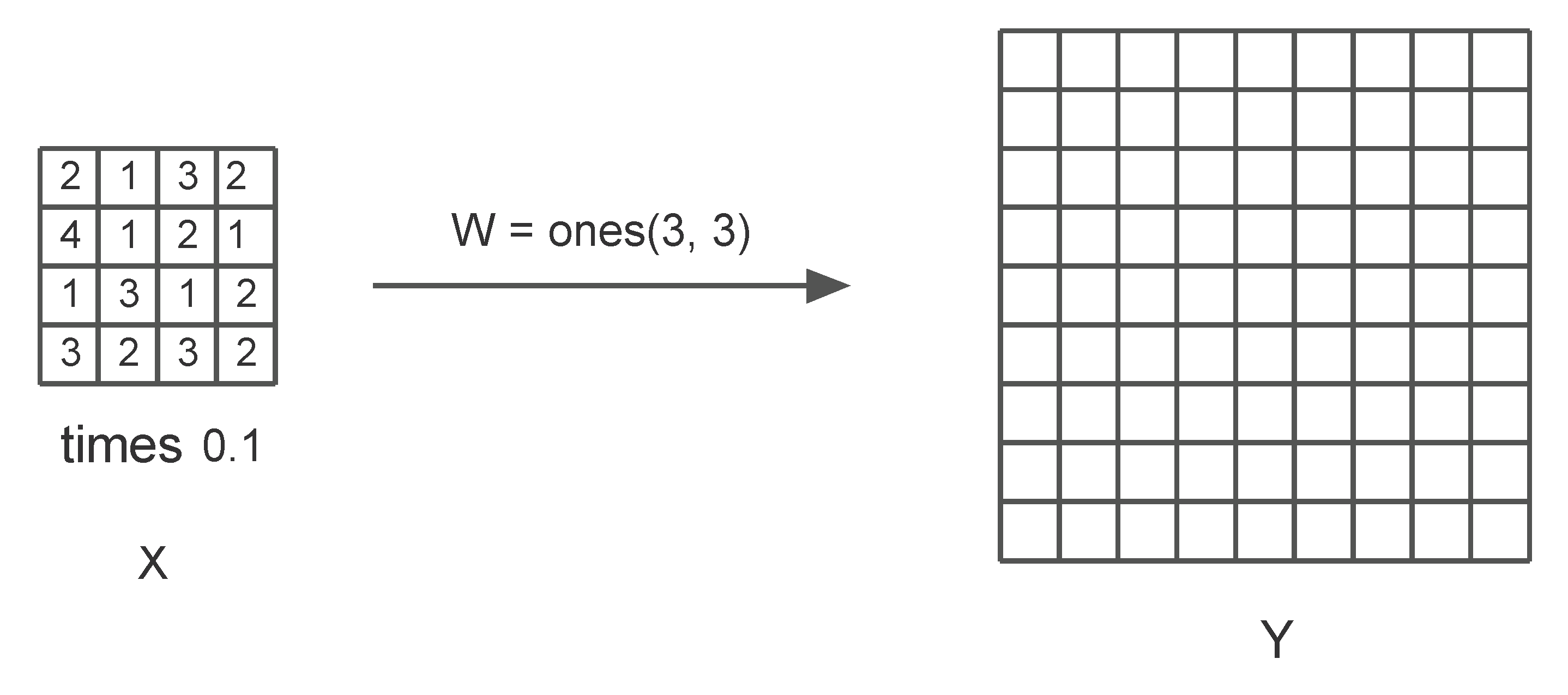Single Image Super Resolution Using Deep Residual Learning

Abstract

Single Image Super Resolution (SSIR) is an intriguing research topic in computer vision where the goal is to create high-resolution images from low-resolution ones using innovative techniques. SSIR has numerous applications in fields such as medical/satellite imaging, remote target identification and autonomous vehicles. Compared to interpolation based traditional approaches, deep learning techniques have recently gained attention in SISR due to their superior performance and computational efficiency. This article proposes an Autoencoder based Deep Learning Model for SSIR. The down-sampling part of the Autoencoder mainly uses 3 by 3 convolution and has no subsampling layers. The up-sampling part uses transpose convolution and residual connections from the down sampling part. The model is trained using a subset of the VILRC ImageNet database as well as the RealSR database. Quantitative metrics such as PSNR and SSIM are found to be as high as 76.06 and 0.93 in our testing. We also used qualitative measures such as perceptual quality.

1. Introduction

In many emerging computer vision applications medical/satellite imaging, remote target identification and autonomous vehicles, there is a need to instantly obtain a high-resolution image from the low resolution image using innovative means. The problem of generating a high-resolution image given a single low-resolution image is commonly referred to as Single Image Super Resolution (SISR). This is a challenging research topic since given a collection of low resolution pixels, there are more than one way to obtain the corresponding high resolution pixels. A usual solution is to constrain the solution space using prior information about the scenery or using the context.

Common techniques for SISR can be mainly divided into three categories: interpolation-based methods, reconstruction-based methods, and learning-based methods. Interpolation based methods such as bi-cubic interpolation [1] and Lanczos re-sampling [2] are fast and straightforward but suffer from poor accuracy. Reconstruction-based models, reported in  [3,4,5,6], typically incorporate complex prior knowledge to constrain the set of feasible solutions and produce high-quality results with detailed outputs. Despite these advantages, many reconstruction-based techniques suffer from diminishing performance as the scaling factor increases, and are often computationally demanding.

Learning-based methods, also known as example-based methods, have gained popularity in recent years. These methods utilize machine learning algorithms to recover the relationship between the low resolution input and its corresponding high resolution counterpart. Learning-based methods have shown better performance and lower computation time requirements compared to most other methods. Very recently, deep convolutional neural networks have emerged as a powerful tool for solving the SISR problem.

A Convolutional Neural Network (CNN) is a type of machine learning algorithm that can automatically learn complex features in input image data [7]. This makes CNN a very powerful tool in various image processing tasks. Autoencoders were originally developed to learn a compressed, low dimensional representation of the data in a large vector [8]. Autoencoders found numerous new applications when scientists realized that the compressed representations could be used to generate a new variation of the original large vector. Consequently, deep Autoencoders were developed recently to create a new variation of the input image by using a type of ‘reverse’ CNN.

Several deep learning-based methods that have been proposed for the SISR problem use different variations on the Autoencoder architectures. These methods have achieved state-of-the-art results in terms of both quantitative metrics and visual quality. However, there are still some challenges that need to be addressed, such as the trade-off between computation time and quality, the extent of generalization of a particular model across different domains and scales, and the need for more realistic evaluation metrics. Despite these challenges, the use of deep networks for SISR continues to be an active area of research, with new methods and architectures being proposed regularly.

In this article, we propose a novel approach to solve the SISR problem using Deep Convolutional Residual Neural Networks. Our model will be based on an Autoencoder structure which has CNN at the first half followed by a ‘reverse’ CNN, mentioned above, in the second half. The ‘reverse’ CNN part will perform up sampling using transpose convolution, and use skipped connections from the CNN part to enrich the collection of feature maps on the second half. The article examines the different metrics and loss functions used to achieve optimal performance. The proposed approach is evaluated using both quantitative and qualitative measures to compare the results of each model, including peak signal-to-noise ratio (PSNR), structural similarity (SSIM), and perceptual quality.

The next section presents a brief overview of related works. Section 3 outlines the evolution of Autoencoders and provides the theory behind them. The problem statement, proposed model, and the used dataset are described in Section 4. The methodology, hyper parameters, and the training details are given in Section 5. The results are discussed in Section 6, followed by conclusions in Section 7.

2. Related Work

This section presents a brief review of the deep learning based SISR reported in recent literature.

Dong et al. [9] proposed a Super Resolution Convolutional Neural Network (SRCNN) that consisted of three major components; patch extraction, non-linear mapping, and reconstruction. In the patch extraction layers, convolution filters extracted the image features without any subsampling. The non-linear mapping was performed by an artificial neural network. The reconstruction layer used bi-cubic interpolation to up-sample the low-resolution image. The model was trained using the Mean Squared Error (MSE) loss function and the results were evaluated using SSIM and MSSIM. It was reported that increasing the number of layers did not result in better performance. The article reported that the architecture is sensitive to learning rate and parameter initialization, and the depth of the network made it very difficult to set appropriate learning rates that guarantee convergence. The architecture reportedly achieved a PSNR of 32.52.

A model that uses a special, pre-trained, loss network instead of the pixel by pixel losses was developed by Johnson et al. [10]. The loss network used perceptual losses that depend on high-level features which produced visually appealing results. The model consisted of two main components; an image transformation network and a loss network. The transformation network used several residual blocks followed by convolutional layers. The results achieved were very visually pleasing. However, quantifying these results seemed to be a problem. In defence of  [10], it should be noted that as reported in [11,12], PSNR and SSIM rely on per-pixel differences and correlate poorly with human assessment of visual quality, which is what this model is supposed to achieve.

Motivated by the small receptive field and the very slow training needed in the SRCNN [9], a Very Deep Super Resolution (VDSR) model was proposed in [13] that makes use of 20 convolutional layers. This very deep CNN network used gradient clipping techniques to handle the exploding gradient problem. Moreover, the model was designed to learn the difference between the target Hi-Res image and the input Lo-Res image rather than learning the Hi-Res image directly. This resulted in significantly reduced training time.

The introduction of ResNet by He et al. [14] opened the door for more advancement in Super Resolution. The core idea of ResNet is to enable a CNN network to be very deep without suffering from the vanishing gradient problem. ResNet layers were reformulated to learn residual functions with reference to the layer inputs, instead of unreferenced functions. These residual networks were easier to optimize and gained higher accuracy with increased network depth. A ResNet block constituted of one or more convolutional layers followed by Batch Normalization and a ReLU activation.

An architecture called Super Resolution Residual Network (SRResNet) was proposed by Ledig et al. [15]. Removing the Batch Normalization (BN) modules in the SRResNet architecture as proposed by Lim et al. [16] achieved better results. The model contained convolutional layers followed by residual blocks. The last part consisted of upsampling and convolution layers.

To make better use of the hierarchical features extracted from Low-Resolution images, Zhang et al. [17] proposed a Residual Dense Network (RDN) for Image Super Resolution that is also based on ResNet architecture. This network modifies the residual blocks by connecting each layer to all subsequent layers in the block.

Since low resolution inputs and features contain low frequency information that are equally treated across channels, Zhang et al. [18] presented a model that selectively emphasizes informative channels in each feature map. This model, named Image Super-Resolution Using Very Deep Residual Channel Attention Network (RCAN), is also based on ResNet architecture.

MSE loss function has its limitations when used in Super Resolution as it encourages average-like solutions that are not visually pleasing. Motivated by this, Ledig et al. [15] proposed a model for image Super Resolution using Generative Adversarial Network (SRGAN), in which the authors suggested a perceptual loss function which consists of an adversarial loss and a content loss. The adversarial loss pushes the solution to the natural image manifold by using a discriminator network that is trained to differentiate between the super-resolved images and the original photo-realistic images. The content loss is motivated by perceptual similarity instead of pixel-wise similarity. The generator network structure mainly consists of residual blocks each of which starts with two convolutional layers followed by batch normalization layers and ReLU as the activation function. One of the metrics used by the authors to evaluate the model is the Mean Opinion Score (MOS), where 26 human observers rated the Hi-Res output images. Compared to other SISR methods, the authors showed that the SRGAN model achieved the highest MOS scores.

Yang et al. [19] reviewed deep learning methods used for SISR and summarized the trends and challenges ahead for Deep Learning (DL) algorithms in tackling the SISR problem. The authors argued that lighter deep architectures for efficient SISR are needed. Even though very high accuracy for Hi-Res images from Lo-Res images was achieved, it is very difficult and impractical to deploy these models to real world scenarios, due to the massive number of parameters and computational needs. They suggested that lighter models should be designed either from scratch or from slimming down current architectures without large compromise on performance. Moreover, the authors believed that more work should be done to bridge the gap in our understanding of deep models for SISR. The success of deep learning is said to be attributed to learning powerful representations. However, to date, these representations are not fully understood, and the deep architectures are treated as a black box. For DL-based SISR, the deep architectures are often viewed as a universal approximation, and the learned representations are often omitted for simplicity. This behavior is not beneficial for further exploration, and the authors argued that more work should be done on why and how these models work. That is, more theoretical explorations are needed. Lastly, the paper addressed the issue of not having rational unified assessment criteria for SISR. Most of the DL methods use the MSE as the loss function despite the fact that it has been shown as a poor criterion for SISR. Clear definitions for assessment criteria for SISR will help designing better optimization objectives and will make the comparison between models more rational.

A Specific activating function, in place of ReLu and MTLU was proposed by Gao et al. [20]. They argued that both ReLu and MTLU provide only a static scaling factor, whereas their new Pixel Attention Activating Function (PAAF) can provide a dynamic pixel-wise scaling factor that is more sensitive to the image features. They demonstrated the advantage of PAAF by providing results that compared PAAF to that obtained with ReLu and MtLU.

Li et al. [21] designed a non-linear global feature fusion (NGFF) module that combined the outputs from the deep feature aggregation blocks (DFAB). Shallow features were extracted from the inputs by a 3 by 3 convolutional filter and the results were sent to NGFF for residual learning. The paper presents PSNR and SSIM results comparing their method to other techniques.

An entirely different approach to SISR that used unsupervised learning was proposed by Yamawaki et al. [22]. The main part of their model is a GAN-like encoder-decoder with skipped connections that was trained to produce a high-resolution image while noise is at the input. A convolutional layer was used to down-sample the output of the GAN to produce a low-resolution image, and this image is compared to the actual low-resolution image in the dataset to create the loss function for the GAN.

Ju et al. [23] focused on the problem of acquiring high definition 3D surface structures in computer vision from low resolution photometric stereo images. Their method uses a dual-position threshold normalization preprocessing scheme, a local affinity feature module, a parallel multi-scale feature extractor, and a shared-weight regressor. The article presents the results of many ablation experiments to justify their method.

In [24], Chen et al. argue that most of the existing deep convolution-based methodologies fail to capture targeted information when the distribution of spatial and channel information is uneven in low-resolution images. To address this issue, they propose a cascade attention blend residual network. A non-local channel and multi-scale attention are considered for channel-wise dependencies and multi-scale receptive fields, respectively. The paper reports promising super resolution results while reducing the number of parameters in the model by about 50%.

An article by Chen et al. [25] combines the spatial and channel dimensions in Transformer to obtain an image representation. They propose Dual Aggregation Trans-former (DAT), for image SR. DAT aggregates features across spatial and channel dimensions, in the inter-block and intra-block, in a dual manner. The paper also proposes an adaptive interaction module (AIM) and the spatial-gate feed-forward network (SGFN) to achieve intra-block feature aggregation.

A detailed study of the latest techniques used for SISR can be found in [26]. Here, 53 different models were evaluated on 7 different datasets. The study tabulated the performances of the various models measured in PSNR and SSIM for scaling factors starting from 2 to 16.

3. Autoencorders

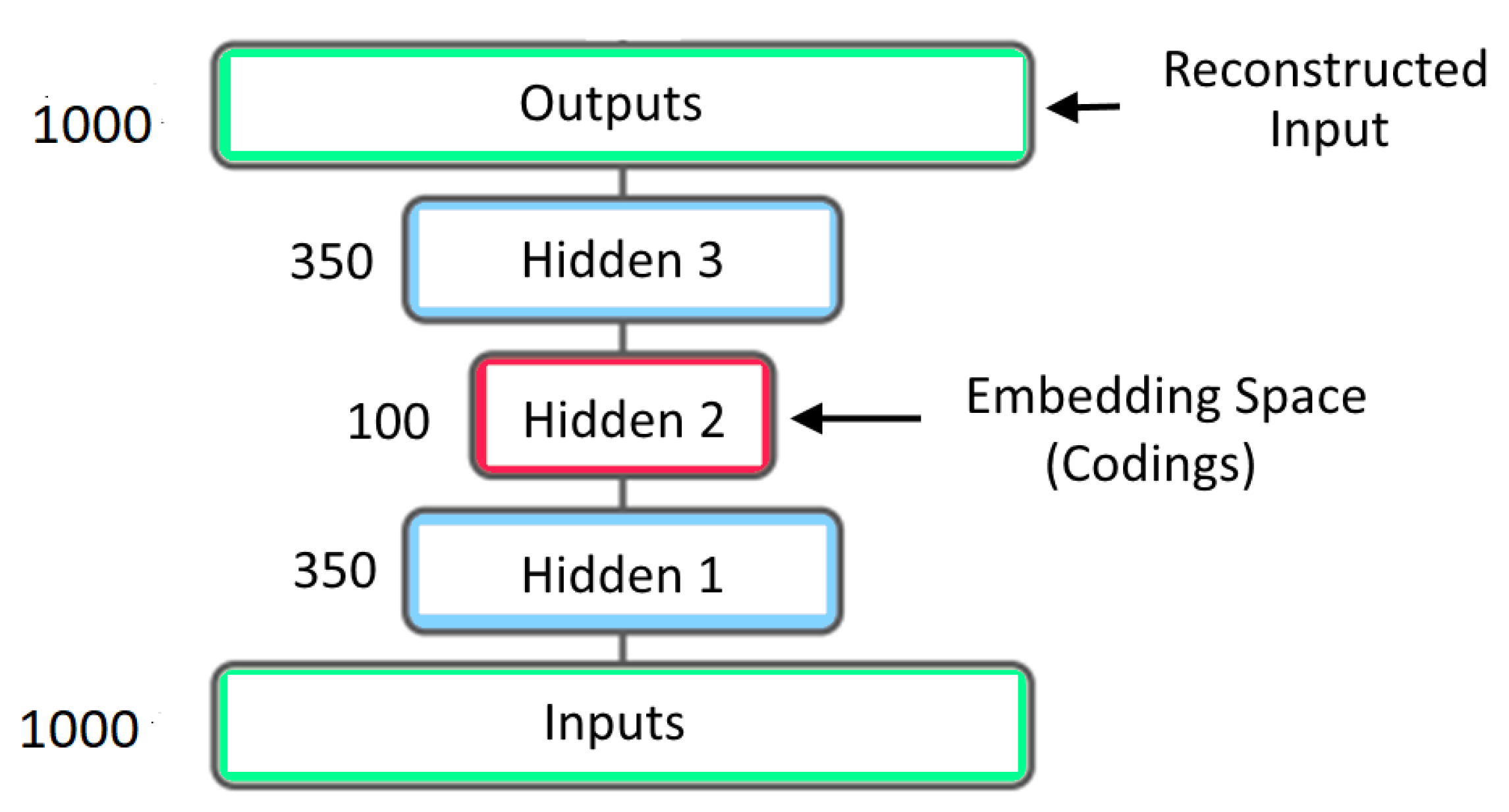
The deep learning model used in this article belongs to a class of networks called Autoencoders. Autoencoders were originally developed for the purpose of dimensionality reduction [8]. They were used to learn a compressed representation of vector data. The simplest Autoencoders are Artificial Neural Networks (ANN) with an hour-glass structure. These Autoencoders were trained with the input vectors as the targets. An Autoencoder that takes in a vector of size 1000 and reduces the dimension to 100 is shown in Figure 1. After training, the outputs from the bottle-neck layer in the middle produces a lower dimensional representation of the input vector.

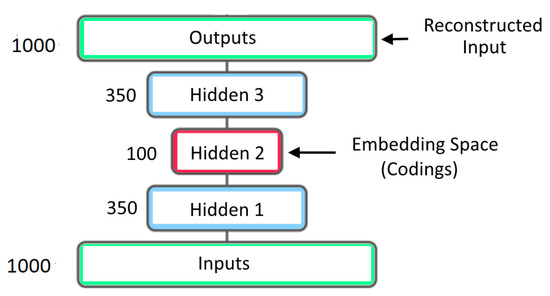
Figure 1. Early Autoencoder Architecture. Different colors indicate different depth of hidden layers.

Later on, researchers surmised that the compressed data could be used to construct a different version of the original input. Note, the inputs were often images rather than vectors. The input images were often flattened and fed to the hour-glass ANN. A well known application of this is image denoising.

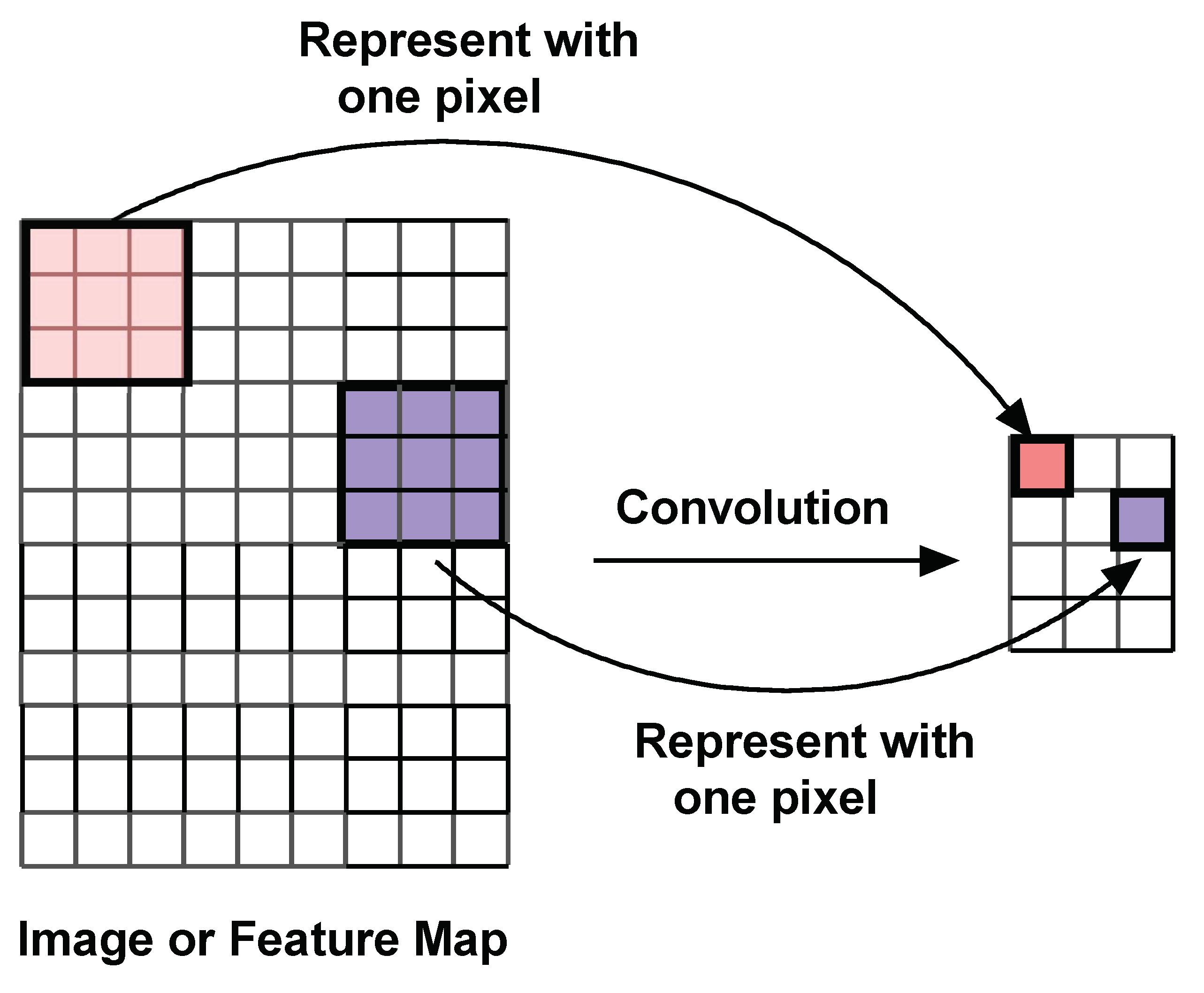
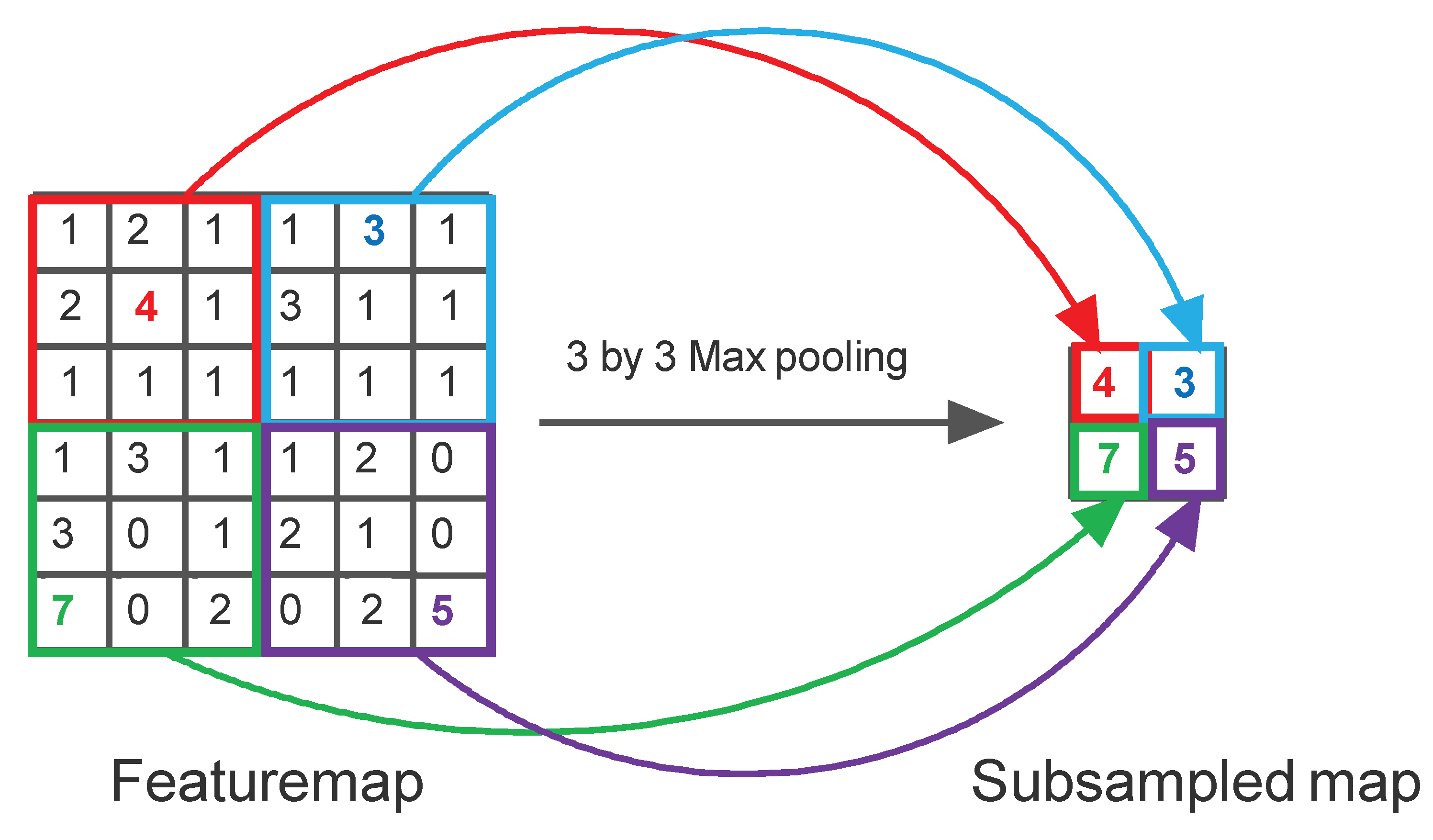
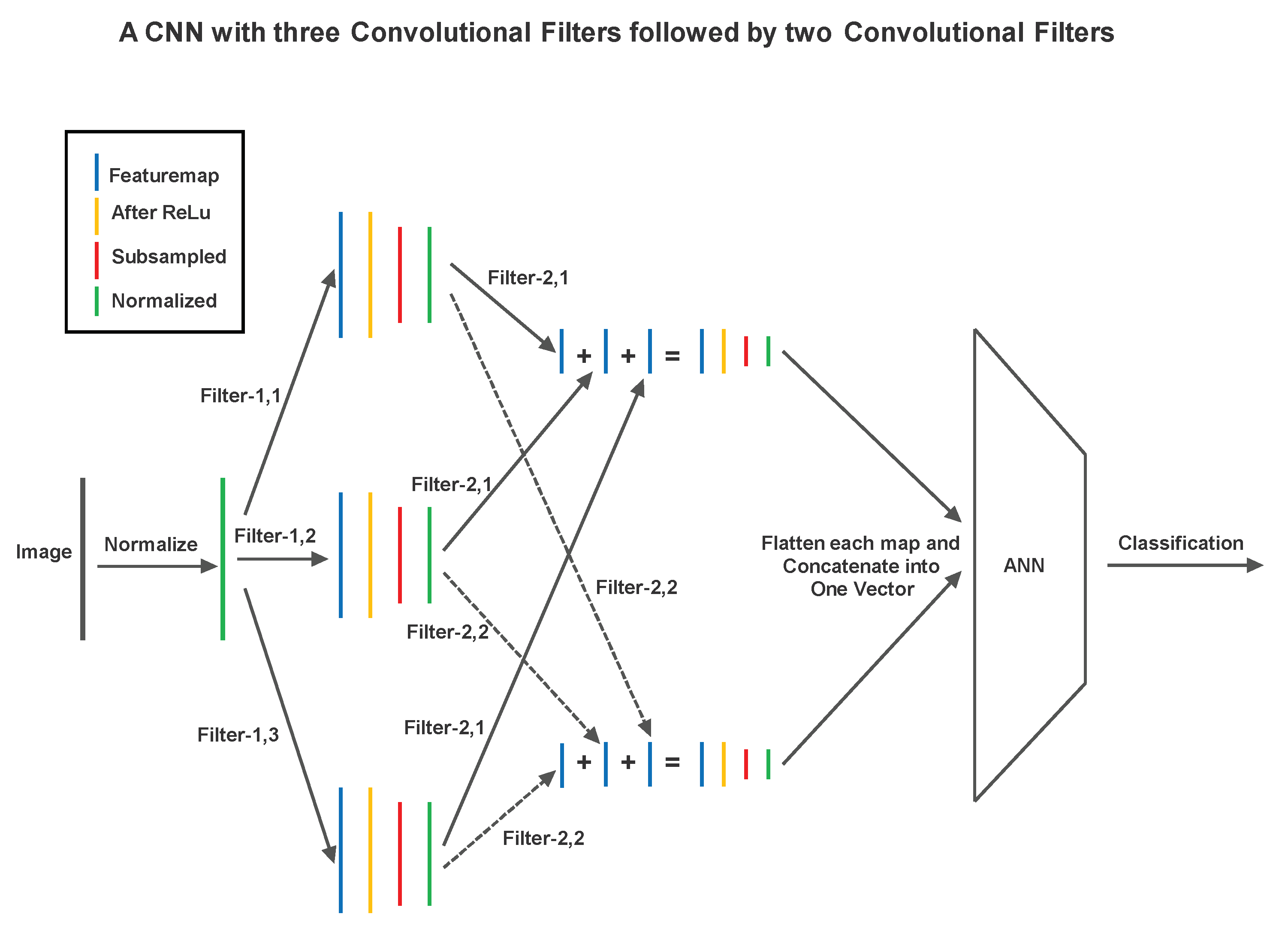
Recently, Image Autoencoders evolved to include the components of CNN [7]. They used a U-shaped architecture, where the left side had a CNN and the right side had a ‘reverse’ CNN. A typical CNN has convolutional filters (Figure 2), featuremap layers, activations, and subsampled maps (Figure 3) followed by an ANN that performs the classification (Figure 4).

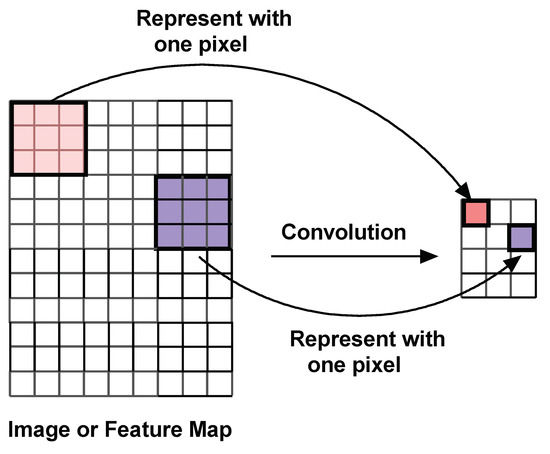
Figure 2. Schematics of 2D Convolution: A moving image filter takes dot-products with a sub-matrix of the image and places the result in a new image called the featuremap.

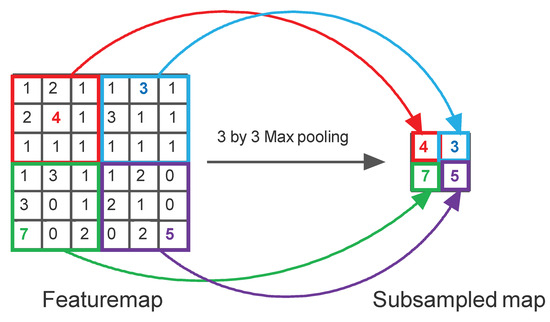
Figure 3. Example of a Subsampling Operation: Maxpooling.

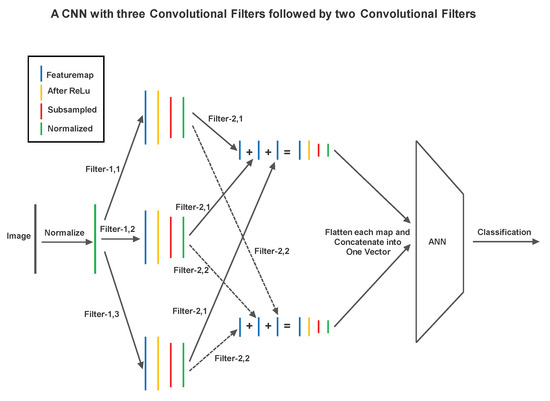
Figure 4. A Simple Schematic of Convolutional Neural Network (CNN).

A convolutional filter moves around the image, takes dot products with the image at each location and places them on a featuremap. The convolution operation is illustrated in Figure 2. Maxpooling is a subsampling operation where a region in a featuremap is replaced by a single representative pixel. Maxpooling is explained in Figure 3. A simple CNN that uses two layers of convolution and maxpooling to extract features, and then uses an ANN to perform image classification is shown in Figure 4.

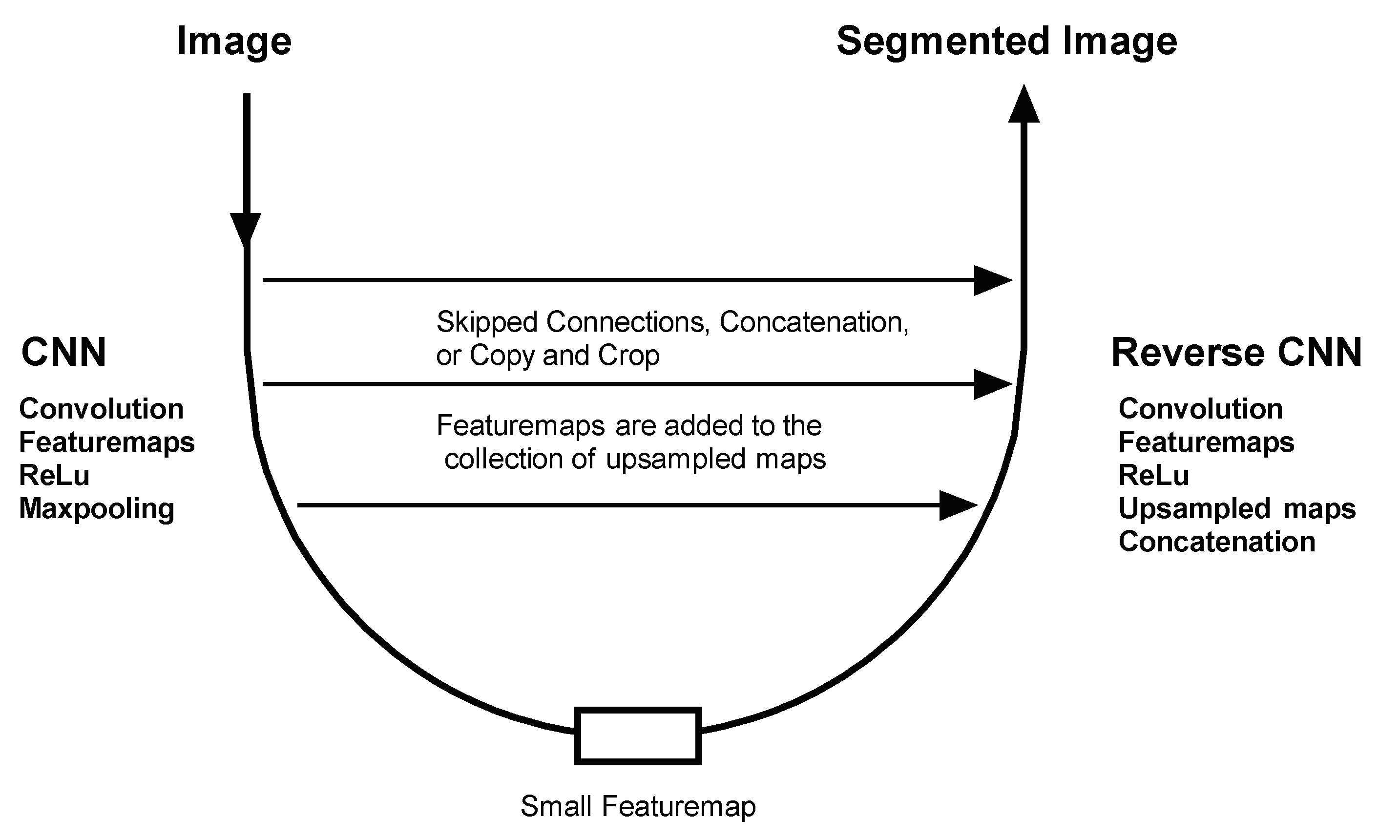
A typical Autoencoder structure is shown in Figure 5. It is important to note that the CNN on the left side of an Autoencoder does not end in an ANN. Rather, the CNN in an Autoencoder ends in a small featuremap. The right side of the Autoencoder starts with this small featuremap and uses transpose convolution and skipped connections from the left side to gradually build up the required output image.

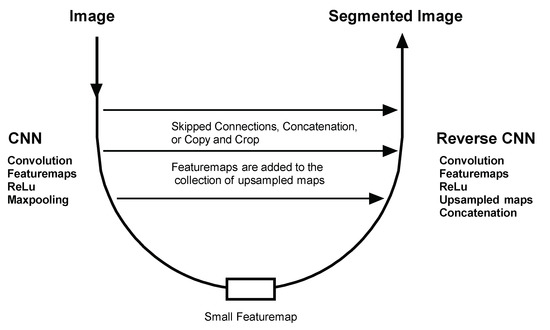
Figure 5. Typical Autoencoder Structure.

The most important operation on the right side of an Autoencoder is the upsampling done by the Transposed convolution. The following example explains this operation. In Figure 6, a 3 by 3 transpose convolution filter operates on a featuremap of shape 4 by 4 pixel by pixel with stride 2 to produce an upsampled map. The filter kernels are multiplied by the pixel value in the top left corner of the feature map to generate a 4 by 4 submatrix. Now the filter moves to the right by one pixel and repeats the computation. The resulting submatrix is placed in the upsampled map after moving two pixels to the right. The calculations are shown step by step below:

$$\begin{array}{cc}\hfill {\displaystyle Y}& =\left[\begin{array}{ccccccccc}0.2& 0.2& 0.2& 0& 0& 0& 0& 0& 0\\ 0.2& 0.2& 0.2& 0& 0& 0& 0& 0& 0\\ 0.2& 0.2& 0.2& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]+\left[\begin{array}{ccccccccc}0& 0& 0.1& 0.1& 0.1& 0& 0& 0& 0\\ 0& 0& 0.1& 0.1& 0.1& 0& 0& 0& 0\\ 0& 0& 0.1& 0.1& 0.1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & +\left[\begin{array}{ccccccccc}0& 0& 0& 0& 0.3& 0.3& 0.3& 0& 0\\ 0& 0& 0& 0& 0.3& 0.3& 0.3& 0& 0\\ 0& 0& 0& 0& 0.3& 0.3& 0.3& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]+\left[\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& 0.2& 0.2& 0.2\\ 0& 0& 0& 0& 0& 0& 0.2& 0.2& 0.2\\ 0& 0& 0& 0& 0& 0& 0.2& 0.2& 0.2\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & +\left[\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0.4& 0.4& 0.4& 0& 0& 0& 0& 0& 0\\ 0.4& 0.4& 0.4& 0& 0& 0& 0& 0& 0\\ 0.4& 0.4& 0.4& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]+\dots \dots \dots \hfill \end{array}$$

(3)

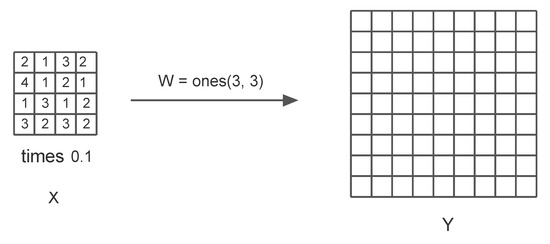
Figure 6. The transpose Convolution.

Skipped connections in Autoencoders refers to the fact that some feature maps from the CNN on the left side are copied and added to the collection of upsampled maps on the ‘reverse’ CNN on the right side.

4. Problem Statement and the Model

The goal of this work is to produce a deep neural network model that is capable of creating high resolution images given the corresponding low resolution image. In particular, the purpose is to develop a lightweight model with a minimum number of parameters, in order to address the computational and resource constraints. The architecture used in the CNN part of the Autoencoder used in this article is borrowed from the state-of-the-art CNN called ResNet.

The first Dataset to be used is a subset from the ImageNet database. This dataset was chosen because it was adopted by most of the models mentioned earlier and represents a benchmark for performance comparison. The second dataset used in this article is the RealSR V1 from Kaggle. This dataset is known for its realistic depiction of the world around us.

5. Proposed Method

5.1. Proposed Network

The Low-Res input image was first reshaped to the size of $256\times 256\times 3$. Let us denote the reshaped input image as $\mathbf{Y}$. The aim is to recover a Hi-Res image $\mathbf{f}\left(\mathbf{Y}\right)$ from $\mathbf{Y}$, and that for $\mathbf{F}\left(\mathbf{Y}\right)$ to be as similar as possible to the ground truth Hi-Res image $\mathbf{X}$.

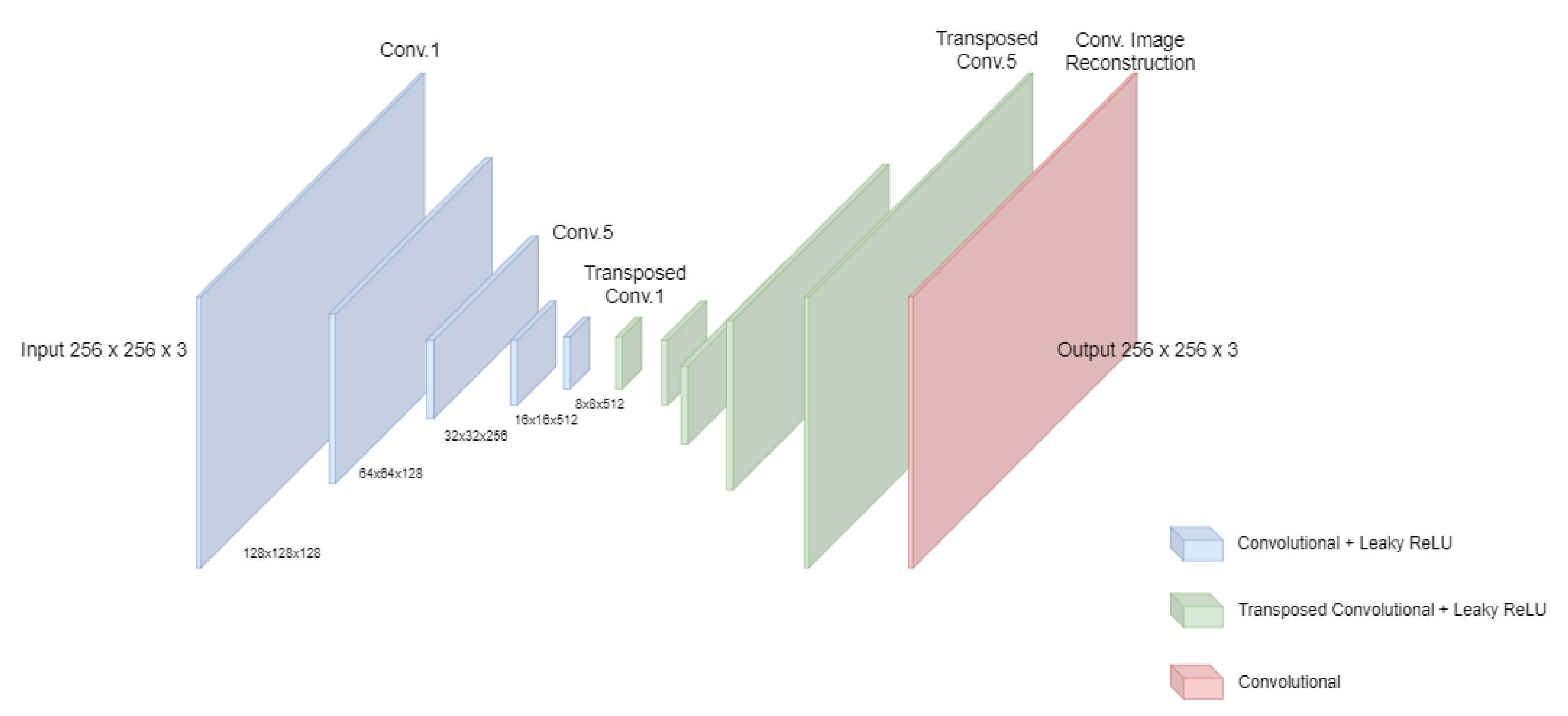
The Autoencoder model used with the ImageNet dataset consists of 5 convolutional layers that down-sample the input image from $256\times 256\times 3$ to $8\times 8\times 512$ after the fifth layer. This is followed by 5 transposed convolutional layers that up-sample the image from $8\times 8\times 512$ to $256\times 256\times 6$. Residual connections were used between the convolutional layers and the transposed convolutional layers as shown in Figure 7. Finally, image reconstruction is achieved by one convolutional layer at the end.

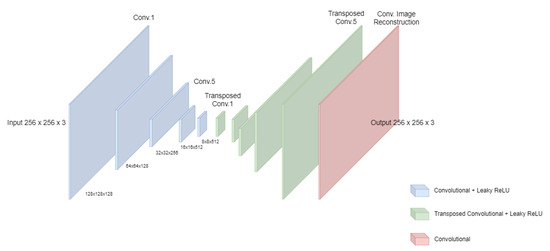
Figure 7. Our Network Structure. Here we have five conv. layers to down sample the input image, followed by five Transposed conv. layers for up-sampling, and one last Conv. layer for image reconstruction. Residual skip connections are not shown in this figure.

All the filters used in the model are of the same kernel size 3 × 3 except for the last image reconstruction layer which has a kernel size of 2 × 2. The number of filters in each layer starts with 128 filters on the first and second convolutional layers and goes to 256, 512, 512 on the third, fourth, and fifth down-sampling layers respectively. Using an increasing number of filters enabled us to stack feature maps and avoid any loss of features between the layers through this down-sampling. As for the decoder part of the model, the number of filters decreases gradually from 512 filters at the first layer to 256, 128, 128, 3 on the other four layers. The last reconstruction layer consists of only 3 filters.

When removing Batch Normalization (BN) modules from the model, better results were achieved with less memory usage. To help tackle the issue of vanishing gradients, the activation function applied through all the layers was the Leaky Rectified Linear Unit (Leaky ReLU).

For the images from the RealSR V1 dataset, the number of convolutional filters were increased to 1024, 1024, 512, and 512, starting from the first layer. The models were implemented using the TensorFlow framework and run on Google Colab. The TensorFlow code is given in Appendix A.

5.2. Training

Learning end-to-end mapping requires the estimation of the network parameters ${\mathbf{W}}_{\mathbf{1}},{\mathbf{W}}_{\mathbf{2}},\dots ,{\mathbf{W}}_{\mathbf{11}}$ and ${\mathbf{B}}_{\mathbf{1}},{\mathbf{B}}_{\mathbf{2}},\dots ,{\mathbf{B}}_{\mathbf{11}}$ where ${\mathbf{W}}_{\mathbf{i}},{\mathbf{B}}_{\mathbf{i}}$ denotes the parameters of the learning filters in the $\mathbf{i}\mathbf{th}$ layer, that minimize the loss between the reconstructed image and the ground truth image. We use the Mean Absolute Error (MAE) as the loss function:

$$\mathrm{Loss}=\frac{1}{n}\sum _{i=1}^n\left|F\left(Y_i\right)-X_i\right|$$

(4)

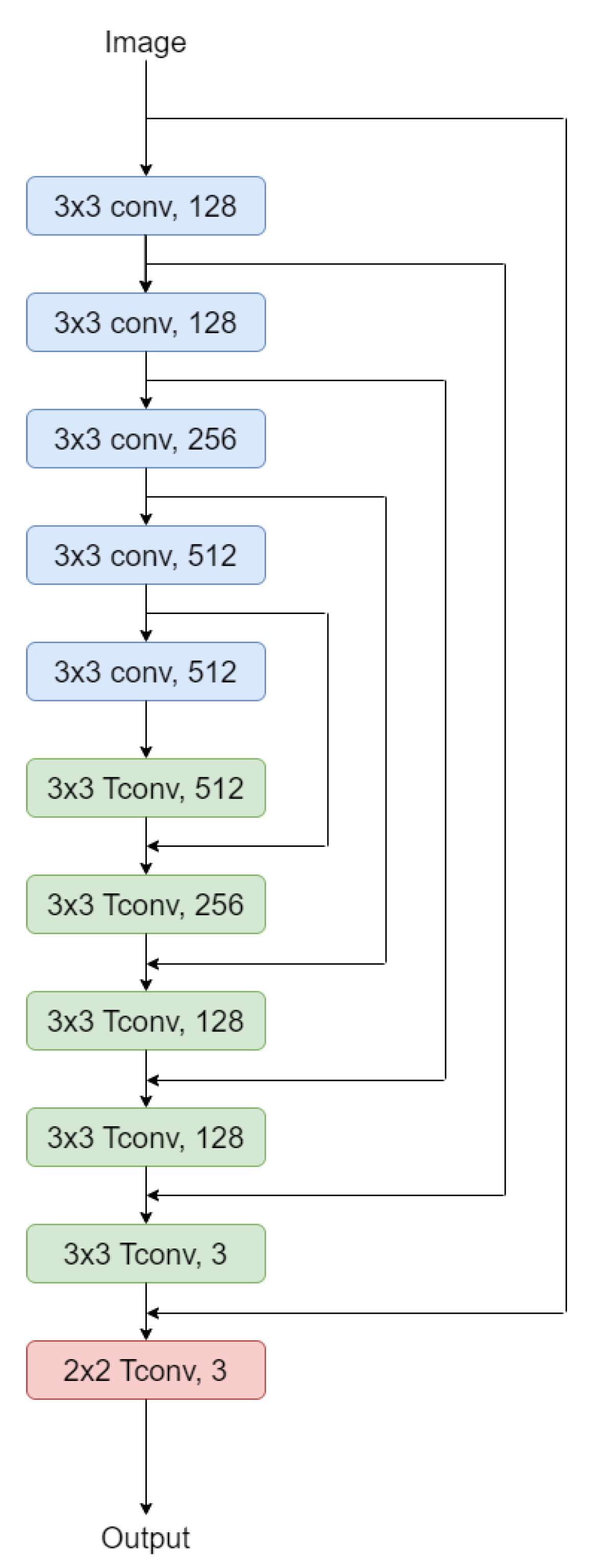
In Super-resolution algorithms, the input image goes through all layers until the output. This requires very-long term memory, and also causes the issue of vanishing gradients. Residual learning with skip connections solve this issue; instead of learning the output directly from the input, the network learn the residual image between the output and input in different layers as shown in Figure 8.

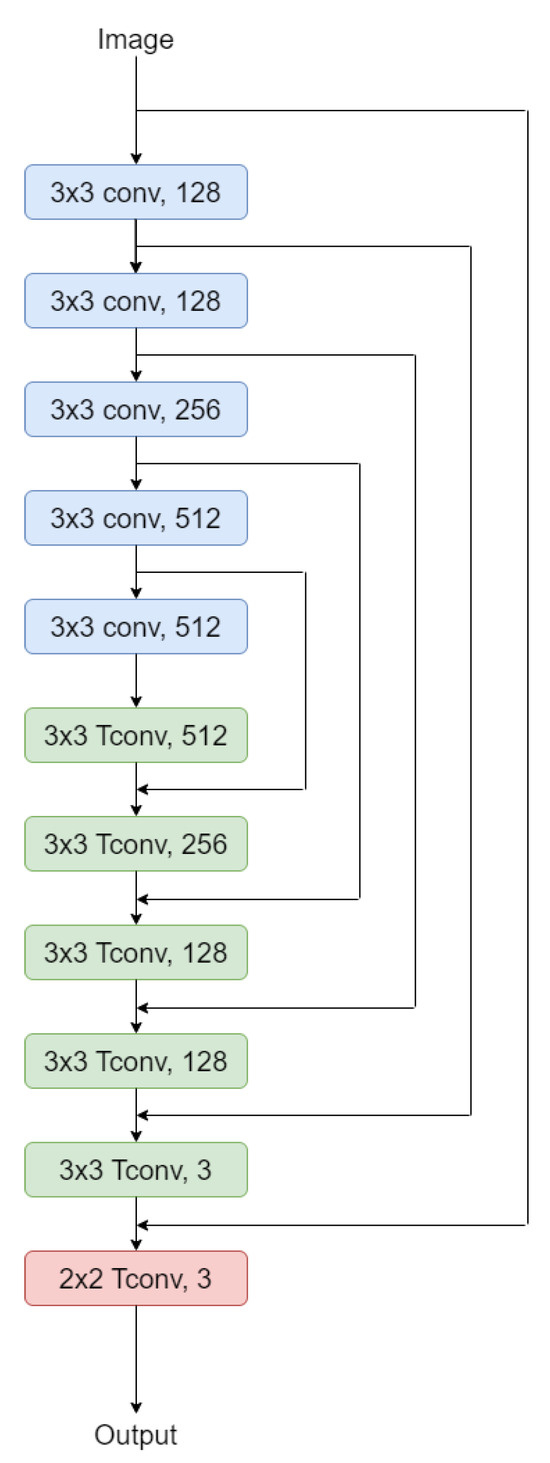
Figure 8. Network Architecture with skip connections.

6. Experiments and Results

6.1. Training Data

Because of limitations in computational time, a subset of the ILSVRC 2013 ImageNet dataset was used in our experiments. The subset consisted of 855 images. Out of the 855 images, 700 images used for training, 130 for validation, and 25 images for testing. In the case of the ReaS V1 dataset, 50 images were used for training, and 32 were used for testing.

On the Google Colab T4 GPU Core, the 700 images from the ImageNet dataset took 5 min and 31 s over 20 Epochs to train and validate on the 130 images. The validation accuracy achieved was 87%. On the same GPU core, the images of RealSR V1 dataset took 16 min and 43 s to achieve a validation accuracy of 81%. On average the testing or inference took 17 micro-seconds per image.

6.2. Training Parameters

For the final model, we selected a network with 11 layers. Filters in all the layers except for the last layer, are of size 3 × 3. This achieved the best results when compared with 5 × 5 filters. The optimizer we use is ’adam’ and the initial learning rate is 0.001. Activation functions through all layers is the Leaky Rectified Linear Unit (Leaky ReLu). We train all experiments over different numbers of epochs, however best results achieved with an epoch equals to 7. Our final model consists of 9,597,646 trainable parameters.

6.3. Model and Performance Trade-Off

Our proposed model was evaluated with different values of learning rate and number of epochs. We computed three metrics to assess the quality of the predicted images: Peak Signal to Noise Ratio (PSNR), Mean Squared Error (MSE), and Structural Similarity Measure (SSIM). We found that increasing the number of epochs generally improves the performance of the network, as reflected by higher values of PSNR and SSIM and lower values of MSE. As for the learning rate, using a lower learning rate achieved better results only when a higher number of epochs is used. Overall, our findings suggest that optimizing the number of epochs while fine tuning the learning rate will further enhance the performance of the model.

The PSNR, MSE, and SSIM results are presented in Table 1, Table 2, Table 3 and Table 4. Each table lists the PSNR, MSE, and SSIM values obtained with different initial learning rates and number of training Epochs. It is worth mentioning here, that the actual range of PSNR values achieved by previous models vary greatly from the PSNR values this model achieved. This is mainly due to the dataset used and the size and complexity of the images.

Table 1. PSNR, MSE, and SSIM values for 9 testing images. These values were obtained with 3 × 3 filters, 11 layers, 7 epochs, and 0.001 step size. Average values for PSNR, MSE, and SSIM are 76.40, 0.005, and 0.89 respectively.

PSNR	MSE	SSIM
73.02	0.01	0.9
75.69	0.01	0.88
75.63	0.01	0.90
75.85	0.01	0.92
73.51	0.01	0.83
82.34	0.001	0.96
79.64	0.002	0.93
77.38	0.003	0.86
74.59	0.01	0.90

Table 2. PSNR, MSE, and SSIM values for 9 testing images. These values were obtained with 3 × 3 filters, 11 layers, 7 epochs, and 0.0001 step size. Average values for PSNR, MSE, and SSIM are 72.76, 0.01, and 0.81 respectively.

PSNR	MSE	SSIM
70.51	0.02	0.81
72.50	0.01	0.78
72.50	0.01	0.81
71.95	0.01	0.84
69.78	0.02	0.68
77.90	0.003	0.93
75.25	0.01	0.88
72.75	0.01	0.76
71.75	0.01	0.81

Table 3. PSNR, MSE, and SSIM values for 9 testing images. These values were obtained with 3 × 3 filters, 11 layers, 20 epochs, and 0.001 step size. Average values for PSNR, MSE, and SSIM are 75.76, 0.01, and 0.91 respectively.

PSNR	MSE	SSIM
73.98	0.01	0.92
75.34	0.01	0.89
76.07	0.004	0.92
75.41	0.01	0.94
73.16	0.01	0.86
79.86	0.002	0.97
77.54	0.003	0.94
75.36	0.01	0.83
75.09	0.01	0.92

Table 4. PSNR, MSE, and SSIM values for 9 testing images. These values were obtained with 3 × 3 filters, 11 layers, 20 epochs, and 0.0001 step size. Average values for PSNR, MSE, and SSIM are 78.25, 0.003, and 0.93 respectively.

PSNR	MSE	SSIM
74.47	0.007	0.93
77.24	0.004	0.92
77.35	0.004	0.94
78.09	0.003	0.95
75.02	0.006	0.89
85.10	0.001	0.98
81.87	0.001	0.95
79.05	0.002	0.90
76.05	0.005	0.93

For visual quality inspection, nine different test images from the ImageNet dataset are shown in Figure 9 and Figure 10. On each Figure, the leftmost picture shows the ground truth high-resolution image. The middle picture depicts the low-resolution input to the model. The right most picture shows the high-resolution output from the model.

Figure 9. Image examples. High Resolution Ground Truth Images are on the left, Low Resolution Input are in the middle, and the High Resolution Output Images are on the right. Note, Low-Res image colors may be different from the original due to TensorFlow.

Figure 10. High Resolution Ground Truth Image on the left, Low Resolution Input in the middle, and the High Resolution Output Image on the right.

The results from the RealSR V1 dataset  [27,28] are shown in Table 5 and Figure 11. These results were obtained over 120 epochs with an initial learning rate of 0.0001.

Table 5. PSNR, MSE, and SSIM values for the 9 testing images from the RealS V1 dataset.

PSNR	MSE	SSIM
73.24	0.0093	0.85
74.70	0.0066	0.90
76.55	0.0043	0.90
71.38	0.0142	0.83
74.03	0.0077	0.86
74.21	0.0074	0.87
70.75	0.0160	0.70
75.01	0.0062	0.90
75.64	0.0053	0.91

Figure 11. High Resolution Ground Truth Image on the left, Low Resolution Input in the middle, and the High Resolution Output Image on the right.

7. Conclusions

In this article, we presented a single image super-resolution technique using deep convolutional residual networks. We obtained remarkable average values for PSNR, MSE, and SSIM. Generally training deep networks is difficult because of the vanishing gradient problem. In this work, we used residual-learning to overcome this issue. The network can be further optimized with larger training datasets. However, they need higher computational power. Moreover, the performance can be possibly improved by exploring more filters and different training strategies.