Predicting Chlorophyll-a in the Mauritanian–Senegalese Coastal Upwelling from Tropical Sea Surface Temperature

Abstract

The Mauritanian–Senegalese Coastal Upwelling exhibits strong interannual variability, which has been found to be driven by El Niño-Southern Oscillation (ENSO). In addition, ENSO has been shown to be triggered by the Indian Ocean and Atlantic Sea Surface Temperature (SST) variability. Nevertheless, how all these basins impact on the upwelling predictability has not been analyzed so far. Using a satellite product of surface chlorophyll-a as a proxy of marine productivity, this work makes an assessment of the predictability of the Mauritanian–Senegalese Coastal Upwelling marine ecosystem. Different statistical approaches are used to evaluate the relative contribution of the tropical basins, including the Pacific, Indian, equatorial and Tropical North Atlantic SSTs. The results indicate that although most of the upwelling variability stands for ENSO, the Atlantic contributions play an important role in shaping the seasonal prediction skill. These results may have strong implications for fisheries and marine ecosystem management in the region.

1. Introduction

The coast of West Africa hosts one of the most important marine ecosystems worldwide: the Mauritanian–Senegalese Coastal Upwelling (MSCU) system. The MSCU is characterized by a marked seasonal cycle in which, from February to May (FMAM), N-S alongshore winds blow parallel to the coast (Figure 1). The friction transferred by the wind stress to the underneath water layers together with the effect of the Coriolis force produce an integrated westward flow known as Ekman transport. The divergence of surface waters, due to the presence of the continental boundary, produce the upwelling of nutrient rich and cold waters from the seabed, supporting primary production, which is closely associated with chlorophyll-a (chl-a) concentration (Figure 1). Chl-a is, thus, an estimate of upwelling strength in the region, as nutrients are the main limiting factor for primary production synthesis [1,2], and there is no critical light-limitation at tropical latitudes [3].

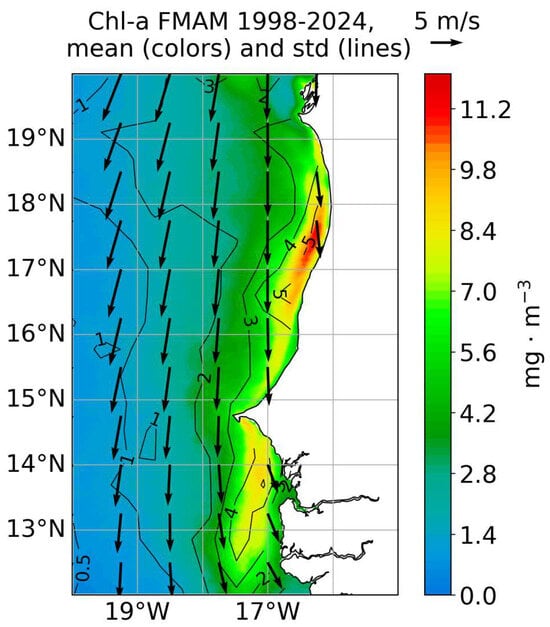
Figure 1. Surface chlorophyll-a (chl-a) concentration (mg·${\mathrm{m}}^{-3}$), mean (colors) and standard deviation (contours) in FMAM during the period 1998–2024. Surface wind (m·${\mathrm{s}}^{-1}$) mean is indicated by arrows.

In the MSCU, predicting changes in alongshore winds can be translated into predicting chl-a anomalies. Variations in alongshore winds can be driven by Sea Surface Temperature (SST) anomalies in remote regions, in the form of SST variability modes. These changes in SST can affect, locally, convection, shifting the Hadley and Walker circulation cells. As a result, atmospheric tropical and extratropical Rossby waves and equatorial Kelvin waves can be triggered, being the former due to conservation of potential vorticity [4,5]. These mechanisms drive the connection between tropical ocean basins, i.e., producing pantropical interactions [6]. Therefore, the ocean–atmosphere interaction processes developed in one basin can be responsible for part of the variability in others [6,7]. In particular, El Niño-Southern Oscillation (ENSO) has a strong influence on the Tropical North Atlantic (TNA) during boreal spring. During El Niño, an atmospheric Rossby wave train is excited over the northern hemisphere in a Pacific–North American (PNA) configuration, which produces a weakening of the Azores high pressure system. As a consequence, there is a reduction in the TNA trade winds. The opposite occurs for La Niña. Also, ENSO can affect the TNA through alterations in the Walker and Hadley cells [8,9] or through a secondary Gill-type response over the Amazon basin [10].

In particular, ENSO is known to influence the MSCU through its impact on surface alongshore winds [11,12]. In fact, some studies have linked ENSO to chl-a concentration, e.g., the 1998–1999 ENSO event [13]; and marine ecosystem variability, e.g., the migratory patterns of round sardinella [14]. Other modes of interannual SST variability have also been linked to chl-a concentration. In the equatorial Atlantic, the Atlantic El Niño [15] modulates chl-a concentration during boreal summer in the eastern equatorial basin through ocean dynamics [16]. Chl-a concentration in the Indian Ocean seems to be modulated primarily by the Indian Ocean Dipole (IOD) [17] and ENSO [18].

A remarkable fact is that ENSO can be triggered, in turn, by other modes of ocean variability, such as the Atlantic El Niño [19,20], SST anomalies in the TNA [5,21] and the Indian Ocean [17,22]. Additionally, the IOD has been found to be followed by a basin-wide warming known as the Indian Ocean Basin (IOB) mode [23,24]. These two Indian Ocean modes can occur independently and affect ENSO [25,26,27]. Thus, different tropical ocean basins can interact with the Pacific, predicting its variability [28,29,30]. Impacts and underlying mechanisms of SST variability modes, beyond ENSO, on anomalous chl-a concentration in the MSCU have been little analyzed. Given that ENSO influences chl-a variability in the MSCU and that ENSO itself can be predicted from SST signals in other ocean basins, it is reasonable to hypothesize that SST variability in these other basins may also serve as a predictor of chl-a fluctuations, potentially extending the horizon of chl-a predictability. To test this, chl-a satellite data is used to assess the influence of different modes of oceanic variability on chl-a concentration in the MSCU in FMAM. In addition, statistical cross-validated hindcasts are generated using SST information from distinct ocean basins as predictors.

2. Materials and Methods

Along this work, SST and chl-a data will be used to feed statistical prediction models. The SST data (°C) have been obtained from the Hadley Centre Global Sea Ice and Sea Surface Temperature dataset (HadISST 1.1) [31], which has a 1° spatial resolution. It covers the period from 1870 to the present. A chl-a product (https://doi.org/10.48670/moi-00281), obtained from satellite observations from the Copernicus Marine Service [32,33], has been used. This product contains the surface chl-a concentration (mg·${\mathrm{m}}^{-3}$), with a 4 km resolution for the period September 1997–present. Geopotential height at 200 hPa (${\mathrm{m}}^2$·${\mathrm{s}}^{-2}$), Sea Level Pressure (SLP, Pa) and 10 m wind speed (m·${\mathrm{s}}^{-1}$) have been used to assess atmospheric teleconnections. These variables come from the ERA5 reanalysis [34], covering the period from January 1940 to the present, with a 0.25° horizontal resolution. In addition, instantaneous wind stress ($\tau$, N·${\mathrm{m}}^{-2}$) from ERA5 was used to characterize upwelling. Upwelling primarily arises from the divergence of Ekman transport. This divergence can result from the presence of a meridionally oriented coastline, as in the MSCU region, where the vertical velocity induced is proportional to the meridional component of the wind stress. In addition, spatial gradients in wind stress (i.e., wind stress curl) can also drive divergence of the Ekman transport, generating vertical motions known as Ekman pumping. These vertical velocities can be estimated as:

$${\displaystyle \frac{1}{{\rho }_{\mathrm{w}}f}}{\nabla }_{\mathrm{z}}\times \tau$$

(1)

where ${\nabla }_{\mathrm{z}}\times \tau$ is the wind stress curl with the subindex z indicating its vertical component, ${\rho }_{\mathrm{w}}$ is the seawater density (assumed constant at 1025 kg·${\mathrm{m}}^{-3}$, following [35]) and f is the Coriolis parameter.

Due to the availability of chl-a data, the analysis in this work is restricted to the period 1998–2024.

Data have been preprocessed by calculating seasonal anomalies. This involved selecting a 4-month season and subtracting the seasonal mean over the entire study period from each year’s data. Given the length of the time series, a linear trend was subtracted from the seasonal anomalies in order to minimize the influence of anthropogenic climate change and low-frequency natural oscillations, thereby isolating interannual variability.

To evaluate spatial patterns of co-variability between SST and chl-a, as well as associated atmospheric teleconnections, many results are presented as regression maps. Their statistical significance is assessed using a non-parametric Monte Carlo test, based on 1000 random permutations. Only those values exceeding the 95% confidence interval are considered statistically significant, and are highlighted accordingly in the figures.

2.1. Identification of Predictors

To identify the tropical basin variability modes preceding chl-a in the MSCU, an Extended Maximum Covariance Analysis (EMCA) is applied. The EMCA is an extension of the classical Maximum Covariance Analysis (MCA) [36,37], which allows for the inclusion of multiple fields either in the predictor or the predictand fields. As designed here, the EMCA involves taking into account several seasons of tropical SSTs by concatenating them year by year in the predictor field [38], starting with AMJJ (−1 yr), where −1 yr refers to the year prior to the MSCU upwelling season (FMAM (0 yr)). AMJJ was chosen as the starting season because it precedes the peak of the Atlantic Niño variability (JJAS) by two months, which has been identified as a potential precursor of ENSO [19,20]. From that point, five additional seasons are considered (JJAS (−1 yr), ASON (−1 yr), ONDJ (−1 yr), DJFM (−1 yr), and FMAM (0 yr)), thus covering from −10 months to 0 lead time before the target chl-a season. The predictand field is defined as the anomalous chl-a concentration in the MSCU (20°–15° W, 12°–20° N, Figure 1 domain) during the upwelling season (FMAM (0 yr)). Chl-a, as a regional impact variable, exhibits greater spatial variability in contrast to the predictor field (tropical SSTs), which primarily varies following large-scale variability modes.

As a result of the EMCA, two time series are obtained: the expansion coefficient Us, which reflects the temporal evolution of the predictor SST field, and the expansion coefficient Vs, which captures the time evolution of the predictand chl-a field (Figure 2a). By regressing the Us series onto the original SST field, a time-evolving SST mode is identified (Figure 2b–g), while the associated chl-a pattern is derived by regressing the same Us series onto the original chl-a field (Figure 2h). These regression patterns describe the spatial structure of the co-variability mode identified between the tropical SST anomalies and chl-a concentration in the MSCU during the upwelling season. The description that follows refers to the positive phase of the mode (positive values of the expansion coefficients Us) while the opposite patterns apply during its negative phase. For an increase in chl-a, a summer Atlantic Niño in AMJJ (−1 yr) appears together with an incipient cooling in the tropical and northern subtropical Pacific (Figure 2b). This Pacific cooling intensifies in subsequent seasons, leading to a fully developed La Niña pattern by ASON (−1 yr), which coincides with a negative IOD (Figure 2d). The IOD subsequently evolves into a basin-wide Indian Ocean cooling, known as the IOB mode in ONDJ (−1 yr) (Figure 2e). From DJFM (−1 yr) onward, a cooling signal also emerges in the TNA (Figure 2f), persisting through FMAM (0 yr), in phase with the ongoing Pacific La Niña (Figure 2g). This specific SST configuration—characterized by La Niña conditions in the Pacific and concurrent cooling in the TNA during boreal late winter—has previously been linked to enhanced upwelling in the MSCU region [12].

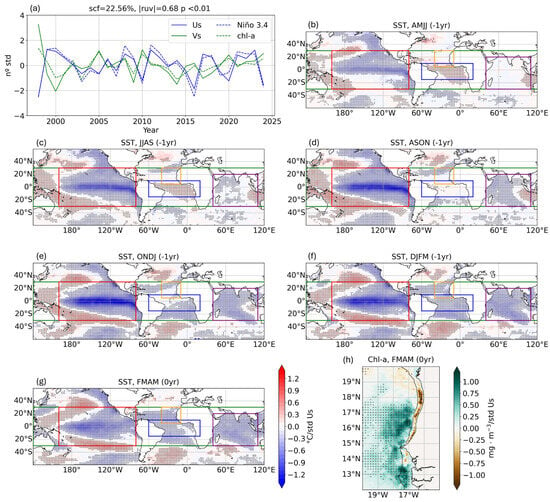
Figure 2. Leading co-variability mode between tropical Sea Surface Temperatures (SSTs) and chlorophyll-a (chl-a) in the Mauritanian–Senegalese Coastal Upwelling (MSCU) for 1998–2024. (a) Standardized expansion coefficients associated with the first mode of variability. The solid blue line is Us (associated with SSTs) and the green Vs (associated with chl-a). The dashed blue line represents the standardized SST anomaly index of Niño 3.4 at DJFM (−1 yr). The green dashed line is the chl-a standardized anomaly index at MSCU in FMAM (0 yr). (b–g) Homogeneous SST regression maps (°C/std) for AMJJ (−1 yr), JJAS (−1 yr), ASON (−1 yr), ONDJ (−1 yr), DJFM (−1 yr) and FMAM (0 yr). Dots indicate the 95% confidence interval based on a Monte Carlo test. The green box, covering all tropics, on each map indicates the region considered for the predictor field in the application of the EMCA. The red, purple, blue and orange boxes indicate the Pacific, Indian, equatorial Atlantic and TNA regions to be used in the statistical prediction models. (h) Heterogeneous regression maps of chl-a (mg·${\mathrm{m}}^{-3}$/std) over the MSCU region in FMAM (0 yr). Dots indicate the 95% confidence interval based on a Monte Carlo test. The 100 m isobath is shown as a black line representing the continental shelf.

This leading co-variability mode explains 22.56% of the total covariance between tropical SSTs and chl-a in the MSCU region, with a correlation coefficient between the expansion coefficients of 0.68, indicating a strong and significant (99% confidence interval) coupling. The reliability of this mode is supported by its strong temporal coherence with independent indices: the SST expansion coefficient (Us) closely follows the Niño 3.4 SST anomaly index during DJFM (−1 yr), suggesting that the mode is predominantly influenced by ENSO-related variability. Simultaneously, the chl-a expansion coefficient (Vs) resembles the chl-a index, calculated as the detrended anomaly of the spatially averaged chl-a time series over the MSCU region during the upwelling season (FMAM (0 yr)). This fact highlights the link between this tropical SST–chl-a mode and surface productivity in the region.

Although the temporal evolution of this tropical SST pattern is largely dominated by ENSO, it provides a useful framework for identifying other drivers of chl-a variability in the MSCU. This, in turn, enables the development of statistical models to predict chl-a anomalies several months in advance. Based on this mode, five potential predictors have been identified, each corresponding to a specific oceanic domain indicated by boxes in Figure 2b–g: the Pacific Ocean (red box, 160° E–70° W, 30° S–30° N), the equatorial Atlantic (blue box, 60° W–20° E, 15° S–10° N), the TNA (orange box, 40°–10° W, 5°–30° N), the Indian Ocean (purple box, 40°–110° E, 30° S–20° N), and the entire tropical latitudinal belt (green box, 30° S–30° N). The potential of each region to predict chl-a anomalies in FMAM (0 yr) will be explored through skill assessment.

2.2. Statistical Prediction Models

To generate cross-validated hindcasts in each of the seasons and using different SST drivers, two statistical prediction tools implemented in python are used: Spy4CAST (version 1.0.0) and NN4CAST (version 1.0.20).

The Spy4CAST tool applies MCA, similarly to Figure 2, but using a single predictor field [39]. The tool identifies the leading modes of co-variability between a predictor and a predictand field (here, SST and chl-a anomalies). In addition, Spy4CAST produces cross-validated hindcasts using a leave-one-year-out methodology: the MCA is repeated omitting one year at a time, and for each omitted year, a reconstructed predictand (chl-a) field is generated using the predictor (SST) information from the remaining years. Prediction skill is evaluated through Anomaly Correlation Coefficient (ACC) maps, which are computed by correlating the original and reconstructed predictand (chl-a) fields. The statistical significance of the ACC values is assessed using a non-parametric Monte Carlo test, based on 1000 random permutations. Values exceeding the 95% confidence interval are highlighted in the figures.

The predictor regions identified in the previous section include the Pacific Ocean, the equatorial Atlantic, the TNA, and the Indian Ocean. For each of the basins, four predictor seasons are considered: AMJJ (−1 yr), JJAS (−1 yr), ASON (−1 yr), and ONDJ (−1 yr), which correspond to lead times of −10, −8, −6, and −4 months with respect to the chl-a season (FMAM (0 yr)). The last season considered is ONDJ (−1 yr), to avoid overlapping with the chl-a predictand season.

For each basin and season, a MCA is applied using Spy4CAST, and the leading mode, which explains the largest fraction of the total covariance, is then used to reconstruct the chl-a field by generating a cross-validated hindcast.

In addition, and in order to corroborate and validate the existence of predictability of chl-a from ocean variability, a deep learning methodology is applied. This methodology has been implemented in python by the creation of an easy Neural Network forecast library. NN4CAST is a model library based on Deep Neural Networks (DNNs) which provides a versatile tool for prediction and non-linear statistical analysis, which can help in the assessment of seasonal predictability [40]. The deep learning model is composed of five hidden layers following an encoder–decoder architecture (with 1024, 256, 64, 256, and 1024 neurons, respectively). In this configuration, the encoder progressively compresses the information from the predictor field into a lower-dimensional latent representation, which captures the essential features of the SST field. The decoder then uses this compact representation to reconstruct and predict the target variable, in this case, the chl-a concentration. The network employs the Exponential Linear Unit activation function, together with batch normalization and a dropout rate of 0.1, to enhance training stability and prevent overfitting. Furthermore, the He initialization and L2 kernel regularization were applied to improve optimization and generalization. The model was trained with a learning rate of 0.0001 over 2500 epochs. As Spy4CAST, NN4CAST produces cross-validated hindcasts. The prediction skill is evaluated, again, by computing ACC maps between the original and reconstructed chl-a fields. The statistical significance of these correlations is assessed using a non-parametric Monte Carlo test, based on 1000 random permutations (95% confidence interval).

3. Results

In this section, the main results derived from the application of both prediction techniques are summarized. The performance of the Spy4CAST model is examined alongside that of the NN4CAST model, which also serves to corroborate and complement the findings from Spy4CAST.

3.1. Assessment of SST Drivers and Chl-a Predictability Derived from MCA. Spy4CAST Model

Figure 3 shows the leading MCA modes using tropical SSTs as predictors of chl-a anomalies in the MSCU region during FMAM (0 yr). The MCA was repeated for four SST seasons: AMJJ (−1 yr), JJAS (−1 yr), ASON (−1 yr), and ONDJ (−1 yr), corresponding to lead times of −10, −8, −6, and −4 months, respectively. The SST patterns in each season (Figure 3a,c,e,g) closely resemble those obtained through the EMCA (Figure 2), reinforcing the idea that the dominant structure of co-variability between tropical SSTs and MSCU chl-a is primarily controlled by ENSO. The spatial coherence across seasons, together with the gradual evolution of the SST patterns, supports the presence of a consistent coupled mode linking tropical SST variability to chl-a in the MSCU. The temporal continuity is further confirmed by strong correlations between the expansion coefficients (Us) from each MCA and those from the EMCA, as well as by high correlations among the individual tropical MCA Us themselves (see Figure S1).

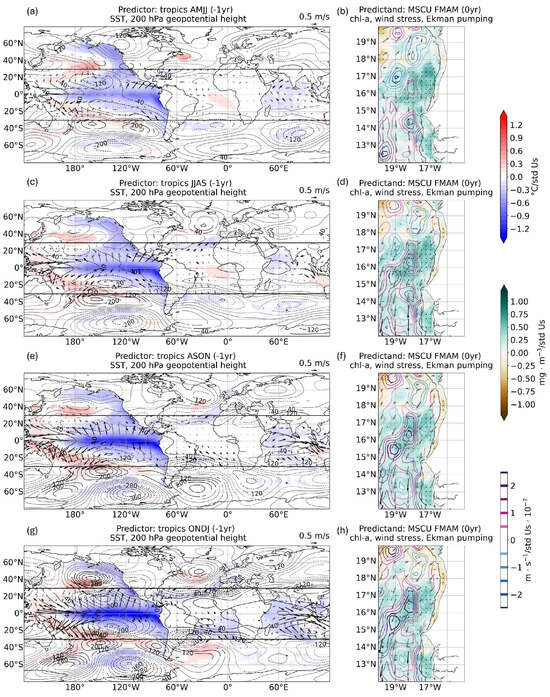
Figure 3. Leading co-variability modes between tropical Sea Surface Temperatures (SSTs) and chlorophyll-a (chl-a) in the Mauritanian–Senegalese Coastal Upwelling (MSCU) for different seasons/lead times. (a) Homogeneous SST regression map (colors, °C/std) derived from the leading co-variability mode between tropical SSTs in AMJJ (−1 yr)/−10 months with MSCU chl-a for FMAM (0 yr). Only values significant at the 95% confidence interval based on a Monte Carlo test are shown. Regressions onto atmospheric variables are also included: geopotential height at 200 hPa (contours, ${\mathrm{m}}^2$·${\mathrm{s}}^{-2}$/std) and surface tropical (30° N–30° S) winds (arrows, m·${\mathrm{s}}^{-1}$/std). Significant values at the 95% level are indicated in black contours/arrows. (b) Heterogeneous regression map of chl-a (mg·${\mathrm{m}}^{-3}$/std) over the MSCU region for FMAM (0 yr) derived from the same co-variability mode. Dots indicate significance at the 95% confidence interval according to a Monte Carlo test. Regression onto the wind stress (arrows, N·${\mathrm{m}}^{-2}$/std) and Ekman pumping velocity (contours, m·${\mathrm{s}}^{-1}$/std) is also included. Significant values at the 95% level are highlighted with thicker contours for Ekman transport and with black arrows for the wind stress. The 100 m isobath is shown as a black line, representing the continental shelf. (c,d) As in (a,b), but for JJAS (−1 yr)/−8 months. (e,f) As in (a,b), but for ASON (−1 yr)/−6 months. (g,h) As in (a,b), but for ONDJ (−1 yr)/−4 months.

In AMJJ (−1 yr) (Figure 3a), a warm SST anomaly emerges in the equatorial Atlantic, although it is notably weaker and narrower than the anomaly identified in the EMCA. This discrepancy may arise because the EMCA integrates information from multiple lead times, including periods when the Pacific has already integrated the potential forcing from the equatorial Atlantic [19]. In contrast, the MCA at AMJJ (−1 yr) captures an earlier stage of the evolution. As such, the SST signal at this lag may not yet reflect the cumulative effect of the Atlantic forcing integrated by the Pacific. This possibility is further explored in a dedicated section examining the Atlantic SSTs role.

In JJAS (−1 yr) (Figure 3c), the Atlantic warming persists, but by ASON (−1 yr), it dissipates, while a negative IOD pattern begins to emerge (Figure 3e). Throughout all seasons, the Pacific La Niña remains active, intensifying toward ONDJ (−1 yr), where the teleconnection patterns become more pronounced (Figure 3g). The geopotential height field at 200 hPa reveals a clear Rossby wave train in the Northern Hemisphere, a counterpart pattern in the Southern Hemisphere, a Gill-type response in the tropical Pacific and a secondary Gill response in the tropical Atlantic—all consistent with the large-scale atmospheric adjustment to persistent La Niña forcing. Additionally, by ONDJ (−1 yr), a cooling signal begins to develop in the TNA, a pattern probably associated with increased upwelling-favorable wind anomalies over the MSCU region in boreal late winter.

Figure 3b,d,f,h display the heterogeneous regression maps of chl-a anomalies associated with the MCA modes for each season. These patterns are consistent with the EMCA-derived chl-a structure (Figure 2h), showing strong resemblance across seasons. In all cases, a pronounced maximum appears between 15° and 18° N, just beyond the continental shelf, while further south the largest positive anomalies are concentrated over the shelf. The chl-a response to tropical SST variability is consistent with previous studies highlighting the influence of ENSO on the MSCU [12,13]. The upwelling signal appears to be primarily driven by wind stress curl, which induces Ekman pumping over the region where the strongest chl-a anomalies are found (Figure 3b,d,f,h). Ekman pumping has been shown to play a key role in supplying nutrients to the euphotic layer and enhancing phytoplankton biomass, thereby supporting increased chl-a concentration [2,41]. In the northern sector, coastal Ekman transport seems less relevant, as the wind stress is not strictly meridional with respect to the coastline and the chl-a anomalies are mainly located offshore. In contrast, in the southern MSCU, where anomalies are concentrated over the continental shelf, coastal Ekman transport may still play a role in explaining the chl-a response.

The predictive skill as ACC maps of Spy4CAST by considering SST anomalies from the tropics and from individual oceanic regions—Pacific, Indian, equatorial Atlantic, and TNA—as predictors of chl-a anomalies in the MSCU region during FMAM (0 yr) are shown in Figure 4. For each predictor region, the MCA was computed independently for four lead seasons: AMJJ (−1 yr), JJAS (−1 yr), ASON (−1 yr), and ONDJ (−1 yr), corresponding to lead times of −10, −8, −6, and −4 months, respectively. The skill of the statistical predictions based on SST anomalies from the different regions is shown as ACC maps.

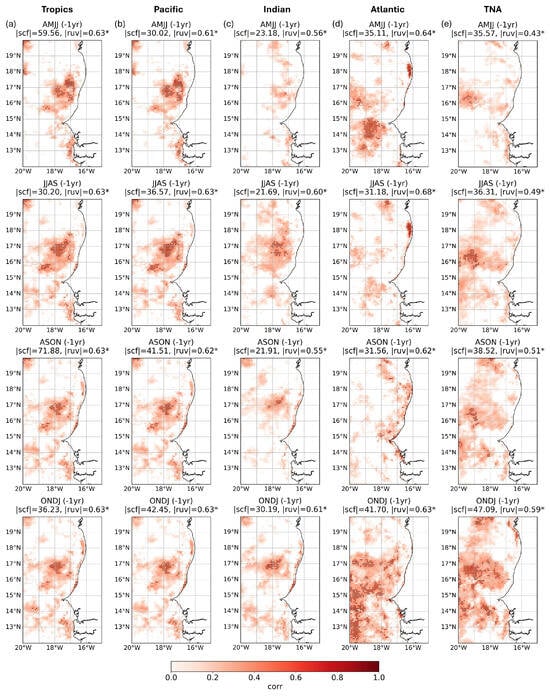
Figure 4. Cross-validated prediction skill maps derived from Spy4CAST. Skill maps as an Anomaly Correlation Coefficient (ACC) between observed chlorophyll-a (chl-a) fields and the corresponding cross-validated hindcasts reconstructed using Maximum Covariance Analysis (MCA)-derived information from Sea Surface Temperature (SSTs) in the column (a) tropics, column (b) Pacific Ocean, column (c) Indian Ocean, column (d) equatorial Atlantic, and column (e) Tropical North Atlantic (TNA). Each row represents a different season/lead time of the SST relative to chl-a in FMAM (0 yr) for the period 1998–2024, from top to bottom: AMJJ (−1 yr)/−10 months, JJAS (−1 yr)/−8 months, ASON (−1 yr)/−6 months and ONDJ (−1 yr)/−4 months. Dots indicate significance at the 95% confidence interval based on a Monte Carlo test. The squared covariance fraction (scf) of the MCA modes indicated above each map, along with the correlation coefficients between the expansion coefficients Us and Vs. Asterisk denote correlations that are statistically significant at the 95% confidence interval based on a Monte Carlo test.

Figure 4a,b, corresponding to the tropics and the Pacific Ocean, show very similar skill maps across all seasons, further confirming that both the detected co-variability mode and the associated predictability are primarily driven by the Pacific. The region with the highest skill is consistently located between 15° and 18° N, offshore and beyond the continental shelf—matching the area of maximum chl-a anomalies captured by the different tropical MCA modes (Figure 3b,d,f,h).

In the case of the Indian Ocean (Figure 4e), JJAS (−1 yr), ASON (−1 yr), and ONDJ (−1 yr) skill maps (second, third, and fourth rows, respectively)—though showing more spatially confined areas of skill—are highly similar to those obtained for the tropics and the Pacific (Figure 4a,b). This suggests that Indian Ocean variability is strongly linked to that of the Pacific, a fact further supported by significant correlations between the corresponding expansion coefficients Us (0.61 in AMJJ (−1 yr) and ASON (−1 yr), 0.78 in JJAS (−1 yr) and 0.87 in ONDJ (−1 yr)).

Regarding the equatorial Atlantic (Figure 4d), this region does not act as a good predictor in JJAS (−1 yr) or ASON (−1 yr). In AMJJ (−1 yr), although the SST signal in the equatorial Atlantic is weak in the individual MCA performed with tropical SSTs (Figure 3a), the mode shows some connection with that identified by the EMCA (correlation coefficient between expansion coefficients Us of 0.48) and a weaker link with the Pacific (0.34). At the same time, it also captures variability that is not entirely associated with these relationships, contributing instead mainly to skill in the southern sector of the MSCU region. In ONDJ (−1 yr), the equatorial Atlantic (Figure 4d, fourth row) also carries relevant predictive information. Therefore, this region emerges as a potentially strong predictor of chl-a anomalies in FMAM (0 yr), again especially in the southern part of the upwelling system. The mechanisms behind the different skill and teleconnection found for the tropical Atlantic will be analyzed in a separate section later on.

Figure 4e shows the ACC skill maps for TNA SSTs as predictor. In general, the predictive skill increases as the predicted season (FMAM (0 yr)) approaches, with ONDJ (−1 yr) (Figure 4e, fourth row) showing the highest skill. This progression mirrors the seasonal development of cold SST anomalies in the TNA seen in the EMCA and in the MCA regression maps (Figure 2b–g and Figure 3a,c,e,g), showing that TNA variability becomes increasingly influential closer to the target season. This influence may operate through changes in surface winds over the TNA and the MSCU region, potentially linked to ENSO but also involving local variability. In contrast, for AMJJ (−1 yr), when the EMCA does not capture a SST signal in the TNA, a small amount of skill is still observed (Figure 4e, first row), indicating that during this season some variability not related to ENSO contributes modestly to predictive skill.

3.2. Assessment of Chl-a Predictability Derived from DNN. NN4CAST Model

To assess the potential predictability of chl-a in the MSCU identified in the previous section, a DNN approach is applied through the NN4CAST model. Figure 5 displays the prediction skill, expressed as an ACC, across the same lead times and SST predictor regions as in Spy4CAST (Figure 4), allowing for a comparison between the two approaches.

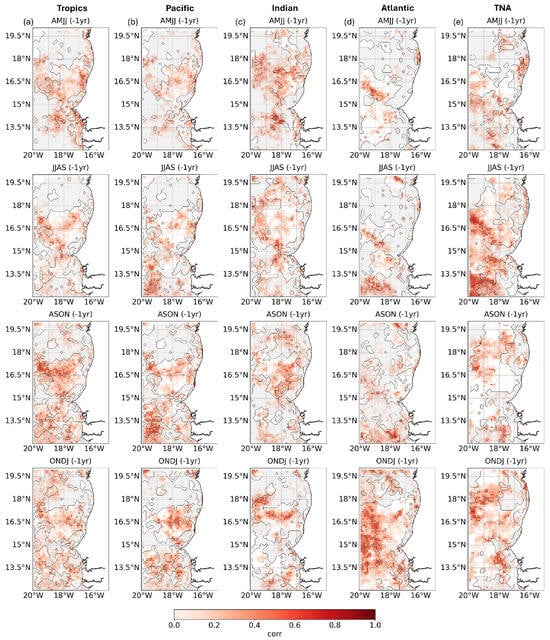
Figure 5. Cross-validated prediction skill maps derived from NN4CAST. Skill maps as an Anomaly Correlation Coefficient (ACC) between observed chlorophyll-a (chl-a) fields and those reconstructed using a neuronal network information from SSTs in the: column (a) tropics, column (b) Pacific Ocean, column (c) Indian Ocean, column (d) equatorial Atlantic, and column (e) Tropical North Atlantic (TNA). Each row corresponds a different season/lead time of the Sea Surface Temperature (SST) relative to chl-a in FMAM (0 yr), covering the period 1998–2024. From top to bottom: AMJJ (−1 yr)/−10 months, JJAS (−1 yr)/−8 months, ASON (−1 yr)/−6 months and ONDJ (−1 yr)/−4 months. Dots indicate significance at the 95% confidence interval based on a Monte Carlo test. Grey contours highlight areas where Spy4CAST does not exhibit skill.

Regarding the tropics and the Pacific (Figure 5a,b, respectively), the skill maps remain highly consistent between them across lead times, once again highlighting the central role of the Pacific in driving predictability. The most extended skill appears at the shorter lead times (ASON (−1 yr) and ONDJ (−1 yr)) where NN4CAST appears to outperform Spy4CAST, particularly in the southern sector of the MSCU, south of 15° N.

For the Indian Ocean (Figure 5c), the predictive skill patterns differ from those associated with the Pacific, suggesting that the covariability between both basins—prominent in the Spy4CAST approach—is not as strongly reflected here. In this case, NN4CAST does not improve skill in the southern part of the MSCU, unlike what was observed for the Pacific. Instead, it shows improved predictive skill in the north, especially during ONDJ (−1 yr), suggesting that the model may be capturing aspects of Indian Ocean variability that are not as tightly linked to the Pacific as in the Spy4CAST framework. This points to the potential of NN4CAST to extract predictive signals from more localized or independent dynamics within the basin.

As for the equatorial Atlantic (Figure 5d), NN4CAST captures some predictability in regions not fully aligned with those highlighted by Spy4CAST, particularly in JJAS and ASON (−1 yr), where skill emerges in the southern MSCU. In AMJJ (−1 yr), the model performance shows some agreement with Spy4CAST, especially between 15° and 17° N. Meanwhile, ONDJ (−1 yr) remains the lead season with the highest overall skill, as in the statistical approach, the area of strong predictability is less extensive, suggesting that NN4CAST may be detecting a more spatially focused or distinct component of the Atlantic-related variability.

In the case of the TNA (Figure 5e), ONDJ (−1 yr), expected to be the best predictive season, reveals notable differences between the two models: while Spy4CAST attains high skill over the MSCU, NN4CAST shows a marked reduction, with the region of maximum predictability shifted northward, around 18–19° N. The greatest agreement between both models occurs in JJAS (−1 yr), and NN4CAST displays enhanced skill, particularly over the southern sector. Finally, during AMJJ (−1 yr) and ASON (−1 yr), NN4CAST still detects some predictive signal.

Overall, NN4CAST shows predictive skill patterns that generally align with those obtained using Spy4CAST, lending support to the signals identified through the statistical approach. However, unlike Spy4CAST, which predicts chl-a anomalies based on the extended co-variability mode identified in the methodology (and therefore provides clearer insights into the origin of predictability), NN4CAST does not offer direct information about the underlying physical linkages driving its forecasts. Although efforts are being made to develop attribution methods that can identify the predictor regions contributing to the predictability, it remains unclear, without further analysis, whether the model relies on the same coupled mode linking tropical basins, or instead draws from different sources of variability. Some of the discrepancies between both approaches may stem from this fundamental difference. Nevertheless, NN4CAST often provides enhanced predictive skill in regions where Spy4CAST is less effective—especially in the southern MSCU. This predictive skill could arise from model-specific artifacts or may reflect NN4CAST capacity to detect non-linear or more complex relationships not accessible through linear statistical methods. More detailed analysis would be required to disentangle these contributions.

3.3. Role of the Atlantic Niño in AMJJ (−1 yr) and Atmospheric Impact in the MSCU

In this section, the role of the Atlantic Niño during AMJJ (−1 yr) in shaping the atmospheric and oceanic conditions that may lead to changes in chl-a concentration in the MSCU during FMAM (0 yr) is explored. To this end, the expansion coefficient Us from the MCA between equatorial Atlantic SSTs in AMJJ (−1 yr) and MSCU chl-a anomalies in FMAM (0 yr) is regressed onto SST fields at various seasons, both prior to and following AMJJ (−1 yr).

Four months before AMJJ (−1 yr) (DJFM (−2 yr)) (Figure 6a), a warm anomaly resembling an Atlantic Niño is already present. This winter Atlantic Niño co-occurs with cold anomalies in the western equatorial Pacific and the North Pacific, particularly in the extratropical northwest region. During the subsequent seasons, the Atlantic warming persists, especially in the western basin, with potential to modulate the Walker circulation. In AMJJ (−1 yr), enhanced divergence of the trade winds over the central equatorial Pacific, contributing to the development of La Niña, are displayed (Figure 6c). This cooling in the equatorial Pacific becomes more defined in ASON (−1 yr), with a clear propagation of the cold tongue anomalies to the east, resembling an oceanic Kelvin wave (Figure 6e), and continues into ONDJ (−1 yr) (Figure 6f), albeit with a weaker intensity than observed in previous sections. These findings suggest that part of the Pacific variability may be influenced or supported by antecedent conditions in the Atlantic, particularly via atmospheric teleconnections, involving changes in the Walker cell, initiated by the Atlantic Niño.

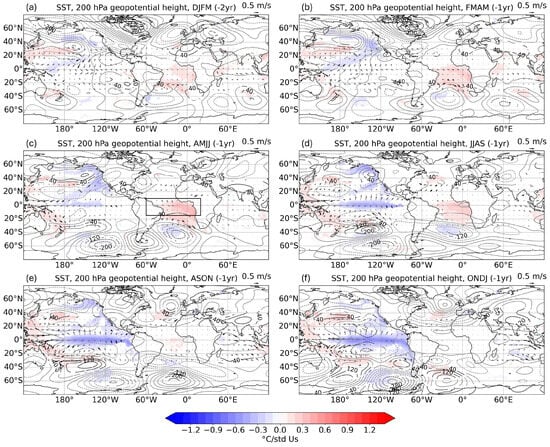
Figure 6. Evolution of global anomalous Sea Surface Temperatures (SSTs) regressed onto the Atlantic mode in AMJJ (−1 yr) impacting on chlorophyll-a (chl-a). Regression maps of the expansion coefficient Us resulting from the Maximum Covariance Analysis (MCA) between equatorial Atlantic SSTs in AMJJ (−1 yr) and chl-a concentration in the Mauritanian–Senegalese Coastal Upwelling (MSCU) in FMAM (0 yr) projected onto the global SSTs (colors, °C/std), 200 hPa geopotential height (contours, ${\mathrm{m}}^2$·${\mathrm{s}}^{-2}$/std) and, tropical (30° N–30° S) winds (arrows, m·${\mathrm{s}}^{-1}$/std). Maps correspond to (a) DJFM (−2 yr), (b) FMAM (−1 yr), (c) AMJJ (−1 yr), (d) JJAS (−1 yr), (e) ASON (−1 yr), and (f) ONDJ (−1 yr). The black box in panel (c) denotes the equatorial Atlantic region used in the MCA. Only SST values significant at the 95% confidence interval based on a Monte Carlo test are shown. Statistically significant anomalies in geopotential height and winds are outlined with black contours and arrows, respectively.

To further investigate the link between equatorial Atlantic SSTs in AMJJ (−1 yr) and the anomalous chl-a concentration in the MSCU during FMAM (0 yr), the associated atmospheric response is analyzed (Figure 7a). At sea level, a pressure anomaly pattern resembling a positive NAO emerges, characterized by a strengthened Azores high pressure system, although this signal does not reach statistical significance. This NAO response could be link to a La Niña in the Pacific [42]. More prominently, over the equatorial Atlantic, a baroclinic structure becomes evident, with corresponding anomalies in both the upper-level geopotential height and the surface pressure. This pattern is consistent with the secondary Gill-type response to an anomalous cooling in the equatorial Pacific. Together, these features help drive the wind field in a cyclonic circulation centered over the southern MSCU. Such a circulation could enhance local upwelling via anomalous Ekman pumping, thus explaining the increased chl-a concentration observed in this region (Figure 7b).

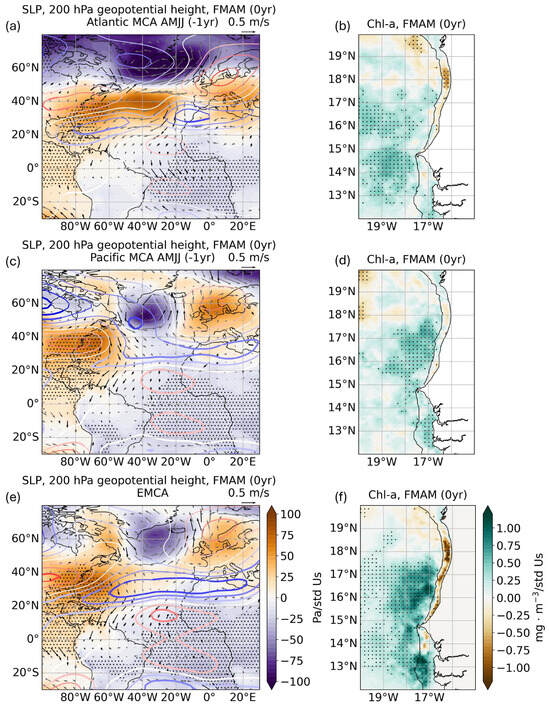
Figure 7. Atmospheric impact of the co-variability modes and associated chlorophyll-a (chl-a) response. (a) Regression maps of the Us expansion coefficient resulting from the Maximum Covariance Analysis (MCA) between equatorial Atlantic SSTs in AMJJ (−1 yr) and chl-a concentration in the Mauritanian–Senegalese Coastal Upwelling (MSCU) during FMAM (0 yr) projected onto the 200 hPa geopotential height (contours, ${\mathrm{m}}^2$·${\mathrm{s}}^{-2}$/std), Sea Level Pressure (SLP, colors, Pa/std) and winds (arrows, m·${\mathrm{s}}^{-1}$/std) in FMAM (0 yr). The zero geopotential height contour is shown in white; positive (negative) contours are in red (blue), drawn every 40 ${\mathrm{m}}^2$·${\mathrm{s}}^{-2}$. Thick contours, black dots in the SLP field, and black arrows indicate significance at the 95% confidence interval based on a Monte Carlo test (with significant meridional wind components only). (b) Heterogeneous regression map of chl-a anomalies (mg·${\mathrm{m}}^{-3}$/std) in FMAM (0 yr) associated with the MCA mode using equatorial Atlantic SSTs in AMJJ (−1 yr). The continental shelf break (100 m isobath) is shown in black. (c,d) As (a,b), but for the MCA mode between Pacific SSTs in AMJJ (−1 yr) and MSCU chl-a in FMAM (0 yr). (e,f) As (a,b), but using the expansion coefficient from the Extended Maximum Covariance Analysis (EMCA) described in Figure 2.

When comparing this response to that associated with Pacific SSTs in AMJJ (−1 yr) (Figure 7c), some differences emerge. In this case, the NAO-like response is absent. However, the Gill-type baroclinic response appears more intense, particularly at upper levels. The associated surface pressure anomalies now formed are located further north compared to the Atlantic case. This shift could account for the observed northward shift in chl-a anomalies (Figure 7d).

As the EMCA mode is largely dominated by Pacific variability, its associated atmospheric response (Figure 7e) closely resembles the pattern linked to Pacific SSTs alone. However, signs of Atlantic influence are also evident. Specifically, the Gill-type secondary response over the equatorial Atlantic appears more prominent than in the Pacific case. Additionally, positive SLP anomalies develop near the Azores, and together with the surface low pressure anomalies induced by the baroclinic structure of the secondary Gill response, they establish a pressure gradient that drives the wind field into a cyclonic circulation over the MSCU. This configuration mirrors the conditions favorable for anomalous upwelling, and indeed, the chl-a pattern (Figure 7f) exhibits southern anomalies similar to those found in the Atlantic-only case.

These results support the idea that the La Niña associated with Atlantic Niño forcing produces a distinct atmospheric teleconnection compared to a La Niña that evolves without important SST anomalies in the equatorial Atlantic. Both processes, operating at interannual scales, may act as separate sources of predictability. The EMCA captures a coupled Atlantic–Pacific mode of variability, where the Atlantic Niño could help modulate the Pacific response. In this sense, the La Niña events that are preceded by an Atlantic warming seem to generate a different teleconnection than those developing independently. Both may contribute to predictability in the MSCU region, and the EMCA structure reflects, in part, their combined influence, although it is largely controlled by the Pacific.

4. Discussion and Conclusions

The Mauritanian–Senegalese Coastal Upwelling (MSCU) is home to one of the world’s richest and most diverse marine ecosystems [43]. Assessing its predictability is crucial for the management and conservation of the region and its fisheries, which are threatened by overfishing and climate change [44,45]. Chlorophyll-a (chl-a) concentration serves as a key proxy for phytoplankton biomass and, consequently, for the base of the marine food web. Understanding the mechanisms that control its variability is therefore essential for anticipating fluctuations in biological productivity and ecosystem health.

Changes in Sea Surface Temperature (SST) anomalies are, among climatic information, one of the most widely approached methods used to predict living marine resources [46,47]. The ocean’s large heat capacity provides memory/inertia that can be used to train predictive models. In this context, predicting chl-a variability based on SST anomalies has become a promising avenue.

To investigate this link, this study applies statistical models trained with historical SST anomalies across different regions and seasons, aiming to evaluate the seasonal predictability of chl-a concentration in the MSCU during the upwelling season, FMAM. Two statistical tools implemented in python are used: Spy4CAST [39], a statistical model based on Maximum Covariance Analysis (MCA), and NN4CAST [40], a deep learning framework based on Deep Neural Networks (DNN). These approaches offers a valuable alternative to dynamical models, especially in areas like the tropical Atlantic and coastal upwelling systems, where physical models still show significant biases [48,49].

Related to the variability of surface chl-a concentration in the MSCU in FMAM, a tropical SST variability mode dominated by El Niño-Southern Oscillation (ENSO) has been identified, evolving from boreal spring (AMJJ) to the following late winter, involving a chain of mechanisms across different tropical ocean basins.

As a synthesis of the study, Figure 8 shows the impact on the chl-a predictability in the MSCU, given by the contribution of each of the basins along time, in a way to wrap up the outcomes from Figure 4 and Figure 5. In the previous spring, 10 months before the peak in chl-a (FMAM), the whole tropics are involved, with the main contribution coming from the Pacific. This contribution reflects the dominant influence of ENSO on the chl-a variability, in agreement with other authors [12,13]. The Indian Ocean does not provide an independent source of predictability, as its contribution largely overlaps with the Pacific signal. Nevertheless, in the southern region of the upwelling system, it can be seen how the equatorial Atlantic plays a crucial role (Figure 8c), a feature that has been also analyzed in this work, highlighting the important role of equatorial Atlantic on ENSO predictability [19]. As ENSO evolves in time, its relation to Tropical North Atlantic (TNA) SST variability strengthens, due to the associated teleconnections, thereby enhancing the role of the TNA in chl-a predictability. From ASON (−1 yr), the equatorial Atlantic also increases its influence on the predictability, although as part of the ENSO pattern. This signal is stronger in the northern MSCU, while the TNA shows a more pronounced influence in the southern sector. The DNN hindcast highlights a stronger contribution from the TNA in the south (Figure 8d), compared to the MCA-based hindcast (Figure 8c).

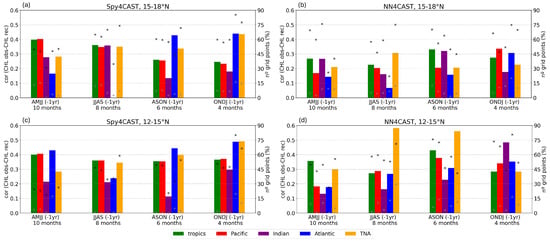
Figure 8. Correlation coefficient between the observed chlorophyll-a (chl-a) anomalous index and the reconstructed chl-a anomalous index in FMAM (0 yr), calculated only over areas with skill (Figure 5), for all Sea Surface Temperature (SST) predictors (tropics (green), Pacific (red), Indian (purple), equatorial Atlantic (blue) and Tropical North Atlantic (TNA, orange)) and all seasons/lead time of the SST relative to chl-a (AMJJ (−1 yr)/10 months, JJAS (−1 yr)/8 months, ASON (−1 yr)/6 months and ONDJ (−1 yr)/4 months). The percentage of grid points contributing to the anomalous index—i.e., where skill is positive—is indicated by a black cross. The percentage of grid points with both positive skill and statistical significance at the 95% confidence interval based on a Monte Carlo test is indicated by a grey cross. (a,c) Show reconstructions obtained with Spy4CAST, while (b,d) use NN4CAST. The chl-a anomalous index is computed over the northern domain (15–18° N) in (a,b), and over the southern domain (12–15° N) in (c,d).

The present study provides, for the first time, a comprehensive analysis of observed surface chl-a concentration predictability from SST variability at seasonal time scales in the MSCU. Considering that chl-a can be used as an estimator of primary productivity in marine ecosystems, the results obtained here represent a useful springboard for the prediction of marine resources in the region. Specifically, using models recently released for global marine ecosystem simulations using historical climate data from the Fisheries and Marine Ecosystem Model Intercomparison Project (FishMIP) [47,50], an assessment of fisheries predictability can now be performed. In addition, individual-based models calibrated for this region can be also applied to test the impact of each of the individual basins, or the time-evolving tropical mode in the way that it was performed by [14], including different species.

The results from this study have important implications for climate services, as they can support the effective management of local resources in the region and contribute to the protection of its marine ecosystem.