Abstract
This paper presents a kind of dual-channel coupled radial magnetic field resolver (DCCRMFR). The exciting winding and signal winding of this resolver adopt the structure of orthogonal phase. The number of turns and distribution of the four phase signal winding have been designed. The rotor has a double-wave magnetic conductive material structure. The variable reluctance mechanism between the stator and the rotor is derived by analytical method, and the feasibility of changing the coupling area for variable reluctance is obtained. The inductance of DCCRMFR was theoretically derived through the winding function method and combined with the finite element simulation method to obtain the inductance variation law and verify the correctness of the resolver design. Then simulation analysis was conducted on the output signal of DCCRMFR to extract the total harmonic distortion (THD) of the envelope of the electromotive force (EMF) output from the signal winding. Taking THD as the optimization objective, the optimized DCCRMFR simulation model is obtained by analyzing the air-gap length between the stator and the rotor and the thickness ratio of rotor. Finally, experimental measurements were conducted on a prototype model of a two pole pairs DCCRMFR, and the measurement results were compared and analyzed with simulation results to verify the correctness of the structural design and optimization of this DCCRMFR.
1. Introduction
The resolver is a key component in power electronics technology, mainly used for signal detection and energy conversion in the fields of electric vehicles and industrial automation [1,2,3]. Resolver uses the principle of electromagnetic induction to convert mechanical rotation angles into electrical signals, providing position and velocity feedback to the control system. In electric vehicles, the resolver detects the real-time position of the motor rotor to ensure the accuracy of torque control and power output. In general, the volume of one pole pair reluctance resolver is relatively small, and the electrical error can reach ±60′.
The design of the reluctance resolver mainly includes the design work of the stator, rotor and winding. Normally, the stator design of the reluctance resolver is similar to that of the motor, consisting of stator teeth, stator slots, stator yokes, etc. Some radial reluctance resolvers and axial reluctance resolvers are provided with an axial slot structure in the axial direction of stator [4]. Ref. [5] uses the tooth pairing method to change the stator tooth shape, which can achieve higher measurement accuracy. The reluctance resolvers may have various design structures of rotor according to different requirements, including wound rotor, radial rotor, axial rotor, and other structures [6]. In Ref. [7], a slant-ring type rotor structure is used in this paper, which cooperates with the cylindrical stator structure to achieve the alternate change of the positive and cosine signals of the output signal. The winding of reluctance resolvers is used for signal input and output, and has various winding forms [8,9,10]. Ref. [11] designed a novel winding arrangement, which simplified the manufacturing process of wound rotor (WR) rotary transformers and improved their accuracy. Ref. [12] proposed a design concept of multi-turn coils, which solved the problem of losing absolute position information. And the sine and cosine winding functions were proposed, which enhanced the reliability of the design. After the structural design of the resolver, parameter adjustment needs to be carried out through characteristic calculation and output signal analysis. It can be seen that research object of existing literature is generally a single-channel structure, which can not achieve absolute measuring position, the minority of dual-channel structures are also realized by multi-functional windings. In this paper, the design concept of dual-channel will be realized by different magnetic belt functions of rotor, which is different from the above literature, and has a simple manufacturing process. It can guarantee the purpose of absolute positioning and high measurement accuracy. The calculation of inductance is an important part of the design of reluctance resolvers, used to measure the performance of reluctance resolvers. The structural parameters directly affect the variation law of inductance [13]. Ref. [14] conducted winding design and configuration through the winding function method, providing support for the design of new resolvers. This winding design concept provides new ideas for the design and analysis of different resolvers. The rotational transformer proposed in Ref. [15] is modeled using a three-dimensional improved winding function method, which combines numerical integration techniques to consider the slot and end effects in the model. The priority assessment is given to the performance evaluation of resolvers. After the structural design is completed, the correctness of the sine and cosine signal outputs can be verified through finite element simulation analysis to meet the requirements of position signal measurement [16]. Ref. [17] employs an analytical modeling approach based on a magnetic equivalent circuit to investigate the output signal of the variable reluctance (VR) resolver with ring winding arrangement. All simulations are carried out by using the time-stepping finite element analysis, and a satisfactory analysis of performance of VR resolver is obtained. In order to improve the measurement accuracy, it is necessary to optimize the analysis of magnetic reluctance type rotary transformer, further select the structural parameters, and find optimal parameters [18,19]. On this basis, it is necessary to measure the error of the reluctance resolver through experiments, so as to verify the correctness of the reluctance resolver design [20]. In general, the radial reluctance resolver realizes the sinusoidal change of induced magnetic field by changing the air gap, and the axial reluctance resolver realizes the sinusoidal change of induced magnetic field by changing the coupling area. In this paper, a new type of reluctance structure is realized by changing the coupling area to form the sinusoidal change of radial magnetic field, which is a principle that has not appeared in the existing literature and is worth studying. Ref. [21] and Ref. [22] proposed a resolver with a slotless structure, which is worth drawing on in the design of resolvers. Ref. [23] proposed the field-reconstruction method, which provides certain assistance for the performance prediction of resolvers. Ref. [24] and Ref. [25] proposed the concept of direct current and alternating current hybrid excitation, which can solve the angle measurement of high-speed running motors. However, the switching between direct current and alternating current would make the design of resolver more complex, which is not the goal pursued by the design concept of this paper.
Based on the design process of the above-mentioned reluctance resolver and the finite element simulation reference, this paper proposes a new type of dual-channel coupled radial magnetic field resolver (DCCRMFR). The structure of the stator, rotor and windings is designed by the analytical method, and the mutual inductance law between different windings is calculated to ensure the design requirements of the reluctance resolver. Then, the designed rotational variation is verified through the finite element analysis method. By summarizing the completed research, the main contributions of this research are as follows:
- (1)
- The mechanism of variable magnetic resistance was derived by the analytical method, and the possibility of variable magnetic resistance by changing the coupling area was obtained. The rotor magnetic belt function is obtained, which is in sinusoidal relationship with the position angle, and provides the possibility for the research of the principle of multi-channel DCCRMFR.
- (2)
- Through theoretical research and finite element simulation analysis, the magnetic field separation of the coarse machine channel and the precise machine channel was achieved, and the decoupling purpose of the output of the coarse machine signal and the precise machine signal was reached. The high-precision output potential signal is obtained.
- (3)
- Through analysis, it is concluded that changing the air gap size and rotor parameters can reduce the zero position error and functional error. And the best structure is found.
DCCRMFR of this paper needs to implement the principle of a dual-channel radial magnetic circuit and meet the purpose of sine and cosine signal output to ensure a high-precision position measurement method. It is hoped that this will provide certain support for the development of reluctance resolvers.
2. Design of Stator and Rotor Structure of DCCRMFR
The DCCRMFR is a high-precision multi-pole brushless reluctance resolver, which is suitable for speed and position sensor of the servo system. Figure 1 shows the model structure of DCCRMFR, position relationship of stator and rotor, unfolding diagram of rotor function.
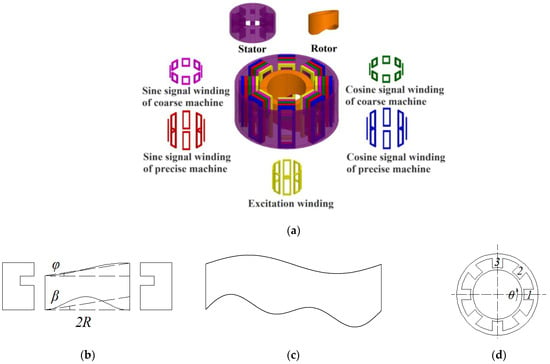
Figure 1.
Structural schematic diagram of DCCRMFR. (a) Overall structural diagram; (b) Position diagram of stator and rotor; (c) Unfolding diagram of rotor; (d) Top view diagram of DCCRMFR.
DCCRMFR consists of a stator and a rotor with equal air gap between them. There are 4NtP identical tooth slots on the inner side of the stator. P is the pole pairs and Nt is a natural number. Five windings are arranged on the stator, which are excitation windings, sine signal windings of coarse machine, cosine signal windings of coarse machine, sine signal windings of precise machine and cosine signal windings of precise machine. The excitation windings, sine signal windings of precise machine and cosine signal windings of precise machine are arranged on the whole stator teeth. The sine signal windings of coarse machine and cosine signal windings of coarse machine are arranged on the upper stator teeth. The number of turns of the excitation windings on each stator tooth is the same, and the direction of the excitation windings on the adjacent stator teeth is opposite. The four groups of signal windings conform to the sinusoidal distribution law, as shown in Figure 2.
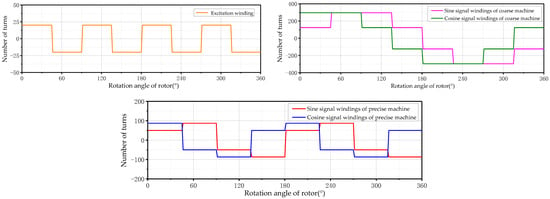
Figure 2.
Winding distribution diagram of the excitation winding and the four-phase signal winding.
The function expression of the four signal winding is as follows:
The resolver studied in this paper adopts the sinusoidal winding mode. This winding mode can effectively improve the precision because of its special structure composition. Reasonable distribution is carried out according to the relationship between the number of teeth and the number of pole pairs. The coarse machine sine signal winding and the coarse machine cosine signal winding are set on the same winding layer and arranged alternately according to one pole pair structure. The setting of the two-phase signal winding of precise machine is similar to that of the two-phase signal winding of coarse machine, arranged to the 2 pole pairs structure. The specific arrangement of signal winding is detailed in Formula (1).
In Figure 1b, the end of rotor is composed of two sine waveforms with different frequencies. The upper waveform of rotor corresponds to the upper teeth of stator, and the lower waveform of rotor corresponds to the lower teeth of stator. The unfolding diagram of rotor structure is shown in Figure 1c. The upper and lower waveforms of rotor can be represented by and respectively:
The upper wave structure is a sine function of 1 times angular frequency, and the lower wave structure is a sine function of P times angular frequency and a sine function of 1 times the angular frequency. This end structure will cause the coupling area between the stator and rotor to change with the rotation angle, as shown in Figure 1d.
When the rotor rotates through one mechanical cycle, the coupling area S changes by P cycles. In order to facilitate the relationship between the coupling area and the rotor angle, the coupling area between the stator teeth and the rotor is derived by taking the 2 pole pairs DCCRMFR as an example. Taking the coupling area of the stator upper teeth as the research object, the rotor is assumed to rotate in the counterclockwise direction, and the coupling length between the center line of the No. 1 stator teeth and the rotor is taken as the initial moment of rotor. That is the initial moment of rotor angle. Figure 3 shows the coupling area between the No. 1 upper teeth of stator and rotor when the rotor angle is 90°, which can be expressed as

Figure 3.
Diagram of coupling area between stator teeth and rotor.
Figure 4 shows the position relationship between the stator teeth and the magnetic conductive part of rotor along the circumferential direction of the stator inner diameter. For the whole stator tooth, the coupling mode of the stator tooth is the same as that of the stator upper tooth, and the coupling area of the stator tooth and the magnetic conductive part of the rotor can be expressed as
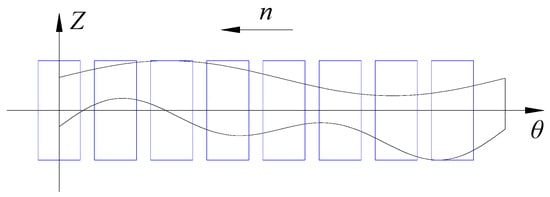
Figure 4.
Corresponding relationship diagram between all stator teeth and rotor.
So the coupling area between the stator teeth and the rotor can be further derived as
Through the derivation of the coupling area corresponding to the coarse and special winding functions, it can be seen that the coupling area satisfies the principle of sinusoidal law which is in line with the stator and rotor design concept of DCCRMFR, and provides a certain supporting role for the subsequent simulation analysis.
3. Inductance Calculation and Simulation of DCCRMFR
This paper uses the winding function method for inductance calculation. The winding function method is a method for calculating the inductance parameters of a motor, proposed by T.A. Lipo of the University of Wisconsin in his book “Analysis of Synchronous Motors”. According to the theory of winding function method, the mutual inductance between any two windings can be written as:
In order to simplify the calculation, the following assumptions are made in the inductance calculation of DCCRMFR:
- (1)
- The stator and rotor cores of DCCRMFR have an infinite magnetic permeability, and the nonlinearity of the magnetic resistance of the stator and rotor cores is ignored;
- (2)
- The influence of magnetic conductor saturation is ignored;
- (3)
- The influence of hysteresis and eddy currents is ignored;
- (4)
- The stator cogging effect is ignored.
3.1. Calculation of Rotor Coupling Length
This paper adopts the finite element method to conduct the simulation analysis of DCCRMFR. The finite element method is an efficient numerical calculation approach. It was initially applied in the field of mechanics. Due to the high precision of its calculation results, it has been widely used in electrical engineering and has become one of the most commonly used methods for analyzing the electromagnetic field of motors. In simple terms, the fundamental principle of finite element method is to transform a continuous infinite problem into a discrete finite problem based on the differential equation of electromagnetic field. The output characteristics of DCCRMFR can be effectively analyzed.
Different from the structure of traditional radial flux reluctance resolver, the magnetic circuit of DCCRMFR distributes along the radial direction. The air-gap length between the stator and rotor remains unchanged along the circumferential direction, and the rotor coupling length is closely related to the structure of rotor. Since the inductance of different windings is caused by the corresponding magnetic links, the direction of the magnetic links will become the decisive factor in determining the coupling length of the rotor.
Taking DCCRMFR with 2 pole pairs as an example, the coupling length can be obtained when the rotor amplitude ratio is 4 (the amplitude ratio is the ratio of the amplitude of the rotor precise machine function to the amplitude of the rotor coarse machine function), and the rotor relative phase angle is 0° as shown in Figure 5. When the influence of stator slots is ignored and the rotor rotates one mechanical cycle, the variation law of the coupling length of the rotor is shown in the shaded area of Figure 5. At this time, the function value corresponding to the shaded area is the axial coupling length between the stator and rotor when the excitation winding and the signal winding generate mutual inductance.
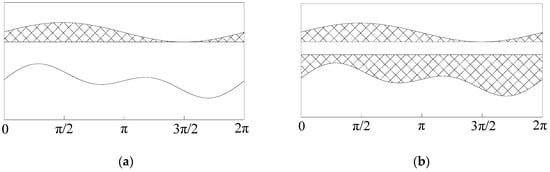
Figure 5.
Coupling length between stator and rotor. (a) The coupling length between the upper teeth of the stator and the rotor; (b) The coupling length between the whole teeth of the stator and the rotor.
Therefore, when the position of the rotor changes, the expression of the rotor coupling length corresponding to the teeth on the stator can be expressed as follows:
The expression of the rotor coupling length corresponding to the whole stator teeth can be expressed as follows:
3.2. Inductance Analytical Calculation Between Windings
From the distribution of each signal winding corresponding to Formula (1), the winding function expression using the sinusoidal winding type can be summarized. After Fourier transform, it can be obtained that:
Since the tooth harmonics of the signal winding function in the sinusoidal winding type are very small and can almost be ignored when , and the high-order tooth harmonics of the signal winding function make the calculation process very complicated, only the tooth harmonics of the signal winding function at m = 1 are taken for calculation here.
According to the winding function method, the mutual inductance expression of the exciting winding and the precise machine sine signal winding under the sinusoidal winding type can be derived as:
Similarly, the mutual inductance expression between the excitation winding and the precise machine cosine signal winding in the sinusoidal winding type can be derived as:
The self-inductance expression of the precise machine sine signal winding under the sinusoidal winding type can be derived as:
Similarly, the self-inductance expression of the precise machine cosine signal winding under the sinusoidal winding type can be derived as:
The mutual inductance expression between the sine signal winding and the cosine signal winding of precise machine in the sinusoidal winding type can be derived as:
Through theoretical research, it can be found that the mutual inductance between the coarse machine signal winding and the precise machine signal winding under the sinusoidal winding type does not affect the harmonic distortion rate of the output potential of the precise machine signal winding. Therefore, theoretical research on the mutual inductance between the coarse machine signal winding and the precise machine signal winding will not be conducted here.
From the above derivation, it can be seen that the inductance of each winding of DCCRMFR in the sinusoidal winding type can be summarized as follows:
- (1)
- LZlijs and LZlijc only contain the P-order fundamental wave component.
- (2)
- In the ideal state, the mutual inductance between the two signal windings of precise machine only contains 2P-order fundamental wave components.
In summary, the theoretical derivation results of inductance are in accordance with the basic principle of DCCRMFR, which verifies the correctness of the design concept of new type of resolver.
3.3. Inductance Simulation Calculation Between Windings
Based on the theoretical analysis of inductance in the previous section, a finite element analysis was conducted on the inductance of DCCRMFR with 2 pole pairs in the sinusoidal winding type here, and the model diagram of DCCRMFR is shown in Figure 1. The simulation software is Ansoft Maxwell 16. The model uses a three-dimensional design method, selects a transient magnetic field solver, and is simulated with an external cylindrical air domain as the balloon boundary condition. The free grid meshing mode is adopted. The current excitation mode is used, the amplitude of excitation current is 500 mA, and the frequency is 1 kHz. The winding material is copper, and the iron core materials of stator and rotor are DW315-50 silicon steel sheets. DW315-50 silicon steel sheets are produced by Dongguan Chang’an Tongxiang Metal Materials Store, located in Dongguan City, Guangdong Province, China.
The main dimensions are shown in Table 1. The setting method of the sinusoidal signal winding of the precision machine is the same as that of the cosine signal winding of the precise machine. However, the phase difference of the both signal windings is 90° electrical angle. Only the inductance of the sinusoidal signal winding of the precise machine needs to be simulated and analyzed.

Table 1.
The main dimensions of DCCRMFR.
The mutual inductance between the excitation winding and the sine signal winding of the precise machine, the self-inductance of the sine signal winding of the precise machine, and the mutual inductance between the sine signal winding and the cosine signal winding of the precise machine were respectively simulated and analyzed. The simulation results are shown from Figure 6, Figure 7 and Figure 8.

Figure 6.
The mutual inductance distribution diagram between the excitation winding and the precise machine sine signal winding when the number of pole pairs is 2.

Figure 7.
Self-inductance distribution diagram of the precise machine sine signal winding when the number of pole pairs is 2.
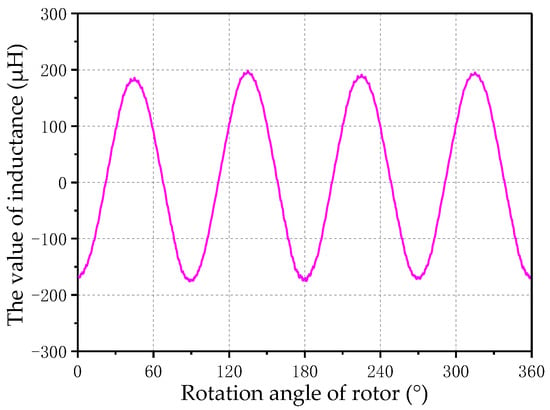
Figure 8.
The mutual inductance distribution diagram of the sine signal winding and the cosine signal winding of the precise machine when the number of pole pairs is 2.
From the above simulation, it can be seen that the simulation results of the inductance in the sinusoidal winding type are basically consistent with the theoretical inductance results calculated by the winding function method, which proves the correctness of DCCRMFR inductance calculation method. Different from the analytical results of inductance, the corresponding simulation results of inductance exist the disturbance. The reason is that the slot effect the stator is ignored by the winding function method, so the analytical value of inductance does not have the problem of disturbance.
4. Simulation and Optimization of DCCRMFR Outputs Signals
The model construction of two pole pairs DCCRMFR was completed based on the main parameters in Table 1, as shown in Figure 1. Simulation and optimization analysis are further carried out.
4.1. Magnetic Density Simulation and EMF Analysis of DCCRMFR
The structure of DCCRMFR has its particularity, which has a large leakage magnetic flux. These leakage fluxes include end leakage flux, slot leakage flux, leakage flux between the upper and lower teeth of the stator, and leakage flux between the air gap of the stator and rotor, etc. In theory, for DCCRMFR without a rotor, the output electromotive force (EMF) of the signal winding should be equal to zero without any displacement between the excitation winding and the signal winding. However, in practical work, the output EMF of the signal winding is not zero. At this time, the output EMF of the signal winding is called residual EMF, which will reduce the sensitivity of the measurement system.
As shown in Figure 9, the internal magnetic circuit of DCCRMFR mainly starts from one stator tooth and passes through the air gap between the stator and rotor to reach the magnetic conductive part inside the rotor, and then returns to the adjacent stator teeth, completing the closure through the stator yoke. The magnetic flux density in the stator teeth gradually decreases from the yoke to the end. This phenomenon is mainly caused by the leakage magnetic field at the stator teeth.
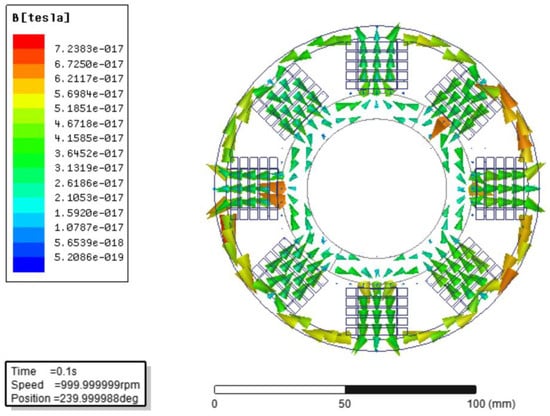
Figure 9.
Magnetic density distribution of two pole pairs DCCRMFR.
DCCRMFR is measured with the accuracy of the output signal as the target, therefore simulation research is needed on the output EMF of the four phase signal winding. The simulation results are shown in Figure 10.

Figure 10.
Waveform diagram of output EMF. (a) Coarse machine signal winding; (b) Pricise machine signal winding.
The simulation results show that the output EMF of the four phase signal winding varies sinusoidally with the change of rotor angle. Moreover, when the rotor rotates one mechanical cycle, the output EMF of the coarse machine signal winding changes by one cycle, while that of the precise machine signal winding changes by two cycles. Therefore, it can be determined that the simulation results shown in Figure 9 meet the basic requirements of the output EMF of DCCRMFR.
4.2. The Influence of Air Gap Size
The spatial harmonic magnetic field in the air gap of DCCRMFR mainly consists of two parts: one part is the winding harmonic magnetic field; Another part is the tooth harmonic magnetic field. The air gap between the stator and rotor not only affects the harmonic magnetic field of the winding, but also has a certain connection with the harmonic magnetic field of the teeth. Therefore, in order to improve the measurement accuracy of DCCRMFR, it is necessary to select the air gap size reasonably. Still taking the 2 pole pairs DCCRMFR as an example, with the main dimensions in Table 1 unchanged, the thickness ratio of rotor is selected as 4, and the relative phase angle between the coarse function and the precise function of rotor is set to 0°. Finite element analysis is performed on the 2 pole pairs DCCRMFR with different air gap lengths. The total harmonic distortion (THD) analysis results of the output EMF of the precision machine signal winding at different air gap lengths are shown in Figure 11.

Figure 11.
The THD distribution of output EMF of the precision machine signal winding at different air gap lengths.
The analysis results show that the amplitude of the output EMF of the precise machine signal winding will decrease as the length of the air gap increases. The THD of the output EMF of the precise machine signal winding tends to decrease as the air gap length increases. When the air gap exceeds 0.7 mm, the decreasing trend becomes gentler. It can be seen that the variation of the air gap between the stator and rotor will change the measurement accuracy of DCCRMFR. Therefore, we can select the air gap based on the output EMF not less than 300 mV and THD not exceeding 3.6%.
Although increasing the air gap between the stator and the rotor is beneficial for improving the measurement accuracy, it also causes a decrease in the amplitude of the signal winding output. Therefore, during the prototype manufacturing process, the air gap length should be reasonably selected according to the actual process requirements and the technical specifications of DCCRMFR. The measurement accuracy can be effectively improved.
Figure 12 shows THD analysis results of the output EMF of the precision machine signal winding at different calculation frequencies. The air gap is 0.8 mm. The analysis results show that as the frequency becomes larger, THD will increase and EMF will decrease. When the frequency reaches 5 KHz, value of THD is 3.82%, which does not exceed the design threshold value of 4%. The value of EMF is 297 mV, which is also within a reasonable range, although it is slightly lower than 300 mV.

Figure 12.
The THD distribution of output EMF of the precision machine signal winding at different calculation frequencies.
4.3. The Influence of the Thickness Ratio of Rotor
The main difference between DCCRMFR and existing reluctance resolver lies in its unique rotor structure. Both the coarse function and precise function of rotor can affect the harmonic content of the signal winding output EMF. Based on the previous derivation, it can be seen that the output EMF of signal winding is affected by the thickness ratio of rotor. However, the magnetic circuit method is rather complex. Here, the finite element method will be adopted to analyze the influence of different rotor fineness ratios on the output potential of the signal winding.
With the main dimensions kept, the relative phase angle between the coarse function and the precise function of rotor is set to 0°. When the thickness ratio of rotor is different, the rotor model of two pole pairs DCCRMFR is shown in Figure 13. The THD of the output EMF of precise machine signal winding was analyzed, and the analysis results are shown in Figure 14.

Figure 13.
Schematic diagrams of rotor models with different thickness ratios of rotor.
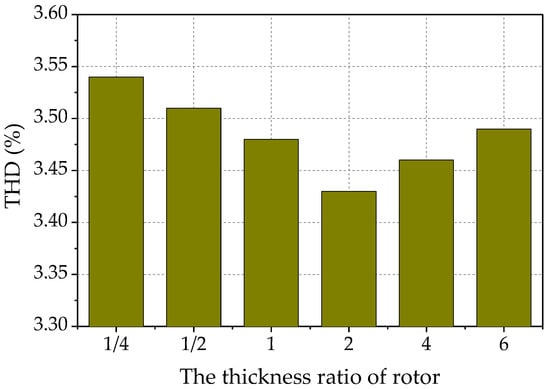
Figure 14.
The THD distribution of output EMF of the precise machine sine signal winding with different thickness ratios of rotor.
With the continuous increase of rotor’s thickness ratio, the THD of the output EMF of the precise machine signal winding first decreases and then increases. When the thickness ratio of rotor is 2, it reaches its minimum, indicating that the THD is very little affected by the coarse function of rotor and leakage inductance at this time. The measurement error is mainly caused by the non-uniform magnetic field within DCCRMFR. When thickness ratio of rotor gradually changes from 2 to both sides, the THD of the output EMF of the precise machine signal winding increases.
4.4. The THD of the Optimized DCCRMFR
The main dimensions of the optimized two pole pairs DCCRMFR can be determined through the analysis of air gap between stator and rotor and the thickness ratio of rotor. The main dimensions are shown in Table 2.

Table 2.
The main dimensions of optimized two pole pairs DCCRMFR.
The structure of the optimized two pole pairs DCCRMFR is the same as that in Figure 1, but the rotor thickness ratio is 2. The harmonic distortion rates of the two-phase output signals obtained through finite element analysis and calculation are shown in Table 3.

Table 3.
The harmonic content of output EMF of precision machine signal winding.
Under ideal conditions, the envelope of the output EMF waveform of resolver should be a standard sine waveform. However, in actual operation, the envelope of resolver will generate harmonics, which can cause the actual output EMF envelope to deviate from the standard sine waveform. This phenomenon is called sine waveform distortion of EMF. The degree of distortion of the output EMF waveform is measured by the sine wave distortion rate of EMF, also known as THD. The expression is as follows,
The analysis results show that the main components of the high-order harmonics in the two-phase output signal of precise machine are the third harmonic, which are 1.38% and 1.31% respectively. The THD of the output signal of the optimized two pole pairs DCCRMFR has been effectively reduced, which are 3.34% and 3.38% respectively. The THD will cause the envelope of the output EMF to deviate from sine waveform, thereby affecting the measurement accuracy of the optimized two pole pairs DCCRMFR. Therefore, the suppression of THD is one of the main evaluation indicators in the design of this resolver. THD is mainly caused by leakage flux caused by uneven structures such as unequal winding turns and the double ripple structure of the rotor. It can be alleviated by injecting third harmonic components into the winding turn distribution function and rotor ripple function. In addition, the setting of score slots and boots of stator teeth can effectively suppress THD.
In this section, the model of two pole pairs DCCRMFR is established by the finite element analysis method, and the thickness ratio of rotor is further studied which ensures that the measurement accuracy meets the design requirements and provides a basis for the manufacture of the prototype.
5. Measurement Accuracy Experiment of DCCRMFR
Since DCCRMFR is a position sensor, it has strict requirements on measuring accuracy. After theoretical derivation and finite element analysis, it is necessary to measure the characteristics of the prototype in actual work and compare them with the finite element simulation results. The experimental prototype adopts a DCCRMFR with two pole pairs and the sinusoidal winding type. The prototype structure is shown in Figure 15. And Figure 16 shows the experimental instrument for precision measurement.

Figure 15.
Schematic diagram of the prototype structure. (a) The stator structure; (b) The rotor structure.

Figure 16.
Schematic diagram of the main experimental instruments.
In Figure 16, the DF1636A low distortion signal generator can produce a sinusoidal input signal, which is applied to the excitation winding. The prototype of DCCRMFR is set on a self-made mechanical rotating table, and the relative positions of the stator and rotor change by rotating at a fixed angle. The YOKOGAWA DLM2022 oscilloscope is used to collect the output signal waveform. The self-made high-precision angle measurement system can conduct accuracy analysis on the output signal waveform and obtain the measurement errors corresponding to different angles, its accuracy can reach . The specific implementation is as follows: The DF1636A low distortion signal generator is connected to the excitation winding of prototype to provide the input signal. The four-phase signal winding are connected to the signal test port of the self-made high-precision angle measurement system for analyzing the function error, and are also connected to the sampling port of the oscilloscope to obtain the waveform. As the self-made mechanical rotating table starts to rotate from 0°, the output signal changes sinusoidal with the rotation angle. These output signals enter the self-made high-precision angle measurement system and calculate the difference with the standard sinusoidal waveform value that changes with the rotation angle. Ultimately, it is converted into a signal error and displayed. The calculation of the error is automatically completed by the program inside the self-made high-precision angle measurement system and is more reliable than the manual measurement results.
The excitation winding of prototype is supplied with a sinusoidal alternating signal. The sinusoidal alternating signal is alternating current with a frequency of 1 kHz and an amplitude of 500 mA. The precision machine signal winding and the coarse machine signal winding are sampled at 50 measurement points per electrical cycle. The functional error of the output EMF of the four-signal winding was measured. Due to the same distribution pattern of the two-phase signal windings in the precise machine, the phase difference is 90° electrical angle. The distribution pattern of the two-phase signal winding of the coarse machine is the same, with a phase difference of 90° electrical angle. It is necessary to measure the functional errors of the output EMF of the sine signal windings of the precise machine and coarse machine, which are shown in Figure 17.
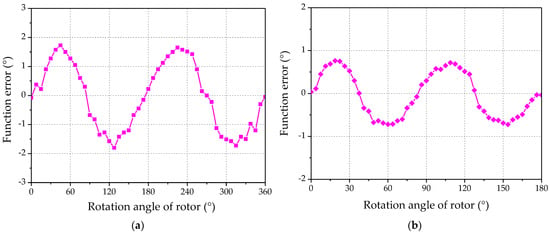
Figure 17.
Schematic diagram of the prototype structure. (a) Sine signal winding of coarse machine; (b) Sine signal winding of precise machine.
From the above measurement results, it can be seen that the basic function error of the output EMF of the coarse machine sine signal winding is , and the basic function error of the output EMF of the fine machine sine signal winding is . The error values for multiple mechanical cycles are . The measurement results indicate that the coarse machine of the two pole pairs DCCRMFR determines the absolute position information of rotating mechanism through preliminary measurements with low accuracy, and then completes high-precision measurements through precise machine, achieving the technical requirements and design goals of DCCRMFR.
6. Conclusions
This paper proposes a novel structure of DCCRMFR. The unique structure of rotor can achieve complete decoupling between the waveform function of one pole pair rotor and that of P pole pairs rotor, effectively reducing the interference between the output signal of coarse machine and that of precise machine, and achieving absolute position measurement. The inductance of DCCRMFR is calculated according to the winding function method and finite element simulation. The mutual inductance between the exciting winding and the precise machine is derived to present P-period variation law, and the mutual inductance between the sine signal winding and the cosine signal winding of precise machine is derived to present 2P-period variation law, which verifies the rationality of DCCRMFR design. After finite element optimization, the THD of EMF of precise machine signal winding has been effectively suppressed. Finally, an experiment is carried out on the prototype of 2-pole pairs DCCRMFR. The functional error of the output voltage is measured for the signal winding of coarse machine and the signal winding of the precise machine, respectively. The correctness of the finite element simulation and theoretical design of DCCRMFR is verified.
Author Contributions
H.W. proposed the research topic, designed the model, performed the simulations and analyzed the data. J.W. was responsible for guidance, proposing the research topic, giving constructive suggestions, and revising the paper. H.C. performed the simulations and analyzed the data. C.L. polished the manuscript and corrected spelling and grammar mistakes. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Shandong Provincial Natural Science Foundation, ZR2020QE219.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Nt | The structural parameter of stator teeth which is a nonzero natural number. | P | The number of pole pairs of resolver. |
| m | The stator tooth number. | ZS | The total number of stator teeth. |
| N1 | Amplitude of the number of turns in the coarse machine signal winding. | N2 | Amplitude of the number of turns in the precise machine signal winding. |
| Ncs | The number of turns in the coarse machine sine signal winding. | Ncc | The number of turns in the coarse machine cosine signal winding. |
| Nps | The number of turns in the precise machine sine signal winding. | Npc | The number of turns in the precise machine cosine signal winding. |
| θ | The rotation angle. | W1(θ) | The upper waveforms of the rotor changes with the rotation angle θ. |
| WP(θ) | The lower waveforms of the rotor changes with the rotation angle θ. | F0 | The constant of waveform. |
| F1 | The coarse waveform amplitude. | FP | The precise waveform amplitude. |
| b | The stator tooth width. | R | The rotor radius. |
| dα | The differential unit of stator tooth width. | φ | The elevation angle of the upper stator teeth. |
| β | The elevation angle of the lower stator teeth. | l0 | The axial position constant of stator teeth. |
| l1 | The rotor coupling length corresponding to the teeth on the stator. | l2 | The rotor coupling length corresponding to the whole stator teeth. |
| S1 | The coupling area between the No. 1 upper teeth of stator and rotor. | SP | The coupling area between the No. 1 whole teeth of stator and rotor. |
| l | Stator axial coupling length. | θr | The position coordinate of the inner surface of the stator. |
| gn(θ,θr) | The calculated air gap function of the motor. | NZcs | The function value of the coarse machine sine signal winding with sinusoidal winding type. |
| NZcc | The function value of the coarse machine cosine signal winding with sinusoidal winding type. | NZjs | The function value of the precise machine sine signal winding with sinusoidal winding type. |
| NZjc | The function value of the precise machine cosine signal winding with sinusoidal winding type. | NZcm | The amplitude of the fundamental wave of the coarse machine signal winding function in the sinusoidal winding type. |
| NZjm | The amplitude of the fundamental wave of the precise machine signal winding function in the sinusoidal winding type. | Nlim | The amplitude of excitation winding. |
| NmZs+1 | The amplitude of the mZS + 1th harmonic component of the coarse machine signal winding function under the sinusoidal winding type. | NmZs−1 | The amplitude of the mZS − 1th harmonic component of the coarse machine signal winding function under the sinusoidal winding type. |
| N’mZ0+1 | The amplitude of the mZ0 + 1th harmonic component of the precise machine signal winding function under the sinusoidal winding type. | N’mZ0−1 | The amplitude of the mZ0 − 1th harmonic component of the precise machine signal winding function under the sinusoidal winding type. |
| Z0 | The number of stator teeth corresponding to each pole. | g | The length of the air gap between the stator and rotor. |
| μ0 | The air permeability. | LZlijs | Mutual inductance between the excitation winding and the sine signal winding of the precise machine in the sinusoidal winding type. |
| LZlijc | Mutual inductance between the excitation winding and the cosine signal winding of the precise machine in the sinusoidal winding type. | LZjsjs | Self-inductance of the sine signal winding of the precise machine in the sinusoidal winding type. |
| LZjcjc | Self-inductance of the cosine signal winding of the precise machine in the sinusoidal winding type. | LZjsjc | Mutual inductance between the sine signal winding and the cosine signal winding of the precise machine in the sinusoidal winding type. |
| T | The thickness ratio of rotor. T = F1/FP | Un | Numerical values of nth harmonic components in the envelope of EMF |
| U1 | Numerical value of fundamental component in EMF envelope |
References
- Kong, T.; Sun, L.; Ding, Y.; Ding, S.; Wang, W. Investigation of a Low-Power Consumption Decoding Method in an Axial Field Variable Reluctance Resolver. IEEE Trans. Transp. Electrif. 2025, 11, 3433–3441. [Google Scholar] [CrossRef]
- Liben, M.J.; Ludois, D.C. A 2-kW, 6.78-MHz, Capacitive Power Transfer and Position Resolver System for Synchronous Machine Rotor Excitation. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 1383–1393. [Google Scholar] [CrossRef]
- Bahari, M.; Tootoonchian, F.; Mahmoudi, A. An Electromagnetic Design of Slotless Variable Reluctance PM-Resolver. IEEE Trans. Ind. Electron. 2023, 70, 5336–5346. [Google Scholar] [CrossRef]
- Abramenko, V.; Petrov, I.; Pyrhönen, J. Variable Reluctance Resolver with a Modular Stator: Main Design Aspects. IEEE Trans. Ind. Appl. 2025, 61, 6236–6247. [Google Scholar] [CrossRef]
- Ghaem-Maghami, M.; Nasiri-Gheidari, Z. Design Optimization of Linear Variable-Reluctance Resolver for Higher Accuracy and Smaller Size. IEEE Sens. J. 2023, 23, 16764–16771. [Google Scholar] [CrossRef]
- Reza, F.; Farid, T. Design and Experimental Investigation of a Two-DOF Planar Resolver. IEEE Trans. Instrum. Meas. 2022, 71, 9000408. [Google Scholar]
- Tootoonchian, F.; Zare, F. A Tubular Variable Reluctance Resolver with Single Coil Excitation Winding. IEEE Sens. J. 2024, 24, 2657–2663. [Google Scholar] [CrossRef]
- Li, X.; Chen, J.; Zhang, Z. Optimization Design of Variable Reluctance Resolver Based on Three-phase Symmetrical Winding. World Electr. Veh. J. 2024, 15, 201. [Google Scholar] [CrossRef]
- Hajmohammadi, S.; Nasiri-Gheidari, Z. Proposal of a Wound-Rotor PCB-Resolver. IEEE Trans. Ind. Electron. 2024, 71, 15122–15129. [Google Scholar] [CrossRef]
- Seyed-Bouzari, S.A.; Eesazadeh, M.R.; Tootoonchian, F.; Nasiri-Gheidari, Z. Development of a Multiturn Linear Variable Reluctance Resolver with Integrated Ferromagnetic Core. IEEE Sens. J. 2024, 24, 29898–29905. [Google Scholar] [CrossRef]
- Saneie, H.; Nasiri-Gheidari, Z.; Tootoonchian, F.; Daniar, A. Simplified winding arrangement for integrated multiturn resolvers. IEEE Trans. Ind. Electron. 2021, 68, 12802–12809. [Google Scholar] [CrossRef]
- Zare, F.; Tootoonchian, F.; Nasiri-Gheidari, Z. A New Resilient Configuration of Wound Rotor Resolver in Mechanical Fault Conditions. IEEE Sens. J. 2025, 25, 19069–19076. [Google Scholar] [CrossRef]
- Cai, Y.; Ni, R.; Zhu, W.; Liu, Y. Modified Approach to Inductance Calculation of Variable Reluctance Resolver Based on Segmented Winding Function Method. IEEE Trans. Ind. Appl. 2023, 59, 5900–5907. [Google Scholar] [CrossRef]
- Ran, X.; Zhao, M.; Shang, J. A novel axial reluctance resolver proposal and its winding configuration optimization using winding function method. Energy Rep. 2022, 8, 705–712. [Google Scholar] [CrossRef]
- Naderi, P.; Ramezannezhad, A. Proposal of a Novel High-Accuracy and Robust Tubular Resolver with Simplified Structure. IEEE Trans. Ind. Electron. 2025, 72, 6530–6538. [Google Scholar] [CrossRef]
- Fateme, Z.; Ali, K.; Zahra, N.-G. Presentation of a Novel Variable Reluctance Tubular Resolver. IEEE Trans. Ind. Electron. 2022, 69, 13773–13780. [Google Scholar] [CrossRef]
- Bahari, M.; Nasiri-Gheidari, Z.; Tootoonchian, F. Modeling, performance analyzing, and prototyping of variable reluctance resolver with toroidal winding. IEEE Sens. J. 2021, 21, 4425–4432. [Google Scholar] [CrossRef]
- Wang, K.; Wu, Z. Oversampling synchronous envelope detection for Resolver-to-Digital conversion. IEEE Trans. Ind. Electron. 2020, 67, 4867–4876. [Google Scholar] [CrossRef]
- Khajueezadeh, M.S.; Emadaleslami, M.; Tootoonchian, F. Comprehensive Investigation of the Resolver’s Eccentricity Effect on the Field-Oriented Control of PMSM. IEEE Sens. J. 2023, 23, 19145–19152. [Google Scholar] [CrossRef]
- Hajmohammadi, S.; Nasiri-Gheidari, Z.; Tootoonchian, F. Proposal of an Integrated Wound-Rotor PCB-Resolver with a PCB Rotary Transformer. IEEE Sens. J. 2025, 25, 23973–23980. [Google Scholar] [CrossRef]
- Sun, L.; Luo, Z.; Hang, J.; Ding, S.; Wang, W. A slotless PM variable reluctance resolver with axial magnetic field. IEEE Trans. Ind. Electron. 2020, 69, 6329–6340. [Google Scholar] [CrossRef]
- Moheyseni, A.; Nasiri-Gheidari, Z.; Alipour-Sarabi, R. Slotless disk type resolver: Asolution to improve the accuracy of multispeedwound rotor resolvers. IEEE Trans. Transp. Electrific 2022, 8, 1493–1500. [Google Scholar] [CrossRef]
- Saneie, H.; Nasiri-Gheidari, Z.; Belahcen, A. On the field reconstruction method for electromagnetic modeling of resolvers. IEEE Trans. Instrum. Meas. 2023, 72, 9000608. [Google Scholar] [CrossRef]
- Moghaddam, G.S.; Nasiri-Gheidari, Z.; Alipour-Sarabi, R. Hybrid Excitation for a Wide Speed Range Linear Sinusoidal Area Variable Reluctance Resolver. IEEE Trans. Instrum. Meas. 2024, 73, 7507007. [Google Scholar] [CrossRef]
- Zhou, J.; Song, Z.; Xiao, X.; Huang, X.; Xie, Y. A Hybrid-Excited Resolver for High-Speed Operation. IEEE Trans. Power Electron. 2024, 39, 4958–4962. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.