Abstract
We conducted an isogeometric analysis (IGA) to evaluate the performance of automobile structural member deformation and crash. In automobile crash analysis, ensuring the accuracy of the acceleration, velocity, and load in time series, as well as the structural deformation behavior, is important. To maintain the aforementioned consistency, accurately reproducing the bending and buckling of structural members is indispensable. In this study, we firstly computed the bending and buckling of structural members using IGA and validated its performance by comparing the results with those of a conventional finite element analysis and experiments. In addition, we utilized IGA for the crash analysis of an automobile body.
1. Introduction
The finite element method (FEM) has become a conventional procedure for evaluating the structural performance of automobiles through computer simulation, and it is widely utilized in the industrial field as commercial software. While computer-aided design (CAD) is used to manage the shapes of automobile structures, recently, the inconsistencies in data between CAD and FEM, such as shape reproducibility and design changes, have become a drawback.
Isogeometric analysis (IGA) [1,2] has been proposed as an alternative analysis method to FEM with the aim of enhancing the compatibility of data used in CAD and analysis, and it is garnering significant attention. The main difference between IGA and FEM lies in the choice of basis functions used to interpolate the internal quantities from the points where the physical quantities are defined. Since the basis functions of IGA use the same spline functions as CAD, their data are compatible. Structural analysis via IGA has already been extensively studied, and research on complicated curved surface structures through trimming and connecting has also been reported [3,4,5]. In addition, there are research examples of simple automobile crashes using computational modeling via IGA [6,7,8]. IGA has also been applied in the medical field, such as analyzing blood flow in the heart and blood vessels through fluid–structure interaction analysis [9].
In this study, we conducted a fundamental investigation into the applicability of IGA for analyzing structural deformations and automobile crashes. Recently, IGA has been implemented in commercial software, and its functions have reached a practical level [10,11]. IGA has also been introduced to the explicit dynamic method used in automobile crash analysis [12]. For automobile crash analysis, consistency is essential not only in the deformation state but also in the actual phenomena, such as acceleration, velocity, and load, in time series. In the aforementioned context, a bending and buckling analysis of structural members was first conducted using IGA, and its applicability was investigated by comparing the results with those of experiments and FEM. Furthermore, IGA was applied to the crash analysis of the automobile body, and its validity was confirmed.
2. Isogeometric Analysis
In this section, we provide an overview of IGA, outlining its features using figures and equations. Interested readers may refer to the literature [1,2] for more details on IGA. While IGA shares many common properties with FEM, the major distinguishing feature is the use of different basis functions. B-spline basis functions are used in IGA. In a B-spline basis function, the curved surface can be accurately reproduced because continuity is maintained on the mesh boundary. Additionally, in IGA, the analysis data can be flexibly improved using corresponding shape changes without the need for CAD [13,14,15,16].
2.1. B-Spline Function
The blue line in Figure 1 shows a second-order B-spline curve. A B-spline curve is composed of a linear combination of B-spline basis functions. The red points are control points and correspond to nodes in the FEM.
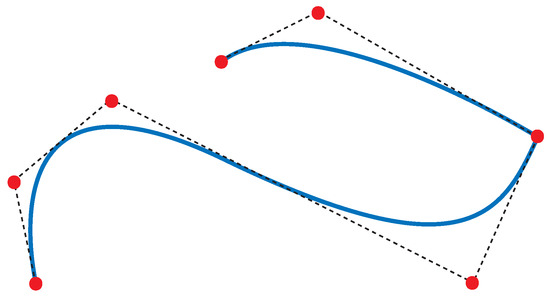
Figure 1.
Second-order B-spline curve (blue) and control points (red).
The B-spline basis function N is defined recursively using the Cox–de Boor recurrence relation [1], as shown in Equations (1) and (2):
Here, represents a knot. Additionally, i represents a control point number, while p denotes the order of the B-spline function. Figure 2 illustrates second- and third-order B-spline basis functions. The B-spline basis function can be contrasted with the FEM basis function in Figure 3. In both figures, the dotted lines indicate the mesh boundaries. continuity and continuity are observed in IGA and FEM, respectively.
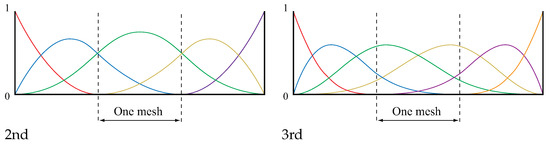
Figure 2.
Second- and third-order B-spline basis functions.
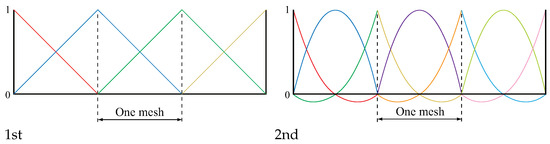
Figure 3.
First- and second-order FEM basis functions.
As shown in Figure 1, B-spline curves are not guaranteed to pass through control points, and in general, they do not. This means that the control points are not on the model in IGA, unlike in FEM. B-spline curve is represented by Equation (3):
where represents the coordinates of the control points.
For the modeling of a shell, a B-spline surface is defined as shown in Figure 4 using the superposition of B-spline functions. To model a three-dimensional solid, the shape is defined by superimposing three B-spline functions.
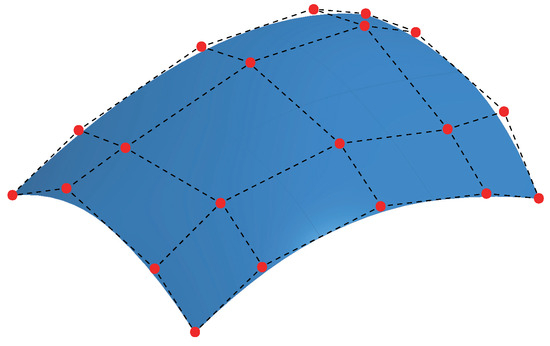
Figure 4.
B-spline surface (blue), control points (red), and control mesh (black).
2.2. NURBS Basis Function
In IGA modeling using the B-spline basis functions described above, there are geometric shapes that cannot be described, such as perfect circles and spheres. To eliminate this disadvantage, Non-Uniform Rational B-Spline (NURBS) basis functions were developed [17]. The NURBS basis is an extension of the concept of the B-spline basis. In a NURBS basis function, by adjusting the weights of the control points as shown in Figure 5, it is possible to model any geometrical shape by controlling the curvature of the curve near the control points.
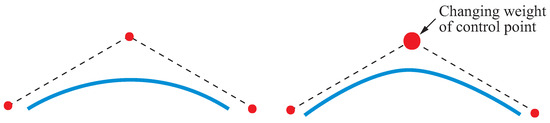
Figure 5.
Curves modeled by changing weights of control points in NURBS.
NURBS basis functions R are represented by Equations (4)–(6). The NURBS basis function for a curve is defined as in Equation (4):
Also, the NURBS basis function for a surface is given by Equation (5):
And the NURBS basis for function for a solid is given by Equation (6):
Here, and are knots similar to . Additionally, M and L are B-spline basis functions similar to N, and q and r are orders of B-spline functions similar to p.
Since the basis functions of IGA and CAD are identical NURBS basis functions, the IGA model can be directly generated from a smooth CAD surface, as shown in Figure 6. Therefore, reducing the effort in analysis is one of the significant advantages of IGA.
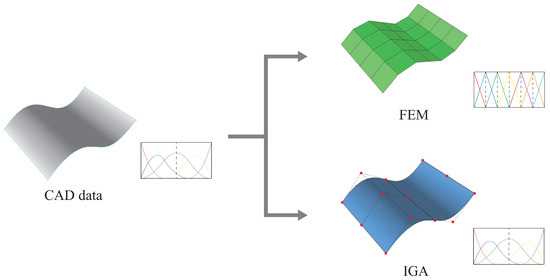
Figure 6.
Generation of FEM and IGA models from CAD.
2.3. Coordinate Transformation by Mapping
In both FEM and IGA, basis functions are used in a coordinate space different from the global coordinate system in which the analyst evaluates various physical quantities. In FEM, since the basis functions are defined within the local coordinate system, each quantity is mapped to the global coordinate system once. On the other hand, in IGA, the B-spline/NURBS basis functions and the local coordinate system are mapped to the global coordinate system through two mappings [2].
3. Deformation Analysis of Structural Members
The three-point bending of the trailing arm using a hot rolled steel plate and compression analysis of aluminum extrusions are computed using IGA. The performance of IGA in bending and buckling behavior was evaluated by comparing the results with those of experiments and FEM. At this point in this study, the commercial software LS-DYNA [18] was employed for both IGA and FEM analyses.
3.1. Three-Point Bending Analysis of Trailing Arm
Figure 7 shows the dimensions of the trailing arm. Figure 8 depicts the three-point bending of the trailing arm, which is discussed here. The distance between the supports was 474 mm, and each support has a cross-sectional shape of a semicircle with a diameter of 30 mm. The cross-sectional shape of an indenter is circular with a diameter of 17 mm. Then, the member was compressed vertically downward with the indenter at 50 mm/min in the experiment. The position of the indenter on the x-y plane of the trailing arm was as shown in Figure 9. The thickness of the trailing arm was 2.3 mm.
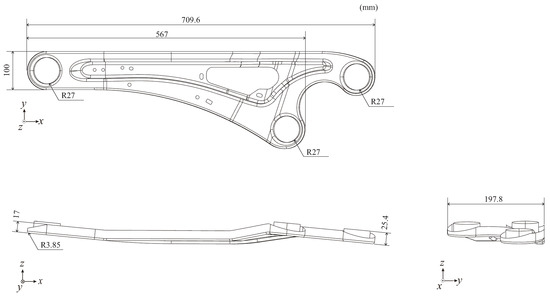
Figure 7.
Model size of trailing arm.
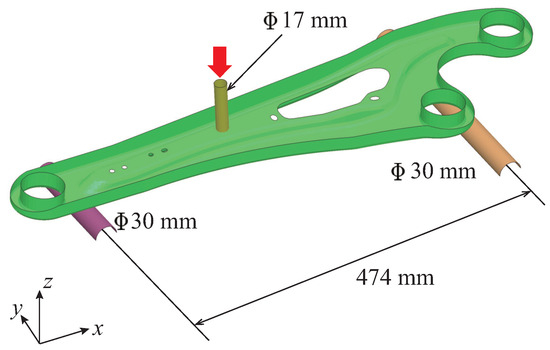
Figure 8.
Three-point bending of trailing arm.
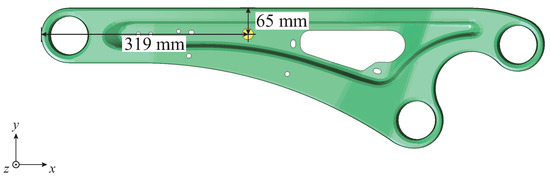
Figure 9.
Position of indenter on x-y plane of trailing arm.
Figure 10 depicts the IGA model for the shell of the trailing arm. In the figure, the black lines represent the boundaries of NURBS patches. These patches are created by combining multiple third-order NURBS patches, and small holes are accurately represented through trimming. Adjacent NURBS patches are connected by sharing control points. In the enlarged view in Figure 10, the blue line represents the boundary of the subregion. A subregion in the IGA corresponds to an element in the FEM, and numerical integration was performed within this subregion.
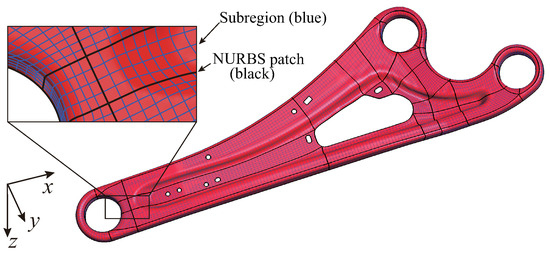
Figure 10.
IGA shell model using NURBS.
Let the in-plane integration point of a third-order IGA model be 3 × 3 for reduced numerical integration within the subregion, with a pitch interval of 5 mm. The FEM model for comparison was a 5 mm sized first-order shell element with in-plane fully numerical integration with assumed strain interpolation [19,20]. The number of integration points in the thickness direction was 5 for both IGA and FEM. In both the IGA and FEM calculations, the indenter speed was set to 5000 mm/min, which is 100 times the experimental value, to enhance the calculation efficiency by increasing the time increment in the explicit dynamic method. The material of the trailing arm was elastoplastic, and the material constants were a mass density of 7860 kg/m3, Young’s modulus of 206 GPa, and Poisson’s ratio of 0.3. The true stress–equivalent plastic strain relationship was set as shown in Figure 11. The indenter and support were rigid bodies.
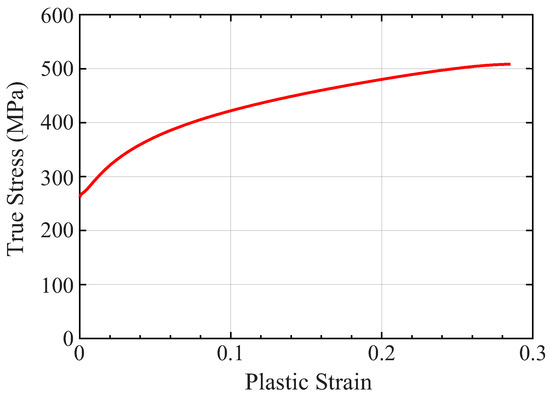
Figure 11.
True stress–plastic strain curve of trailing arm.
Figure 12 compares the load–stroke curves at the indentation point obtained from three experiments with the FEM and IGA analyses. In both FEM and IGA, the load–stroke curves are qualitatively consistent with the experimental results. However, in both cases, the load peak is lower than in the experiments. This is because the trailing arm includes changes in plate thickness and work hardening during forming in the experiment. On the other hand, these forming histories are not considered in the analysis. The load–stroke curve of IGA is slightly lower than that of FEM because IGA uses higher-order basis functions. Investigating contact parameters for suppressing oscillations in load–stroke curves due to the indenter speed being 100 times faster than in the experiments is a future task. Figure 13 displays the deformation and a contour of the von Mises stress for the trailing arm. A stress distribution similar to that of FEM can be obtained in IGA. In contrast to this, a distinct deformation is observed at the bottom center of the enlarged model. This is because this location is where consistent deformation could not be achieved even in multiple experiments.
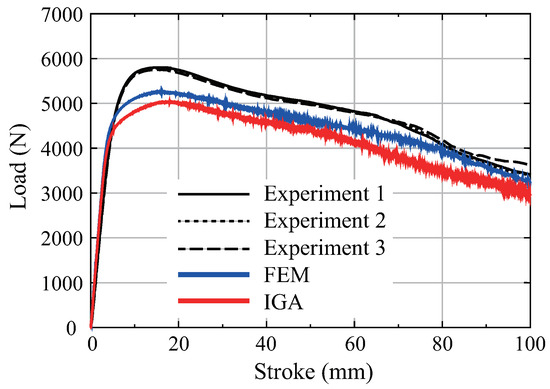
Figure 12.
Load–stroke curves of trailing arm.
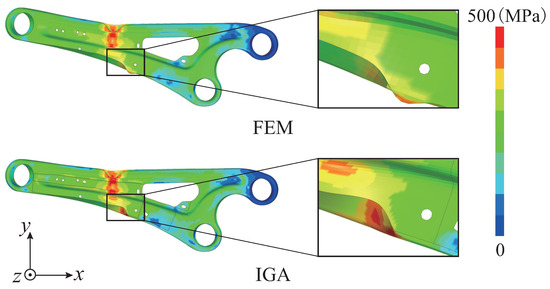
Figure 13.
Deformations and von Mises stress of trailing arm.
3.2. Compression Analysis of Aluminum Extrusions
Figure 14 shows the dimensions of aluminum extrusions based on actual measurements. Figure 15 is the cross-sectional dimension with two cavities. A compression analysis was conducted using an aluminum extrusion with this cross-section to evaluate the performance of IGA in buckling deformation.
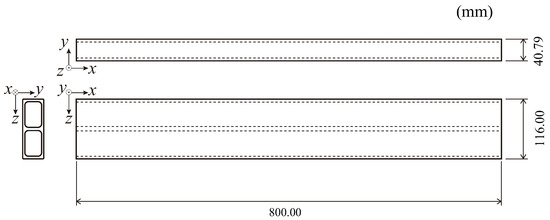
Figure 14.
Model size of aluminum extrusion.
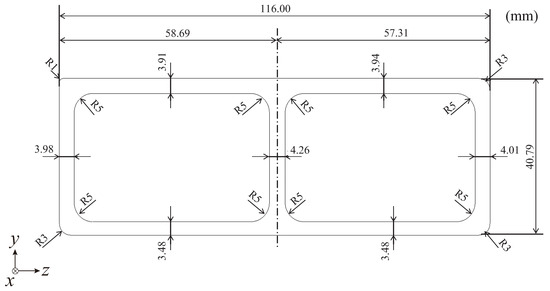
Figure 15.
Cross-section of aluminum extrusion.
A model of a thick plate, such as an aluminum extrusion, is treated. A solid model was employed instead of the shell to obtain sufficient accuracy for the bending of members. Figure 16 depicts the aluminum extrusion model created using NURBS solids. The black line in the figure represents the boundary of the NURBS patch on the model section, and the extruded model was generated by sweeping along the yellow edge. Figure 17 shows the element division via FEM and the subregion via IGA in the cross-section. In FEM, one-point reduced (Reduce) and selective reduced (S/R) integration were used with eight-node 3D solid elements. The third-order NURBS solids with 3 × 3 × 3 integration points for reduced integration were used in the IGA. In addition, in the normal IGA model, control points were crowded at the corners of the cross-section. To prevent a decrease in the time increment in the explicit dynamic method caused by the crowded control points, a remesh model was also created, similar to the IGA model (Remesh) shown in Figure 17. However, in the remeshed model, poor reproducibility of the cross-sectional shape was observed through the widening of the control point interval.
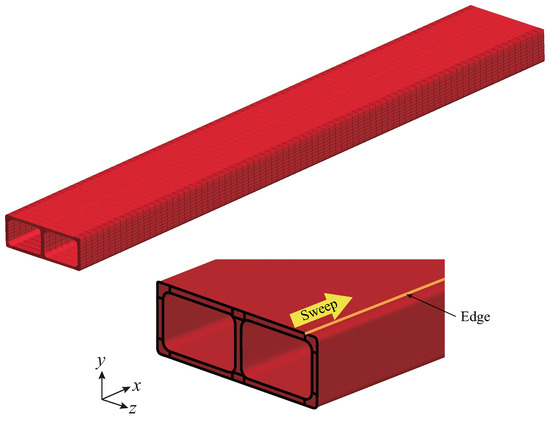
Figure 16.
IGA solid model of aluminum extrusion.
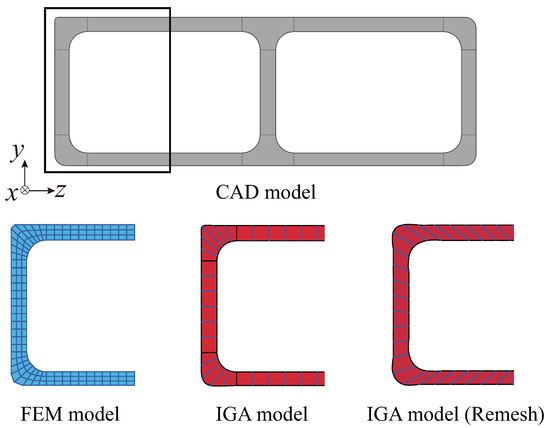
Figure 17.
Mesh division of cross-section.
Figure 18 shows the compression analysis conditions. The aluminum extruded member (cross-sectional) was placed upright on a flat plate, and the center of the member was compressed vertically downward with an indenter with a radius of 148 mm and a width of 100 mm. Although the indenter speed was 50 mm/min in the experiments, the indenter speed was adjusted to 500 mm/s in the analysis to enhance the calculation efficiency of the explicit dynamic method. The aluminum extruded member was an elastic–plastic material with a mass density of 2740 kg/m3, a Young’s modulus of 68.95 GPa, and a Poisson’s ratio of 0.33. Figure 19 shows the true stress–equivalent plastic strain relationship of the aluminum extrusions. Here, the plate and the indenter were assumed to be rigid bodies. In this analysis, fracture was not introduced.
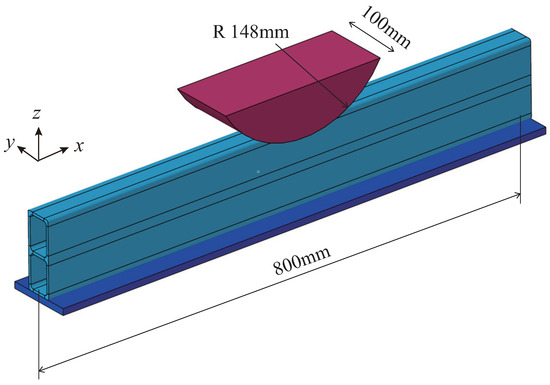
Figure 18.
Computational model of aluminum extrusion.
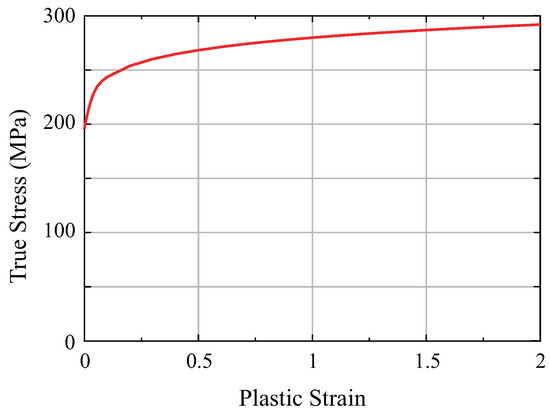
Figure 19.
True stress–plastic strain curve of aluminum extrusion.
Figure 20 shows the load–stroke curve obtained from the experiment and the deformation state of the structure. The load initially increases and then decreases as the upper part of the structure starts to buckle. When the deformation of the lower part of the structure begins, the load increases once more, and then the load decreases due to the buckling of the lower part of the structure. Figure 21 shows the load–stroke curves of the indenter obtained from this analysis and the experiment. FEM Reduce and FEM S/R denote the one-point integration and selective reduced integration of eight-node 3D solid elements in FEM, respectively. All FEMs and IGAs exhibited strong agreement with the experimental results in the initial slopes. However, after this, although the load decreased and then increased again in the experiment, the load increased again without decreasing in the analysis. This is because the fracture criterion was not considered in the present analysis. In the region where the gradient of the load–stroke curve was negative in experiments, there is inconsistency between the analysis and experimentation due to fracture occurrence. However, in the region where fracture does not affect and the gradient is positive, consistency between the analysis and experimentation is observed in the gradient and the increase in load. Figure 22 shows the deformation and von Mises stress distribution of the central cross-section of the member at various stroke levels. For the eight-node 3D solid elements used in FEM, selective reduced integration (FEM S/R) is generally known to provide greater accuracy than one-point integration (FEM Reduce). For Figure 22, the buckling mode of IGA was the same as that of the selective reduced integration of FEM (FEM S/R). This result indicates the high performance of IGA. In the experiment, a buckling mode in which the unevenness is reversed on the front and back of the cross-section was observed. On the other hand, in this analysis, we could not reproduce this buckling mode because the introduction of fracture conditions is insufficient.
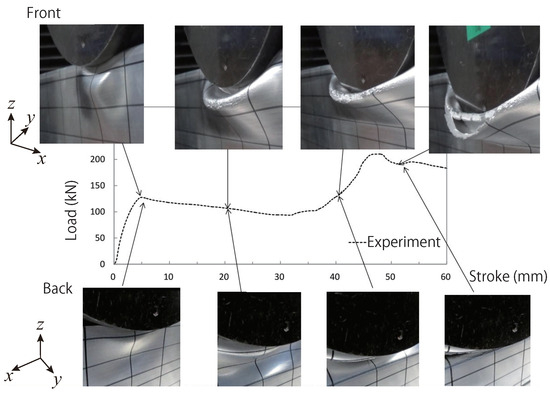
Figure 20.
Load–stroke curve and deformations of upper part in experiment.
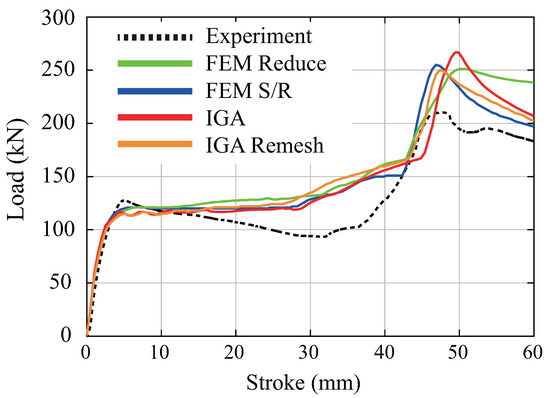
Figure 21.
Load–stroke curves of aluminum extrusion.
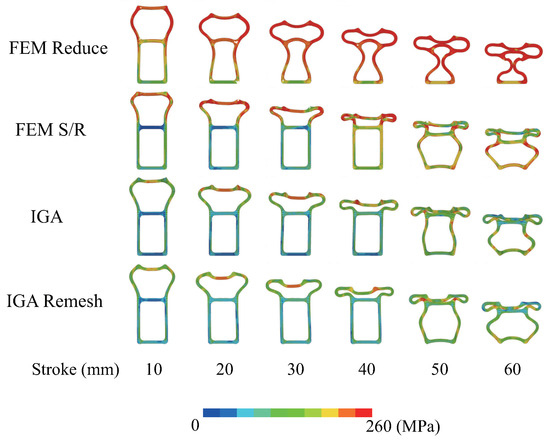
Figure 22.
Deformations and von Mises stress on central cross-section.
The fracture of IGA can be evaluated by eliminating each subregion in the same way as eliminating elements in FEM, but determining the fracture condition while considering the differences in each size is indispensable.
Table 1 shows the time increments and computational times for each solid model in the compression analysis of aluminum extrusions. In the IGA model, the time increment is reduced, and the computational time is increased compared to FEM because the control points were crowded in the corner areas. On the other hand, in the IGA Remesh model, widening the intervals between control points results in larger time increments compared to FEM, and the computational time becomes almost the same as that of FEM S/R. From the above, we confirm that in the IGA solid model, by adjusting the intervals between control points, the time increment can be increased, resulting in a computational cost equivalent to that of FEM.

Table 1.
Time increment and computational times for each solid model (seconds).
4. Crash Analysis of Automobile
In this study, IGA was applied to a crash analysis of the automobile body. In the deformation analysis of the structural members mentioned above, the computational results were compared with experimental data. In this analysis, the validity of IGA in automobile crash analysis was examined by comparing it with the analysis results of FEM.
4.1. Automobile Body Model
Figure 23 shows the computational automobile body model. This model consists of 367 components and 2000 spot-welded points. In the spot-welded locations, first-order one-element beams are connected using free nodes within a patch, similar to FEM, without considering fractures. At the front of the B-pillar, nodes are fully constrained, and the automobile body is subjected to impact due to the rigid wall’s displacement from the front of the automobile. The velocity of the rigid body was 18 km/h, but this speed was determined for analytical purposes without practical significance. Here, only the front part of the automobile body, which mainly affects the analysis results, was modeled using IGA, and the region beyond that was modeled using FEM.
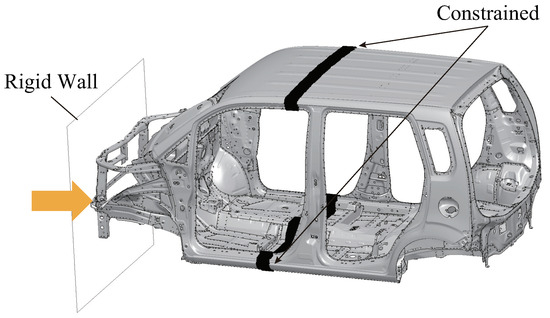
Figure 23.
Automobile body model.
Figure 24 represents an analysis model that combines IGA and FEM. The 114 components in the red area were modeled using IGA shells, while the gray area was modeled using FEM shells. As mentioned above, the deformation of the automobile body becomes dominant in front of the constrained B-pillar. Therefore, for a comparison with the analysis results of the entire automobile body structure modeled with FEM shells, only the front part was modeled using IGA shell modeling. The IGA regions were divided into subdomains of sizes 5 mm and 10 mm, while the FEM regions were divided into elements of a uniform size of 5 mm. Furthermore, for the IGA subdomains and FEM elements, the same order and number of integration points, as validated in the previous section on the three-point bending analysis of the trailing arm in Section 3.1, were employed. Figure 25 depicts the mesh divisions under FEM (5 mm), IGA (5 mm), and IGA (10 mm).
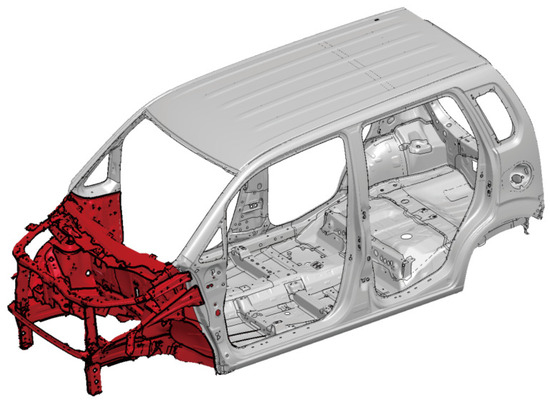
Figure 24.
IGA and FEM model of automobile body. Red and gray zones show IGA and FEM modeling, respectively.
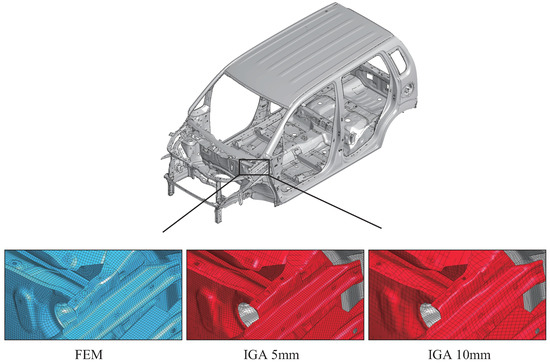
Figure 25.
Mesh divisions of automobile body with FEM and IGA models.
4.2. Computational Results
Figure 26 depicts the load–stroke curves for the rigid wall for each of the respective models. The results obtained from the IGA model with a 5 mm subdomain size closely correspond to the reference results from the FEM analysis. In contrast, the results from the IGA model with a 10 mm subdomain size indicate an increase in strength.
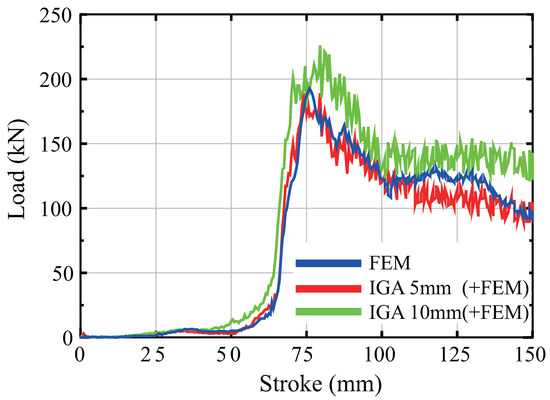
Figure 26.
Load–stroke curves of automobile body.
The deformation states will be considered next. Figure 27 and Figure 28 show deformation views from the front and top of the automobile, respectively. The deformation of the IGA model with a 5 mm subdomain size is highly consistent with the deformation states observed in the FEM analysis. In comparing the deformation of the IGA model with a 10 mm subdomain size to the FEM model, it is observed that the locations of buckling are nearly identical, but the deformation tends to be small.

Figure 27.
Deformations from front view of automobile.
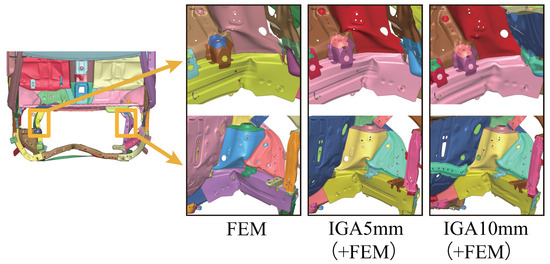
Figure 28.
Deformations from top view of automobile.
This is because the reproducibility of the curved surface, which is possible with the IGA model with a 5 mm subdomain size, has decreased in the IGA model with a 10 mm subdomain size. The shape of the buckling location becomes smoother, resulting in increased buckling load. Therefore, local deformations are constrained.
In the IGA model with a 10 mm subdomain size, a significant difference from the others is the occurrence of localized buckling in the A-pillar on the left side of the automobile, as shown in the right image in Figure 27. The reason for this is that the localized deformation is constrained as mentioned above, leaving no outlet for the release of internal energy, resulting in buckling at the A-pillar on the left side.
4.3. Computational Time
The computational time for each model is presented in Table 2. In parallel computation with 16 domain partitions, uniform time increments are used for all analyses employing the mass scaling of the explicit dynamic method. As evident from this table, the IGA model with a 5 mm domain exhibits approximately double the computational time compared to the FEM, while the IGA model with a 10 mm domain results in nearly equivalent computation times. Hence, the analysis results obtained using the IGA shell model with a 10 mm domain size for the automobile body are nearly identical to those obtained for the entire FEM shell model. Regarding computational time, both models perform approximately equally.

Table 2.
Computational times for each automobile body model (seconds).
5. Conclusions
To verify the applicability of IGA to automobile crash analysis, performance evaluations of the bending and buckling deformations of structural components were conducted using an explicit dynamic method. Furthermore, IGA was applied to the crash analysis of the automobile body. Through these investigations, it was confirmed that structural analysis with IGA using the explicit dynamic method provides analysis accuracy and computational efficiency comparable to those of FEM, while also being highly practical. Furthermore, due to compatibility with CAD data, IGA can reduce the most time-consuming process of model generation in structural analysis, leading to an overall cost reduction in the structural analysis time.
One future challenge is to enhance the shape representation accuracy by improving the modeling adjusted to weight functions in IGA. Furthermore, quantitative consistency with experiments will be improved through the examination of fracture conditions for components and joints under IGA. In this study, we investigated the performance and computational efficiency of IGA compared to those of FEM. Ultimately, we aimed to tackle problems where generating computational models from CAD for large-scale structures occupies a significant portion of the analysis time and demonstrate its practical effectiveness.
Author Contributions
Conceptualization, Y.Y.; methodology, Y.Y.; validation, Y.Y. and K.N.; formal analysis, Y.Y.; investigation, H.S.; writing-original draft preparation, Y.Y.; writing-review and editing, Y.Y. and S.O.; supervision, I.M.; project administration, S.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
Authors Yuta Yokoyama and Shigenobu Okazawa were employed by the company Diver Technology Corporation. Authors Kei Nagasaka and Idemitsu Masuda were employed by the company Suzuki Motor Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis, CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Cottrell, J.A.; Hughes, T.J.R.; Bazilevs, Y. Isogeometric Analysis, Toward Integration of CAD and FEA; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Nagy, A.P.; Benson, D.J. On the numerical integration of trimmed isogeometric elements. Comput. Methods Appl. Mech. Eng. 2015, 284, 165–185. [Google Scholar] [CrossRef]
- Guo, Y.; Ruess, M. Nitsch’s method for a coupling of isogeometric thin shells and blended shell structures. Comput. Methods Appl. Mech. Eng. 2015, 284, 881–905. [Google Scholar] [CrossRef]
- Schuß, S.; Dittmann, M.; Wohlmuth, B.; Klinkel, S.; Hesch, C. Multi-patch isogeometric analysis for Kirchhoff-Love shell elements. Comput. Methods Appl. Mech. Eng. 2019, 349, 91–116. [Google Scholar] [CrossRef]
- Leidinger, L.F.; Breitenberger, M.; Bauer, A.M.; Hartmann, S.; Wuechner, R.; Bletzinger, K.-U.; Duddeck, F.; Song, L. Explicit dynamic isogeometric B-Rep analysis of penalty-coupled trimmed NURBS shells. Comput. Methods Appl. Mech. Eng. 2019, 351, 891–927. [Google Scholar] [CrossRef]
- Leidinger, L.; Hartmann, S.; Benson, D.; Nagy, A.; Rorris, L.; Chalkidis, I. Hybrid IGA/FEM vehicle crash simulations with trimmed NURBS-based shells in LS-DYNA. In Proceedings of the 13th European LS-DYNA Conference, Ulm, Germany, 5–7 October 2021. [Google Scholar]
- Bauer, F.; Yugeng, T.; Leidinger, L.; Hartmann, S. Experience with crash simulations using an IGA body in white. In Proceedings of the 14th European LS-DYNA Conference, Baden-Baden, Germany, 18–19 October 2023. [Google Scholar]
- Morganti, S.; Auricchio, F.; Benson, D.J.; Gambarin, F.I.; Hartmann, S.; Hughes, T.J.R.; Reali, A. Patient-specific isogeometric structural analysis of aortic valve closure. Comput. Methods Appl. Mech. Eng. 2015, 284, 508–520. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, S.P.; Faruque, O.; Alanoly, J.; El-Essawi, M.; Baskaran, R. Current status of LS-DYNA Iso-geometric analysis in crash simulation. In Proceedings of the 14th International LS-DYNA Users Conference, Dearborn, MI, USA, 12–14 June 2016. [Google Scholar]
- Hartmann, S.; Nagy, A.P.; Benson, D.J. Advances in IGA for sheet metal forming applications. In Proceedings of the 11th European LS-DYNA Users Conference, Salzburg, Austria, 9–11 May 2017. [Google Scholar]
- Hartmann, S.; Benson, D.J. Mass scaling and stable time step estimates for isogeometric analysis. Int. J. Numer. Methods Eng. 2015, 102, 671–687. [Google Scholar] [CrossRef]
- Casquero, H.; Bona-Casas, C.; Gomez, H. A NURBS-based immersed methodology for fluid-structure interaction. Comput. Methods Appl. Mech. Eng. 2015, 84, 943–970. [Google Scholar] [CrossRef]
- Caseiro, J.F.; Valente, R.A.F.; Reali, A.; Kiendl, J.; Auricchio, F.; Alves de Sousa, R.J. Assumed natural strain NURBS-based solid-shell element for the analysis of large deformation elasto-plastic thin-shell structures. Comput. Methods Appl. Mech. Eng. 2015, 284, 861–880. [Google Scholar] [CrossRef]
- Kiendl, J.; Hsu, M.C.; Wu, M.C.; Reali, A. Isogeometric Kirchhoff-Love shell formurations for general hyperelastic materials. Comput. Methods Appl. Mech. Eng. 2015, 291, 280–303. [Google Scholar] [CrossRef]
- Hu, P.; Hu, Q.; Xia, Y. Order reduction for locking free isogeometric analysis of Timoshenko beams. Comput. Methods Appl. Mech. Eng. 2016, 308, 1–22. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Book; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- LS-DYNA theory Manual, Livermore Software Technology (LST), An ANSYS Company. 2023. Available online: https://lsdyna.ansys.com/manuals/ (accessed on 8 April 2024).
- Pian, T.H.H.; Sumihara, K. Rational approach for assumed stress finite elements. Int. J. Numer. Methods Eng. 1984, 20, 1685–1695. [Google Scholar] [CrossRef]
- Simo, J.C.; Hughes, T.J.R. On the variational foundations of assumed strain methods. J. Appl. Mech. 1986, 53, 51–54. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).