Conceptual Study on Car Acceleration Strategies to Minimize Travel Time, Fuel Consumption, and CO2-CO Emissions
Abstract
1. Introduction
1.1. Overview
1.2. Literature Review
1.3. The Present Study
2. Problem Description
2.1. Problem Definition
2.2. The Car
- Mass (m): 1150 kg;
- Front surface area (Af): 2 m2;
- Drag coefficient (CD): 0.33;
- Maximum power (W): 90 kW;
- Maximum crankshaft rotating speed: 5500 rpm;
- Cylinders: four in line;
- Piston diameter (b); 77 mm;
- Crank length (LC): 43 mm;
- Connecting rod length (LCR): 144 mm;
- Total displacement: 1600 cm3;
- Compression ratio: 11:1;
- Total moment of inertia of rotating parts (I_R): 0.55 kg·m2;
- Admission valve closing: 50 deg after bottom dead center;
- Exhaust valve opening: 50 deg before top dead center
2.3. Acceleration Scenarios
2.3.1. Acceleration Scenario 1
- The car accelerated from 20 m/s (72 km/h) up to 35 m/s (126 km/h) along a horizontal plane 1000 m long, see Figure 1;
- Acceleration at both the beginning and end points was zero;
- Three velocity trajectories (time laws) were considered. They were modelled via Bezier polynomials, and represented nearly constant acceleration (T1), fast acceleration first and slow acceleration later (T2), and slow acceleration first and fast acceleration later (T3). Each Bezier polynomial had 1000 points;
- The transmission ratio was 23 km/h per 1000 rpm.
2.3.2. Acceleration Scenario 2 (AC2)
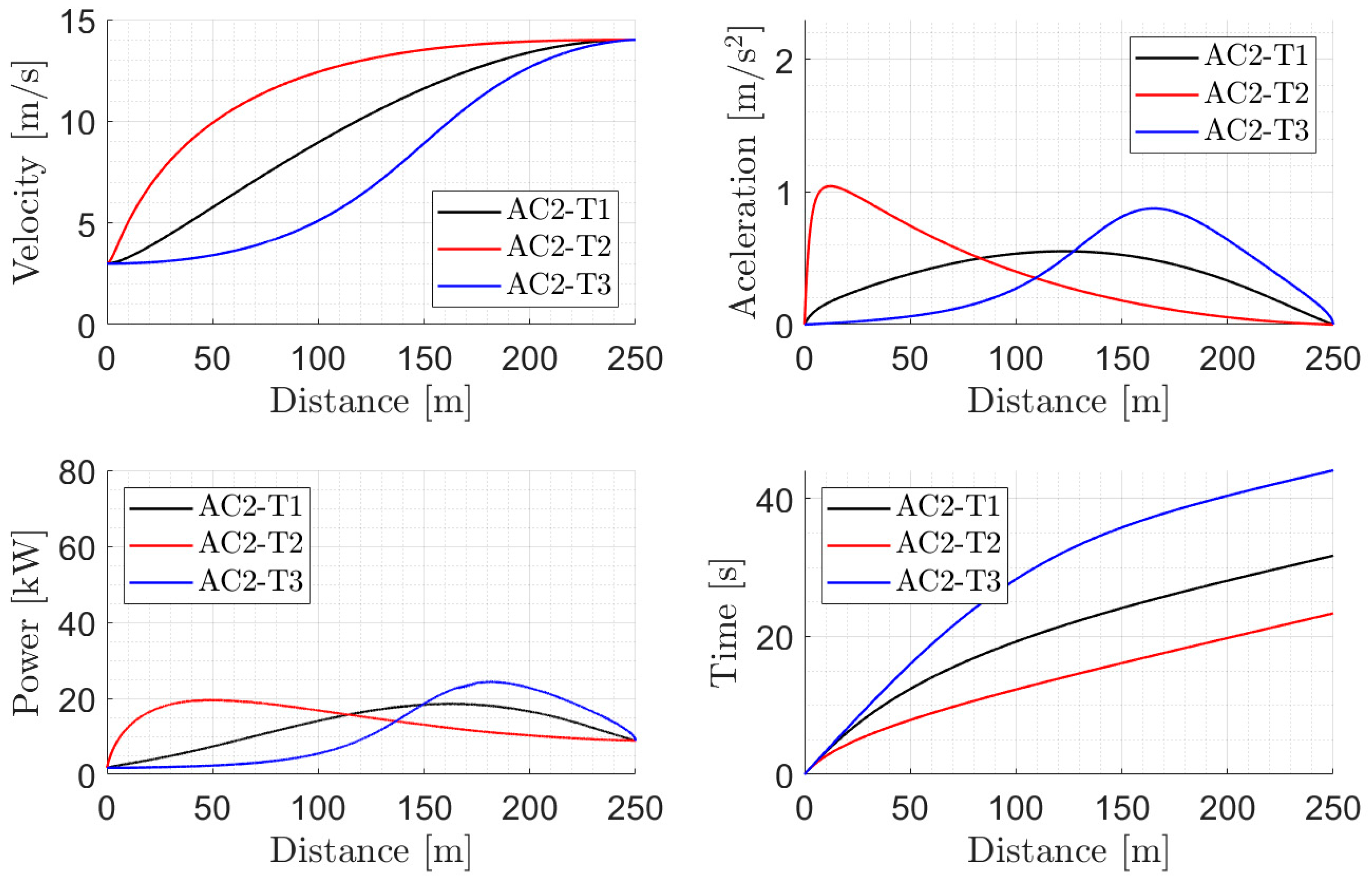
- The car accelerated from 3 m/s (11 km/h) to 14 m/s (50 km/h) along an inclined plane (5% slope) 250 m long, see Figure 2;
- The transmission ratio was 10.8 km/h per 1000 rpm;
- An additional term was included in the right-hand side of Equation (1) to account for the gain of potential energy per unit time when climbing the slope:
3. Methodology
3.1. Overview of the Methodology
3.2. Engine Model
- Gasoline Otto cycle;
- Zero-dimensional (time is the only independent variable);
- Heat transfer to the outside is accounted for in all thermodynamic cycle processes;
- Pressure losses through the intake and exhaust valves are modelled;
- Combustion takes place with 10 species: CO2, H2O, OH, CO, H2, H, O2, O, N2, and N, considered to be chemical equilibrium;
- Atmospheric engine (no compressor);
- The model is made up of 35 integral–differential equations that involve all processes of the thermodynamic cycle.
3.3. Tensor Mirror Model
3.4. Densified Surrogate Tensor Model
3.5. Generic Description of the Optimization Process
3.6. Objective Function
3.7. Detailed Description of the Optimization Process
- The starting engine operating point, P0, in the (PA, IT, RPM) data tensor corresponds to the initial point of the acceleration path. This point has constant vehicle velocity and engine RPM’s, zero acceleration, minimum fuel consumption, C, and minimum CO2 and CO emissions. It provides the power needed to propel the vehicle at the prescribed constant velocity, and its risk of engine knocking is smaller than 1.
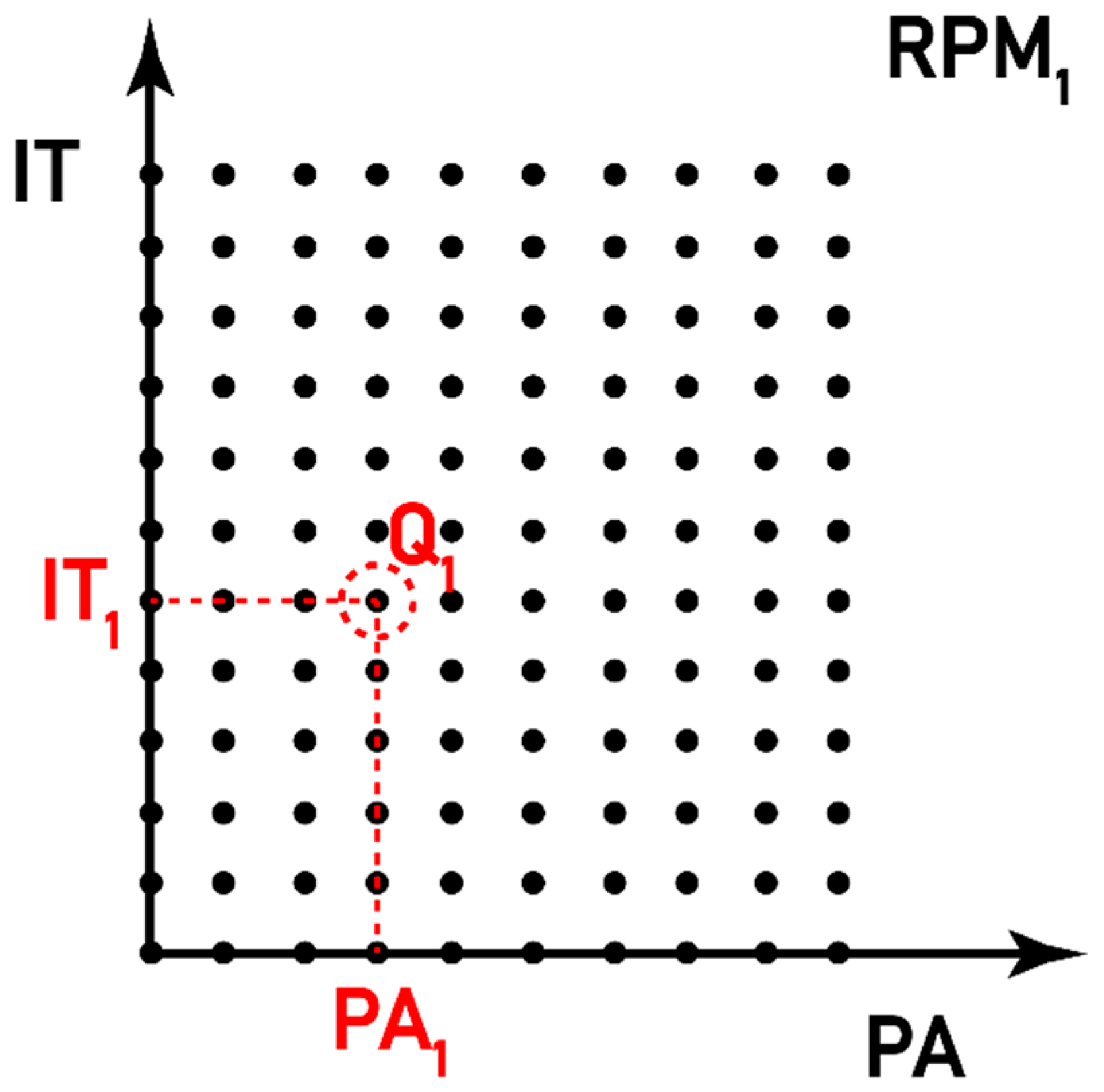
- Once the variable RPM is prescribed (it is called RPM1 for convenience), the objective function , as defined in Equation (2), is computed for all points located in the plane of constant RPM1 of the (PA, IT, RPM) data tensor. The number of points where evaluation of takes place is 141 × 121 = 17,061.
- Out from the 17,061 evaluations of , the one that delivers the minimum value, , is selected. This point where corresponds to an associated pair of PA and IT (denoted with the subscript “1” for convenience). Then, the next optimum point in the data tensor of operation variables is (PA1, IT1, RPM1).
- The process is repeated iteratively until the end point of the acceleration path is reached.
- Finally, integrals of the time evolution of fuel consumption, C, and CO2 and CO emissions along the optimum path inside the data tensor are computed to obtain the total values of fuel consumed and pollutant emissions: , , and , respectively.
4. Results
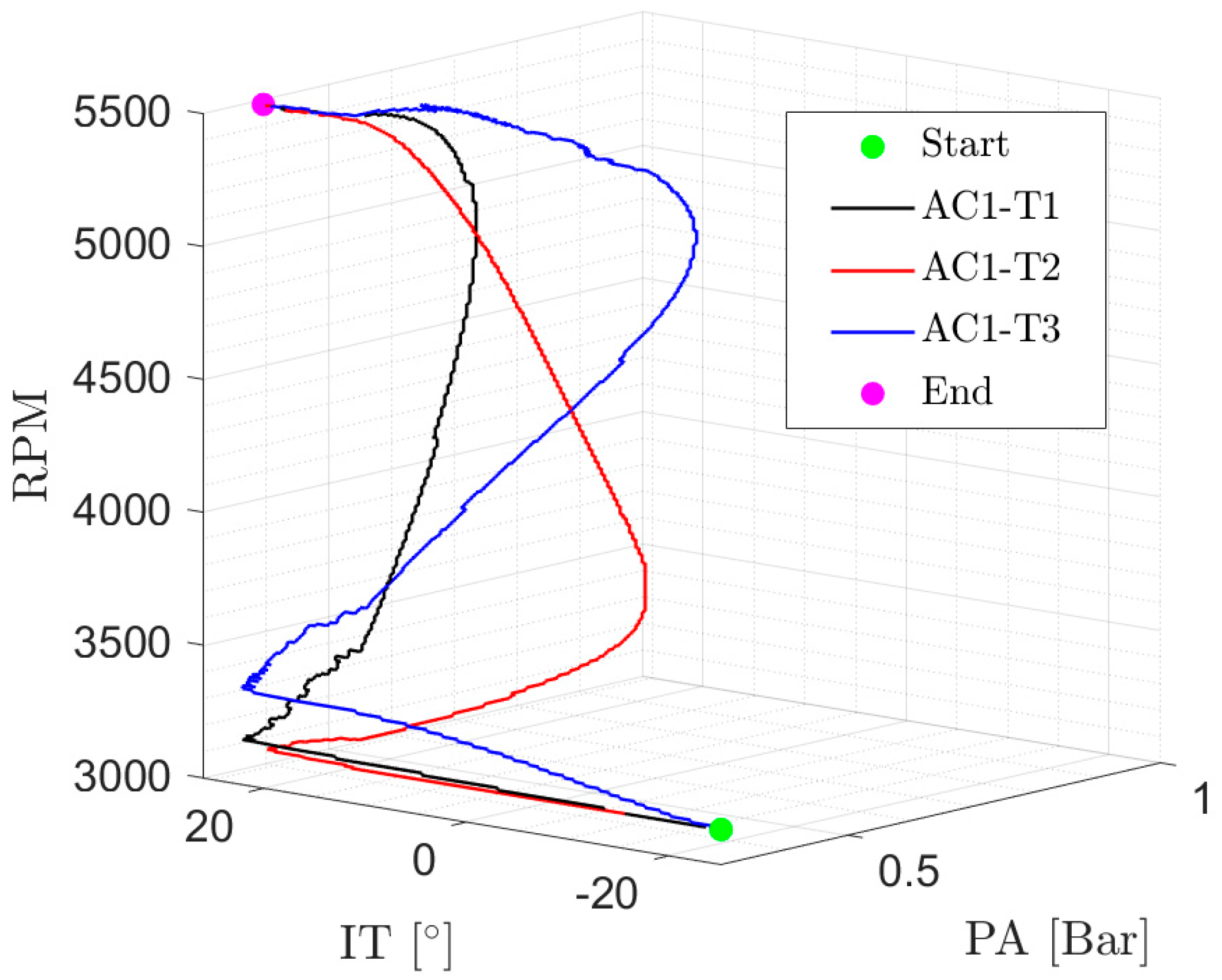
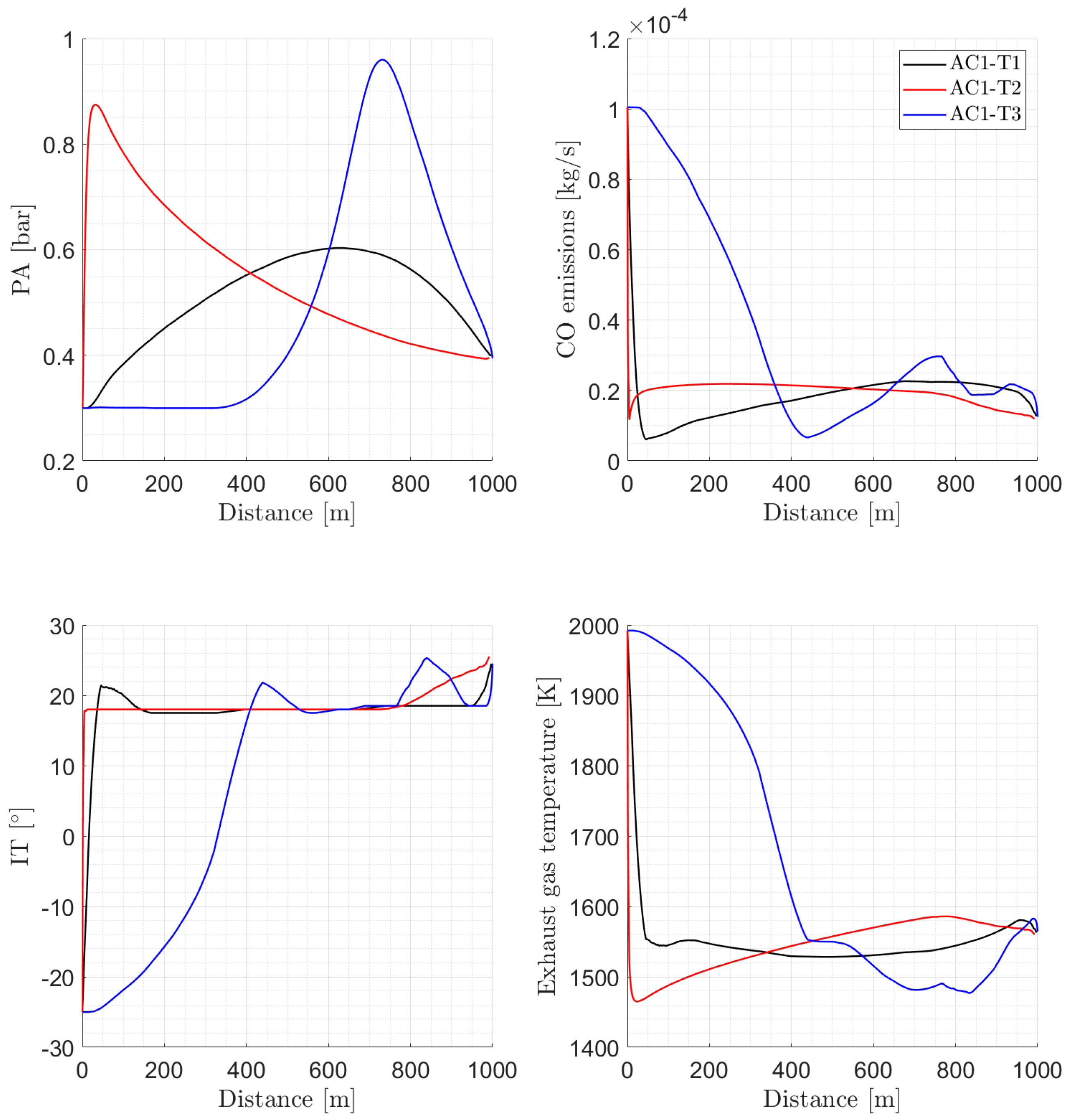
4.1. Acceleration Scenario AC1
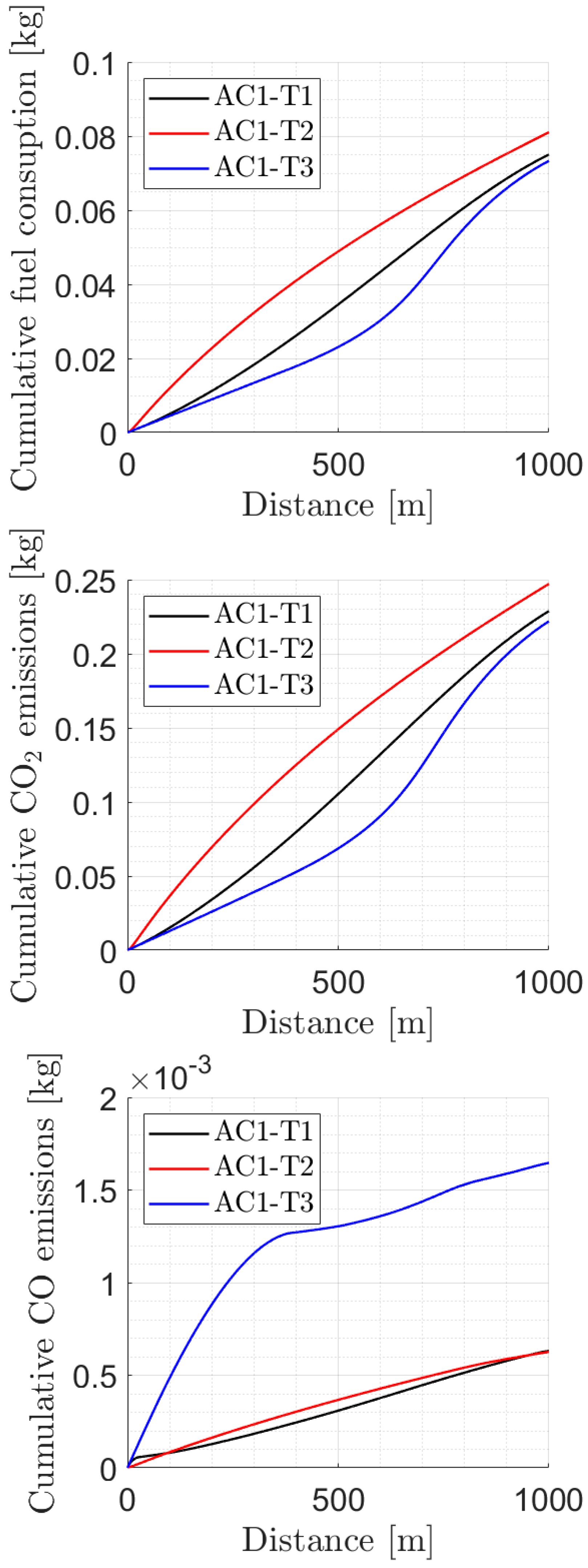
- The integrals of the CO2 emissions alongside the 1 km long trajectories, T1, T2, T3, were similar. They were all in a band of 0.232 kg ± 6%. The integral of CO emissions varied between 0.631 × 10−3 kg and 1.646 × 10−3 kg. The ratio of the integral of CO2 emissions to the integral of CO emissions had values between 362 and 134.
- Total CO emissions in trajectory T3 nearly tripled those of trajectories T1 and T2. The reason is that the initial point of the trajectories had a high CO emission (see Table 1). Then, while T1 and T2 trajectories rapidly increase their velocity and acceleration, thereby moving away from the high CO emissions operating region, trajectory T3 keeps close to the initial operation point for a significant part of the trajectory. Thus, the integral of the CO emissions (that is the variable represented in Figure 5) is larger than its counterparts of trajectories T1 and T2. Then, T3 is discarded as a practical option when compared to trajectories T1 and T2.
- Trajectories T1 and T2 present a similar lever of total CO emissions. Fuel consumption and CO2 emissions of trajectory T2 are 8% larger than in trajectory T1. However, trajectory T2 saves time (by a factor of 11%) as compared to trajectory T1.
- All this suggests that trajectories T1 and T2 are preferable in acceleration scenario AC1. Specific selection of each of them could be based on either minimizing emissions (T1) or reducing travel time (T2). In any case, all acceleration profiles that range from nearly constant acceleration to fast acceleration first and slow acceleration later might be acceptable in a practical driving situation. This provides a reasonable margin to the designer of intelligent driving approaches when these criteria are to be combined with other concerns related to the interaction of the vehicle with the surrounding traffic flow.
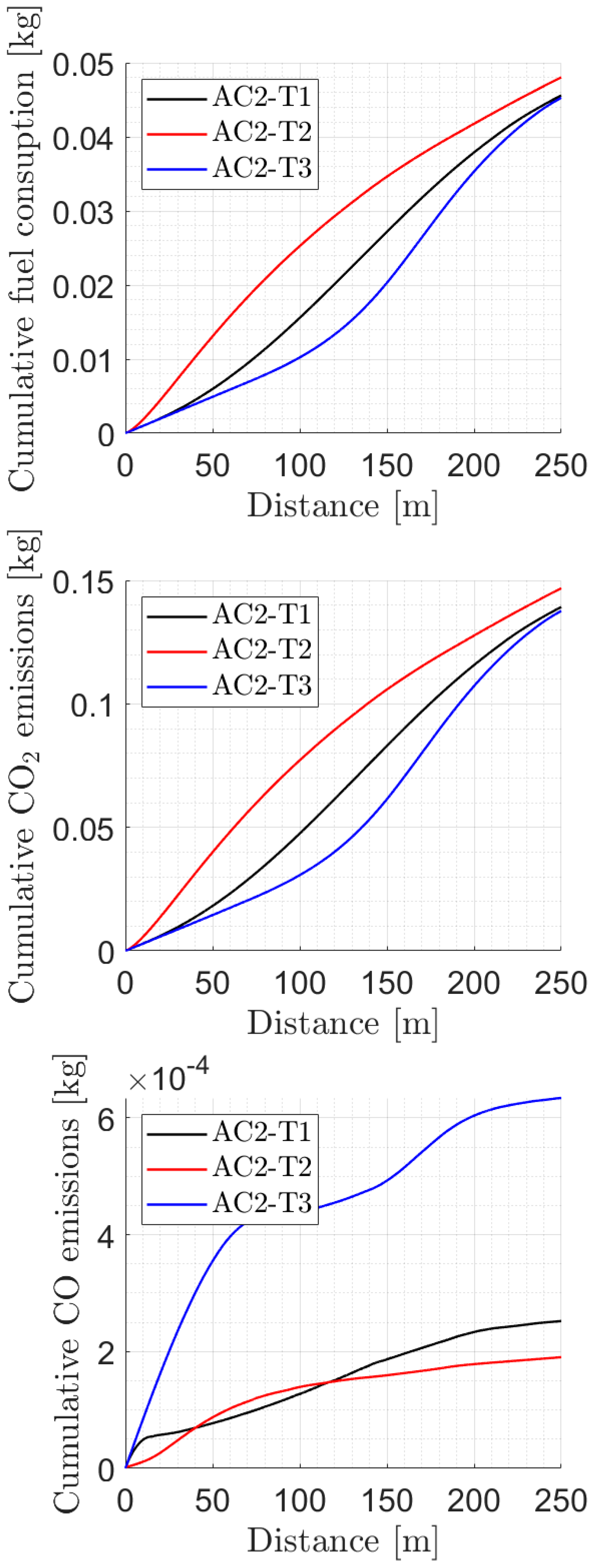
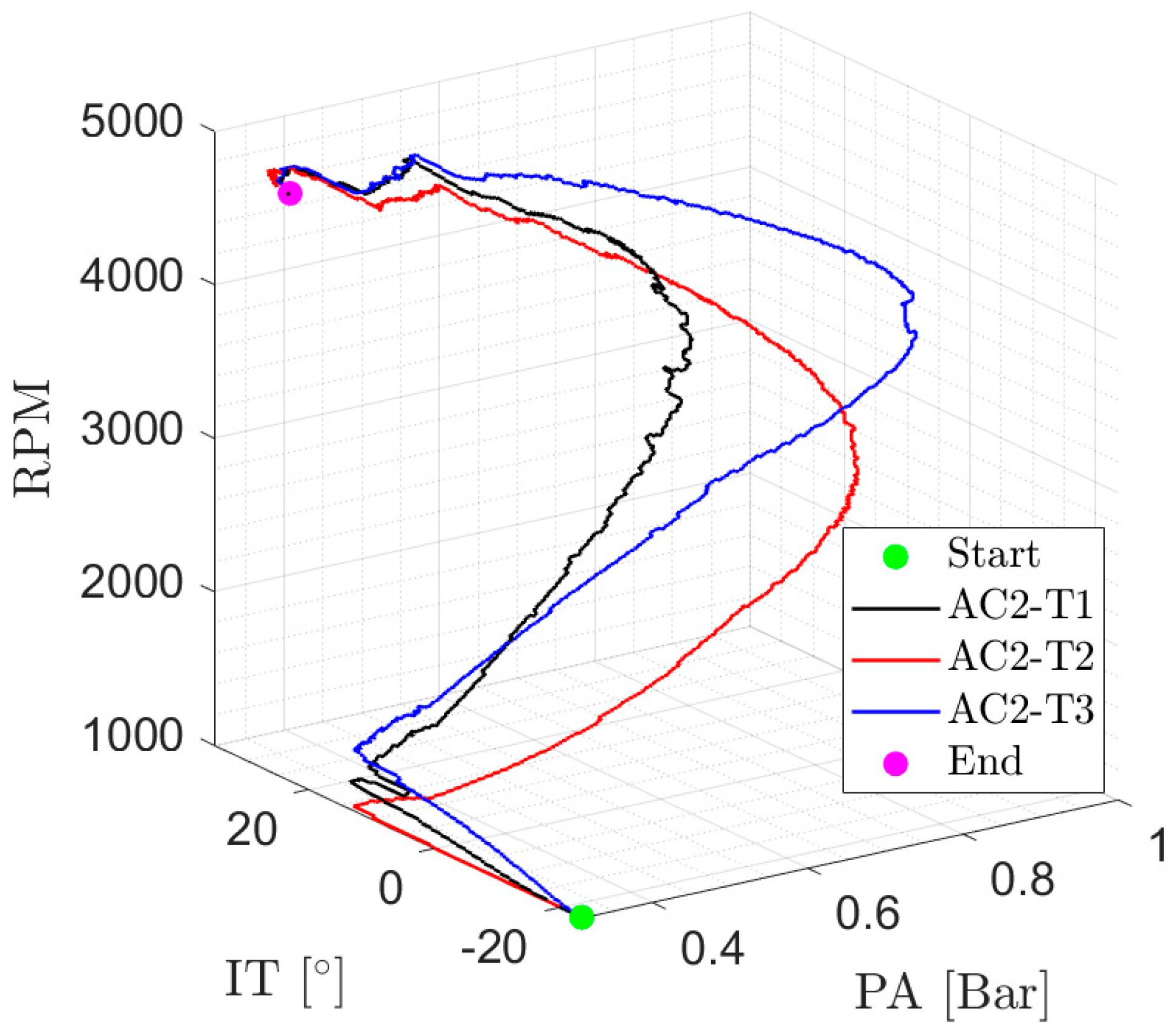
4.2. Acceleration Scenario AC2
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Engine Model Description
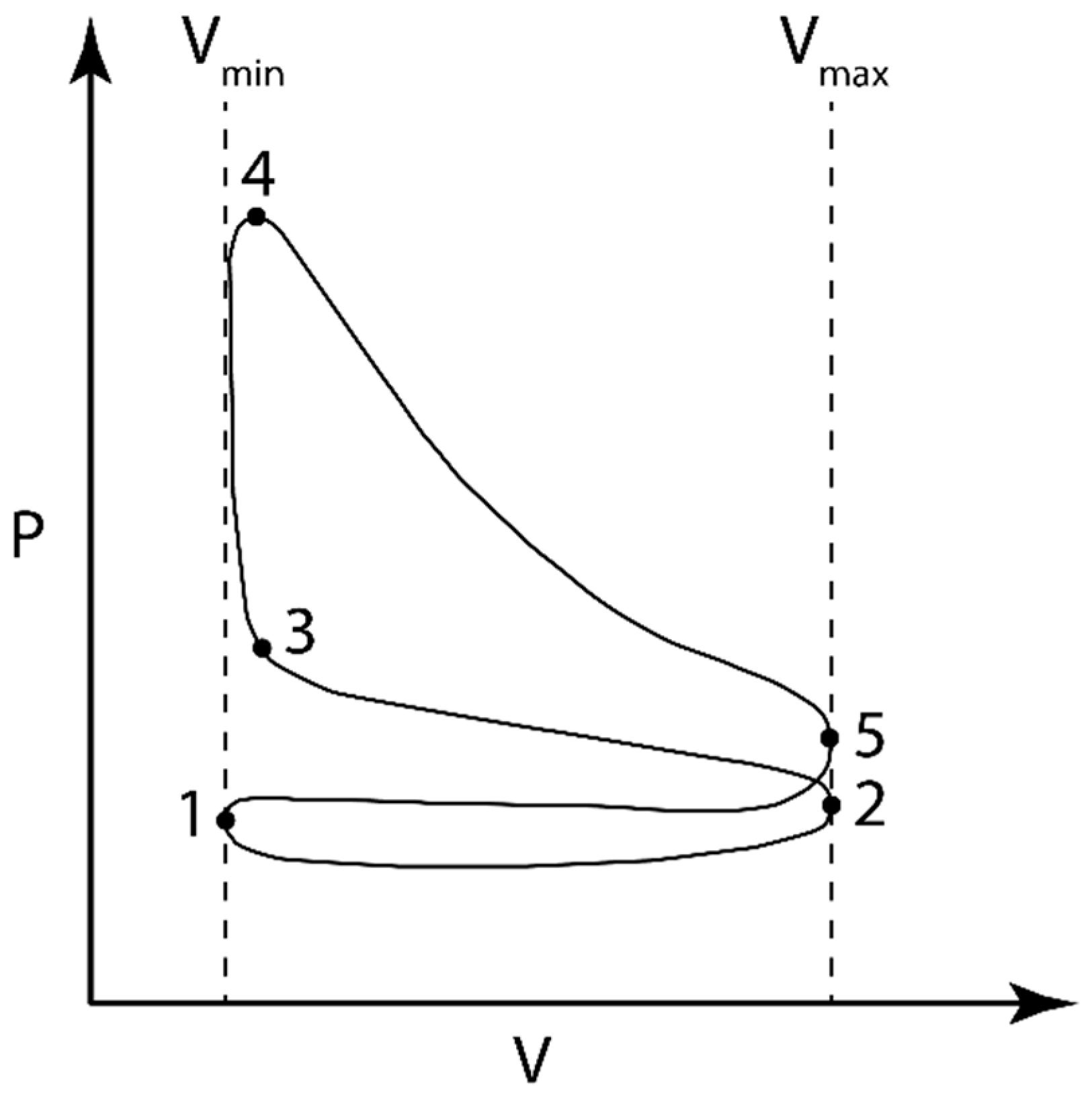
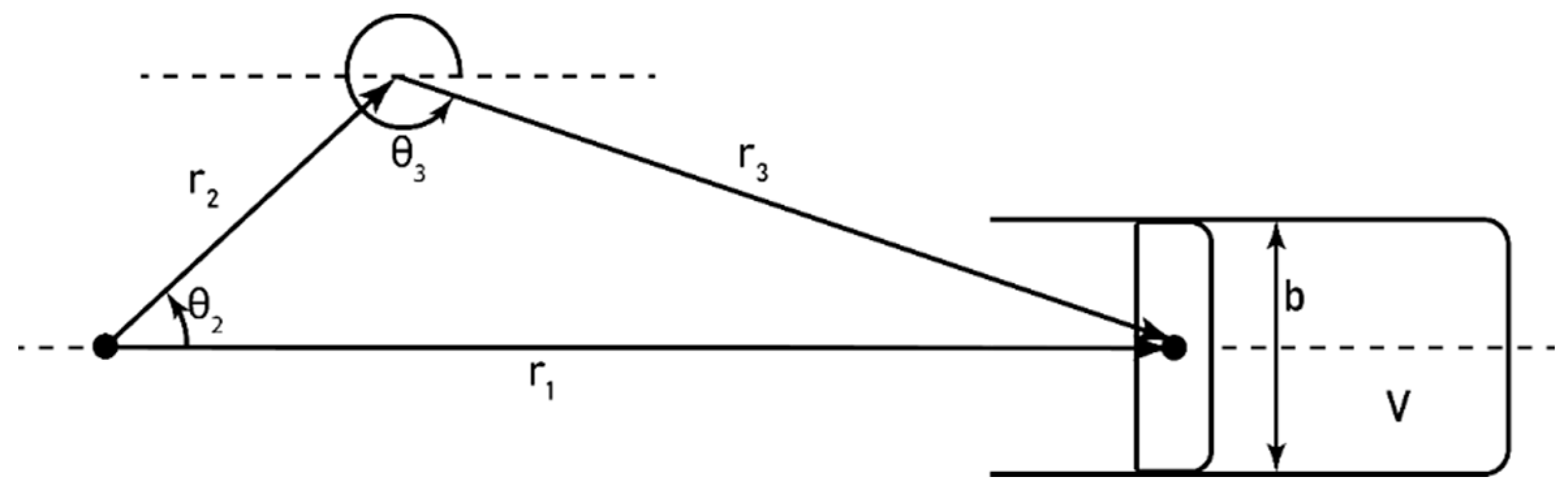
Appendix A.1. Intake
Appendix A.2. Compression
Appendix A.3. Combustion
Appendix A.4. Expansion
Appendix A.5. Exhaust
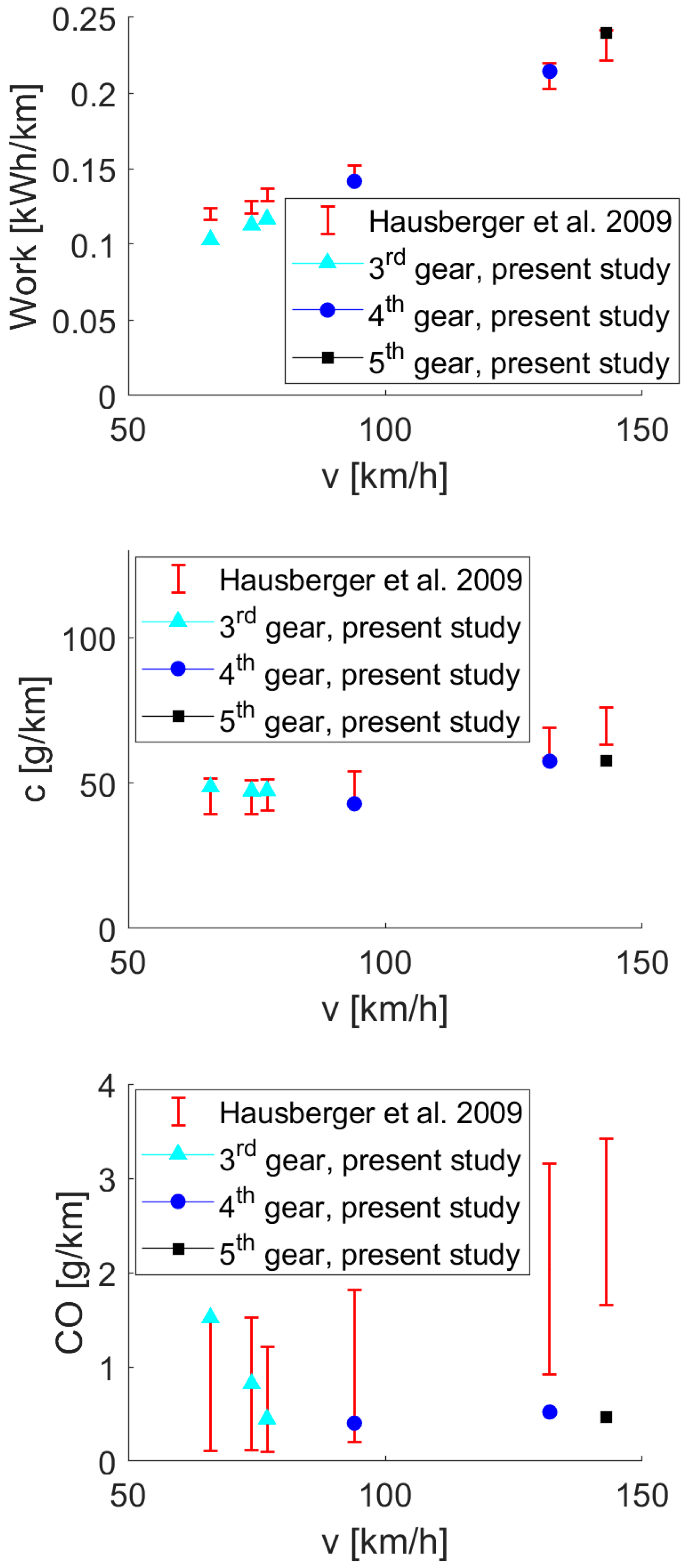
Appendix B. Engine Model Validation
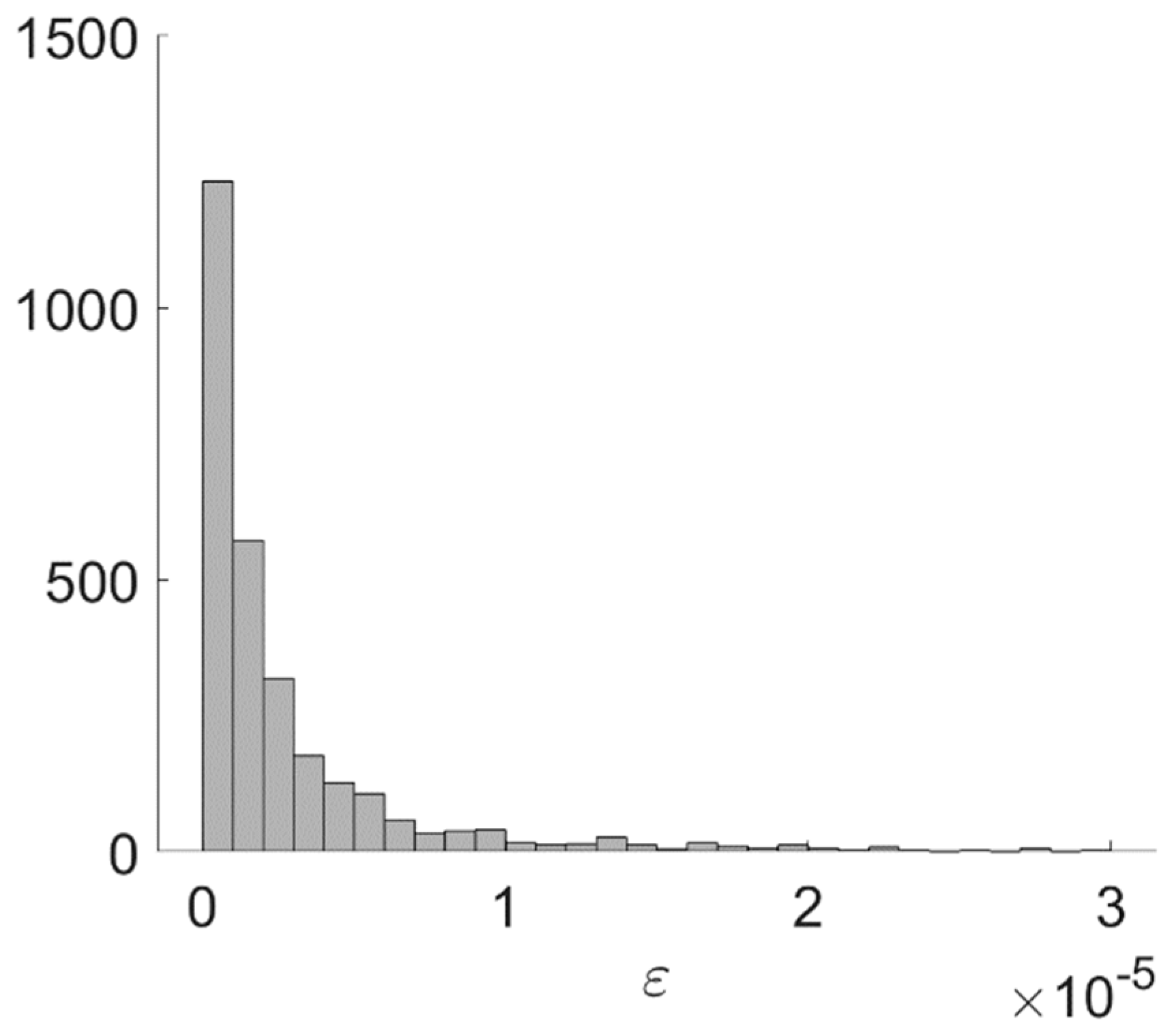
Appendix C. Quality of Tensor Densification via HOSVD
References
- Langhorst, J.; Chan, K.W.; Meerpohl, C.; Büskens, C. Computing safe stop trajectories for autonomous driving utilizing clustering and parametric optimization. Vehicles 2024, 6, 590–610. [Google Scholar] [CrossRef]
- Li, X.; Guvenc, L.; Aksun-Guvenc, B. Vehicle state estimation and prediction for autonomous driving in a round intersection. Vehicles 2023, 5, 1328–1352. [Google Scholar] [CrossRef]
- Diachuk, M.; Easa, S.M. Improved technique for autonomous vehicle motion planning based on integral constraints and sequential optimization. Vehicles 2022, 4, 1122–1157. [Google Scholar] [CrossRef]
- Diachuk, M.; Easa, S.M. Motion planning for autonomous vehicles based on sequential optimization. Vehicles 2022, 4, 344–374. [Google Scholar] [CrossRef]
- Choudhury, C.F.; Islam, M.M. Modelling acceleration decisions in traffic streams with weak lane discipline: A latent leader approach. Transp. Res. Part C Emerg. Technol. 2016, 67, 214–226. [Google Scholar] [CrossRef]
- Goñi-Ros, B.; Knoop, V.L.; Takahashi, T.; Sakata, I.; van Arem, B.; Hoogendoorn, S.P. Optimization of traffic flow at freeway sags by controlling the acceleration of vehicles equipped with in-car systems. Transp. Res. Part C Emerg. Technol. 2016, 71, 1–18. [Google Scholar] [CrossRef]
- Ivanchev, J.; Eckhoff, D.; Knoll, A. System-level optimization of longitudinal acceleration of autonomous vehicles in mixed traffic. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 1968–1974. [Google Scholar]
- Manolis, D.; Spiliopoulou, A.; Vandorou, F.; Papageorgiou, M. Real time adaptive cruise control strategy for motorways. Transp. Res. Part C Emerg. Technol. 2020, 115, 102617. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Cai, B.; Liu, J. Combined alignment effects on deceleration and acceleration: A driving simulator study. Transp. Res. Part C Emerg. Technol. 2019, 104, 172–183. [Google Scholar] [CrossRef]
- Ard, T.; Guo, L.; Dollar, R.A.; Fayazi, A.; Goulet, N.; Jia, Y.; Vahidi, A. Energy and flow effects of optimal automated driving in mixed traffic: Vehicle-in-the-loop experimental results. Transp. Res. Part C Emerg. Technol. 2021, 130, 103168. [Google Scholar] [CrossRef]
- Bishop, J.D.; Stettler, M.E.; Molden, N.; Boies, A.M. Engine maps of fuel use and emissions from transient driving cycles. Appl. Energy 2016, 183, 202–217. [Google Scholar] [CrossRef]
- Guo, Q.; Angah, O.; Liu, Z.; Ban, X.J. Hybrid deep reinforcement learning based eco-driving for low-level connected and automated vehicles along signalized corridors. Transp. Res. Part C Emerg. Technol. 2021, 124, 102980. [Google Scholar] [CrossRef]
- Hibberd, D.L.; Jamson, A.H.; Jamson, S.L. The design of an in-vehicle assistance system to support eco-driving. Transp. Res. Part C Emerg. Technol. 2015, 58, 732–748. [Google Scholar] [CrossRef]
- Sun, Z.; Hao, P.; Ban, X.J.; Yang, D. Trajectory-based vehicle energy/emissions estimation for signalized arterials using mobile sensing data. Transp. Res. Part D Transp. Environ. 2015, 34, 27–40. [Google Scholar] [CrossRef]
- Tsanakas, N.; Ekström, J.; Olstam, J. Generating virtual vehicle trajectories for the estimation of emissions and fuel consumption. Transp. Res. Part C Emerg. Technol. 2022, 138, 103615. [Google Scholar] [CrossRef]
- Hausberger, S.; Rexeis, M.; Zallinger, M.; Luz, R. Emission Factors from the Model PHEM for the HBEFA Version 3. Report Nr. I-20/2009 Haus-Em 33/08/679. Institute for Internal Combustion Engines and Thermodynamics, 2009; Technical University of Grazt, Austria. [Google Scholar]
- Kim, W.-G.; Kim, C.-K.; Lee, J.-T.; Kim, J.-S.; Yun, C.-W.; Yook, S.-J. Fine particle emission characteristics of a light-duty diesel vehicle according to vehicle acceleration and road grade. Transp. Res. Part D Transp. Environ. 2017, 53, 428–439. [Google Scholar] [CrossRef]
- Chandrashekar, C.; Chatterjee, P.; Pawar, D.S. Estimation of CO2 and CO emissions from auto-rickshaws in Indian heterogeneous traffic. Transp. Res. Part D Transp. Environ. 2022, 104, 103202. [Google Scholar] [CrossRef]
- Kuppili, S.K.; Alshetty, V.D.; Diya, M.; Nagendra, S.M.S.; Ramadurai, G.; Ramesh, A.; Gulia, S.; Namdeo, A.; Maji, K.; Bell, M.; et al. Characteristics of real-world gaseous exhaust emissions from cars in heterogeneous traffic conditions. Transp. Res. Part D Transp. Environ. 2021, 95, 102855. [Google Scholar] [CrossRef]
- Suarez, J.; Makridis, M.; Anesiadou, A.; Komnos, D.; Ciuffo, B.; Fontanaras, G. Benchmarking the driver acceleration impact on vehicle energy consumption and CO2 emissions. Transp. Res. Part D Transp. Environ. 2022, 107, 103282. [Google Scholar] [CrossRef]
- Zhang, Y.; Lv, J.; Wang, W. Evaluation of vehicle acceleration models for emission estimation at an intersection. Transp. Res. Part D Transp. Environ. 2013, 18, 46–50. [Google Scholar] [CrossRef]
- US Environmental Protection Agency. Development of Emission Rates for Light-duty Vehicles in the Motor Vehicle Emissions Simulator, EPA-420-P-09-002 August 2009, (MOVES2009).
- Blokpoel, R.; Hausberger, S.; Krajzewicz, D. Emission optimised control and speed limit for isolated intersections. IET Intell. Transp. Syst. 2017, 11, 174–181. [Google Scholar] [CrossRef]
- Crolla, D. (Ed.) Automotive Engineering, Powertrain, Chassis System and Vehicle Body; Elsevier: Amsterdam, The Netherlands, 2009; pp. 306–309. [Google Scholar]
- De Lathauwer, L.; De Moor, B.; Vandewalle, J. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 2000, 21, 1253–1278. [Google Scholar] [CrossRef]
- Garcia-Magarino, A.; Sor, S.; Velazquez, A. Data reduction method for droplet deformation experiments based on High Order Singular Value Decomposition. Exp. Therm. Fluid Sci. 2016, 79, 13–24. [Google Scholar] [CrossRef]
- Ferguson, C.R.; Kirkpatrick, A.T. Internal Combustion Engines; John Wiley & Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Stull, D.R.; Prophet, H. JANAF Thermochemical Tables, 2nd ed.; USA Department of Commerce, National Bureau of Standards: Washington DC, USA, 1971.
- The Handbook of Emissions Factors for Road Transport, HBEFA Version 3; INFRAS: Zurich, Switzerland, 2010.


| Starting Point | End Point | |
|---|---|---|
| Velocity [m/s] | 20 | 35 |
| RPM | 3129 | 5483 |
| Power [kW] | 3.2 | 16.3 |
| Distance [m] | 0 | 1000 |
| C [kg/s] | 0.89 × 10−3 | 2.01 × 10−3 |
| CO2 [kg/s] | 2.57 × 10−3 | 6.15 × 10−3 |
| CO [kg/s] | 0.100 × 10−3 | 0.012 × 10−3 |
| Starting Point | End Point | |
|---|---|---|
| Velocity [m/s] | 3 | 14 |
| RPM | 1000 | 4669 |
| Power [kW] | 1.7 | 8.8 |
| Distance [m] | 0 | 250 |
| C [kg/s] | 0.30 × 10−3 | 1.59 × 10−3 |
| CO2 [kg/s] | 0.86 × 10−3 | 4.88 × 10−3 |
| CO [kg/s] | 0.026 × 10−3 | 0.004 × 10−3 |
| T1 | T2 | T3 | |
|---|---|---|---|
| Total C [kg] | 0.075 | 0.081 | 0.073 |
| Total CO2 [kg] | 0.228 | 0.247 | 0.222 |
| Total CO [kg] | 0.631 × 10−3 | 0.626 × 10−3 | 1.646 × 10−3 |
| Total time [s] | 35.9 | 31.9 | 41.1 |
| T1 | T2 | T3 | |
|---|---|---|---|
| Total C [kg] | 0.045 | 0.048 | 0.045 |
| Total CO2 [kg] | 0.139 | 0.146 | 0.137 |
| Total CO [kg] | 0.25 × 10−3 | 0.19 × 10−3 | 0.63 × 10−3 |
| Total time [s] | 31.7 | 23.4 | 44.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acosta, O.; Sastre, F.; Arias, J.R.; Velazquez, Á. Conceptual Study on Car Acceleration Strategies to Minimize Travel Time, Fuel Consumption, and CO2-CO Emissions. Vehicles 2024, 6, 984-1007. https://doi.org/10.3390/vehicles6020047
Acosta O, Sastre F, Arias JR, Velazquez Á. Conceptual Study on Car Acceleration Strategies to Minimize Travel Time, Fuel Consumption, and CO2-CO Emissions. Vehicles. 2024; 6(2):984-1007. https://doi.org/10.3390/vehicles6020047
Chicago/Turabian StyleAcosta, Olivia, Francisco Sastre, Juan Ramón Arias, and Ángel Velazquez. 2024. "Conceptual Study on Car Acceleration Strategies to Minimize Travel Time, Fuel Consumption, and CO2-CO Emissions" Vehicles 6, no. 2: 984-1007. https://doi.org/10.3390/vehicles6020047
APA StyleAcosta, O., Sastre, F., Arias, J. R., & Velazquez, Á. (2024). Conceptual Study on Car Acceleration Strategies to Minimize Travel Time, Fuel Consumption, and CO2-CO Emissions. Vehicles, 6(2), 984-1007. https://doi.org/10.3390/vehicles6020047









