Next Article in Journal
A Sensor (Optode) Based on Cellulose Triacetate Membrane for Fe(III) Detection in Water Samples
Previous Article in Journal
New Polymorph of β-Cyclodextrin with a Higher Bioavailability
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Chemistry
Volume 6
Issue 1
10.3390/chemistry6010004
chemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

4,4-Bis(isopropylthio)-1,1-diphenyl-2-azabuta-1,3-diene Adducts with Cadmium(II), Mercury(II) and Copper(I) Iodides: Crystal, Molecular and Electronic Structures of d10 Transition Metal Chelate Complexes

by
Rodolphe Kinghat
1,
Abderrahim Khatyr
1,
Michael Knorr
1,*,
Carsten Strohmann
2 and
Marek M. Kubicki
3,*
1
Institut UTINAM UMR 6213 CNRS, Université de Franche-Comté, 16, Route de Gray, 25030 Besançon, France
2
Anorganische Chemie, Technische Universität Dortmund, Otto-Hahn-Str. 6, 44227 Dortmund, Germany
3
Institut ICMUB UMR 6302 CNRS, Université de Bourgogne, 9, Avenue Alain Savary, 21078 Dijon, France
*
Authors to whom correspondence should be addressed.
Chemistry 2024, 6(1), 62-80; https://doi.org/10.3390/chemistry6010004
Submission received: 14 November 2023 / Revised: 22 December 2023 / Accepted: 22 December 2023 / Published: 25 December 2023
(This article belongs to the Section Crystallography)
Browse Figures
Versions Notes

Abstract

:
The thioether-functionalized 2-azabutadiene (iPrS)2C=C(H)-N=CPh2 L ligates to CdI2 and HgI2 to form the chelate compounds [CdI2{(iPrS)2C=C(H)-N=CPh2] (1) and [HgI2(iPrS)2C=C(H)-N=CPh2] (2). Their crystal structures were solved via X-ray diffraction. Both crystallize in the non-centrosymmetric space groups: monoclinic P21 (1) and orthorhombic P212121 (2), respectively. The closed-shell d10 metal centers are four-coordinated (two iodides and S and N coordinating atoms from the ligand L) in both complexes. The geometrical indexes τ indicate that a highly distorted trigonal pyramidal is adopted for 1 and a seesaw geometry for 2. The comparative nature of metal–ligand bonds is discussed on the basis of metric parameters and of QT-AIM (quantum theory of atoms in molecules) calculations. L was also treated with CuI to obtain the dinuclear species [LCu(μ2-I2)CuL] (3), in which the two Cu(I) centers are linked by a short metal–metal bond. The geometric and electronic properties of 3 are compared with those of 1 and 2.

1. Introduction

In contrast to the plethora of 1,4-diazabutadien (α-diimine) complexes [1,2,3], 2-azabutadienes R2C=C(H)-N=CR′2 (R, R′ = Hal, alkyl, aryl) featuring a π-conjugated C=C(H)-N=C array are far less common as ligands in coordination chemistry [4]. We have developed an access to π-conjugated Cl2C=C(H)-N=CAr2 via 1,3-dipolar cycloaddition and demonstrated that the chlorine atoms therein can be readily substituted with alcoholates, amides and thiolates [5,6,7,8,9]. The latter ditopic thioether-functionalized 2-azabutadienes (RS)2C=C(H)-N=CAr2 in turn represent versatile ligands in coordination chemistry, since they dispose of both a harder imine-type N-donor site and a soft S-thioether site, allowing a chelating coordination on various transition metal centers. For example, coordination of crystallographically characterized derivative (iPrS)2C=C(H)-N=CPh2 (L) on Mo(CO)5THF yields cis-(OC)4Mo{(iPrS)2C=C(H)-N=CPh2}] [10], and using [Re(μ-Br)(CO)3(THF)]2 as a starting material allowed the synthesis of octahedral fac-[(OC)3ReBr{(iPrS)2C=C(H)-N=CPh2}] [11]. We have even demonstrated that the ortho-H atoms of the aryl groups can be activated for cyclometallation reactions producing the luminescent C,N,S-pincer complexes [(iPrS)2C=C(H)-N=C(Ph)C6H4)MCl] with M = Pd or Pt [10]. The 16-membered bimetallic macrocyclic complex [{Cu2Br2{p-iPrSC6H4)2C=N-C(H)=C(SiPr)2}2] has also been synthesized and characterized [9].
We have now extended our investigation on the coordination chemistry of (iPrS)2C=C(H)-N=CPh2 to the closed-shell metal salts CdI2, HgI2 and CuI and present the synthesis of the resulting chelate complexes, which were structurally characterized using X-ray diffraction studies. AIM (atoms in molecules) topological analyses of the electron densities were performed, bringing clarifications about the nature of bonding around the d10 metallic centers.
After having analyzed in detail the structural properties of the group 12 CdI2 and HgI2 complexes 1 and 2 featuring a closed-shell d10 configuration, we turned our attention to CuI. The diamagnetic Cu(I) ion, which has in the ground state a 3d104s0 rather than a 3d94s1 electronic configuration (Aufbau principle inversion), also belongs to the d10 avenue and is considered according to the HSAB principle as a soft metal cation. Although MI2 salts may form after complexation of soft sulfur and phosphorus donor ligands dinuclear halide-bridged compound, CuI forms after coordination with soft sulfur and phosphorus donor and harder N-donor ligands quasi-invariably in both rhomboid-shaped dinuclear [LnCu(μ2-I2)CuLn] (n = 1,2) and polynuclear CunIn clusters. Examples are the wide-spread closed-cubane clusters Cu4I4L4 (L = S, N, P, As) [12,13,14,15,16]. But with SMe2 and PPh3, other tetranuclear partially opened isomeric forms are also known, such as the flower-basket-shaped 2D polymer [(Me2S)3{Cu4(μ-I)4}]n or the open chair (open cubane tetramer) Cu4I4(PPh3)4 cluster [17,18,19]. With N,S coordinating site ligands, dinuclear complexes featuring [Cu2I2] rhomboids are formed in most cases [20,21,22,23,24].

2. Experimental Section

The ligand L was prepared according to the procedure described in the literature [9].
General procedure for the preparation of the complexes 1 and 2: A solution of 4,4-bis(isopropylthio)-1,1-diphenyl-2-azabuta-1,3-diene (L) (113 mg, 0.318 mmol) in 4 mL of ethanol/dichloromethane (1/1) was added to a solution of MI2 (0.318 mmol) (M = Cd or Hg) in 4 mL of ethanol. The resulting yellow solution was refluxed for 3 h and then stirred for 1 day, after which the solvent was evaporated until a yellow solid appeared. Crystals suitable for X-ray diffraction were obtained via slow evaporation of methanol/chloroform solution of the dry yellow solid.
[CdI2{(iPrS)2C=C(H)-N=CPh2}] 1: Yellow crystal. Yield: 48%; IR-ATR: 1594 (C=C), 1511 (C=N) cm−1; UV–vis (CH2Cl2) [λmax nm (ε)]: 269 (47,800 M−1 cm−1), 311 sh (31,000 M−1 cm−1), 375 (33,800 M−1 cm−1), C21H25CdI2NS2 (721.78): Anal. calcd. C 34.94, H 3.49, N 1.94, S 8.88; found: C 34.86, H 3.37, N 1.89, S 8.81.
[HgI2{(iPrS)2C=C(H)-N=CPh2}] 2: Yellow crystal. Yield: 44%; IR-ATR: 1595 (C=C), 1489 (C=N) cm−1; UV–vis (CH2Cl2) [λmax nm (ε)]: 252 (59,500 M−1 cm−1), 378 (38,800 M−1 cm−1); C21H25HgI2NS2 (809.96): Anal. calcd. C 31.14, H 3.11, N 1.73, S 7.92; found: C 31.06, H 3.05, N 1.69, S 7.88.
Synthesis of [{Cu(µ-I)}2{Ph2C=N-CH=C(S-iPr)2}] 3: A solution of CuI (190 mg, 1 mmol) in 5 mL of acetone was added to a solution of the ligand L (711 mg, 2 mmol) in 5 mL of dichloromethane. The mixture was stirred at room temperature for 2 h and the layering with diethyl ether afforded red-coloured crystals, suitable for X-ray diffraction. Red crystal. Yield: 75%. Anal. calcd. for C42H50Cu2I2N2S4 C, 46.19; H, 4.62; N, 2.57; S, 11.75. Found: C, 46.08; H, 4.57; N, 2.49; S, 11.64. IR-ATR: ν(C=C) 1596, ν(C=N) 1514 cm−1; 1H NMR: δ/ppm 1.17 (d, 3J = 6.7 Hz, 12H, 4CH3), 1.34 (d, 3J = 6.7 Hz, 12H, 4CH3), 3.25 (sept, 3J = 6.7 Hz, 2H, SCH), 3.73 (sept, 3J = 6.7 Hz, 2H, SCH), 7.14–7.42 (m, 16Har + 2HC=C), 7.69 (d, 3J = 7.5 Hz, 4Har); 13C{1H} NMR: δ/ppm 22.8 (s, CH3), 23.0 (s, CH3), 37.9 (s, SCH), 38.6 (s, SCH), 128.2-132.4 (9s, Car + C=CH), 136.6 (s, C=CH), 139.2 (s, C=N). UV–vis: 231 (62,000), 259 (60,300), 373 (43,800), 498 sh (4500).

2.1. Apparatus

Infrared spectra were obtained with a Shimadzu IR affinity-1 spectrometer using the ATR technique (germanium crystal). UV–vis spectra were measured with a VARIAN-Cary 100 spectrophotometer in CH2Cl2 at room temperature. The 1H, 13C{1H} NMR spectra were recorded with a Bruke Avance 400 HD spectrometer operating at 400 and 100 MHz, respectively. The Supplemental Materials contain samples of 1H, 13C-NMR and IR spectra of the products (Figures S8–S12).

2.2. X-ray Diffraction

X-ray diffraction intensities were measured on Oxford Xcalibur (1), Nonius KappaCCD (2) and Stoe IPDS (3) diffractometers. The unit cell refinements, data reductions and scale corrections were performed using CrysAlis CCD (Oxford Diffraction, 2012, Rigaku, Tokyo, Japan), CrysAlis RED (Oxford Diffraction, 2012) and “Integrate” in IDPS (Stoe & Cie, 1999, Darmstadt, Germany) for 1 and 3 and DENZO and SCALEPACK [25] for 2. The structures were solved either with SHELXS [26] (for 1 and 3) or with SIR92 [27] (for 2). Multi-scan absorption correction (CrysAlis PRO; Oxford Diffraction, 2012) was applied for 1 and the empirical RefDelF [28], FACEIT in IPDS (Stoe & Cie, 1999) and DIFABS [29] for 3 and 2. The models were refined via least squares with SHELXL [30]. Olex2 (Durham, England) was used as a graphical interface [31].
In all three structures, the nonhydrogen atoms, except those of CH2Cl2 solvent molecule in 2, were refined with anisotropic thermal parameters. Solvent molecules were refined in the isotropic model. All H atoms were placed in calculated positions and treated in a riding model. C-H distances were set to 0.95 Å (aromatic) and 0.98 Å (methyl) with Uiso(H) = xUeq(C), where x = 1.5 for idealized methyls refined as rotating groups and 1.2 for all C-H groups.
Highly disordered CH2Cl2 solvent molecules are present in the structure of 2. They are placed close to the screw axes 21 (x, 0.25, 0.5) and 21 (x, 0.75, 0) running along the X direction of the crystal (see Figure S5 in SI), which renders their modeling difficult. This structure was refined as a 2-component inversion twin with site occupancies refined to 0.65(1) and 0.35(1). There is also a slight disorder of the iodine atom in the structure of 3. The site occupancies were refined to 0.93 and 0.07. Crystal data, data collection and structure refinement details are summarized in Table 1.
Crystallographic data were deposited with the Cambridge Crystallographic Data Centre: deposition numbers CCDC 941423 (1), 941424 (2) and 941425 (3) contain detailed crystallographic data for this publication. These data may be obtained free of charge from the Cambridge Crystallographic Data Centre through www.ccdc.cam.ac.uk/data_request/cif (accessed on 21 December 2023).

2.3. Computational Studies

The wave functions for AIM topological analyses were calculated with the Gaussian 09 package [32] with the hybrid B3LYP functional [33,34]. The 6-31G(d,p) standard basis set was applied for all but the iodine and metallic atoms. Since the AIM theory should preferentially use the whole electron and not the ECP (effective core potential) basis sets, the high-quality 6-311G(d,p) basis set was applied for iodine [35], and the double zeta polarized DZP-DKH basis sets of Jörge for Cd and Hg atoms [36,37]. Because we were interested in comparative interpretation of metric parameters found in the structures, these calculations were performed on the molecular geometries really present in the crystal structures of 1 and 2. It is notable, however, that attempts to optimize the geometries even with an ECP basis set like LANL2DZ failed, probably because of the flatness of potential energy surfaces. Topological parameters were calculated using the AIM2000 and AIMALL packages [38,39]. GausSum [40] was used for analysis of the TD-DFT files. The calculations were performed either at the Centre of Calculations of the University of Burgundy or on the local PC with GW09-W [32].

3. Results and Discussion

3.1. Synthesis of the CdI2, HgI2 and CuI Adduct Complexes

The synthesis of cadmium and mercury complexes of the types [MI2{(iPrS)2C=C(H)-N=CPh2}] (1) and (2) was carried out via reacting solutions of the CdI2 or HgI2 salts in ethanol in the presence of ligand L under reflux (Scheme 1).
Pure air-stable complexes 1 and 2 were obtained in the form of yellow crystals after evaporation of the solvent and recrystallization from a methanol/chloroform mixture with yields of 48 and 55%, respectively. According to elemental analysis, one L molecule is attached per MI2 motif (M = Cd or Hg). The IR spectra confirmed the complexation of L on Cd(II) or Hg(II) (Figures S8 and S9); the UV–vis spectra are discussed in more detail below. The 1H and 13C NMR spectra are similar to that recorded for ligand L [9]. Furthermore, two X-ray diffraction studies corroborate the S,N-chelating coordination of L. Upon addition of an equimolar amount of L to a solution of CuI in a mixture of dichloromethane/acetone, the dinuclear compound [LCu(μ2-I2)CuL] (3) was formed straightforwardly and was isolated in the form of deep-red crystals (Scheme 2).

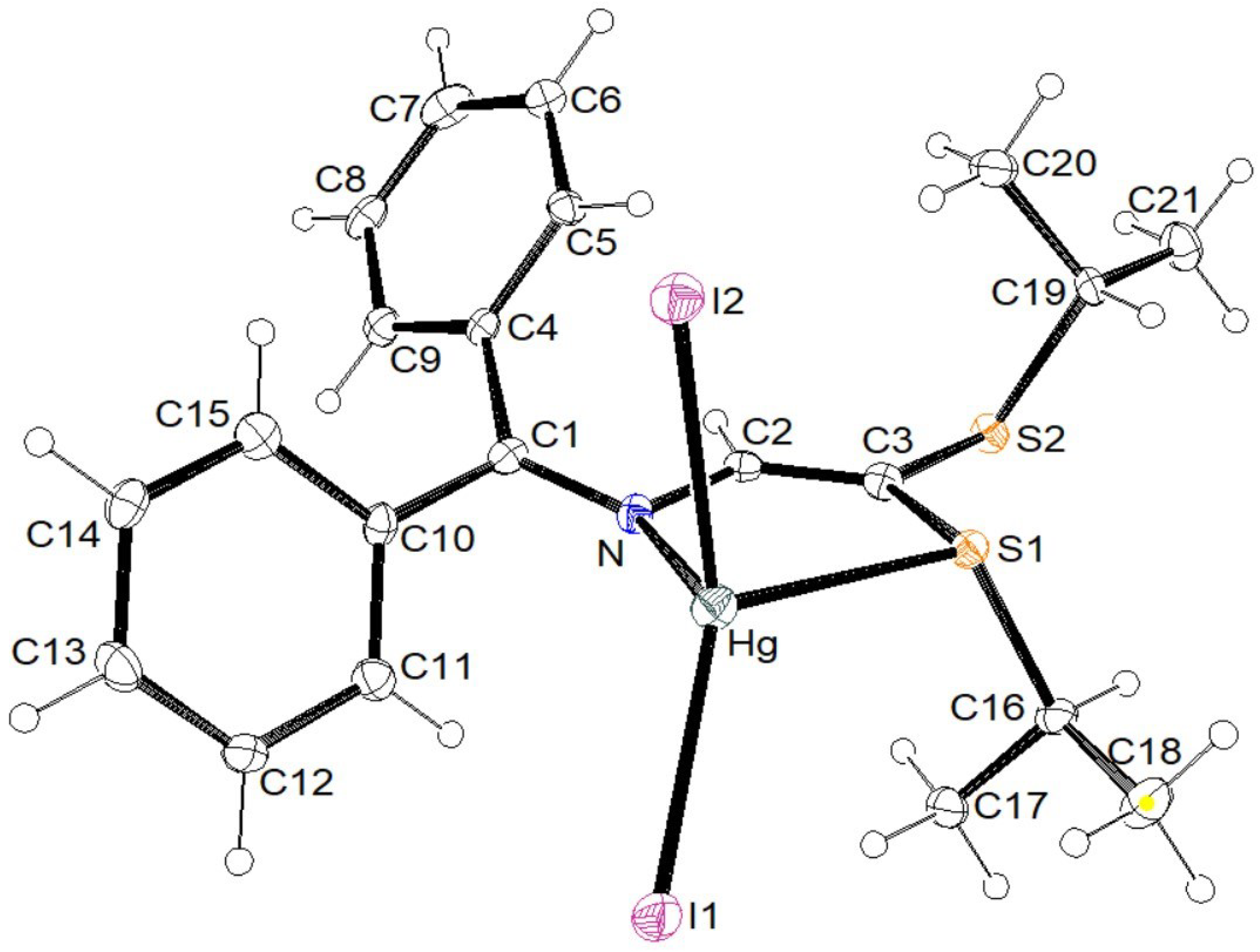
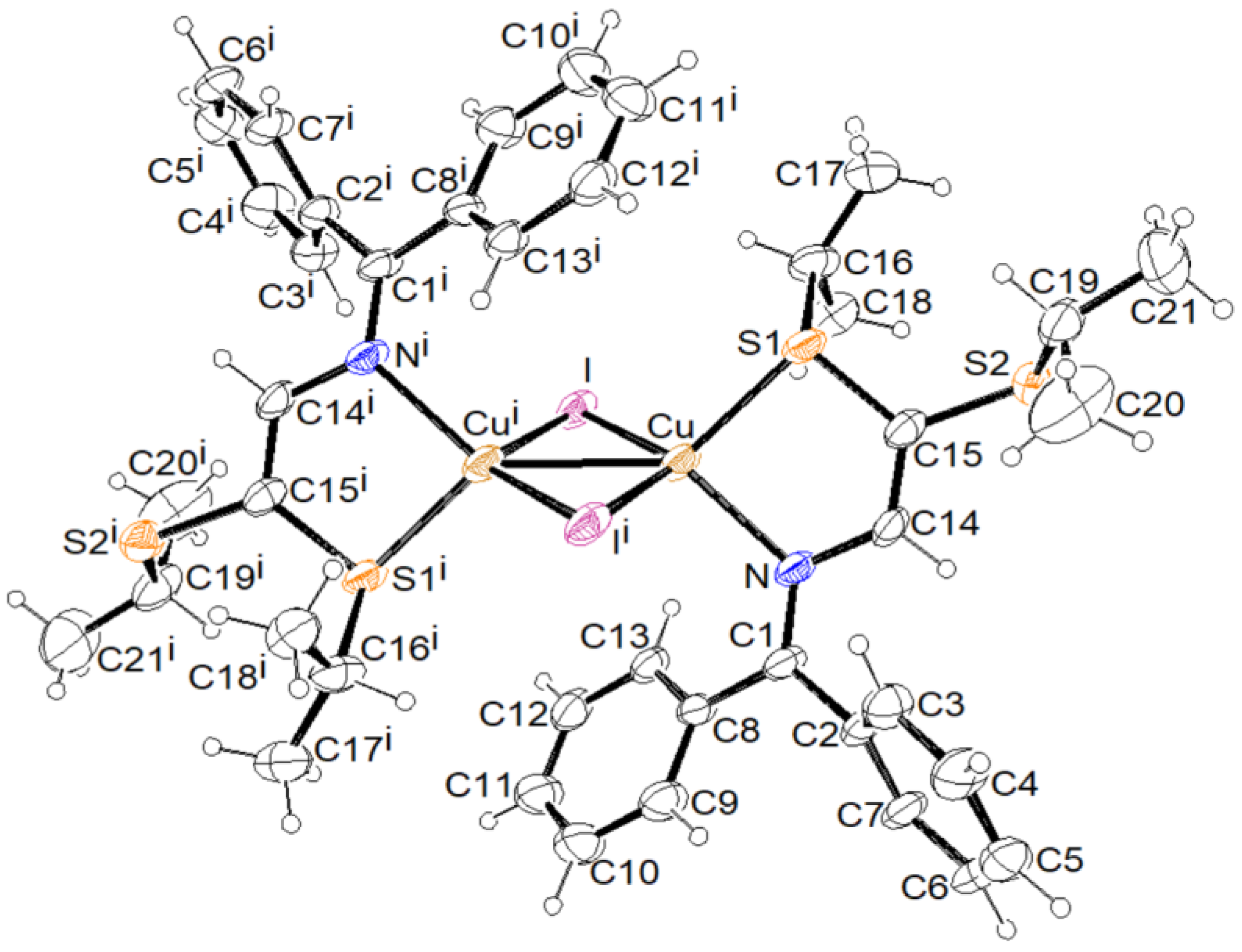
3.2. X-ray Structural Studies

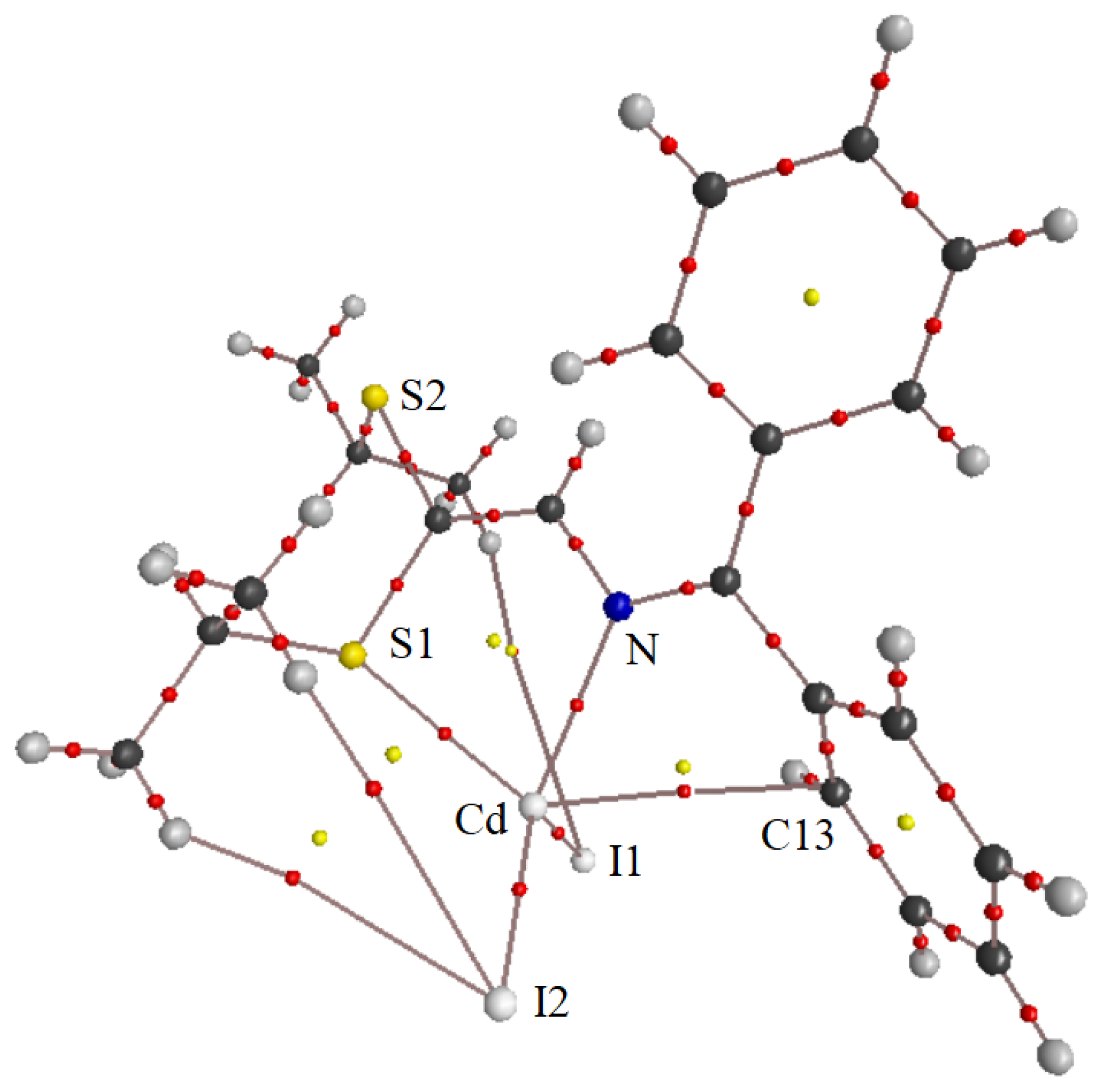
3.2.1. Molecular Structures

The molecular architectures of mononuclear complexes 1 and 2 are depicted in Figure 1 and Figure 2, respectively. They show the presence of two iodides and of S and N coordination sites from the azabutadiene ligand. The metal centers are thus four-coordinated with coordination polyhedra severely distorted from regular tetrahedral geometries. The Cambridge Crystallographic Database (version CSD 5.43, November 2021) contains three entries for four-coordinate HgI2 adducts with N and S coordinating atoms [41,42]. On the other hand, there is no example of a purely four-coordinate CdI2 N,S adduct. Instead, two entries for pentacoordinate complexes are present [43,44]. The CdI2 compound 1 described here thus represents the first four-coordinate complex of CdI2 bearing a N,S donor set.
The five-membered metallacycles M-S-C-C-N are almost planar with the highest deviations from mean planes observed for N atoms, which are equal to 0.14 Å (Cd) and 0.06 Å (Hg). These planes are roughly perpendicular to I-M-I planes with dihedral angles equal to 81.3(1)° (Cd) and 83.4(1)° (Hg).
The values of the four-coordinate geometry index τ4 [45] are 0.83 and 0.71, and those of τ4′ [46] are equal to 0.81 and 0.66 for 1 and 2, respectively. For the Cd complex 1, these values are very close to the theoretical value of 0.83 for a trigonal pyramidal geometry, far from the value of 1 for an ideal tetrahedral coordination sphere. The case of Hg adduct 2 is more complicated. It is common in the crystal chemistry of mercury cations that they easily form covalently bonded linear rods, like, e.g., in the structure of the yellow polymorph of HgI2 [47,48], or in that of cinnabar HgS [49]. We thus turned our attention to the seesaw (disphenoidal) geometry (https://en.wikipedia.org/wiki/Seesaw_molecular_geometry accessed on 21 December 2023). The expected values of the τ4 and τ4′ indexes for bidentate ligands depend on the opening of the bite angle. The τ4 varies from 0.42 (bite angle equal to 120°) to 0.64 (bite angle of 90°) whereas the values of τ4′ vary from 0.24 to 0.36 for the same bite angles. One may conclude that with a bite angle for S-Hg-N equal to 74.5(2)°, the value of (especially) the τ4 index for 2 (0.71) favors the seesaw geometry. The most significant bond lengths and angles are gathered in Table 2. Data for complex 3 are also included therein.
The bond lengths observed for the mercury complex 2 (Hg–Imean = 2.667 Å, Hg–S = 2.689(2) Å, Hg–N = 2.496(7) Å) roughly match the corresponding values found in 1,8-di-2-pyridyl-3,6-dithiaoctane-N,N′,S,S′)-tetraiodo-dimercury(II) of 2.666(1), 2.714(4) and 2.417(9) Å, respectively [41]; in 2,5-dioxa-13,19-dithia-16-azatricyclo[19.4.0.06,11]pentacosa-1(21),6,8,10,22,24-hexaene)-diiodomercury(II) of 2.668(1), 2.710(2) and 2.454(5)Å [42] and in μ2-1,4-bis(2,5-dioxa-13,19-dithia-16-azatricyclo[19.4.0.06,11]pentacosa-1(21),6,8,10,22,24-hexaene)benzene)-tetraiodo-dimercury(II) of 2.695 (mean), 2.625(2) and 2.435(6) Å [42]. The Hg–I distances are longer than in the yellow metastable polymorph of HgI2 built of linear HgI2 rods (mean 2.617(6) Å) and in its yellow high-temperature (414 K) structure containing the bent molecular HgI2 units (mean 2.491 Å). They are, however, shorter than in the most stable red polymorph of HgI2 where the mercury atom has a tetrahedral geometry (2.783(3) Å) [10]. The Cd–I (mean 2.696 Å), Cd–S (2.662(2) Å) and Cd–N (2.321(5) Å) bond lengths observed in 1 apparently show some noncoherent differences when compared with the parameters calculated for 2. The mean length of the Cd I bonds (2.70 Å) is slightly longer than that of the Hg–I ones (2.67 Å), but the Cd–S is slightly shorter (0.04 Å) and the Cd–N is greatly shorter (0.18 Å) than the corresponding distances in 2. In order to understand these features, we appeal to the hard/soft acid/base theory of interatomic interactions (HSAB) [50,51,52]. The Cd atom is harder than the Hg one and the softness of donor atoms decreases from iodide to sulfur, and nitrogen is considered as a hard site. Moreover, one easily assumes that in a hard–hard couple the bond has an ionic nature while in a soft–soft combination the bond is covalent. Consequently, the Hg–I bond should have the highest covalency, whereas Cd–N is expected to be an ionic bond. We look now on the covalent and ionic radii of the metals. In four-coordinated environments, the ionic radius of Cd2+ (0.78 Å) is smaller by 0.18 Å than that of Hg2+ (0.96 Å) [53]. On the other hand, a recent compilation of covalent radii derived from those of C, N and O atoms gives, because of lanthanide contraction, the opposite values: 1.44 Å for Cd against 1.32 Å for Hg [54]. Thus, in light of these values of ionic and covalent radii and the expected nature of bonding discussed above, the observed bond lengths are not surprising.
The dinuclear framework of 3 was ascertained via an X-ray diffraction study. The molecular structure is shown in Figure 3 and consists of a centrosymmetric Cu(μ2-I2)Cu core, in which the Cu centers are in a close contact of only 2.672(2) Å, considerably below the sum of the van der Waals radii of two Cu atoms (2.8 Å). There is a slight disorder of the bridging iodine atom that splits in two sites with occupancies equal to 0.93 and 0.07. Rhomboid dimers of the type [L2Cu(μ2-I2)CuL2] (L = N, S), SNCu2I2SN, have been extensively investigated in the past by us and other research groups. A literature survey indicates that the Cu⋯Cu separations vary significantly in the molecular Cu2I2 compound and SBUs in coordination polymers, underpinning the structural flexibility of this motif. In the majority of cases of this type of dimers, the Cu⋯Cu distance comprises between 2.55 Å and 2.70 Å (CSD version 5.44, April 2023). The shortest value of 2.4641(16) Å, which is even shorter than the Cu⋯Cu distance of 2.56 Å in metallic copper, has been reported for tetrakis(µ2-iodo)-bis(µ2-4,6-bis((pyrid-2-ylmethyl)sulfanylmethyl)dibenzo(b,d)furan)-tetracopper(I) [55,56]. Other examples of short Cu⋯Cu distances close to that of 3 are observed in [Cu2I2(THT)4] (THT = tetrahydrothiophene) and the dithioether-functionalized tetrathiafulvalene complex [(ttf)Cu(l-I)2 Cu(ttf)] with metal–metal separations of 2.675(2) and 2.6469(15) Å [57,58].
Conversely, a much longer Cu⋯Cu separation of 3.18 Å has been reported for [Cu2I2(dtpcp)2] • THF (dtpcp = 2,11-dithia[3.3]paracyclophane) [59], but it may reach up to 3.243 Å in [CuI(mbix)]n (mbix = 1,3-bis(imidazole-1-yl-methyl)benzene) [60,61]. This wide range of experimentally observed Cu⋯Cu separations in dinuclear Cu2I2 units indicates a certain degree of structural flexibility.
Considering only the iodide atoms (I and Ii) of the major site of occupancy 0.93 and neglecting the Cu⋯Cu interaction, the value of the four-coordinate geometry index τ4 [45] is equal to 0.81 and consequently the coordination polyhedron around the Cu atom may be considered, like for the Cd atom in 1, as a trigonal pyramid. The five-membered metallacycle Cu-S1-C14-C15-N is almost planar, with the highest deviation from the mean plane (0.06 Å) observed for the C15 atom. This plane is roughly perpendicular to the I–Cu–Ii plane, with a dihedral angle of 99.9°.
All Cu–ligand distances in 3 are shorter than the metal–ligand bonds in 1 and 2 (Table 2). This is an expected feature because even if the covalent radius of Cu is equal, like that of Hg, to 1.32 Å [54], the ionic one of 0.60 Å is much smaller [55]. The Cu–N bond length of 2.143(5) Å is shorter by 0.18 Å than the Cd–N one and by 0.36 Å than the Hg–N bond. These differences exactly match the differences in ionic radii of the central cations, and it may be concluded from that the ionic nature is dominant for M–N bonds. In the case of M–S bonds, a difference of 0.36 Å is also observed between Cu–S and Hg–S bonds, but the Cd–S bond does not follow the trend. The differences in M–I bond lengths are still smaller, confirming the more covalent nature of these bonds.

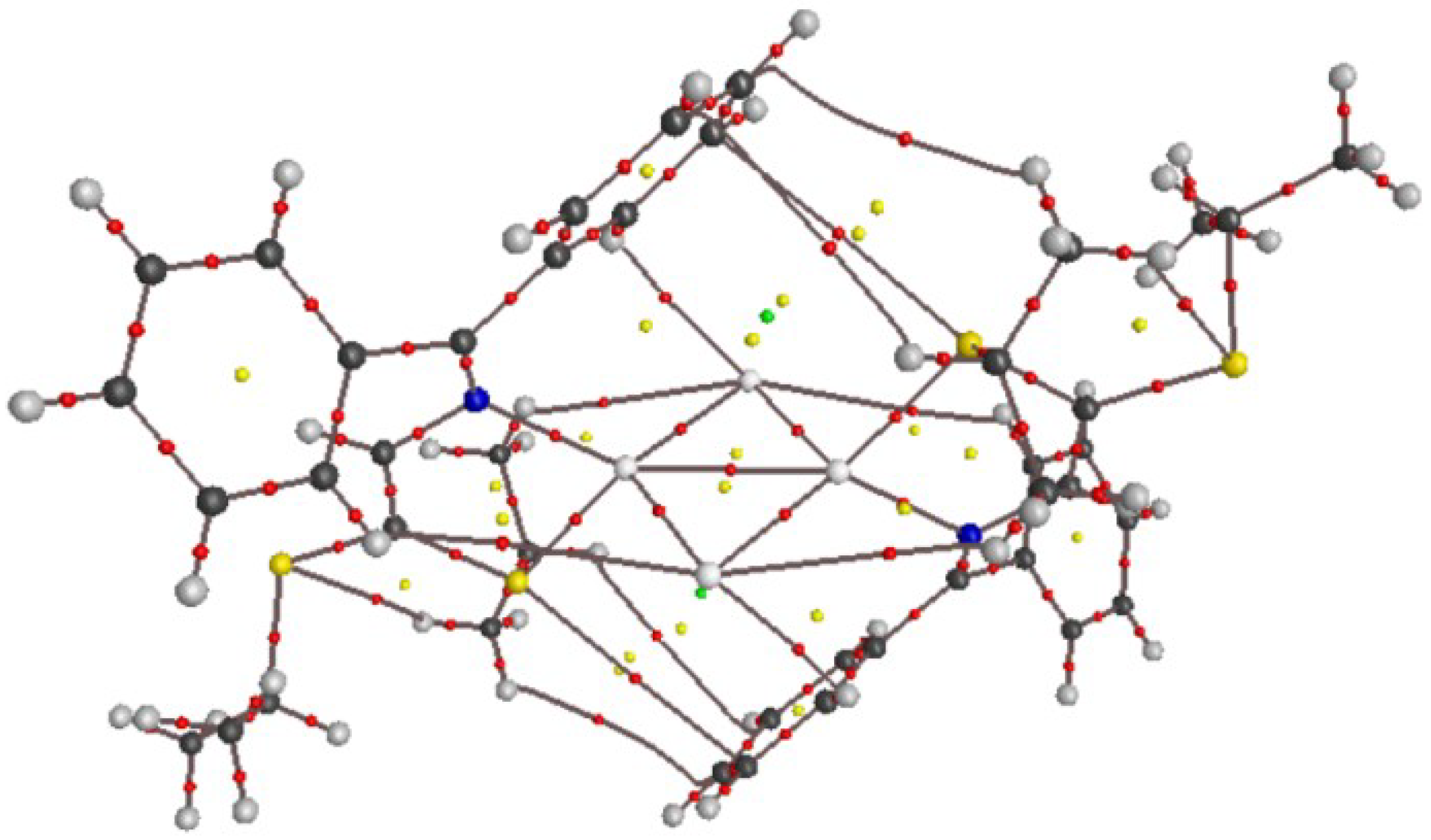
3.2.2. Crystal Structures and Supramolecular Features

Compounds 1 and 2 crystallize in the non-centrosymmetric monoclinic polar P21 (1) and orthorhombic P212121 (2) space groups, respectively, whereas the copper adduct 3 crystallizes in the centrosymmetric triclinic P 1 ¯ space group. Their structures are built of coordination molecular MI2L adducts for 1 and 2 and of (CuIL)2 dimers for 3. Highly disordered solvent CH2Cl2 molecules are present in the crystals of 2.
The complexes in the crystal lattices are connected by very week noncovalent interactions responsible for the stability of the structures. In the structure of 1, these interactions are of the type CH⋯π between the phenyl groups of neighboring molecules (Figure S1 in the Supporting Material) and of the π⋯π type, which concerns a kind of stacking between phenyl rings through the C9⋯C12 contacts at the limit of the van der Waals radii (3.39 Å, contraction by 0.01 Å). They are shown in Figure S2. The noncovalent interactions in the structure of 2 are also very weak. The sole contact shorter than the sum of the van der Waals radii between complex molecules concerns the CH⋯π interactions of hydrogen (H21B) atoms of iPr substituent with carbon (C1) atoms of azabutadiene linkage (2.86 Å, shortening by 0.04 Å) (Figure S5). They form the 1D chains connected through the CH (iPr)⋯Cl (solvent) interactions.
The system of weak noncovalent interactions in 3 is also poor and limited to the C-H⋯I kind of hydrogen bonds with I⋯H distances at the limit of the sum of the van der Waals radii. They consist of I⋯H7 (3.221 Å), which form the chains parallel to the 0a [1 0 0] direction of the unit cell (Figure S6) and I⋯H17C (3.271 Å) parallel to the 0b [0 1 0] direction (Figure S7).

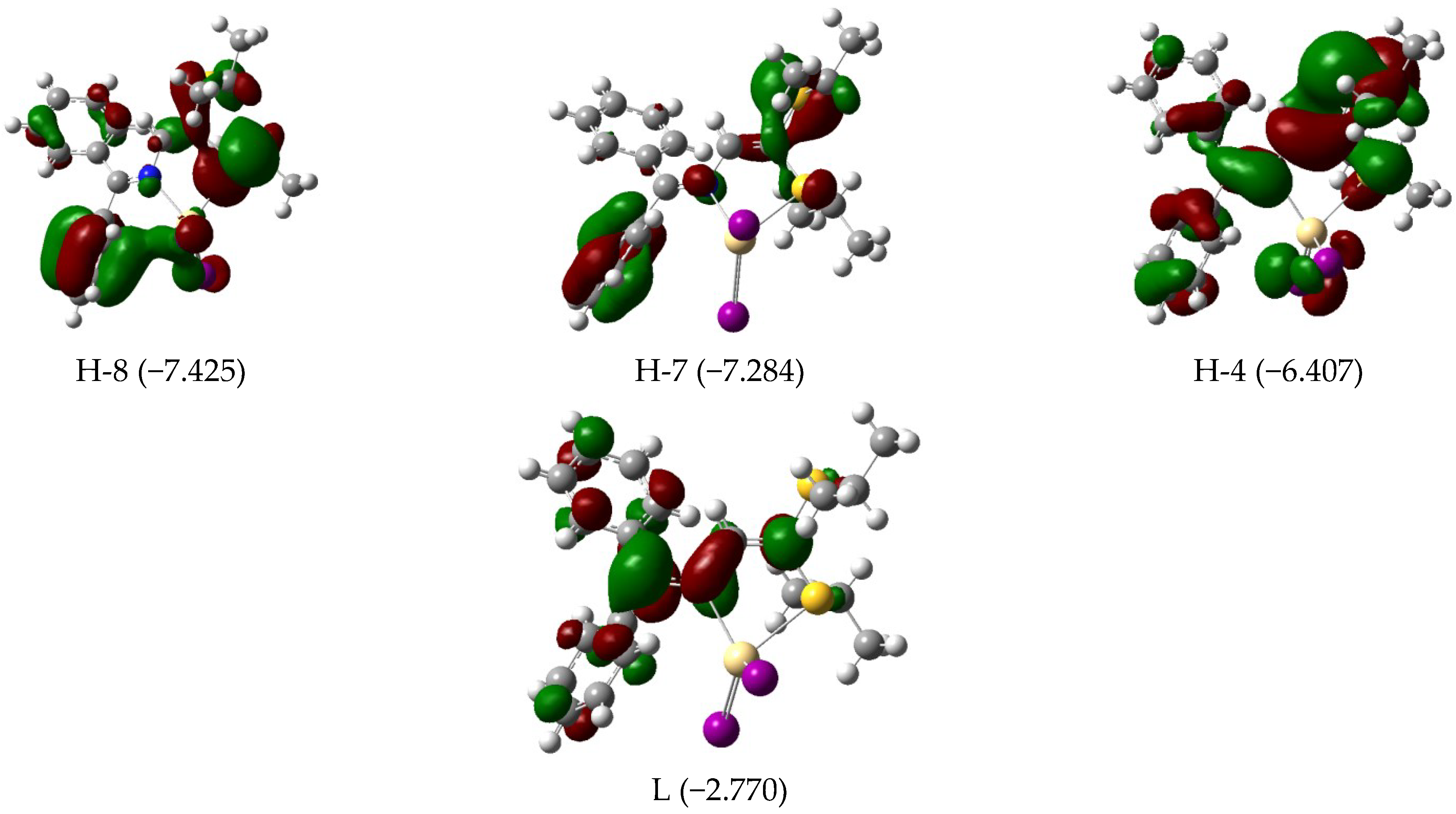
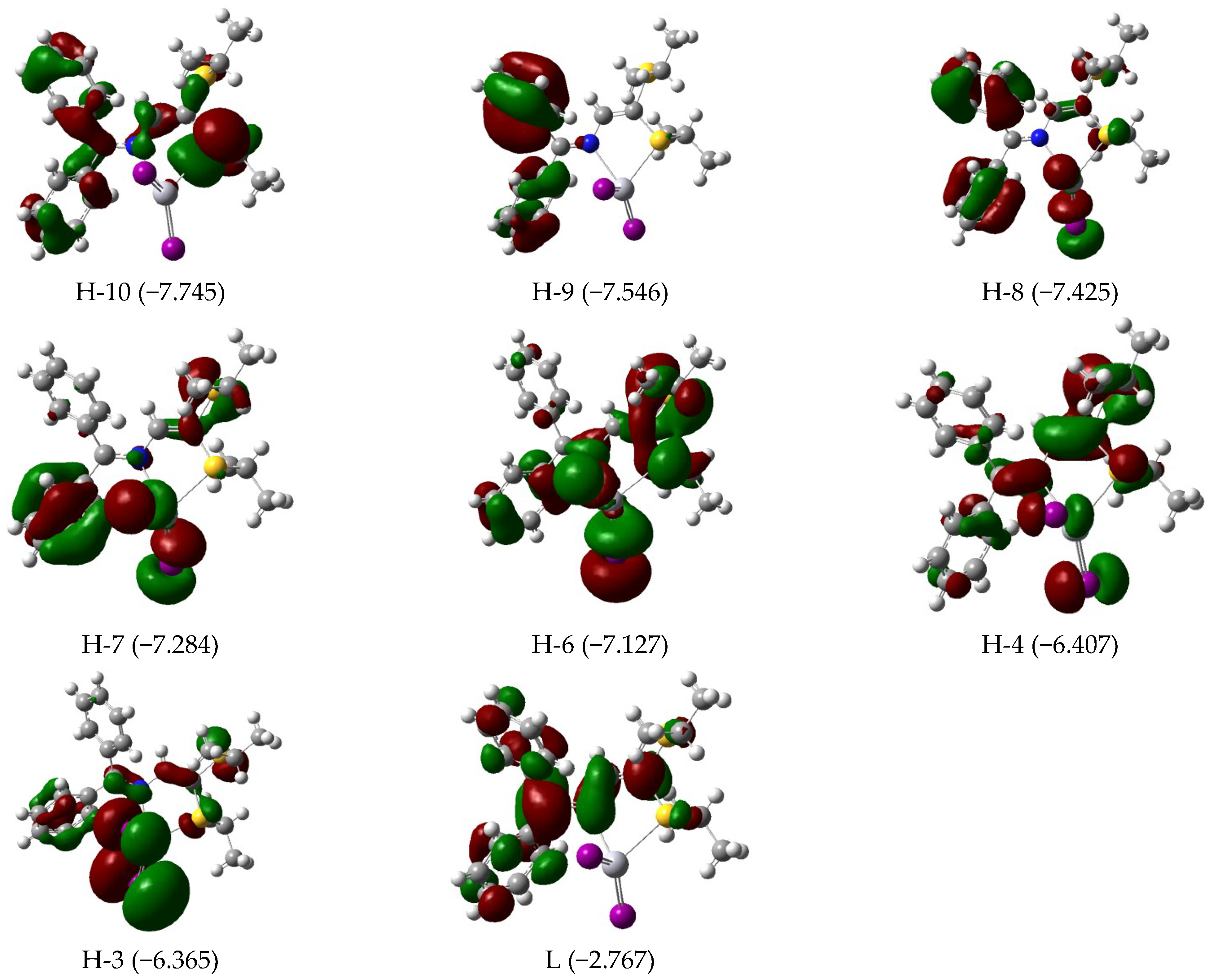
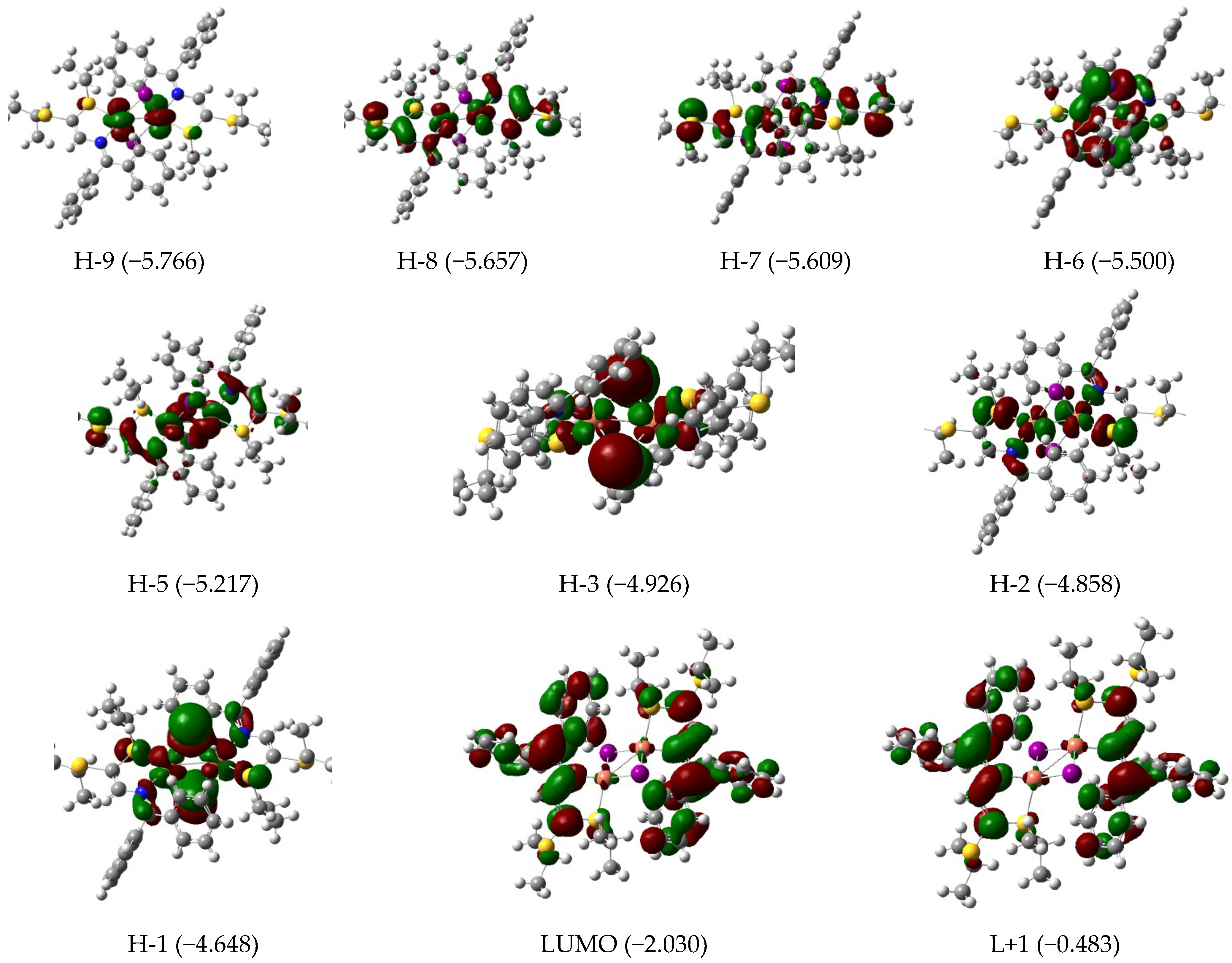
3.3. Electronic Features and AIM Approach

The UV–vis absorption spectra of 1 and 2 exhibit two intense bands in the UV region close to 380 nm and 255 nm, respectively, and in the case of Cd complex 2 a weak additional shoulder near 300–325 nm (Figure 4 (top)).
The theoretical UV–vis spectra (Figure 4 (bottom)) were generated using time-dependent DFT calculations. The spectrum calculated for Cd complex 1 matches well with the experimental one, whereas in the case of Hg complex 2, the calculated shoulder of 1 becomes a band which is not detectable in the experimental spectrum. The TD-DFT results allow recognition of the nature of experimental transitions in 1 and 2. They are summarized in Table 3.
The target molecular orbital (MO) in all calculated transitions for 1 and 2 is the LUMO one. The low-energy band in both spectra (close to 390 nm) is generated by HOMO-4 with the contribution of HOMO-3 in 2. The shoulder in complex 1 is composed of four weak transitions from HOMO-7 to HOMO-11 and the corresponding band in 2 contains the transitions from H-6 to H-9, which have similar shapes. The high-energy band calculated near 280 nm originates from the mixing of H-11 and H-10 for 1 and from H-10 for 2. The molecular orbitals involved in these transitions are depicted in Figure 5 and Figure 6. The LUMO corresponds principally to the LUMO π molecular orbital of 2-azabutadiene molecule delocalized over lateral C atoms and the central C-N bond (Figure 7) [7], whereas the HOMO-4 exhibits alternating π lobes from one phenyl ring through the azabutadiene array to sulfur atoms. The azabutadiene molecule introduces into this H-4 MO its HOMO π MO covering the C=N and C=C bonds. It is worth noting that the four highest occupied MOs (HOMO to HOMO-3) in both complexes 1 and 2 are formed in more than 90% by contributions of the p atomic orbitals of iodine atoms.
As a reference, the frontier MOs of 4-dichloro-2-aza-butadiene are presented as Figure S13 in the Supporting Material [7].
According to the shapes of these MOs, the low-energy band in 1 and 2 is assigned mainly to the π–π intra-ligand transition localized on the C=N-C=C linkage. The high-energy band contains, besides small contributions stemming from the azabutadiene chain, also those from the phenyl rings. For the shoulder in 1 or the intermediate energy band in 2, the main contributions stem from the phenyl rings and MI2 unit. Selected MOs for complex 3 are presented in Figure 7.
The calculations show that in complex 3, the low-energy large band near 560 nm, responsible for its red color, is due to the transitions from the H-1, H-2 and H-3 molecular orbitals that have contributions from the Cu2I2 ring towards the LUMO and LUMO+1 corresponding to the π system of the ligand L. The metallic orbitals (H-9) also contribute to the strong high-energy transition at 380 nm together with the π orbitals of L (H-7 and H-8), giving rise to the mixing of the M-L charge transfer and π–π transitions.
In order to confirm our conclusions concerning the nature of bonding, we calculated the wave functions on complex molecules present in the structures of 1, 2 and 3. They were further used in the QT-AIM analysis (quantum theory of atoms in molecules) developed by Bader [60,62]. We recall briefly the main features of this theory. A topological analysis of electron density is a powerful tool for the study of different weak interatomic interactions (hydrogen bonding [63], van der Waals, σ–π and π–π [64,65,66]) as well as for studying the nature of metal–metal [67,68,69] and metal–ligand [69,70] interactions in addition to the classic case of covalent bonds. Various topological properties at bond critical points (BCPs defined with (rank, signature) code (3,−1)) are used for these purposes [44,46]. These topological parameters include principally the electron charge density (ρ, e−/a03), the Laplacian of electron density (∇2ρ, e−/a05), the local kinetic, potential and total energy densities (G, V and H, Ha/a03) and the derived quantities like the bond degree (H/ρ, Ha/e−) and a dimensionless ratio |V|/G at the BCP [60,61,62,63]. The potential energy density V (always negative) is related to the covalent contribution to the bond, whereas the kinetic G (always positive) one is related to its ionic part. Thus, the total energy density H (sum of potential and kinetic contributions) is negative for predominantly covalent bonds, while the positive value of H indicates the ionic or weak noncovalent nature of the bond. The integrations of electron density over atomic basins allow, among other properties, the calculations of delocalization indexes (DIA-B) that indicate the number of electron pairs localized between atoms A and B and are thus roughly related to the bond orders. Similar information may be obtained from Wiberg bond indexes calculated in the frame of natural bond orbitals (NBOs) [71].
QT-AIM classifies the chemical interacting systems into three main types depending on the values of the parameters mentioned above. These are the following:
  • 1—shared–shared (SS), covalent, (∇2ρ < 0, H < 0 and |V|/G > 2;
  • 2—shared–closed (SC), transit or intermediate, (∇2ρ > 0, H < 0 and 1< |V|/G < 2;
  • 3—closed–closed (CC), ionic, van der Waals…, (∇2ρ> 0, H > 0 and |V|/G < 1.
The molecular graphs built on bond paths for 1 and 2 are shown in Figure 8 and Figure 9 and the topological parameters calculated on geometries found in the crystal structures of 1 and 2 are gathered in Table 4. The Wiberg bond indexes are also included in this table.
The molecular graph of complex 1 (Figure 8) shows the presence of four expected bond paths of Cd with I, S and N atoms, the intramolecular C–H⋯I hydrogen bonds and an additional bonding interaction of the central Cd atom with the π system of one phenyl ring via the Cd–C13 bond path. The presence of this BCP indicates a favorable distribution of electron density for attractive interaction in this region of the molecule. It is worth noting that the H-9 molecular orbital of complex 1 depicted in Figure 5 also exhibits a favorable overlap of electron density for this interaction. This observation may also suggest a tendency of the Cd atom to extend its coordination sphere, thus explaining the lack of purely four-coordinated CdI2 adducts with S,N ligands in CCDC.
The molecular graph of complex 2 (Figure 9) exhibits the expected four Hg–ligand bond paths as well as the intramolecular C–H⋯I hydrogen bonds.
Inspection of the data in Table 4 provides a significant amount of information about the nature of the metal–ligand bonds. The parameters calculated for complexes 1 and 2 are discussed first. All values of the Laplacian of electron density ∇2ρ are positive, which means that no bond around the metals is shared–shared (purely covalent). The values of total energy densities H confirm the suggestions derived from HSAB considerations. They increase in the order I < S < N (order of increasing hardness) and are more negative for Hg than for Cd (higher covalency/softness of Hg). All M–I bonds have negative total energy densities and are thus typical coordination bonds. This is also true for the Hg–S bond, but there is an ambiguity concerning the Cd–S one since the total energy density H for this bond is slightly positive (see Table 4). One may consider this bond as being at the limit of covalent contribution. The Hg–N bond remains a coordination bond; however, the Cd–N bond lost its covalency and falls within the closed–closed region. It may thus be considered as an ionic bond. The derived values of |V|/G confirm in a similar manner the conclusions of the above discussion. The bonding between Cd–I, Hg–I, Hg–S and Hg–N can be considered as coordination bonds, but the Cd–S and Cd–N bonds have an ionic character.
One may argue that the higher values of ρ at BCP are not a sufficient criterion, allowing us to conclude that (i) higher ρ means a stronger bond in interactions involving atoms with a different number of electron shells, as is the case here (Cu vs. Cd vs. Hg and I vs. S vs. N), and that (ii) a more adequate quantity for making comparisons in that case is the pressure of total energy density per electron or bond degree H/ρ. Data gathered in Table 3 indicate that the H/ρ values are more negative (higher covalency and probably higher strengths) for Hg–ligand than for Cd–ligand bonds.
All calculated delocalization indexes DIcalc of bonds involving metal and ligands are surprisingly higher for Cd than for Hg bonds. Moreover, the sum of these indexes is equal to 2.283 for Cd but only to 1.620 for Hg, which is significantly different from the expected values, which are close to 2. An attempted explanation of these unexpected features may reside in some weaknesses or imperfections of all electron basis sets DKH-DZP applied in calculations for the heavy metals. After corrections introduced via normalization of the calculated indexes to 2 (sum of expected bond orders), the normalized ones, DInorm, agree with the precedent discussions, showing that all but the M–N bonds are stronger with mercury than with Cd. A similar situation is observed for the Wiberg bond indexes, which were calculated with the same basis sets.
The weak noncovalent Cd⋯phenyl bond path detected in the molecular graph of complex 1 (Figure 8) has all the properties of the closed–closed system and may be classified by analogy with C-H⋯π interactions as a metal⋯π path.
It is interesting now to compare the topological parameters calculated for dinuclear complex 3, in which the iodine atoms are bridging, with those of the mononuclear complexes 1 and 2, in which the iodides are terminal. It is generally accepted in crystal chemistry that the bridging bonds are weaker than the terminal ones, but the Cu–S and Cu–N bonds and above all the influence of the relative hardness of Cu(I) with respect to Cd(II) and Hg(II) on the AIM parameters reported in Table 4 warrant discussion. Parr and Pearson reported the following values of hardness for the cations employed in this study: 10.3 eV (Cd2+), 7.7 eV (Hg2+) and 6.3 eV (Cu+) [72,73]. Following their classification, Cu+ is slightly softer than Hg2+ and Cd2+ is the hardest one among these three soft cations. The molecular graph of complex 3 is presented in Figure 10.
Like in 1 and 2, all Laplacians (∇2ρ) at the BCP of the Cu–ligand bonds in 3 are positive. The total energy densities H are negative, except in the case of Cu–N which belongs, like Cd–S and Cd–N bonds, to a closed–closed ionic system. The values of H also indicate that the covalency of Cu–I bonds (H2 < H3 < H1) is intermediate between those of Hg–I and Cd–I, and the covalency of the Cu–S bond (H3 < H2 < H1) is slightly higher than that of the Hg–S bond, both being significantly higher than the total energy of the Cd–S bond. This last observation may be related to the known affinity of Hg(II) and Cu(I) towards the sulfur coordination sites. The values of |V|/G agree with the trends deduced from the values of H. The delocalization indexes DI confirm the weaker Cu–I bridging bonds compared with the terminal Hg–I and Cd–I ones. These DI indexes also indicate that the Cu–S and Hg–S bonds are stronger than the Cd–S one. The topological properties of the Cu–Cu BCP fall well into the shared/closed system and are typical of metal–metal bonds [51,52].

4. Conclusions

The two apparently similar MI2-azabutadiene (M = Cd, Hg) and CuI-azabutadiene adducts described in this article are four-coordinated around the metallic centers. Their coordination polyhedra are severely distorted from tetrahedral geometry. The geometry indexes τ indicate that a trigonal pyramid better describes the coordination sphere of the Cd atom in complex 1 and of Cu in complex 3, but a seesaw geometry seems to be the most adequate for the Hg atom in complex 2. The observed bond lengths around the Cd and Hg centers were discussed first on the basis of the HSAB theory considering the hardness/softness of each atom involved therein and of the covalent and ionic radii of the metals. The most covalent nature is expected for Hg–I and Cu–I bonds, whereas the most ionic should be the Cd–N bond. These hypotheses were further confirmed via AIM topological analyses of electron densities.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/chemistry6010004/s1, Figure S1: CH⋯π (phenyl⋯phenyl) interactions in 1; Figure S2: Two chains running along the screw axes connected through π⋯π interactions in the structure of 1; Figure S3: π⋯π chain running along 21 (½, y, 0) in the structure of 1; Figure S4: Two chains running along the screw axes 21 at (1, y, 0) and at (0, y, 1) related through the screw 21 at (½, y, ½) in the structure of 1; Figure S5: Three 1D channels running down the twofold screw axes 21(x, ¼, 0; x, 3/4, ½; x, ¼, 1) formed by intermolecular interactions in the structure of 2; Figures S6 and S7: I⋯H interactions occurring in the structure of 3; Figures S8–S10: IR-ATR spectrum of complexes 1, 2 and 3; Figures S11 and S12: NMR spectra (CDCl3) of complex 3; Figure S13: Recall of the frontier MOs of 4-dichloro-2-aza-butadiene.

Author Contributions

R.K. and A.K. prepared and analyzed the complexes; M.M.K. and C.S. collected the X-ray data and solved the structures; M.M.K. performed the quantum (molecular orbitals and AIM) calculations; M.M.K. and M.K. designed the study, analyzed the data and wrote the paper; A.K., M.M.K. and M.K. contributed to the conceptualization. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article and supplementary materials.

Acknowledgments

M.M.K. acknowledges Y. Rousselin (ICMUB, University of Burgundy) for his help in the modeling of the disorder of CH2Cl2 solvent molecules in the structure of 2. Annika Schmitt (Universität Dortmund) is acknowledged for her contribution to the final refinement of the structure of 3. Quantum calculations were performed using HPC resources from DNUM CCUB (Centre de Calcul de l’Université de Bourgogne).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Coleman, A.; Brennan, C.; Vos, J.G.; Pryce, M.T. Photophysical properties and applications of Re(I) and Re(I)–Ru(II) carbonylpolypyridyl complexes. Coord. Chem. Rev. 2008, 252, 2585–2595. [Google Scholar] [CrossRef]
  2. Raghavana, A.; Venugopal, A. Review: Structurally characterized α-diimine complexes of s- and p-block elements. J. Coord. Chem. 2014, 67, 2530–2549. [Google Scholar] [CrossRef]
  3. Zhang, R.; Wang, Y.; Zhao, Y.; Redshaw, C.; Fedushkin, I.L.; Wu, B.; Yang, X.-J. Main-group metal complexes of α-diimine ligands: Structure, bonding and reactivity. Dalton Trans. 2021, 50, 13634–13650. [Google Scholar] [CrossRef] [PubMed]
  4. Knorr, M.; Schmitt, G.; Kubicki, M.M.; Vigier, E. Formation of (σ-alkenyl)- and (μ-vinylidene)palladium and -platinum complexes by oxidative addition of 4,4-dichloro-1,1-diphenyl-2-azabuta-1,3-diene—The molecular structure of an unusual asymmetric (μ-vinylidene)Pd-Pd complex. Eur. J. Inorg. Chem. 2003, 2003, 514–517. [Google Scholar] [CrossRef]
  5. Jacquot, S.; Belaissaoui, A.; Schmitt, G.; Laude, B.; Kubicki, M.M.; Blacque, O. Reaction of diphenyldiazomethane with N-methyloxy- and N-ethyloxycarbonyl-N-(2,2,2-trichloroethylidene)amines. Eur. J. Org. Chem. 1999, 1999, 1541–1544. [Google Scholar] [CrossRef]
  6. Jacquot, S.; Schmitt, G.; Laude, B.; Kubicki, M.M.; Blacque, O. Nucleophilic additions of sodium alkoxides to 4,4-dichloro-1,1-diphenyl- 2-azabuta-1,3-diene. Eur. J. Org. Chem. 2000, 2000, 1235–1239. [Google Scholar] [CrossRef]
  7. Jacquot-Rousseau, S.; Schmitt, G.; Khatyr, A.; Knorr, M.; Kubicki, M.M.; Vigier, E.; Blacque, O. Reactivity of 4,4-Dichloro-1,1-diphenyl-2-azabutadiene Towards Alkoxides and Thiolates: Synthesis of Functionalised π-Conjugated 2-Azabutadienes and Unexpected 1,4-Thiazine Formation. Eur. J. Org. Chem. 2006, 2006, 1555–1562. [Google Scholar] [CrossRef]
  8. Kinghat, R.; Boudiba, H.; Khatyr, A.; Knorr, M.; Kubicki, M.M. 4,4-Bis(4-methylphenylsulfanyl)-1,1-diphenyl-2-azabuta-1,3-diene. Acta Cryst. 2008, E64, o370. [Google Scholar] [CrossRef]
  9. Kinghat, R.; Schmitt, G.; Ciamala, K.; Khatyr, A.; Knorr, M.; Jacquot-Rousseau, S.; Rousselin, Y.; Kubicki, M.M. 1,3-Dipolar cycloaddition of diaryldiazomethanes across N-ethoxy-carbonyl-N-(2,2,2-trichloroethylidene)amine and reactivity of the resulting 2-azabutadienes towards thiolates and cyclic amides. Comptes Rendus Chim. 2016, 19, 320–332. [Google Scholar] [CrossRef]
  10. Jacquot-Rousseau, S.; Khatyr, A.; Schmitt, G.; Knorr, M.; Kubicki, M.M.; Blacque, O. Synthesis and reactivity of an 2-azabutadiene-based π-conjugated dithioether: Formation of a N,S-ligated molybdenum chelate complex and C,N,S-pincer complexes of palladium and platinum. Inorg. Chem. Commun. 2005, 8, 610–613. [Google Scholar] [CrossRef]
  11. Schlachter, A.; Juvenal, F.; Kinghat Tangou, R.; Khatyr, A.; Guyon, F.; Karsenti, P.L.; Strohmann, C.; Kubicki, M.M.; Rousselin, Y.; Harvey, P.D.; et al. 2-Azabutadiene complexes of rhenium(I): S,N-chelated species with photophysical properties heavily governed by the ligand hidden traits. Dalton Trans. 2021, 50, 2945–2963. [Google Scholar] [CrossRef] [PubMed]
  12. Schramm, V. Crystal and molecular structure of tetrameric copper(I) iodide-piperidine, a complex with a tetrahedral tetrakis[copper(I) iodide] core. Inorg. Chem. 1978, 17, 714–718. [Google Scholar] [CrossRef]
  13. Jasinski, J.P.; Rath, N.P.; Holt, E.M. Structural comparison of (CuICH3CN4·dibenzo-18-crown-6 (I) and (CuICH3CN)x (II) fluorescent copper(I) materials. Inorg. Chim. Acta 1985, 7, 91–97. [Google Scholar] [CrossRef]
  14. Vega, A.; Saillard, J.-Y. Bonding in Tetrahedral Cu4(μ3-X)4L4 Copper(I) Clusters:  A DFT Investigation. Inorg. Chem. 2004, 43, 4012–4018. [Google Scholar] [CrossRef] [PubMed]
  15. Harvey, P.D.; Knorr, M. Luminescent Coordination Polymers Built Upon Cu4X4 (X = Br,I) Clusters and Mono- and Dithioethers. Macromol. Rapid Commun. 2010, 31, 808–826. [Google Scholar] [CrossRef] [PubMed]
  16. Kitagawa, H.; Ozawa, Y.; Toriumi, K. Flexibility of cubane-like Cu4I4 framework: Temperature dependence of molecular structure and luminescence thermochromism of [Cu4I4(PPh3)4] in two polymorphic crystalline states. Chem. Commun. 2010, 46, 6302–6304. [Google Scholar] [CrossRef] [PubMed]
  17. Benito, Q.; Le Goff, X.F.; Nocton, G.; Fargues, A.; Garcia, A.; Berhault, A.; Kahlal, S.; Saillard, J.-Y.; Martineau, C.; Trébosc, J.; et al. Geometry Flexibility of Copper Iodide Clusters: Variability in Luminescence Thermochromism. Inorg. Chem. 2015, 54, 4483–4494. [Google Scholar] [CrossRef] [PubMed]
  18. Zhou, J.; Bian, G.-Q.; Dai, J.; Zhang, Y.; Zhu, Q.-Y.; Lu, W. Luminescent 2-D Double-layered Polymer, [(CuI)4(CH3SCH3)3]∞, Containing Helical Chains Constructed by Flower-Basket-Shaped Cu4I4 Clusters. Inorg. Chem. 2006, 45, 8486–8488. [Google Scholar] [CrossRef]
  19. Knorr, M.; Bonnot, A.; Lapprand, A.; Khatyr, A.; Strohmann, C.; Kubicki, M.M.; Rousselin, Y.; Harvey, P.D. Reactivity of CuI and CuBr toward Dialkyl Sulfides RSR: From Discrete Molecular Cu4I4S4 and Cu8I8S6 Clusters to Luminescent Copper(I) Coordination Polymers. Inorg. Chem. 2015, 54, 4076–4409. [Google Scholar] [CrossRef]
  20. Cran, G.A.; Gibson, C.L.; Handa, S.; Kennedy, A.R. Scalemic β-Amino Sulfide Ligands: Use in Enantioselective Conjugate Additions and X-ray Analysis of a Dimeric Copper(I) Complex. Tetrahedron Asymmetry 1996, 7, 2511–2514. [Google Scholar] [CrossRef]
  21. Zhang, S.-M.; Hu, T.-L.; Du, J.-L.; Bu, X.-H. Tuning the formation of copper(I) coordination architectures with quinoxaline-based N,S-donor ligands by varying terminal groups of ligands and reaction temperature. Inorg. Chim. Acta. 2009, 362, 3915–3924. [Google Scholar] [CrossRef]
  22. Cheon, S.; Kim, T.H.; Jeon, Y.; Kim, J.; Park, K.-M. Novel heptanuclear copper(I) iodide cluster with a pinwheel shape. CrystEngComm 2013, 15, 451–454. [Google Scholar] [CrossRef]
  23. Lee, H.-H.; Park, I.-H.; Kim, S.; Lee, E.; Ju, H.; Jung, J.H.; Ikeda, M.; Habatac, Y.; Lee, S.S. Anion exchange coupled with the reduction and dimerisation of a copper(II) nitrate complex of tripyridyl dithioether via a single-crystal-to-single-crystal transformation. Chem. Sci. 2017, 8, 2592–2596. [Google Scholar] [CrossRef] [PubMed]
  24. Curcio, M.; Pankhurst, J.; Sproules, R.S.; Mignard, D.; Love, J.B. Triggering Redox Activity in a Thiophene Compound: Radical Stabilization and Coordination Chemistry. Angew. Chem. Int. Ed. 2017, 56, 7939–7943. [Google Scholar] [CrossRef] [PubMed]
  25. Otwinowski, Z.; Minor, W. Processing of X-ray diffraction data collected in oscillation mode. Methods Enzymol. 1997, 276, 307–326. [Google Scholar] [CrossRef]
  26. Sheldrick, G.M. SHELXS-97 and SHELXL-97, Program for Crystal Structure Solution and Refinement; University of Göttingen: Göttingen, Germany, 1997. [Google Scholar]
  27. Altomare, A.; Cascarano, G.; Giacovazzo, C.; Guagliardi, A. Completion and refinement of crystal structures with SIR92. J. Appl. Cryst. 1993, 26, 343–350. [Google Scholar] [CrossRef]
  28. Parkin, S.; Moezzi, B.; Hope, H. XABS2: An empirical absorption correction program. J. Appl. Crystal. 1995, 28, 53–56. [Google Scholar] [CrossRef]
  29. Walker, N.; Stuart, D. An Empirical Method for Correcting Diffractometer Data for Absorption Effects. Acta Cryst. 1983, A39, 158–166. [Google Scholar] [CrossRef]
  30. Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Cryst. 2015, A71, 3–8. [Google Scholar] [CrossRef]
  31. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  32. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; C.01, revision; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
  33. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
  34. Kohn, W.; Becke, A.D.; Parr, R.G. Density functional theory of electronic structure. J. Phys. Chem. 1996, 100, 12974–12980. [Google Scholar] [CrossRef]
  35. Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. A New Basis Set Exchange: An Open, Up-to-date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef] [PubMed]
  36. Barros, C.L.; de Oliveira, P.J.P.; Jörge, F.E.; Canal Neto, A.; Campos, M. Gaussian basis set of double zeta quality for atoms Rb through Xe: Application in non-relativistic and relativistic calculations of atomic and molecular properties. Mol. Phys. 2010, 108, 1965–1972. [Google Scholar] [CrossRef]
  37. Canal Neto, A.; Jörge, F.E. All-electron double zeta basis sets for the most fifth-row atoms: Application in DFT spectroscopic constant calculations. Chem. Phys. Lett. 2013, 582, 158–162. [Google Scholar] [CrossRef]
  38. Biegler-König, F.; Schönbohm, J.; Bayles, D. AIM2000—A Program to Analyze and Visualize Atoms in Molecules. J. Comp. Chem. 2001, 22, 545–559. [Google Scholar] [CrossRef]
  39. Keith, T.A. AIMAll, version 17.11.14; TK Gristmill Software: Overland Park, KS, USA, 2017. [Google Scholar]
  40. O’Boyle, N.M.; Tenderholt, A.L.; Langner, K.M. Cclib: A library for package-independent computational chemistry algorithms. J. Comp. Chem. 2008, 29, 839–845. [Google Scholar] [CrossRef]
  41. Castineiras, A.; Diaz, G.; Florenzio, F.; Garcia-Blanco, S.; Martinez-Carrera, S. Crystal and molecular structure of tetraiodo (1,8-di-2-pyridyl-3,6-dithiaoctane-N,S,S′,N′)dimercury(II). J. Crystallogr. Spectrosc. Res. 1988, 18, 395–401. [Google Scholar] [CrossRef]
  42. Lee, E.; Lee, I.S.-G.; Park, I.-H.; Kim, S.; Ju, H.; Jung, J.H.; Ikeda, M.; Habata, Y.; Lee, S.S. Endo- and Exocyclic Coordination of a 20-Membered N2O2S2-Macrocycle and Cascade Complexation of a 40-Membered N4O4S4-Macrocycle. Inorg. Chem. 2018, 57, 6289–6299. [Google Scholar] [CrossRef]
  43. Zhang, J.-A.; Pan, M.; Zhang, J.-Y.; Kang, B.-S.; Su, C.-Y. Syntheses, structures and bioactivities of cadmium(II) complexes with a tridentate heterocyclic N- and S-ligand. Inorg. Chim. Acta 2009, 362, 3519–3525. [Google Scholar] [CrossRef]
  44. Kim, S.; Huiyeong, J.; Park, K.-M.; Jung, J.H.; Lee, S.S.; Lee, E. Influence of the Reaction Sequence on the Complexation of an NS4-Macrocycle with CdII and CuI Salts Leading to the Formation of Supramolecular Isomers and an Endo/Exocyclic CuI Complex. Inorg. Chem. 2021, 60, 13637–13645. [Google Scholar] [CrossRef] [PubMed]
  45. Yang, L.; Powell, D.R.; Houser, R.P. Structural variation in copper(I) complexes with pyridylmethylamide ligands: Structural analysis with a new four-coordinate geometry index, τ4. J. Chem. Soc. Dalton Trans. 2007, 9, 955–964. [Google Scholar] [CrossRef] [PubMed]
  46. Okuniewski, A.; Rosiak, D.; Chojnacki, J.; Becker, B. Coordination polymers and molecular structures among complexes of mercury(II) halides with selected 1-benzoylthioureas. Polyhedron 2015, 90, 47–57. [Google Scholar] [CrossRef]
  47. Hostettler, M.; Birkedal, H.; Schwarzenbach, D. Polymorphs and structures of mercuric iodide. Chimia 2001, 55, 541–545. [Google Scholar] [CrossRef]
  48. Jeffrey, G.A.; Vlasse, M. On the Crystal Structures of the Red, Yellow, and Orange Forms of Mercuric Iodide. Inorg. Chem. 1967, 6, 396–399. [Google Scholar] [CrossRef]
  49. Auvray, P.; Genet, F. Affinement de la structure cristalline du cinabre α–HgS. Bull. Soc. Fr. Minéral. 1973, 96, 218–219. [Google Scholar]
  50. Pearson, R.G. Hard and Soft Acids and Bases. J. Am. Chem. Soc. 1963, 85, 3533–3539. [Google Scholar] [CrossRef]
  51. Pearson, R.G. Hard and soft acids and bases, HSAB, part I: Fundamental principles. J. Chem. Educ. 1968, 45, 581–586. [Google Scholar] [CrossRef]
  52. Pearson, R.G. Hard and soft acids and bases, HSAB, part II: Underlying theories. J. Chem. Educ. 1968, 45, 643–648. [Google Scholar] [CrossRef]
  53. Shannon, R.D.; Prewitt, C.T. Effective Ionic Radii on Oxides and Fluorides. Acta Cryst. 1969, B25, 925–945. [Google Scholar] [CrossRef]
  54. Cordero, B.; Gómez, V.; Platero-Prats, A.E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S. Covalent radii revisited. Dalton Trans. 2008, 21, 2832–2838. [Google Scholar] [CrossRef] [PubMed]
  55. Allen, F.H.; Davies, J.E.; Galloy, J.J.; Johnson, O.; Kennard, O.; Macrae, C.F.; Mitchell, E.M.; Mitchell, G.F.; Smith, J.M.; Watson, D.G. The Development of Versions 3 and 4 of the Cambridge Structural Database System. J. Chem. Inf. Comput. Sci. 1991, 31, 187–204. [Google Scholar] [CrossRef]
  56. Caradoc-Davies, P.L.; Hanton, L.R. Molecular rectangles from metallomacrocycles: Development of dibenzofuranligands. Dalton Trans. 2003, 9, 1754–1758. [Google Scholar] [CrossRef]
  57. Noren, B.; Oskarsson, A. Bond Length Variations in Tetrahydrothiophene Solvates of the Coinage Metals. The Crystal Structure of Di-mu-iodo-bis[bis(tetrahydrothiophene)copper(I)]. Acta Chem. Scand. 1987, A41, 12–17. [Google Scholar] [CrossRef]
  58. Lu, W.; Yan, Z.-M.; Dai, J.; Zhang, Y.; Zhu, Q.-Y.; Jia, D.-X.; Guo, W.-J. Coordination Assembly of TTF Derivatives through CuI Bridges. Eur. J. Inorg. Chem. 2005, 2005, 2339–2345. [Google Scholar] [CrossRef]
  59. Munakata, M.; Wu, L.P.; Kuroda-Sowa, T.; Maekawa, M.; Suenaga, Y.; Nakagawa, S.J. One-, two- and three-dimensional copper(I) and silver(I) complexes of 2,11-dithia[3.3]paracyclophane. J. Chem. Soc. Dalton Trans. 1996, 25, 1525–1530. [Google Scholar] [CrossRef]
  60. Bader, R.F.W. Atoms in Molecules, A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
  61. Zhou, H.; Lin, P.; Li, Z.-H.; Du, S.-W. Four new coordination polymers based on multinuclear Cu(I) halide clusters and 1,3-bis(imidazol-1-yl-methyl)-benzene. J. Mol. Struct. 2008, 881, 21–27. [Google Scholar] [CrossRef]
  62. Popelier, P. Atoms in Molecules, an Introduction; Prentice Hall: Essex, UK, 2000. [Google Scholar]
  63. Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X-H⋯F-Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
  64. Alkorta, I.; Blanco, F.; Elguero, J. The use of a molecular balance derived from 5,5′-bipyrazole to calculate π−π stacking interactions. Tetrahedron Lett. 2008, 49, 7246–7249. [Google Scholar] [CrossRef]
  65. Biswas, C.; Drew, M.G.B.; Escudero, D.; Frontera, A.; Ghosh, A. Anion–π, lone-pair–π, π–π and hydrogen-bonding interactions in a CuII complex of 2-picolinate and protonated 4,4′-bipyridine: Crystal structure and theoretical studies. Eur. J. Inorg. Chem. 2009, 15, 2238–2246. [Google Scholar] [CrossRef]
  66. Estarellas, C.; Frontera, A.; Quinonero, D.; Deya, P.M. Theoretical ab initio study of substituted benzene trimer: Interplay between hydrogen bonding and π-π interactions. Comput. Theor. Chem. 2011, 975, 106–110. [Google Scholar] [CrossRef]
  67. Dinda, S.; Samuelson, A.G. The nature of bond critical points in dinuclear copper(I) complexes. Chem. Eur. J. 2012, 18, 3032–3042. [Google Scholar] [CrossRef] [PubMed]
  68. Bianchi, R.; Gervasio, G.; Marabello, D. Experimental electron density analysis of Mn2(CO)10: Metal-metal and metal-ligand bond characterization. Inorg. Chem. 2000, 39, 2360–2366. [Google Scholar] [CrossRef] [PubMed]
  69. Farrugia, L.J.; Senn, H.M. Metal-metal and metal-ligand bonding at a QTAIM catastrophe: A combined experimental and theoretical charge density study on the alkylidyne cluster Fe3(μ-H)(μ-COMe)(CO)10. J. Phys. Chem. A 2010, 114, 13418–13433. [Google Scholar] [CrossRef] [PubMed]
  70. Varadwaj, P.R.; Marques, H.M. The physical chemistry of coordinated aqua-, ammine-, and mixed-ligand Co2+ complexes: DFT studies on the structure, energetics, and topological properties of the electron density. Phys. Chem. Chem. Phys. 2010, 12, 2126–2138. [Google Scholar] [CrossRef]
  71. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular Interactions from a Natural Bond Orbital, Donor—Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  72. Pearson, R.G. Absolute electronegativity and hardness: Application to inorganic chemistry. Inorg. Chem. 1988, 27, 734–740. [Google Scholar] [CrossRef]
  73. Parr, R.G.; Pearson, R.G. Absolute Hardness: Companion Parameter to Absolute Electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
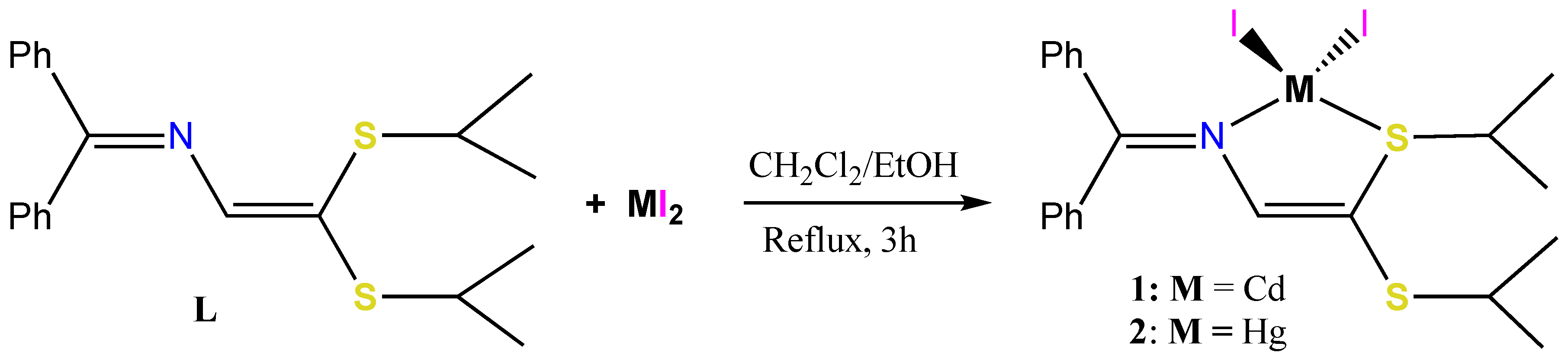
Chemistry 06 00004 sch001
Scheme 1. Synthesis of the mononuclear complexes 1 and 2.
Scheme 1. Synthesis of the mononuclear complexes 1 and 2.
Chemistry 06 00004 sch001
Chemistry 06 00004 sch002
Scheme 2. Synthesis of the dinuclear complex 3.
Scheme 2. Synthesis of the dinuclear complex 3.
Chemistry 06 00004 sch002
Chemistry 06 00004 g001
Figure 1. ORTEP (50% probability level) of the molecule of the Cd complex found in the crystal structure of 1.
Figure 1. ORTEP (50% probability level) of the molecule of the Cd complex found in the crystal structure of 1.
Chemistry 06 00004 g001
Chemistry 06 00004 g002
Figure 2. ORTEP (50% probability level) of the molecule of Hg complex found in the crystal structure of 2.
Figure 2. ORTEP (50% probability level) of the molecule of Hg complex found in the crystal structure of 2.
Chemistry 06 00004 g002
Chemistry 06 00004 g003
Figure 3. ORTEP (30% probability level) of the molecular structure of Cu adduct in the structure of 3. Only the major site of occupancy equal to 0.93 is shown for the μ2-iodide bridge. Symmetry transformations used to generate equivalent atoms: i1-x, 2-y, 2-z.
Figure 3. ORTEP (30% probability level) of the molecular structure of Cu adduct in the structure of 3. Only the major site of occupancy equal to 0.93 is shown for the μ2-iodide bridge. Symmetry transformations used to generate equivalent atoms: i1-x, 2-y, 2-z.
Chemistry 06 00004 g003
Chemistry 06 00004 g004
Figure 4. Experimental (top) and calculated UV–vis spectra (bottom) of 1 (blue), 2 (red) and 3 (green); ε, molar absorptivity; λ, wavelength; f, oscillator strength.
Figure 4. Experimental (top) and calculated UV–vis spectra (bottom) of 1 (blue), 2 (red) and 3 (green); ε, molar absorptivity; λ, wavelength; f, oscillator strength.
Chemistry 06 00004 g004
Chemistry 06 00004 g005aChemistry 06 00004 g005b
Figure 5. Selected molecular orbitals for complex 1. The energies (eV) are given in brackets.
Figure 5. Selected molecular orbitals for complex 1. The energies (eV) are given in brackets.
Chemistry 06 00004 g005aChemistry 06 00004 g005b
Chemistry 06 00004 g006
Figure 6. Selected molecular orbitals for complex 2. The energies in eV are given in brackets.
Figure 6. Selected molecular orbitals for complex 2. The energies in eV are given in brackets.
Chemistry 06 00004 g006
Chemistry 06 00004 g007
Figure 7. Selected molecular orbitals for complex 3. The energies in eV are given in brackets.
Figure 7. Selected molecular orbitals for complex 3. The energies in eV are given in brackets.
Chemistry 06 00004 g007
Chemistry 06 00004 g008
Figure 8. Molecular graph of the complex molecule in the crystal structure of 1. Colors of critical points: bond (BCP 3,−1) is red and ring (RCP 3,+1) is yellow.
Figure 8. Molecular graph of the complex molecule in the crystal structure of 1. Colors of critical points: bond (BCP 3,−1) is red and ring (RCP 3,+1) is yellow.
Chemistry 06 00004 g008
Chemistry 06 00004 g009
Figure 9. Molecular graph of the complex molecule in the crystal structure of 2. Colors of critical points: bond (BCP 3,−1) is red and ring (RCP 3,+1) is yellow.
Figure 9. Molecular graph of the complex molecule in the crystal structure of 2. Colors of critical points: bond (BCP 3,−1) is red and ring (RCP 3,+1) is yellow.
Chemistry 06 00004 g009
Chemistry 06 00004 g010
Figure 10. Molecular graph of dimeric molecule in the crystal structure of 3. Colors of critical points: bond (BCP 3,−1) is red, ring (RCP 3,+1) is yellow and cage (CCP 3,+3) is green.
Figure 10. Molecular graph of dimeric molecule in the crystal structure of 3. Colors of critical points: bond (BCP 3,−1) is red, ring (RCP 3,+1) is yellow and cage (CCP 3,+3) is green.
Chemistry 06 00004 g010
Table 1. Crystal data, data collection and structure refinement for 1, 2 and 3.
Table 1. Crystal data, data collection and structure refinement for 1, 2 and 3.
Compound123
FormulaC21H25CdI2NS2C22H27Cl2HgI2NS2C22H25CuI2NS2
Formula weight721.74894.85545.98
Temperature/K173115193.15
Wavelength/Å0.710730.710730.71073
Crystal systemmonoclinicorthorhombictriclinic
Space groupP21P212121P 1 ¯
a/Å9.006(3)9.7582(2)9.3935(19)
b/Å9.454(3)15.7719(3)9.6540(19)
c/Å15.081(4)17.9490(4)13.689(3)
a/°90.090101.92(3)
β/°101.587(6)9096.52(3)
γ/°90.09090.30(3)
Volume/Å31257.9(6)2762.45(10)1206.3(4)
Z242
ρ(calc.) g/cm31.9062.1521.503
μ/mm−13.4958.1622.363
F(000)6881672544
Crystal size/mm0.16 × 0.15 × 0.120.10 × 0.10 × 0.080.20 × 0.20 × 0.10
θ range for data collection/°2.308 to 26.9972.611 to 27.4764.366 to 49.998
Index ranges−11 ≤ h ≤ 11,
−11 ≤ k ≤ 12,
−19 ≤ l ≤ 19		−12 ≤ h ≤ 12,
−20 ≤ k ≤ 20,
−23 ≤ l ≤ 23		−11 ≤ h ≤ 11,
−00 ≤ k ≤ 10,
−0 ≤ l ≤ 16
Reflections collected20,40962993965
Independent reflections5388 [R(int) = 0.0273]62993965 [R(int) = 0.0651]
Refl. greater [I > 2σ(I)]532554452805
Absorption correction
Transmission max
Transmission min
Refinement method		CrysAlis PRO
0.999
0.704
Full-matrix least squares on F2		DIFABS
0.4419
0.3386
Full-matrix least squares on F2		FACEIT in IPDS
0.7980
0.6494
Full-matrix least squares on F2
Data/restraints/parameters5388/1/2486299/0/2773695/6/249
Goodness-of-fit on F2
Flack parameter		1.124
0.02(2)		1.044
0.014(7)		1.012
-
Final R indexes [I > 2σ(I)]R1 = 0.0292,
wR2 = 0.0774		R1 = 0.0368,
wR2 = 0.0601		R1 = 0.0894,
wR2 = 0.1456
R indexes (all data)R1 = 0.0297,
wR2 = 0.0787		R1 = 0.0484,
wR2 = 0.0633		R1 = 0.0805,
wR2 = 0.1549
Largest diff. peak
and hole/e.Å−3		0.95 and −0.371.08 and −0.800.67 and −0.75
Table 2. Selected bond lengths (Å) and angles (°) found in the structures of 1, 2 and 3.
Table 2. Selected bond lengths (Å) and angles (°) found in the structures of 1, 2 and 3.
1 Cd2 Hg3 Cu 1 Cd2 Hg3 Cu
M–I1 (a)2.6787(8)2.6412(7)2.576(2)I1-M-I2124.80(2)138.56(2)119.09(5)
M–I2 (a)2.7140(9)2.6941(7)2.692(2)I1-M-S118.25(4)117.93(5)112.4(1)
M–S2.662(2)2.689(2)2.342(2)I1-M-N114.5(1)121.1(2)127.4(2)
M–N2.321(5)2.496(7)2.143(5)I2-M-S97.93(4)96.04(5)108.6(1)
I2-M-N112.7(1)88.9(2)98.0(2)
Cu–Cu 2.672(2)S-M-N78.1(1)74.5(2)86.0(2)
(a) Iodine atom on the major site of occupancy equal to 0.93(1) (see experimental section).
Table 3. Contribution of molecular orbitals to electronic transitions; λ (nm) wavelength, oscillation strength (f) and major contributions (%) of molecular orbitals (MO) involved therein. For 1 and 2, all transitions occur in the LUMO.
Table 3. Contribution of molecular orbitals to electronic transitions; λ (nm) wavelength, oscillation strength (f) and major contributions (%) of molecular orbitals (MO) involved therein. For 1 and 2, all transitions occur in the LUMO.
Complex 1Complex 2Complex 3
λ (nm)Osc.
Strength		MOλ (nm)Osc.
Strength		MOλ (nm)Osc.
Strength		MO
3930.23H-4 (95)3880.29H-4 (80)
H-3 (19)		5670.07H-3/L+1 (10)
H-2/L (73)
H-1/L+1 (12)
3230.08H-7 (87)3280.08H-6 (95)5500.03H-1/L+1 (84)
3110.03H-8 (82)3180.08H-7 (92)4570.02H-7/L+1 (14)
H-5/L (63)
3040.04H-9 (80)3090.03H-8 (93)4190.04H-9/L (14)
H-6/L (76)
2900.05H-11 (21)
H-10 (66)		2990.05H-9 (87)3800.50H-9/L (33)
H-8/L+1 (21)
H-7/L+1 (24)
2830.15H-11 (61)
H-10 (19)		2870.11H-10 (91)
Table 4. Topological properties of bond critical points (3,-1 BCP) in complex molecules of 1(Cd) and 2(Hg): d, bond distance; ρ, electron density; (∇2ρ, Laplacian of ρ; V, G and H, potential, kinetic and total energy densities; H/ρ, pressure of total energy per electron (a kind of “bond degree”); DIcalc, calculated delocalization index; DInorm, delocalization index normalized to 2; Wbxcalc, calculated Wiberg bond indexes; Wbxnorm, Wiberg bond indexes normalized to 2. All but d (interatomic distances) data are given in atomic units.
Table 4. Topological properties of bond critical points (3,-1 BCP) in complex molecules of 1(Cd) and 2(Hg): d, bond distance; ρ, electron density; (∇2ρ, Laplacian of ρ; V, G and H, potential, kinetic and total energy densities; H/ρ, pressure of total energy per electron (a kind of “bond degree”); DIcalc, calculated delocalization index; DInorm, delocalization index normalized to 2; Wbxcalc, calculated Wiberg bond indexes; Wbxnorm, Wiberg bond indexes normalized to 2. All but d (interatomic distances) data are given in atomic units.
Bond
Property		M—I1
Cd Hg Cu		M—I2
Cd Hg Cu		M—S
Cd Hg Cu		M—N
Cd Hg Cu		Cd–C13Cu–Cu
d, Å2.679  2.641  2.5762.714  2.694  2.6922.662  2.689  2.3422.321  2.496  2.1433.157(5)2.672
ρ, e−/a030.060  0.064  0.0540.056  0.059  0.0460.044  0.045  0.0640.057  0.043  0.0610.0100.031
∇2ρ, e−/a050.127  0.180  0.1090.119  0.165  0.0850.149  0.150  0.2140.301  0.184  0.2950.0310.021
−V, Ha/a030.048  0.079  0.0510.044  0.070  0.0410.037  0.051  0.0730.059  0.052  0.0733−0.00540.0288
G, Ha/a030.040  0.062  0.0390.037  0.055  0.0310.037  0.044  0.0610.067  0.049  0.07360.00660.0177
−H, Ha/a030.008  0.017  0.0120.007  0.014  0.010−0.0003  0.006  0.010−0.008  0.003  −0.0003−0.00120.0105
−H/ρ, Ha/e−0.136  0.266  0.2190.126  0.244  0.218−0.048  0.144  0.149−0.143  0.065  −0.0043−0.0390.341
|V|/G1.203  1.276  1.3031.192  1.258  1.3190.992  1.150  1.1890.879  1.058  0.9960.8181.605
DIcalc0.778  0.589  0.5870.728  0.523  0.4790.367  0.287  0.4830.372  0.221  0.3790.0380.149
DInorm0.682  0.727  0.5650.638  0.646  0.4610.322  0.354  0.4650.326  0.273  0.3650.0180.143
Wbxcalc0.785  0.563  0.2300.756  0.471  0.1920.306  0.168  0.1410.216  0.101  0.1000.0260.097
Wbxnorm0.752  0.8090.724  0.7580.293  0.2700.207  0.1630.025-
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kinghat, R.; Khatyr, A.; Knorr, M.; Strohmann, C.; Kubicki, M.M. 4,4-Bis(isopropylthio)-1,1-diphenyl-2-azabuta-1,3-diene Adducts with Cadmium(II), Mercury(II) and Copper(I) Iodides: Crystal, Molecular and Electronic Structures of d10 Transition Metal Chelate Complexes. Chemistry 2024, 6, 62-80. https://doi.org/10.3390/chemistry6010004

AMA Style

Kinghat R, Khatyr A, Knorr M, Strohmann C, Kubicki MM. 4,4-Bis(isopropylthio)-1,1-diphenyl-2-azabuta-1,3-diene Adducts with Cadmium(II), Mercury(II) and Copper(I) Iodides: Crystal, Molecular and Electronic Structures of d10 Transition Metal Chelate Complexes. Chemistry. 2024; 6(1):62-80. https://doi.org/10.3390/chemistry6010004

Chicago/Turabian Style

Kinghat, Rodolphe, Abderrahim Khatyr, Michael Knorr, Carsten Strohmann, and Marek M. Kubicki. 2024. "4,4-Bis(isopropylthio)-1,1-diphenyl-2-azabuta-1,3-diene Adducts with Cadmium(II), Mercury(II) and Copper(I) Iodides: Crystal, Molecular and Electronic Structures of d10 Transition Metal Chelate Complexes" Chemistry 6, no. 1: 62-80. https://doi.org/10.3390/chemistry6010004

APA Style

Kinghat, R., Khatyr, A., Knorr, M., Strohmann, C., & Kubicki, M. M. (2024). 4,4-Bis(isopropylthio)-1,1-diphenyl-2-azabuta-1,3-diene Adducts with Cadmium(II), Mercury(II) and Copper(I) Iodides: Crystal, Molecular and Electronic Structures of d10 Transition Metal Chelate Complexes. Chemistry, 6(1), 62-80. https://doi.org/10.3390/chemistry6010004

Article Metrics

Back to TopTop