Extending WSN Lifetime via Optimized Mobile Sink Trajectories: Linear Programming and Cuckoo Search Approaches with Overhearing-Aware Energy Models
Abstract
1. Introduction
- Formalizing a new energy model that considers overhearing as one of the main sources of energy consumption.
- Solving the maximization problem using Linear Programming while considering the new energy model and assessing the impact of overhearing on the WSN lifetime.
- Solving the optimization problem using an enhanced swarm-intelligence-based solution.
- Evaluating and comparing both models in terms of the achieved WSN lifetime and execution time.
- Finding the Sink’s shortest path to cover all the sojourn points for both models using the Traveling Salesman Problem (TSP) algorithm.
2. Related Work
2.1. LP-Based Sink Mobility Models
2.2. AI-Based Sink Mobility Models
2.3. Non-LP/AI Sink Mobility Models
2.4. Discussion
2.4.1. Comparative Analysis
2.4.2. Critical Gaps in the Literature
- Overhearing:Consistently overlooked in prior research, compromising the accuracy of energy consumption estimation models.
- Optimal Mobile Sink Trajectory: Predominantly addressed through heuristic or partial solutions, leaving the determination of truly optimal trajectories largely unexplored.
- Dynamic Adaptability: Significantly enhanced in AI-based models compared to LP or non-LP/AI approaches when responding to changing network conditions.
- Environment and Scalability: Severely limited in LP approaches when applied to large networks, restricted to small-to-medium networks in non-LP/AI methods, and rarely accounting for environmental factors across all approaches.
- Lifetime vs. Energy: Theoretically maximized in LP methods despite limited practical adaptability, while primarily focused on energy balancing rather than lifetime maximization in AI and non-LP/AI approaches.
2.4.3. Research Contribution
- Incorporates overhearing effects to significantly enhance energy consumption estimation accuracy.
- Integrates both AI-based optimization techniques (Cuckoo Search algorithm) and Linear Programming approaches.
- Dynamically optimizes routing paths and Sink positioning strategies across variable network scales.
- Maximizes WSN lifetime through strategic energy balancing and consumption optimization.
- Accounts for critical real-world environmental factors to ensure effective practical deployment (e.g., overhearing phenomena).
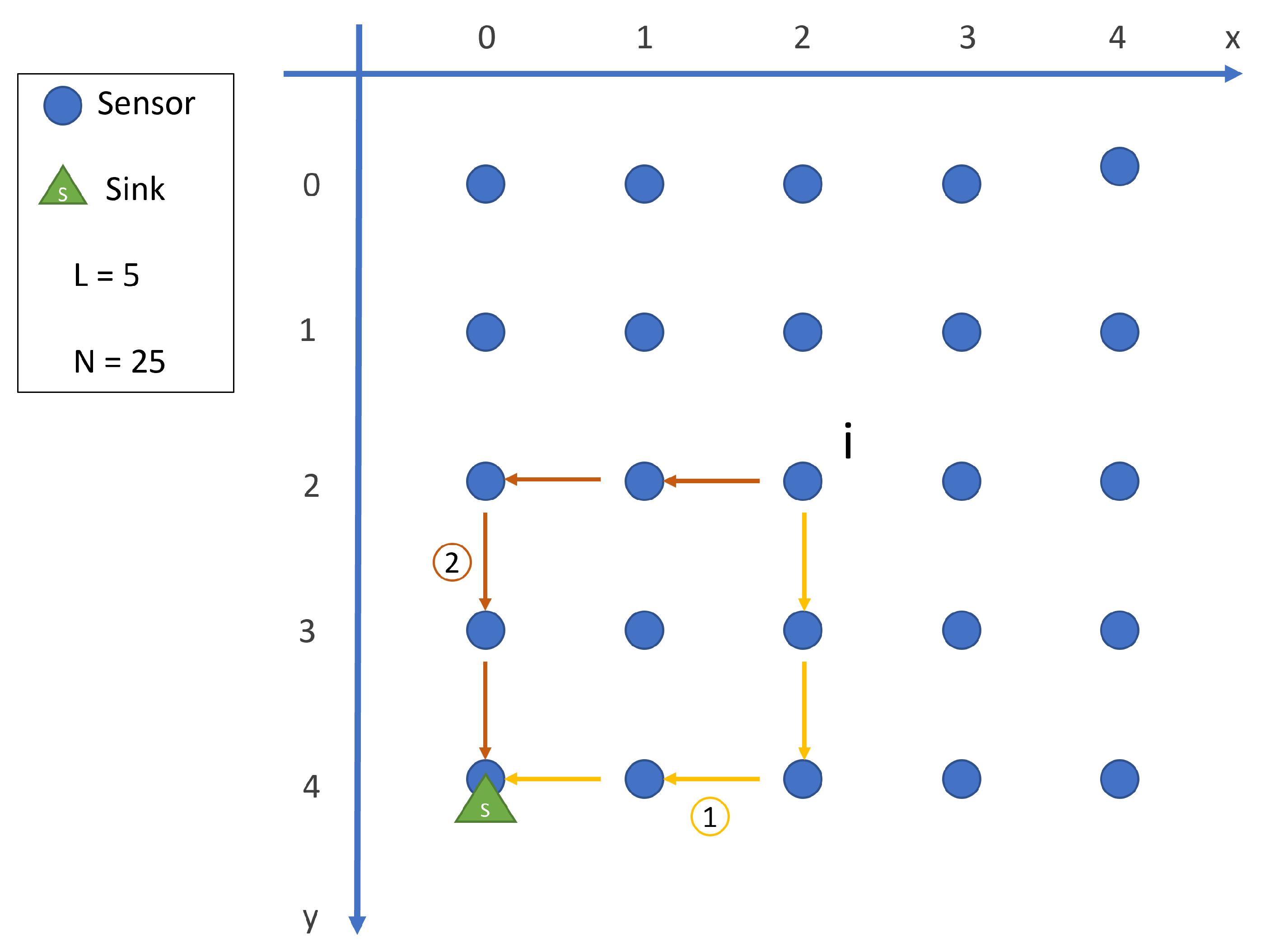
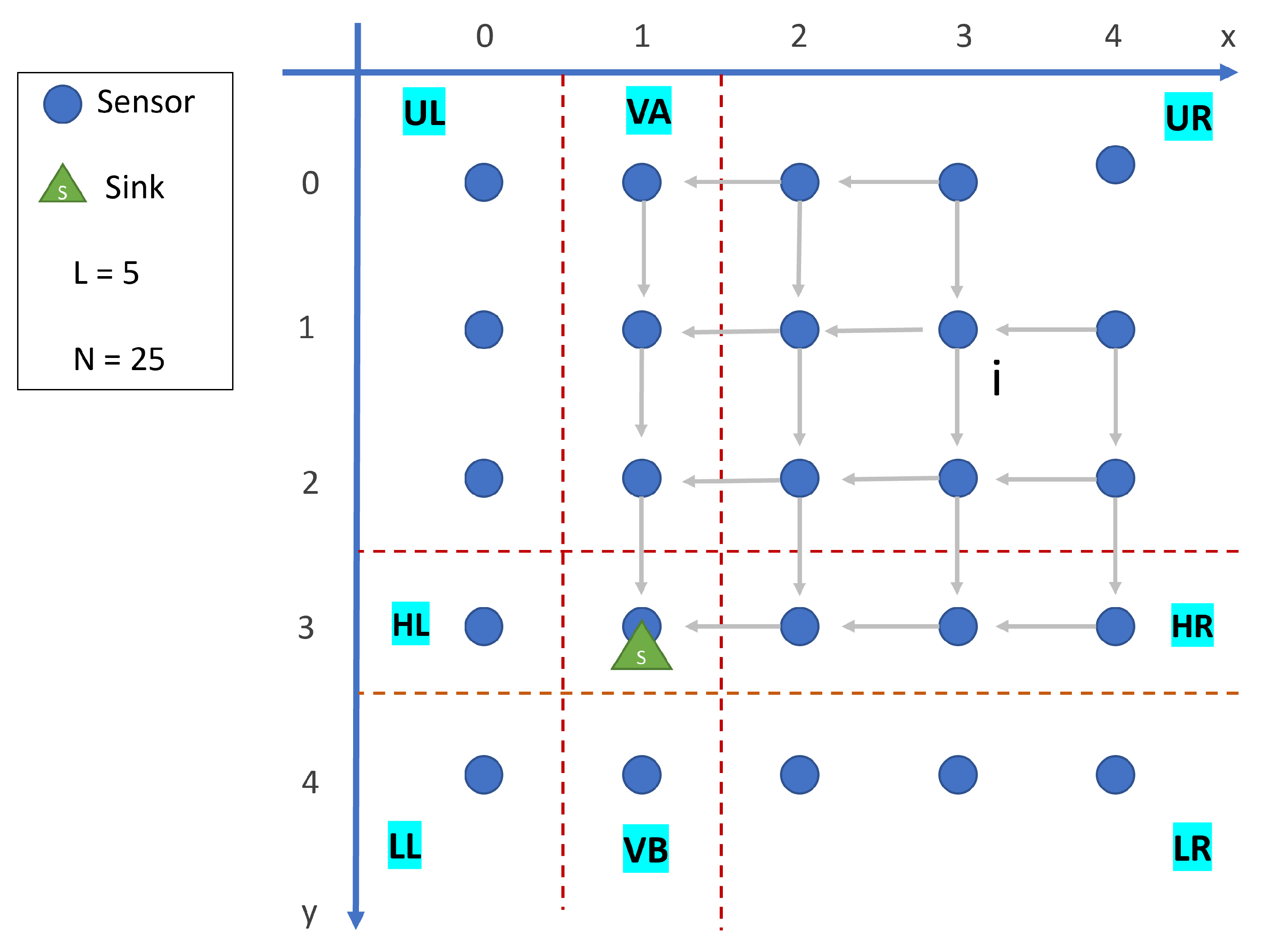
3. System Model
3.1. Main Constraints of Sink Mobility Approach
- The energy constraint: this constraint states that the total energy consumed at each node by the data reception and transmission must not overextend its initial allocated energy.
- The flow conservation law: every node should satisfy the equality between the total incoming flow rates added to the self-generated data rate and the sum of the resulting outgoing flow rates at any time.
- The total traffic received by the Sink in a given duration must equal the total of the data generated by all the sensor nodes in the same duration.
3.2. Assumptions and Network Topology
- The network consists of a bi-dimensional square grid with size , where N represents the total number of static sensors.
- The Sink can move among nodes in the grid to collect data, with negligible moving time compared to its sojourn time.
- All sensors can communicate with the Sink during its sojourn time through either one-hop or multi-hop communication schemes.
- The primary sources of energy consumption are data reception, transmission, and overhearing. Notably, the consideration of overhearing constitutes our main contribution.
- All sensors are homogeneous, possessing identical data generation rates, power consumption rates, and transmission ranges.
- Communication channels are error-free, symmetric, and bi-directional.
- All sensors are equipped with the same limited initial energy and unlimited buffer size.
- When the Sink is neither co-located with a sensor nor directly connected to it, communication between them occurs through the shortest path in the multi-hop scheme.
3.3. Problem Description
4. Mathematical Formulation
4.1. Parameters
- L: Number of sensors along each edge of the square grid.
- N: Total number of sensors in the square grid ().
- : Initial energy (J) allocated to each node, from which energy is deducted during each operation.
- e: Energy consumption rate (J/bit).
- r: Sensor data generation rate (bits/s), constant across all sensors.
- : Data transmission rate between nodes when the Sink is positioned at sojourn point k (bits/s).
- : Set of neighboring nodes for node i.
- : Power consumption rate at sensor node i, while the Sink remains at sojourn point k (J/s).
- : Overhearing rate between the sensor node and its neighbors.
- : Additional overhead for specific conditions or locations within the grid.
4.2. Decision Variables
- : Sink sojourn duration (s) at node k.
4.3. Objective Function
- Maximize T, representing the total WSN lifetime, defined as the sum of all Sink sojourn durations across all possible sojourn points (s).
4.4. Linear Programming Formulation
5. LP-Based Analytical Result
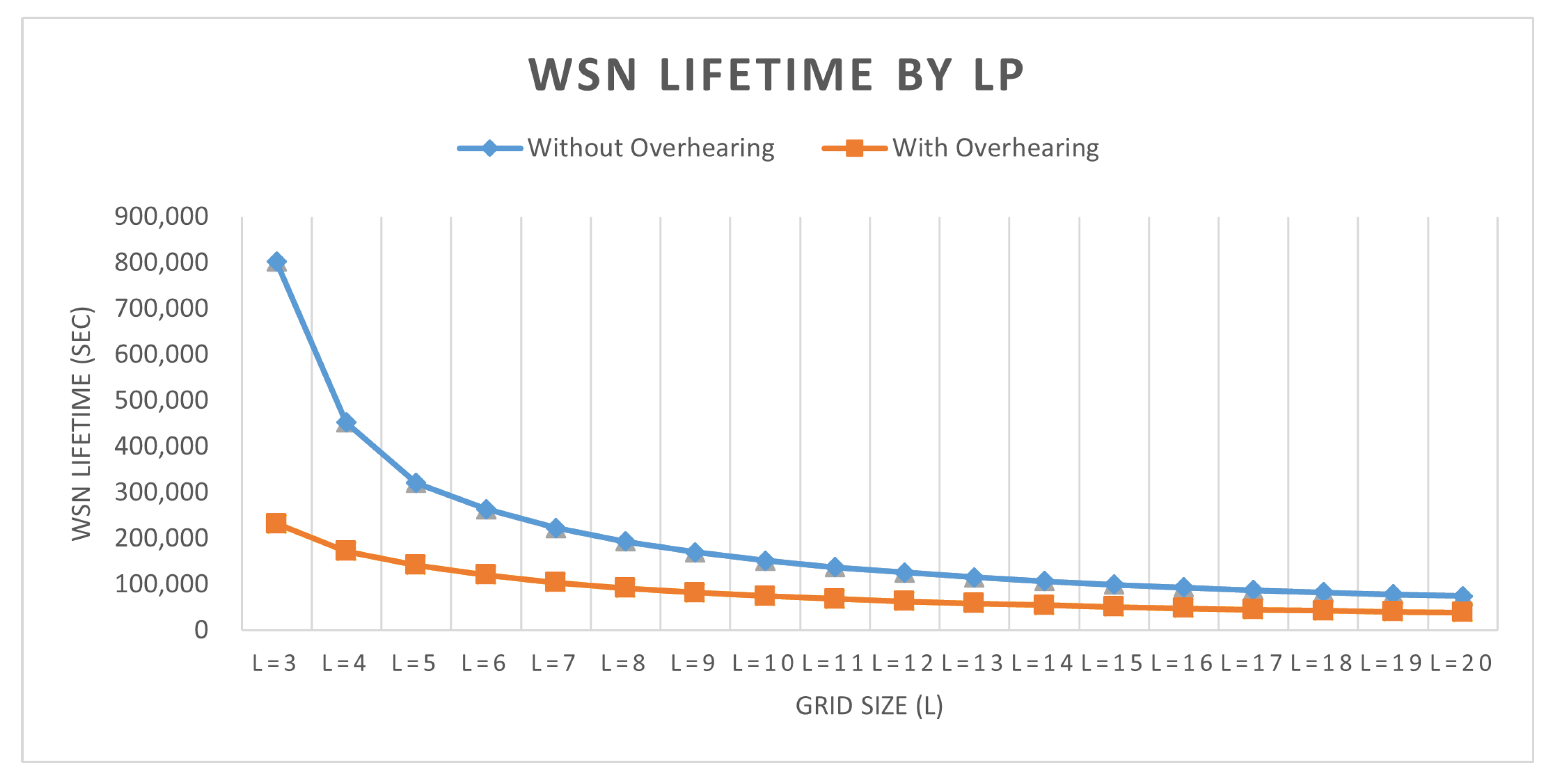
5.1. Achieved WSN Lifetime
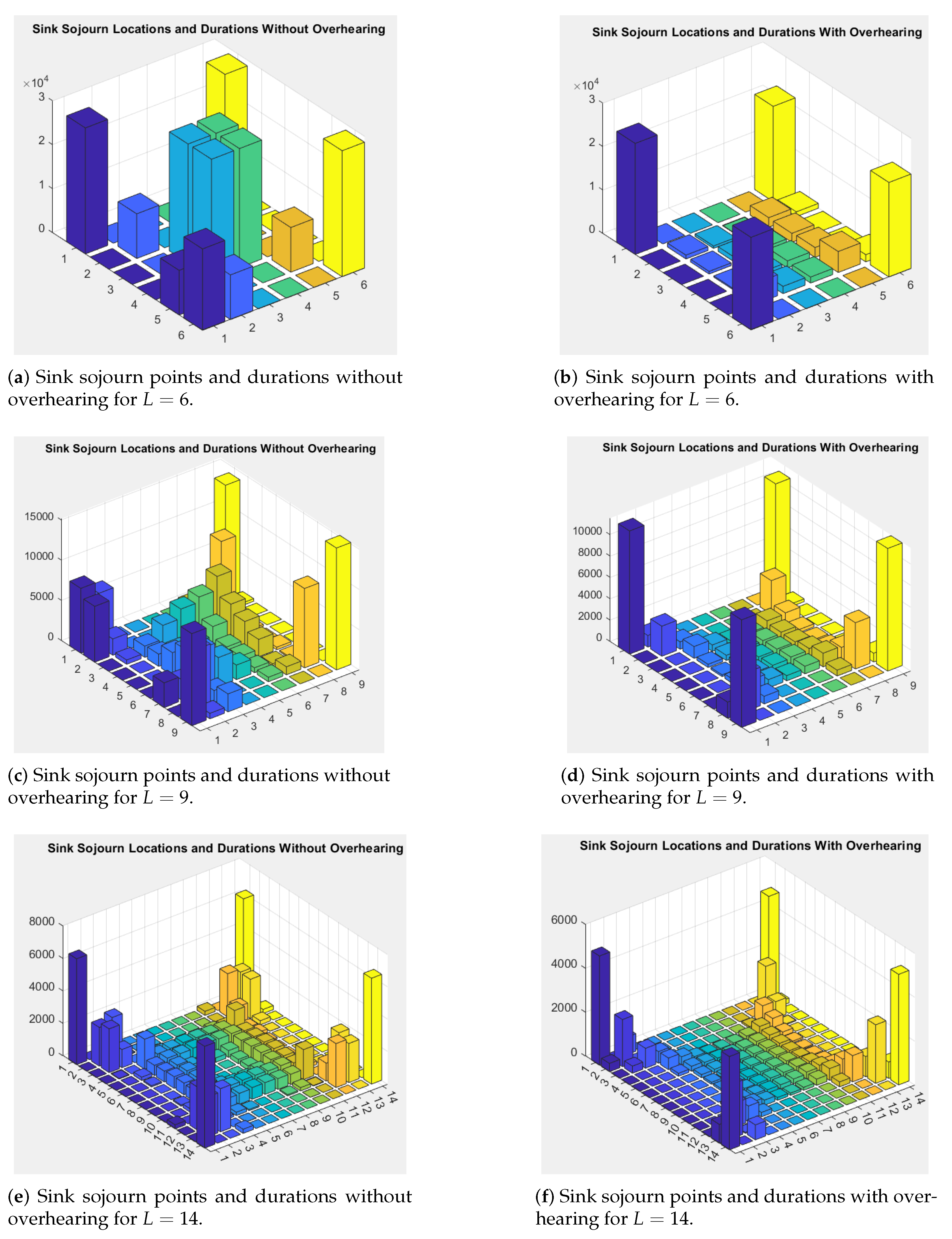
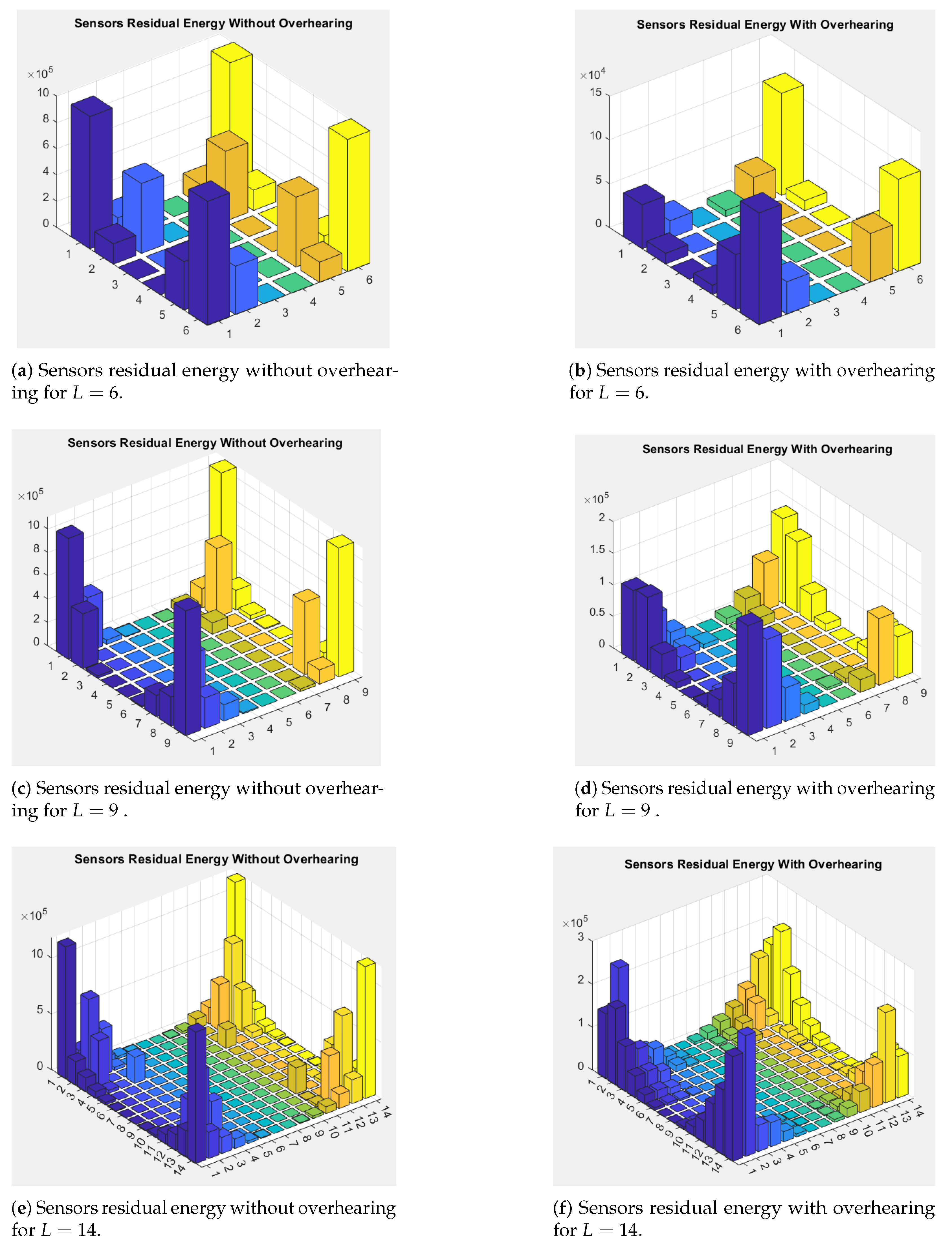
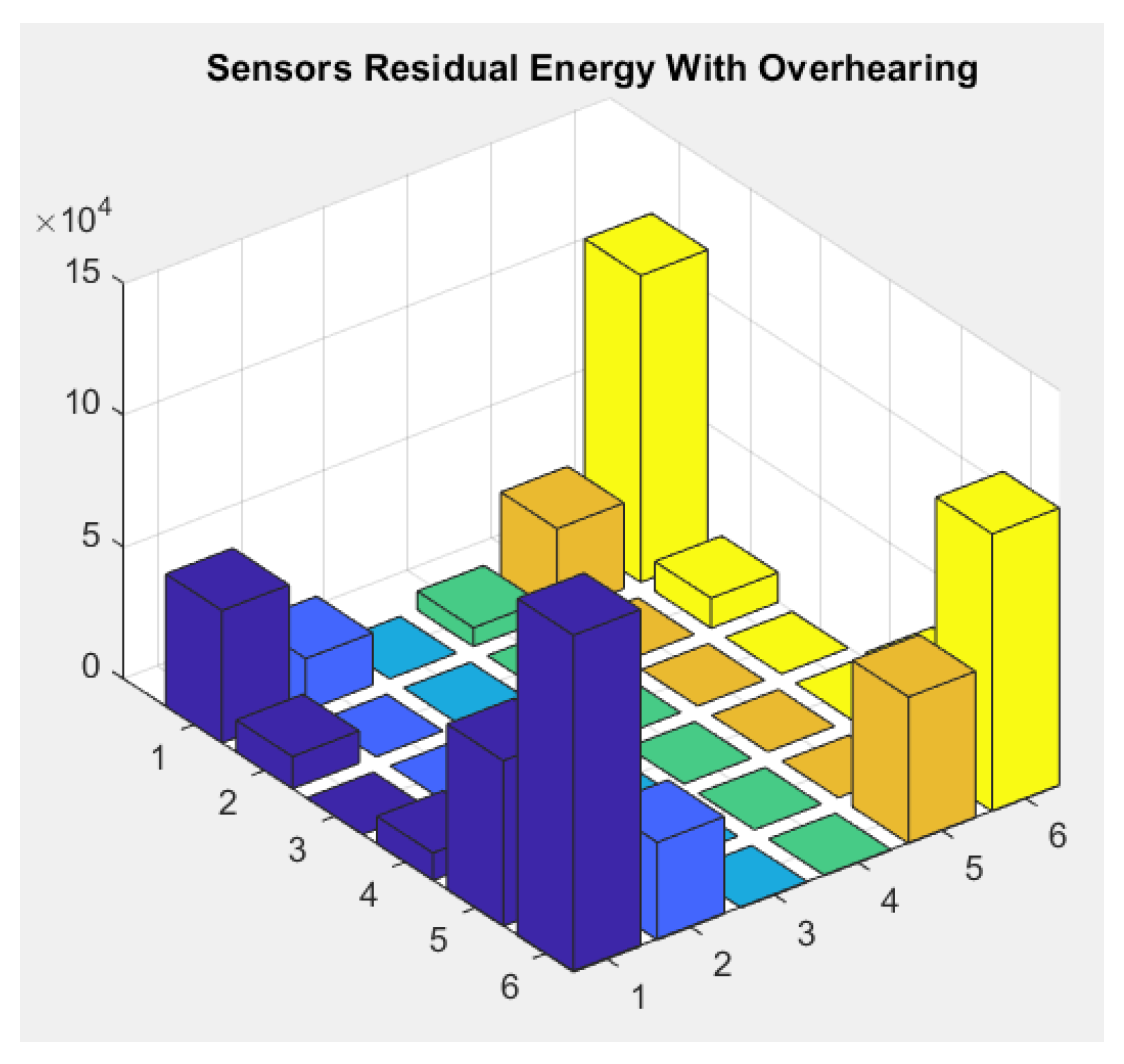
5.2. Sink’s Sojourn and Sensors’ Residual Energy Distribution
6. AI-Based Solution
6.1. Cuckoo Search Optimization
- Initialize the population with a predetermined number of host nests.
- Each cuckoo generates a single egg and deposits it in a randomly selected nest from the initialized population.
- At each iteration, a new candidate nest is generated from a randomly selected nest using LV. If the new nest has a better egg value (fitness value) than the selected one, then it is replaced. Only nests containing superior eggs progress to the subsequent generation.
- The nests are sorted according to their fitness value.
- A discovery probability, denoted as , represents the likelihood of host birds detecting foreign eggs. Consequently, a proportion of nests equivalent to is eliminated from consideration.
- The final optimal solution is found upon reaching the maximum number of iterations or if a stop criterion is satisfied, whereupon the highest-quality nest is returned as the best solution.
| Algorithm 1 Original CS algorithm. |
|
Parameters
- : Candidate solution vector (nest).
- d: Dimensionality of the optimization problem (number of decision variables per nest; where , since not all potential sojourn points necessarily receive positive sojourn durations, indicating that the Sink may not visit all candidate locations).
- t: Iteration index.
- M: Maximum number of iterations.
- C: Population counter for tracking solution generation.
- S: Population size (number of nests).
- : Fitness evaluation function (representing total WSN lifetime).
- : Discovery probability (fraction of abandoned nests).
- : Solution vector i at iteration t.
6.2. Proposed Improved Cuckoo Search
6.2.1. Improved Cuckoo Search Solution’s Structure
- Each nest has a full solution as a matrix of , which is the Sink sojourn point and duration in WSN.
- The fitness function of each solution, , is the objective function, which is maximizing the WSN lifetime, .
6.2.2. Enhanced Initialization Phase
6.2.3. Generating First Population
6.2.4. Search Process
6.3. Analytical Results
| Algorithm 2 Improved Cuckoo Search (CS) algorithm. |
Input:
Output:
|
6.3.1. Achieved WSN Lifetime
6.3.2. Execution Time
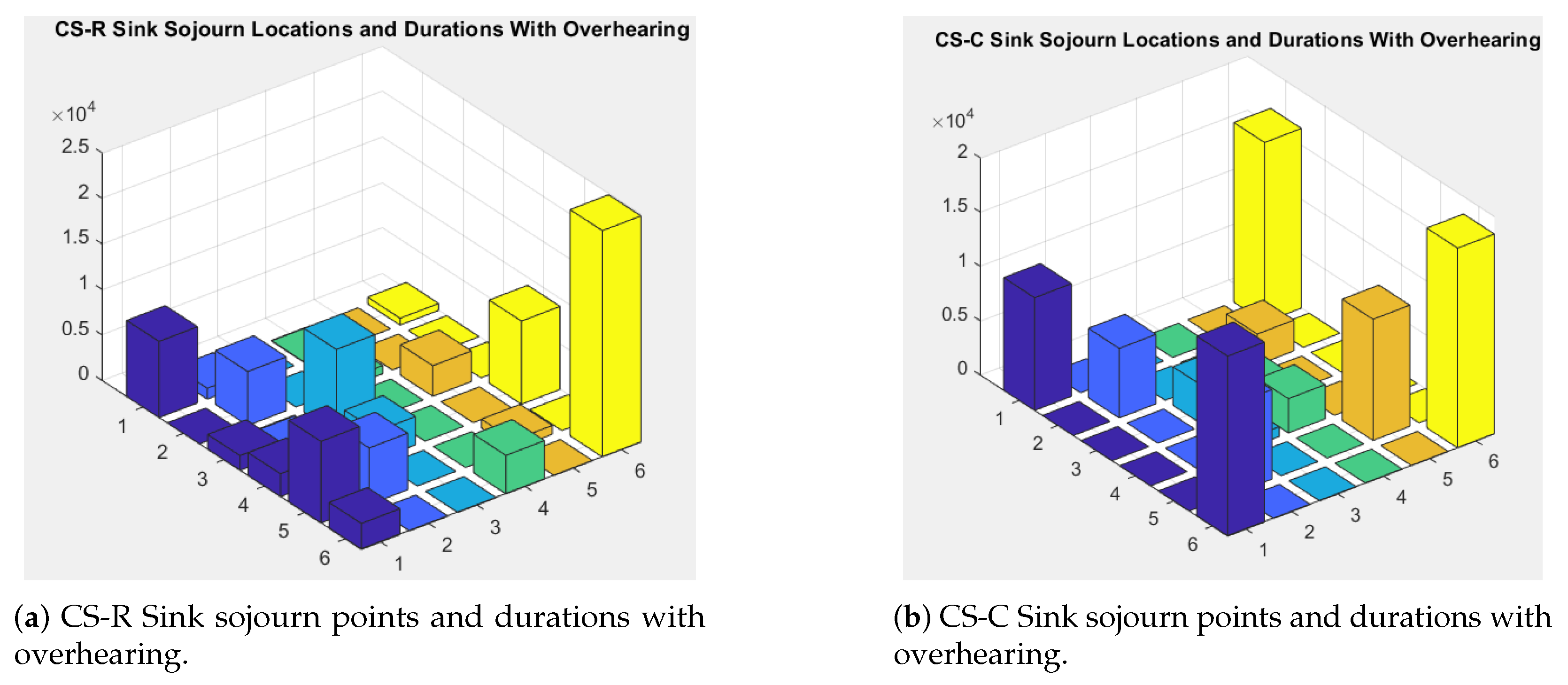
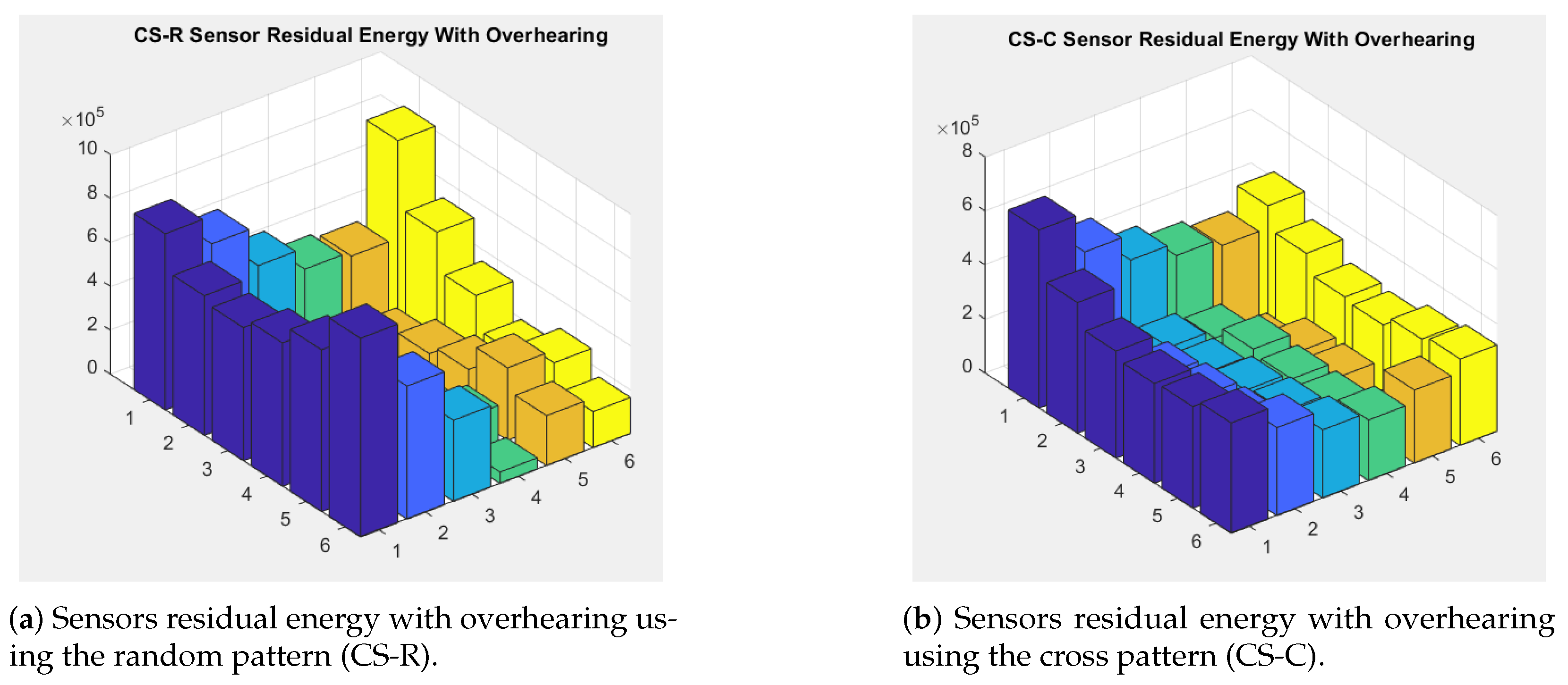
6.3.3. Sink’s Sojourn and Sensors’ Residual Energy Distribution
7. Comparative Analysis
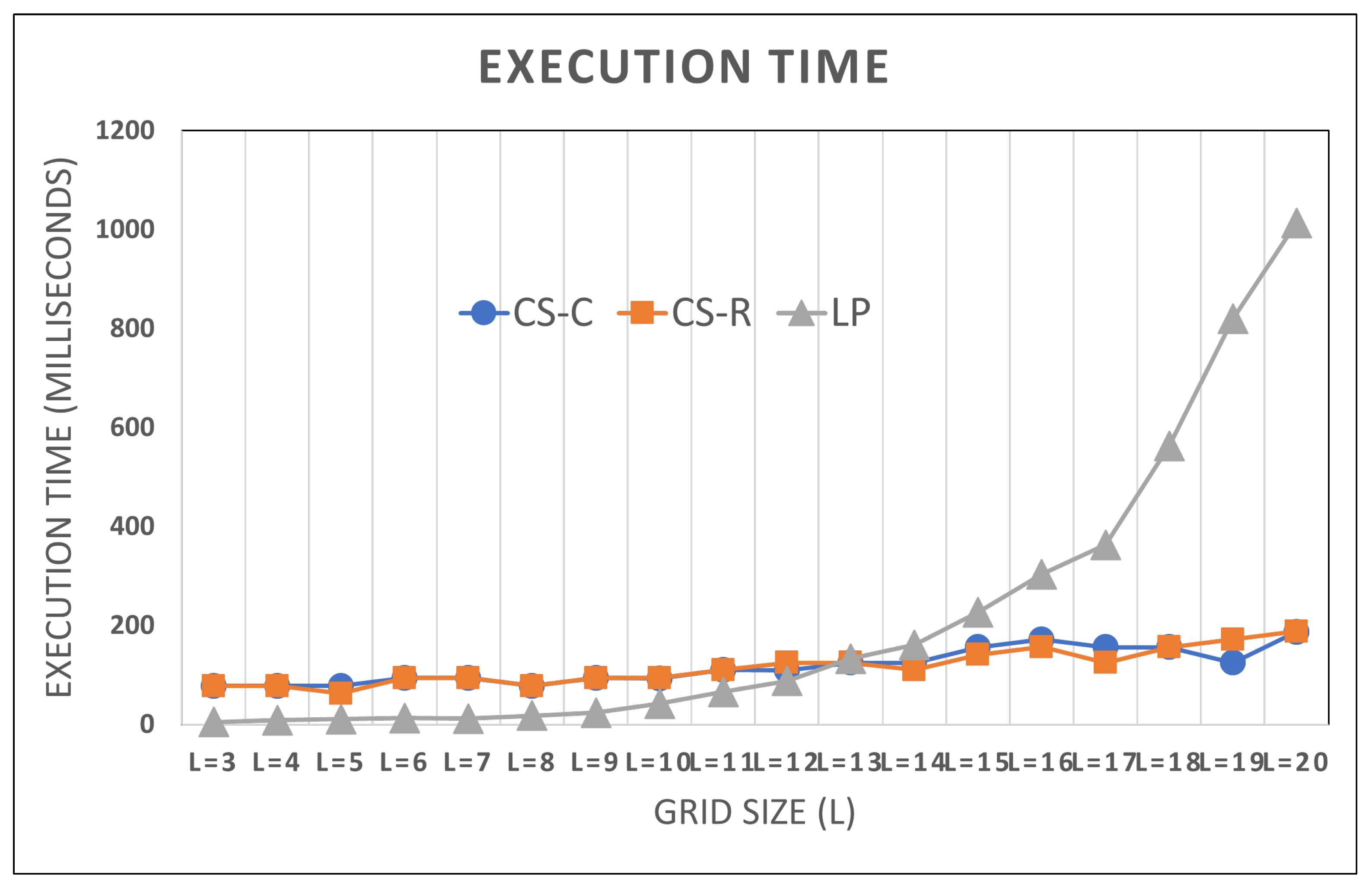
7.1. Execution Time
7.2. Achieved WSN Lifetime
7.3. Sensors Residual Energy
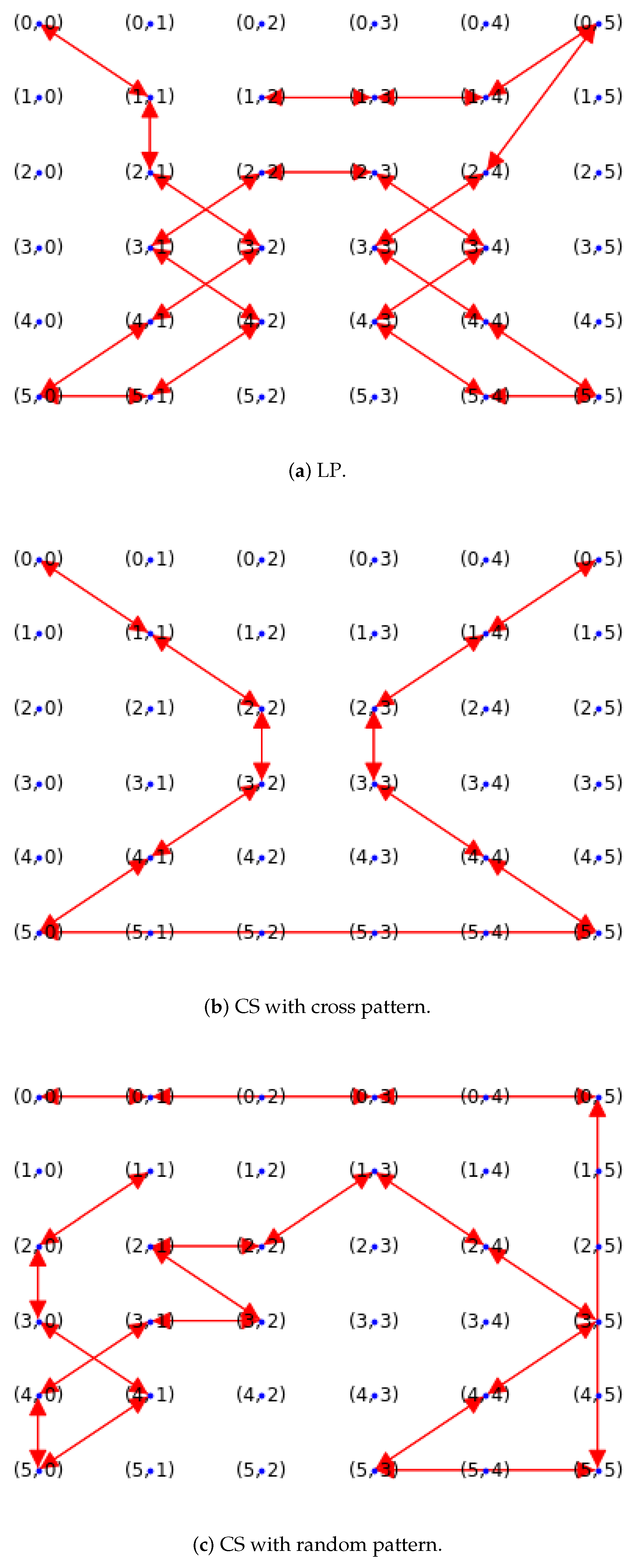
8. Optimal Sink Trajectory Planning Using TSP-Based Mobility Optimization
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allakonda, M.; Anjareddy, G.; Shanthi, B.; Kuntala, R.; Venkata Balamurali Krishna, K.; Reddy, P.N. Enhancing Military Surveillance Through WSN-Machine Learning Fusion for Anomaly Detection and Threat Identification. In Proceedings of the Third International Conference on Cognitive and Intelligent Computing (ICCIC 2023), Hyderabad, India, 8–9 December 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 587–596. [Google Scholar]
- Vinoth Kumar, P.; Jayanthi, R.; Sivaranjani, S.; Pradeep, S. Clustering Technique Based on ARSH-FATI for Data Transmission in WSN-IoT Healthcare System. In Proceedings of the 2025 International Conference on Multi-Agent Systems for Collaborative Intelligence (ICMSCI), Erode, India, 20–22 January 2025. [Google Scholar] [CrossRef]
- Mohamed, B.; Abdellatif, E. Fog-Enabled IoT Robotic System for Efficient Date Palm Monitoring in Moroccan Oases. IoT 2025, 6, 16. [Google Scholar] [CrossRef]
- Sharmin, N.; Karmaker, A.; Lambert, W.L.; Alam, M.S.; Shawkat, M.S.A. Minimizing the energy hole problem in wireless sensor networks: A wedge merging approach. Sensors 2020, 20, 277. [Google Scholar] [CrossRef]
- Shafique, T.; Gantassi, R.; Soliman, A.H.; Amjad, A.; Hui, Z.Q.; Choi, Y. A review of Energy Hole mitigating techniques in multi-hop many to one communication and its significance in IoT oriented Smart City infrastructure. IEEE Access 2023, 11, 121340–121367. [Google Scholar] [CrossRef]
- D’Andreagiovanni, F.; Nardin, A. Towards the fast and robust optimal design of wireless body area networks. Appl. Soft Comput. 2015, 37, 971–982. [Google Scholar] [CrossRef]
- Hung, C.W.; Zhuang, Y.D.; Lee, C.H.; Wang, C.C.; Yang, H.H. Transmission power control in wireless sensor networks using fuzzy adaptive data rate. Sensors 2022, 22, 9963. [Google Scholar] [CrossRef]
- Asadollahi, H.; Zandi, S.; Asharioun, H. Maximizing Network Lifetime in Many-to-One Wireless Sensor Networks (WSNs). Wirel. Pers. Commun. 2022, 123, 2971–2983. [Google Scholar] [CrossRef]
- Joon, R.; Tomar, P.; Kumar, G.; Balusamy, B.; Nayyar, A. Unequal clustering energy hole avoidance (UCEHA) algorithm in cognitive radio wireless sensor networks (CRWSNs). Wirel. Netw. 2025, 31, 735–757. [Google Scholar] [CrossRef]
- Yadav, A.; Kumar, S.; Vijendra, S. Network Life Time Analysis of WSNs Using Particle Swarm Optimization. Procedia Comput. Sci. 2018, 132, 805–815, International Conference on Computational Intelligence and Data Science. [Google Scholar] [CrossRef]
- Wu, X.; Chen, Z.; Zhong, Y.; Zhu, H.; Zhang, P. End-to-end data collection strategy using mobile Sink in wireless sensor networks. Int. J. Distrib. Sens. Netw. 2022, 18, 15501329221077932. [Google Scholar] [CrossRef]
- Sridhar, M.; Pankajavalli, P. Adaptive data aggregation scheme with optimal hop selection using optimized distributed Voronoi-based cooperation with energy-aware dual-path geographic routing protocol. Wirel. Pers. Commun. 2023, 130, 2215–2230. [Google Scholar] [CrossRef]
- Fu, X.; Yang, Y.; Postolache, O. Sustainable multipath routing protocol for multi-Sink wireless sensor networks in harsh environments. IEEE Trans. Sustain. Comput. 2020, 6, 168–181. [Google Scholar] [CrossRef]
- Alsolai, H.; Maashi, M.; Saeed, M.K.; Mohamed, A.; Assiri, M.; Abdelbagi, S.; Drar, S.; Abdelmageed, A.A. Leveraging metaheuristic unequal clustering for hotspot elimination in energy-aware wireless sensor networks. Sensors 2023, 23, 2636. [Google Scholar] [CrossRef]
- Wang, Z.; Duan, J. An Unequal Clustering and Multi-Hop Routing Protocol Based on Fuzzy Logic and Q-Learning in WSNs. Entropy 2025, 27, 118. [Google Scholar] [CrossRef]
- Sherazi, H.H.R.; Grieco, L.A.; Boggia, G. A comprehensive review on energy harvesting MAC protocols in WSNs: Challenges and tradeoffs. Ad Hoc Netw. 2018, 71, 117–134. [Google Scholar] [CrossRef]
- Amengu, A.A.; Abdulai, J.D.; Katsriku, F.A.; Adu-Manu, K.S. SMAC-Based WSN Protocol-Current State of the Art, Challenges, and Future Directions. J. Comput. Netw. Commun. 2022, 2022, 6707413. [Google Scholar] [CrossRef]
- Yun, Y.; Xia, Y.; Behdani, B.; Smith, J.C. Distributed Algorithm for Lifetime Maximization in a Delay-Tolerant Wireless Sensor Network with a Mobile Sink. IEEE Trans. Mob. Comput. 2013, 12, 1920–1930. [Google Scholar] [CrossRef]
- Wang, Y.C.; Chen, K.C. Efficient Path Planning for a Mobile Sink to Reliably Gather Data from Sensors with Diverse Sensing Rates and Limited Buffers. IEEE Trans. Mob. Comput. 2019, 18, 1527–1540. [Google Scholar] [CrossRef]
- Xie, L.; Shi, Y.; Hou, Y.T.; Lou, W.; Sherali, H.D.; Zhou, H.; Midkiff, S.F. A Mobile Platform for Wireless Charging and Data Collection in Sensor Networks. IEEE J. Sel. Areas Commun. 2015, 33, 1521–1533. [Google Scholar] [CrossRef]
- Çorapsız, M.F. Lifetime maximization of wireless sensor networks while ensuring intruder detection. Soft Comput. 2024, 28, 4197–4215. [Google Scholar] [CrossRef]
- El-Fouly, F.H.; Altamimi, A.B.; Ramadan, R.A. Energy and environment-aware path planning in wireless sensor networks with mobile Sink. Sensors 2022, 22, 9789. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Han, G.; Zhang, H. A honeycomb structure based data gathering scheme with a mobile Sink for wireless sensor networks. Peer -Peer Netw. Appl. 2017, 10, 484–499. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Shu, W.; Chou, J. Ant colony optimization algorithm based on mobile Sink data collection in industrial wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 152. [Google Scholar] [CrossRef]
- Jong, G.J.; Aripriharta; Hendrick; Horng, G.J. A Novel Queen Honey Bee Migration (QHBM) Algorithm for Sink Repositioning in Wireless Sensor Network. Wirel. Pers. Commun. 2017, 95, 3209–3232. [Google Scholar] [CrossRef]
- Iwendi, C.; Maddikunta, P.K.R.; Gadekallu, T.R.; Lakshmanna, K.; Bashir, A.K.; Piran, M.J. A metaheuristic optimization approach for energy efficiency in the IoT networks. Softw. Pract. Exp. 2021, 51, 2558–2571. [Google Scholar] [CrossRef]
- Dash, L.; Pattanayak, B.K.; Laha, S.R.; Pattnaik, S. Enhanced network lifetime with EPMS: An energy-aware PSO based routing algorithm with mobile Sink support for hot spot mitigation in WSNs. Int. J. Intell. Syst. Appl. Eng. 2023, 11, 18–26. [Google Scholar]
- Han, X.; Mu, X.; Zhong, J. HGFF: A Deep Reinforcement Learning Framework for Lifetime Maximization in Wireless Sensor Networks. IEEE Trans. Artif. Intell. 2024, 6, 859–873. [Google Scholar] [CrossRef]
- Sangeetha, S.; Victoire, T.; Premkumar, M.; Sowmya, R. ExAq-MSPP: An Energy-Efficient Mobile Sink Path Planning Using Extended Aquila Optimization Algorithm. Int. J. Comput. Intell. Syst. 2024, 17, 1–21. [Google Scholar] [CrossRef]
- Al-Salahat, N.N.; Eljaafreh, Y.G. Maximizing the Lifetime of Wireless Sensor Networks with Mobile Sink. J. Commun. 2023, 18, 613–620. [Google Scholar] [CrossRef]
- Abu Taleb, A.; Abu Al-Haija, Q.; Odeh, A. Efficient mobile Sink routing in wireless sensor networks using bipartite graphs. Future Internet 2023, 15, 182. [Google Scholar] [CrossRef]
- Mohapatra, S.; Behera, P.K.; Sahoo, P.K.; Ojha, M.K.; Swarup, C.; Singh, K.U.; Pandey, S.K.; Kumar, A.; Goswami, A. Modified ring routing protocol for mobile Sinks in a dynamic sensor network in smart monitoring applications. Electronics 2023, 12, 281. [Google Scholar] [CrossRef]
- Ye, W.; Heidemann, J.; Estrin, D. An energy-efficient MAC protocol for wireless sensor networks. In Proceedings of the Proceedings. Twenty-First Annual Joint Conference of the IEEE Computer and Communications Societies, New York, NY, USA, 23–27 June 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 3, pp. 1567–1576. [Google Scholar]
- Wang, Z.M.; Basagni, S.; Melachrinoudis, E.; Petrioli, C. Exploiting Sink Mobility for Maximizing Sensor Networks Lifetime. In Proceedings of the 38th Annual Hawaii International Conference on System Sciences, Big Island, HI, USA, 6 January 2005; p. 287a, ISSN 1530-1605. [Google Scholar] [CrossRef]
- Google OR-Tools. 2008. Available online: https://developers.google.com/optimization (accessed on 19 July 2008).
- Mohammed, L.A.; Hasan, A.M.; Hamza, E.K. Optimizing Energy Efficiency in Wireless Sensor Networks Using Dijkstra’s Algorithm. Instrum. Mes. Metrol. 2024, 23, 307. [Google Scholar] [CrossRef]
- Houssein, E.H.; Saad, M.R.; Djenouri, Y.; Hu, G.; Ali, A.A.; Shaban, H. Metaheuristic algorithms and their applications in wireless sensor networks: Review, open issues, and challenges. Clust. Comput. 2024, 27, 13643–13673. [Google Scholar] [CrossRef]
- Yang, X.S. Harmony Search as a Metaheuristic Algorithm. In Music-Inspired Harmony Search Algorithm: Theory and Applications; Geem, Z.W., Ed.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–14. [Google Scholar] [CrossRef]
- Civicioglu, P.; Besdok, E. A conceptual comparison of the Cuckoo-search, particle swarm optimization, differential evolution and artificial bee colony algorithms. Artif. Intell. Rev. 2013, 39, 315–346. [Google Scholar] [CrossRef]
- Wang, T.; Meskin, M.; Grinberg, I. Comparison between particle swarm optimization and Cuckoo Search method for optimization in unbalanced active distribution system. In Proceedings of the 2017 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 14–17 August 2017; pp. 14–19. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Hessin, A.N.; Abdel-Fatah, L. A comprehensive study of cuckoo-inspired algorithms. Neural Comput. Appl. 2018, 29, 345–361. [Google Scholar] [CrossRef]
- Reddy, M.R.; Chandra, M.L.R.; Dilli, R. Enhanced Cuckoo Search Optimization with Opposition-Based Learning for the Optimal Placement of Sensor Nodes and Enhanced Network Coverage in Wireless Sensor Networks. Appl. Sci. 2025, 15, 8575. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy flights. In Proceedings of the 2009 World Congress on Nature Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar] [CrossRef]
- Bonabeau, E.; Dorigo, M.; Theraulaz, G.; Theraulaz, G. Swarm Intelligence: From Natural to Artificial Systems; Oxford University Press: Oxford, UK, 1999; Number 1. [Google Scholar]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. (CSUR) 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Frome, UK, 2010. [Google Scholar]
- Adekanmbi, O.; Green, P. Conceptual comparison of population based metaheuristics for engineering problems. Sci. World J. 2015, 2015, 936106. [Google Scholar] [CrossRef] [PubMed]
- RinnooyKan, A.; Telgen, J. The complexity of linear programming. Stat. Neerl. 1981, 35, 91–107. [Google Scholar] [CrossRef]
- Reinelt, G. The Traveling Salesman: Computational Solutions for TSP Applications; Springer: Berlin/Heidelberg, Germany, 2003; Volume 840. [Google Scholar]
- Christofides, N. Worst-Case Analysis of a New Heuristic for the Travelling Salesman Problem; Technical Report; Carnegie-Mellon University, Management Sciences Research Group: Pittsburgh, PA, USA, 1976. [Google Scholar]
- Andrews, J.; Sethian, J. Fast marching methods for the continuous traveling salesman problem. Proc. Natl. Acad. Sci. USA 2007, 104, 1118–1123. [Google Scholar] [CrossRef] [PubMed]







| Reference | Approach | Key Features | Advantages | Limitations | Overhearing | Energy Balancing/Lifetime |
|---|---|---|---|---|---|---|
| Yun et al. [18] | LP + fractional knapsack | Distributed algorithm with energy, flow, and traffic constraints | Near-optimal lifetime, distributed decisions | Single Sink, limited scalability | No | Lifetime |
| Wang et al. [19] | LP + mobile relay and Sink | Trade-off analysis, relay placement | Suitable for dense large networks | Higher communication and computation overhead | No | Lifetime |
| Xie et al. [20] | LP + Wireless Charging Vehicle (WCV) | Balanced data collection and recharging | Continuous operation | Path discretization and complex timing | No | Lifetime and energy |
| WSNDID [21] | MILP + Lagrangean heuristic | Scheduling, routing, intruder detection | High detection rate, scalable | High computational cost | No | Lifetime and detection |
| El-Fouly et al. [22] | 0/1 ILP + Swarm Intelligence | Path planning, Cluster Heads | Improved energy saving and timely delivery | ILP complexity, approximate solution | No | Lifetime |
| Reference | Approach | Key Features | Advantages | Limitations | Overhearing | Energy Balancing vs. Lifetime |
|---|---|---|---|---|---|---|
| Zhu C. et al. [23] | Honeycomb + RM/DGM/EGM | Partitioned nodes, movement strategies | Reduces energy waste, DGM best | Limited dynamic adaptability | No | Energy balancing |
| Zhang H. et al. [24] | Ant Colony + entropy weighting | Rendezvous node selection, energy balance | Balances node energy | Does not maximize network lifetime | No | Energy balancing |
| Jong G. J [25] | QHBM (bee-inspired) | CHs as scouts, Sink follows CH | Reduces routing overhead | Random CH selection | No | Energy balancing |
| Iwendi et al. [26] | Hybrid WOA + SA | Optimal CH selection | Outperforms other metaheuristic tasks | Medium computational complexity | No | Energy balancing |
| Dash et al. [27] | EPMS (PSO + Mobile Sink) | Cluster formation + Sink path optimization | High energy efficiency | Computational overhead for large networks | No | Energy balancing |
| Han et al. [28] | HGFF (GNN + DRL) | Graph representation, greedy Sink policy | Outperforms heuristics, practical | Requires training, complex for very large networks | No | Lifetime and energy |
| Sangeetha et al. [29] | ExAq-MSPP (Aquila Optimization) | Voronoi placement, optimized Sink path | Energy efficient, reduces delay, improves throughput | Computationally intensive | No | Lifetime and energy |
| Reference | Approach | Key Features | Advantages | Limitations | Overhearing | Energy Balancing vs. Lifetime |
|---|---|---|---|---|---|---|
| Nusaiba N. et al. [30] | Enhanced LEACH + Mobile Sink | Sink selects CH based on geographic location and data load | Improves residual energy, slight increase in alive nodes | Small network, minor improvement | No | Energy balancing |
| Abu Taleb et al. [31] | Bipartite graph + BFS traversal | Sink visits two disjoint sets iteratively | Reduces buffer overflow and delay | Limited to medium networks | No | Energy balancing |
| Mohapatra et al. [32] | Virtual ring + greedy geographic Sink movement | Ring shares Sink location, dynamic CH selection | Reduces overhead, improves throughput and energy | Reconfiguration needed if nodes die or Sink moves | No | Energy balancing |
| Parameter | Value |
|---|---|
| 1,350,000 J | |
| e | 0.62 J/bit |
| r | 1 bit/s |
| WSN Size | WSN Lifetime (s) | Decrease in Percentage | ||
|---|---|---|---|---|
| Without Overhearing | With Overhearing | |||
| 3 | 9 | 802,207 | 231,751 | 71% |
| 4 | 16 | 451,917 | 171,888 | 62% |
| 5 | 25 | 320,054 | 141,999 | 56% |
| 6 | 36 | 263,601 | 120,256 | 54% |
| 7 | 49 | 222,869 | 104,031 | 53% |
| 8 | 64 | 193,126 | 91,773 | 52% |
| 9 | 81 | 169,493 | 82,153 | 52% |
| 10 | 100 | 151,529 | 74,416 | 51% |
| 11 | 121 | 137,219 | 68,028 | 50% |
| 12 | 144 | 125,451 | 62,680 | 50% |
| 13 | 169 | 115,285 | 58,114 | 50% |
| 14 | 196 | 106,707 | 54,176 | 49% |
| 15 | 225 | 99,423 | 50,742 | 49% |
| 16 | 256 | 93,075 | 47,725 | 49% |
| 17 | 289 | 87,360 | 45,050 | 48% |
| 18 | 324 | 82,370 | 42,658 | 48% |
| 19 | 361 | 77,978 | 40,510 | 48% |
| 20 | 400 | 73,986 | 38,569 | 48% |
| 25,562.38 | 0 | 0 | 0 | 0 | 21,909.61 |
| 0 | 883.449 | 548.3728 | 97.8 | 2198.067 | 1100 |
| 0 | 621.3749 | 1083.469 | 1233.625 | 2070 | 0 |
| 0 | 281.4028 | 1324.894 | 1626.36 | 2270 | 0 |
| 0 | 4842.191 | 1676.129 | 1386.798 | 4818.932 | 1654.615 |
| 21,310.66 | 0 | 0 | 0 | 0 | 21,761.73 |
| 28,662.13 | 0 | 0 | 0 | 28,662.13 | |
| 0 | 10,155.87 | 0 | 10,155.87 | ||
| 0 | 0 | 27,082.33 | 27,082.33 | 0 | |
| 0 | 0 | 27,082.33 | 27,082.33 | 0 | |
| 10,155.87 | 0 | 0 | 0 | 10,155.87 | 0 |
| 18,506.26 | 10,155.87 | 0 | 0 | 0 | 28,662.13 |
| 1,008,862 | 0 | 0 | 155,317 | 1,008,862 | |
| 155,317 | 533,116 | 0 | 0 | 533,116 | |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 369,403 | 167,910 | 0 | 0 | 533,116 | 155,317 |
| 945,896 | 369,403 | 0 | 0 | 155,317 | 1,008,862 |
| 50,199 | 0 | 7129 | 32,501 | 116,321 | |
| 12,193 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 10,414 | 0 | 0 | 0 | 0 | 0 |
| 62,786 | 0 | 0 | 0 | 0 | 28,915 |
| 127,713 | 36,975 | 0 | 0 | 55,530 | 105,229 |
| WSN Size | WSN Lifetime (s) | ||
|---|---|---|---|
| L | CS-C | CS-R | |
| 3 | 9 | 210,974 | 219,545 |
| 4 | 16 | 150,958 | 145,280 |
| 5 | 25 | 119,392 | 116,982 |
| 6 | 36 | 100,243 | 96,687 |
| 7 | 49 | 76,036 | 79,712 |
| 8 | 64 | 72,692 | 67,319 |
| 9 | 81 | 63,213 | 60,118 |
| 10 | 100 | 50,876 | 53,057 |
| 11 | 121 | 49,578 | 49,908 |
| 12 | 144 | 44,127 | 45,621 |
| 13 | 169 | 39,406 | 38,157 |
| 14 | 196 | 34,685 | 36,575 |
| 15 | 225 | 33,559 | 34,011 |
| 16 | 256 | 31,516 | 35,496 |
| 17 | 289 | 28,853 | 33,100 |
| 18 | 324 | 26,220 | 28,600 |
| 19 | 361 | 24,240 | 29,259 |
| 20 | 400 | 24,851 | 25,945 |
| WSN Size | Execution Time (ms) | ||
|---|---|---|---|
| L | CS-C | CS-R | |
| 3 | 9 | 78 | 78 |
| 4 | 16 | 78 | 78 |
| 5 | 25 | 78 | 63 |
| 6 | 36 | 94 | 94 |
| 7 | 49 | 94 | 94 |
| 8 | 64 | 78 | 78 |
| 9 | 81 | 94 | 94 |
| 10 | 100 | 93 | 94 |
| 11 | 121 | 110 | 110 |
| 12 | 144 | 109 | 125 |
| 13 | 169 | 125 | 125 |
| 14 | 196 | 125 | 110 |
| 15 | 225 | 156 | 141 |
| 16 | 256 | 172 | 157 |
| 17 | 289 | 156 | 125 |
| 18 | 324 | 156 | 156 |
| 19 | 361 | 125 | 172 |
| 20 | 400 | 187 | 188 |
| 10,377 | 0 | 0 | 0 | 0 | 16,539 |
| 0 | 6398 | 0 | 0 | 2842 | 0 |
| 0 | 0 | 3555 | 2100 | 0 | 0 |
| 0 | 0 | 893 | 3154 | 0 | 0 |
| 0 | 8259 | 0 | 0 | 11,157 | 0 |
| 16,575 | 0 | 0 | 0 | 0 | 18,395 |
| 8357 | 1186 | 0 | 53 | 0 | 755 |
| 0 | 5917 | 0 | 890 | 0 | 0 |
| 1617 | 92 | 9211 | 0 | 3359 | 0 |
| 2520 | 2419 | 3116 | 0 | 0 | 9122 |
| 8965 | 6208 | 0 | 0 | 972 | 0 |
| 2849 | 0 | 0 | 4232 | 0 | 24,846 |
| 659,133 | 512,992 | 417,816 | 369,595 | 342,141 | 423,985 |
| 483,226 | 184,553 | 187,643 | 156,897 | 59,030 | 340,416 |
| 396,100 | 240,853 | 188,655 | 208,816 | 134,606 | 271,644 |
| 369,115 | 254,863 | 214,567 | 190,987 | 131,476 | 260,444 |
| 376,228 | 260,031 | 230,128 | 187,529 | 53,114 | 300,831 |
| 408,338 | 325,932 | 252,761 | 224,174 | 270,365 | 319,989 |
| 801,790 | 674,567 | 494,162 | 396,622 | 375,142 | 820,061 |
| 635,307 | 326,539 | 204,844 | 78,149 | 98,269 | 518,727 |
| 606,102 | 348,652 | 42,217 | 27,057 | 162,243 | 345,890 |
| 652,494 | 387,962 | 207,113 | 95,626 | 206,146 | 195,826 |
| 736,766 | 501,756 | 289,361 | 174,622 | 329,407 | 271,329 |
| 904,800 | 605,811 | 369,220 | 52,100 | 227,572 | 164,864 |
| WSN Size | Sink Mobility Model Type | Route | Distance (Number of Nodes) |
|---|---|---|---|
| L = 6 | LP | 22 | |
| CS-C | 20 | ||
| CS-R | 25 | ||
| L = 9 | LP | 53 | |
| CS-C | 32 | ||
| CS-R | 50 |
| WSN Size | Sink Mobility Model Type | Route | Distance (Number of Nodes) |
|---|---|---|---|
| L = 6 | LP | 24 | |
| CS-C | 20 | ||
| CS-R | 27 | ||
| L = 9 | LP | 46 | |
| CS-C | 32 | ||
| CS-R | 52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Mamari, G.T.; Bouabdallah, F.; Cherif, A. Extending WSN Lifetime via Optimized Mobile Sink Trajectories: Linear Programming and Cuckoo Search Approaches with Overhearing-Aware Energy Models. IoT 2025, 6, 54. https://doi.org/10.3390/iot6030054
Al-Mamari GT, Bouabdallah F, Cherif A. Extending WSN Lifetime via Optimized Mobile Sink Trajectories: Linear Programming and Cuckoo Search Approaches with Overhearing-Aware Energy Models. IoT. 2025; 6(3):54. https://doi.org/10.3390/iot6030054
Chicago/Turabian StyleAl-Mamari, Ghada Turki, Fatma Bouabdallah, and Asma Cherif. 2025. "Extending WSN Lifetime via Optimized Mobile Sink Trajectories: Linear Programming and Cuckoo Search Approaches with Overhearing-Aware Energy Models" IoT 6, no. 3: 54. https://doi.org/10.3390/iot6030054
APA StyleAl-Mamari, G. T., Bouabdallah, F., & Cherif, A. (2025). Extending WSN Lifetime via Optimized Mobile Sink Trajectories: Linear Programming and Cuckoo Search Approaches with Overhearing-Aware Energy Models. IoT, 6(3), 54. https://doi.org/10.3390/iot6030054






