Abstract
Gravitational Waves (GW) from coalescence of a Binary Neutron Star (BNS) and its accompanying short Gamma-Ray Burst (GRB) GW/GRB 170817A confirmed the presumed origin of these puzzling transients and opened up the way for relating properties of short GRBs to those of their progenitor stars and their surroundings. Here we review an extensive analysis of the prompt gamma-ray and late afterglows of this event. We show that a fraction of polar ejecta from the merger had been accelerated to ultra-relativistic speeds. This structured jet had an initial Lorentz factor of about 260 in our direction, which was from the jet’s axis, and was a few orders of magnitude less dense than in typical short GRBs. At the time of arrival to circum-burst material the ultra-relativistic jet had a close to Gaussian profile and a Lorentz factor in its core. It had retained in some extent its internal collimation and coherence, but had extended laterally to create mildly relativistic lobes—a cocoon. Its external shocks on the far from center inhomogeneous circum-burst material and low density of colliding shells generated slowly rising afterglows, which peaked more than 100 days after the prompt gamma-ray. The circum-burst material was somehow correlated with the merger. As non-relativistic outflows or tidally ejected material during BNS merger could not have been arrived to the location of the external shocks before the relativistic jet, circum-burst material might have contained recently ejected materials from resumption of internal activities, faulting and mass loss due to deformation and breaking of stars crusts by tidal forces during latest stages of their inspiral but well before their merger. By comparing these findings with the results of relativistic Magneto-Hydro-Dynamics (MHD) simulations and observed gravitational waves we conclude that progenitor neutron stars were most probably old, had close masses and highly reduced magnetic fields.
1. Introduction
As a light dominated species we are usually more confident about nature of objects when we can see them in our very restricted electromagnetic band of 380 nm to 740 nm -the visible band. For this reason since the discovery of Gamma-Ray Bursts (GRBs) in 1960’s efforts for understanding these enigmatic transients have relied on detecting their counterparts in optical and other electromagnetic bands with our extended eyes—the ground and space based telescopes. Observation of X-ray counterpart of GRB 970228 [1,2] by BeppoSAX satellite [3] led to its detection in optical by the William Herschel Telescope [4]. For the first time these observations proved that GRBs are extragalactic and in contrast to prediction of some models, have a broad band of electromagnetic emissions. Since then observation of thousands of GRBs and their afterglows in X-ray, for roughly all confirmed GRB detected by the Neil Gehrels Swift [5] and other spatial Gamma-ray observatories such as the Burst And Transient Source Experiment (BATSE) [6] and Fermi [7], and in optical/IR and radio for large fraction of them, have clarified many aspects of origin and physical mechanisms involved in their production. Notably, discovery of supernovae type Ib and Ic associated to long GRBs confirmed collapsar hypothesis and proved that they are produced by ultra-relativistic jets ejected from exploding massive stars—also called collapsars—at the end of their life. However, no direct evidence of the origin of short GRBs was available until the breakthrough observation of gravitational waves from merger of a binary neutron star by the Laser Interferometer Gravitational waves Observatory (LIGO) [8] and Virgo [9].
In many respects the short GRB 170817A associated to the first detection of gravitation waves from a Binary Neutron Star (BNS) merger [10,11,12,13] was unusual:
- The prompt gamma-ray was intrinsically faint and somehow softer than any other short GRB with known redshift;
- Its X-ray afterglow was not detected—despite several attempts as early as ∼ days [14,15], where T is the Fermi trigger time;
- It was finally detected at ∼ days [16], but surprisingly rather than fainting, its flux increased and peaked at ∼ days;
- The same behaviour was observed in radio bands;
- By contrast, the kilonova emission [17,18,19] in UV was brighter than expected [20].
Initially, the simplest explanation seemed to be an off-axis view of an otherwise ordinary short GRB [21,22] with a uniform (top hat) or structured ultra-relativistic jet [23,24]. Alternatively, the burst might have been formed by a mildly relativistic magnetized cocoon, i.e., an outflow with a Lorentz factor ∼2–3 at its breakout [25] from the envelop of merged stars [26,27,28,29,30,31], or a wide spiraling outflow [32]. However, further observations and detection of the decline of flux in all 3 observed energy bands, i.e., radio [29,33,34,35], optical/Infra-Red (IR) [36,37,38], and X-ray [39,40,41,42,43,44] after ≳ days was much earlier than the prediction of a fully off-axis jet, or a cocoon/jet breakout. In addition, detailed modeling of the prompt gamma-ray [45] showed that the most plausible initial Lorentz factor for the jet was , which is a few fold less than those of typical short GRBs [45,46]. Its density along our line of sight was also much less than other short GRBs.
Gradually it became clear that an additional source of X-ray [47] or presence of a highly relativistic component with a Lorentz factor of – in the outflow at late times is inevitable [38,39,48]. This meant that at least a fraction of the initial ultra-relativistic jet had survived internal shocks and energy dissipation up to long distances. These conclusions from analysis of afterglows are consistent with those obtained from modeling of the prompt gamma-ray emission alone. On the other hand, detection of the superluminal motion of the radio afterglow [49,50] proved off-axis view of the jet at late times and simulations of emissions from such a system led to estimation of a viewing angle – for its source [34,48,49].
In this review we first briefly summarize multi-probe multi-wavelength observations of Gravitational Waves/Gamma-Ray Burst (GW/GRB) 170817A in Section 2 and compare some of properties of this transient with other short GRBs. Then, in Section 3 we use a phenomenological model of relativistic shocks and synchrotron/self-Compton emission [46,51] (reviewed in [52]) to analyze both prompt gamma-ray and afterglows of this GRB. Interpretation of models and what they teach us about ejecta from the merger and its environment are discussed in Section 4. In Section 5 we use predictions of General Relativistic Magneto-Hydro-Dynamics (GRMHD) simulations and physics of neutron stars and compare them with conclusions obtained from multi-wavelength observations of GW/GRB 170817A and their analysis to see what we can learn about progenitor neutron stars, their life history, physical properties, and environment just before their coalescence. Finally, in Section 6 as outline we give a qualitative description of this transient and briefly discuss prospectives for deeper understanding of compact objects with increasing data and new probes.
We should remind that this review is concentrated on the GRB component of the merger and does not address other components, namely the ejected disk/torus and its kilonova emission and the merger remnant. They are very important subjects by their own and need separate analyses.
2. Review of Multi-Probe, Multi-Wavelength Observations of GW/GRB 170817A
GW 170817A was the first gravitation wave source detected in a panoramic range of electromagnetic energy bands. In this section we briefly review its observations and their findings.
2.1. Gravitational Waves (GW)
At 12:41:04 UTC on 17 August 2017 the Advanced LIGO and Advanced Virgo gravitational wave detectors registered a low amplitude signal lasting for ∼100 s, starting at 24 Hz frequency [10]. These are hallmarks of gravitational wave emission from inspiral of low mass compact binary objects, where is the solar mass. Further analysis of gravitational wave data confirmed a chirp mass , a total mass , and individual masses of – and – [11]. These masses are in neutron star mass range and led to conclusion that a BNS merger was the source of the observed GW signal.
Due to low sensitivity of LIGO-Virgo detectors at frequencies Hz—necessary for analysing post-merger signal—estimation of radius, tidal deformability, and Equation of States (EoS) of progenitors are model dependent. To estimate radius and deformability of progenitor neutron stars using gravitation wave data only—except for the position, which was fixed to that of electromagnetic counterpart—LIGO-Virgo Collaboration employed two approaches in their Markov chain search for the best model [53]. The first method uses directly deformability . In the second approach equation of state is sampled from a family of 4-parameter functions. p and are pressure and density of nuclear matter of the neutron stars, respectively. Results of this analysis marginalized over the selection methods can be summarized as the followings: Radius of the progenitors – km and – km; Tidal deformability parameters , and ; Stiff EoS such as H4 and MPA1 disfavored. The estimated radius of progenitors are well in the expected range [54], but constraints obtained for deformability from this analysis are not strong.
Authors of [55] use gravitational wave data, assume a power-law relation between mass ratio and deformability ratio, and add priors from observed mass ratio of galactic binary neutron stars and pulsars to their analysis to reduce the volume of parameter space. Under this additional input they find and – km, where binary tidal deformability is defined as:
and is the radius for a neutron star of mass . These ranges of radius and deformability cover results for various choices of mass ration prior. In an analysis by [56] a more fundamental formulation of equation of state using chiral effective field theory and without any prior on mass ration leads to and – km. Additionally, authors of [57] use LIGO-Virgo findings as posterior for simulations of kilonova emission to model optical/IR emissions of GW/GRB/Kilonova 170817 by one or two dynamical component with velocities . They find a lower limit of for binary deformability of progenitor BNS. This independent estimation further decreases the allowed range of and thereby rules out very soft equations of state.
The range of neutron stars radius obtained by LIGO-Virgo analysis is on the middle of the range obtained by [55,56]. Moreover, according to these analyses a small radius of km for stars in a close mass BNS with masses similar to what is concluded from GW is consistent with optical emission of a blue kilonova with a relatively low neutron content. The observed excess of blue/UV emission [20,58] (see also Section 2.4) can be explained by an excess of shock heated dynamical ejecta. However, such a compact progenitor couldn’t make a sufficiently massive accretion disk to explain IR emission at days [59]. A neutrino heated magnetically accelerated wind from a Hyper-Massive Neutron Star (HMNS) living for ∼ 0.1–1 s may explain dichotomy of dynamical ejecta from kilonova concluded in [57] and reconcile observed blue and red light curves. However, hydrodynamical simulations of HMNS shows that viscous shear may be not enough and reprocessing of photons and/or magnetic pressure should be involved in ejection of significant mass with high velocity [60].
In summary, theoretical knowledge about very complex physics of neutron stars, their evolution, and how they influence measurable outcomes of BNS merger is not still sufficiently mature and interpretation of data in this review and elsewhere should be considered as preliminary.
2.2. Prompt Gamma-Ray
GRB 170817A was detected by the Fermi Gamma-ray Burst Monitor (GBM) [61] and the Integral imager IBIS [62] detectors at about s after the end of inspiral stage of gravitational waves. It lasted for about 2 s, had an integrated fluence of erg cm in the 10 keV to 1 MeV Fermi-GBM band and erg cm in the Integral-IBIS 75 keV to 2 MeV band. The peak energy was keV. No extended emission was detected by these instruments. Unfortunately at the time of prompt gamma-ray emission the source was not in the field of view of the Swift Burst Alert Telescope (BAT). For this reason no early follow-up data from days is available, except for an upper limit of >4-sigma on any excess from background in 10 keV to 10 MeV band from Konus-Wind satellite [63].
Despite lack of early follow up, detection of the gravitational waves by both LIGO and Virgo resulted to a sky-localization area much smaller than previous GW events. This helped confirmation of coincidence between GRB 170817A and GW 170817 and follow up of the event in low energy electromagnetic bands [11]. The host galaxy of the transient was identified to be NGC 4993 [64,65] at , that is at a distance of Mpc for a vanilla CDM cosmology with km s Mpc, and . Such a distance makes GRB 170817A the closest GRB with known distance so far, see e.g., [66] for a review of properties of short GRBs and their hosts.
2.3. X-ray Afterglow
The earliest observation of GW/GRB 170817A in X-ray was at about s by the Swift-X-RayTelescope (XRT) [14]. There is also an upper limit of ∼ erg s cm in 0.3–10 keV band at around days on any excess of X-ray flux obtained from observations of the Swift-XRT in the sky area calculated from gravitational wave signal. Upper limit on the early X-ray afterglow from Chandra observations is erg s cm at ∼ days [15]. Although this limit is lower than flux of any previous short GRB with known redshift at similar epoch [67], it is higher than early flux of many short GRBs without redshift. Therefore, in an observational sense it is not very restrictive.
A X-ray counterpart was finally found by Chandra observatory [16,68] at ∼ days with a flux of erg s cm in 0.3–8 keV. Moreover, further observations [39] showed that the afterglow was gradually brightening. Late time brightening in X-ray and optical is claimed in a few other short [69] and long [70,71] GRBs. However, in contrast to prediction of off-axis models that brightening could last several hundreds of days, X-ray light curve peaked somewhere in the interval of ∼110–134 days [42] and began to decline afterward [40,41,43,44].
2.4. Optical/IR Afterglow
Despite low spatial resolution of LIGO-Virgo and Fermi-GBM, follow up of GW/GRB 170817A by a plethora of ground and space based telescopes [12,13] allowed to find optical/IR counterpart of the transient, known also as AT 2017 gfo [58,65], SSS17a [64,72], and DLT17ck [73]. The earliest detection of the optical counterpart was at ∼41 ksec ∼ days and further observations were performed at ∼ days onward [65]. Its magnitude was: , [58,65] and [64,72]. Spectroscopy data showed that optical/IR flux was dominated by a kilonova emission [19,20]. However, the UV emission seemed to be too bright. The initial conclusion was that the afterglow of the GRB might have had contributed, otherwise the mass of slow kilonova ejecta had to be larger than ∼0.01–0.03 predicted by kilonova models [19,20].
Later observations [34,36,37,38,39] showed that as expected, the kilonova/afterglow emission had rapidly declined. Unfortunately between ∼ days and 110 days there was no follow up observation in optical/IR bands. Nonetheless, later observations showed that the decline of the source continued with somehow shallower slope until ∼ days and then became steeper. The shallower slope in ∼– can be interpreted as when the decay of isotopes and cooling of kilonova ejecta [17,36,39] had reduced its optical/IR flux and contribution of GRB afterglow in visible bands became dominant.
2.5. Radio Afterglow
The counterpart of GW/GRB 170817 was also observed in gigahertz (GHz)radio band relatively early, that is at ∼ days onward [28,74]. But, earlier observations at ∼ days didn’t find any excess in the direction of the source [74]. Thus, similar to the X-ray emission the afterglow had been brightening. This conclusion was indeed confirmed by further observations [29,39] and was considered as a confirmation of off-axis view of a relativistic jet [39] or a mildly relativistic large opening angle outflow (a cocoon) [29]. The peak and turnover of the light curve was observed at ∼ days [33] and confirmed by later observations [34,35,49]. They ruled out a highly off-axis/side view of a relativistic jet or break out of a mildly relativistic cocoon as the origin of this weak GRB.
Overall, these observations showed that at late times the jet had to include a relativistic component [34,35,38,39,48,49]. In addition, the detection of superluminal motion of the radio source with an estimated apparent velocity of [49,50] confirmed its oblique view and allowed to obtain a lower limit for source’s Lorentz factor. This information along with simulation of the jet and consistency with other observations led to estimation of viewing angle – with respect to symmetry axis of the jet [34,39,48,49]. This off-axis angle is consistent with estimation of the orbit inclination [75] using only gravitational wave data.
2.6. Comparison with Other Short GRB-Kilonova Events
With an isotropic luminosity erg in 10 keV to 1 MeV band, at present GRB 170817A is intrinsically the faintest short burst with known redshift, see Figure 1. Moreover, the peak energy of this burst was close to the lowest peak energy of short bursts observed by Fermi-GBM, see Figure 31 in [76]. Therefore, it is not a surprise that its afterglows, specially in X-ray, were intrinsically the faintest among short bursts with known redshift, see e.g., [67]. However, it is not sure that GW/GRB 170817 could be classified as X-ray dark at early times, see Figure 2 and Section 4.2.1 for more discussion. Some short GRB’s such as GRB 070724A [77,78,79], GRB 111020A [80], GRB 130912A [81,82], and GRB 160821B [83,84] had similar or smaller fluxes than upper limit on X-ray mission from GRB 170817A at ∼ days after trigger. Notably, GRB 111020A is an interesting case because its host galaxy is most probably at redshift 0.02 [85]. It had a flux of ∼ erg s cm in 0.3–10 keV at ∼ s, and had to be decayed to ∼ erg s cm at ∼ days.
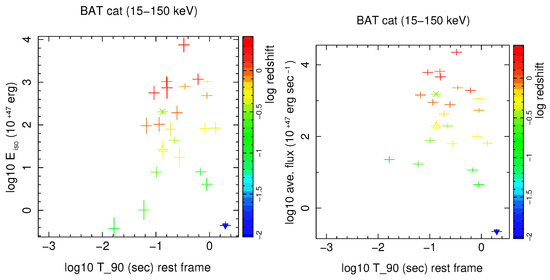
Figure 1.
Left: of short GRB’s with known redshift in the Swift-BAT 15–150 keV energy band. Right: Average flux of the same data. The data is taken from the Swift GRB on-line database https://swift.gsfc.nasa.gov/archive/grb_table/ using as selection criteria s, where is duration containing energy of all detected photons. Redshift is color coded. As GRB 170817A was not in the field of view of the Swift-BAT, we have used fluence measured in the Fermi-GBM 10 keV–2 MeV band. Thus, and average flux of GRB 170817A shown here are upper limits and shown with an inverse triangle as the symbol of upper limit. Star symbol presents kilonova/GRB 130603B and up-right triangle is GRB 160624A at , the only GRB with known redshift since 01 September 2015, considered as the beginning of the Advanced LIGO operation, which its GW could be apriori observed if it was at a lower redshift.
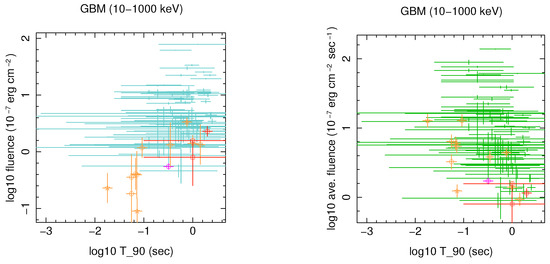
Figure 2.
Fluence and flux of nearby Swift short GRBs, GW-BNS events and Swift X-ray dark short GRBs. Left: Fluence in keV band; Right: Average flux. Symbols: Nearby short GRBs (star), X-ray dark (circle), GW events (square), Fermi-GBM short GRBs (data without symbol). GRB 080121 is distinguished by its color/grey level from other X-ray dark GRBs. For LIGO-Virgo 190425z and LIGO-Virgo 190510g only upper limit on gamma-ray is available and a s is used to calculate average flux.
The outline of this section is the importance of early discovery of electromagnetic (EM) counterpart of gravitational wave events for the identification and study of their sources. Specifically, it is crucial to improve angular resolution of gravitational wave detectors by multiplying their number, and gamma-ray telescopes by increasing their surface and resolution. This will help to reduce sky area to be searched for afterglows in lower energies.
3. Analysis and Modeling of GW/GRB 170817A Data
Observations of thousands of gamma-ray bursts and their afterglows by Swift, Fermi, Konus-wind, and other high energy satellites and ground based robotic telescopes have demonstrated that the main component in the prompt gamma-rays and their afterglows in lower energies is synchrotron emission generated in relativistic or mildly relativistic shocks. In this section we first briefly review a phenomenological shock and synchrotron emission formalism developed in [46,51]. Then, we use it to analyse both prompt gamma-ray and afterglows of GW/GRB 170817A. A more extensive review of the model can be found in [52]. The advantage of this formalism, despite its simplicity, is that it can be applied to both internal and external shocks, and thereby make it possible to construct a consistent and overall picture about: relativistic ejecta from compact objects such as collapsars, BNS and NS-BH mergers; clarify relations between properties of jets and their progenitors; and characteristics of the environment around progenitors, which influence GRB afterglows.
3.1. Phenomenological Formulation of Relativistic Shocks and Synchrotron/Self-Compton Emission
The phenomenological model of [46,51] assumes that GRB emissions are synchrotron/self-Compton produced by accelerated charged leptons in a dynamically active region in the head front—wake—of shocks between density shells inside a relativistic jet for prompt and with surrounding material for afterglows in lower energies. In addition to the magnetic field generated by Fermi processes in the active region, an external magnetic field precessing with respect to the jet axis may contribute in the production of synchrotron emission. Origin of this field is not relevant for this simple model. It can be the magnetic field of central object or Poynting flow imprinted into the jet/outflow.
An essential aspect of this model, which distinguishes it from other phenomenological GRB formulations, is the evolution of parameters with time. Moreover, simulation of each burst consists of a few time intervals—regimes—each corresponding to an evolution rule (model) for phenomenological quantities such as: fraction of kinetic energy transferred to fields and its variation; variation of the thickness of synchrotron/self-Compton emitting—active—region; etc. Division of simulated bursts to these intervals allows to change parameters and phenomenological evolution rules which are kept constant during one time interval. Physical motivation for such fine-tuning is the fact that GRB producing shocks are in a highly non-equilibrium and fast varying state. In fact, multiple variation of the slope of afterglows light curves, which presumably are produced by external shocks on the ISM or circumburst material is an evidence that they are not completely uniform and their anisotropies affect the emission. Definition of parameters of the model and phenomenological expressions used for the evolution of active region, which in the framework of this model cannot be calculated from first principles are given in Appendix A.
An important issue, specially when considering the best models for a specific burst, is the fact that parameters of the model are not completely independent from each others. For instance, fractions of kinetic energy transferred to induced electric and magnetic fields should depend on the strength of the shock, which in turn is determined by the density difference of colliding shells and their relative Lorentz factor. But there is no simple first principle way to incorporate these dependencies to the model.
Originally, the goal of the shock formalism developed in [46,51] was modeling prompt and early afterglow emissions, which are presumably generated by a fast and compact ejecta. For this reason, the model assumes uniform properties for the matter in the colliding shells and treats their evolution self-similarly. In other words, evolution of shocks and their synchrotron emission depend only on time or equivalently distance from the center, rather than to both time and distance as independent variables. Due to these simplifications, the formalism cannot take into account lateral variation of properties in the jet/outflow. However, as suggested in the literature [26,27,29,42,86] and we give more arguments in its favour in this review, the observed late afterglows of GW/GRB 170817A might have been produced by a continuous flow with a time varying profile of density and Lorentz factor. To take into account these variations we simulate afterglows as being generated by a composite jet with different density and speed for each component. They are simulated separately and can be considered as presenting part of the outflow with corresponding properties. We emphasize that these components are effective presentation of the sections of the jet or outflow, which due to the simplicity of the model could not be properly simulated as a single entity. Therefore, it is meaningless to e.g., consider their interaction with each others, just as interaction between parts of a split apple is meaningless.
3.2. Prompt Emission
The large number of parameters of the model used here make a systematic exploration of the parameter space too time consuming. For instance, on a 3.06 GHz Intel Duo CPU T9900 processor each simulation takes about 20–30 min for 3 regimes without inverse Compton and about 2 times longer with inverse Compton. If only 5 of parameters are changed with only 5 nodes for each, total calculation time without inverse Compton would be about minutes or about 130 days. To facilitate the search for plausible models for GW/GRB 170817A we use simulations of typical short GRBs in [46] as a departure point and adjust parameters, notably physically most important ones, namely: , p, , , , , , , and around their prototype values to obtain an acceptable fit to the Fermi-GBM prompt gamma-ray light curve and spectrum. We emphasize that as the exploration of parameter space of the model was not systematic, values of parameters for best models should be considered as order of magnitude estimation.
Giving the unusual characteristics of GRB 170817A, we try 3 ranges of Lorentz factor to see which one lead to a satisfactory model. Additionally, this exercise allows to explore the well known parameter degeneracy of shock/synchrotron model of gamma-ray bursts. The Lorentz factor intervals divide the models to 3 categories:
- Ultra-relativistic jet with [87,88,89], see also simulations in [46];
- Structured relativistic jet with [16,18];
- Mildly relativistic cocoon with [22,25,26,27,90].
Here a cocoon means a mildly relativistic, mildly collimated outflow with a Lorentz factor of ∼2–3 in its center, but its angular extension far from its core may have smaller Lorentz factors. This slow part of the outflow is not relevant for the high energy prompt emission but as we show in the next subsection it can be important for the radio afterglow.
Our tests show that a cocoon model cannot reproduce Fermi data. Therefore, we do not discuss such models further in this section. Examples of such models are discussed in [45]. We should also remind that cocoon models here are not exactly the same as cocoon break out model [25] suggested by [27,30], which is produced by different mechanisms. In any case, as we show in Section 3.3 a cocoon or cocoon break out or a chocked jet in the cocoon break out alone cannot explain prompt gamma-ray or afterglows, because X-ray afterglow needs a jet with an ultra-relativistic component.
Figure 3 shows light curves of 4 simulated bursts with best chi-square fits to the Fermi-GBM’s 10 keV–1 MeV band data. The two peaks in the observed light curve are simulated separately and adjusted in time such that the sum of two peaks minimize the chi-square fit. Figure 4 shows light curves in narrower bands for each peak. Table 1 shows the value of parameters for these simulations. Examples of light curves and spectra of simulations which were explored to find best fits to the data are given in [45] and interested readers can refer to that work. In addition, those simulations were necessary to understand degeneracy of the model and how they might impact interpretation of the results.
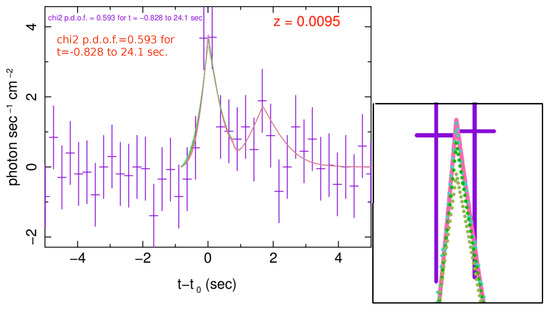
Figure 3.
Light curves of 4 best simulations in 10 keV–1 MeV. The data is from observationsof Fermi-GBM [61]. This plot shows that these simulations have very similar light curves. The inset is a zoom on the first peak and shows the slight difference of the amplitude of the first peak in these models. The value of is for the full line corresponding to model No. 2 in Table 1 for the first peak and model No. 3 for the second peak. Other curves (doted lines) correspond to model No. 1 with and without an external magnetic field (blue and dark green curves, respectively), and an off-axis model with all parameters the same as model No. 2, except column density of ejecta which is cm (light green). The value of per degree of freedom of the first two simulations are about larger than model No. 2 and that of the last model is ∼0.03 larger.
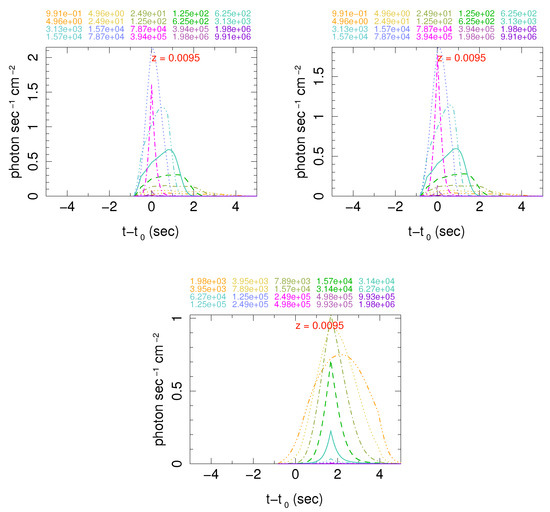
Figure 4.
Light curves of simulated models in energy bands covered by Fermi-GBM and Integral SPI-ACS instruments: (Left) Simulation No. 2; (Center) Simulation No. 1 without external magnetic field; (Right) Second peak, that is simulation No. 3. All simulation numbers refer to Table 1. Minimum and maximum of each energy band in eV is written in the corresponding color on the top of each plot. Notice that the second peak is simulated in lower energy bands than the first peak. The lag between highest energy bands is roughly zero and consistent with observation of short GRBs.

Table 1.
Parameter set of simulated prompt emission models.
Degeneracy of light curve can be partially resolved by fitting the spectrum of the first peak to data shown in Figure 5. We do not fit the spectrum of the second peak because Fermi spectrum of this peak [61] includes only 2 measured points at lowest energies and the rest are upper limits. It is evident that model d) in Figure 5 has a weaker fit to data than other models. However, in view of uncertainties of the data, their differences are too small to provide a statistically significant criteria in favour of one of these models. Nonetheless, comparison of spectra in Figure 5a,b, which their only difference is an external magnetic field in the former, may be interpreted as the necessity of a weak magnetic field in addition to the field induced by Fermi processes in the shock front. Indeed, in the next section we show that the remnant of the jet after internal shocks had preserved its collimation and coherence well after prompt shocks. Therefore, it had to have an intrinsic magnetic field—a Poynting flow. As for degeneracy between ultra-relativistic and relativistic jet models , they can be ultimately removed when the same formalism is used to analyse afterglows of this burst.
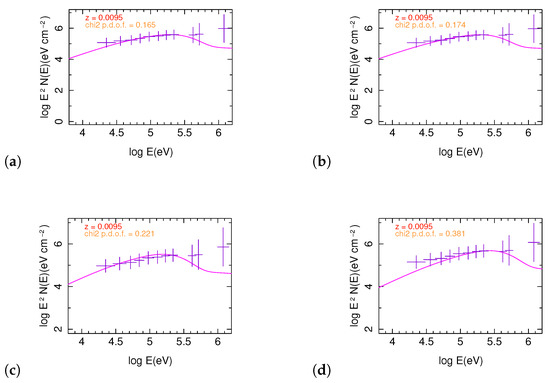
Figure 5.
Spectra of simulated models fitted to Fermi-GBM data: (a) Model No. 1; (b) Model No. 1 without external magnetic field; (c) Model No. 2; (d) A model with the same parameters as models No. 2 except for cm. As the published spectral data in [61] is in count rate, after changing it to energy flux we used peak energy from [61] to normalize the data such that at keV observed and simulated spectra have the same amplitude. For this reason, spectra of simulated models have much smaller than their corresponding light curves.
Parameters of the best models of the prompt emission show that in comparison with other short GRBs with accompanying kilonova such as GRB 130603B [91,92] Lorentz factor and densities of colliding shells of GRB 170817 in our direction was at least a few folds smaller, see [45] for details. Although off-axis view of the jet may be somehow responsible for the weakness of this burst, there are compelling evidence for the involvement of intrinsic characteristics of the BNS and its environment. An evidence for this claim is the absence of bright short GRBs at low redshifts in Figure 1, which may points to an evolutionary effect. The caveat of this argument is small number of bursts with redshift. On the other hand, even a small amount of lateral expansion of the core during internal shocks had to brought enough material to the line of sight and generate significant extended emission. The absence of such emission in gamma-ray and stringent upper limit on the early X-ray mission, which is presumably dominated by off-axis (high latitude) emission of internal shocks [93] is in contradiction with off-axis view of a typical jet as origin of the faintness of the prompt gamma-ray. Further arguments in favor of this conclusion are given in the next subsection and in Section 5. A summary of all arguments can be found in Section 6.
3.3. Late Afterglows
As we discussed in Section 2 electromagnetic afterglows of GW/GRB 170817A were the most unusual among both short and long GRBs. Notably, long lasting brightening had never been observed in any other GRB. It is however useful to remind that at present no other GRB had follow up observations for as long as this burst. In particular, follow up of other short GRBs have been limited to just a few days. Thus, we ignore how exceptional is the late time behaviour of the afterglows of GW/GRB 170817A. In other words, whether slow brightening of afterglows for more than 100 days is common in short GRBs or not.
Although, off-axis view of a structured jet predicts late brightening of afterglows [21,22,24,39], the observed decline of X-ray flux at ≲ days [42] is inconsistent with simulations of significantly off-axis emission [24], which predict a break after a few hundred days. Other simulations, for instance those reported in [39,94] predict earlier break, but cannot discriminate between off-axis structured jet and cocoon models [29] and need polarimetry for identifying the nature of outflow [94]. In any case, initially it seemed reasonable to assume that at late times the section of the jet along our line of sight, which even before prompt shocks was not as dense and boosted as in typical short GRBs, had to have dissipated its energy, and its Lorentz factor and density should have been decreased to negligibly small values. In this case the late brightening had to have another origin, for instance MHD instabilities leading to an increase in magnetic energy dissipation [95,96]; external shock on the ISM/circum-burst material of a mildly relativistic thermal cocoon ejected at the same time as the dissipated relativistic GRB making jet [90,97]; late outflows from an accretion disk [98]; or decay of isotopes in the kilonova [47,99]. Therefore, it was not certain that late afterglows were directly related to the relativistic jet models concluded from analysis of the prompt emission, see also the commentary of [100] on the issue of finding a reliable explanation for this exceptional discovery.
Here we first discuss simulations of external shocks of a mildly relativistic outflow on the ISM/circum-burst material in the framework of formalism reviewed in Section 3.1 and highlight shortcomings of such models for afterglows of GW/GRB 170817A. Then, we discuss models which can explain the data.
3.3.1. Shortcomings of a Mildly Relativistic Outflow
Irrespective of energy dissipation mechanism most of explanations described in the previous paragraphs predict a mildly relativistic outflow with a Lorentz factor as the ultimate origin of the afterglows. Indeed, as shown in Figure 3 and Figure 5 one of the best prompt models discussed in Section 3.2 has a Lorentz factor . Energy dissipation of such a jet, for instance through weak internal shocks and interaction with materials close to the merger, could easily reduce its Lorentz factor to 2–3, as had been suggested in the early literature on afterglows of GW/GRB 170817A. Figure 6 shows a few examples of synchrotron emission from external shocks of such outflows. It is clear that none of them can fit all the multiband data. Although models in Figure 6a,b fit well X-ray data, they over-produce both optical and radio emission. By contrast, models (c) and (d) in this figure have an acceptable fit to radio data, but not enough X-ray and both of them over-produce optical emission by a large amount.
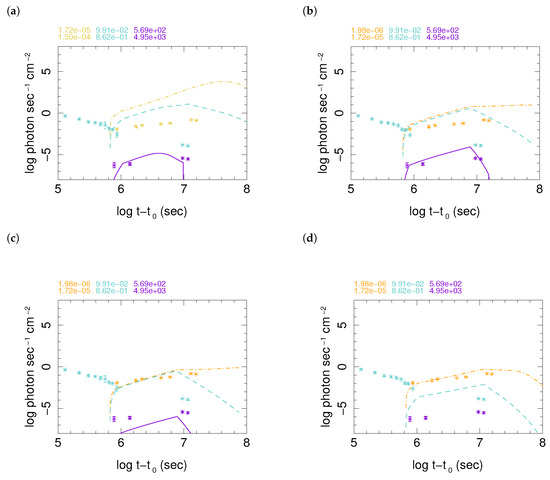
Figure 6.
X-ray, optical, and radio light curves of simulated models without taking into account synchrotron self-absorption. Stars present data taken from: [39,43] (X-ray), [18,36,42,65] (optical), [28,33,74] (radio). Model (a) has ; (b), (c) and (d) have . Complete list of parameters for these simulations can be found in [47]. If it is assumed that the centroid of outflow is oblique with respect to the line of sight, the effect of projection must be taken into account and the Lorentz factor should be considered to be larger by a factor of , where is the angle between centroid of outflow and the line of sight.
Regarding performance of these simulations, several issues need more clarification. It is well known that synchrotron self-absorption of radio emission can be important. In this case, one can assume that most of radio emission in the model (a) which has higher Lorentz factor is absorbed and only radio from a slower and less dense section of outflow, presented by models (c) and (d), can escape the shocked region. Examples of the effect of self-absorption are presented in [47]. On the other hand, this explanation cannot solve the problem of over-production of optical photons. Although the simulated optical band in Figure 6 is wider than HST F606W and SDSS r’ filters or its equivalents used for acquiring data shown in these plots, it is unlikely that multiple orders of magnitude deviation between these models and data can be due to the wider simulated band. The reason for wide simulation bands is the fixed number of bands in the simulation code. To cover a broad range of energies, from radio to X-ray, the width of individual bands should be large. Moreover, it is crucial to remind that the optical data is dominated by kilonova mission, which has very different origin and spectrum. Therefore, the optical data must be considered as an upper limit to any contribution from the GRB. This makes models shown in Figure 6 even more distant from data, unless optical photons are strongly observed. Alternatively, one can make simulations consistent with optical data, but an additional source of X-ray would be necessary to explain these observations.
The outline of this exercise is that the assumption about extreme energy dissipation in the jet after prompt emission is not realistic. To increase the contribution of X-ray emission and decrease the number of soft photons, the spectrum of synchrotron emission must be harder, i.e., its peak must be pushed to higher energies such that low energy emissions fall on the fast declining side of the spectrum, see examples of synchrotron/self-Compton spectra of GRBs in [46,52]. To satisfy this requirement Lorentz factor of the jet must be larger. Moreover, the fact that combination of two simulations gives a better fit to data than each component alone reminds us that the formulation of [51] assumes a jet with uniform Lorentz factor and density. But numerical simulations of ejecta from BNS [101,102,103,104] and its further acceleration by transfer of Poynting to kinetic energy [105] shows that both these processes are inhomogeneous. Consequently, the final relativistic jet should have a profile with varying , density, and extension. Another crucial characteristic of emissions from a relativistic jet is their beaming for a far observer. Due to this relativistic effect only an angle around the line of sight is visible to the observer. As we discussed in Section 3.2 at the time of prompt emission the jet is ultra-relativistic and . Therefore, beaming allows to see emissions only from a small part of the jet along the line of sight. Consequently, anisotropy of the jet is not visible, specially when only a relatively narrow gamma-ray band is observed. By contrast, afterglows are usually observed in broad bands, from gamma and X-rays to radio, and low energy emissions from side lobes—high latitudes—of the jet would be visible and have significant contribution in their flux.
3.3.2. Multi-Component Models
Theoretical shortcomings of models developed in [46,51] and simulation of [47] can be compensated by constructing multi-component models in which each component presents approximately an angular section of the jet with different Lorentz factor, density and extension. In addition, as argued in the previous subsection, we allow the presence of an ultra-relativistic component. This strategy, leads to a model and a few of its variants which fit X-ray and radio data well and satisfy the upper limit constraint imposed by the observed optical data [48]. Parameters of the components of the model are shown in Table 2. Figure 7 shows light curves of components of this model and their sum in each band. As this model and some of its variants shown in Figure 8 fit well radio and X-ray data, we presume that their predictions for optical emission of the GRB afterglow should be reliable. Under this assumption, these models show that after ∼ days kilonova emission in optical/IR bands was not anymore significant and the afterglow was dominated by synchrotron emission from external shocks of the relativistic polar outflow from the merger.

Table 2.
Parameter set of simulated afterglow components.
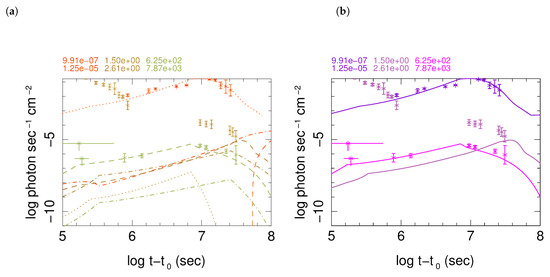
Figure 7.
(a) Radio, optical/IR, and X-ray light curves of simulated 3-component. Left: Light curves of the 3 components: ultra-relativistic (C1) (dash lines), relativistic (C2) (dash-dot), mildly relativistic (C3) (dotted lines). The energy range for each band is written on the top of each plot in the same colour/gray scale as the curves. Stars present data taken from: [39,41,43,44] (X-ray), [18,36,37,38,42,65] (optical), [28,33,35,74] (radio). The upper limit of X-ray flux at is from Neil Gehrels Swift-XRT [14] and the upper limit at ∼ is from Chandra observations [16]. (b) Sum of the light curves of the 3 components: radio (magenta/light grey), optical (purple/medium grey), X-ray (dark purple/dark grey).
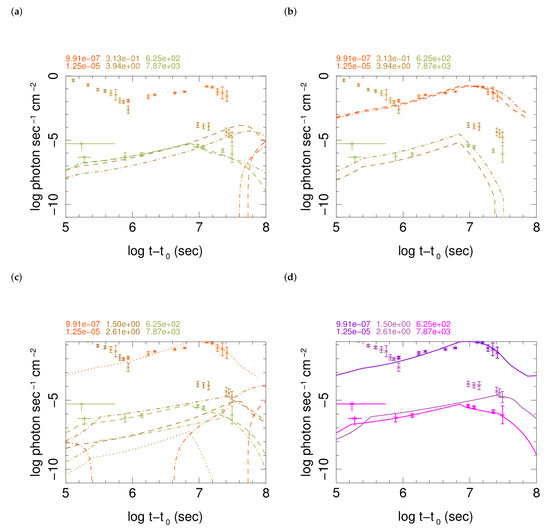
Figure 8.
Variants of components of the model of Table 2 which fit the data: (a) A variant of component C1 with , cm (dash-dot); (b) A variant of C3 with , cm, , cm, cm (dash-dot); (c) Variant of C2 component with , , cm, cm (dash-dot); In all these plots dashed lines correspond to the components described in Table 2; (d) Total light curves for a model with C1 and C2 as in Table 2 and C2 as shown in (c).
Spectra of the components and total spectrum of the model are shown in Figure 9. They show a good consistency between simulated spectrum and the data, and as expected, amplitude of optical emission at ∼ days is higher than the afterglow model. Moreover, due to the dominance of kilonova contribution, the shape of pseudo-spectrum of energy flux shown in Figure 5b at this epoch is significantly different from those at later times. In addition, Figure 5c shows a crude broad-band spectral slope, which is determined from radio and X-ray data only and thereby is not contaminated by kilonova emission. Ignoring large uncertainties of calculated slopes, they show a behaviour similar to other GRB afterglows, namely softer spectrum during earliest observations around days, which gradually becomes harder until the peak of emissions around days, and finally softens at later times. Therefore, despite unusual brightening of afterglows of GRB 170817, they have the same spectral trend as other GRBs.
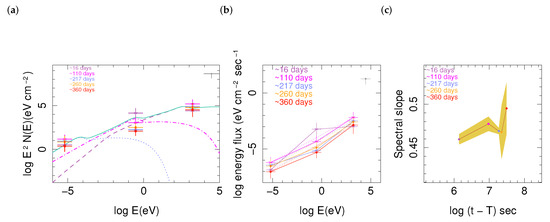
Figure 9.
(a) Spectra of components and their sum : ultra-relativistic (C1) (dash line), relativistic (C2) (dash-dot), mildly relativistic (C3) (dotted line), sum of 3 components (full line). Crosses present observations at different times in radio, optical/IR, and X-ray, optical and radio bands. When data for a time interval was not available an interpolation has been used. The width of crosses presents the width of the corresponding filter and are much larger than observational uncertainties. The upper limit at 16–50 keV is from the Swift-BAT survey data [106]. To generate a pseudo-spectrum from flux measurements, we have normalized data such that X-ray at days become equal to maximum of simulated spectrum in the simulated energy interval. (b) Spectrum of energy flux. The lines connecting the data points are added to facilitate the illustration of spectral variation. (c) Evolution of the slope of pseudo-spectrum using only radio and X-ray data, that is slope of dotted lines in (b). The shaded region is the estimate of uncertainty of calculated slopes according to variation rule.
3.3.3. Degeneracies
Despite the fact that the model described in Table 2 provides a good fit to the data some issues should be considered before making any conclusion. Notably, as we explained in Section 3.1, parameters of the phenomenological formalism of [46,51] are not completely independent, and models may be degenerate. For this reason, before interpreting this model and concluding properties of the jet from it, we must consider implications of degeneracies. For this purpose, change of the characteristics of the model as a function of their variation is studied in some extent in [48]. Here we summarize them by showing in Figure 8 a few variants for components of the model which can fit the data as good as those presented in Table 2. Specifically, Figure 8a shows an alternative to component C1 with smaller ISM/circum-burst density but longer jet extent. It fits X-ray data as good as C1 in Table 2, but future observations should be able to distinguish between them.
Variant of C3 shown in Figure 8b is important because it has a Lorentz factor consistent with superluminal motion of radio counterpart [49,50], whereas the Lorentz factor of C3 in Table 2 is too small to generate a significant apparent superluminal motion of the source. Alternatively, with slight modification of column densities and/or thicknesses of active regions in these models we can consider both of them as components of the full model. Evidence for a mildly relativistic component with small Lorentz factor—a cocoon—is observed in long GRB 171205A and its associated supernova SN2017uk [107]. It has , corresponding to , i.e., similar to C3 component in Table 2. Therefore, model C3 and its variant in Figure 8b may present sectors further and closer to the jet axis, respectively.
Another important conclusion from the study of parameter degeneracy is the influence of distance between merger and location of external shocks on the slope of the light curve and time of its turnover. See [48] for examples of models with shorter distances than cm used in the model of Table 2. The peak light curves in these models are too early and inconsistent with the data.
3.4. Other Models and Their Consistency with Data
In our knowledge [45] is the only detailed modeling and analysis of the prompt gamma-ray emission of GW/GRB 170817A. Therefore, here we only compare afterglow models described in Section 3.3 with some of the proposed models in the literature.
Fitting afterglow data with a multi-component model in [48] is not unique and some other authors have similarly modelled late afterglows of GW/GRB 170817A in this manner. For instance, [34,39] consider a two component structured jet model with a top-hat ultra-relativistic component and in its inner , where is angle with respect to symmetry axis of the outflow, and a component with a decreasing Lorentz factor in the angular interval with a mean . They use a relativistic jet simulation code to find that a line of sight angle from the jet axis . This model is very similar to the model described in the latest version of [24], but Lorentz factor and energy profile of the jet in the two works are different. Authors of [108] also conclude an initially ultra-relativistic jet from their analysis of afterglows. Authors of [38] consider two profiles for the jet, one similar to 2-component model of [34,39] and the other with Gaussian energy and Lorentz factor profiles. Both models find a small central core opening angle of ≲. In their 2-component model high and low Lorentz factors are ∼100 and ∼5, respectively. However, in the Gaussian model on-axis Lorentz factor can be as large as 900. A phenomenological function which effectively has two coupled components is used by [35].
It should be pointed out that asymptotic formulation of synchrotron emission from external shock formulation in [109], which is used in all the cited works, considers a uniform spherical ejecta. Therefore, conclusions about viewing angle of the jet in the cited works is based on the value of Lorentz factor and beaming of emissions from a relativistic source [110]. An interpretation of the multi-component model of Table 2 in the framework of [109] formulation can be found in [48].
4. Interpretation of Models
In this section we use models of prompt and afterglows described in the previous section to check their consistency, remove degeneracies, and correlate them to properties of progenitor neutron stars, their environment and merger, and its ejecta.
4.1. Selecting between Prompt Models
Although simulations of prompt gamma-ray emission show that both an ultra-relativistic jet with a Lorentz factor of and a relativistic jet with a Lorentz factor of are consistent with data, afterglows rule out the latter case. However, analysis of the prompt gamma-ray of GRB 170817A in [45] was performed well before the relatively early turn over of its afterglows. Therefore, they could not be used to distinguish between the two possible range of initial Lorentz factor, which might additionally discriminate between a significantly off-axis view of the jet and otherwise. For this reason, in [45] several other arguments were given in favour of an ultra-relativistic jet with . Here we briefly review them because this approach may be useful for analysing future GW/GRB events.
Giving relation between emitted and received power from a relativistic source , it is clear that if the jet is uniform, off-axis view alone cannot explain intrinsic faintness of the burst. Therefore, GW/GRB 170817 had to have a structured jet. On the other hand, even during prompt internal shocks energy dissipation significantly reduces Lorentz factor, see Figure 10, and scattering of particles by induced electromagnetic fields generates a lateral expansion. This process should bring dissipated material and its emission to the line of sight [21] and should have been detectable as a tail emission. Such extended emission is detected in some short bursts. Moreover, lateral expansion should have generated bright early afterglows. None of these emissions are observed in GW/GRB 170817A event. Thus, according to this argument an off-axis view of a structured jet alone cannot explain the faintness of the prompt gamma-ray and afterglows at early times, and late and slow brightening of the latter.
Another criteria for choosing between low and high Lorentz factor candidate models of Table 1 is plausibility of parameters which characterize shocks and synchrotron emission. Table 1 shows that in the moderately relativistic Model 2 smaller Lorentz factor is compensated by a higher fraction of energy transferred to electrons (more generally charged leptons), which is ∼3 times larger than in the ultra-relativistic jet Model 1. However, apriori due to the low density of the jet in this model interaction between charged particles and their scattering had to be rarer and induced electric and magnetic fields weaker. Moreover, low electron yield of neutron rich BNS ejecta [102,111,112] should have made the transfer of kinetic energy to electrons even harder. Estimation of electron yield for various components of the ejecta of GW 170817 event based on the observation of r-process products [103,113,114] are: for dynamical component, for wind, and in another wind component [18]. Considering the value of in the low Lorentz factor Model 2, the effective fraction of kinetic energy transferred to electrons had to be , which is much higher than found in Particle In Cell (PIC) simulations [115,116,117]. By contrast of Model 1 is comfortably in the PIC range.
In conclusion, Model 1 seems more plausible than Model 2. Considering parameters of Model 1 as approximately presenting properties of the jet before prompt internal shocks, according to simulations of [46] its bulk Lorentz factor in our direction was a few folds smaller than typical short bursts. Additionally, densities of colliding shells were more than one order of magnitude less than brighter short GRBs.
4.2. Kinematic of the Jet at Late Times
The structure of 3-component jet model at late times, that is > days, discussed in Section 3.3 is in agreement with our arguments in favour of an ultra-relativistic prompt jet with a Lorentz factor at the end of internal shocks. As discussed earlier, exploration of the parameter space of external shocks in [47,48] to find a model with only relativistic or mildly relativistic Lorentz factor was not successful. Apriori Lorentz factor of the jet at the location of external shocks should have been smaller than its value at the end of internal shocks at because weaker internal shocks and cooling of shocked material should have reduced its kinetic energy. Therefore, the presence of an ultra-relativistic component with roughly the same Lorentz factor in the afterglow model means that despite all odds, a fraction of ultra-relativistic jet had survived up to long distances. However, comparison of the column density of the prompt jet in Table 1 with that of component C1 in Table 2 show that column density of ultra-relativistic section of the jet at the time of external shocks was reduced by a factor of ∼200. If the jet were an adiabatically expanding cone, its column density had to decline by a factor of . The much smaller dilation factor according to the models described here means that the material inside the jet had an internal coherence and collimation—most probably due to imprinted electric and magnetic fields in the plasma. Thus, we conclude that its geometry and expansion were closer to a boosted cylinder rather than an adiabatic cone. In addition, in [48] it is shown that non-adiabatic expansion of the jet cannot be associate to accretion of material, which could completely extinguish its boost.
4.2.1. Late Time Jet Structure and Interpretation of Components
As discussed earlier, unusual characteristics of GRB 170817A may be in some extent due to the off-axis view of the jet. Indeed, observation of gravitational waves from this transient indicates an orbital inclination angle of [75]. Moreover, superluminal motion of radio afterglow with an apparent speed of [49,50] is evidence of an oblique view of its source.
Due to relativistic beaming of photons, off-axis view of the jet has significant consequences for observations. A far observer receives synchrotron emission only from a cone with half angle with respect to the line of sight. For components C1, C2, and C3 of the afterglow model listed in Table 2 these angles are , , and and for C3 in Table 2 and the model in Figure 8b as its alternative or an additional component, respectively. This leads us to conclude that the 3 (or 4)-component model of the jet at the time of external shocks presents a structured jet and components of the model approximately present its angular structure and characteristics of its shock on the surrounding material from our line of sight up to its outer boundary. In particular, their Lorentz factors and column densities present azimuthal variation of material load of the polar outflow and its velocity up to a factor, that is , where is angle between centroid of component i of the model and the line of sight. It should be reminded that the simulation code used in [48] uses an analytical expression for determining synchrotron/self-Compton flux. In addition, terms depending on higher order of angle between emitting element and the line of sight are neglected. This is a good approximation when . Under this simplification dependence is only through a factor, which must be integrated between and . However, angular size of emitting surface may be smaller than . In this case, integration over maximum visible angle over-estimate the flux. But the difference would be at most a factor of few and comparable to other uncertainties of the model. Indeed, for this and other simplifications and approximations applied to the model and its simulations that we should consider parameters as order of magnitude estimations.
Figure 11 shows a schematic presentation of this interpretation, components of the model, and their positions with respect to our line of sight. We remind that jet axis may be inclined with respect to rotation axis of the merger [105]. Considering this possibility and estimated inclination of orbit, viewing angle is constraint to . This is consistent with estimations of [34,39,49], but not very restrictive. Moreover, it does not provide any information about Lorentz factor of the invisible core of the jet. Additionally, the maximum off-axis of components according to their Lorentz factor does not fix their centroid. To estimate these quantities we assume a Gaussian profile for the jet and apply constraints on the centroid angles and on the parameters of the profile, see [48] for details. From this analytical approximation we find: –, –, assuming on-axis Lorentz factor . In [48] it is shown that the range of allowed values for the viewing angle is strongly correlated with and is restricted to for and to for . For alternative C3 model in Figure 8b the range of allowed angles is even more restricted: –, for and –, for , and , , for any standard deviation of the Gaussian profile as long as . Marginalizing over other parameters, the angle between jet axis and rotation axis is constraint to –. An exponential profile does not lead to acceptable values for the parameters and is ruled out.
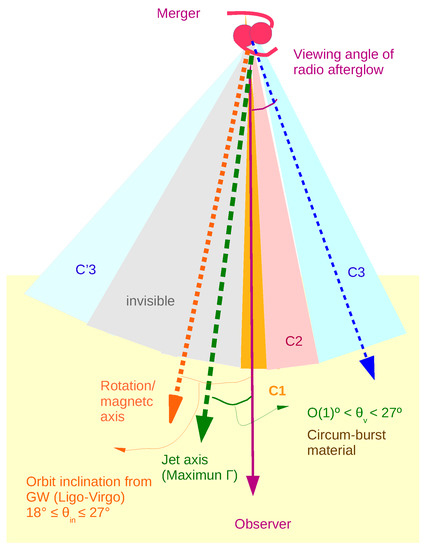
Figure 11.
Schematic description of polar outflow of merger at the time of its encounter with circum-burst material. C1, C2, C3 refer to components of the simulated model. Grey shaded region on the opposite side of the jet with respect to observer’s line of sight is approximately invisible because of its large Lorentz factor and off-axis angle. Nonetheless, C’3 region which has even larger off-axis may be visible if its Lorentz factor is sufficiently low. Therefore, there can be a contribution to component C3 of the model from emission of this region. In any case, due to its large off-axis contribution of C3’ would be subdominant. For the sake of simplicity here we have assumed that magnetic field direction and rotation axis coincide. This may not be true.
Although above constraints are more restrictive than those only based on the orbit inclination, due to degeneracies in the parameter space it is still impossible to judge whether the core of the jet had a typical Lorentz factor of ∼500 [46] or had a smaller boost. The latter case means that off-axis viewing angle was only partially responsible for unusual properties of GRB 170817A. We remind that the probability of viewing a jet exactly on axis is very small and in any GRB some degrees of deviation is expected. Moreover, prompt gamma-ray emission of GRB 170817A is somehow similar to dark short bursts—those without an X-ray counterpart at ksec, see Figure 2. Although some of these GRB candidates may be faint flares from Soft Gamma-ray Repeaters (SGR) in nearby galaxies, others—specially those with longer —might be related to BNS mergers similar to GW/GRB 170817A and to two other BNS merger gravitational wave candidate events LIGO-Virgo 190425z and LIGO-Virgo 190510g at redshift and , respectively. For latter events, which were about 6 times further than GW/GRB 170817A only upper limits on any electromagnetic emission is available. Additionally, the host of the faint X-ray dark short GRB 080121 [118] may belong to a galaxy group at redshift [119]. If true, this burst was intrinsically only 2 times brighter than GRB 170817A, which its was a few orders of magnitude fainter than typical short bursts, see Figure 1.
The faintness or absence of GRB in gravitation wave events associated to BNS may be interpreted as a natural consequence of jets directionality. However, it does not explain the absence of optical emission from ejected disk/torus, which its emission is roughly spherical—presumably due to its faintness. Therefore, despite the impact of off-axis view of GW/GRB 170817A, intrinsic properties of the progenitor BNS, in particular magnetic field of neutron stars, their spin, and their age, might have been involved in its weakness. In [45] this subject is discussed in detail and we summarize its conclusions in Section 5.
4.2.2. Delayed Brightening
In the literature, along with its intrinsic faintness, the late brightening of GW/GRB 170817A afterglows is usually considered as an exceptional characteristic of this burst.
Afterglows of GRBs up to few thousands of seconds are most probably a superposition of weak internal shocks in what remains from the relativistic jet after the main prompt shock, and emission from external shocks [93]. Assuming a narrow prompt spike, the delay between the prompt and onset of afterglow emission is , where c is the speed of light. For the model of Table 2 s This delay is much shorter than any automatic follow up and practically unobservable. Thus, the shape of X-ray light curve depends on relative importance of decreasing emission from internal shocks and increasing emission from external shocks. The absence of early brightening or even a plateau in many short GRBs means that their early X-ray is dominated by what we call the tail emission of internal shocks. Thus, as pointed out earlier, in absence of long follow up observation of short GRBs we do not usually detect the second component and ignore how its light curve look like at late times. Short GRB’s with a plateau in their X-ray light curve may be those in which the afterglow takes off quickly and peaks a few hours or days after prompt gamma-ray.
The initial suggestions about brightening of afterglows due to the reduction of off-axis view when the jet become dissipated and its content scatter to our line of sight is not consistent with relatively early break of light curves in all three energy bands after ∼ days. Therefore, viewing angle cannot be the only reason for the late brightening of afterglows. On the other hand, our simulations show that in the case of GW/GRB170817A the slow rise of the afterglow was due to the long distance of ISM/circum-burst material from center, its low density and low column density of the jet. Dilution of the jet was partially due to the intrinsically low density and low Lorentz factor of polar ejecta—at least in our direction—and partially the result of large distance of surrounding material from center, that is ∼1000 AU (see Table 2) rather than e.g., ∼200 AU for recently detected NIR emitting material around the isolated neutron star RXJ0806.4-4123 [120]. Consequently, jet’s column density was extensively reduced by lateral expansion.
It is however cautious to consider that our conclusion about the effect of distance may be somehow biased and correlated to spatial resolution of our simulations. Nonetheless, estimation of shock distance for this GRB in the literature and for other GRBs with various methods, such as cooling of thermal emission [121] show that the range of distances obtained from simulation of GRBs by the formalism used here [46] are realistic.
5. Properties of GW/GRB 170817 Progenitors and Their Environment
If the unusual properties of GW/GRB 170817A and presumed faintness of other nearby candidate BNS mergers are merely due to an off-axis view, they tell little about properties of their progenitor neutron stars. By contrast, if the faintness is at least in some extent intrinsic, it may be an evidence for evolution of BNS population. Assuming an intrinsic origin, in this section we use results from observation and modeling of the GRB 170817A along with those of GRMHD simulations of BNS merger and observed properties of neutron stars and pulsar, which are mostly young, that is an age less than Myr, to understand properties of the nearby——BNS and their merger, and see which set of characteristics might have influenced GRB 170817A event.
5.1. Equation of State, Magnetic Field and Spin
In addition to the relation between mass and radius, the Equation of State (EoS) of neutron stars determines core and crust density and their buoyancy, and thereby their tidal deformability [122], which affects high frequency post-merger gravitational waves at the end of binary’s inspiral. Although resolution of LIGO-Virgo at high frequency is not sufficient for detailed discrimination between numerous equations of state in the literature, it is sufficient for distinguishing between stiff EoS such as H4 and SLy, and soft ones such as APR4 and WFF1 [53]. In the case of GW 170817 stiff equations of state are disfavored by GW signal [10].
For close mass BNS merger such as GW 170817 the density of inner part of the accretion disk and poloidal magnetic field of the merger are smaller for softer EoS [102,123,124]. Moreover, simulations of [102] show that in equal mass BNS merger, if the initial magnetic fields of progenitors are aligned with each other and anti-aligned with the orbital rotation axis, the average poloidal magnetic field of the polar ejecta is about 5 times weaker than when both initial fields are aligned with the rotation axis. Additionally, if the initial fields are anti-aligned with each other, the average poloidal field is even smaller by a factor of few. In addition, the merger have smaller magnetic field far from rotation axis than the aligned case. These results reflect the fact that the potential energy of two dipole magnets is minimum when they are anti-aligned. On the other hand, coupling of progenitors magnetic fields and its evolution depend on the BNS surrounding material, structure of inner layers, and strength and geometry of the fields. Specifically, the coupling may become stronger through electromagnetic coupling of the surrounding plasma [125,126] or a direction flip occur suddenly through a viscosity driven instability [127]. In any case, although a priori anti-aligned field configuration is energetically favored and more stable, other processes such as spinning and vorticity in superfluid neutron rich layer and superconducting type of proton layer [128] and their interaction with the crust may alter anti-aligned configuration.
Above processes and characteristics have direct impact on attainable Lorentz factor when ejected polar material is accelerated by transfer of magnetic to kinetic energy [105]. Observations show that star population of the host galaxy NGC 4993 of GW/GRB 170817A is relatively old [129,130]. Using measurements of magnetic field and period and their relation with ages of neutron stars—see e.g., Figure 1 of [131]—magnetic fields of the progenitor neutron stars might have been as low as – G or smaller if their age was Gyr, i.e., similar to dominant population of the host [132]. In this case, they were quite cold because after Myr the crust of neutron stars cool roughly exponentially and their interior linearly [133] but its slope depends on the equation of state [134]. If the BNS of GW/GRB 170817A was formed dynamically during a relatively recent merger of NGC 4993 with another galaxy, its age could be Gyr [135]. However, even this younger age is long enough for cooling the progenitors such that their temperature can be considered as approximately zero.
GRB data and its modeling cannot be directly used to estimate the magnetic field of progenitors. Nonetheless, assuming that the external magnetic field in the simulations of prompt gamma-ray originates on the merger and decay with square of distance, the magnetic field at a distance of about 11 km, that is approximately one neutron star radius, was ∼– G, i.e., a plausible but weak field for a BNS merger or short living HMNS—the most probable outcome of the merger [57,60,136,137]. On the other hand, simulations show that just before merging the magnetic field between neutron stars would be amplified by a few orders of magnitude [138]. In this case magnetic fields of the progenitors of GW/GRB 170817A before their encounter had to be a few orders of magnitude less than the above estimation and consistent with what is observed in neutron stars older than Gyr [131]. However, if the external field was a Poynting flow imprinted in the jet’s plasma, it might have decayed much slower and its amplitude at ejection was not much different from its value at the onset of internal shocks. On the other hand, both a central field and a Poynting flow had to be present, because the jet was collimated. Therefore, most probably the magnetic field of the central object was the dominant external magnetic field at the position of internal shocks, and the Poynting was the second to it. Unfortunately model of [46,51] is not able to distinguish these components. A priori power spectrum (Fourier transform) of gamma-ray light curve can be used to separate the two components because in general their precession frequency would not be the same. However, for various reasons, which are explained in details in [46] signature of a periodicity in the light curves is smeared. For this reason, although a weak evidence exists in many GRBs, it is clearly detected only for GRB 090709A [46,139].
Initial spins of progenitor neutron stars, which carry a fingerprint of their evolution history, have a crucial role in the dynamics of their merging. In particular, they affect the amount of ejecta, density and extent of accretion disk/torus, and spin of the short living HMNS and the final black hole. Unfortunately, GW 170817 event was too faint and spin of progenitors could not be determined from gravitational waves. Therefore, here we discuss situations which may explain reduced jet and excess of blue kilonova emission according to GRMHD simulations, but remind that conclusions must be considered conservatively.
If the progenitor stars were old recycled millisecond pulsars, they had to be fast rotating [131,140]. In this case, the larger angular momentum leads to smaller binding energy and it should be easier for tidal force to eject material from merger. Of course there is no direct evidence that the neutron stars were old. But statistically it is more probable because dominant population of the host is old.
Simulations by [104,141] show that if tidal force is the dominant process for mass ejection, larger spin leads to larger ejecta. Moreover, if spin axes are aligned with orbital rotation, binding energy of BNS is even weaker, inspiral regime longer, and the amount of ejected mass larger. These findings is consistent with the observed bright blue kilonova of GW/GRB 170817A. However, these effects depend on the mass ratio of progenitors and their effects are less significant for equal mass binaries, which seems to be the case in this event. Therefore, high and aligned spin and tidal force may not be enough to explain observations, and as explained in Section 2.1 internal interactions and heating by neutrinos may be needed [60]. If shocks and internal interactions, rather than tidal force are the main cause of mass ejection [57,142,143] the effect of spin would depend on the equation of state, temperature, mass, and nuclear content of the progenitors [144]. In particular, fast spins aligned with the orbital rotation can have an inverse effect and reduce the amount of ejecta, and thereby kilonova emission. On the other hand, equations of state studied in [142,143], may be more suitable for young neutron stars [144,145], which are not dominant population in the host galaxy NGC 4993.
In summary, without a better understanding of interplay between gravitational and non-gravitational processes in neutron stars and their evolution with time it is premature to make strong conclusion about initial spin of progenitors, that is whether they were fast rotating recycled neutron stars, and what was the alignment of their spins.
5.2. Environment of Progenitor BNS
The afterglow model described in Section 3.3 requires that density of external material depends on the azimuthal angle with respect to jet axis. Despite degeneracy of the parameters, the directional anisotropy of ISM/circum-burst material may be real because we could not find consistent model without it. This means that circum-burst material was not only the ISM. Moreover, origin of additional material and its properties were somehow correlated with progenitors.
In young neutron stars and pulsars the distance to wind Termination Shock (TS) depends on the rate of mass loss and wind pressure inside wind nebular, which is balanced by the ISM pressure, and its typical value is pc cm [146]. In old neutrons it is expected that the reduction of glitching activities due to the solidification of crust and dissipation of magnetic field gradually decreases mass loss and . However, detection of this population is very difficult and information about their properties is extremely rare. An exception is the isolated neutron star RXJ0806.4-4123 with an age of Myr for which thermal material at a relatively short distance of ∼200 AU cm is detected [120].
Our simulations of the afterglows estimates cm, which is between the above values. The reason may be an age larger than most observed neutron stars and pulsars, estimated to be yr, and younger than Myr age of RXJ0806.4-4123. It is also plausible that the progenitor neutron stars were even older, but during early stages of inspiral, that is well before generation of detectable gravitational waves, strong tidal forces had induced crustal faults and resumed internal interactions, glitching and mass loss. If this explanation is correct, ejected material had to be also existed at shorter distances and inside the wind bubble at the time of merging. To estimate their average column density we employ the distribution used in the afterglow model for ISM/circum-burst material, that is and extend it to . For model C1 this estimation gives a column density of cm, which is much smaller than column density of the components of model. It is also smaller than swept circum-burst material in the first s after the onset of the external shocks, and therefore completely negligible. On the other hand, if we consider much denser circum-burst material at shorter distances, much higher X-ray flux generated by the shocks violates upper limits at ∼ days, see additional simulations for this purpose in [48]. Using these two extreme cases, we conclude that the column density of material inside cm bubble was cm or equivalently its average density was cm.
6. Outline and Prospectives for Future
From analysis of prompt and afterglows of GW/GRB170817A along with information acquired from gravitational wave observation we conclude that the faintness and other unusual properties of this burst cannot be fully explained by off-axis view of a structured jet. The arguments discussed in various occasions in this review can be summarized as the followings:
- -
- Absence of bright short GRBs at low redshift is probably a signature of population evolution;
- -
- Absence of extended gamma-ray or X-ray emission from lateral expansion of the jet during internal shocks, which had to bring additional material to the line of sight.
- -
- Due to degeneracies, a core Lorentz factor as small as ∼250–300 cannot be ruled out. This is much smaller than what is predicted for typical short GRBs.
- -
- Simulations show that the properties of circum-burst material, notably its distance from center, rather than those of the jet are responsible for the late brightening of afterglows.
These arguments point to intrinsic weakness of the structured relativistic jet in this burst, probably due to the characteristics of the progenitor BNS. Using both analysis reviewed here and results of BNS merger simulations in the literature, we can draw the following consistent picture for the first BNS merger event extensively followed up in multi-wavelength by multi-probe instruments:
- -
- Progenitors were old and thereby cool neutron stars with close masses;
- -
- They had soft equations of state and small initial magnetic fields of ≲ G. Their fields were probably anti-aligned with respect to orbital rotation axis and each other.
- -
- The merger produced a HMNS with a moderate magnetic field of ≲– G.
- -
- The HMNS eventually collapsed to a black hole and created a moderately magnetized disk/torus and a low density, low magnetized outflow.
- -
- A total amount of ∼0.03–0.05 material, including – of tidally stripped pre-merger and a post-merger wind were ejected to high latitudes. They were subsequently collimated and accelerated by transfer of Poynting to kinetic energy. The same process increased electron yield by segregation of charged particles.
- -
- A small mass fraction of the polar ejecta was accelerated to ultra-relativistic velocities and made a relatively weak GRB. The reason for low Lorentz factor, density, and extent of this component was the weakness of the magnetic field.
- -
- For the same reasons, the ultra-relativistic section of the jet was narrow and our off-axis view of ∼ was enough to reduce the emission of high energy photons in our direction.
- -
- After prompt internal shocks the jet had a wide angular distribution with varying density and Lorentz factor. But despite significant energy dissipation in its core, a tiny fraction of the jet had preserved its coherence and boost up to its collision with circum-burst material at ∼ cm from merger.
- -
- In addition to the ISM, circum-burst material included a component which its origin was correlated with the BNS.
- -
- The late brightening of afterglows was due to the relatively long distance of circum-burst material and low density of material inside the wind bubble surrounding the BNS.
- -
- Angular variation in the jet was also responsible for domination of emission in lower energies from high latitude side lobes and thereby observation of superluminal motion of the radio afterglow.
This qualitative picture and redshift distribution of short GRBs point to an evolutionary effect on their properties. This conclusion is somehow strengthen by failure of finding an electromagnetic counterpart for two recent candidate BNS merger gravitational wave events. Although the absence of a GRB may be due to our off-axis viewing angle, it does not explain the failure of kilonova detection. In any case, number of such events is still too small to make any statistically meaningful conclusion. Nonetheless, this analysis demonstrates the importance of multi-probe observation of this and other categories of transients detected through their gravitational waves.
A highly desired capability is to detect gravitational waves from compact object collisions well before their merger such that the evolution of the source can be followed by other probes [147]. This needs detectors working at lower frequencies, such as LISA. On the other hand, higher frequencies are necessary for studying post-merger regime. They enable us to follow deformation of merging objects, which can be then related to a state of quantum matter and and Quantum Chromo-Dynamics (QCD) interactions impossible to reproduce in laboratory. Additionally, improving angular resolution of GW detectors is crucial for accelerating follow up by other probes and increasing the chance of detecting electromagnetic counterparts. Synchronized and automatic wide field observations in ultra-violet/optical/IR are important because apriori they do not have the issue of directionality of high energy emission from a narrow jet. At present the only way to increase angular resolution of gravitational wave detectors is their multiplication. In this respect the upcoming detectors Kagra [148] and LIGO-India [149] will be significantly helpful.
In addition to astronomical applications, multiwavelength observations are crucial for using gravitational wave detection for testing general relativity and Einstein gravity, and determining cosmological parameters such as the Hubble constant. Both these applications need a high precision determination of redshift of the events, which cannot be achieved by using only gravitational waves [150]. The detection of GW 170817 and its electromagnetic counterparts was a benchmark for these applications and allowed to determine Hubble constant with ∼16% precision completely independent of electromagnetic signal, except for the redshift [150]. Although this measurement is impressive, it does not solve the discrepancy between measurements of by Planck satellite using the Cosmic Microwave Background (CMB) [151] and those obtained from observation of standard candles, that is supernovae [152], Cepheids [153], and Quasi-Star Objects (QSO) lensing [154]. Cross-correlations between LIGO-Virgo measurements and the CMB [155], electromagnetic counterpart of GW/GRB 170817A [156] and galaxy surveys [157] were not useful either and have rather increased confusion and controversies. Nonetheless, increasing number of gravitational wave events with electromagnetic counterpart should reduce uncertainties and make GW a valuable cosmological probe.
Observation of gravitational waves, specially from GW/GRB 170817A has stringently constrained many classes of modified gravity models [158,159]. Nonetheless, increasing resolution of detectors at high frequencies should make possible to improve these constraints and extend them to scalar-tensor models including higher order derivatives than second order in Einstein gravity and are still viable [160]. Another method for finding deviation from general relativity and Einstein gravity is the measurement of difference between propagation time of gravitational and electromagnetic signals [161]. A modified propagation time and dispersion relation can be for example due to a classical Yukawa interaction or the result of photons and gravitons interaction with quantum structure of the spacetime during their propagation at cosmological distances. These tests need very precise information about processes involved in the generation of electromagnetic signals, their properties, and their production delay with respect to gravitational waves, thus better theoretical modeling and multiprobe measurements. Additionally, some of models suggested as solution for apparent loss of quantum information in black holes, such various versions of firewall and fuzzball, predict a finite thickness for black hole horizon, which leads to presence of gravitation wave echos well after the end of ringdown of binary black hole merger. Although there is already claim of the detection of such echos [162,163], their existence is not yet accepted by the community. Confirmation or constraining such a signal would be a significant step toward test of quantum gravity models [164,165].
Gravitational wave detectors have opened a whole new channel by which we can see events and phenomena completely hidden from us until now. Nonetheless, complementary observations of electromagnetic emission, neutrinos and cosmic rays from these events are necessary for achieving a full understanding of underlying physical processes.
Funding
This research received no external funding.
Conflicts of Interest
The author declare no conflict of interest.
Appendix A. Definition of Parameters and Models of Active Region
Table A1 summarizes parameters of this model. Despite their long list, simulations of typical long and short GRBs in [46] show that the range of values which lead to realistic bursts are fairly restricted.
In the phenomenological model of [51] the evolution of cannot be determined from first principles. For this reason we consider the following phenomenological models:
The initial width in Model = 1 & 3 is zero. Therefore, they are suitable for description of initial formation of an active region in internal or external shocks. Other models are suitable for describing more moderate growth or decline of the active region. In tables of models the column mod. corresponds to numbers given in A1- and indicates which evolution rule is used in a simulation regime.

Table A1.
Parameters of the phenomenological prompt model.
Table A1.
Parameters of the phenomenological prompt model.
| Model (mod.) | Model for evolution of active region with distance from central engine; See Appendix A and [46,51] for more details. |
| (cm) | Initial distance of shock front from central engine. |
| Initial (or final, depending on the model) thickness of active region. | |
| p | Slope of power-law spectrum for accelerated electrons; See Equation (3.8) of [46]. |
| Slopes of double power-law spectrum for accelerated electrons; See Equation (3.14) of [46]. | |
| Cut-off Lorentz factor in power-law with exponential cutoff spectrum for accelerated electrons; See Equation (3.11) of [46]. | |
| Initial Lorentz factor of fast shell with respect to slow shell. | |
| Index in the model defined in Equation (3.28) of [46]. | |
| Index in the model defined in Equation (3.29) of [46]. | |
| Electron yield defined as the ratio of electron (or proton) number density to baryon number density. | |
| Fraction of the kinetic energy of falling baryons of fast shell transferred to leptons in the slow shell (defined in the slow shell frame). | |
| Power index of as a function of r. | |
| Fraction of baryons kinetic energy transferred to induced magnetic field in the active region. | |
| Power index of as a function of r. | |
| Baryon number density of slow shell. | |
| Power-law index for N’ dependence on . | |
| Column density of fast shell at . | |
| Lorentz factor of slow shell with respect to far observer. | |
| Magnetic flux at . | |
| f | Precession frequency of external field with respect to the jet. |
| Power-law index of external magnetic field as a function of r. | |
| Initial phase of precession, see [46] for full description. |
1 The phenomenological model discussed in [51] and its simulation [46] depends only on the combination . For this reason only the value of this combination is given for simulations; 2 The model neglects variation of physical properties along the jet or active region. They only depend on the average distance from center r, that is ; 3 Quantities with prime are defined with respect to rest frame of slow shell, and without prime with respect to central object, which is assumed to be at rest with respect to a far observer. Power indices do not follow this rule; † According to this definition for external shocks (index e for external shock)and (index i for internal shock.
References
- Costa, E.; Feroci, M.; Frontera, F.; Zavattini, G.; Nicastro, L.; Palazzi, E.; Spoliti, G.; Di Ciolo, L.; Coletta, A.; D’Andreta, G.; et al. IAU Circular 6572: GRB 970228; International Astronomical Union: Paris, France, 1997. [Google Scholar]
- Costa, E.; Frontera, F.; Heise, J.; Feroci, M.; In’t Zand, J.; Fiore, F.; Cinti, M.N.; Dal Fiume, D.; Nicastro, L.; Orlandini, M.; et al. Discovery of the X-ray Afterglow of the Gamma-Ray Burst of February 28 1997. Nature 1997, 387, 783. [Google Scholar] [CrossRef]
- Boella, G.; Butler, R.C.; Perola, G.C.; Piro, L.; Scarsi, L.; Bleeker, J.A.M. BeppoSAX, the wide band mission for X-ray astronomy. Astron. Astrophys. Suppl. 1997, 122, 299. [Google Scholar] [CrossRef]
- Groot, P.J.; Galama, T.J.; van Paradijs, J.; Strom, R.; Telting, J.; Rutten, R.G.M.; Pettini, M.; Tanvir, N.; Naber, R.; Kouveliotou, C.; et al. IAU Circular 6584: GRB 970228; International Astronomical Union: Paris, France, 1997. [Google Scholar]
- Gehrels, N.; Chincarini, G.; Giommi, P.; Mason, K.O.; Nousek, J.A.; Wells, A.A.; White, N.E.; Barthelmy, S.D.; Burrows, D.N.; Cominsky, L.R.; et al. The Swift Gamma-Ray Burst Mission. Astrophys. J. 2004, 611, 1005. [Google Scholar] [CrossRef]
- Fishman, G.J.; Meegan, C.A.; Wilson, R.B.; Paciesas, W.S.; Pendleton, G.N. Proc. GRO Science Workshop; Johnson, W.N., Ed.; NASA/GSFC: Greebelt, UK, 1989; pp. 2–29. [Google Scholar]
- Dingus, B.L. EGRET observations of >30 MeV emission from the brightest bursts detected by BATSE. Space Sci. 1995, 231, 187. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration. A gravitational wave observatory operating beyond the quantum shot-noise limit. Nat. Phys. 2011, 7, 962. [Google Scholar] [CrossRef]
- The Virgo Collaboration. Advanced Virgo: A 2nd generation interferometric gravitational wave detector. Class. Quant. Grav. 2015, 32, 024001. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Scientific Collaboration. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- The LIGO Scientific Collaboration; The Virgo Collaboration. On the Progenitor of Binary Neutron Star Merger GW170817. Astrophys. J. Lett. 2017, 850, L40. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration; Virgo Collaboration; Fermi GBM; INTEGRAL; IceCube Collaboration; AstroSat Cadmium Zinc Telluride Imager Team; IPN Collaboration; The Insight-Hxmt Collaboration; ANTARES Collaboration; The Swift Collaboration; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration; Virgo Collaboration; Fermi Gamma-Ray Burst Monitor Collaboration; INTEGRAL Collaboration. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Evans, P.A.; Cenko, S.B.; Kennea, J.A.; Emery, S.W.K.; Kuin, N.P.M.; Korobkin, O.; Wollaeger, R.T.; Fryer, C.L.; Madsen, K.K.; Harrison, F.A.; et al. Swift and NuSTAR observations of GW170817: detection of a blue kilonova. Science 2017, 358, 1565. [Google Scholar] [CrossRef] [PubMed]
- Margutti, R.; Berger, E.; Fong, W.; Guidorzi, C.; Alexander, K.D.; Metzger, B.D.; Blanchard, P.K.; Cowperthwaite, P.S.; Chornock, R.; Eftekhari, T.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/VIRGO GW170817. V. Rising X-ray Emission from an Off-Axis Jet. Astrophys. J. Lett. 2017, 848, L20. [Google Scholar] [CrossRef]
- Troja, E.; Piro, L.; van Eerten, H.; Wollaeger, R.T.; Im, M.; Fox, O.D.; Butler, N.R.; Cenko, S.B.; Sakamoto, T.; Fryer, C.L.; et al. The X-ray counterpart to the gravitational wave event GW 170817. Nature 2017, 551, 71. [Google Scholar] [CrossRef]
- Metzger, B.D. Welcome to the Multi-Messenger Era! Lessons from a Neutron Star Merger and the Landscape Ahead. arXiv 2017, arXiv:1710.05931. [Google Scholar]
- Pian, E.; D’Avanzo, P.; Benetti, S.; Branchesi, M.; Brocato, E.; Campana, S.; Cappellaro, E.; Covino, S.; D’Elia, V.; Fynbo, J.P.U.; et al. Spectroscopic identification of r-process nucleosynthesis in a double neutron-star merger. Nature 2017, 551, 67. [Google Scholar] [CrossRef]
- Kasen, D.; Metzger, B.; Barnes, J.; Quataert, E.; Ramirez-Ruiz, E. Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event. Nature 2017, 551, 80. [Google Scholar] [CrossRef]
- Smartt, S.J.; Chen, T.W.; Jerkstrand, A.; Coughlin, M.; Kankare, E.; Sim, S.A.; Fraser, M.; Inserra, C.; Maguire, K.; Chambers, K.C.; et al. A kilonova as the electromagnetic counterpart to a gravitational-wave source. Nature 2017, 551, 75. [Google Scholar] [CrossRef]
- Lazzati, D.; Deich, A.; Morsony, B.J.; Workman, J.C. Off-axis emission of short gamma-ray bursts and the detectability of electromagnetic counterparts of gravitational wave detected binary mergers. Mon. Not. R. Astron. Soc. 2017, 471, 1652. [Google Scholar] [CrossRef]
- Kathirgamaraju, A.; Barniol Duran, R. Giannios, D. Off-axis short GRBs from structured jets as counterparts to GW events. Mon. Not. R. Astron. Soc. 2018, 473, L121. [Google Scholar] [CrossRef]
- Lamb, G.P.; Kobayashi, S. Electromagnetic Counterparts to Structured Jets from Gravitational Wave Detected Mergers. Mon. Not. R. Astron. Soc. 2017, 472, 4953. [Google Scholar] [CrossRef]
- Lazzati, D.; Perna, R.; Morsony, B.J.; López-Cámara, D.; Cantiello, M.; Ciolfi, R.; Giacomazzo, B.; Workman, J.C. Late time afterglow observations reveal a collimated relativistic jet in the ejecta of the binary neutron star merger GW170817. Phys. Rev. Lett. 2018, 120, 241103. [Google Scholar] [CrossRef] [PubMed]
- Nakar, E.; Sari, R. Relativistic shock breakouts—A variety of gamma-ray flares: from low luminosity gamma-ray bursts to type Ia supernovae. Astrophys. J. 2012, 747, 88. [Google Scholar] [CrossRef]
- Kasliwal, M.M.; Nakar, E.; Singer, L.P.; Kaplan, D.L.; Cook, D.O.; Van Sistine, A.; Lau, R.M.; Fremling, C.; Gottlieb, O.; Jencson, J.E.; et al. Illuminating gravitational waves: A concordant picture of photons from a neutron star merger. Science 2017, 358, 1559. [Google Scholar] [CrossRef] [PubMed]
- Gottlieb, O.; Nakar, E.; Piran, T.; Hotokezaka, K. A cocoon shock breakout as the origin of the γ-ray emission in GW170817. Mon. Not. R. Astron. Soc. 2017, 479, 588. [Google Scholar] [CrossRef]
- Hallinan, G.; Corsi, A.; Mooley, K.P.; Hotokezaka, K.; Nakar, E.; Kasliwal, M.M.; Kaplan, D.L.; Frail, D.A.; Myers, S.T.; Murphy, T.; et al. A Radio Counterpart to a Neutron Star Merger. Science 2017, 358, 1579. [Google Scholar] [CrossRef] [PubMed]
- Mooley, K.P.; Nakar, E.; Hotokezaka, K.; Hallinan, G.; Corsi, A.; Frail, D.A.; Horesh, A.; Murphy, T.; Lenc, E.; Kaplan, D.L.; et al. A mildly relativistic wide-angle outflow in the neutron star merger GW170817. Nature 2018, 554, 207. [Google Scholar] [CrossRef] [PubMed]
- Nakar, E.; Gottlieb, O.; Piran, T.; Kasliwal, M.M.; Hallinan, G. From γ to Radio—The Electromagnetic Counterpart of GW 170817. Astrophys. J. 2018, 867, 18. [Google Scholar] [CrossRef]
- Piro, A.L.; Kollmeier, J. Evidence for Cocoon Emission from the Early Light Curve of SSS17a. Astrophys. J. 2018, 855, 103. [Google Scholar] [CrossRef]
- Fargion, D.; Khlopov, M.; Oliva, P. Could GRB170817A be really correlated to a NS-NS merging? Int. J. Mod. Phys. D 2018, 27, 1841001. [Google Scholar] [CrossRef]
- Dobie, D.; Kaplan, D.L.; Murphy, T.; Lenc, E.; Mooley, K.P.; Lynch, C.; Corsi, A.; Frail, D.; Kasliwal, M.; Hallinan, G. A turnover in the radio light curve of GW170817. Astrophys. J. 2018, 858, L15. [Google Scholar] [CrossRef]
- Alexander, K.D.; Margutti, R.; Blanchard, P.K.; Fong, W.; Berger, E.; Hajela, A.; Eftekhari, T.; Chornock, R.; Cowperthwaite, P.S.; Giannios, D.; et al. A Decline in the X-ray through Radio Emission from GW170817 Continues to Support an Off-Axis Structured Jet. Astrophys. J. Lett. 2018, 863, L18. [Google Scholar] [CrossRef]
- Mooley, K.P.; Frail, D.A.; Dobie, D.; Lenc, E.; Corsi, A.; De, K.; Nayana, A.J.; Makhathini, S.; Heywood, I.; Murphy, T.; et al. A Strong Jet Signature in the Late-Time Lightcurve of GW170817. Astrophys. J. Lett. 2018, 868, L11. [Google Scholar] [CrossRef]
- Lyman, J.D.; Lamb, G.P.; Levan, A.J.; Mandel, I.; Tanvir, N.R.; Kobayashi, S.; Gompertz, B.; Hjorth, J.; Fruchter, A.S.; Kangas, T.; et al. The optical afterglow of the short gamma-ray burst associated with GW170817. Nat. Astron. 2018, 2, 751. [Google Scholar] [CrossRef]
- Rossi, A.; Cantiello, M.; Testa, V.; Paris, D.; Melandri, A.; Covino, S.; Salafia, O.S.; D’Avanzo, P.; Campana, S.; Nicastro, L.; et al. GW170817/GRB170817A: LBT Optical Detection. 2018. Available online: https://gcn.gsfc.nasa.gov/gcn3/22763.gcn3 (accessed on 15 July 2019).
- Lamb, G.P.; Lyman, J.D.; Levan, A.J.; Tanvir, N.R.; Kangas, T.; Fruchter, A.S.; Gompertz, B.; Hjorth, J.; Mandel, I.; Oates, S.R.; et al. The optical afterglow of GW170817 at one year post-merger. Astrophys. J. Lett. 2019, 870, L15. [Google Scholar] [CrossRef]
- Margutti, R.; Alexander, K.D.; Xie, X.; Sironi, L.; Metzger, B.D.; Kathirgamaraju, A.; Fong, W.; Blanchard, P.K.; Berger, E.; MacFadyen, A.; et al. The Binary Neutron Star event LIGO/VIRGO GW170817 a hundred and sixty days after merger: synchrotron emission across the electromagnetic spectrum. Astrophys. J. Lett. 2018, 856, L18. [Google Scholar] [CrossRef]
- Hajela, A.; Alexander, K.D.; Eftekhari, T.; Margutti, R.; Fong, W.; Berger, E. Chandra Observations of GW170817 260 Days Since Merger: First Statistically Significant Evidence for an X-ray Decay. Available online: https://gcn.gsfc.nasa.gov/gcn3/22692.gcn3 (accessed on 15 July 2019).
- Troja, E.; Piro, L.; Ryan, G. Chandra Observations of GW170817 Reveal a Fading Afterglow. 2018. Available online: https://gcn.gsfc.nasa.gov/gcn3/22693.gcn3 (accessed on 15 July 2019).
- D’Avanzo, P.; Campana, S.; Ghisellini, G.; Melandri, A.; Bernardini, M.G.; Covino, S.; D’Elia, V.; Nava, L.; Salvaterra, R.; Tagliaferri, G.; et al. The evolution of the X-ray afterglow emission of GW 170817/GRB 170817A in XMM-Newton observations. Astron. Astrophys. 2018, 613, L1. [Google Scholar] [CrossRef]
- Nynka, M.; Ruan, J.J.; Haggard, D. Fading of the X-ray Afterglow of Neutron Star Merger GW170817/GRB170817A at 260 days. Astrophys. J. Lett. 2018, 862, L19. [Google Scholar] [CrossRef]
- Haggard, D.; Nynka, M.; Ruan, J.J. Chandra X-ray Observations of GW170817 at 1 Year Post-Merger: Increasingly Rapid Fading. 2018. Available online: https://gcn.gsfc.nasa.gov/gcn3/23140.gcn3 (accessed on 15 July 2019).
- Ziaeepour, H. Prompt gamma-ray emission of GRB 170817A associated to GW 170817: A consistent picture. Mon. Not. R. Astron. Soc. 2018, 478, 3233. [Google Scholar] [CrossRef]
- Ziaeepour, H.; Gardner, B. Broad band simulation of Gamma Ray Bursts (GRB) prompt emission in presence of an external magnetic field. J. Cosmol. Astrop. Phys. 2011, 12, 001. [Google Scholar] [CrossRef][Green Version]
- Ziaeepour, H. Late afterglows of GW/GRB 170817A. arXiv 2018, arXiv:1806.11161. [Google Scholar]
- Ziaeepour, H. Properties of jet and surrounding material of GW/GRB 170817A. arXiv 2019, arXiv:1901.10792. [Google Scholar]
- Mooley, K.P.; Deller, A.T.; Gottlieb, O.; Nakar, E.; Hallinan, G.; Bourke, S.; Frail, D.A.; Horesh, A.; Corsi, A.; Hotokezaka, K. Superluminal motion of a relativistic jet in the neutron star merger GW170817. Nature 2018, 561, 355. [Google Scholar] [CrossRef] [PubMed]
- Ghirlanda, G.; Salafia, O.S.; Paragi, Z.; Giroletti, M.; Yang, J.; Marcote, B.; Blanchard, J.; Agudo, I.; An, T.; Bernardini, M.G.; et al. Compact radio emission indicates a structured jet was produced by a binary neutron star merger. Science 2019, 363, 968. [Google Scholar] [CrossRef] [PubMed]
- Ziaeepour, H. Gamma Ray Bursts Cook Book I: Formulation. Mon. Not. R. Astron. Soc. 2009, 397, 361. [Google Scholar] [CrossRef][Green Version]
- Ziaeepour, H. Prompt gamma-ray emission in GRBs and its simulation. In Horizons in World Physics; Nova Science Inc.: New York, NY, USA, 2015; Volume 286. [Google Scholar]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Bauswein, A.; Just, O.; Janka, H.T.; Stergioulas, N. Neutron-star radius constraints from GW170817 and future detections. Astrophys. J. Lett. 2017, 850, L34. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef] [PubMed]
- Tews, I.; Margueron, J.; Reddy, S. A critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys. Rev. C 2018, 98, 045804. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Dietrich, T.; Doctor, Z.; Kasen, D.; Coughlin, S.; Jerkstrand, A.; Leloudas, G.; McBrien, O.; Metzger, B.D.; O’Shaughnessy, R.; et al. Constraints on the neutron star equation of state from AT2017gfo using radiative transfer simulations. Mon. Not. R. Astron. Soc. 2018, 480, 3871. [Google Scholar]
- Arcavi, I.; Hosseinzadeh, G.; Howell, D.A.; McCully, C.; Poznanski, D.; Kasen, D.; Barnes, J.; Zaltzman, M.; Vasylyev, S.; Maoz, D.; et al. Optical emission from a kilonova following a gravitational-wave-detected neutron-star merger. Nature 2017, 551, 64. [Google Scholar] [CrossRef]
- Metzger, B.D.; Thompson, T.A.; Quataert, E. A magnetar origin for the kilonova ejecta in GW170817. Astrophys. J. 2018, 856, 101. [Google Scholar] [CrossRef]
- Fahlman, S.; Fernández, R. Hypermassive Neutron Star Disk Outflows and Blue Kilonovae. Astrophys. J. Lett. 2018, 869, L3. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An Ordinary Short Gamma-Ray Burst with Extraordinary Implications: Fermi-GBM Detection of GRB 170817A. Astrophys. J. Lett. 2017, 848, L14. [Google Scholar] [CrossRef]
- Savchenko, V.; Ferrigno, C.; Kuulkers, E.; Bazzano, A.; Bozzo, E.; Brandt, S.; Chenevez, J.; Courvoisier, T.J.-L. INTEGRAL Detection of the First Prompt Gamma-Ray Signal Coincident with the Gravitational Wave Event GW170817. Astrophys. J. Lett. 2017, 848, L15. [Google Scholar] [CrossRef]
- Svinkin, D.; Golenetskii, S.; Aptekar, R.; Frederiks, D.; Oleynik, P.; Ulanov, M.; Tsvetkova, A.; Lysenko, A.; Kozlova, A.; Cline, T. LIGO/Virgo G298048: Konus-Wind Observations. 2017. Available online: https://gcn.gsfc.nasa.gov/gcn3/21746.gcn3 (accessed on 15 July 2019).
- Coulter, D.A.; Foley, R.J.; Kilpatrick, C.D.; Drout, M.R.; Piro, A.L.; Shappee, B.J.; Siebert, M.R.; Simon, J.D.; Ulloa, N.; Kasen, D.; et al. Swope Supernova Survey 2017a (SSS17a), the Optical Counterpart to a Gravitational Wave Source. Science 2017, 358, 1556. [Google Scholar] [CrossRef] [PubMed]
- Soares-Santos, M.; Holz, D.E.; Annis, J.; Chornock, R.; Herner, K.; Berger, E.; Brout, D.; Chen, H.; Kessler, R.; Sako, M.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. I. Dark Energy Camera Discovery of the Optical Counterpart. Astrophys. J. Lett. 2017, 848, L16. [Google Scholar] [CrossRef]
- Berger, E. Short-Duration Gamma-Ray Bursts. Annu. Rev. Astron. Astrophys. 2014, 52, 43. [Google Scholar] [CrossRef]
- Fong, W.F.; Berger, E.; Blanchard, P.K.; Margutti, R.; Cowperthwaite, P.S.; Chornock, R.; Alexander, K.D.; Metzger, B.D.; Villar, V.A.; Nicholl, M.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/VIRGO GW170817. VIII. A Comparison to Cosmological Short-duration Gamma-ray Bursts. Astrophys. J. Lett. 2017, 848, L29. [Google Scholar] [CrossRef]
- Haggard, D.; Nynka, M.; Ruan, J.J.; Kalogera, V.; Cenko, S.B.; Evans, P.A.; Kennea, J.A. A Deep Chandra X-ray Study of Neutron Star Coalescence GW170817. Astrophys. J. Lett. 2017, 848, L25. [Google Scholar] [CrossRef]
- Fong, W.F.; Berger, E.; Metzger, B.D.; Margutti, R.; Chornock, R.; Migliori, G.; Foley, R.J.; Zauderer, B.A.; Lunnan, R.; Laskar, T.; et al. Short GRB 130603B: Discovery of a jet break in the optical and radio afterglows, and a mysterious late-time X-ray excess. Astrophys. J. 2013, 780, 118. [Google Scholar] [CrossRef]
- Cummings, J.R.; Barthelmy, S.D.; Gronwall, C.; Holland, S.T.; Kennea, J.A.; Marshall, F.E.; Palmer, D.M.; Perri, M.; Stamatikos, M.; Vetere, L.; et al. GRB 060712: Swift Detection of a Burst. 2006. Available online: https://gcn.gsfc.nasa.gov/gcn3/5301.gcn3 (accessed on 15 July 2019).
- De Pasquale, M.; Barthelmy, S.D.; Campana, S.; Cummings, J.R.; Godet, O.; Guidorzi, C.; Hill, J.E.; Holland, S.T.; Kennea, J.A. GRB 060807: Swift Detection of a Burst. 2006. Available online: https://gcn.gsfc.nasa.gov/gcn3/5409.gcn3 (accessed on 15 July 2019).
- Buckley, D.A.H.; Andreoni, I.; Barway, S.; Cooke, J.; Crawford, S.M.; Gorbovskoy, E.; Gromadski, M.; Lipunov, V.; Mao, J.; Potter, S.B.; et al. A comparison between SALT/SAAO observations and kilonova models for AT 2017gfo: the first electromagnetic counterpart of a gravitational wave transient—GW170817. Mon. Not. R. Astron. Soc. 2018, 474, L71. [Google Scholar] [CrossRef]
- Valenti, S.; Sand, D.J.; Yang, S.; Cappellaro, E.; Tartaglia, L.; Corsi, A.; Jha, S.W.; Reichart, D.E.; Haislip, J.; Kouprianov, V. The discovery of the electromagnetic counterpart of GW170817: kilonova AT 2017gfo/DLT17ck. Astrophys. J. Lett. 2017, 848, L24. [Google Scholar] [CrossRef]
- Alexander, K.D.; Berger, E.; Fong, W.; Williams, P.K.G.; Guidorzi, C.; Margutti, R.; Metzger, B.D.; Annis, J.; Blanchard, P.K.; Brout, D.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/VIRGO GW170817. VI. Radio Constraints on a Relativistic Jet and Predictions for Late-Time Emission from the Kilonova Ejecta. Astrophys. J. Lett. 2017, 848, L21. [Google Scholar] [CrossRef]
- Mandel, I. The orbit of GW170817 was inclined by less than 28 degrees to the line of sight. Astrophys. J. 2018, 853, L12. [Google Scholar] [CrossRef]
- Gruber, D.; Goldstein, A.; von Ahlefeld, V.W.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Byrne, D.; Cleveland, W.H.; Connaughton, V.; Diehl, R.; et al. The Fermi GBM Gamma-Ray Burst Spectral Catalog: Four Years Of Data. Astrophys. J. Suppl. 2014, 211, 27. [Google Scholar] [CrossRef]
- Ziaeepour, H.; Barthelmy, S.D.; Parsons, A.; Page, K.L.; De Pasquale, M.; Schady, P. GRB 070724: Swift Detection of a Burst. 2007. Available online: https://gcn.gsfc.nasa.gov/gcn3/6654.gcn3 (accessed on 15 July 2019).
- Berger, E.; Cenko, S.B.; Fox, D.B.; Cucchiara, A. Discovery of the Very Red Near-Infrared and Optical Afterglow of the Short-Duration GRB 070724A. Astrophys. J. 2009, 704, 877. [Google Scholar] [CrossRef]
- Kocevski, D.; Thone, C.C.; Ramirez-Ruiz, E.; Bloom, J.S.; Granot, J.; Butler, N.R.; Perley, D.A.; Modjaz, M. Limits on Radioactive-Powered Emission Associated With a Short-Hard GRB 070724A in a Star-Forming Galaxy. Mon. Not. R. Astron. Soc. 2010, 404, 963. [Google Scholar] [CrossRef]
- Sakamoto, T.; Chester, M.M.; Cummings, J.R.; Evans, P.A.; Guidorzi, C.; Mangano, V.; Page, K.L.; Palmer, D.M.; Romano, P. GRB 111020A: Swift Detection of a Short Burst. 2011. Available online: https://gcn.gsfc.nasa.gov/gcn3/12460.gcn3 (accessed on 15 July 2019).
- D’Elia, V.; Chester, M.M.; Cummings, J.R.; Malesani, D.; Markwardt, C.B.; Page, K.L.; Palmer, D.M. GRB 130912A: Swift Detection of a Short Burst. 2013. Available online: https://gcn.gsfc.nasa.gov/gcn3/15212.gcn3 (accessed on 15 July 2019).
- Zhu, B.; Zhang, F.W.; Zhang, S.; Jin, Z.P.; Wei, D.M. The long-lasting optical afterglow plateau of short burst GRB 130912A. Astron. Astrophys. 2015, 576, A71. [Google Scholar] [CrossRef][Green Version]
- Siegel, M.H.; Barthelmy, S.D.; Burrows, D.N.; Lien, A.Y.; Marshall, F.E.; Palmer, D.M.; Sbarufatti, B. GRB 160821B: Swift Detection of a Short Burst. 2016. Available online: https://gcn.gsfc.nasa.gov/gcn3/19833.gcn3 (accessed on 15 July 2019).
- Kasliwal, M.M.; Korobkin, O.; Lau, R.M.; Wollaeger, R.; Fryer, C.L. Infrared emission from kilonovae: The case of the nearby short hard burst GRB 160821B. Astrophys. J. Lett. 2017, 843, L34. [Google Scholar] [CrossRef]
- Tunnicliffe, R.L.; Levan, A.J.; Tanvir, N.R.; Rowlinson, A.; Perley, D.A.; Bloom, J.S.; Cenko, S.B.; O’Brien, P.T.; Cobb, B.E.; Wiersema, K.; et al. On the nature of the ’hostless’ short GRBs. Mon. Not. R. Astron. Soc. 2014, 437, 1495. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kiuchi, K.; Shibata, M.; Nakar, E.; Piran, T. Synchrotron radiation from the fast tail of dynamical ejecta of neutron star mergers. Astrophys. J. 2018, 867, 95. [Google Scholar] [CrossRef]
- Zhang, B.B.; Qin, Y.P. Parameters of the Prompt Gamma-Ray Burst Emission Estimated with the Opening Angle of Jets. 2005. Available online: https://arxiv.org/abs/astro-ph/0504070 (accessed on 15 July 2019).
- Zhao, X.H.; Li, Z.; Bai, J. The bulk Lorentz factors of Fermi-LAT GRBs. Astrophys. J. 2010, 726, 87. [Google Scholar]
- Evans, P.A.; Osborne, J.P.; Willingale, R.; O’Brien, P.T. Spectral evolution and the onset of the X-ray GRB afterglow. AIP Conf. Proc. 2011, 1358, 117. [Google Scholar]
- Nakar, E.; Piran, T. The Observable Signatures of GRB Cocoons. Astrophys. J. 2016, 834, 28. [Google Scholar] [CrossRef]
- Berger, E.; Fong, W.; Chornock, R. An r-Process Kilonova Associated with the Short-Hard GRB 130603B. Astrophys. J. Lett. 2013, 774, L23. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Levan, A.J.; Fruchter, A.S.; Hjorth, J.; Hounsell, R.A.; Wiersema, K.; Tunnicliffe, R. A “kilonova” associated with short-duration gamma-ray burst 130603B. Nature 2013, 500, 547. [Google Scholar] [CrossRef]
- Willingale, R.; O’Brien, P.; Osborne, J.P.; Godet, O.; Page, K.L.; Goad, M.R.; Burrows, D.N.; Zhang, B.; Rol, E.; Gehrels, N.; et al. Testing the standard fireball model of GRBs using late X-ray afterglows measured by Swift. Astrophys. J. 2007, 662, 1093. [Google Scholar] [CrossRef]
- Gill, R.; Granot, J. Afterglow Imaging and Polarization of Misaligned Structured GRB Jets and Cocoons: Breaking the Degeneracy in GRB 170817A. Mon. Not. R. Astron. Soc. 2018, 478, 4128. [Google Scholar] [CrossRef]
- Levinson, A.; Begelman, M.C. Collimation and confinement of magnetic jets by external media. Astrophys. J. 2013, 764, 148. [Google Scholar] [CrossRef]
- Bromberg, O.; Tchekhovskoy, A. Relativistic MHD simulations of core-collapse GRB jets: 3D instabilities and magnetic dissipation. Mon. Not. R. Astron. Soc. 2016, 456, 1739. [Google Scholar] [CrossRef]
- De Colle, F.; Lu, W.; Kumar, P.; Ramirez-Ruiz, E.; Smoot, G. Thermal and non-thermal emission from the cocoon of a gamma-ray burst jet. Mon. Not. R. Astron. Soc. 2017, 478, 4553. [Google Scholar] [CrossRef]
- Murase, K.; Toomey, M.W.; Fang, K.; Oikonomou, F.; Kimura, S.S.; Hotokezaka, K.; Kashiyama, K.; Ioka, K.; Meszaros, P. Double Neutron Star Mergers and Short Gamma-Ray Bursts: Long-Lasting High-Energy Signatures and Remnant Dichotomy. Astrophys. J. 2018, 854, 60. [Google Scholar] [CrossRef]
- Korobkin, O.; Hungerford, A.M.; Fryer, C.L.; Mumpower, M.R.; Wendell Misch, G.; Sprouse, T.M.; Lippuner, J.; Surman, R.; Couture, A.J.; Bloser, P.F.; et al. Gamma-rays from kilonova: a potential probe of r-process nucleosynthesis. arXiv 2019, arXiv:1905.05089. [Google Scholar]
- Wijers, R. A chirp, a roar and a whisper. Nature 2018, 554, 178. [Google Scholar] [CrossRef] [PubMed]
- Foucart, F.; Desai, D.; Brege, W.; Duez, M.D.; Kasen, D.; Hemberger, D.A.; Kidder, L.E.; Pfeiffer, H.P.; Scheel, M.A. Dynamical ejecta from precessing neutron star-black hole mergers with a hot, nuclear-theory based equation of state. Class. Quant. Grav. 2017, 34, 044002. [Google Scholar] [CrossRef]
- Kawamura, T.; Giacomazzo, B.; Kastaun, W.; Ciolfi, R.; Endrizzi, A.; Baiotti, L.; Perna, R. Binary Neutron Star Mergers and Short Gamma-Ray Bursts: Effects of Magnetic Field Orientation, Equation of State, and Mass Ratio. Phys. Rev. D 2016, 94, 064012. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Okawa, H.; Sekiguchi, Y.I.; Shibata, M.; Taniguchi, K. The mass ejection from the merger of binary neutron stars. Phys. Rev. D 2013, 87, 024001. [Google Scholar] [CrossRef]
- Dietrich, T.; Bernuzzi, S.; Ujevic, M.; Tichy, W. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of the stars’ rotation. Phys. Rev. D 2017, 95, 044045. [Google Scholar] [CrossRef]
- Komissarov, S.; Vlahakis, N.; Konigl, A.; Barkov, M. Magnetic acceleration of ultra-relativistic jets in gamma-ray burst sources. Mon. Not. R. Astron. Soc. 2009, 394, 1182. [Google Scholar] [CrossRef]
- Krimm, H.A. (Swift Science Team, National Science Foundation, Alexandria, VA, USA). Private communication, 2018.
- Izzo, L.; de Ugarte Postigo, A.; Maeda, K.; Thöne, C.C.; Kann, D.A.; Della Valle, M.; Sagues Carracedo, A.; Michałowski, M.J.; Schady, P.; Schmidl, S.; et al. Signatures of a jet cocoon in early spectra of a supernova associated with a γ-ray burst. Nature 2019, 565, 324. [Google Scholar] [CrossRef] [PubMed]
- Murguia-Berthier, A.; Ramirez-Ruiz, E.; Kilpatrick, C.D.; Foley, R.J.; Kasen, D.; Lee, W.H.; Piro, A.L.; Coulter, D.A.; Drout, M.R.; Madore, B.F.; et al. A Neutron Star Binary Merger Model for GW170817/GRB170817a/SSS17a. Astrophys. J. Lett. 2017, 848, L34. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. 1998, 497, 17. [Google Scholar] [CrossRef]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; Wieley-VCH verlag GmbH & Co.KGaA: Wienheim, Germany, 2004. [Google Scholar]
- Rezzolla, L.; Giacomazzo, B.; Baiotti, L.; Granot, J.; Kouveliotou, C.; Aloy, M.A. The missing link: Merging neutron stars naturally produce jet-like structures and can power short Gamma-Ray Bursts. Astrophys. J. Lett. 2011, 732, L6. [Google Scholar] [CrossRef]
- Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Shibata, M.; Wada, T. High resolution numerical relativity simulations for the merger of binary magnetized neutron stars. Phys. Rev. D 2014, 90, 041502. [Google Scholar] [CrossRef]
- Siegel, D.M.; Metzger, B.D. Three-dimensional GRMHD simulations of the remnant accretion disks from neutron star mergers: Outflows and r-process nucleosynthesis. Phys. Rev. Lett. 2017, 119, 231102. [Google Scholar] [CrossRef] [PubMed]
- Siegel, D.M.; Metzger, B.D. Three-dimensional GRMHD simulations of neutrino-cooled accretion disks from neutron star mergers. Astrophys. J. 2018, 858, 52. [Google Scholar] [CrossRef]
- Spitkovsky, A. Particle acceleration in relativistic collisionless shocks: Fermi process at last? Astrophys. J. 2008, 682, 5. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Particle Acceleration in Relativistic Magnetized Collisionless Electron-Ion Shocks. Astrophys. J. 2011, 726, 75. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Acceleration of Particles at the Termination Shock of a Relativistic Striped Wind. Astrophys. J. 2011, 741, 39. [Google Scholar] [CrossRef]
- Cummings, J.R.; Palmer, D.M. GRB 080121: Swift-BAT Detection of a Very Weak, Short Burst. 2008. Available online: https://gcn.gsfc.nasa.gov/gcn3/7209.gcn3 (accessed on 15 July 2019).
- Perley, D.A.; Foley, R.J.; Bloom, J.S. GRB 080121: Nearby SDSS Galaxies. 2008. Available online: https://gcn.gsfc.nasa.gov/gcn3/7210.gcn3 (accessed on 15 July 2019).
- Posselt, B.; Pavlov, G.G.; Ertan, Ü.; Çalışkan, S.; Luhman, K.L.; Williams, C.C. Discovery of extended infrared emission around the neutron star RX J0806.4-4123. Astrophys. J. 2018, 865, 1. [Google Scholar] [CrossRef]
- Olivares, F.; Greiner, J.; Schady, P.; Rau, A.; Klose, S.; Krühler, T.; Afonso, P.M.J.; Updike, A.C.; Nardini, M.; Filgas, R.; et al. The Fast Evolution of SN 2010bh associated with XRF 100316D. Astron. Astrophys. 2012, 539, A76. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and Equation of State of Neutron Stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401. [Google Scholar] [CrossRef]
- Stepanovs, D.; Fendt, C. An extensive numerical survey of the correlation between outflow dynamics and accretion disk magnetization. Astrophys. J. 2016, 825, 14. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433. [Google Scholar] [CrossRef]
- Wu, K. Magnetic Interaction in Ultra-compact Binary Systems. Astron. Astrophys. 2009, 3, 725. [Google Scholar] [CrossRef]
- Piro, A.L. Magnetic Interactions in Coalescing Neutron Star Binaries. Astrophys. J. 2012, 755, 80. [Google Scholar] [CrossRef]
- Dall’Osso, S.; Stella, L.; Palomba, C. Neutron star bulk viscosity, “spin-flip” and GW emission of newly born magnetars. Mon. Not. R. Astron. Soc. 2018, 480, 1353. [Google Scholar] [CrossRef]
- Haskell, B.; Pizzochero, P.M.; Seveso, S. Investigating superconductivity in neutron star interiors with glitch models. Astrophys. J. Lett. 2013, 784, L25. [Google Scholar] [CrossRef]
- Blanchard, P.K.; Berger, E.; Fong, W.; Nicholl, M.; Leja, J.; Conroy, C.; Alexander, K.D.; Margutti, R.; Williams, P.K.G.; Doctor, Z.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/VIRGO GW170817. VII. Properties of the Host Galaxy and Constraints on the Merger Timescale. Astrophys. J. Lett. 2017, 848, L22. [Google Scholar] [CrossRef]
- Im, M.; Yoon, Y.; Lee, S.K.; Lee, H.M.; Kim, J.; Lee, C.U.; Kim, S.L.; Troja, E.; Choi, C.; Lim, G.; et al. Distance and properties of NGC 4993 as the host galaxy of a gravitational wave source, GW170817. Astrophys. J. Lett. 2017, 849, L16. [Google Scholar] [CrossRef]
- Harding, A.K.; Lai, D. Physics of Strongly Magnetized Neutron Stars. Rep. Prog. Phys. 2006, 69, 2631. [Google Scholar] [CrossRef]
- Levan, A.J.; Lyman, J.D.; Tanvir, N.R.; Hjorth, J.; Mandel, I.; Stanway, E.R.; Steeghs, D.; Fruchter, A.S.; Troja, E.; Schrøder, S. L; et al. The environment of the binary neutron star merger GW170817. Astrophys. J. Lett. 2017, 848, L28. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Gnedin, O.Y.; Gusakov, M.E.; Kaminker, A.D.; Levenfish, K.P.; Potekhin, A.Y. Neutron star cooling. Nucl. Phys. A 2005, 752, 590. [Google Scholar] [CrossRef]
- Wei, J.-B.; Burgio, G.F.; Schulze, H.-J. Neutron star cooling with microscopic equations of state. Mon. Not. R. Astron. Soc. 2019, 484, 5162. [Google Scholar] [CrossRef]
- Palmese, A.; Hartley, W.; Tarsitano, F.; Conselice, C.; Lahav, O.; Allam, S.; Annis, J.; Lin, H.; Soares-Santos, M.; Tucker, D.; et al. Evidence for Dynamically Driven Formation of the GW170817 Neutron Star Binary in NGC 4993. Astrophys. J. Lett. 2017, 849, L34. [Google Scholar] [CrossRef]
- Margalit, B.; Metzger, B.D. Constraining the Maximum Mass of Neutron Stars From Multi-Messenger Observations of GW170817. Astrophys. J. Lett. 2017, 850, L19. [Google Scholar] [CrossRef]
- Ruiz, M.; Shapiro, S.L.; Tsokaros, A. GW170817, General Relativistic Magnetohydrodynamic Simulations, and the Neutron Star Maximum Mass. Phys. Rev. D 2018, 97, 021501. [Google Scholar] [CrossRef] [PubMed]
- Price, D.J.; Rosswog, S. Producing Ultrastrong Magnetic Fields in Neutron Star Mergers. Science 2006, 312, 719. [Google Scholar] [CrossRef]
- Markwardt, C.B.; Gavriil, F.P.; Palmer, D.M.; Baumgartner, W.H.; Barthelmy, S.D. GRB 090709A: Quasiperiodic Variations in the BAT Light Curve. 2009. Available online: https://gcn.gsfc.nasa.gov/gcn3/9645.gcn3 (accessed on 15 July 2019).
- Krastev, P.G.; Li, B.A. Nuclear limits on properties of pulsars and gravitational waves. In Pulsars: Theory, Categories and Applications; Morozov, A.D., Ed.; Nova Science Publishers: New York, NY, USA, 2010. [Google Scholar]
- Bernuzzi, S.; Dietrich, T.; Tichy, W.; Bruegmann, B. Mergers of binary neutron stars with realistic spin. Phys. Rev. D 2014, 89, 104021. [Google Scholar] [CrossRef]
- Kastaun, W.; Ciolfi, R.; Endrizzi, A.; Giacomazzo, B. Structure of Stable Binary Neutron Star Merger Remnants: Role of Initial Spin. Phys. Rev. D 2017, 96, 043019. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Tsokaros, A.; Rezzolla, L. Impact of high spins on the ejection of mass in GW170817. arXiv 2019, arXiv:1904.04220. [Google Scholar]
- Togashi, H.; Nakazato, K.; Takehara, Y.; Yamamuro, S.; Suzuki, H.; Takano, M. Nuclear equation of state for core-collapse supernova simulations with realistic nuclear forces. Nucl. Phys. A 2017, 961, 78. [Google Scholar] [CrossRef]
- Banik, S.; Hempel, M.; Bandyopadhyay, D. New Hyperon Equations of State for Supernovae and Neutron Stars in Density-dependent Hadron Field Theory. Astrophys. J. Suppl. 2014, 214, 22. [Google Scholar] [CrossRef]
- Slane, P. Pulsar Wind Nebulae. In Handbook of Supernovae; Alsabti, A.W., Murdin, P., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Akcay, S. Forecasting Gamma-Ray Bursts using Gravitational Waves. Ann. Phys. 2019, 531, 1800365. [Google Scholar] [CrossRef]
- The Kagra Collaboration. KAGRA: 2.5 Generation Interferometric Gravitational Wave Detector. arXiv arXiv:1811.08079.
- LIGO-India. Available online: http://www.ligo-india.in/ (accessed on 15 July 2019).
- The LIGO Scientific Collaboration; The Virgo Collaboration. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85. [Google Scholar] [CrossRef]
- The Planck Collaboration. Planck 2018 results. VI. Cosmological parameters. arXiv 2018, arXiv:1807.06209. [Google Scholar]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics Beyond LambdaCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Taubenberger, S.; Suyu, S.H.; Komatsu, E.; Jee, I.; Birrer, S.; Bonvin, V.; Courbin, F.; Rusu, C.E.; Shajib, A.J.; Wong, K.C. The Hubble Constant determined through an inverse distance ladder including quasar time delays and Type Ia supernovae. arXiv 2019, arXiv:1905.12496. [Google Scholar]
- Di Valentino, E.; Melchiorri, A. First cosmological constraints combining Planck with the recent gravitational-wave standard siren measurement of the Hubble constant. Phys. Rev. D 2018, 97, 041301. [Google Scholar] [CrossRef]
- Guidorzi, C.; Margutti, R.; Brout, D.; Scolnic, D.; Fong, W.; Alexander, K.D.; Cowperthwaite, P.S.; Annis, J.; Berger, E.; Blanchard, P.K.; et al. Improved constraints on H0 from a combined analysis of gravitational-wave and electromagnetic emission from GW170817. Astrophys. J. Lett. 2017, 851, L36. [Google Scholar] [CrossRef]
- Soares-Santos, M.; The DES Collaboration; the LIGO Scientific Collaboration; the Virgo Collaboration. First measurement of the Hubble constant from a dark standard siren using the Dark Energy Survey galaxies and the LIGO/Virgo binary-black-hole merger GW170814. Astrophys. J. Lett. 2019, 876, L7. [Google Scholar] [CrossRef]
- Baker, T.; Bellini, E.; Ferreira, P.G.; Lagos, M.; Noller, J.; Sawicki, I. Strong constraints on cosmological gravity from GW170817 and GRB 170817A. Phys. Rev. Lett. 2017, 119, 251301. [Google Scholar] [CrossRef] [PubMed]
- The LIGO Scientific Collaboration; The Virgo Collaboration. Tests of General Relativity with GW170817. Phys. Rev. Lett. 2019, 123, 011102. [Google Scholar] [CrossRef]
- Copeland, E.J.; Kopp, M.; Padilla, A.; Saffin, P.M.; Skordis, C. Dark energy after GW170817, revisited. Phys. Rev. Lett. 2019, 122, 061301. [Google Scholar] [CrossRef] [PubMed]
- Shoemaker, I.M.; Murase, K. Constraints from the Time Lag between Gravitational Waves and Gamma Rays: Implications of GW 170817 and GRB 170817A. Phys. Rev. D 2018, 97, 083013. [Google Scholar] [CrossRef]
- Abedi, J.; Dykaar, H.; Afshordi, N. Echoes from the abyss: Tentative evidence for Planck-scale structure at black hole horizons. Phys. Rev. D 2017, 96, 082004. [Google Scholar] [CrossRef]
- Abedi, J.; Afshordi, N. Echoes from the Abyss: A Highly Spinning Black Hole Remnant for the Binary Neutron Star Merger GW170817. arXiv 2018, arXiv:1803.10454. [Google Scholar]
- Testa, A.; Pani, P. Analytical template for gravitational-wave echoes: signal characterization and prospects of detection with current and future interferometers. Phys. Rev. D 2018, 98, 044018. [Google Scholar] [CrossRef]
- Oshita, N.; Afshordi, N. Probing microstructure of black hole spacetimes with gravitational wave echoes. Phys. Rev. D 2019, 99, 044002. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).