Abstract
This paper presents a novel method of tensor rank regularization with bias compensation for channel estimation in a hybrid millimeter wave MIMO-OFDM system. Channel estimation is challenging due to the unknown number of multipath components that determines the channel rank. In general, finding the intrinsic rank of a tensor is a non-deterministic polynomial-time (NP) hard problem. However, by leveraging the sparse characteristics of millimeter wave channels, we propose a modified CANDECOMP/PARAFAC (CP) decomposition-based method that jointly estimates the tensor rank and channel component matrices. Our approach differs from most existing works that assume the number of channel paths is known and the proposed method is able to estimate channel parameters accurately without the prior knowledge of number of multipaths. The objective of this work is to estimate the tensor rank by a novel sparsity-promoting prior that is incorporated into a standard alternating least squares (ALS) function. We introduce a weighting parameter to control the impact of the previous estimate and the tensor rank estimation bias compensation in the regularized ALS. The channel information is then extracted from the estimated component matrices. Simulation results show that the proposed scheme outperforms the baseline l1 strategy in terms of accuracy and robustness. It also shows that this method significantly improves rank estimation success at the expense of slightly more iterations.
1. Introduction
Millimeter wave (mmWave) transmission technology is an attractive candidate technology for next-generation wireless communication systems []. The main benefit of utilizing mmWave carrier frequencies is the larger spectral bandwidth available for higher data rates facilitating the ever-increasing communication traffic []. To compensate for the significant path-loss at such high frequencies, large antenna arrays are common at both the base station (BS) and the mobile station (MS) to provide sufficient beamforming gain []. Compared to conventional multiple-input multiple-output (MIMO) systems, the large antenna arrays in mmWave systems make it unlikely to have a dedicated radio frequency (RF) chain for each antenna without costly hardware []. A hybrid analog/digital structure uses fewer RF chains to reduce the number of power-consuming devices, such as analog-to-digital converters (ADCs) or digital-to-analog converters (DACs) []. To achieve considerable beamforming gain in the precoding stage, accurate channel state information (CSI) is required through channel estimation.
Channel estimation in mmWave hybrid systems is challenging due to the hybrid precoding structure and the large number of antennas. The mmWave channel can be modeled in parametric form based on the path angles, i.e., directions of arrival and departure (DoA/DoD), and the corresponding complex path gains. As a result, mmWave channel estimation is a problem of estimating the path angles and gains rather than estimating the conventional MIMO channel matrix [,]. An attractive approach to directly estimate the mmWave channel parameters is to use compressive sensing (CS) based methods [,,,,,,]. Due to the limited propagation range of mmWave channels, the parametric form of the channel description generally has few active paths. Therefore, these CS-based methods leverage the sparsity of the channel to cast estimation as a sparse recovery problem. The virtual angular representation [] or angle grids [] are used to describe the path angles. There is a gain coefficient for each angle grid point that represents a pair of DoA/DoD. Because of the spatial sparsity of the mmWave channel, most of the gain coefficients are negligible. The sparse recovery approach intends to recover the significant gain coefficients providing estimates of the path directions and reducing training overhead. A compressive architecture for estimating and tracking sparse spatial channels in mmWave picocellular networks with large arrays was proposed and investigated in []. In [], it considered multi-user massive MIMO systems and deployed CS-based techniques to reduce the training and feedback overhead in the channel state information at the transmitter estimation. In [,], the authors showed that significant reductions in training overhead can be achieved via CS-based methods in mmWave MIMO communication systems. [] developed a system that uses CS-based estimation on the uplink to configure precoders and combiners for the downlink in a hybrid mmWave MIMO system.
In addition to CS-based methods, tensor-based methods for mmWave MIMO communication have been studied in [,,,,,], which formulate a third order tensor with multiple dimensions containing information about the channel parameters. A two-stage tensor decomposition-based method for mmWave time-varying channel estimation was proposed in []. The CP decomposition aided method is used to estimate the DOAs/DODs in the first stage. The estimated angles are then used to estimate the path gains and doppler shifts. A spatial channel covariance estimation method, proposed in [], is based on higher-order tensor decomposition for the hybrid single-input multiple-output (SIMO) architecture over uplink time-varying frequency-selective channels. The Vandermonde structure of the component matrix of a third-order low-rank tensor model was proposed in [], which developed a non-iterative structured CP decomposition-aided channel estimation algorithm and showed the advantages of avoiding random initialization and iterations. The authors in [] also proposed a tensor rank estimation method by applying singular value decomposition (SVD) to a tensor unfolding matrix, which is suitable in a noiseless channel. A CP decomposition-based method for mmWave channel parameter estimation with frequency selectivity in a hybrid orthogonal frequency division multiplexing (OFDM)-MIMO scenario was proposed in [], which showed advantages over a compressed sensing (CS)-based method. A novel tensor-decomposition channel estimation method for IRS-assisted mmWave OFDM systems was proposed in []. By exploiting the inherent sparse structure of the cascade channel, the authors formulate the received signal as a low-rank third-order tensor. Only a very small amount of training overhead is used to obtain a reliable estimate of the cascade channel because of the low rank structure. A sparse Bayes tensor and DOA tracking inspired channel estimation for V2X millimeter wave massive MIMO system was proposed in []. This paper dealt with accurate channel estimation in highly mobile scenarios. The sparse Bayes tensor is used to calculate the angle offset. Then a direction of arrival (DOA) tracking method is developed to acquire the angle value at the next moment by exploiting the sparse Bayes tensor.
These methods rely on knowing, or estimating, the rank of the tensors. Tensor rank is analogous to matrix rank, but the properties of matrix and tensor ranks are quite different. It is not clear how to define a nuclear norm surrogate for tensors because singular values defined by the Tucker decomposition are not generally related to the rank of a tensor. Usually, finding the tensor rank is NP-hard [], and even very simple tensors stubbornly resist rank determination, such as for the × × tensor whose rank is only known to be between 19 and 23 []. While the tensor rank is difficult to compute precisely, it is not known whether the rank can be approximated. A regularization term of the CP decomposition factors capturing the tensor’s rank was proposed in []. The proposed regularization term relies on an alternative characterization of the nuclear norm based on a low-rank factorization of its matrix argument. A method to simultaneously perform CP decomposition and tensor rank approximation was proposed in [], which divided a third-order low rank CP tensor into 4 blocks, i.e., 3 component matrices and 1 weighting vector. In this paper, we propose a novel CP decomposition based method to jointly estimate the tensor rank and channel component matrices for the hybrid MIMO architecture. We construct the received signal into a third-order tensor and exploit the low rank characteristics of mmWave channel.
The main contributions of the paper are summarized as follows:
- First, we propose a novel CP decomposition-based method to jointly estimate both the tensor rank and component matrices of the received signal tensor. We formulate the received signals into a third-order tensor in the form of the CP structure of a hybrid MIMO-OFDM system. Unlike the conventional tensor signal analysis assumed a-priori knowledge of the rank, we focus on determining the tensor rank which is often unknown in practice. We also develop a novel sparsity-promoting prior to determine tensor rank, and then estimate channel information from low rank component matrix representations.
- Second, we analyze the effectiveness of the weighting parameter in our proposed new prior. Based on the numerical results, we show that the proposed scheme outperforms the conventional strategies in [,] in terms of estimation accuracy and robustness.
- Third, we discuss the trade-off between convergence and rank estimation accuracy for our proposed rank regularization method. Through numerical experiments, we find that our method significantly improves rank estimation success at the expense of slightly more iterations.
The rest of the paper is organized as follows. Section 2 briefly introduces some tensor basics. The system model is discussed in Section 3. In Section 4, we propose a novel CP decomposition-based joint method for mmWave channel estimation. The computational complexity of the proposed method and the conventional CP decomposition method without known rank are analyzed in Section 5. Simulation results are shown in Section 6. Conclusions are provided in Section 7.
Notations: We use the following notations throughout this paper: y is a scalar, y is a vector, Y is a matrix, and is a tensor. , , , and are transpose, conjugate, conjugate transpose, and Moore-Penrose pseudoinverse, respectively. and are the i-th row and the j-th column of the matrix Y. A⊗B, A⊛B, and A⊙B denote the Kronecker product, the Hadamard product, and the column-wise Khatri-Rao product. a∘b denotes the outer product, which is also known as the tensor product. Let Rank () and denote the rank and Kruskal-rank of a matrix , respectively. Let Re(Y) and Im(Y) denote the real part and the imaginary part of Y. d(Y) denotes a vector of diagonal entries of Y, and D(y) denotes a diagonal matrix constructed from y.
2. Tensor Preliminaries
In this section, we briefly introduce the foundations of tensor algebra that will be used in this paper. Readers who are interested in more details about tensors can refer to [,].
2.1. Tensor Basics
Simply speaking, a tensor is a multi-dimensional array. The order of a tensor is defined as the number of dimensions of the tensor. Vectors and matrices can be viewed as special cases of tensors with one and two orders, respectively. Let an N-th order tensor be denoted as with ()-th entry . Fibers are the higher-order analogue of matrix rows and columns. The mode-n fibers of are defined as —dimensional vectors obtained by fixing all but one index . Slices are two-dimensional sections of a tensor, defined by fixing all but two indices. The mode-n unfolding (i.e., matricization) is an operation that transforms a tensor into a matrix. The mode-n unfolding of a tensor , denoted as , arranges the mode-n fibers as the columns of the resulting unfolding matrix.
2.2. CP Tensor Decomposition
A tensor is called a rank-one tensor if it can be written as the outer product of vectors
where , .
The canonical polyadic decomposition (CPD), which is also known as CANDECOMP/PARAFAC decomposition, factorizes a tensor into a sum of component rank-one tensors. The CPD of is defined as
where for . The minimum achievable value is referred to as the rank of the tensor.
3. Signal Model
We consider a massive MIMO-OFDM system consisting of a base station and multiple mobile stations operating at mmWave frequencies. To facilitate the hardware implementation, hybrid analog/digital architectures are employed by both the BS and the MS, shown in Figure 1. We assume that the BS is equipped with antennas and RF chains (), and each MS is equipped with antennas and RF chains (). The OFDM system occupies subcarriers for data transmission, among which subcarriers are selected for training purposes. In the downlink scenario, we only need to consider a single user system because the channel estimation is conducted by each mobile user []. For the -th subcarrier, the BS utilizes an analog RF precoder . Similarly, the MS employs an analog combiner for analog signal processing. The digital processors follow and in BS, and MS performs channel estimation and digital precoding []. The elements of and are assumed to be random phases with a unit amplitude.
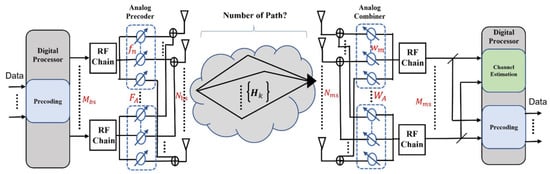
Figure 1.
Architecture of the proposed Hybrid-MIMO system.
Both the BS and MS employ uniform linear arrays (ULA) with antenna element spacing of half the signal wavelength. The extended Saleh-Valenzuela model [,], is adopted to characterize the sparse mmWave channel with multipath between the MS and the BS. The frequency-domain channel matrix associated with the k-th subcarrier can be obtained as
where is the system sampling rate, is the complex gain of the rth path in the frequency domain, is the time delay, the DoD—θr and the DoA—φr. and are the steering vectors of the MS and BS, respectively.
The MS employs combining vectors with all the RF chains to simultaneously combine the n-th pilot precoded by a beamforming vector . The BS switches beamforming vectors at successive time slots, while the MS maintains the combining matrix . Then, adopting the same strategy of [], the received signals for the -th subcarrier can be represented as
where , is the transmitted symbol matrix for successive time slots, and is the equivalent noise after the combining process. We assume that the pilot matrix is for simplicity [].
Then substituting the frequency domain channel matrix (3) into (4), we obtain
where and are the equivalent array response vectors.
By combining of selected subcarriers, the received signals can be expressed by a third-order tensor . We notice that each frontal slice of the tensor is a weighted sum of a common set of rank-one outer products, which makes the tensor admit the definition of the CP model as
where we assume subcarriers are assigned for the training process for simplicity and is the phase vector caused by delay. is the equivalent noise tensor.
Due to the sparse nature of mmWave channels, the number of paths is typically small relative to the dimension of the tensor [,]. Therefore, inherently has a low-rank nature, which ensures that the CP decomposition is unique up to scaling and permutation ambiguities. An estimation of channel parameters {, , , } can be obtained by processing the CP decomposition results from . Define
These three component matrices , , and are associated with a noiseless version of .
4. The Proposed Algorithm
4.1. Joint CP Tensor Decomposition
If the number of active paths, or rank , is known, the CP decomposition of can be accomplished by a standard alternating least squares (ALS) method [].
It is likely that the rank is unknown in practice. In this case, the CP decomposition of can be accomplished by minimizing the cost function
where is an estimation of the true rank . Instead of estimating tensor rank individually, we seek a more comprehensive CP decomposition-based technique to estimate component matrices and rank jointly. A method of combining CP decomposition and sparsity-promoting prior is presented as an l1 regularization LS method [] by solving
where is a tuning parameter for the rank regularization term. The regularizer relies on an alternative characterization of the nuclear norm based on a low-rank factorization of its matrix argument.
The optimization problem (11) can also be solved by ALS. However, because the rank is unknown, an overestimated CP rank, , must be chosen initially. The objective function (11) can be divided into three sub-problems:
Sub-problems (12)–(14) do not contain sparsity-promoting prior. However, the entire ALS procedure promotes sparse results because the restraint in (11) is incorporated in the three sub-problems. can be estimated by removing all negligible rank-one tensor components after convergence. The least squares solutions are derived as follows:
According to [], (15)–(17) are also special cases of the iteratively regularized Gauss-Newton method with a linear bounded operator and initial guess set as 0. Equations (15)–(17) have corresponding iterative sequences. Consider (15) as an example and transform to its iterative sequence as follows:
From the above iterative sequence, one can easily get back to (15) when (18) approaches the convergence.
Equations (15)–(17) are the well-known ridge regression solutions. However, there is a bias issue according to [,]. For example, the bias can be demonstrated by transforming the least squares solution (15) as follows,
When the solution converges, , , , (with noise in ). Substitute , , into the right-hand side of (19), we can get . Substitute , , into the left-hand side of (19), we can get . If we compare two sides, it leads to (19) invalid due to common term exists in both sides. Therefore, in (19) is called the bias term. It is desirable to compensate for the effect of the bias term by introducing an additional term as the algorithm converges to the desired solution. To compensate the regularization term we can add to the right-hand side the similar term which gradually removes the bias as , where is the estimate of
After some manipulation we get
Likewise, we can compensate the estimation bias of and by using
According to [,], (21)–(23) are least square solutions of the regularized alternating least squares (RALS) objective function
The second term in (24) penalizes the difference between the current values and previous iterates. However, the limit points of (24) are the critical points of a standard ALS-the first term in (24) without the regularization term. Equation (24) can be divided into three sub-problems:
The iteration approaches (25)–(27) work well for CP tensor decomposition with faster convergence if the rank is known. If the rank is unknown, objective function (24) is incapable of obtaining tensor rank because its solutions are not critical points of the regularized version. According to [,], the sub-problems (25)–(27) are variational characterizations of the Levenberg–Marquardt method with linear bounded operator. We need to seek a compromise between estimation bias and sparsity promotion.
4.2. Proposed CP Tensor Decomposition with Weighted Bias
We propose a novel regularized alternating least squares (RALS) with sparsity promoting and weighted bias compensation as follows,
where is the weighting parameter. The objective function (28) can be divided into three sub-problems:
The least square solutions of (29)–(31) as follows
To explore the role of the weighting parameter , we will consider the iteration of matrix A from (32). First, (32) can be transformed to an iterative sequence as follows
When the solution in (35) approaches convergence: , we have
According to [], (36) is a modified Levenberg-Marquardt function with variable decay rate when . We will therefore restrict the range of to (0, 1). Sub-problems (29)–(31) can be considered modified Levenberg–Marquardt variational characterizations. Compared to LS solution (15) which is a Levenberg-Marquardt function, we know that will affect both the direction and step size of each iteration []. The scaled identity matrix in the modified Levenberg-Marquardt method in (36) also controls the direction of each iteration to favor low-rank solutions through the modified pseudoinverse calculation ) of (36). Compared to that of the LS solution (15), the added term 1 will slightly change the direction of (15) and still favor low rank solutions because we restrict .
Moreover, compared to the LS solution (15) and RALS solution (21), the weighting parameter in (32) controls the bias compensation. The analyses to and are similar.
The estimated component matrices from the novel joint CP tensor decomposition-based method are associated with the weighting parameter. The novel joint CP tensor decomposition-based method is summarized in Algorithm 1.
| Algorithm 1. The Proposed Joint CP Tensor Decomposition-Based Estimation Method. |
| Input, an initial selection for rank(), and the regularization parameters , weighting parameter , threshold , number of Iterations iter = 0, Output: Estimated Rank , Estimated Component Matrices , , , iter 1. Derive unfolding matrices: , , 2. Generate normally distributed pseudorandom initial matrices , , 3. The initialization of the cost function is : 4. while do 5. iter = iter + 1 6. Calculate 7. Calculate 8. Calculate 9. Recalculate cost in Equation (10) 10. End while 11. Calculate column power of 12. Set the number of columns whose power > as and construct the new by using these columns 13. Based on the index number obtained from 11, we select the columns from and to construct new and new 14. Return , , |
After obtaining the estimated component matrices: , and , we turn to the channel parameters estimation by using the correlation-based scheme adopted by [].
5. Computational Complexity Analysis
We analyze the computational complexity of the proposed CP decomposition-based joint estimation method and the baseline l1 regularization LS method.
The major computational task of the proposed joint rank and component matrices estimation method involves solving the three least squares problems (32)–(34) at each iteration. Considering the calculation of , we have (32). The complexity of calculating consists of three steps:
- (1)
- To calculate , the complexity is ,
- (2)
- To calculate , the complexity is ,
- (3)
- To calculate , the complexity is .
Thus, the total number of flops required to compute is of order .
The major computational task of l1 regularization LS joint rank and component matrices estimation method involves solving three least squares problems (15)–(17) at each iteration. The complexity of the calculation in (15) is the same as the computational complexity (32) above because the calculations of matrix sum, matrix transpose, matrix conjugate, and matrix multiplication by a constant can be ignored in the complexity evaluation.
Similarly, we can analyze the complexity of (33) and (34) as above.
6. Numerical Experiments
We present simulation results to demonstrate the performance of the proposed method. We consider a scenario where the BS employs a uniform linear array with = 64 antennas and RF chains = 6, the MS employs a uniform linear array with = 32 antennas and RF chains = 6. The separation between neighboring antenna elements is assumed to be half the signal wavelength. In our simulations, the mmWave MIMO channel is generated according to the wideband geometric channel model, in which the DoAs and DoDs are randomly distributed in [0, 2π], the delay spread for each path is uniformly distributed between 0 and 100 nanoseconds, and the complex gain is a random variable following a circularly symmetric Gaussian distribution (0, 1/R). We set = 28 GHz, the total number of subcarriers = 128, the number of subcarriers selected for training K = 6, and the sampling rate = 0.32 GHz.
The beamforming matrix and the combining matrix are randomly generated with their entries uniformly chosen from a unit circle. Because the sparse scattering nature of mmWave channels, the number of paths R is usually small [,]. Thus, we select the number of paths equal to R = 4, 5, and 6 to form a low rank channel scenario in our simulations. We assume the initial rank to be an overestimation of the true rank. To compare the rank estimation performance, the signal-to-noise ratio (SNR) is defined as the ratio of the signal component to the noise component, i.e.,
Figure 2 shows the estimated ranks versus regularization tuning parameter in the interval to 1 based on the baseline l1 regularization LS method (11) when R = 4 with the selected SNR values. It is observed that tensor rank can be approximately recovered when = .
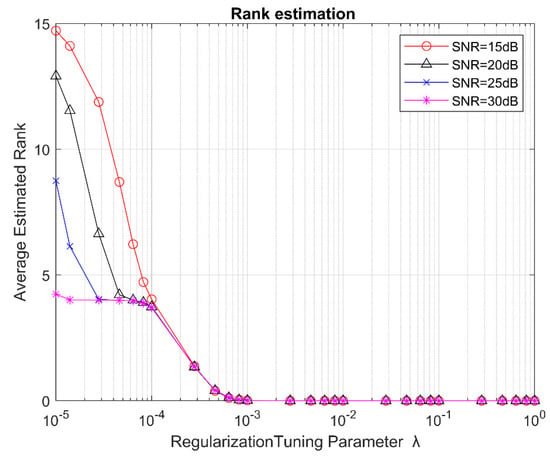
Figure 2.
Rank estimation performance of the l1 Regularization LS method as a function of with real rank = 4.
To evaluate the rank estimation performance of the proposed method as a function of weighting parameter , Figure 3 depicts the performance comparison of rank estimation versus SNR with = and real rank = 4. It also indicates the proposed method leads to smaller rank estimation error when is no larger than 0.5 with SNRs between 20 dB and 30 dB than that of the l1 regularization LS method.
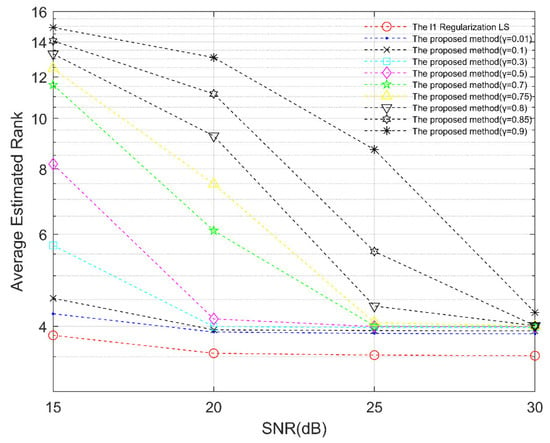
Figure 3.
Comparison of the rank estimation performance of the proposed method as a function of and the l1 regularization LS versus SNR with = and real rank = 4.
The comparison between the proposed method and the l1 regularization LS in terms of robustness is shown in Figure 4. The simulation is based on the true rank R = 4, =, = 0.3, SNR = 20 dB. We select the initial rank as some integers between 4 and 32 and calculate the estimated rank with the same stop criterion. The selection of the upper bound of the initial rank is bounded by the characteristics of , and . We make these three Khatri-Rao products as overdetermined matrices to guarantee the ALS-based method has a unique solution. So, It can be observed from Figure 4 that the proposed method (the top red line) converges to the real rank R = 4 under the different initializations, while l1 regularization LS method only converges at a large initial . Thus, the rank estimation performance of the proposed method is much more robust than that of the l1 regularization LS in terms of initialization.
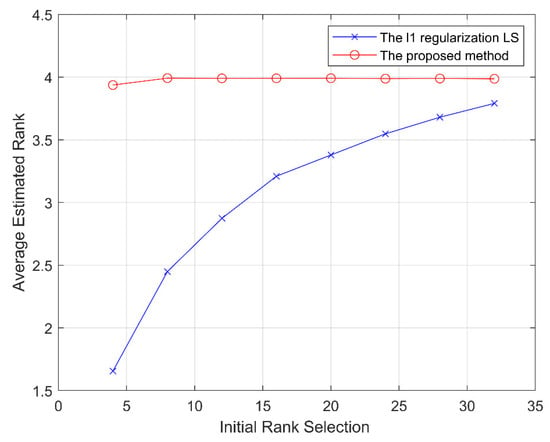
Figure 4.
Robustness of the proposed method regrading different initial rank values with = 4, SNR = 20 dB, = and = 0.3.
The performance comparisons between the proposed method and the l1 regularization LS in terms of robustness in success rate is shown in Figure 5. The simulation settings are the same as that of Figure 4. In Figure 5, the success rate is defined as the ratio of the number of the correctly estimated ranks over the total number of trails. This result shows the proposed method can converge to the true rank value under different initial rank selections with a success rate of over 90%.
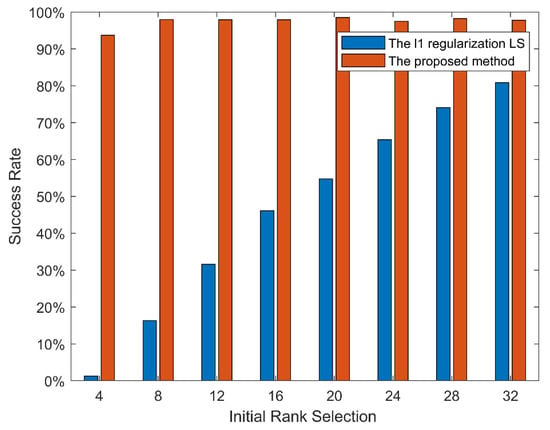
Figure 5.
Robustness of the proposed method in success rate regrading different values of initial rank with = 4, SNR = 20 dB, = and = 0.3.
The performance comparisons between the proposed method and the l1 regularization LS () in terms of success rate for different values of with same initial rank 24 are shown in Figure 6. It shows the proposed method with some values of can achieve much better rank estimation success rate than that of the baseline l1 regularization method when SNR = 20 dB. For example, the rank estimation success rate is above 98% when = 0.3.
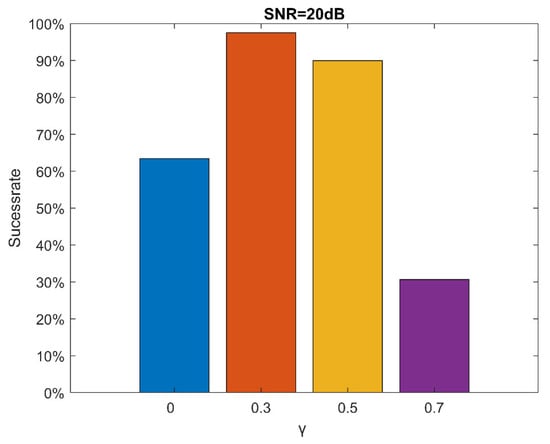
Figure 6.
Success rate regrading different values of with = 4, SNR = 20 dB, =.
The plots in Figure 7a–d show the relative error versus the number of iterations converging to the threshold when 0, 0.3, 0.5, 0.7, respectively. For example, the proposed method takes about 300 iterations to reach the threshold in Figure 7b, compared to the baseline l1 regularization with roughly 200 iterations in Figure 7a. Rank estimation is crucial for channel estimation when the number of multipath is unknown. It is worthy to get a significantly improved rank estimation success rate at the expense of slightly more iterations.
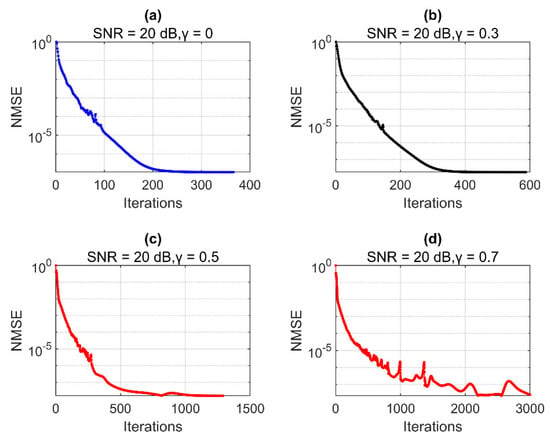
Figure 7.
Relative error vs. Iteration using the proposed method for different values of with = 4, SNR = 20 dB, =. (a) , (b) , (c) , (d) .
We then turn to the overall channel estimation performance of our proposed scheme, which is measured by the normalized mean squared error: Channel NMSE = . Figure 8 depicts the channel NMSE performance versus the system SNR derived by the proposed scheme, which is compared with that of l1 regularization LS method (). It is observed that some values of (i.e., at SNR = 20 dB) give us smaller NMSE or better channel estimation performance.
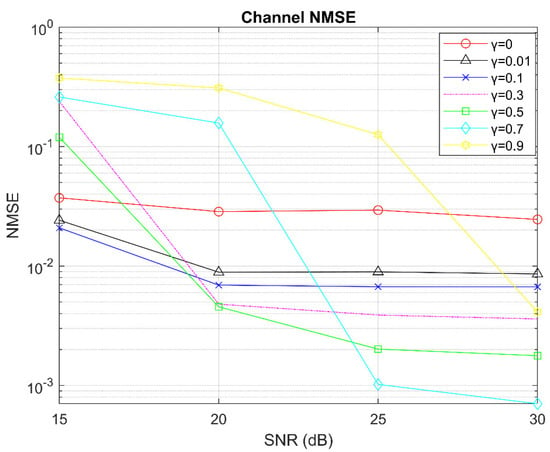
Figure 8.
NMSEs of channel estimation schemes versus the system SNR and values of with = 4, =.
The robustness of the proposed method for different true rank R in terms of success rate is shown in Table 1. The simulation is based on the true rank R = 4, 5, and 6, = , = 0.3, SNR = 20 dB. It can be observed that our proposed method can converge to the true ranks with high probability for different true rank R.

Table 1.
Robustness of the proposed method in success rate with different real rank.
The rank estimation performance versus different and ranks is shown in Figure 9. In this simulation, we assume the true rank R = 4, 5, and 6, = , SNR = 20 dB. When in (28) the proposed algorithm is equivalent to l1 regularization LS (11). It can be observed that the average estimated ranks are very close to the true ranks with weighting parameter from 0.1 to 0.4. Otherwise, we get large rank estimation errors.
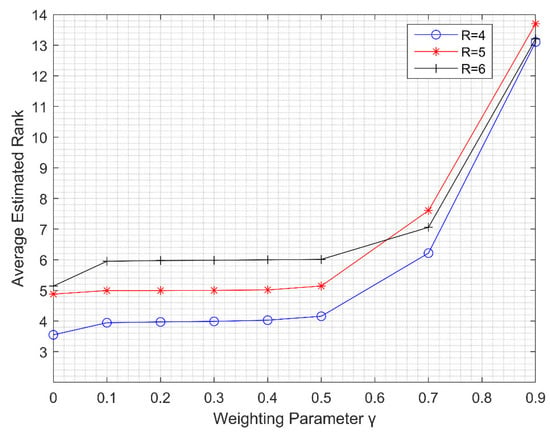
Figure 9.
Rank estimation performance of the proposed method as a function of weighting parameter with real rank = 4, 5, and 6, SNR = 20 dB, =.
Figure 10 depicts the number of iterations that the proposed method converges for each trail as a function of weighting parameter with real rank R = 4, 5, and 6, SNR = 20 dB, =. Our simulation shows fast convergence for the weighting parameter 0.5. It can be observed that the number of iterations to converge to the real ranks is much smaller than that of 0.5.
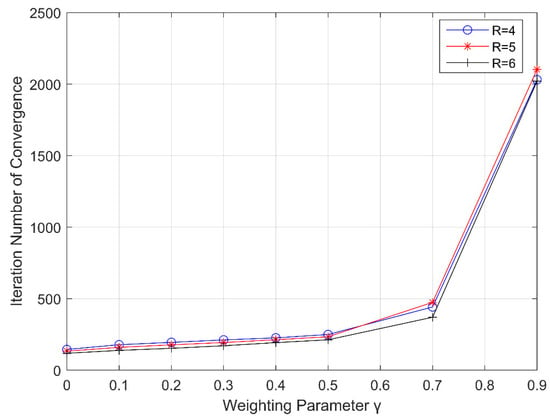
Figure 10.
Number of iterations for each trail of the proposed method as a function of weighting parameter with real rank = 4, 5, and 6, SNR = 20 dB, =.
7. Conclusions
In this paper, we presented a novel CP decomposition-based method to jointly estimate both tensor rank and component matrices of the received signal for the mmWave hybrid MIMO-OFDM systems. The proposed method is able to estimate channel parameters accurately without the prior knowledge of number of multipaths. Our approach differs from most existing works that assume the number of channel paths is known, instead, we aimed to determine the tensor rank or the number of multipath in the mmWave channel. We proposed a novel rank regularization method with a weighting parameter that can control the impact of the estimates from the previous iteration and compensate the tensor estimation bias. Compared to the baseline l1 regularization LS method, our proposed method shows that we can significantly increase the rank estimation success by reducing rank estimation bias. Compared to the RALS, our proposed method is capable of promoting sparsity for low rank CP tensor with selected values of the weighting parameter. Numerical experiments show that the proposed method outperforms the conventional l1 strategy in terms of accuracy and robustness in high SNR situation with a marginal cost to computation.
Author Contributions
Conceptualization, F.H., A.H. and L.Y.Y.; formal analysis, F.H., methodology, F.H., A.H. and L.Y.Y.; writing—original draft preparation, F.H.; writing—review and editing, F.H., A.H. and L.Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pi, Z.; Khan, F. An introduction to millimeter-wave mobile broad-band systems. IEEE Commun. Mag. 2011, 49, 101–107. [Google Scholar] [CrossRef]
- Rangan, S.; Rappaport, T.S.; Erkip, E. Millimeter-Wave Cellular Wireless Networks: Potentials and Challenges. Proc. IEEE. 2014, 102, 366–385. [Google Scholar] [CrossRef]
- Heath, R.W., Jr.; Gonzalez-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A.M. An Overview of Signal Processing Techniques for Millimeter Wave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Andrews, J.G.; Bai, T.; Kulkarni, M.N.; Alkhateeb, A.; Gupta, A.K.; Heath, R.W., Jr. Modeling and Analyzing Millimeter Wave Cellular Systems. IEEE Trans. Commun. 2017, 65, 403–430. [Google Scholar] [CrossRef]
- Mo, J.; Schniter, P.; Prelcic, N.G.; Heath, R.W. Channel estimation in millimeter wave MIMO systems with one-bit quantization. In Proceedings of the Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 2014; pp. 957–961. [Google Scholar]
- Bajwa, W.U.; Haupt, J.; Sayeed, A.M.; Nowak, R. Compressed Channel Sensing: A New Approach to Estimating Sparse Multipath Channels. Proc. IEEE 2010, 98, 1058–1076. [Google Scholar] [CrossRef]
- Lee, J.; Gil, G.-T.; Lee, Y.H. Exploiting spatial sparsity for estimating channels of hybrid MIMO systems in millimeter wave communications. In Proceedings of the IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 3326–3331. [Google Scholar]
- Marzi, Z.; Ramasamy, D.; Madhow, U. Compressive Channel Estimation and Tracking for Large Arrays in mm-Wave Picocells. IEEE J. Sel. Top. Signal Process. 2016, 10, 514–527. [Google Scholar] [CrossRef]
- Rao, X.; Lau, V.K.N. Distributed Compressive CSIT Estimation and Feedback for FDD Multi-User Massive MIMO Systems. IEEE Trans. Signal Process. 2014, 62, 3261–3271. [Google Scholar]
- Alkhateeb, A.; El Ayach, O.; Leus, G.; Heath, R.W. Channel Estimation and Hybrid Precoding for Millimeter Wave Cellular Systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 831–846. [Google Scholar] [CrossRef]
- Alkhateeb, A.; Leus, G.; Heath, R.W. Compressed sensing based multi-user millimeter wave systems: How many measurements are needed? In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP’15), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 2909–2913. [Google Scholar]
- González-Coma, J.P.; Rodriguez-Fernandez, J.; González-Prelcic, N.; Castedo, L.; Heath, R.W. Channel estimation and hybrid precoding for frequency selective multiuser mmWave MIMO systems. IEEE J. Sel. Top. Signal Proc. 2018, 12, 353–367. [Google Scholar] [CrossRef]
- Cheng, L.; Yue, G.; Xiong, X.; Liang, Y.; Li, S. Tensor Decomposition-Aided Time-Varying Channel Estimation for Millimeter Wave MIMO Systems. IEEE Wirel. Commun. Lett. 2019, 8, 1216–1219. [Google Scholar] [CrossRef]
- Park, S.; Ali, A.; Gonzalez-Prelcic, N.; Heath, R.W. Spatial Channel Covariance Estimation for Hybrid Architectures Based on Tensor Decompositions. IEEE Trans. Wirel. Commun. 2019, 19, 1084–1097. [Google Scholar] [CrossRef]
- Lin, Y.; Jin, S.; Matthaiou, M.; You, X. Structured Tensor Decomposition-Based Channel Estimation for Wideband Millimeter Wave MIMO. In Proceedings of the Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 3–6 November 2019; pp. 421–426. [Google Scholar]
- Zhou, Z.; Fang, J.; Yang, L.; Li, H.; Chen, Z.; Blum, R.S. Low-Rank Tensor Decomposition-Aided Channel Estimation for Millimeter Wave MIMO-OFDM Systems. IEEE J. Sel. Areas Commun. 2017, 35, 1524–1538. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, P.; Fang, J.; Li, H. Compressed Channel Estimation for IRS-Assisted Millimeter Wave OFDM Systems: A Low-Rank Tensor Decomposition-Based Approach. IEEE Wirel. Commun. Lett. 2022, 11, 1258–1262. Available online: https://arxiv.org/pdf/2203.16164.pdf (accessed on 30 March 2022). [CrossRef]
- Luo, K.; Zhou, X.; Wang, B.; Huang, J.; Liu, H. Sparse Bayes Tensor and DOA Tracking Inspired Channel Estimation for V2X Millimeter Wave Massive MIMO System. Sensors 2021, 21, 4021. [Google Scholar] [CrossRef]
- Håstad, J. Tensor rank is NP-complete. J. Algorithms 1990, 11, 644–654. [Google Scholar] [CrossRef]
- Swernofsky, J. Tensor Rank Is Hard to Approximate; Electronic Colloquium on Computational Complexity, Report No. 86; Schloss Dagstuhl—Leibniz Center for Informatics: Wadern, Germany, 2018. [Google Scholar]
- Bazerque, J.A.; Mateos, G.; Giannakis, G.B. Rank Regularization and Bayesian Inference for Tensor Completion and Extrapolation. IEEE Trans. Signal Process. 2013, 61, 5689–5703. [Google Scholar] [CrossRef]
- Karim, R.G.; Guo, G.; Yan, D.; Navasca, C. Accurate Tensor Decomposition with Simultaneous Rank Approximation for Surveillance Videos. In Proceedings of the Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 3–6 November 2020; pp. 842–846. [Google Scholar]
- Kolda, T.; Bader, B.W. Tensor Decompositions and Applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Sidiropoulos, N.D.; De Lathauwer, L.; Fu, X.; Huang, K.; Papalexakis, E.E.; Faloutsos, C. Tensor Decomposition for Signal Processing and Machine Learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Dai, L.; Wang, Z.; Yang, Z. Spectrally Efficient Time-Frequency Training OFDM for Mobile Large-Scale MIMO Systems. IEEE J. Sel. Areas Commun. 2013, 31, 251–263. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, X.; Heng, W. Millimeter-Wave Channel Estimation Based on 2-D Beamspace MUSIC Method. IEEE Trans. Wirel. Commun. 2017, 16, 5384–5394. [Google Scholar] [CrossRef]
- Qi-Nian, J. On the iteratively regularized Gauss-Newton method for solving nonlinear ill-posed problems. Math. Comput. 2000, 69, 1603–1624. [Google Scholar] [CrossRef]
- Cichocki, A.; Zdunek, R. Regularized Alternating Least Squares Algorithms for Non-negative Matrix/Tensor Factorization. In Proceedings of the 4th International Symposium on Neural Networks, Nanjing, China, 3–7 June 2007. [Google Scholar]
- Wang, J.-H.; Hopke, P.K.; Hancewicz, T.M.; Zhang, S.L. Application of modified alternating least squares regression to spectroscopic image analysis. Anal. Chim. Acta 2003, 476, 93–109. [Google Scholar] [CrossRef]
- Wang, X.; Navasca, C.; Kindermann, S. On accelerating the regularized alternating least-squares algorithm for tensors. ETNA-Electron. Trans. Numer. Anal. 2018, 48, 1–14. [Google Scholar] [CrossRef]
- Li, N.; Kindermann, S.; Navasca, C. Some convergence results on the Regularized Alternating Least-Squares method for tensor decomposition. Linear Algebra Its Appl. 2013, 438, 796–812. [Google Scholar] [CrossRef]
- Deuflhard, P.; Engl, H.W.; Scherzer, O. A convergence analysis of iterative methods for the solution of non-linear ill-posed problems under affinely invariant conditions. Inverse Probl. 1998, 14, 1081–1106. [Google Scholar] [CrossRef]
- Kaltenbacher, B. Some Newton-type methods for the regularization of nonlinear ill-posed problems. Inverse Probl. 1997, 13, 729–753. [Google Scholar] [CrossRef]
- Chen, T.C.; Han, D.J.; Au, F.T.; Tham, L.G. Acceleration of Levenberg-Marquardt Training of Neural Net-works with Variable Decay Rate. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA, 20–24 July 2003; pp. 1873–1878. [Google Scholar]
- Madsen, K.; Nielsen, H.B.; Tingleff, O. Methods for Non-Linear Least Squares Problems, 2nd ed.; Technical University of Denmark: Lyngby, Denmark, 2004; pp. 24–26. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).