Abstract
Datasets with many zero outcomes are common in real-world studies and often exhibit overdispersion and strong correlations among predictors, creating challenges for standard count models. Traditional approaches such as the Zero-Inflated Poisson (ZIP), Zero-Inflated Negative Binomial (ZINB), and Hurdle models can handle extra zeros and overdispersion but struggle when multicollinearity is present. This study introduces the Ridge-Hurdle Negative Binomial model, which incorporates L2 regularization into the truncated count component of the hurdle framework to jointly address zero inflation, overdispersion, and multicollinearity. Monte Carlo simulations under varying sample sizes, predictor correlations, and levels of overdispersion and zero inflation show that Ridge-Hurdle NB consistently achieves the lowest mean squared error (MSE) compared to ZIP, ZINB, Hurdle Poisson, Hurdle Negative Binomial, Ridge ZIP, and Ridge ZINB models. Applications to the Wildlife Fish and Medical Care datasets further confirm its superior predictive performance, highlighting RHNB as a robust and efficient solution for complex count data modeling.
1. Introduction
Count data, representing event frequencies across domains such as transportation safety, epidemiology, and insurance, present persistent methodological challenges due to zero-inflation and the presence of multicollinearity. Negative Binomial (NB) regression model serves as the primary framework for count data analysis, incorporating a dispersion parameter that accommodates variance exceeding the mean, a phenomenon known as overdispersion [1,2]. Despite this flexibility, NB models encounter significant limitations when datasets exhibit zero inflation, characterized by observed zero counts substantially exceeding theoretical expectations under standard distributions [3].
Zero inflation manifests through dual mechanisms: structural zeros emerge when events become inherently impossible for specific population subsets, while sampling zeros result from stochastic processes [4,5,6]. This complexity necessitates sophisticated modeling approaches that can simultaneously address overdispersion and excess zeros.
Two-component models address zero inflation effectively, such as the Zero-Inflated Poisson (ZIP) and Zero-Inflated Negative Binomial (ZINB) models [7]. They combine a binary mechanism for classifying structural zeros with a count process that generates observations, including potential zeros. These frameworks have demonstrated substantial utility across highway safety [8], health sciences [9,10], and ecological modeling [11].
Hurdle models provide distinct two-part architectures where all zeros come from the binary component, while the count component uses truncated distributions to model only positive values, in contrast to ZINB approaches that allow zeros from both components [12,13,14]. This structure is valuable when factors influencing activity initiation differ from those affecting intensity, as shown in transportation research distinguishing crash occurrence from frequency [15].
Unlike ZIP models that assume Poisson-distributed positive counts and suffer from equidispersion constraints, Hurdle NB accommodates overdispersion in the positive count component through the gamma-distributed heterogeneity parameter [16]. Compared to ZINB models, Hurdle NB provides more precise conceptual interpretation by completely separating the zero-generating process from positive count generation, eliminating potential confusion about zero sources [17,18]. The additional dispersion parameter in Hurdle NB effectively captures unobserved heterogeneity that Hurdle Poisson cannot accommodate, resulting in improved model fit and more accurate predictions [19,20]. Likelihood ratio tests often favor Hurdle NB over Hurdle Poisson in real datasets, highlighting the importance of modeling overdispersion in the positive count component [21,22].
Multicollinearity among predictors introduces additional analytical complications, inflating coefficient standard errors and compromising inferential stability, especially problematic in high-dimensional datasets where covariate control remains challenging [23,24]. Traditional solutions like variable selection or principal component regression often sacrifice interpretability or exclude crucial covariates. Regularization techniques have emerged as powerful solutions for multicollinearity and enhanced predictive performance. Ridge regression incorporates L2 penalties that shrink coefficients toward zero without elimination, stabilizing estimates amid correlated predictors [25].
Recent developments have extended regularization to count data through penalized generalized linear models, including penalized NB regression [26,27,28]. Akram et al. (2024) developed a ridge-type estimator for zero-inflated negative binomial [29]. Zeeshan et al. (2024) proposed a new ridge-type estimator for zero-inflated Poisson regression [30]. Penalized models demonstrate superior predictive accuracy, interpretability, and coefficient stability in high-dimensional or multicollinear contexts [31]. These advances have extended to zero-inflated models with penalization applied to both components [32].
Despite substantial progress, Hurdle models remain underexplored in penalized regression literature. While numerous studies have introduced regularized ZIP and ZINB models [33,34,35,36,37,38], limited research addresses penalized Hurdle frameworks, particularly regarding simultaneous zero inflation and multicollinearity management.
This study addresses a critical methodological gap by proposing an innovative Ridge-Hurdle Negative Binomial model that integrates L2 regularization into the truncated NB count component. The approach stabilizes coefficient estimates under highly correlated predictors while maintaining the interpretability and flexibility inherent in Hurdle architectures for zero-inflated scenarios.
This study systematically compares performance across multiple count regression models: ZIP, ZINB, Hurdle Ridge, Hurdle Negative Binomial, Ridge ZIP, Ridge ZINB, and the proposed Ridge-Hurdle Negative Binomial under diverse data conditions. Through comprehensive simulation frameworks, the study evaluates model performance across varying zero inflation levels, predictor multicollinearity degrees, and sample sizes, using Mean Squared Error (MSE) as the primary assessment criterion.
The remainder of this paper is structured as follows. Section 2 presents the models under comparison, introduces the proposed estimator, and discusses its key statistical properties. Section 3 describes the design of the Monte Carlo simulations and reports the results across multiple scenarios based on the mean squared error criterion. Section 4 demonstrates the application of two real-world datasets, providing comparative analyses and discussions that highlight the reinforcement of theoretical findings. Finally, Section 5 concludes the paper with a summary of key insights and potential directions for future research.
2. Materials and Methods
This study employs a rigorous analytical framework to assess the effectiveness of competing count data models, contrasting traditional approaches (ZIP, ZINB, Hurdle Ridge, Hurdle Negative Binomial) against regularized alternatives (Ridge ZIP and Ridge ZINB) and the novel Ridge-Hurdle Negative Binomial (RHNB) methodology. The experimental design unfolds through two strategic phases: executing extensive simulation studies that explore model behavior under challenging conditions of excessive zeros and correlated predictors, and demonstrating practical applicability through empirical data analysis. The entire computational workflow leverages R statistical software (Version 4.5.1) to guarantee methodological transparency and replicable results.
2.1. Zero-Inflated Poisson (ZIP) Model
Let be a count variable with excess zeros. The ZIP model assumes: each observation is zero with probability or comes from a Poisson distribution with mean with probability [4]. The Poisson PMF is:
In ZIP, and , giving:
Let and be covariate matrices, and . The log-likelihood for independent observations is:
Define . For the Poisson part (non-zero counts), the score and information matrix are approximated as:
The approximate estimator is:
2.2. Zero-Inflated Negative Binomial (ZINB) Model
The ZINB model extends the ZIP by assuming a Negative Binomial distribution for the count component [4,7]. Let denote a count response with overdispersion and excess zeros.
The NB PMF is [2]
In ZINB, zeros arise either from a structural process with probability , or from the NB distribution with probability . Thus,
with
The observed information (negative Hessian) for is
with the weight matrix from second derivatives. The estimator is approximated by
2.3. Hurdle Poisson Model
Hurdle models, introduced by Mullahy (1986) and refined by Cameron and Trivedi (1998), address excess zeros in count data by modeling the probability of crossing a hurdle before generating positive counts from a zero-truncated distribution [1,13].
Let denote the binary (hurdle) process and the count model. Then the Hurdle PMF is defined as [11]:
where is the zero-truncated version of , and . If is Poisson with mean , and the hurdle is Bernoulli-logistic with , the Hurdle Poisson (HP) model is
with
where (count covariates) and (hurdle covariates). The mean and variance are
2.4. Hurdle Negative Binomial (Hurdle NB) Model
The Hurdle NB model extends hurdle regression to accommodate overdispersed count data using a zero-truncated negative binomial (ZTNB) distribution for positive counts [39]. The model consists of two parts:
Binary component (zero vs. positive count), modeled via logistic regression:
where is the design matrix for the binary part, the associated parameters, and . The odds ratio is .
Thus,
Positive count component (for ), modeled via a zero-truncated negative binomial:
where is the design matrix for the count part, and are the parameters. Now, the Hurdle NB probability mass function
The MLE is obtained by solving using Newton-Raphson. In matrix form:
where is a diagonal weight matrix depending on and , and is the pseudo-response vector from the score expansion.
2.5. Ridge Zero-Inflated Poisson (Ridge ZIP) Model
Let be a vector of count responses (non-negative integers), be the design matrix of predictors, and be the coefficient vector. The Poisson regression model, which assumes that each observation , where the mean is related to the predictors through a log link function:
However, when the predictors in are highly correlated (i.e., multicollinearity), the MLE can be unstable and lead to overfitting [40].
Hoerl and Kennard (1970) introduced ridge regression to handle multicollinearity by minimizing squared residuals with a constraint on the sum of squared coefficients [25]. This concept extends to count data through GLMs, particularly the Poisson model, where with . Multicollinearity can make the MLE unstable. The Ridge ZIP model extends the standard ZIP model to handle excessive zeros and multicollinearity. The ZIP PMF is [41]:
with and . The ridge estimator maximizes the penalized log-likelihood:
In matrix form, the Ridge ZIP estimator for is:
where is the count design matrix, the weight matrix from the Fisher scoring, the adjusted response, the ridge penalty, and the identity.
2.6. Ridge Zero-Inflated Negative Binomial (Ridge ZINB) Model
Multicollinearity among explanatory variables can destabilize regression estimates, making the standard ZINB estimator unreliable when the eigenvalues of are small. To address this, the ridge estimator adds a positive constant to the diagonal of , producing the Ridge ZINB estimator [42]:
where is the design matrix for the count component, is the weight matrix from ZINB, with , is the standard ZINB estimate, is the ridge parameter, and is the identity matrix.
Properties:
- reducing variance and improving stability under multicollinearity
2.7. Proposed Ridge-Hurdle Negative Binomial (RHNB) Model
In Section 2.4, denoted the MLE obtained from the positive-count component of the Hurdle NB model. The proposed RHNB estimator introduces a ridge penalty to control for multicollinearity or overfitting in the count component of the Hurdle NB model. The following is the estimator of the RHNB, adding a weight matrix.
where : design matrix for the count component (excluding zero counts), : diagonal weight matrix with elements , : ridge penalty parameter, identity matrix, and when . Here, plays an analogous role to the diagonal weight matrix in Section 2.4, Section 2.5, Section 2.6.
Let the eigen-decomposition of be:
Let the true coefficient vector be expressed in terms of this eigenbasis:
Then the MSE of is:
where -th eigenvalue of , : corresponding orthonormal eigenvector, : projection of the true coefficient vector onto the eigenvector , and : estimated residual dispersion.
A conceptual flowchart of the models compared in this study is shown in Figure 1.
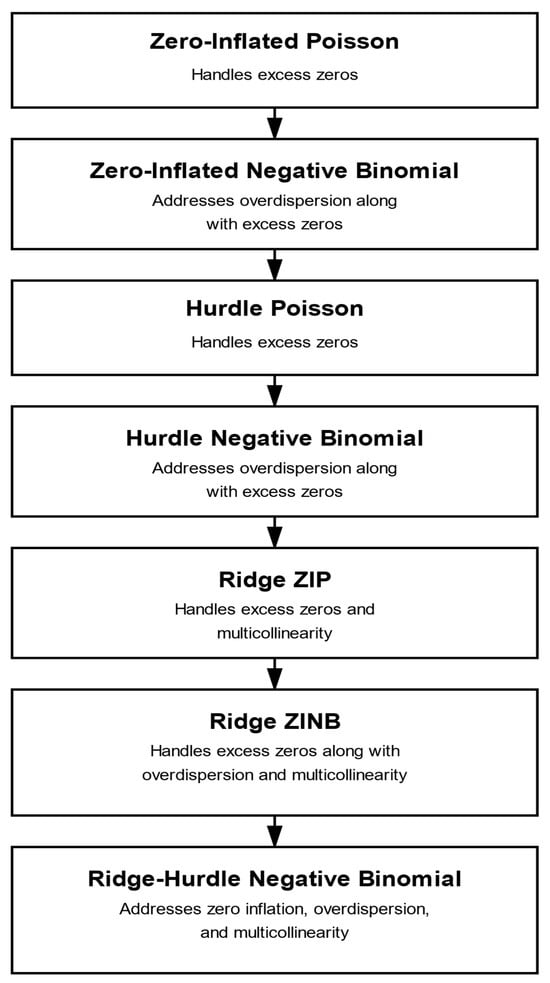
Figure 1.
Conceptual flowchart of the models compared in this study.
The proposed RHNB estimator theoretically surpasses the HNB, Ridge ZIP, and Ridge ZINB models by integrating the ridge penalty directly into the zero-truncated NB component, thereby reducing estimator variance and enhancing stability when exhibits small eigenvalues (multicollinearity). Unlike Ridge ZIP and Ridge ZINB, which conflate zero and count processes, RHNB separates structural zeros from positive counts, ensuring efficient estimation under overdispersion and zero inflation. Its MSE expression confirms a favorable bias–variance trade-off, yielding lower total error and improved robustness in high-dimensional or correlated count data contexts.
3. Simulation Study
This section outlines the simulation design, varying sample sizes, correlation structures, and levels of zero inflation, and presents results that reveal the relative strengths, limitations, and robustness of each method under diverse and challenging data-generating processes.
3.1. Simulation Design
The data generation process followed a well-established methodology [43,44,45,46]. Correlated predictors were generated as
where is the number of predictors, and controls intercorrelation. The response variable followed a zero-inflated negative binomial mechanism:
with linear predictor , zero-inflation probability , and dispersion . Simulation scenarios varied by the number of predictors (), high to severe correlation levels (), sample sizes (), and zero-inflation intercepts (), corresponding to approximately and structural zeros [47,48]. Overdispersion was incorporated through , with higher values inducing greater variability [49]. Each configuration was replicated times for robust evaluation [50].
Model performance was assessed using mean squared error (MSE), computed as [51]
where is an estimator and the true coefficient vector, aligned with the normalized eigenvector of associated with its largest eigenvalue. Lower MSE values indicate superior estimator performance.
The ridge penalty parameter in this study for Ridge ZIP, Ridge ZINB, and RHNB models was optimized through cross-validation to ensure a fair balance between model bias and variance. Specifically, for both the Poisson and logistic components of the regularized models, was selected using -fold cross-validation (with ) across a logarithmic grid of candidate values [52].
At each fold, the model was refitted on the training data and evaluated on the validation subset using appropriate loss functions-mean squared error (MSE) for Poisson models and log-loss for logistic models. The optimal penalty was chosen as [53]
where denotes the fold-specific validation loss. This data-driven approach ensures that the ridge term effectively stabilizes parameter estimation under high multicollinearity and overdispersion, providing a sensitivity-controlled, empirically tuned penalty rather than an arbitrarily fixed one.
3.2. Results Discussion
This simulation study evaluates the performance of various count data models for zero-inflated and overdispersed count outcomes in roadway safety analysis. The study examines how model performance, measured by Mean Squared Error (MSE), is influenced by sample size, number of predictors, predictor correlation, intercept logit, and overdispersion levels. Models evaluated include traditional approaches (ZIP, ZINB, Hurdle Poisson, Hurdle NB) and regularized variants (Ridge ZIP, Ridge ZINB, RHNB). Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7 and Table A8 in Appendix A present the MSE of the models under various scenarios.
3.2.1. Effectiveness Relative to Sample Size
Across all compared models, larger sample sizes consistently improved estimation accuracy, as reflected by declining MSE values in Table A1 and Table A2. Yet, the RHNB model stood out for its remarkable stability and reliability, even when data were limited. Unlike traditional zero-inflated and hurdle models that showed volatility in small samples, RHNB maintained low variability and robust predictive precision. The results in Table A1 illustrate that its accuracy improved steadily with increasing n, while Table A2 confirms that this pattern held even under stronger correlation conditions where competing models suffered from overfitting and inflated error. Overall, these findings demonstrate that RHNB effectively balances bias and variance, ensuring dependable performance across varying sample sizes.
3.2.2. Effectiveness Relative to the Number of Predictors
As the number of predictors increased, most models exhibited noticeable performance deterioration, underscoring their sensitivity to dimensionality (Table A5 and Table A8). Traditional ZIP and ZINB models, in particular, showed severe instability as multicollinearity intensified. In contrast, the RHNB model demonstrated strong resistance to variance inflation, with only a slight rise in error even when the predictor set doubled. This stability highlights the regularization effect of the ridge penalty, which effectively mitigates overfitting and preserves accuracy in high-dimensional and highly correlated environments. Overall, the results confirm that RHNB maintains reliable estimation performance as model complexity increases, outperforming conventional alternatives across all predictor settings.
3.2.3. Effectiveness Relative to Correlation Coefficients
Increasing correlation among predictors substantially impaired the performance of traditional models, as reflected in Table A1 to Table A2, Table A2 to Table A3, and Table A3 to Table A4. However, the RHNB model maintained strong resilience, showing only modest increases in error even under extreme multicollinearity. While all models experienced some degradation as correlation approached 0.99, RHNB consistently preserved estimation stability and predictive accuracy, unlike ZIP and ZINB, which deteriorated sharply. These results emphasize the model’s ability to counteract multicollinearity through ridge regularization, ensuring reliable inference and minimizing overfitting across varying correlation strengths.
3.2.4. Effectiveness Relative to Intercept Logit
Higher intercept logits, which correspond to stronger zero-inflation, posed major challenges for traditional models, as reflected in Table A1 and Table A7. In these scenarios, RHNB consistently exhibited exceptional robustness, maintaining stable and low error levels even when competing models failed. While ZIP and ZINB suffered from extreme error inflation under heavy zero-inflation, RHNB preserved accuracy across different correlations and dimensionalities. This demonstrates the model’s capacity to handle severe zero-inflated conditions through its ridge penalty, which effectively stabilizes estimation and curbs variance amplification when structural zeros dominate the data.
3.2.5. Effectiveness Relative to Overdispersion
Overdispersion posed significant difficulties for traditional count models, especially those without explicit mechanisms to handle extra-Poisson variation (Table A5, Table A6 and Table A8). While ZINB and Hurdle NB offered moderate resilience, the RHNB model consistently demonstrated superior adaptability. Its performance remained stable and accurate even as overdispersion intensified, reflecting the combined benefits of the hurdle framework and ridge regularization. Unlike ZIP and ZINB, which showed escalating error under high variance, RHNB effectively controlled instability and preserved predictive precision. These findings underscore its robustness in managing overdispersed data, a common feature of real-world count processes.
4. Application
To validate the robustness and practical applicability of the proposed count data models under various complex scenarios, two real-world datasets were analyzed. The analysis aimed to determine if the performance trends from the simulation study apply in real-world settings with multicollinearity, overdispersion, and excess zeros. The real data findings validate and strengthen the simulation results, enhancing the reliability of the comparison among the modeling methods.
In real-world applications, lower MSE values indicate greater predictive reliability and closer alignment between true and estimated coefficients, underscoring the model’s practical interpretability and usefulness for decision-making.
4.1. Wildlife Fish Data
This dataset contains 250 observations with five predictors: X1 (nofish) indicates whether the trip was not solely for fishing, X2 (livebait) indicates whether live bait was used, X3 (camper) indicates whether a camper was brought, X4 (persons) indicates the total number of participants, and X5 (child) indicates the number of children present. The response variable y is the number of fish caught [54]. The histogram in Figure 2 reveals clear zero inflation along with a few extreme values of interest for truncation. Additionally, the condition number of 10.25 suggests moderate multicollinearity in the dataset.
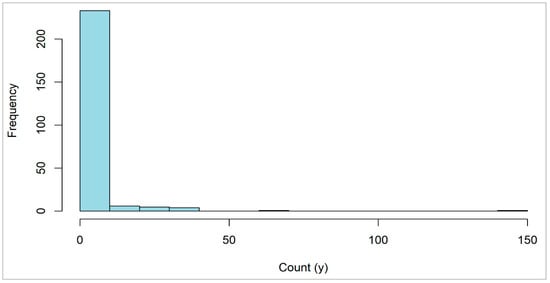
Figure 2.
Zero-Inflated response of wildlife fish data.
The study assessed overdispersion in the fish count data by fitting a Poisson regression model. Although the residual deviance-to-degrees-of-freedom ratio was close to 1 (1.03), a formal score-based test using the R function dispersiontest() under the AER package indicated significant overdispersion (dispersion = 1.36, p = 0.025), showing that the variance of the counts exceeds the Poisson assumption. Table A9 in Appendix B showed that the coefficient and standard error vary from model to model, especially the standard error was smallest for the regularized models.
Figure 3 illustrates the MSE values across competing models, where the proposed RHNB model achieves the lowest error (0.718), clearly outperforming both traditional (ZIP, ZINB, HP, Hurdle NB) and regularized (Ridge ZIP, Ridge ZINB) alternatives. This superior performance reinforces the findings from the simulation study, highlighting RHNB’s robustness in handling zero inflation, overdispersion, and multicollinearity in the fish catch data.
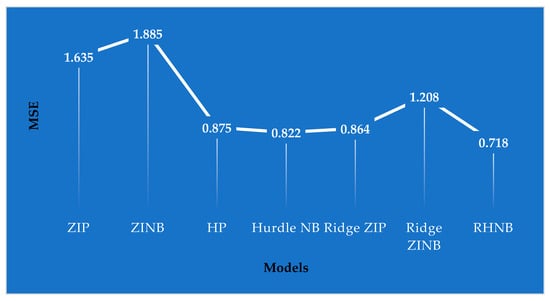
Figure 3.
MSE of the models for the wildlife fish data.
4.2. Medical Care Data
The Medical Care dataset (NMES1988) consists of 4406 Medicare-covered individuals aged 66 and older, drawn from the U.S. National Medical Expenditure Survey of 1987–1988 [9,55]. The response variable, ovisits (number of physician outpatient visits), exhibits clear evidence of zero inflation, as shown in Figure 4. Alongside measures of health-care utilization such as emergency visits and hospital stays, the dataset includes demographic, socioeconomic, and health-status indicators (e.g., age, gender, income, chronic conditions, activity limitations, and insurance coverage). Notably, the condition number of 212.22 signals severe multicollinearity among covariates, underscoring the need for robust modeling approaches.
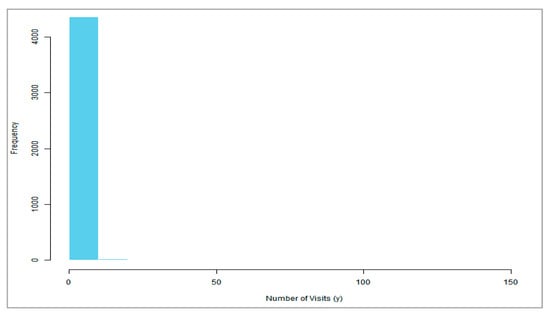
Figure 4.
Zero-inflated response of the data.
The analysis also evaluated overdispersion in the medical care visit data by fitting a Poisson regression model. The residual deviance relative to the degrees of freedom was substantially greater than 1 (2.77), and a formal score-based test using the R function dispersiontest() function from the AER package confirmed significant overdispersion (dispersion = 16.67, p = 0.001), indicating that the variance of the count outcome exceeds the assumptions of the Poisson model. Table A10 in Appendix B for this dataset showed that the coefficient and standard error vary from model to model, especially the standard error was the smallest for the proposed RHNB model.
Residual analysis further highlights the superiority of the proposed RHNB model, which demonstrates more stable variance and improved fit compared to its ridge counterparts, such as Ridge ZIP and Ridge ZINB. The comprehensive residual diagnostic plots supporting these findings are presented in Figure A1, Figure A2, and Figure A3 respectively in Appendix C.
Figure 5 presents the MSE values for the Medicare data, highlighting the clear superiority of the proposed RHNB model, which achieves the lowest error (0.068). Traditional models such as ZIP and ZINB, as well as their ridge counterparts, show notably higher errors, indicating their limitations in handling the complexities of this dataset. The results further demonstrate that RHNB effectively addresses both zero inflation and multicollinearity, leading to substantial gains in predictive accuracy. These findings are consistent with and strongly validate the insights obtained from the simulation study.
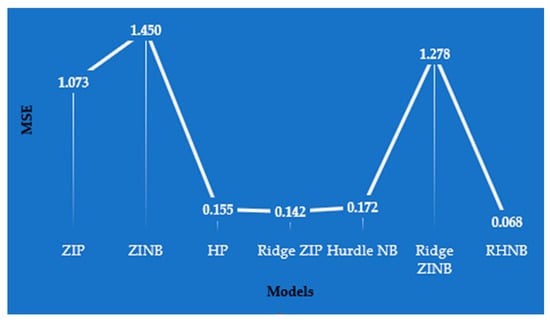
Figure 5.
MSE of the Medical Care Data.
5. Conclusions
This study introduces the Ridge-Hurdle NB model, a novel framework that integrates the hurdle structure with ridge regularization to effectively address zero inflation, overdispersion, and multicollinearity in count data. Unlike earlier work on penalized Poisson and negative binomial models, the incorporation of ridge penalization within a hurdle-based design marks a unique methodological advancement.
Simulation experiments, along with applications to the Wildlife Fish Catch dataset and the Medicare dataset, consistently showed that the RHNB outperforms both traditional and regularized alternatives, validating its robustness and practical utility. While RHNB offers strong performance, its effectiveness depends on the careful selection of the ridge tuning parameter and may require a high configuration computer. Beyond its immediate contributions, this work lays the foundation for future research on regularized mixture models that jointly accommodate structural zeros, overdispersion, and predictor dependencies. Potential directions include developing open-source software for broader adoption, extending the framework to Bayesian inference and nonlinear effects, and adapting the model to longitudinal or spatially correlated count processes. Taken together, RHNB offers a powerful and flexible tool for applied domains such as health sciences, ecology, and transportation safety, where complex count data challenges are the norm.
Author Contributions
Conceptualization, H.N. and B.M.G.K.; methodology development, H.N. and B.M.G.K.; formal analysis and interpretation, H.N. and B.M.G.K.; writing—original draft preparation, H.N. and B.M.G.K.; writing—review and editing, H.N. and B.M.G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors are grateful to the editor and reviewers for their constructive comments and suggestions, which have certainly helped improve the presentation and quality of the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Simulation Results Tables

Table A1.
MSEs for Simulation when p = 10 and correlation = 0.80.
Table A1.
MSEs for Simulation when p = 10 and correlation = 0.80.
| Models | Intercept Logit | Overdispersion Parameter = 1 | Overdispersion Parameter = 5 | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Sample Size | ||||||
| 100 | 200 | 500 | 100 | 200 | 500 | ||
| ZIP | 1 | 6.146 | 0.406 | 0.224 | 0.368 | 0.191 | 0.156 |
| ZINB | 0.899 | 0.302 | 0.182 | 0.361 | 0.189 | 0.147 | |
| Hurdle Poisson | 0.671 | 0.349 | 0.192 | 0.263 | 0.175 | 0.153 | |
| Ridge ZIP | 0.146 | 0.156 | 0.155 | 0.154 | 0.150 | 0.153 | |
| Ridge ZINB | 0.202 | 0.136 | 0.131 | 0.107 | 0.104 | 0.111 | |
| Hurdle NB | 0.604 | 0.204 | 0.121 | 0.250 | 0.156 | 0.124 | |
| RHNB | 0.063 | 0.057 | 0.056 | 0.085 | 0.058 | 0.041 | |
| ZIP | 2 | 872.117 | 1.356 | 0.334 | 425.184 | 0.467 | 0.181 |
| ZINB | 699.379 | 1.498 | 0.553 | 762.497 | 0.557 | 0.252 | |
| Hurdle Poisson | 14.000 | 2.521 | 0.292 | 15.660 | 0.314 | 0.188 | |
| Ridge ZIP | 4.084 | 0.208 | 0.200 | 7.004 | 0.181 | 0.173 | |
| Ridge ZINB | 3.385 | 0.164 | 0.116 | 5.529 | 0.114 | 0.165 | |
| Hurdle NB | 14.262 | 2.426 | 0.189 | 11.638 | 0.304 | 0.248 | |
| RHNB | 0.070 | 0.059 | 0.058 | 0.055 | 0.051 | 0.036 | |

Table A2.
MSEs for Simulation when p = 10 and correlation = 0.90.
Table A2.
MSEs for Simulation when p = 10 and correlation = 0.90.
| Models | Intercept Logit | Overdispersion Parameter = 1 | Overdispersion Parameter = 5 | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Sample Size | ||||||
| 100 | 200 | 500 | 100 | 200 | 500 | ||
| ZIP | 1 | 1.083 | 0.583 | 0.339 | 0.509 | 0.226 | 0.188 |
| ZINB | 0.947 | 0.478 | 0.215 | 0.519 | 0.213 | 0.167 | |
| Hurdle Poisson | 1.146 | 0.550 | 0.310 | 0.434 | 0.223 | 0.192 | |
| Ridge ZIP | 0.167 | 0.177 | 0.179 | 0.144 | 0.162 | 0.168 | |
| Ridge ZINB | 0.172 | 0.158 | 0.128 | 0.120 | 0.096 | 0.116 | |
| Hurdle NB | 0.858 | 0.321 | 0.162 | 0.396 | 0.187 | 0.146 | |
| RHNB | 0.073 | 0.063 | 0.061 | 0.069 | 0.065 | 0.047 | |
| ZIP | 2 | 81.739 | 7.798 | 0.501 | 93.461 | 0.858 | 0.256 |
| ZINB | 92.304 | 7.765 | 0.617 | 96.643 | 1.189 | 0.388 | |
| Hurdle Poisson | 27.219 | 7.694 | 0.456 | 10.644 | 0.499 | 0.253 | |
| Ridge ZIP | 9.695 | 2.193 | 0.318 | 2.184 | 0.288 | 0.225 | |
| Ridge ZINB | 7.884 | 1.080 | 0.306 | 1.588 | 0.266 | 0.219 | |
| Hurdle NB | 26.916 | 3.396 | 0.345 | 6.039 | 0.471 | 0.246 | |
| RHNB | 0.338 | 0.054 | 0.032 | 0.053 | 0.047 | 0.040 | |

Table A3.
MSEs for Simulation when p = 10 and correlation = 0.95.
Table A3.
MSEs for Simulation when p = 10 and correlation = 0.95.
| Models | Intercept Logit | Overdispersion Parameter = 1 | Overdispersion Parameter = 5 | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Sample Size | ||||||
| 100 | 200 | 500 | 100 | 200 | 500 | ||
| ZIP | 1 | 35.598 | 0.900 | 0.520 | 1.050 | 0.320 | 0.236 |
| ZINB | 3.270 | 0.698 | 0.338 | 1.081 | 0.295 | 0.192 | |
| Hurdle Poisson | 2.828 | 0.959 | 0.539 | 0.835 | 0.324 | 0.253 | |
| Ridge ZIP | 0.203 | 0.182 | 0.207 | 0.190 | 0.161 | 0.176 | |
| Ridge ZINB | 0.392 | 0.178 | 0.143 | 0.153 | 0.106 | 0.114 | |
| Hurdle NB | 1.759 | 0.511 | 0.245 | 0.621 | 0.265 | 0.174 | |
| RHNB | 0.088 | 0.067 | 0.060 | 0.128 | 0.085 | 0.074 | |
| ZIP | 2 | 95.822 | 45.154 | 0.953 | 63.818 | 1.107 | 0.819 |
| ZINB | 48.022 | 27.661 | 0.984 | 13.268 | 1.292 | 0.474 | |
| Hurdle Poisson | 55.013 | 3.105 | 0.938 | 19.409 | 0.779 | 0.334 | |
| Ridge ZIP | 18.737 | 1.184 | 0.337 | 6.902 | 0.271 | 0.227 | |
| Ridge ZINB | 14.367 | 1.070 | 0.233 | 3.969 | 0.198 | 0.196 | |
| Hurdle NB | 35.742 | 2.425 | 0.464 | 5.397 | 0.738 | 0.250 | |
| RHNB | 0.051 | 0.040 | 0.032 | 0.052 | 0.041 | 0.029 | |

Table A4.
MSEs for Simulation when p = 10 and correlation = 0.99.
Table A4.
MSEs for Simulation when p = 10 and correlation = 0.99.
| Models | Intercept Logit | Overdispersion Parameter = 1 | Overdispersion Parameter = 5 | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Sample Size | ||||||
| 100 | 200 | 500 | 100 | 200 | 500 | ||
| ZIP | 1 | 62.282 | 3.347 | 2.041 | 4.283 | 1.092 | 0.612 |
| ZINB | 59.227 | 2.046 | 1.826 | 4.451 | 0.852 | 0.378 | |
| Hurdle Poisson | 53.279 | 1.503 | 1.300 | 3.504 | 0.641 | 0.708 | |
| Ridge ZIP | 7.347 | 0.232 | 0.205 | 0.915 | 0.388 | 0.307 | |
| Ridge ZINB | 3.107 | 0.274 | 0.193 | 0.783 | 0.330 | 0.141 | |
| Hurdle NB | 50.644 | 1.056 | 0.741 | 2.244 | 0.515 | 0.341 | |
| RHNB | 0.117 | 0.082 | 0.070 | 0.221 | 0.113 | 0.102 | |
| ZIP | 2 | 159.496 | 21.902 | 6.955 | 77.842 | 8.615 | 2.191 |
| ZINB | 181.909 | 14.263 | 8.638 | 82.632 | 9.955 | 2.081 | |
| Hurdle Poisson | 63.205 | 9.728 | 4.219 | 39.622 | 6.061 | 1.257 | |
| Ridge ZIP | 42.266 | 5.180 | 3.169 | 11.012 | 1.338 | 0.288 | |
| Ridge ZINB | 35.939 | 3.882 | 2.595 | 8.304 | 0.499 | 0.209 | |
| Hurdle NB | 57.773 | 6.268 | 3.836 | 15.620 | 5.675 | 0.793 | |
| RHNB | 1.050 | 0.040 | 0.027 | 0.285 | 0.051 | 0.024 | |

Table A5.
MSEs for Simulation when p = 20 and correlation = 0.80.
Table A5.
MSEs for Simulation when p = 20 and correlation = 0.80.
| Models | Intercept Logit | Overdispersion Parameter = 1 | Overdispersion Parameter = 5 | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Sample Size | ||||||
| 100 | 200 | 500 | 100 | 200 | 500 | ||
| ZIP | 1 | 540.361 | 0.593 | 0.249 | 187.591 | 0.196 | 0.119 |
| ZINB | 670.843 | 4.823 | 0.161 | 271.596 | 0.213 | 0.115 | |
| Hurdle Poisson | 35.106 | 0.523 | 0.226 | 25.376 | 0.177 | 0.115 | |
| Ridge ZIP | 0.132 | 0.165 | 0.155 | 0.127 | 0.122 | 0.132 | |
| Ridge ZINB | 77.343 | 2.589 | 0.115 | 29.410 | 0.100 | 0.092 | |
| Hurdle NB | 1.647 | 0.292 | 0.101 | 1.451 | 0.159 | 0.088 | |
| RHNB | 0.069 | 0.050 | 0.042 | 0.039 | 0.029 | 0.014 | |
| ZIP | 2 | 136.156 | 10.505 | 0.415 | 68.248 | 14.224 | 0.147 |
| ZINB | 120.916 | 18.819 | 0.528 | 46.596 | 6.385 | 0.366 | |
| Hurdle Poisson | 90.868 | 19.959 | 0.385 | 3.038 | 2.557 | 0.136 | |
| Ridge ZIP | 68.451 | 0.268 | 0.227 | 11.926 | 0.240 | 0.211 | |
| Ridge ZINB | 52.083 | 7.739 | 0.293 | 9.443 | 7.978 | 0.220 | |
| Hurdle NB | 85.981 | 3.190 | 0.236 | 3.196 | 2.417 | 0.125 | |
| RHNB | 0.781 | 0.062 | 0.060 | 0.034 | 0.025 | 0.017 | |

Table A6.
MSEs for Simulation when p = 20 and correlation = 0.90.
Table A6.
MSEs for Simulation when p = 20 and correlation = 0.90.
| Models | Intercept Logit | Overdispersion Parameter = 1 | Overdispersion Parameter = 5 | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Sample Size | ||||||
| 100 | 200 | 500 | 100 | 200 | 500 | ||
| ZIP | 1 | 292.209 | 0.937 | 0.435 | 222.253 | 0.241 | 0.160 |
| ZINB | 208.681 | 0.684 | 0.247 | 472.061 | 0.397 | 0.134 | |
| Hurdle Poisson | 158.013 | 0.917 | 0.424 | 66.112 | 0.242 | 0.162 | |
| Ridge ZIP | 0.223 | 0.204 | 0.242 | 0.207 | 0.216 | 0.193 | |
| Ridge ZINB | 15.563 | 0.176 | 0.143 | 14.220 | 0.150 | 0.095 | |
| Hurdle NB | 15.127 | 1.678 | 0.154 | 0.942 | 0.223 | 0.103 | |
| RHNB | 0.140 | 0.082 | 0.058 | 0.092 | 0.061 | 0.051 | |
| ZIP | 2 | 558.922 | 238.307 | 0.820 | 95.895 | 13.309 | 0.267 |
| ZINB | 331.164 | 118.676 | 22.851 | 73.794 | 17.524 | 0.659 | |
| Hurdle Poisson | 26.671 | 17.324 | 0.801 | 2.672 | 2.531 | 0.251 | |
| Ridge ZIP | 98.440 | 0.368 | 0.398 | 40.858 | 0.228 | 0.281 | |
| Ridge ZINB | 28.347 | 6.460 | 5.327 | 41.582 | 13.158 | 0.283 | |
| Hurdle NB | 5.510 | 1.018 | 0.451 | 2.672 | 2.502 | 0.202 | |
| RHNB | 0.759 | 0.250 | 0.115 | 0.071 | 0.048 | 0.029 | |

Table A7.
MSEs for Simulation when p = 20 and correlation = 0.95.
Table A7.
MSEs for Simulation when p = 20 and correlation = 0.95.
| Models | Intercept Logit | Overdispersion Parameter = 1 | Overdispersion Parameter = 5 | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Sample Size | ||||||
| 100 | 200 | 500 | 100 | 200 | 500 | ||
| ZIP | 1 | 574.206 | 1.761 | 0.976 | 317.659 | 1.399 | 0.882 |
| ZINB | 443.453 | 1.174 | 0.869 | 94.783 | 0.605 | 0.786 | |
| Hurdle Poisson | 120.674 | 1.076 | 0.793 | 34.198 | 0.417 | 0.340 | |
| Ridge ZIP | 35.565 | 0.443 | 0.317 | 10.521 | 0.323 | 0.315 | |
| Ridge ZINB | 15.327 | 0.261 | 0.163 | 8.729 | 0.189 | 0.135 | |
| Hurdle NB | 82.297 | 0.975 | 0.546 | 18.508 | 0.359 | 0.236 | |
| RHNB | 0.448 | 0.108 | 0.100 | 0.147 | 0.073 | 0.067 | |
| ZIP | 2 | 747.036 | 74.734 | 1.551 | 95.486 | 12.151 | 1.413 |
| ZINB | 422.694 | 60.561 | 1.177 | 25.926 | 10.058 | 1.163 | |
| Hurdle Poisson | 96.235 | 5.940 | 1.086 | 13.300 | 1.937 | 1.009 | |
| Ridge ZIP | 36.803 | 2.726 | 0.362 | 8.046 | 1.296 | 0.740 | |
| Ridge ZINB | 21.693 | 1.424 | 0.325 | 5.178 | 1.085 | 0.532 | |
| Hurdle NB | 57.651 | 2.679 | 0.674 | 10.711 | 1.347 | 0.987 | |
| RHNB | 0.438 | 0.200 | 0.122 | 0.586 | 0.436 | 0.079 | |

Table A8.
MSEs for Simulation when p = 20 and correlation = 0.99.
Table A8.
MSEs for Simulation when p = 20 and correlation = 0.99.
| Models | Intercept Logit | Overdispersion Parameter = 1 | Overdispersion Parameter = 5 | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Sample Size | ||||||
| 100 | 200 | 500 | 100 | 200 | 500 | ||
| ZIP | 1 | 678.909 | 8.075 | 4.038 | 804.014 | 2.087 | 1.843 |
| ZINB | 708.676 | 4.747 | 2.200 | 890.000 | 2.569 | 1.122 | |
| Hurdle Poisson | 66.509 | 2.554 | 1.189 | 421.420 | 2.104 | 0.891 | |
| Ridge ZIP | 12.326 | 1.514 | 0.874 | 22.211 | 1.953 | 0.536 | |
| Ridge ZINB | 8.847 | 1.039 | 0.365 | 16.261 | 0.618 | 0.307 | |
| Hurdle NB | 27.635 | 1.832 | 0.951 | 73.422 | 1.508 | 0.657 | |
| RHNB | 1.009 | 0.659 | 0.315 | 0.937 | 0.334 | 0.140 | |
| ZIP | 2 | 492.554 | 190.133 | 6.664 | 190.918 | 96.810 | 2.828 |
| ZINB | 235.260 | 88.416 | 5.770 | 136.842 | 82.092 | 2.376 | |
| Hurdle Poisson | 49.965 | 8.778 | 2.225 | 30.201 | 9.722 | 1.922 | |
| Ridge ZIP | 44.265 | 2.662 | 1.909 | 18.829 | 2.169 | 0.936 | |
| Ridge ZINB | 34.371 | 1.857 | 1.602 | 13.374 | 1.194 | 0.514 | |
| Hurdle NB | 45.966 | 4.459 | 2.021 | 25.873 | 3.190 | 1.314 | |
| RHNB | 19.144 | 0.967 | 0.512 | 1.573 | 0.552 | 0.311 | |
Appendix B. Real Data Results

Table A9.
Coefficient and Standard Error of the models for Wildlife Fish data.
Table A9.
Coefficient and Standard Error of the models for Wildlife Fish data.
| Predictors | ZIP | ZINB | Hurdle Poisson | Hurdle NB | Ridge ZIP | Ridge ZINB | Ridge Hurdle NB | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coef. | SE | Coef. | SE | Coef. | SE | Coef. | SE | Coef. | SE | Coef. | SE | Coef. | SE | |
| nofish | −0.04 | 0.14 | −0.09 | 0.17 | −0.05 | 0.14 | −0.03 | 0.17 | −0.11 | 0.04 | −0.08 | 0.05 | −0.03 | 0.05 |
| livebait | 0.43 | 0.27 | 0.09 | 0.30 | 0.66 | 0.34 | 0.50 | 0.38 | 0.13 | 0.04 | 0.05 | 0.05 | 0.20 | 0.05 |
| camper | −0.04 | 0.11 | −0.01 | 0.14 | −0.12 | 0.10 | −0.09 | 0.14 | −0.03 | 0.04 | −0.01 | 0.05 | 0.10 | 0.05 |
| persons | 0.05 | 0.05 | 0.01 | 0.07 | 0.07 | 0.05 | 0.05 | 0.07 | 0.09 | 0.02 | 0.09 | 0.03 | 0.34 | 0.03 |
| child | −0.71 | 0.13 | −0.38 | 0.16 | −0.48 | 0.13 | −0.24 | 0.16 | −0.32 | 0.04 | −0.23 | 0.05 | −0.03 | 0.05 |
| xb | 0.99 | 0.03 | 1.17 | 0.07 | 0.95 | 0.04 | 1.09 | 0.07 | 0.78 | 0.02 | 0.91 | 0.03 | 0.61 | 0.03 |
| zg | 0.27 | 0.04 | 0.50 | 0.07 | 0.24 | 0.04 | 0.30 | 0.06 | 0.38 | 0.01 | 0.48 | 0.02 | 0.28 | 0.02 |

Table A10.
Coefficient and Standard Error of the models for Medical Care data.
Table A10.
Coefficient and Standard Error of the models for Medical Care data.
| Predictors | ZIP | ZINB | Hurdle Poisson | Hurdle NB | Ridge ZIP | Ridge ZINB | Ridge Hurdle NB | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coef. | SE | Coef. | SE | Coef. | SE | Coef. | SE | Coef. | SE | Coef. | SE | Coef. | SE | |
| emergency | −0.08 | 0.04 | 0.14 | 0.09 | −0.09 | 0.03 | 0.27 | 0.14 | −0.08 | 0.04 | 0.15 | 0.03 | 0.25 | 0.000012 |
| hospital | 0.08 | 0.04 | 0.43 | 0.09 | 0.07 | 0.02 | 0.21 | 0.10 | 0.27 | 0.04 | 0.42 | 0.04 | 0.23 | 0.000015 |
| health | 0.05 | 0.03 | −0.30 | 0.15 | 0.07 | 0.06 | −0.08 | 0.25 | −0.05 | 0.03 | −0.30 | 0.02 | −0.13 | 0.000024 |
| chronic | 0.07 | 0.05 | 0.23 | 0.05 | 0.06 | 0.02 | 0.14 | 0.07 | 0.13 | 0.05 | 0.23 | 0.05 | 0.14 | 0.000029 |
| adl | −0.47 | 0.03 | −0.68 | 0.15 | −0.48 | 0.06 | −1.02 | 0.23 | −0.50 | 0.03 | −0.60 | 0.02 | −0.57 | 0.000023 |
| region | −0.09 | 0.05 | −0.16 | 0.05 | −0.09 | 0.02 | −0.23 | 0.08 | −0.15 | 0.05 | −0.16 | 0.04 | −0.19 | 0.000033 |
| age | −0.27 | 0.04 | −0.56 | 0.10 | −0.24 | 0.04 | −0.16 | 0.16 | −0.57 | 0.04 | −0.55 | 0.04 | −0.18 | 0.000092 |
| afam | 1.25 | 0.02 | 1.07 | 0.17 | 1.23 | 0.06 | 2.07 | 0.32 | 0.89 | 0.02 | 0.82 | 0.02 | 0.71 | 0.000004 |
| gender | 0.26 | 0.03 | −0.01 | 0.13 | 0.29 | 0.05 | 0.39 | 0.19 | 0.09 | 0.03 | −0.03 | 0.03 | 0.20 | 0.000018 |
| married | 0.14 | 0.03 | 0.03 | 0.13 | 0.14 | 0.06 | −0.16 | 0.19 | 0.06 | 0.03 | 0.02 | 0.03 | −0.13 | 0.000010 |
| school | −0.03 | 0.03 | 0.01 | 0.02 | −0.04 | 0.01 | 0.00 | 0.03 | −0.01 | 0.03 | 0.01 | 0.03 | −0.04 | 0.000144 |
| income | −0.03 | 0.04 | −0.01 | 0.02 | −0.03 | 0.01 | −0.06 | 0.04 | −0.01 | 0.04 | −0.01 | 0.04 | −0.06 | 0.000048 |
| employed | −0.16 | 0.02 | −0.19 | 0.18 | −0.13 | 0.09 | 0.12 | 0.29 | −0.22 | 0.02 | −0.15 | 0.02 | 0.06 | 0.000004 |
| insurance | 0.11 | 0.02 | 0.59 | 0.16 | 0.06 | 0.07 | −0.24 | 0.32 | 0.49 | 0.02 | 0.47 | 0.02 | −0.18 | 0.000012 |
| medicaid | −0.05 | 0.02 | −0.15 | 0.22 | −0.05 | 0.09 | −0.37 | 0.41 | −0.07 | 0.02 | −0.12 | 0.01 | 0.02 | 0.000003 |
Appendix C. Residual Analysis of Medical Care Data
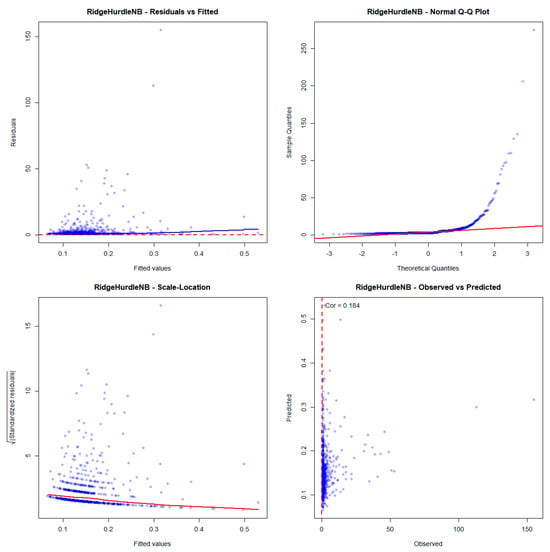
Figure A1.
Residual Analysis of RHNB model.
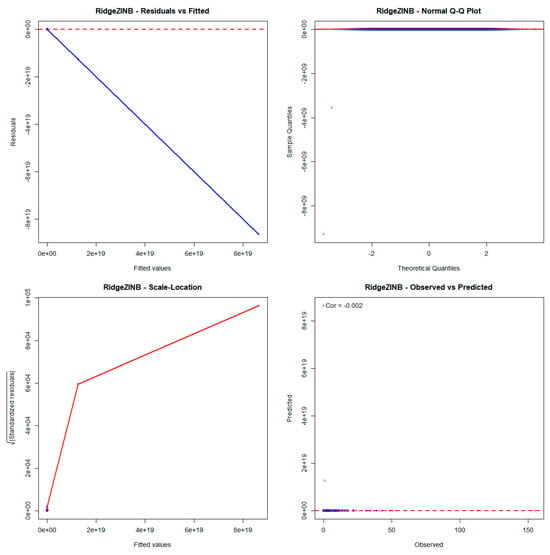
Figure A2.
Residual Analysis of Ridge ZINB model.
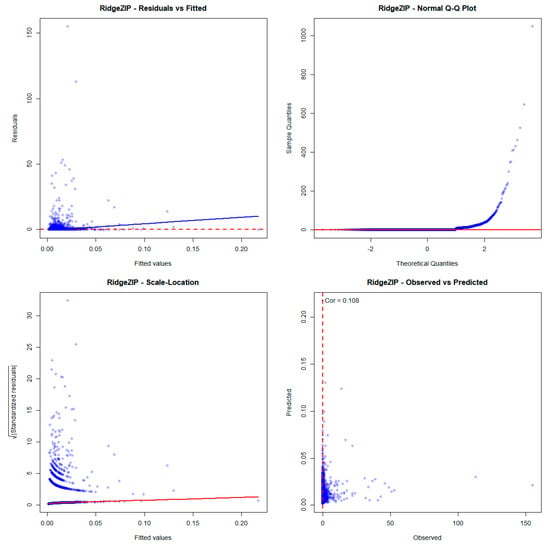
Figure A3.
Residual Analysis of Ridge ZIP model.
References
- Cameron, A.C.; Trivedi, P.K. Regression Analysis of Count Data, 2nd ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Schober, P.; Vetter, T.R. Count data in medical research: Poisson regression and negative binomial regression. Anesth. Analg. 2021, 132, 1378–1379. [Google Scholar] [CrossRef] [PubMed]
- Akram, M.N.; Abonazel, M.R.; Amin, M.; Kibria, B.G.; Afzal, N. A new Stein estimator for the zero-inflated negative binomial regression model. Concurr. Comput. Pract. Exp. 2022, 34, e7045. [Google Scholar] [CrossRef]
- Lambert, D. Zero-inflated Poisson regression, with an application to defects in manufacturing. Technometrics 1992, 34, 1–14. [Google Scholar] [CrossRef]
- Ridout, M.; Demétrio, C.G.; Hinde, J. Models for count data with many zeros. In Proceedings of the International Biometric Conference, Cape Town, South Africa, 14–18 December 1998; Volume 19, pp. 179–192. [Google Scholar]
- Greene, W.H. Accounting for Excess Zeros and Sample Selection in Poisson and Negative Binomial Regression Models; NYU Working Paper; New York University: New York, NY, USA, 1994. [Google Scholar]
- Amalia, R.N.; Sadik, K.; Notodiputro, K.A. A study of ZIP and ZINB regression modeling for count data with excess zeros. J. Phys. Conf. Ser. 2021, 1863, 012022. [Google Scholar] [CrossRef]
- Lord, D.; Mannering, F. The statistical analysis of crash-frequency data: A review and assessment of methodological alternatives. Transp. Res. A 2010, 44, 291–305. [Google Scholar] [CrossRef]
- Deb, P.; Trivedi, P.K. Demand for medical care by the elderly: A finite mixture approach. J. Appl. Econ. 1997, 12, 313–336. [Google Scholar] [CrossRef]
- Abonazel, M.R.; El-Sayed, S.M.; Saber, O.M. Performance of robust count regression estimators in the case of overdispersion, zero inflated, and outliers: Simulation study and application to German health data. Commun. Math. Biol. Neurosci. 2021, 2021, 55. [Google Scholar] [CrossRef]
- Rose, C.E.; Martin, S.W.; Wannemuehler, K.A.; Plikaytis, B.D. On the use of zero-inflated and hurdle models for modeling vaccine adverse event count data. J. Biopharm. Stat. 2006, 16, 463–481. [Google Scholar] [CrossRef]
- Feng, C.X. A comparison of zero-inflated and hurdle models for modeling zero-inflated count data. J. Stat. Distrib. Appl. 2021, 8, 8. [Google Scholar] [CrossRef]
- Mullahy, J. Specification and testing of some modified count data models. J. Econom. 1986, 33, 341–365. [Google Scholar] [CrossRef]
- Cragg, J.G. Some statistical models for limited dependent variables with application to the demand for durable goods. Econometrica 1971, 39, 829–844. [Google Scholar] [CrossRef]
- Lee, J.; Mannering, F.L.; Kim, D.K. Statistical modeling of highway safety data: Hurdle models revisited. Anal. Methods Accid. Res. 2021, 30, 100165. [Google Scholar]
- Xu, L.; Paterson, A.D.; Turpin, W.; Xu, W. Assessment and selection of competing models for zero-inflated microbiome data. PLoS ONE 2015, 10, e0129606. [Google Scholar] [CrossRef]
- Min, Y.; Agresti, A. Random effect models for repeated measures of zero-inflated count data. Stat. Model 2005, 5, 1–19. [Google Scholar] [CrossRef]
- Ghosh, P.; Mukerjee, R.; Chatterjee, S. Bayesian analysis of zero-inflated regression models. J. Stat. Plan. Inference 2012, 142, 1393–1403. [Google Scholar] [CrossRef]
- Famoye, F.; Singh, K.P. Zero-inflated generalized Poisson regression model with an application to domestic violence data. J. Data Sci. 2006, 4, 117–130. [Google Scholar] [CrossRef]
- Gurmu, S.; Trivedi, P.K. Excess zeros in count models for recreational trips. J. Appl. Econ. 1996, 11, 341–358. [Google Scholar] [CrossRef]
- Winkelmann, R. Econometric Analysis of Count Data, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hilbe, J.M. Negative Binomial Regression, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 5th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Kibria, B.M.G.; Månsson, K.; Shukur, G. A simulation study of some biasing parameters for the ridge type estimation of Poisson regression. Commun. Stat. Simul. Comput. 2015, 44, 943–957. [Google Scholar] [CrossRef]
- Khan, A.; Ullah, M.A.; Amin, M. Poisson regression diagnostics with ridge estimation. Commun. Stat. Simul. Comput. 2023, 52, 4174–4192. [Google Scholar] [CrossRef]
- Rady, E.A.; Abonazel, M.R.; Taha, I.M. Ridge estimators for the negative binomial regression model with application. In Proceedings of the 53rd Annual Conference on Statistics, Computer Science, and Operation Research, Cairo, Egypt, 3–5 December 2018; pp. 3–5. [Google Scholar]
- Akram, M.N.; Afzal, N.; Amin, M.; Batool, A. Modified ridge-type estimator for the zero inflated negative binomial regression model. Commun. Stat.-Simul. Comput. 2024, 53, 5305–5322. [Google Scholar] [CrossRef]
- Zeeshan, M.; Khan, A.; Amanullah, M.; Bakr, M.E.; Alshangiti, A.M.; Balogun, O.S.; Yusuf, M. A new modified biased estimator for Zero inflated Poisson regression model. Heliyon 2024, 10, e24225. [Google Scholar] [CrossRef]
- McGough, S.F.; Incerti, D.; Lyalina, S.; Copping, R.; Narasimhan, B.; Tibshirani, R. Penalized regression for left-truncated and right-censored survival data. Stat. Med. 2021, 40, 5487–5500. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Kibria, B.M.G.; Månsson, K.; Shukur, G. A Ridge Regression Estimator for the Zero-Inflated Poisson Model; CESIS Working Paper; Royal Institute of Technology: Stockholm, Sweden, 2011. [Google Scholar]
- Kibria, B.M.G.; Månsson, K.; Shukur, G. Some ridge regression estimators for the zero-inflated Poisson model. J. Appl. Stat. 2013, 40, 721–735. [Google Scholar] [CrossRef]
- Yüzbaşi, B.; Asar, A. Ridge type estimation in the zero-inflated negative binomial regression. Econom. Methods Appl. 2018, 93. [Google Scholar]
- Qasim, M.; Månsson, K.; Amin, M.; Kibria, B.M.G.; Sjölander, P. Biased adjusted Poisson ridge estimators—Method and application. Iran. J. Sci. Technol. Trans. A Sci. 2020, 44, 1775–1789. [Google Scholar] [CrossRef]
- Aladeitan, B.B.; Adebimpe, O.; Lukman, A.F.; Oludoun, O.; Abiodun, O.E. Modified Kibria–Lukman (MKL) estimator for the Poisson regression model: Application and simulation. F1000Research 2021, 10, 548. [Google Scholar] [CrossRef] [PubMed]
- Raihan, M.A.; Alluri, P.; Wu, W.; Gan, A. Estimation of bicycle crash modification factors (CMFs) on urban facilities using zero-inflated negative binomial models. Accid. Anal. Prev. 2019, 123, 303–313. [Google Scholar] [CrossRef] [PubMed]
- Bhaktha, N. Properties of Hurdle Negative Binomial Models for Zero-Inflated and Overdispersed Count Data. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2018. [Google Scholar]
- Park, M.Y.; Hastie, T. L1-regularization path algorithm for generalized linear models. J. R. Stat. Soc. B. 2007, 69, 659–677. [Google Scholar] [CrossRef]
- Al-Taweel, Y.; Algamal, Z. Almost unbiased ridge estimator in the zero-inflated Poisson regression model. TWMS J. Appl. Eng. Math. 2022, 12, 235–246. [Google Scholar]
- Kibria, B.M.G. Performance of some new ridge regression estimators. Commun. Stat. Simul. Comput. 2003, 32, 419–435. [Google Scholar] [CrossRef]
- Hoque, M.A.; Kibria, B.M. Some one and two parameter estimators for the multicollinear Gaussian linear regression model: Simulations and applications. Surv. Math. Appl. 2023, 18, 183–221. [Google Scholar]
- Hoque, M.A.; Kibria, B.G. Performance of some estimators for the multicollinear logistic regression model: Theory, simulation, and applications. Res. Stat. 2024, 2, 2364747. [Google Scholar] [CrossRef]
- Nayem, H.M.; Aziz, S.; Kibria, B.M.G. Comparison among ordinary least squares, ridge, lasso, and elastic net estimators in the presence of outliers: Simulation and application. Int. J. Stat. Sci. 2024, 24, 25–48. [Google Scholar] [CrossRef]
- Yasmin, N.; Kibria, B.M. Performance of some improved estimators and their robust versions in presence of multicollinearity and outliers. Sankhya B 2025, 87, 173–219. [Google Scholar] [CrossRef]
- Fletcher, D.; MacKenzie, D.; Villouta, E. Modelling skewed data with many zeros: A simple approach combining ordinary and logistic regression. Environ. Ecol. Stat. 2005, 12, 45–54. [Google Scholar] [CrossRef]
- Hua, H.; Tang, W.; Wang, W.; Paul, C. Structural zeroes and zero-inflated models. Shanghai Arch. Psychiatry 2014, 26, 236. [Google Scholar]
- Bertoli, W.; Conceição, K.S.; Andrade, M.G.; Louzada, F. A Bayesian approach for some zero-modified Poisson mixture models. Stat. Model. 2020, 20, 467–501. [Google Scholar] [CrossRef]
- Alheety, M.I.; Nayem, H.M.; Kibria, B.M.G. An unbiased convex estimator depending on prior information for the classical linear regression model. Stats 2025, 8, 16. [Google Scholar] [CrossRef]
- Nayem, H.M.; Aziz, S.; Kibria, B.M.G. Evaluating estimator performance under multicollinearity: A trade-off between MSE and accuracy in logistic, lasso, elastic net, and ridge regression with varying penalty parameters. Stats 2025, 8, 45. [Google Scholar] [CrossRef]
- Yu, Y.; Yang, L.; Shen, Y.; Wang, W.; Li, B.; Chen, Q. An iterative and shrinking generalized ridge regression for ill-conditioned geodetic observation equations. J. Geod. 2024, 98, 3. [Google Scholar] [CrossRef]
- Patil, P.; Du, J.H.; Tibshirani, R.J. Optimal ridge regularization for out-of-distribution prediction. arXiv 2024, arXiv:2404.01233. [Google Scholar] [CrossRef]
- Seifollahi, S.; Bevrani, H.; Algamal, Z.Y. Shrinkage estimators in zero-inflated Bell regression model with application. J. Stat. Theory Pract. 2025, 19, 1. [Google Scholar] [CrossRef]
- Zeileis, A.; Kleiber, C.; Jackman, S. Regression models for count data in R. J. Stat. Softw. 2008, 27, 1–25. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).