Robustness of the Trinormal ROC Surface Model: Formal Assessment via Goodness-of-Fit Testing

Abstract

Receiver operating characteristic (ROC) surfaces provide a natural extension of ROC curves to three-class diagnostic problems. A key summary index is the volume under the surface (VUS), representing the probability that a randomly chosen observation from each of the three ordered groups is correctly classified. A parametric estimation of VUS typically assumes trinormality of the class distributions. However, a formal method for the verification of this composite assumption has not appeared in the literature. Our approach generalizes the two-class AUC-based GOF test of Zou et al. to the three-class setting by exploiting the parallel structure between empirical and trinormal VUS estimators. We propose a global goodness-of-fit (GOF) test for trinormal ROC models based on the difference between empirical and trinormal parametric estimates of the VUS. To improve stability, a probit transformation is applied and a bootstrap procedure is used to estimate the variance of the difference. The resulting test provides a formal diagnostic for assessing the adequacy of trinormal ROC modeling. Simulation studies illustrate the robustness of the assumption via the empirical size and power of the test under various distributional settings, including skewed and multimodal alternatives. The method’s application to COVID-19 antibody level data demonstrates the practical utility of it. Our findings suggest that the proposed GOF test is simple to implement, computationally feasible for moderate sample sizes, and a useful complement to existing ROC surface methodology.

1. Introduction

Receiver operating characteristic (ROC) analysis is a cornerstone of diagnostic test evaluation [1,2,3]. While the two-class ROC curve and its area under the curve (AUC) have been extensively studied, many clinical problems involve three or more diagnostic categories. The ROC surface generalizes the ROC curve to the three-class setting, and its summary statistic, the volume under the surface (VUS), extends the AUC [4,5,6,7,8,9,10,11,12,13].

A common modeling framework is the trinormal model, which assumes that test results from the three groups (e.g., healthy, intermediate, diseased) are independent normals with increasing means or that they can be transformed to normality through a common monotone transformation [14,15,16,17]. In practice, the latter assumption is often overlooked: researchers may typically verify only marginal normality within each group. Yet departures from normality for the independent groups do not necessarily invalidate the trinormal assumption as already known from the ROC curve framework [18,19], while it is reasonable to hypothesize that significant departures such as skewness, heavy tails, or multimodality can invalidate the trinormal model, bias VUS estimation, and undermine inference. Despite this vague reality, a formal assessment of the model’s adequacy has received little attention in the literature.

In the two-class case, Zou et al. [20] developed a large-sample goodness-of-fit (GOF) test for binormal (and bi-Weibull) ROC models. Their method compares a nonparametric AUC estimator with its model-based counterpart, applying a variance-stabilizing transformation (e.g., probit or logit) to enable valid asymptotics. The appeal of this approach is its interpretability: if the parametric model is correct, the two estimates agree up to sampling error; otherwise, their discrepancy reflects a lack of fit.

No analogous GOF procedure has been available for ROC surfaces. Yet the ingredients are parallel: the VUS admits both a nonparametric U-statistic estimator and a closed-form expression under the trinormal model [21,22]. In this work we provide a natural extension of the Zou et al. framework to the three-class case: compare empirical and trinormal VUS estimates, possibly after transformation, using resampling to calibrate inference.

Such an extension matters because the trinormal model is pervasive in ROC surface analysis, especially for very large samples where nonparametric estimates can be computationally expensive or even infeasible, but real biomedical data may not adhere to trinormality assumptions. The two-class “binormal” framework illustrates this issue: in strict form it posits independent normals with distinct means and variances; in a broader sense, it assumes existence of a monotone transformation yielding approximate normality, exploiting ROC invariance to monotone changes in scale. Transformation-based methods (e.g., Box–Cox with a common exponent) formalize this broader view [23,24], yet without a GOF check, adequacy remains unverified.

By importing the GOF philosophy to the three-class setting, we provide a practical diagnostic for trinormal ROC models. Contrasting empirical and parametric VUS estimates highlights when parametric summaries are reliable and when departures from trinormality call for alternative modeling. This brings needed transparency to the routine use of ROC surface methods in practice.

2. Methods

2.1. The Two-Class, Binormal ROC Curve Framework

In the two-class case, receiver operating characteristic (ROC) analysis evaluates the ability of a continuous marker, X, to distinguish between a non-diseased group ($X_0$) and a diseased group ($X_1$), assuming $X_0<X_1$.

Suppose $X_0\sim F_0$ is the cumulative distribution function (CDF) of the marker for non-diseased subjects and $X_1\sim F_1$ is the CDF for diseased subjects. The ROC curve is defined as $ROC\left(t\right)=1-F_1(F_0^{-1}(1-t)$, $u\in [0,1]$. Under the binormal model, we assume

$$X_0\sim N({\mu }_0,{\sigma }_0^2),X_1\sim N({\mu }_1,{\sigma }_1^2),$$

with independent samples, possibly after a common transformation to normality that will allow for the efficient use of the model. The ROC curve can then be written in closed form as

$$ROC\left(t\right)=\Phi \left({\displaystyle \frac{{\mu }_1-{\mu }_0}{{\sigma }_1}}+{\displaystyle \frac{{\sigma }_0}{{\sigma }_1}}{\Phi }^{-1}\left(t\right)\right),0<t<1,$$

(1)

where $\Phi (·)$ is the standard normal distribution function and t is the false positive rate (FPR). The area under the curve (AUC), which summarizes overall discriminatory ability, has the simple expression $AUC=P(X_0<X_1)$. Equivalently, the AUC can be interpreted as the probability that a randomly chosen diseased subject will have a higher marker value than a randomly chosen non-diseased subject. For the binormal model, denoting AUC simply by A, this becomes

$$A=\Phi \left({\displaystyle \frac{{\mu }_1-{\mu }_0}{\sqrt{{\sigma }_0^2+{\sigma }_1^2}}}\right),$$

(2)

with $\Phi (·)$ as the standard normal distribution function [25]. This form highlights that, in the binormal setting, the AUC depends only on the standardized mean difference between groups.

2.2. Box–Cox for Binormal ROC

A pragmatic route to approximate binormality for continuous diagnostic markers is to apply a common monotone power transformation across groups prior to model fitting [23]. Let

$$T_{\lambda }\left(u\right)=\left\{\begin{array}{cc}{\displaystyle \frac{u^{\lambda }-1}{\lambda },}\hfill & \lambda \ne 0,\hfill \\ logu,\hfill & \lambda =0,\hfill \end{array}\right.$$

(3)

and suppose $T_{\lambda }\left(X_0\right)$ and $T_{\lambda }\left(X_1\right)$ are approximately normal with distinct means/variances for a single $\lambda$ shared by both classes. Because the ROC curve is invariant to monotone transformations, estimation and inference can proceed on the transformed scale while reporting cutoffs back on the original scale. A comprehensive binormal workflow based on this idea, including point and interval estimation for AUC, the maximized Youden index, its cutoff and joint $(\mathrm{TPR},\mathrm{FPR})$ inference, as well as two-marker comparisons, has been developed by Bantis et al. [26] and implemented in the rocbc package, with procedures that account for the uncertainty in $\widehat{\lambda }$ and tools to check whether a Box–Cox transformation can plausibly achieve approximate normality [27].

In practice, $\lambda$ is estimated (e.g., by profile likelihood under normality on $T_{\lambda }\left(X_0\right),T_{\lambda }\left(X_1\right)$). This yields semi-parametric robustness (via transformation) without abandoning the interpretability and efficiency of binormal ROC when the transformed model is adequate.

2.3. Goodness-of-Fit Testing in the Binormal Framework

To formally assess the binormal assumption in ROC curve analysis, Zou et al. [20] proposed a global goodness-of-fit test based on comparing nonparametric and parametric estimates of the area under the curve (AUC). The nonparametric AUC is given by

$${\widehat{A}}_N={\displaystyle \frac{1}{n_H{n}_D}}\sum _{j=1}^{n_H}\sum _{i=1}^{n_D}I\{X_{0j}<X_{1i}\},$$

(4)

where $X_{0j}$ and $X_{1i}$ denote test results from the non-diseased and diseased samples, respectively. Under the binormal model, $X_0\sim N({\mu }_{X_0},{\sigma }_{X_0}^2)$ and $X_1\sim N({\mu }_{X_1},{\sigma }_{X_1}^2)$, the parametric AUC is

$${\widehat{A}}_P=\Phi \left({\displaystyle \frac{\widehat{a}}{\sqrt{1+{\widehat{b}}^2}}}\right),\widehat{a}={\displaystyle \frac{\overline{X_1}-\overline{X_0}}{s_{X_0}}},\widehat{b}={\displaystyle \frac{s_{X_1}}{s_{X_0}}}.$$

(5)

Since AUC values are confined to (0, 1), both ${\widehat{A}}_N$ and ${\widehat{A}}_P$ are conveniently transformed to take values over the entire real line via the probit transform, $W={\Phi }^{-1}\left(A\right)$. The test statistic is then constructed as

$$\widehat{D}={\displaystyle \frac{{\widehat{W}}_N-{\widehat{W}}_P}{\widehat{\mathrm{SE}}({\widehat{W}}_N-{\widehat{W}}_P)}},$$

(6)

where the standard error in the denominator is estimated by a stratified bootstrap resampling of the diseased and non-diseased groups [28]. Under the null hypothesis that the binormal model is correct, $\widehat{D}$ is asymptotically standard normal, and the two-sided p-value is $p=2\{1-\Phi (|\widehat{D}\left|\right)\}$.

2.4. The Three-Class, ROC Surface Framework

Let $X_0$, $X_1$, and $X_2$ denote independent test results from healthy, intermediate, and diseased populations with cumulative distributions $F_0, F_1, F_2$, respectively. The VUS is defined as $\mathrm{VUS}=P(X_0<X_1<X_2).$ It represents the probability that the diagnostic marker correctly orders a randomly selected triplet. The nonparametric estimator of VUS is a U-statistic:

$${\widehat{\mathrm{VUS}}}_{emp}={\displaystyle \frac{1}{n_0{n}_1{n}_2}}\sum _{i=1}^{n_0}\sum _{j=1}^{n_1}\sum _{k=1}^{n_2}I(X_{0i}<X_{1j}<X_{2k}),$$

(7)

where $n_0,n_1,$ and $n_2$ are class sample sizes. This estimator is unbiased but computationally intensive for large n [29]. To adjust for ties, the indicator function in Equation (7) becomes $I(X_{0i}<X_{1j}<X_{2k})+\frac{1}{2}I(X_{0i}=X_{1j}<X_{2k})+\frac{1}{2}I(X_{0i}<X_{1j}=X_{2k})+\frac{1}{3}I(X_{0i}=X_{1j}=X_{2k})$.

Under the trinormal model, $X_0\sim N({\mu }_0,{\sigma }_0^2)$, $X_1\sim N({\mu }_1,{\sigma }_1^2)$, $X_2\sim N({\mu }_2,{\sigma }_2^2)$. The trinormal ROC surface and corresponding VUS have closed-form expressions [30].

The closed-form expression for VUS is derived as follows. Let

$${\delta }_{01}={\displaystyle \frac{{\mu }_1-{\mu }_0}{\sqrt{{\sigma }_0^2+{\sigma }_1^2}}},{\delta }_{12}={\displaystyle \frac{{\mu }_2-{\mu }_1}{\sqrt{{\sigma }_1^2+{\sigma }_2^2}}},\rho =-{\displaystyle \frac{{\sigma }_1^2}{\sqrt{({\sigma }_0^2+{\sigma }_1^2)({\sigma }_1^2+{\sigma }_2^2)}}}.$$

Denote by ${\Phi }_2(·,·;\rho )$ the standard bivariate normal CDF with correlation $\rho$,

$${\Phi }_2(x,y;\rho )={\int }_{-\infty }^x{\int }_{-\infty }^y{\displaystyle \frac{1}{2\pi \sqrt{1-{\rho }^2}}}exp\left(-{\displaystyle \frac{u^2-2\rho uv+v^2}{2(1-{\rho }^2)}}\right)\mathrm{d}v\mathrm{d}u.$$

(8)

Then, under the trinormal model,

$$\mathrm{VUS}=Pr(X_0<X_1<X_2)=Pr\left(X_1-X_0>0,X_2-X_1>0\right)={\Phi }_2\left({\delta }_{01},{\delta }_{12};\rho \right).$$

(9)

For the equivalent $(a,b,c,d)$ form pertinent to the four-parameter trinormal ROC surface model, define

$$a={\displaystyle \frac{{\sigma }_1}{{\sigma }_0}},b={\displaystyle \frac{{\mu }_0-{\mu }_1}{{\sigma }_0}},c={\displaystyle \frac{{\sigma }_1}{{\sigma }_2}},d={\displaystyle \frac{{\mu }_2-{\mu }_1}{{\sigma }_2}}.$$

Then,

$${\delta }_{01}={\displaystyle \frac{-b}{\sqrt{1+a^2}}},{\delta }_{12}={\displaystyle \frac{d}{\sqrt{1+c^2}}},\rho =-{\displaystyle \frac{ac}{\sqrt{(1+a^2)(1+c^2)}}},$$

hence,

$$\mathrm{VUS}={\Phi }_2\left({\displaystyle \frac{-b}{\sqrt{1+a^2}}},{\displaystyle \frac{d}{\sqrt{1+c^2}}};-{\displaystyle \frac{ac}{\sqrt{(1+a^2)(1+c^2)}}}\right).$$

(10)

The VUS is estimated by maximum likelihood fitting of the class-specific normals. We denote this estimator by ${\widehat{VUS}}_{trin}$. These expressions follow the standard trinormal ROC parameterization reviewed in Noll et al. [14] and Xiong et al. [30].

2.5. Box–Cox for Trinormal ROC Surfaces

The Box–Cox ROC curve framework extends to three-class ROC surface analysis by applying a common Box–Cox transformation to all three groups, and then we fit a trinormal model to $T_{\lambda }\left(X_0\right),T_{\lambda }\left(X_1\right),T_{\lambda }\left(X_2\right)$ and compute VUS on the transformed scale. Methodology and software exist for this pathway: trinROC includes boxcoxROC for the automatic selection of a common $\lambda$ and transformed-scale fitting. Noll et al. [14] formalized inference and testing for ROC surfaces under the trinormal model and explicitly connected these procedures with Box–Cox-type transformations.

Transformation-based modeling does not obviate the need to verify the trinormal working model. Even with good empirical performance, adequacy should be tested rather than assumed. In the two-class case, goodness-of-fit testing compares a nonparametric AUC to its model-based counterpart after variance-stabilizing transformation; an analogous comparison for VUS provides a principled diagnostic for trinormal ROC surfaces. Embedding a Box–Cox pre-processing step and a subsequent GOF test adds essential formalism to the routine use of binormal/trinormal ROC models, clarifying when parametric summaries are trustworthy and when departures from trinormality warrant alternatives [26].

2.6. Proposed Trinormal GOF Test

Extending the two-class framework [20], we compare the empirical and parametric trinormal VUS estimates. Because VUS $\in (0,1)$, we apply a probit transformation, $W={\Phi }^{-1}\left(\widehat{\mathrm{VUS}}\right)$, where ${\Phi }^{-1}$ is the standard normal quantile function. We define $\Delta =W_{emp}-W_{trin}$. We estimate $\mathrm{Var}(\Delta )$ by bootstrap resampling (resampling within each class). The test statistic is

$$D={\displaystyle \frac{|\Delta |}{\sqrt{\widehat{\mathrm{Var}}(\Delta )}}},$$

(11)

which is asymptotically $N(0,1)$ under the null hypothesis that the trinormal model is valid. Large values of D indicate a lack of fit, with two-sided p-values obtained accordingly.

The procedure was implemented in R, using the trinROC package for empirical and trinormal VUS estimation and boxcoxROC for optional transformation to normality. We provide the code in Appendix A.

3. Simulation Scenarios and Results

To assess the impact of distributional assumptions and potential deviations from trinormality on the estimation of VUS, we conducted a series of simulation experiments under nine distinct data-generating scenarios (A–I), reviewed in

Table 1. Empirical VUS vs. naive trinormal plug-in VUS (Scenarios A–I). Sample sizes of 2000, averages of r = 300,000 replicates given for empirical and naive trinormal VUS.

Scenario (Approximate Target Empirical VUS)	Empirical VUS	Naive Trinormal VUS	${\mathit{X}}_0$	${\mathit{X}}_1$	${\mathit{X}}_2$
A (≈0.80)	0.818	0.811	$\Gamma (1,2)$	$\frac{1}{2}N(3,0.6^2)+\frac{1}{2}N(7,0.6^2)$	$N(8.5,1.6^2)$
B (≈0.55)	0.555	0.562	$\mathrm{LN}(0,0.6)$	$\frac{1}{2}N(2.5,0.9^2)+\frac{1}{2}N(7,0.6^2)$	${\chi }_6^2+N(0,0.5^2)$
C (≈0.60)	0.592	0.584	$\Gamma (1,2)$	$\Gamma (5,1)$	$\Gamma (2,5)$
D (≈0.50)	0.504	0.511	$N(0,1^2)$	$N(0.9,1^2)$	$N(1.8,1^2)$
E (≈0.50)	0.523	0.525	$N(0,1^2)$	$N(1.2,1.5^2)$	$N(2.4,1^2)$
F (≈0.50)	0.493	0.507	$N(0,0.5^2)$	$N(2.2,2.5^2)$	$N(4.4,4^2)$
G (≈0.30)	0.295	0.209	$\mathrm{LN}(0,1)$	$\mathrm{LN}(0.406,1)$	$\mathrm{LN}(0.812,1)$
H (≈0.70)	0.699	0.427	$\mathrm{LN}(0,0.6)$	$\mathrm{LN}(1.4,1)$	$\mathrm{LN}(2.8,1.2)$
I (≈0.20)	0.214	0.602	$\mathrm{LN}(-0.2,0.6)$	$0.7N(0.1,0.5^2)+0.3N(10.5,0.8^2)$	$8.5+\Gamma (2,1)+N(0,0.5^2)$

Notes: $N(\mu ,{\sigma }^2)$ is normal with mean $\mu$ and variance ${\sigma }^2$, with $100+\mu$ for scenarios D–F. $\Gamma (k,\theta )$ is gamma with shape k and scale $\theta$. $\mathrm{Lognormal}(\mu ,\sigma )$, denoted as $LN$, uses $(\mu ,\sigma )$ as log-scale parameters (meanlog, sdlog). Mixture weights are shown explicitly; e.g., $0.7N(·)+0.3N(·)$.

and illustrated visually in Figure 1. Increments in means across groups were maintained to enforce an ordering of disease severity. Each scenario was constructed to represent common or challenging situations encountered in diagnostic test evaluation, ranging from symmetric Gaussian distributions with increasing means and skewed lognormal or gamma settings to mixture models and heavy-tailed distributions.

• Scenarios A–C: Skewed and/or mixture distributions. Scenario A combines a gamma distribution for $X_0$, a two-component normal mixture for $X_1$, and a shifted normal for $X_2$, yielding a high empirical VUS around 0.82. Scenario B introduces a lognormal distribution for $X_0$, a mixture distribution for $X_1$, and a chi-square plus normal noise for $X_2$, producing moderate discrimination (empirical VUS $\approx 0.56$). Scenario C adopts gamma distributions with increasing shape/scale parameters across groups, targeting a VUS of 0.60. At the same time, these are scenarios where the Box–Cox transformation (or the simpler log one) are expected to fail in transforming to normality. The proposed GOF test is expected to exhibit some power to reject the trinormal hypothesis even at low to moderate sample sizes.
• Scenarios D–F: Trinormal benchmarks with equal or unequal variances. Scenario D sets means equally spaced at 0, 0.9, and 1.8 with equal unit variance, while Scenarios E and F gradually increase variance heterogeneity across groups, yielding empirical VUS values close to the 0.50 null benchmark. For these scenarios, even the simple log transformation is expected to perform rather well in transforming to normality, with the Box–Cox providing optimal results. The test is expected to approximate the nominal size of $\alpha =0.05$ used throughout.
• Scenarios G–I: Strong departures from normality. Scenario G uses lognormal distributions with scaling factors, leading to pronounced skewness and low empirical VUS ($\approx 0.30$). Scenario H further exaggerates skewness by shifting the lognormal parameters, targeting VUS $\approx 0.70$. Finally, Scenario I combines a lognormal, $X_0$, a normal mixture, $X_1$, and a highly skewed gamma plus normal noise, $X_2$, resulting in the lowest discrimination (VUS $\approx 0.20$). A naive estimation of VUS based on a trinormal assumption is expected to fail, while Box–Cox should show robustness and be a valid option for the use of parametric assumptions.

The diversity of scenarios ensures that both mild and extreme violations of the trinormal assumption are represented, allowing us to evaluate robustness across a wide range of practical conditions. For each scenario of Table 1, the empirical VUS was estimated via Equation (7). We approximated $\mathrm{VUS}=P(X_0<X_1<X_2)$ using averages of $r = 300,000$ Monte Carlo replicates with independent samples of size 2000 drawn from distributions assigned to the three diagnostic groups, denoted $X_0,X_1,$ and $X_2$. The naive trinormal plug-in VUS was obtained by estimating group means and variances via maximum likelihood under the normal model and applying the trinormal VUS formula of Equation (10). The standard errors of these VUS estimates are negligible (in the vicinity of 0.001) given the number of replicates and sample sizes used. These estimates represent the “true” difference between the empirical and naive trinormal VUS estimates for each scenario.

Furthermore, the scenarios listed in Table 1 span a wide range of complexities:

• In Scenarios A–F, the empirical and naive trinormal VUS values are broadly consistent, with differences typically below 0.02. For example, Scenario A yields an empirical VUS of 0.818 and a naive VUS of 0.811, while Scenario D (trinormal null) shows 0.504 vs. 0.511. This suggests that moderate skewness or variance heterogeneity does not strongly bias parametric estimates when sample sizes are large.
• Scenarios G–I demonstrate severe discrepancies. In Scenario G, the empirical VUS is 0.295, but the naive trinormal estimate drops to 0.209, substantially underestimating diagnostic performance. In Scenario H, the empirical VUS is 0.699, yet the naive trinormal VUS falls to 0.427, a striking underestimation. Conversely, in Scenario I, the naive estimate (0.602) vastly overstates the empirical VUS (0.214). These results indicate that naive normal modeling can misrepresent discrimination strength, either attenuating or inflating it, when strong departures from normality or mixture structures are present.

The proposed GOF test should reject when $|\Delta |$ is high for the scenarios of Table 1. A comprehensive assessment of the proposed GOF test was performed by comparing the empirical VUS, estimated nonparametrically, with three plug-in VUS estimates: (i) the naïve trinormal estimate obtained by fitting normal distributions to each class without regard to the true underlying distributions, (ii) the trinormal estimate after applying a simple log transformation, and (iii) the trinormal estimate after applying the Box–Cox transformation, used as an optimal method for normalizing continuous diagnostic test results within the ROC framework. The aim was also to evaluate the usefulness of simple log and Box–Cox transformations in situations where the naive VUS estimator fails.

Table 2. Monte Carlo power by scenario. Entries are rejection proportions over $R=5000$ replicates for balanced designs (n per class) and the unbalanced design $(20,40,80)$.

Scenario	$\mathit{n}=20$			$\mathit{n}=40$			$\mathit{n}=80$			Unbalanced (20, 40, 80)
	Box–Cox	Log	None	Box–Cox	Log	None	Box–Cox	Log	None	Box–Cox	Log	None
A	0.020	0.022	0.019	0.053	0.079	0.049	0.096	0.205	0.065	0.046	0.072	0.039
B	0.026	0.036	0.018	0.069	0.083	0.029	0.119	0.211	0.034	0.040	0.066	0.035
C	0.021	0.026	0.024	0.032	0.079	0.037	0.057	0.182	0.043	0.026	0.058	0.037
D	0.026	0.024	0.033	0.026	0.041	0.034	0.038	0.047	0.041	0.027	0.028	0.037
E	0.029	0.024	0.051	0.035	0.039	0.051	0.033	0.047	0.045	0.033	0.029	0.059
F	0.029	0.029	0.190	0.040	0.040	0.336	0.035	0.043	0.477	0.030	0.029	0.367
G	0.345	0.345	0.500	0.034	0.355	0.655	0.042	0.353	0.553	0.042	0.347	0.680
H	0.504	0.509	0.716	0.514	0.520	0.945	0.523	0.523	0.999	0.511	0.510	0.978
I	0.992	0.996	0.994	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000

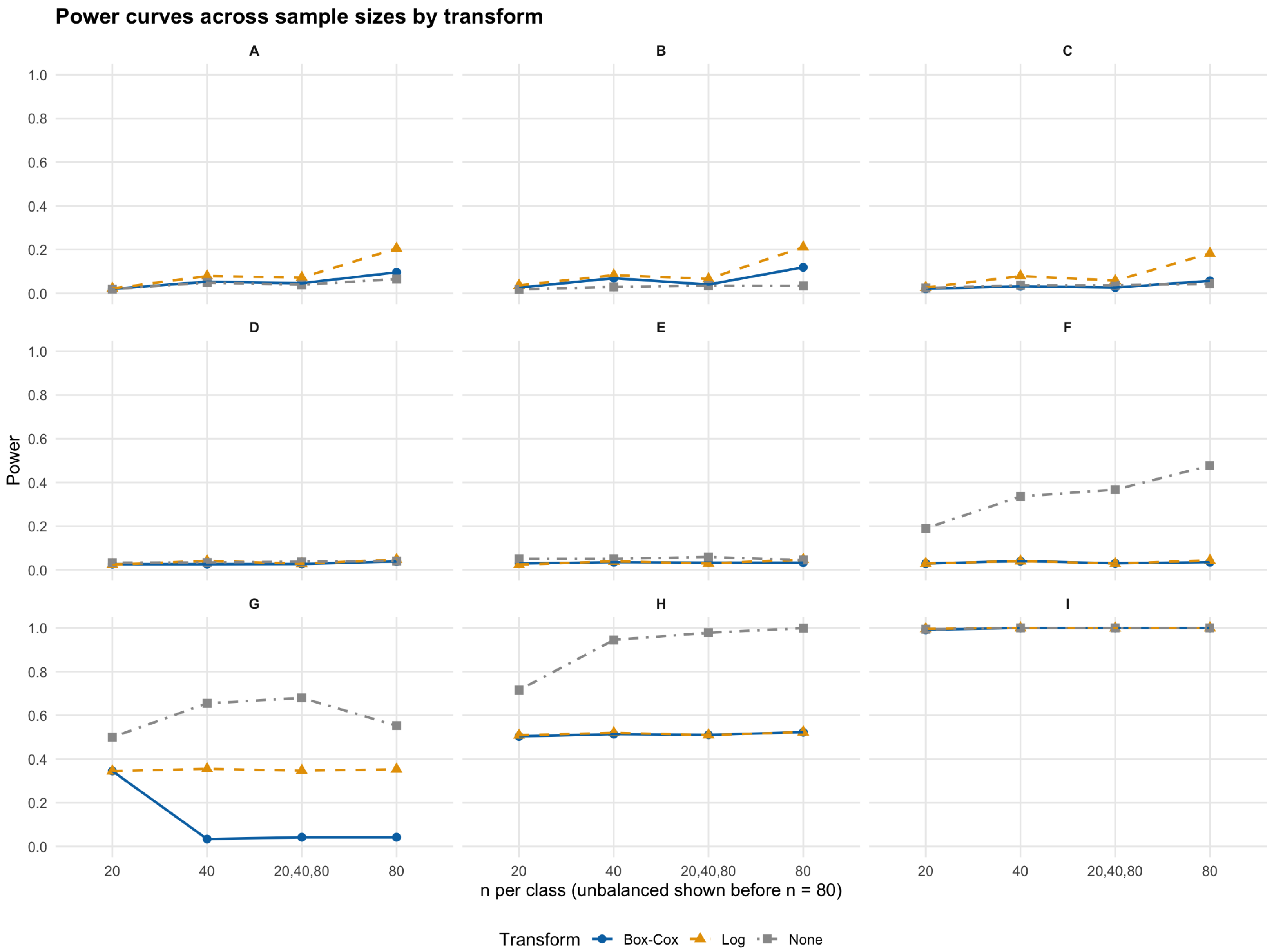
displays the results and Figure 2 provides the corresponding visual illustration:

• For Scenarios A–C, when the naive trinormal VUS estimate is close to the empirical, rejection rates are close to the nominal size of 0.05. No transformation appears to be needed regardless of underlying distributions. Transformations may even distort the true underlying discrimination pattern, a fact that is apparent as the sample size grows larger. Specifically, for the log transformation, rejection rates are in the vicinity of 0.2, although the trinormal model is expected to provide an appropriate parametric framework based on the underlying sampling distributions.
• For Scenarios D–F, even if underlying distributions are in fact normal, the naive trinormal VUS estimator will fail if significant scale differences exist between the underlying actually normal distribution. This is a very important finding, given that the underlying independent normality of the distributions of the three classes does not ensure an accurate estimation of the VUS using the naive trinormal model. The naive trinormal model approach results in high rejection rates, even near 0.5 for sample sizes of 80, although the trinormal model is again hypothesized to provide the appropriate parametric framework. Even a simple log transformation will yield the needed normalization to trinormality, allowing for the use of the parametric VUS model.
• For Scenarios G–I, Box–Cox behaves very well for moderate or larger sample sizes when differences between empirical and naive trinormal VUS estimates are within the range of $0.1$ (Scenario G, underlying lognormal distributions), while the simple log transformation does not provide an adequately accurate result. Only Box–Cox appears to result in rejection rates close to the nominal size of 0.05 for sample sizes of above 40. As a result, when $|\Delta |$ is as large as 0.1 in absolute terms, the Box–Cox transformation is suggested as the appropriate normalizing method for the accurate use of the trinormal model. The proposed GOF test exhibits high power in detecting departures from the trinormal model (especially for Scenarios H and I). Even when the underlying distributions are lognormal, both transformation choices offer little help and the GOF test results in high power, i.e., consistently above 0.5 for Scenario H and even 1 for the extreme Scenario I. In such cases, resorting to nonparametric methods is the recommended approach.

In sum, our simulation study demonstrates that naive trinormal VUS estimates are robust to mild departures from normality but can be severely misleading in some skewed or mixture scenarios where the empirical estimate diverges significantly from the naive trinormal or even when significant scale differences exist between underlying normal distributions. This emphasizes the need for approximate transformations to normality (e.g., via Box–Cox or simple log) in the three-class diagnostic setting where biases can propagate into erroneous clinical inference. The use of nonparametric approaches is recommended for extreme differences of empirical versus naive trinormal VUS estimates. THe use of the proposed GOF test is the suggested gatekeeping procedure in the sense that when the GOF test rejects the trinormal model, it would be absolutely necessary to either resort to nonparametric approaches or use the Box–Cox transformation. If the GOF test rejects it even after Box–Cox, nonparametric approaches are recommended.

4. Application: COVID-19 Antibody Data

As a motivating illustration, consider the situation during the initial phase of the COVID-19 vaccination campaign when antibody titers were collected to assess vaccine response but demographic data were often withheld to preserve anonymity. Because vaccination at that stage was prioritized for medical personnel and subsequently for older adults, linking titer measurements with age could inadvertently reveal individual identities. For instance, in a small hospital cohort where only one 63-year-old physician had been vaccinated, recording the exact age would have immediately identified that individual. Consequently, laboratory datasets were released without age information. In such a setting, the antibody titer values themselves could serve as indirect markers for age group (e.g., 40–49, 50–59, 60–69), given the systematic differences in both immune response magnitude and the timing of vaccination across these strata. This creates a natural, though unconventional, diagnostic scenario, using continuous antibody titers as the test variable to classify subjects into age groups, thereby providing a useful example for evaluating transformation-based ROC and VUS estimation methods under realistic data constraints.

For the application, we illustrate our methodology using antibody data following the first dose of the BNT162b2 COVID-19 vaccine, as reported by [31]. The original study recruited 425 Greek healthcare workers and measured IgG levels against the SARS-CoV-2 spike protein 14 days post-immunization. Their findings indicated robust immunogenicity, with more than 90% of participants developing detectable antibody responses. Importantly, antibody titers displayed a clear age gradient: levels were highest among younger individuals (20–49 years), declined markedly in the 50–59 age group, and dropped further among participants aged 60 years or older. This pattern makes the dataset particularly suitable for exploring three-class ROC methodology, with the age strata serving as distinct groups. In our analysis, we restricted attention to the most relevant age ranges 40–49, 50–59, and 60–69 years, thereby creating three groups with progressively decreasing antibody concentrations.

Figure 3 illustrates smoothed histograms and boxplots of the raw, log-transformed, and Box–Cox measurements, while Figure 4 illustrates the corresponding ROC surface estimates according to the possible models used through standard output of the trinROC package. Applying our trinormal goodness-of-fit test framework, we examined the adequacy of the trinormal assumption under different transformations.

Table 3. Results of trinormal goodness-of-fit tests under different transformations.

Case	VUS Empirical (se)	VUS Trinormal (se)	D	p-Value
None	0.335 (0.037)	0.180 (0.033)	3.865	1.11 $\times {10}^{-4}$
Log	0.335 (0.037)	0.295 (0.036)	2.254	0.024
Box–Cox	0.335 (0.037)	0.306 (0.035)	1.674	0.094

summarizes the results. The raw data showed clear deviations from normality, and the log transformation improved model fit but still left some departures. By contrast, the Box–Cox transformation provided the best adherence to trinormality, yielding more stable estimates of the volume under the surface (VUS). This example highlights the practical relevance of transformation choice in ROC surface analysis: while simpler transformations such as the logarithm can mitigate skewness, the more flexible Box–Cox approach can better accommodate the distributional characteristics of immunogenicity data, ultimately leading to more reliable inference.

5. Discussion

It is well known that the binormal ROC curve model exhibits a level of certain robustness to departures from normality in the underlying group distributions. For example, Hanley [18] noted that binormal ROC analysis can still provide useful summaries even when the marker distributions are skewed or heavy-tailed, provided the deviation from normality is not extreme. Nevertheless, the binormal framework remains a parametric model, and its use implicitly assumes validity of the underlying distributional form. In practice, this assumption is seldom tested in ROC curve analysis, though analogous assumptions are routinely checked in classical inference problems such as the t-test or one-way ANOVA. The same issue carries over to ROC surface analysis, where the trinormal model can be adopted in practice, and must be adopted for large sample sizes where computational cost becomes an issue, but is not subjected to formal GOF evaluation. While ROC surface methodology has matured substantially, a formal consideration of distributional adequacy remains underdeveloped. This gap motivates the development of dedicated GOF procedures for ROC surfaces, ensuring that parametric estimates of diagnostic accuracy are not unduly biased by violations of normality.

We proposed a global GOF test for trinormal ROC surfaces based on comparing empirical and parametric VUS estimates. The test generalizes two-class AUC-based GOF tests [20] to three-class settings. The test maintains correct type I error when trinormality holds and has good power against skewed or multimodal alternatives even for moderate sample sizes. Transformations such as Box–Cox can markedly improve model adequacy as tested using the proposed GOF framework. Limitations include the computational cost of the empirical VUS for large n, though our implementation remains feasible for $n<150$ per group. Extensions to higher-class ROC manifolds represent future work. The current contribution provides the basis for a straightforward generalization to the multiple-class case but an elaboration on the effect of underlying distributions on the size and power of the test is needed.

The proposed GOF test provides a simple and interpretable way to check trinormal assumptions in ROC surface analysis. It complements parametric modeling by highlighting when results are robust and when alternative approaches may be needed. Such model adequacy tests could become routine practice even for standard methods that rely on parametric assumptions, such as the ANOVA.