Abstract
In this paper, we introduce a kernel-based nonlinear Bayesian model for a right-censored survival outcome data set. Our kernel-based approach provides a flexible nonparametric modeling framework to explore nonlinear relationships between predictors with right-censored survival outcome data. Our proposed kernel-based model is shown to provide excellent predictive performance via several simulation studies and real-life examples. Unplanned hospital readmissions greatly impair patients’ quality of life and have imposed a significant economic burden on American society. In this paper, we focus our application on predicting 30-day readmissions of patients. Our survival Bayesian additive regression kernel model (survival BARK or sBARK) improves the timeliness of readmission preventive intervention through a data-driven approach.
1. Introduction
The Centers for Medicare and Medicaid Services (CMS) has defined hospital readmission as an admission to an acute care hospital within 30 days of a discharge from the index admission in the same or another acute care hospital [1]. Hospital readmissions have emerged as a global concern due to their high frequency and high associated cost. In the United States, 15.5% of Medicare beneficiaries were readmitted unplanned within 30 days after discharge during July 2014 to June 2015 [2]. It has been estimated that unplanned readmissions account for USD 17.4 billion in Medicare expenditures annually [3]. Although the causes are complicated, unplanned hospital readmissions are frequently seen as related to the substandard quality of care received during index admissions [4,5,6]. The pressure to reduce cost and improve healthcare quality has triggered the implementation of the Hospital Readmissions Reduction Program (HRRP) [1] in the United States in 2012. In the fiscal year 2017, 79% of hospitals were penalized by the HRRP, with estimated penalties of USD 528 million [7].
In recent years, we are seeing a growing body of literature on the development of hospital readmission predictive models for both hospital profiling purposes and clinical decision support, with the ultimate goal of reducing readmissions [8]. The most widely used approach is to treat readmission prediction as a binary classification or a probability regression problem with statistical or machine-learning-based algorithms. However, 30-day hospital readmission data is naturally right-censored, making it inappropriate to directly apply traditional prediction algorithms. A patient’s probability of being readmitted varies with the time after discharge. For example, a patient may be readmitted on the 31st day after discharge. Because it is outside of the monitoring time window (30 days), it is considered as no readmission within 30 days. However, the time is very close to the threshold, making it hard to contrast the readmissions within the window (e.g., 29th day, 30th day, etc.). This is one reason why most readmission models cannot achieve good performance. Therefore, it is more appropriate to study patients’ probability of readmission as a function of time within the observation time window.
Survival analysis has been one of the most important branches of statistics to estimate the duration of time until the occurrence of an event of interest [9]. The key characteristic of the survival analysis problem is the presence of censored instances whose event outcomes cannot be observed at some time point or when the event outcome does not occur within the monitoring time window [10]. As a result, regular statistical and machine learning predictive algorithms cannot be directly applied to survival analysis problems. Based on the assumption about the distribution of time, statistical survival models can be classified as either parametric, nonparametric, or semiparametric. Parametric models assume survival time follows some particular distribution, such as normal, exponential, and Weibull distributions. One popular parametric survival model is the accelerated failure time (AFT) model [11]. The AFT model assumes failure time is accelerated by some constant. For example, it is known that dogs become older seven times faster than human beings, and the probability of one dog surviving t years is equivalent to that of one human surviving 7t years [12]. Nonparametric models assume no distributions for the survival time. The survival function can be empirically estimated by the Kaplan–Meier [13], Nelson–Aalen estimator [14], or Life-Table [15] methods. Semiparametric methods do not require the knowledge of the distribution of the time to event. The Cox regression model [16] is the most popular semiparametric method. Wang et al. (2017) [10] have provided a comprehensive survey of both the statistical and machine-learning-based survival analysis methods.
In recent years, many machine-learning-based survival analysis models have been developed to complement the traditional statistical survival models [10]. Ensemble trees have been one of the most interesting base machine learning algorithm families for survival analysis because of their generally good performance in handling nonlinear relationships. The random survival forest (RSF) is another widely cited random forest model that can work with right-censored data [17]. This work defined a new predictive outcome called ensemble mortality. Bayesian additive regression trees (BART) [18] are a nonparametric “sum-of-trees” model constructed based on a fully Bayesian approach. Sparapani et al. (2016) [19] created a nonparametric survival analysis model in a discrete-time fashion based on the BART model. In their work, the survival analysis problem has been handled by transforming into a regular binary classification problem. Bonato et al. (2011) [20] modified the BART model further based on three classical statistical survival models and created an ensemble-based proportional hazards regression model, an ensemble-based Weibull regression model, and an ensemble-based AFT model.
Kernel learning models are another popular candidate for survival analysis. Support vector machines (SVM) were extended to support survival analysis by regression and ranking approaches [21]. In the regression problem, the censored data is handled by modifying the loss function [22,23]. In addition to that, relevance vector machines (RVM) have been extended to support parametric survival analysis based on the Weibull AFT model [24]. The classical SVM algorithm can only make point predictions without reporting predictive distributions for future observations. As a result, the uncertainty of the predictions is not known. To address this issue, RVM was developed as a probabilistic alternative of SVM [25]. By estimating prior parameters with type II maximum likelihood, RVM can deliver posterior distributions with Bayesian inference. However, this is not a fully Bayesian approach and the inferences might be unreliable. To address this issue, hierarchical Bayes SVM and hierarchical Bayes RVM [26,27] have been developed based on reproducing kernel Hilbert space (RKHS) [28] methodology under a complete Bayesian framework [26,27]. By using a similar approach, Maity et al. (2011) [29] performed a fully Bayesian analysis of proportional hazards (PH) regression based on SVM and RVM by using RKHS. Where the functional form of the baseline hazard function [30] was specified by a nonparametric Bayesian approach. Bayesian additive regression kernels (BARK) is a fully Bayesian kernel learning method, which was developed by using the symmetric α-stable (SαS) Lévy random field to induce the prior distribution [26]. Compared with classical SVM and RVM, BARK does not restrict the number of kernel functions and supports simultaneous feature selection through soft shrinkage and hard shrinkage.
The electronic health record (EHR) is a comprehensive electronic medical history which longitudinally records patients’ demographics, vital signs, medications, laboratory data, procedures, diagnoses, clinical notes, and other information pertaining to hospital encounters [31]. Compared with traditional medical data sets accumulated by recruiting patients, EHR data can provide a larger number of subjects and conditions [32]. Survival analysis has seen many applications in the studies of EHR data because subjects may lose follow-up or die [32].
In this work, a survival kernel learning model (sBARK) was developed based on the BARK (Bayesian additive regression kernel) model to analyze the 30-day hospital readmissions extracted from EHR data. sBARK is a fully Bayesian survival model fitted by MCMC. The survival time is assumed to be based on the covariates and a baseline survival time. The inherent features of BARK, such as the support of feature selection and the unrestricted number of kernels, make sBARK more flexible than other survival kernel learning algorithms. The remaining part of this paper is organized as follows. Section 2 discusses the theoretical background and the fitting method of sBARK. The evaluations on the simulated data and a standard benchmark data are detailed in Section 3. Section 4 is dedicated to solving the 30-day hospital readmission prediction based on our sBARK model. In Section 5, we provide our detailed discussion along with the future possibilities and extensions.
2. Bayesian Additive Regression Kernel Model for Survival Outcome
In this study, we state the survival analysis problem as the prediction of the survival time for a subject i, represented by is the vector of predictor variables of size p and is the indicator of whether the instance is censored or not [10]. is the observed time and can be represented as, where is the survival time for an uncensored instance and is the survival time for a censored instance. The goal is to estimate the time to event for a new instance i given . The survival analysis problem can also be understood as the study of survival probability as a function of time. Figure 1 shows an example of right censoring.
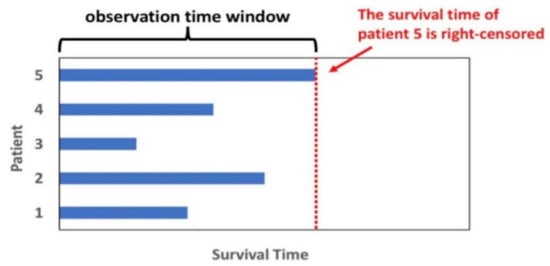
Figure 1.
Subject’s survival status within an observation time window. Subject #5 survives at the end of the observation and the data is missing outside the monitor window (right-censored).
2.1. A Quick Background of Bayesian Additive Regression Kernels (BARK)
In this section, we give a quick overview of the BARK method, which is the cornerstone of our kernel-based nonparametric survival analysis model. In the BARK algorithm [26] models, the observed covariates and responses are expressed as the sum of weighted kernel functions , where is the kernel regression coefficient, is the kernel location parameter, and is the independent additive Gaussian noise. The number of kernel functions J is not fixed and needs to be learned. In addition to that, a Gaussian kernel function is adopted with and independent scale parameter for each predictor variable. The full BARK model can be written as follows:
where:
- -
- : observed covariate vectors in .
- -
- : responses.
- -
- : regression coefficient.
- -
- : kernal location parameter in X.
- -
- : independent additive Gaussian noise.
The Gaussian kernel function was used in the original BARK construction [26] by assigning a scale parameter for each predictor variable. The Gaussian kernel function has the following form:
where:
- -
- : the scale parameter, which measures the contribution of the lth variable in the kernel function.
- -
- : no contribution made by the lth variable through the kernel function.
- -
- is large: the lth variable is important in the kernel function.
2.1.1. Use of Symmetric α-Stable (SαS) Lévy Random Field as Prior Distribution on the Mean Function f(x)
The unknown mean function f(x) can be represented as a stochastic integral of a kernel function with respect to a random signed measure.
where:
- -
- : the random signed measure.
Putting a prior distribution on the mean function f(x) is exactly the same as putting a prior on the above random signed measure. To be noted here, the linear mapping from an L2 (square integrable) function to random variables by a random measure is called a random field. One such specific random field is the symmetric α-stable (SαS) Lévy random field defined by the (SαS) Lévy measure [26] as:
where:
- -
- .
- -
- the probability measure on X.
- -
- : the stable index.
- -
- : the intensity parameter.
The above SαS Lévy random measure was used to induce the joint prior distribution for the number of kernels , regression coefficient and kernel parameter . Because the SαS Lévy random measure is not finite, two methods were used for approximation. The first method approximated it by truncation of with respect to a given threshold and had a finite mass as:
The second method is based on continuous approximation and had a finite mass as:
2.1.2. Automatic Feature Selection in BARK
Suppose the prior distribution for the sum of all s is , which is indefinitely divisible. Here, and are the shape parameter and scale parameter of Gamma distribution, respectively. There are four types of feature selections that are automatically built into the BARK structure, as mentioned in [26]. They are as follows:
- Equal weights: All kernel scale parameters are the same and follow the same Gamma distribution as:
- Different weights: All kernel scale parameters are different, and each follows a different Gamma distribution as:
- Equal weights with hard shrinkage and selection: Introduce a vector to indicate if a variable is selected or not. Each indicator follows a Bernoulli distribution. If the indicator is 1, the corresponding Note that here all selected kernel scale parameters are the same as in Equal weights.
- Different weights with hard shrinkage and selection: Exactly the same formulation as in 3, however, each selected kernel scale parameter has its own Gamma distribution where d is the number of nonzero kernel scale parameters.
2.1.3. Likelihood and the Posterior Distribution
Under continuous response with normal error explained in the beginning of Section 2.1, our likelihood of the training set can be written as:
where:
- -
- K: the kernel matrix, with .
Apart from the feature selection prior and the α-stable (SαS) Lévy random field prior, we also put a noninformative prior on ϕ as .
By Bayes rule, the full posterior distribution can be written as:
For a new observation at x*, the posterior predictive distribution for y* can be written as:
In the next section, we extend the above-mentioned BARK modeling architecture for a right-censored survival time data set.
2.2. Nonparametric Survival Analysis with BARK
The implementation of nonparametric survival BARK is based on the data modification method discussed in [19]. There is no assumption about the distribution of the time to event and we put no functional restriction on the proportional hazard structure. Here, we handle the survival analysis problem in a discrete-time fashion by converting into a binary classification problem [19], which can then be directly modelled by BARK and the help of latent variable data augmentation.
2.2.1. Data Transformation Method: Converting Right-Censored Data to Binary Classification
Let us consider the survival data with the following form: , Where : covariates of subject ; : the event/censoring time of subject ; and : the indicator of status of subject : 1—event, 0—right-censoring.
For subjects, there can be distinct events and censoring times. Because two different subjects can have the same event or censoring times, . Order the distinct event and censoring times as:
Then, for each subject , use a new binary indicator to indicate the status at each distinct time up to and including the subject’s original observation time . In other words, each subject has a series of binary indicators to indicate its status at all discrete time points earlier than (inclusive) the original observation time . That means = 0 for all j before the last indicator as the original observation time does not match with the ordered distinct time . Note that the last indicator in the series is the original status indicator .
For example, suppose there are three subjects in a dataset as follows: ’s are omitted because they are not directly involved in the data transformation.
Order the distinct event/censoring times and obtain:
For the subject 1, its observation time is the second place in the ordered distinct event and censoring times. It has two binary indicators and to represent its status at time and : . For the instance 2, its observation time is the first place in the ordered distinct event and censoring times. It has one binary indicator to represent its status at time : . For the instance 3, its observation time is the third place in the ordered distinct event and censoring times. It has three binary indicators , and to represent its status at time and : . Note that because it is right-censored at . In this way, the original dataset with three instances can be transformed into a dataset with six records. The time is used as a new covariate together with the original covariates . Figure 2 shows the full transformation result for this example.

Figure 2.
Transform the original survival dataset into a binary classification dataset.
2.2.2. Bayesian Additive Kernel-Based Survival Model for the Transformed Data (sBARK)
Based on our data transformation method discussed before, we transformed our right-censored survival outcome data to binary outcome data. Here, we formulate a BARK model to handle the binary data based on data augmentation by [33,34]. Our hierarchical BARK model with data augmentation is given as below:
where:
- -
- : the probability of an event at time given no previous event for instance .
- -
- : the probit link function.
- -
- : the predicted event status.
- -
- : the baseline, which equals to 0 for centered outcome.
- -
- : truncated normal latent variable.
- -
- : the nonlinear function that connects the binary response with the set of predictors. The f function [35] is modeled nonparametrically using the BARK architecture discussed previously in detail.
Please note that after our data transformation method as described in Section 2.2 and in Figure 2, we can write the model for yij as a nonparametric probit regression of yij on the time t(j) and the covariates xi [36], and then utilize the Albert–Chib (1993) truncated normal latent variables zij to reduce it to the continuous outcome BARK model of Equations (1)–(3) applied to z’s. That is why, in Equation (10), f() is a function of time t(j) and the covariates xi. The in Equation (10) means [37] follows the same BARK architecture as explained in Equation (3) in Section 2.1. However, now the new covariate vector is x* = (t, x).
The survival function at the discrete time points is given by (for details see [38,39,40])
where
The drawings of posteriors after burning in were used to create the survival function. For the sake of simplicity, we call our above-described BARK survival model sBARK or survival BARK.
2.3. MCMC Algorithm to Fit sBARK
Because the integral of the posterior distribution is analytically intractable, the MCMC method is used to fit our sBARK model. The full MCMC process is shown below:
- Sample the latent variables conditional on all other parameters from the truncated normal distribution described in (10). The truncation scheme is based on the value of described above in (10). The truncated normal distribution has mean which is based on the posterior sample of from BARK output and variance is 1.
- Update all parameters of BARK architecture with the MCMC process built in the BARK algorithm. The full MCMC scheme to generate the BARK parameters are documented in detail in [26] and in https://github.com/merliseclyde/bark, accessed on 20 November 2019.
- The zij’s are centered around a known constant µ0, which is equivalent to centering the probabilities pij around p0 = Φ(µ0). By default, we set µ0 = 0, which means pij are centered around 0.5.
2.4. Prior and MCMC Parameter Selection for sBARK
In all our simulation studies and real data analysis in our sBARK model, we set . These choices of prior parameters ensure that our prior is near-diffuse, but the posterior is a proper density. For automatic variable selection, we use the Option 4: different weights with hard shrinkage and selection prior with Bernoulli parameter set to 0.20. In all our simulation studies and real data analysis, we ran MCMC chain with 200,000 iterations and used the first 100,000 as burn in. To reduce autocorrelation, we keep every 5th draw. All our MCMC chain convergences are verified via inspection of trace plots and running the Gelman–Rubin diagnostic [34]. For the survival BART, we used 200 trees with near-diffuse prior settings exactly as suggested in [19]. For survival BART, we generated 200,000 MCMC iterations with the first 100,000 as burn in.
3. Simulation Study and a Benchmark Real Data Analysis
In this section, we conduct a simulation study and we also apply our model to a standard right-censored survival outcome data: the kidney catheter data [27].
3.1. Simulated Data
One simulated data set is created to test sBARK’s performance. The simulation was performed with the simple.surv.sim() function in the “survsim” package [35] in R. In this simulation, 80 cases are generated. The maximum observation time is set to be 365 days. The time to event follows a log-normal distribution. Each subject has seven covariates, with each following a standard normal distribution. The mean function of the log-normal distribution is given by . The simulated dataset has a total of 12 attributes, including the instance id “nid”, the observation start time “start”, the observation end time “stop”, the status indicator “status” (1: event, 0: censored), the individual heterogeneity “z”, and seven covariates. Of the 80 instances, 20 are censored. We chose to conduct the simulation study with 80, as in a typical data set we are often restricted to small samples. Traditionally, with machine learning models, they always tend to perform better with large data volume, but it is always a challenge working with reasonably small data. So, we showed our model can work well even with a small sample size. In Figure 3, we report the estimated survival function based on popular survival models such as Kaplan–Meier, survival Bayesian additive regression tree (BART), and our survival BARK or sBARK model. We can see clearly that our sBARK is equally effective in estimating the underlying survival probability curve. To be noted here is that the role of our Figure 3 is not to show better performance of sBARK but to validate that based on Equation (11) our sBARK model can also estimate the survival curve. The survival curve produced by our sBARK is like the ones provided by Kaplan–Meier and the survival BART. The point we are trying to make through Figure 3 is that our sBARK was implemented by transforming the survival analysis problem into a regular binary classification problem, which then handled by BARK architecture can retrieve/estimate the underlying survival curve/function as accurately as Kaplan–Meier and the survival BART. In Table 1 we list the root mean square error (RMSE) based on 5-fold cross-validation of our simulated data based on survival BARK, survival BART [19], and the more traditional Cox proportional hazards model [16]. From Table 1, it is clearly seen that our survival BARK model’s root mean square error across all included time points is always lower than its closest competitor, the survival BART. In the BART package/model, which is the main competitor of our sBARK model, the authors used the traditional RMSE formula with the original survival predicted outcome, which can be calculated using our Equation (11). We also adopted the same approach for the calculation in all reported RMSE calculations. The censoring information is implicitly taken into account in the construction of the survival function at the discrete time points. Like in our main competitor survival BART, in our sBARK calculation of RMSE we did not carry out anything additional to it for censored times.
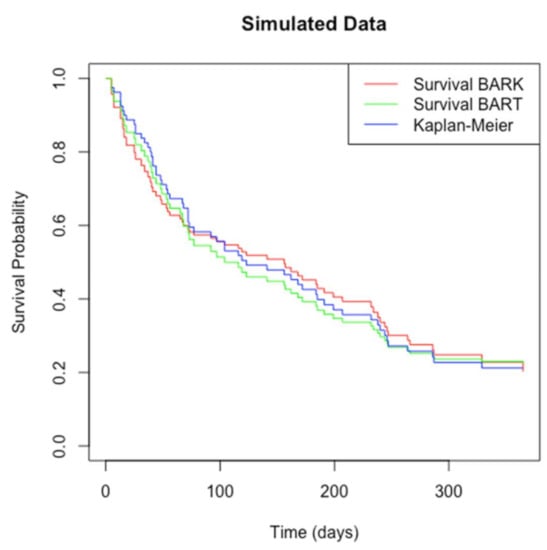
Figure 3.
Estimated survival probability curves for the simulated dataset by nonparametric survival BARK, survival BART, and Kaplan–Meier method.

Table 1.
RMSE from 5-fold cross-validation performance of Survival BARK, Survival BART, and Cox-PH Model on the simulated dataset.
3.2. Benchmark Data Analysis with Kidney Catheter Data
In this section, we demostrate the performance of our survival BART with respect to the kidney catheter data [36]. This data is available in the “survival” package [37] in R and has been widely used as a benchmark. The data set records the recurrence of infection in patients who are using a portable dialysis machine. The infection may occur when the catheter is inserted. In this case, the catheter must be removed from the patient. It can be re-inserted only after the infection has been treated. The recurrence time is the time from the insertion until the next infection. This data is right-censored because the catheter may be removed for other reasons. This data has 76 instances and seven attributes, including patient ID, survival time, status indicator (1: event, 0: censored), age, sex, disease type, and estimated frailty. Of the 76 instances, 18 are censored. Figure 4 shows the survival probability as a function of time (days) obtained by the nonparametric survival BARK, the nonparametric survival BART, and the Kaplan–Meier estimator on the kidney catheter dataset. The Kaplan–Meier method only considers the event time when constructing the survival function curve. The survival BARK and survival BART take both event time and covariates into consideration when estimating the survival probability. Using the Kaplan–Meier curve as a baseline, it can be seen that the survival probability estimated by the nonparametric survival BARK tends to be higher over time. The survival curve by the nonparametric survival BART is closer to the Kaplan–Meier curve, and the survival probability tends to be lower. Moreover, from Table 2, it is clearly demonstrated that our survival BARK has completely outperformed its best contender survival BART and traditional models such as the Cox proportional hazards model.

Figure 4.
Estimated survival probability curves for the kidney catheter dataset by survival BARK, survival BART, and Kaplan–Meier method.

Table 2.
RMSE from 5-fold cross-validation performance of Survival BARK, Survival BART, and Cox-PH Model on the kidney catheter dataset.
4. Analysis of 30-Day Hospital Readmission Data
The 30-day hospital readmission data was obtained from Medical Information Mart for Intensive Care (MIMIC III), a public accessible deidentified EHR database of critical care encounters at the Beth Israel Deaconess Medical Center between 2001 and 2012 (https://mimic.mit.edu/ (accessed on 20 November 2019)) [38]. It contains 58,977 encounters of 46,521 unique patients. A total of 43,407 encounters are unplanned (emergency or urgent). To be eligible as a readmission, the encounter needs to meet the following criteria: (1) the patient has to be older than 18 at the time of index admission; (2) the patient does not expire during the index admission or after discharge from the index admission; (3) the gap between index admission and readmission is between one day and 30 days; and (4) ff a patient has more than one eligible index admission–readmission episode, only the latest episode is kept. Of the 43,407 unplanned encounters, 1434 eligible index admission–readmission episodes were identified. Another 1434 admissions with censored outcome (not readmitted within 30 days) were randomly sampled from the remaining unplanned encounters to balance the data set. The data set has 45 attributes including patients’ socio-demographics information (age, sex, religion, marital status, ethnicity, and insurance), index admission type, index admission length of stay, index admission discharge disposition, minimum/mean/maximum of vital signs before discharge (heart rate, systolic blood pressure, diastolic blood pressure, and respiratory rate), and minimum/mean/maximum of laboratory test results before discharge (hemoglobin, serum sodium, magnesium, calcium, glucose, urea, creatinine, platelet count, and white blood cell count). Categorical variables were transformed into dummy variables, and as a result, the number of attributes increased to 85. Cases with missing values and outliers (greater than three times the standard deviation) in any attribute were removed. The cleaned data set has 1228 censored cases and 1307 uncensored cases.
In Table 3, we summarized our findings with respect to our survival BARK model and its competitors. In terms of out-of-sample prediction from Table 3, we observe that our survival BARK does at least 2 times better than its competitors in an early prediction model of readmission by incorporating detailed medical history such as diagnoses, procedures, medications, lab test results, vital signs, and healthcare utilization. In Figure 5, we report the posterior probability plot for each of the predictors for the purpose of variable selection. In this paper, we adopted a posterior probability threshold of 0.50, and from Figure 5 we see that out of 85, 10 variables are selected based on the 0.50 probability threshold. Based on our survival BARK model, the 10 selected predictors for 30-day hospital readmission are minimum heart rate, minimum respiratory rate, minimum urea content, Medicaid status, Medicare status, marital status, white race, long-term care status, age group 50 to 64, and age group 65 to 79.

Table 3.
RMSE from 5-fold cross-validation performance of Survival BARK, Survival BART, and Cox- PH Model on the 30-day Hospital Readmission Data.
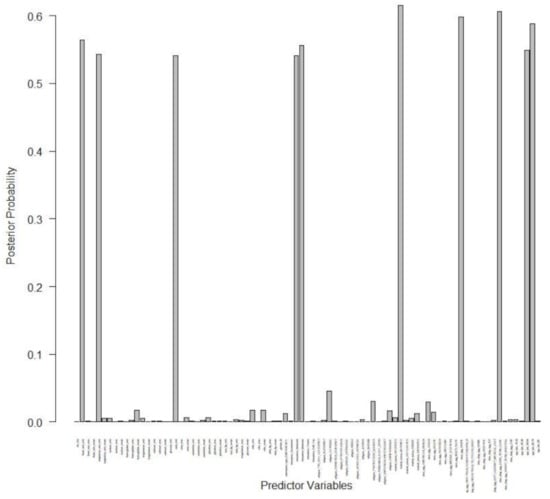
Figure 5.
Posterior probability plot for the 30-day hospital readmission data.
5. Conclusions
Modelling of 30-day hospital readmission has been a popular research topic in recent years. Although survival analysis is more appropriate than traditional binary classification methods in this scenario, very few studies have treated readmission prediction as a survival analysis problem. In this paper, we developed a kernel-based machine learning method for readmission predictions. Our developed survival BARK or sBARK model supports survival analysis based on flexible kernel machines. The sBARK, which is based on a kernel machine learning model, has the flexibility of nonlinear methods. Our survival BARK has been implemented in a discrete-time fashion. The dataset is restructured to transform the survival analysis problem into a regular binary classification problem, which can be handled by BARK. In the restructured data, the binary response variable indicates the status at each distinct time up to and including the instance’s original observation time. The distinct discrete time points before and including the instance’s observation time are used as a new predictor attribute in BARK. In addition to that, Equation (11) provides a direct way to calculate the survival curves based on our sBARK model. The survival probability curves of the two datasets estimated by survival BARK and the survival BART have similar trends. In all simulation studies and benchmark data analyses, and on the real-life 30-day hospital readmission data, our survival BARK has convincingly outperformed its other nonlinear tree-based competitor survival BART with respect to prediction performance.
BARK can also be extended based on other survival analysis models, such as the parametric Weibull model and the semiparametric Cox proportional hazards model. Moreover, there is huge potential to make our survival BARK work with big data scenarios such as electronic health record data, which is in the order of hundreds of millions. However, to make our survival BARK model scalable for such big data sets, we need to modify the sBARK algorithm to optimize its time and space complexity. Along with that, the searching and ordering steps also require to be further optimized. It is also possible to parallelize the computations by taking advantage of multicore processors. It can also be ported to the Spark environment to allow for more flexible computing resource management. These are some of our potential directions of work for future extensions.
Author Contributions
Conceptualization, S.C. and P.Z.; methodology, S.C.; software, P.Z.; validation, S.C., T.D. and P.Z.; formal analysis, S.C. and P.Z.; data curation, P.Z.; writing—original draft preparation, S.C., P.Z., Y.H. and T.D.; writing—review and editing, S.C., P.Z., Y.H. and T.D.; visualization, S.C., P.Z., Y.H. and T.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not Applicable.
Data Availability Statement
https://mimic.mit.edu/ (accessed on 7 June 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Readmissions Reduction Program (HRRP). Available online: https://www.cms.gov/medicare/medicare-fee-for-service-payment/acuteinpatientpps/readmissions-reduction-program.html (accessed on 20 November 2019).
- Hospital Quality Initiative—Outcome Measures 2016 Chartbook. Available online: https://www.cms.gov/Medicare/Quality-Initiatives-Patient-Assessment-Instruments/HospitalQualityInits/OutcomeMeasures.html (accessed on 20 November 2019).
- Jencks, S.F.; Williams, M.V.; Coleman, E.A. Rehospitalizations among Patients in the Medicare Fee-for-Service Program. N. Engl. J. Med. 2009, 360, 1418–1428. [Google Scholar] [CrossRef] [PubMed]
- Weissman, J.S.; Ayanian, J.Z.; Chasan-Taber, S.; Sherwood, M.J.; Roth, C.; Epstein, A.M. Hospital Readmissions and Quality of Care. Med. Care 1999, 37, 490–501. [Google Scholar] [CrossRef] [PubMed]
- Polanczyk, C.A.; Newton, C.; Dec, G.W.; Di Salvo, T.G. Quality of care and hospital readmission in congestive heart failure: An explicit review process. J. Card. Fail. 2001, 7, 289–298. [Google Scholar] [CrossRef]
- Luthi, J.-C.; Lund, M.J.; Sampietro-Colom, L.; Kleinbaum, D.G.; Ballard, D.J.; McClellan, W.M. Readmissions and the quality of care in patients hospitalized with heart failure. Int. J. Qual. Health Care 2003, 15, 413–421. [Google Scholar] [CrossRef] [PubMed]
- Boccuti, C.; Casillas, G. Aiming for Fewer Hospital U-turns: The Medicare Hospital Readmission Reduction Program. Policy Brief. 2017, 1–10. [Google Scholar]
- Kansagara, D.; Englander, H.; Salanitro, A.; Kagen, D.; Theobald, C.; Freeman, M.; Kripalani, S. Risk prediction models for hospital readmission: A systematic review. JAMA 2011, 306, 1688–1698. [Google Scholar] [CrossRef]
- Miller, R.G. Survival Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Wang, P.; Li, Y.; Reddy, C.K. Machine Learning for Survival Analysis: A Survey. arXiv 2017, arXiv:1708.04649. Available online: https://arxiv.org/abs/1708.04649 (accessed on 28 February 2020).
- Klein, J.P.; Moeschberger, M.L. Survival Analysis: Techniques for Censored and Truncated Data, 2nd ed.; Springer: New York, NY, USA, 2003; Volume 9, pp. 302–308. [Google Scholar]
- Dätwyler, C.; Stucki, T. Parametric Survival Models. 2011. Available online: http://stat.ethz.ch/education/semesters/ss2011/seminar/contents/handout_9.pdf (accessed on 15 February 2020).
- Kaplan, E.L.; Meier, P. Nonparametric Estimation from Incomplete Observations. J. Am. Stat. Assoc. 1958, 53, 457. [Google Scholar] [CrossRef]
- Andersen, P.K.; Borgan, O.; Gill, R.D.; Keiding, N. Statistical Models Based on Counting Processes; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Cutler, S.J.; Ederer, F. Maximum Utilization of the Life Table Method in Analyzing Survival. In Annals of Life Insurance Medicine; Springer: Berlin/Heidelberg, Germany, 1964; pp. 9–22. [Google Scholar]
- Cox, D.R. Regression Models and Life-Tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–220. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random survival forests. Ann. Appl. Stat. 2008, 2, 841–860. [Google Scholar] [CrossRef] [PubMed]
- Chipman, H.A.; George, E.I.; McCulloch, R.E. BART: Bayesian additive regression trees. Ann. Appl. Stat. 2012, 6, 266–298. [Google Scholar] [CrossRef]
- Sparapani, R.; Logan, B.R.; McCulloch, R.E.; Laud, P.W. Nonparametric survival analysis using Bayesian Additive Regression Trees (BART). Stat. Med. 2016, 35, 2741–2753. [Google Scholar] [CrossRef] [PubMed]
- Bonato, V.; Baladandayuthapani, V.; Broom, B.M.; Sulman, E.P.; Aldape, K.D.; Do, K.-A.; Anh, K. Bayesian ensemble methods for survival prediction in gene expression data. Bioinformatics 2010, 27, 359–367. [Google Scholar] [CrossRef] [PubMed]
- Van Belle, V.; Pelckmans, K.; Van Huffel, S.; Suykens, J.A.K. Support vector methods for survival analysis: A comparison between ranking and regression approaches. Artif. Intell. Med. 2011, 53, 107–118. [Google Scholar] [CrossRef] [PubMed]
- Khan, F.M.; Zubek, V.B. Support Vector Regression for Censored Data (SVRc): A Novel Tool for Survival Analysis. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2008; pp. 863–868. [Google Scholar]
- Shivaswamy, P.K.; Chu, W.; Jansche, M. A support vector approach to censored targets. In Proceedings of the IEEE International Conference on Data Mining, ICDM 2007, Omaha, NE, USA, 28–31 October 2007; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2008; pp. 655–660. [Google Scholar]
- Kiaee, F.; Sheikhzadeh, H.; Eftekhari Mahabadi, S. Relevance Vector Machine for Survival Analysis. In IEEE Transactions on Neural Networks and Learning Systems; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2015; Volume 27, pp. 648–660. [Google Scholar]
- Tipping, M. Sparse Bayesian Learning and the Relevance Vector Mach. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Ouyang, Z. Bayesian Additive Regression Kernels; Duke University: Durham, NC, USA, 2008. [Google Scholar]
- Chakraborty, S.; Ghosh, M.; Mallick, B.K. Bayesian nonlinear regression for large p small n problems. J. Multivar. Anal. 2012, 108, 28–40. [Google Scholar] [CrossRef]
- Aronszajn, N. Theory of reproducing kernels. Trans. Am. Math. Soc. 1950, 68, 337–404. [Google Scholar] [CrossRef]
- Maity, A.; Mallick, B.K. Proportional Hazards Regression Using Bayesian Kernel Machines. In Bayesian Modeling in Bioinformatics; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2011; pp. 317–336. [Google Scholar]
- Kalbfleisch, J.D. Non-Parametric Bayesian Analysis of Survival Time Data. J. R. Stat. Soc. Ser. B 1978, 40, 214–221. [Google Scholar] [CrossRef]
- Electronic Health Records. Available online: https://www.cms.gov/Medicare/E-Health/EHealthRecords/index.html (accessed on 20 November 2019).
- Hodgkins, A.J.; Bonney, A.; Mullan, J.; Mayne, D.; Barnett, S. Survival analysis using primary care electronic health record data: A systematic review of the literature. Health Inf. Manag. J. 2017, 47, 6–16. [Google Scholar] [CrossRef]
- Albert, J.H.; Chib, S. Bayesian Analysis of Binary and Polychotomous Response Data. J. Am. Stat. Assoc. 1993, 88, 669. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Moriña, D.; Navarro, A. The R Package survsim for the Simulation of Simple and Complex Survival Data. J. Stat. Softw. 2014, 59, 1–20. [Google Scholar] [CrossRef]
- McGilchrist, C.A.; Aisbett, C.W. Regression with Frailty in Survival Analysis. Biometrics 1991, 47, 461. [Google Scholar] [CrossRef] [PubMed]
- Therneau, T.; Grambsch, P. Modeling Survival Data: Extending the Cox Model, 1st ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Johnson, A.E.W.; Pollard, T.J.; Shen, L.; Lehman, L.-W.H.; Feng, M.; Ghassemi, M.; Moody, B.; Szolovits, P.; Celi, L.A.; Mark, R.G. MIMIC-III, a freely accessible critical care database. Sci. Data 2016, 3, 160035. [Google Scholar] [CrossRef] [PubMed]
- Fahrmeir, L. Encyclopedia of Biostatistics. Discrete Survival-Time Models; Wiley: Hoboken, NJ, USA, 1998; pp. 1163–1168. [Google Scholar]
- Masyn, K.E. Discrete-Time Survival Mixture Analysis for Single and Recurrent Events Using Latent Variables. Unpublished Doctoral Dissertation, University of California, Los Angeles, CA, USA, 2003. Available online: http://www.statmodel.com/download/masyndissertation.pdf (accessed on 20 April 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).