Comparing the Robustness of the Structural after Measurement (SAM) Approach to Structural Equation Modeling (SEM) against Local Model Misspecifications with Alternative Estimation Approaches
Abstract
1. Introduction
2. Estimation under Local Model Misspecification
2.1. Numerical Analysis of Sensitivity to Model Misspecifications
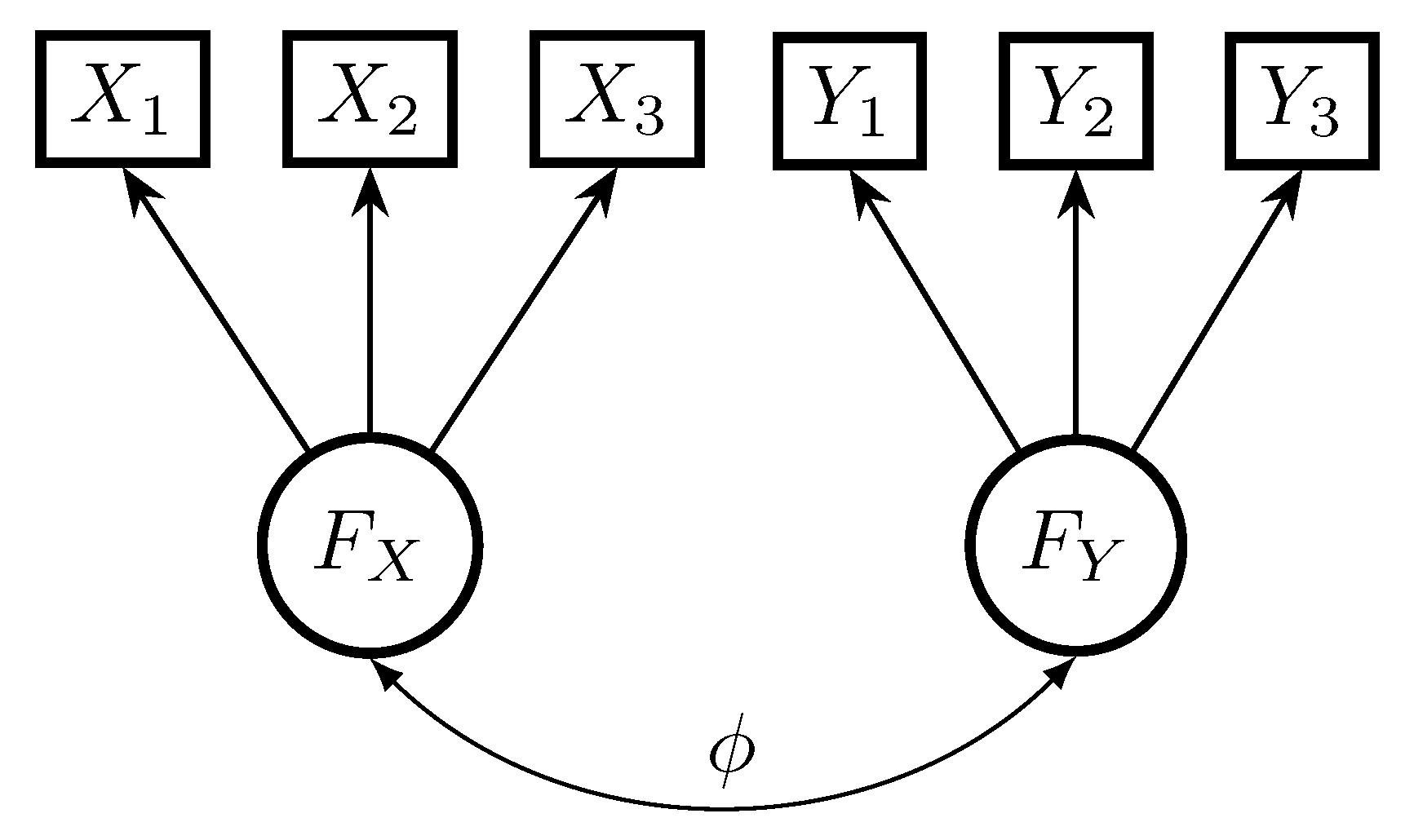
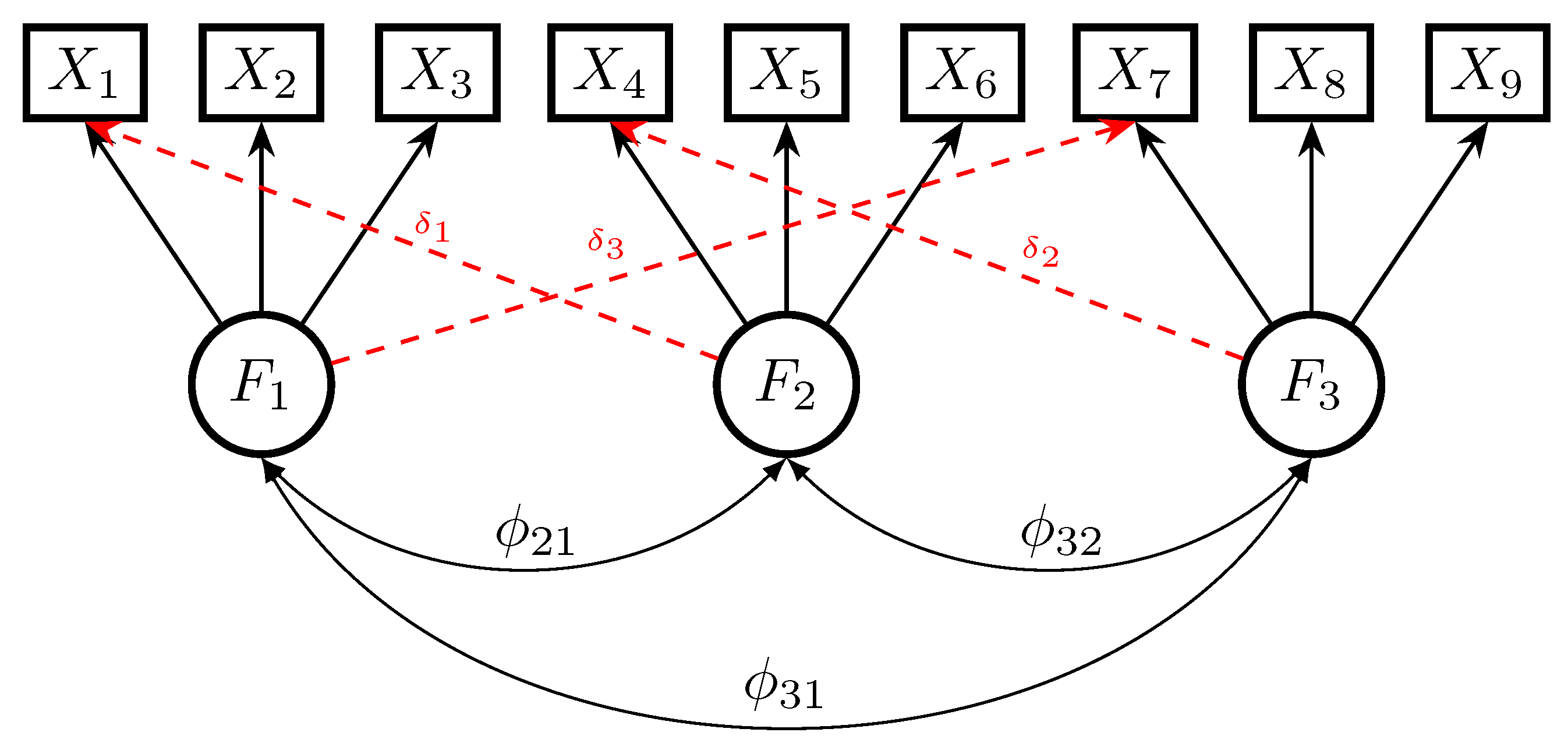
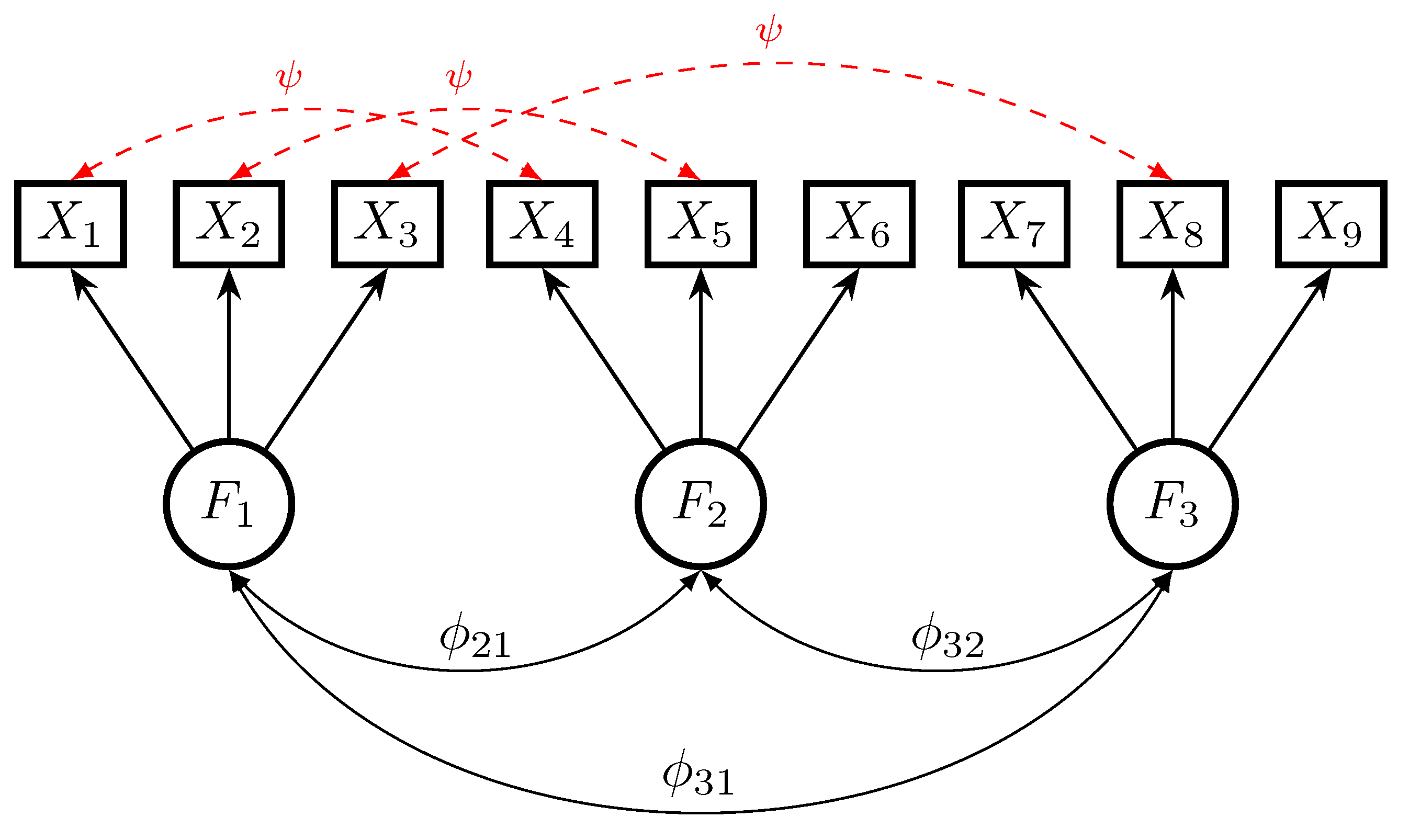
2.2. Two-Factor CFA Model with Local Model Misspecifications
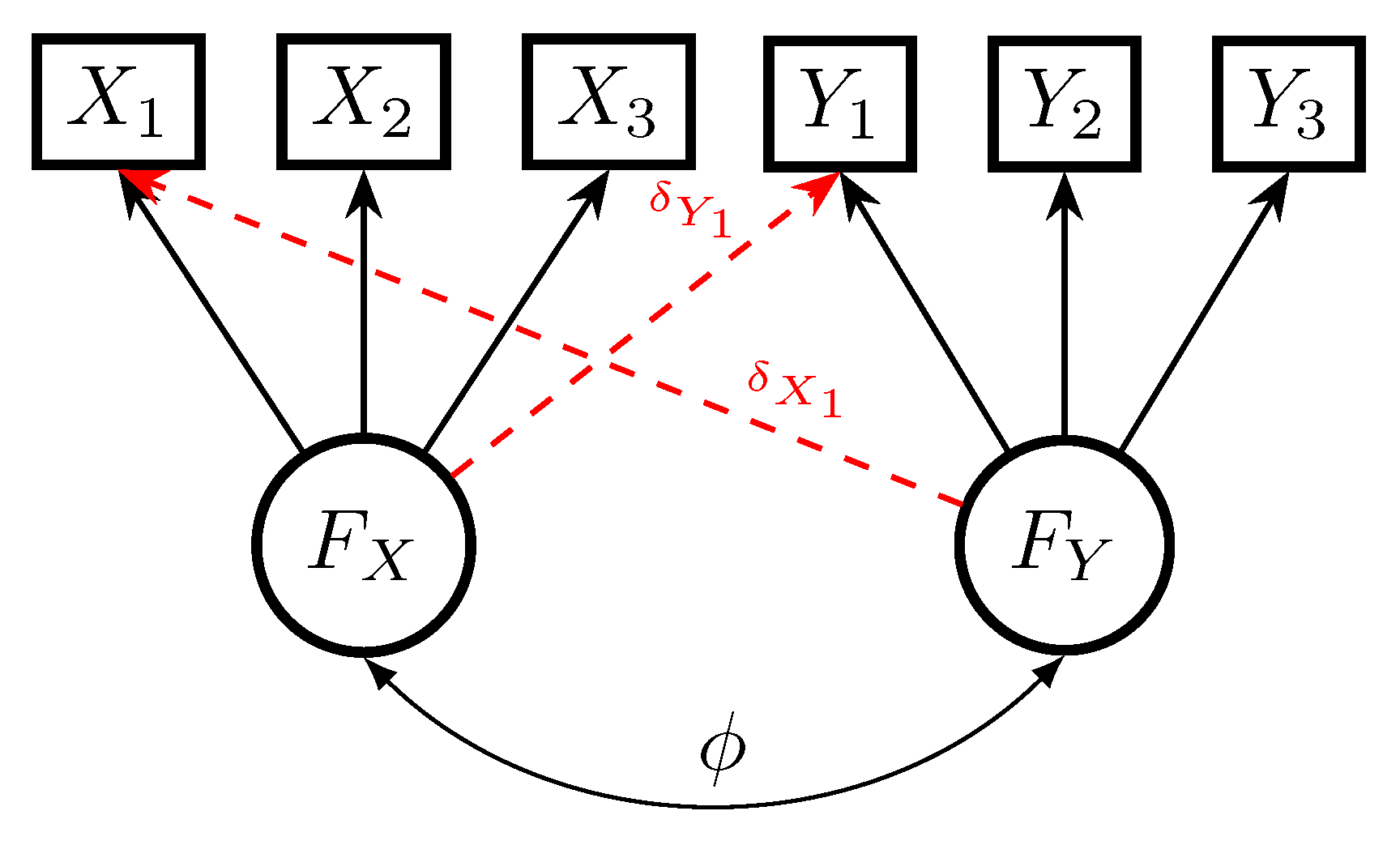
2.3. Nonrobustness of the LSAM Approach
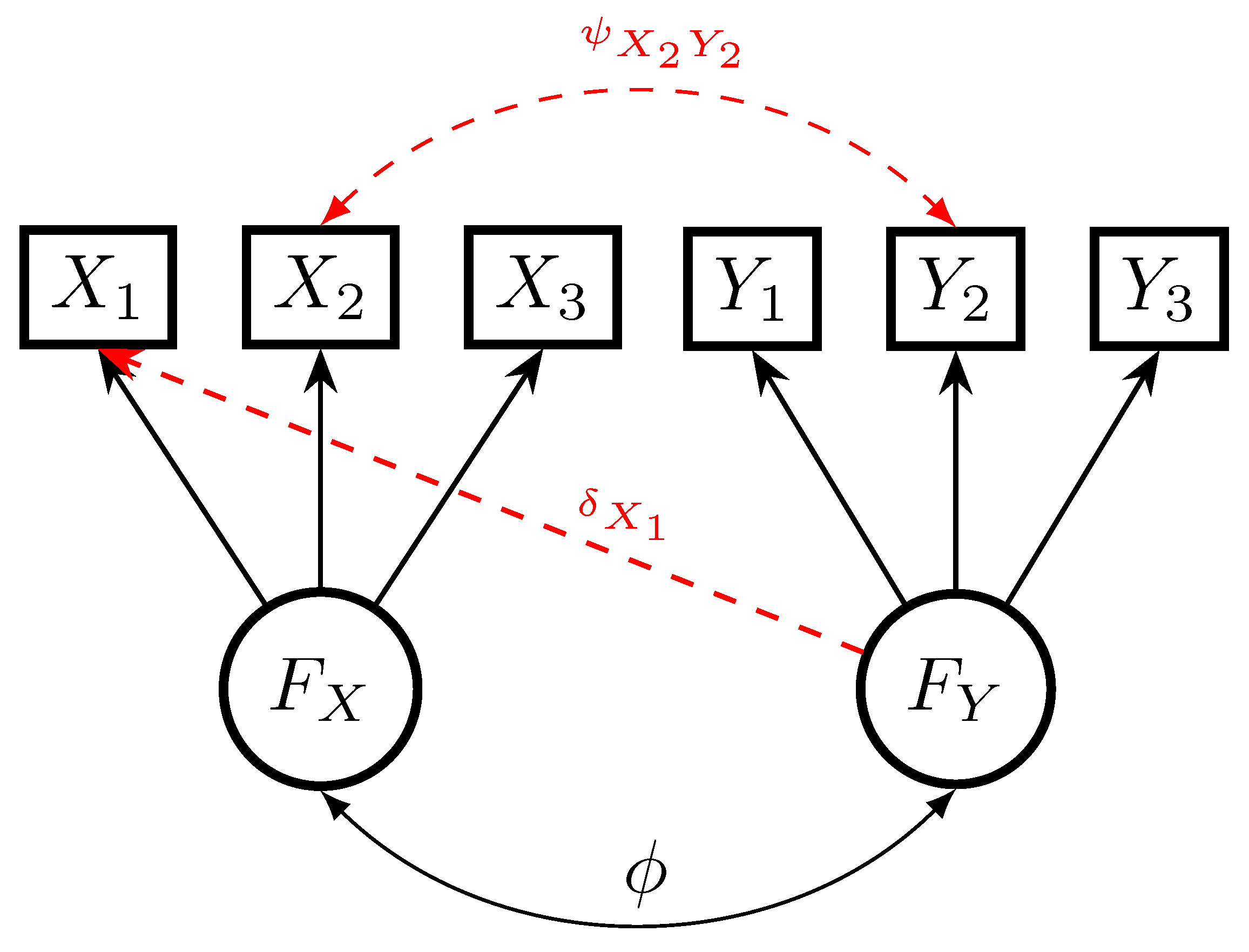
2.4. Comparison of ULS and GSAM in a Congeneric Measurement Model
2.5. Equivalence of ULS and SAM for the Tau-Equivalent Measurement Model
3. Alternative Model-Robust Estimation Approaches
3.1. Robust Moment Estimation (RME)
3.2. GSAM with Robust Moment Estimation (GSAM-RME)
3.3. Factor Rotation with Thresholding the Error Correlation Matrix
4. Simulation Studies
4.1. Simulation Study 1: Correlated Residual Errors in the Two-Factor Model
4.1.1. Method
4.1.2. Results
4.1.3. Focused Simulation Study 1A: Choice of Model Identification
4.1.4. Focused Simulation Study 1B: Investigating the Small-Sample Bias of LSAM
4.1.5. Focused Simulation Study 1C: Bootstrap Bias Correction of the LSAM Method
4.2. Simulation Study 2: Cross Loadings in the Two-Factor Model
4.2.1. Method
4.2.2. Results
4.3. Simulation Study 3: Correlated Residual Errors and Cross Loadings in the Two-Factor Model
4.3.1. Method
4.3.2. Results
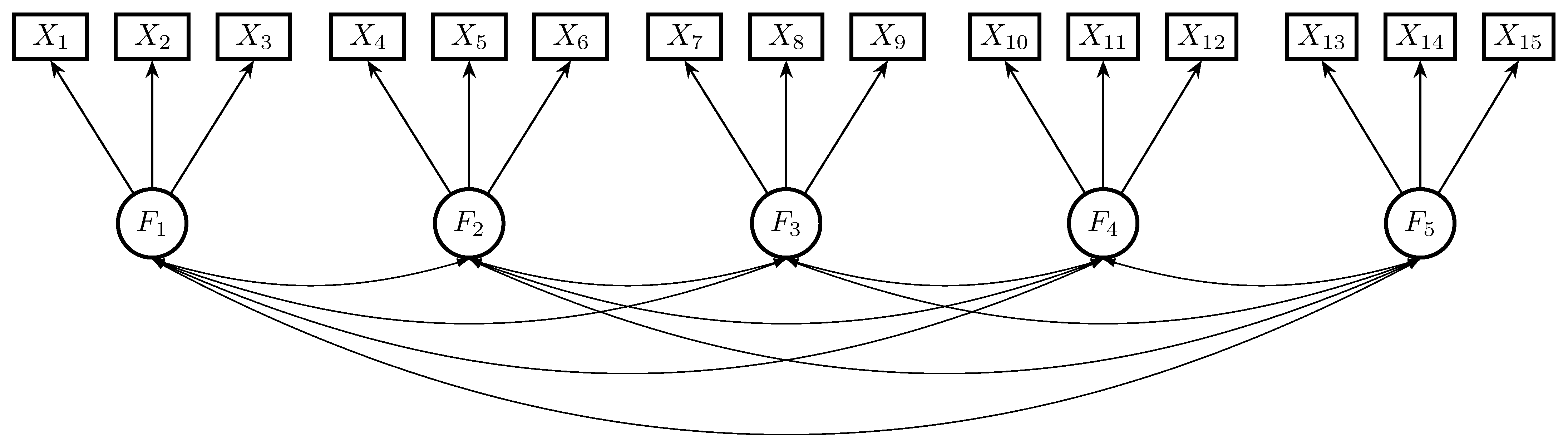
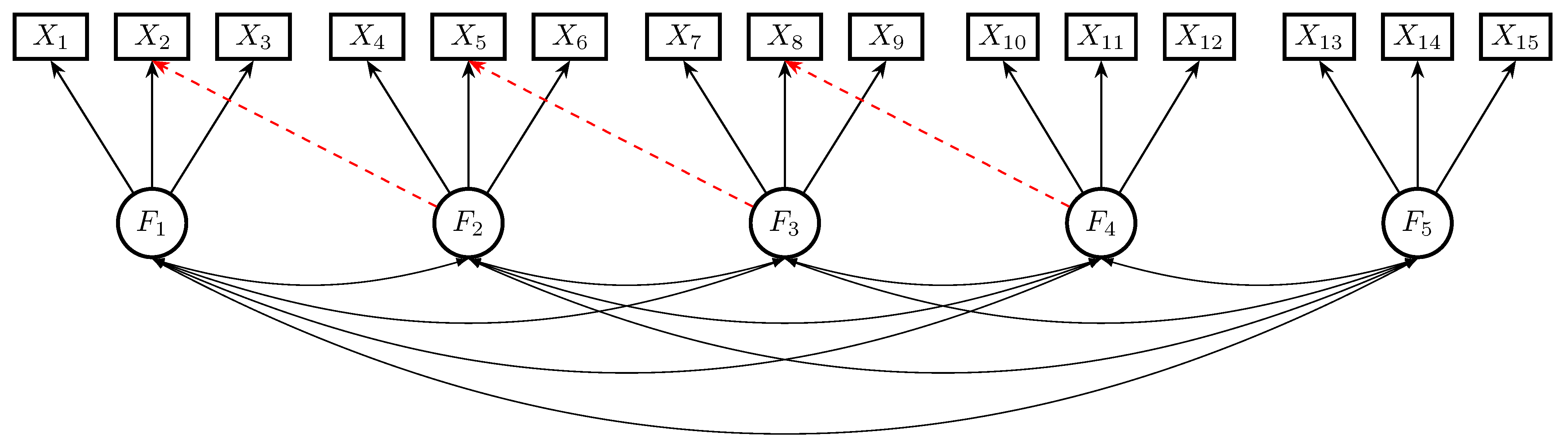
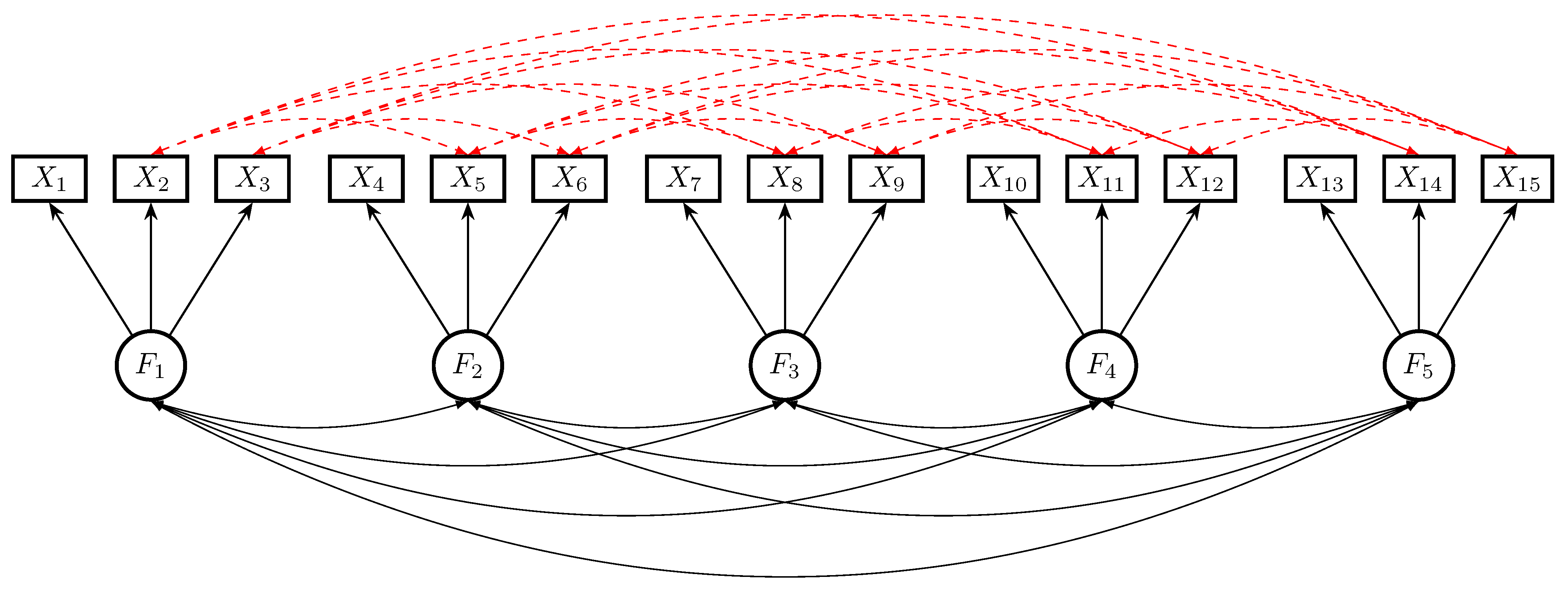
4.4. Simulation Study 4: A Five-Factor Model Very Close to the Rosseel-Loh Simulation Study
4.4.1. Method
4.4.2. Results
4.4.3. Focused Simulation Study 4A: Varying the Size of Factor Correlations
4.5. Simulation Study 5: Comparing SAM and SEM in a Three-Factor Model with Cross Loadings
4.6. Simulation Study 6: Comparing SAM and SEM in a Three-Factor Model with Residual Correlations
5. Discussion
5.1. Regularized Estimation and Misspecified Models
5.2. Why the SAM Approach Should Generally Be Preferred over SEM
5.3. Why We Do Not Bother about a Violation of Measurement Invariance Due to Model Misspecifications
5.4. Why We Should Not Rely on a Factor Model in Two-Step SEM Estimation
5.5. Why We Should Model Errors Report as Additional Parameter Uncertainty
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BBC | bootstrap bias correction |
| CFA | confirmatory factor analysis |
| EFA | exploratory factor analysis |
| GSAM | global stuctural after measurement |
| LSAM | local stuctural after measurement |
| ML | maximum likelihood |
| RL | Rosseel and Loh |
| RME | robust moment estimation |
| RMSE | root mean square error |
| SAM | stuctural after measurement |
| SCAD | smoothly clipped absolute deviation |
| SD | standard deviation |
| SEM | stuctural equation model |
| ULI | unit loading identification |
| UVI | unit latent variance identification |
| ULS | unweighted least squares |
Appendix A. Additional Results for Simulation Studies
| Bias | RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | 100 | 250 | 500 | 1000 | 2500 | 100 | 250 | 500 | 1000 | 2500 | ||
| One negative residual correlation | ||||||||||||
| ML | −0.06 | −0.05 | −0.04 | −0.05 | −0.05 | −0.05 | 0.23 | 0.14 | 0.10 | 0.08 | 0.06 | 0.05 |
| ULS | −0.04 | −0.04 | −0.04 | −0.05 | −0.05 | −0.05 | 0.21 | 0.13 | 0.09 | 0.08 | 0.06 | 0.05 |
| RME | −0.04 | −0.02 | −0.01 | −0.01 | −0.01 | 0.00 | 0.23 | 0.15 | 0.11 | 0.07 | 0.05 | 0.01 |
| LSAM | −0.20 | −0.11 | −0.08 | −0.07 | −0.06 | −0.05 | 0.28 | 0.17 | 0.12 | 0.09 | 0.07 | 0.05 |
| GSAM-ML | −0.20 | −0.11 | −0.08 | −0.07 | −0.06 | −0.05 | 0.28 | 0.17 | 0.12 | 0.09 | 0.07 | 0.05 |
| GSAM-ULS | −0.16 | −0.09 | −0.07 | −0.06 | −0.06 | −0.05 | 0.25 | 0.15 | 0.11 | 0.09 | 0.07 | 0.05 |
| GSAM-RME | −0.16 | −0.08 | −0.04 | −0.03 | −0.01 | 0.00 | 0.28 | 0.17 | 0.11 | 0.08 | 0.05 | 0.01 |
| Geomin | −0.36 | −0.31 | −0.29 | −0.27 | −0.26 | −0.27 | 0.39 | 0.33 | 0.30 | 0.28 | 0.27 | 0.27 |
| Lp | −0.37 | −0.30 | −0.26 | −0.22 | −0.19 | −0.16 | 0.39 | 0.33 | 0.28 | 0.24 | 0.20 | 0.16 |
| Geomin(THR) | −0.35 | −0.30 | −0.26 | −0.25 | −0.24 | −0.27 | 0.37 | 0.31 | 0.28 | 0.26 | 0.26 | 0.27 |
| Lp(THR) | −0.36 | −0.29 | −0.25 | −0.21 | −0.18 | −0.16 | 0.38 | 0.32 | 0.27 | 0.23 | 0.20 | 0.16 |
| Geomin(RME) | −0.13 | −0.09 | −0.08 | −0.05 | −0.03 | −0.01 | 0.28 | 0.20 | 0.14 | 0.09 | 0.05 | 0.01 |
| Lp(RME) | −0.05 | 0.01 | 0.03 | 0.01 | 0.00 | 0.00 | 0.29 | 0.20 | 0.15 | 0.14 | 0.14 | 0.03 |
| Geomin(THR,RME) | −0.12 | −0.09 | −0.07 | −0.05 | −0.03 | −0.01 | 0.28 | 0.20 | 0.14 | 0.09 | 0.05 | 0.01 |
| Lp(THR,RME) | −0.03 | 0.03 | 0.04 | 0.02 | 0.00 | 0.00 | 0.28 | 0.20 | 0.15 | 0.14 | 0.14 | 0.03 |
| Two negative residual correlations | ||||||||||||
| ML | −0.11 | −0.10 | −0.10 | −0.10 | −0.10 | −0.10 | 0.25 | 0.16 | 0.13 | 0.12 | 0.11 | 0.10 |
| ULS | −0.09 | −0.09 | −0.10 | −0.10 | −0.10 | −0.10 | 0.23 | 0.15 | 0.13 | 0.12 | 0.11 | 0.10 |
| RME | −0.07 | −0.06 | −0.04 | −0.03 | −0.02 | 0.00 | 0.25 | 0.17 | 0.12 | 0.08 | 0.05 | 0.01 |
| LSAM | −0.23 | −0.16 | −0.13 | −0.12 | −0.11 | −0.11 | 0.30 | 0.20 | 0.16 | 0.14 | 0.12 | 0.11 |
| GSAM-ML | −0.23 | −0.16 | −0.13 | −0.12 | −0.11 | −0.11 | 0.30 | 0.20 | 0.16 | 0.14 | 0.12 | 0.11 |
| GSAM-ULS | −0.20 | −0.14 | −0.12 | −0.12 | −0.11 | −0.11 | 0.27 | 0.19 | 0.15 | 0.13 | 0.12 | 0.11 |
| GSAM-RME | −0.19 | −0.11 | −0.07 | −0.05 | −0.02 | 0.00 | 0.29 | 0.19 | 0.13 | 0.09 | 0.05 | 0.01 |
| Geomin | −0.40 | −0.37 | −0.34 | −0.32 | −0.29 | −0.21 | 0.42 | 0.38 | 0.35 | 0.33 | 0.30 | 0.21 |
| Lp | −0.38 | −0.34 | −0.30 | −0.26 | −0.23 | −0.23 | 0.40 | 0.36 | 0.32 | 0.28 | 0.24 | 0.23 |
| Geomin(THR) | −0.38 | −0.33 | −0.30 | −0.28 | −0.25 | −0.09 | 0.40 | 0.35 | 0.31 | 0.30 | 0.27 | 0.14 |
| Lp(THR) | −0.38 | −0.31 | −0.27 | −0.23 | −0.18 | −0.04 | 0.40 | 0.34 | 0.30 | 0.25 | 0.21 | 0.08 |
| Geomin(RME) | −0.18 | −0.12 | −0.09 | −0.07 | −0.04 | 0.00 | 0.32 | 0.23 | 0.17 | 0.12 | 0.07 | 0.01 |
| Lp(RME) | −0.07 | −0.04 | −0.02 | 0.01 | 0.01 | 0.03 | 0.31 | 0.22 | 0.17 | 0.13 | 0.10 | 0.10 |
| Geomin(THR,RME) | −0.16 | −0.13 | −0.10 | −0.08 | −0.04 | −0.01 | 0.32 | 0.23 | 0.16 | 0.11 | 0.06 | 0.01 |
| Lp(THR,RME) | −0.06 | 0.00 | 0.01 | 0.01 | 0.00 | −0.02 | 0.29 | 0.22 | 0.17 | 0.14 | 0.12 | 0.10 |
| Bias | RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | 100 | 250 | 500 | 1000 | 2500 | 100 | 250 | 500 | 1000 | 2500 | ||
| One negative cross-loading | ||||||||||||
| ML | −0.11 | −0.08 | −0.08 | −0.08 | −0.08 | −0.08 | 0.26 | 0.16 | 0.12 | 0.10 | 0.09 | 0.08 |
| ULS | −0.08 | −0.08 | −0.08 | −0.08 | −0.08 | −0.08 | 0.24 | 0.16 | 0.12 | 0.10 | 0.09 | 0.08 |
| RME | −0.07 | −0.05 | −0.04 | −0.03 | −0.02 | 0.00 | 0.25 | 0.17 | 0.12 | 0.08 | 0.05 | 0.01 |
| LSAM | −0.25 | −0.16 | −0.12 | −0.10 | −0.10 | −0.09 | 0.32 | 0.21 | 0.15 | 0.12 | 0.11 | 0.09 |
| GSAM-ML | −0.25 | −0.16 | −0.12 | −0.10 | −0.10 | −0.09 | 0.32 | 0.21 | 0.15 | 0.12 | 0.11 | 0.09 |
| GSAM-ULS | −0.22 | −0.14 | −0.12 | −0.10 | −0.10 | −0.10 | 0.29 | 0.19 | 0.15 | 0.12 | 0.11 | 0.10 |
| GSAM-RME | −0.22 | −0.13 | −0.09 | −0.06 | −0.03 | −0.01 | 0.32 | 0.21 | 0.15 | 0.10 | 0.06 | 0.01 |
| Geomin | −0.39 | −0.31 | −0.25 | −0.21 | −0.18 | −0.16 | 0.41 | 0.33 | 0.27 | 0.23 | 0.18 | 0.16 |
| Lp | −0.40 | −0.33 | −0.27 | −0.22 | −0.17 | −0.01 | 0.42 | 0.36 | 0.31 | 0.28 | 0.25 | 0.02 |
| Geomin(THR) | −0.39 | −0.32 | −0.26 | −0.22 | −0.18 | −0.16 | 0.40 | 0.34 | 0.28 | 0.23 | 0.19 | 0.16 |
| Lp(THR) | −0.40 | −0.33 | −0.28 | −0.22 | −0.17 | −0.01 | 0.42 | 0.36 | 0.32 | 0.28 | 0.25 | 0.02 |
| Geomin(RME) | −0.18 | −0.15 | −0.13 | −0.12 | −0.11 | −0.03 | 0.35 | 0.29 | 0.26 | 0.27 | 0.26 | 0.10 |
| Lp(RME) | −0.17 | −0.14 | −0.15 | −0.15 | −0.16 | −0.14 | 0.35 | 0.29 | 0.30 | 0.28 | 0.29 | 0.19 |
| Geomin(THR,RME) | −0.16 | −0.14 | −0.13 | −0.13 | −0.11 | −0.03 | 0.34 | 0.29 | 0.27 | 0.28 | 0.26 | 0.10 |
| Lp(THR,RME) | −0.15 | −0.14 | −0.15 | −0.15 | −0.16 | −0.14 | 0.35 | 0.30 | 0.29 | 0.27 | 0.29 | 0.19 |
| Two negative cross-loadings | ||||||||||||
| ML | −0.22 | −0.19 | −0.17 | −0.17 | −0.16 | −0.16 | 0.37 | 0.27 | 0.21 | 0.19 | 0.17 | 0.16 |
| ULS | −0.19 | −0.17 | −0.16 | −0.17 | −0.17 | −0.17 | 0.35 | 0.25 | 0.20 | 0.19 | 0.17 | 0.17 |
| RME | −0.15 | −0.13 | −0.09 | −0.06 | −0.03 | 0.00 | 0.33 | 0.24 | 0.18 | 0.12 | 0.07 | 0.01 |
| LSAM | −0.36 | −0.29 | −0.25 | −0.22 | −0.21 | −0.20 | 0.42 | 0.33 | 0.27 | 0.24 | 0.21 | 0.20 |
| GSAM-ML | −0.36 | −0.29 | −0.25 | −0.22 | −0.21 | −0.20 | 0.42 | 0.33 | 0.27 | 0.24 | 0.21 | 0.20 |
| GSAM-ULS | −0.32 | −0.28 | −0.25 | −0.23 | −0.22 | −0.21 | 0.84 | 0.32 | 0.27 | 0.24 | 0.23 | 0.21 |
| GSAM-RME | −0.33 | −0.27 | −0.21 | −0.14 | −0.08 | −0.01 | 0.76 | 0.33 | 0.26 | 0.19 | 0.11 | 0.02 |
| Geomin | −0.44 | −0.41 | −0.38 | −0.36 | −0.34 | −0.30 | 0.45 | 0.42 | 0.39 | 0.37 | 0.34 | 0.30 |
| Lp | −0.43 | −0.41 | −0.40 | −0.41 | −0.46 | −0.53 | 0.45 | 0.43 | 0.43 | 0.45 | 0.49 | 0.53 |
| Geomin(THR) | −0.43 | −0.41 | −0.39 | −0.36 | −0.34 | −0.30 | 0.45 | 0.43 | 0.40 | 0.38 | 0.34 | 0.30 |
| Lp(THR) | −0.43 | −0.42 | −0.40 | −0.41 | −0.46 | −0.53 | 0.45 | 0.43 | 0.43 | 0.45 | 0.49 | 0.53 |
| Geomin(RME) | −0.26 | −0.24 | −0.20 | −0.12 | −0.05 | −0.01 | 0.41 | 0.34 | 0.26 | 0.17 | 0.10 | 0.01 |
| Lp(RME) | −0.19 | −0.17 | −0.17 | −0.18 | −0.19 | −0.07 | 0.40 | 0.34 | 0.32 | 0.31 | 0.30 | 0.20 |
| Geomin(THR,RME) | −0.25 | −0.23 | −0.20 | −0.13 | −0.05 | −0.01 | 0.39 | 0.34 | 0.27 | 0.18 | 0.10 | 0.01 |
| Lp(THR,RME) | −0.18 | −0.16 | −0.18 | −0.18 | −0.19 | −0.07 | 0.41 | 0.34 | 0.33 | 0.32 | 0.30 | 0.20 |
Appendix B. lavaan Syntax for Model Estimation
Appendix C. lavaan Syntax for ULI Estimation in Focused Simulation Study 1A
References
- Bartholomew, D.J.; Knott, M.; Moustaki, I. Latent Variable Models and Factor Analysis: A Unified Approach; Wiley: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Basilevsky, A.T. Statistical Factor Analysis and Related Methods: Theory and Applications; Wiley: New York, NY, USA, 2009; Volume 418. [Google Scholar] [CrossRef]
- Bollen, K.A. Structural Equations with Latent Variables; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar] [CrossRef]
- Browne, M.W.; Arminger, G. Specification and estimation of mean-and covariance-structure models. In Handbook of Statistical Modeling for the Social and Behavioral Sciences; Arminger, G., Clogg, C.C., Sobel, M.E., Eds.; Springer: Boston, MA, USA, 1995; pp. 185–249. [Google Scholar] [CrossRef]
- Jöreskog, K.G. Factor analysis and its extensions. In Factor Analysis at 100; Cudeck, R., MacCallum, R.C., Eds.; Lawrence Erlbaum: Mahwah, NJ, USA, 2007; pp. 47–77. [Google Scholar]
- Jöreskog, K.G.; Olsson, U.H.; Wallentin, F.Y. Multivariate Analysis with LISREL; Springer: Basel, Switzerland, 2016. [Google Scholar] [CrossRef]
- Mulaik, S.A. Foundations of Factor Analysis; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar] [CrossRef]
- Shapiro, A. Statistical inference of covariance structures. In Current Topics in the Theory and Application of Latent Variable Models; Edwards, M.C., MacCallum, R.C., Eds.; Routledge: London, UK, 2012; pp. 222–240. [Google Scholar] [CrossRef]
- Yanai, H.; Ichikawa, M. Factor analysis. In Handbook of Statistics, Volume 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 257–297. [Google Scholar] [CrossRef]
- Yuan, K.H.; Bentler, P.M. Structural equation modeling. In Handbook of Statistics, Volume 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 26, pp. 297–358. [Google Scholar] [CrossRef]
- Arminger, G.; Schoenberg, R.J. Pseudo maximum likelihood estimation and a test for misspecification in mean and covariance structure models. Psychometrika 1989, 54, 409–425. [Google Scholar] [CrossRef]
- Browne, M.W. Generalized least squares estimators in the analysis of covariance structures. S. Afr. Stat. J. 1974, 8, 1–24. [Google Scholar] [CrossRef]
- Curran, P.J.; West, S.G.; Finch, J.F. The robustness of test statistics to nonnormality and specification error in confirmatory factor analysis. Psychol. Methods 1996, 1, 16–29. [Google Scholar] [CrossRef]
- Yuan, K.H.; Bentler, P.M.; Chan, W. Structural equation modeling with heavy tailed distributions. Psychometrika 2004, 69, 421–436. [Google Scholar] [CrossRef]
- Yuan, K.H.; Bentler, P.M. Robust procedures in structural equation modeling. In Handbook of Latent Variable and Related Models; Lee, S.Y., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 367–397. [Google Scholar] [CrossRef]
- Avella Medina, M.; Ronchetti, E. Robust statistics: A selective overview and new directions. WIREs Comput. Stat. 2015, 7, 372–393. [Google Scholar] [CrossRef]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics; Wiley: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Maronna, R.A.; Martin, R.D.; Yohai, V.J. Robust Statistics: Theory and Methods; Wiley: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Ronchetti, E. The main contributions of robust statistics to statistical science and a new challenge. Metron 2021, 79, 127–135. [Google Scholar] [CrossRef]
- Rosseel, Y.; Loh, W.W. A structural after measurement (SAM) approach to structural equation modeling. Psychol. Methods. 2022. Forthcoming. Available online: https://osf.io/pekbm/ (accessed on 28 March 2022).
- Briggs, N.E.; MacCallum, R.C. Recovery of weak common factors by maximum likelihood and ordinary least squares estimation. Multivar. Behav. Res. 2003, 38, 25–56. [Google Scholar] [CrossRef]
- Cudeck, R.; Browne, M.W. Constructing a covariance matrix that yields a specified minimizer and a specified minimum discrepancy function value. Psychometrika 1992, 57, 357–369. [Google Scholar] [CrossRef]
- Kolenikov, S. Biases of parameter estimates in misspecified structural equation models. Sociol. Methodol. 2011, 41, 119–157. [Google Scholar] [CrossRef]
- MacCallum, R.C.; Tucker, L.R. Representing sources of error in the common-factor model: Implications for theory and practice. Psychol. Bull. 1991, 109, 502–511. [Google Scholar] [CrossRef]
- MacCallum, R.C. 2001 presidential address: Working with imperfect models. Multivar. Behav. Res. 2003, 38, 113–139. [Google Scholar] [CrossRef]
- MacCallum, R.C.; Browne, M.W.; Cai, L. Factor analysis models as approximations. In Factor Analysis at 100; Cudeck, R., MacCallum, R.C., Eds.; Lawrence Erlbaum: Mahwah, NJ, USA, 2007; pp. 153–175. [Google Scholar]
- Tucker, L.R.; Koopman, R.F.; Linn, R.L. Evaluation of factor analytic research procedures by means of simulated correlation matrices. Psychometrika 1969, 34, 421–459. [Google Scholar] [CrossRef]
- Yuan, K.H.; Marshall, L.L.; Bentler, P.M. Assessing the effect of model misspecifications on parameter estimates in structural equation models. Sociol. Methodol. 2003, 33, 241–265. [Google Scholar] [CrossRef]
- Boos, D.D.; Stefanski, L.A. Essential Statistical Inference; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Huber, P.J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Ronchetti, E. The historical development of robust statistics. In Proceedings of the 7th International Conference on Teaching Statistics (ICOTS-7), Salvador, Brazil, 2–7 July 2006; pp. 2–7. Available online: https://bit.ly/3aueh6z (accessed on 22 June 2022).
- Stefanski, L.A.; Boos, D.D. The calculus of M-estimation. Am. Stat. 2002, 56, 29–38. [Google Scholar] [CrossRef]
- White, H. Maximum likelihood estimation of misspecified models. Econometrica 1982, 50, 1–25. [Google Scholar] [CrossRef]
- Gourieroux, C.; Monfort, A.; Trognon, A. Pseudo maximum likelihood methods: Theory. Econometrica 1984, 52, 681–700. [Google Scholar] [CrossRef]
- Wu, J.W. The quasi-likelihood estimation in regression. Ann. Inst. Stat. Math. 1996, 48, 283–294. [Google Scholar] [CrossRef]
- Aronow, P.M.; Miller, B.T. Foundations of Agnostic Statistics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Robitzsch, A. Estimation methods of the multiple-group one-dimensional factor model: Implied identification constraints in the violation of measurement invariance. Axioms 2022, 11, 119. [Google Scholar] [CrossRef]
- Shapiro, A. Statistical inference of moment structures. In Handbook of Latent Variable and Related Models; Lee, S.Y., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 229–260. [Google Scholar] [CrossRef]
- Chun, S.Y.; Shapiro, A. Construction of covariance matrices with a specified discrepancy function minimizer, with application to factor analysis. SIAM J. Matrix Anal. Appl. 2010, 31, 1570–1583. [Google Scholar] [CrossRef][Green Version]
- Savalei, V. Understanding robust corrections in structural equation modeling. Struct. Equ. Model. 2014, 21, 149–160. [Google Scholar] [CrossRef]
- Fox, J.; Weisberg, S. Robust Regression in R: An Appendix to an R Companion to Applied Regression, Second Edition. 2010. Available online: https://bit.ly/3canwcw (accessed on 22 June 2022).
- Siemsen, E.; Bollen, K.A. Least absolute deviation estimation in structural equation modeling. Sociol. Methods Res. 2007, 36, 227–265. [Google Scholar] [CrossRef]
- van Kesteren, E.J.; Oberski, D.L. Flexible extensions to structural equation models using computation graphs. Struct. Equ. Model. 2022, 29, 233–247. [Google Scholar] [CrossRef]
- Asparouhov, T.; Muthén, B. Multiple-group factor analysis alignment. Struct. Equ. Model. 2014, 21, 495–508. [Google Scholar] [CrossRef]
- Pokropek, A.; Lüdtke, O.; Robitzsch, A. An extension of the invariance alignment method for scale linking. Psych. Test Assess. Model. 2020, 62, 303–334. [Google Scholar]
- Robitzsch, A. Lp loss functions in invariance alignment and Haberman linking with few or many groups. Stats 2020, 3, 246–283. [Google Scholar] [CrossRef]
- She, Y.; Owen, A.B. Outlier detection using nonconvex penalized regression. J. Am. Stat. Assoc. 2011, 106, 626–639. [Google Scholar] [CrossRef]
- Battauz, M. Regularized estimation of the nominal response model. Multivar. Behav. Res. 2020, 55, 811–824. [Google Scholar] [CrossRef]
- Oelker, M.R.; Tutz, G. A uniform framework for the combination of penalties in generalized structured models. Adv. Data Anal. Classif. 2017, 11, 97–120. [Google Scholar] [CrossRef]
- Fabrigar, L.R.; Wegener, D.T. Exploratory Factor Analysis; Oxford University Press: Oxford, UK, 2011. [Google Scholar] [CrossRef]
- Browne, M.W. An overview of analytic rotation in exploratory factor analysis. Multivar. Behav. Res. 2001, 36, 111–150. [Google Scholar] [CrossRef]
- Hattori, M.; Zhang, G.; Preacher, K.J. Multiple local solutions and geomin rotation. Multivar. Behav. Res. 2017, 52, 720–731. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wallin, G.; Chen, Y.; Moustaki, I. Rotation to sparse loadings using Lp losses and related inference problems. arXiv 2022, arXiv:2206.02263. [Google Scholar]
- Jennrich, R.I. Rotation to simple loadings using component loss functions: The oblique case. Psychometrika 2006, 71, 173–191. [Google Scholar] [CrossRef]
- Fan, J.; Liao, Y.; Mincheva, M. Large covariance estimation by thresholding principal orthogonal complements. J. R. Stat. Soc. Series B Stat. Methodol. 2013, 75, 603–680. [Google Scholar] [CrossRef]
- Bai, J.; Liao, Y. Efficient estimation of approximate factor models via penalized maximum likelihood. J. Econom. 2016, 191, 1–18. [Google Scholar] [CrossRef]
- Pati, D.; Bhattacharya, A.; Pillai, N.S.; Dunson, D. Posterior contraction in sparse Bayesian factor models for massive covariance matrices. Ann. Stat. 2014, 42, 1102–1130. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Rothman, A.J.; Levina, E.; Zhu, J. Generalized thresholding of large covariance matrices. J. Am. Stat. Assoc. 2009, 104, 177–186. [Google Scholar] [CrossRef]
- Scharf, F.; Nestler, S. Should regularization replace simple structure rotation in exploratory factor analysis? Struct. Equ. Model. 2019, 26, 576–590. [Google Scholar] [CrossRef]
- McDonald, R.P. Test Theory: A Unified Treatment; Lawrence Erlbaum: Mahwah, NJ, USA, 1999. [Google Scholar] [CrossRef]
- Lüdtke, O.; Ulitzsch, E.; Robitzsch, A. A comparison of penalized maximum likelihood estimation and Markov Chain Monte Carlo techniques for estimating confirmatory factor analysis models with small sample sizes. Front. Psychol. 2021, 12, 615162. [Google Scholar] [CrossRef]
- Ulitzsch, E.; Lüdtke, O.; Robitzsch, A. Alleviating estimation problems in small sample structural equation modeling—A comparison of constrained maximum likelihood, Bayesian estimation, and fixed reliability approaches. Psychol. Methods 2021. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 11 January 2022).
- Rosseel, Y. lavaan: An R package for structural equation modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Bernaards, C.A.; Jennrich, R.I. Gradient projection algorithms and software for arbitrary rotation criteria in factor analysis. Educ. Psychol. Meas. 2005, 65, 676–696. [Google Scholar] [CrossRef]
- Robitzsch, A. sirt: Supplementary Item Response Theory Models. R package version 3.12-66. 2022. Available online: https://CRAN.R-project.org/package=sirt (accessed on 17 May 2022).
- Dhaene, S.; Rosseel, Y. Resampling based bias correction for small sample SEM. Struct. Equ. Model. 2022. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar] [CrossRef]
- Chen, J. Partially confirmatory approach to factor analysis with Bayesian learning: A LAWBL tutorial. Struct. Equ. Model. 2022. [Google Scholar] [CrossRef]
- Hirose, K.; Terada, Y. Sparse and simple structure estimation via prenet penalization. Psychometrika 2022. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.H.; Chen, H.; Weng, L.J. A penalized likelihood method for structural equation modeling. Psychometrika 2017, 82, 329–354. [Google Scholar] [CrossRef]
- Huang, P.H. lslx: Semi-confirmatory structural equation modeling via penalized likelihood. J. Stat. Softw. 2020, 93, 1–37. [Google Scholar] [CrossRef]
- Jacobucci, R.; Grimm, K.J.; McArdle, J.J. Regularized structural equation modeling. Struct. Equ. Model. 2016, 23, 555–566. [Google Scholar] [CrossRef]
- Li, X.; Jacobucci, R.; Ammerman, B.A. Tutorial on the use of the regsem package in R. Psych 2021, 3, 579–592. [Google Scholar] [CrossRef]
- Muthén, B.; Asparouhov, T. Bayesian structural equation modeling: A more flexible representation of substantive theory. Psychol. Methods 2012, 17, 313–335. [Google Scholar] [CrossRef] [PubMed]
- Rowe, D.B. Multivariate Bayesian Statistics: Models for Source Separation and Signal Unmixing; Chapman and Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar] [CrossRef]
- Liang, X. Prior sensitivity in Bayesian structural equation modeling for sparse factor loading structures. Educ. Psychol. Meas. 2020, 80, 1025–1058. [Google Scholar] [CrossRef] [PubMed]
- Lodewyckx, T.; Tuerlinckx, F.; Kuppens, P.; Allen, N.B.; Sheeber, L. A hierarchical state space approach to affective dynamics. J. Math. Psychol. 2011, 55, 68–83. [Google Scholar] [CrossRef] [PubMed]
- Devlieger, I.; Mayer, A.; Rosseel, Y. Hypothesis testing using factor score regression: A comparison of four methods. Educ. Psychol. Meas. 2016, 76, 741–770. [Google Scholar] [CrossRef]
- Devlieger, I.; Talloen, W.; Rosseel, Y. New developments in factor score regression: Fit indices and a model comparison test. Educ. Psychol. Meas. 2019, 79, 1017–1037. [Google Scholar] [CrossRef]
- Kelcey, B.; Cox, K.; Dong, N. Croon’s bias-corrected factor score path analysis for small-to moderate-sample multilevel structural equation models. Organ. Res. Methods 2021, 24, 55–77. [Google Scholar] [CrossRef]
- Zitzmann, S.; Helm, C. Multilevel analysis of mediation, moderation, and nonlinear effects in small samples, using expected a posteriori estimates of factor scores. Struct. Equ. Model. 2021, 28, 529–546. [Google Scholar] [CrossRef]
- Zitzmann, S.; Lohmann, J.F.; Krammer, G.; Helm, C.; Aydin, B.; Hecht, M. A Bayesian EAP-based nonlinear extension of Croon and Van Veldhoven’s model for analyzing data from micro-macro multilevel designs. Mathematics 2022, 10, 842. [Google Scholar] [CrossRef]
- Anderson, J.C.; Gerbing, D.W. Structural equation modeling in practice: A review and recommended two-step approach. Psychol. Bull. 1988, 103, 411–423. [Google Scholar] [CrossRef]
- Burt, R.S. Interpretational confounding of unobserved variables in structural equation models. Sociol. Methods Res. 1976, 5, 3–52. [Google Scholar] [CrossRef]
- Fornell, C.; Yi, Y. Assumptions of the two-step approach to latent variable modeling. Sociol. Methods Res. 1992, 20, 291–320. [Google Scholar] [CrossRef]
- McDonald, R.P. Structural models and the art of approximation. Perspect. Psychol. Sci. 2010, 5, 675–686. [Google Scholar] [CrossRef] [PubMed]
- Marsh, H.W.; Morin, A.J.S.; Parker, P.D.; Kaur, G. Exploratory structural equation modeling: An integration of the best features of exploratory and confirmatory factor analysis. Annu. Rev. Clin. Psychol. 2014, 10, 85–110. [Google Scholar] [CrossRef]
- Brennan, R.L. Misconceptions at the intersection of measurement theory and practice. Educ. Meas. 1998, 17, 5–9. [Google Scholar] [CrossRef]
- Uher, J. Psychometrics is not measurement: Unraveling a fundamental misconception in quantitative psychology and the complex network of its underlying fallacies. J. Theor. Philos. Psychol. 2021, 41, 58–84. [Google Scholar] [CrossRef]
- Grønneberg, S.; Foldnes, N. Factor analyzing ordinal items requires substantive knowledge of response marginals. Psychol. Methods 2022. [Google Scholar] [CrossRef]
- Jorgensen, T.D.; Johnson, A.R. How to derive expected values of structural equation model parameters when treating discrete data as continuous. Struct. Equ. Model. 2022. [Google Scholar] [CrossRef]
- Rhemtulla, M.; Brosseau-Liard, P.É.; Savalei, V. When can categorical variables be treated as continuous? A comparison of robust continuous and categorical SEM estimation methods under suboptimal conditions. Psychol. Methods 2012, 17, 354–373. [Google Scholar] [CrossRef]
- Robitzsch, A. Why ordinal variables can (almost) always be treated as continuous variables: Clarifying assumptions of robust continuous and ordinal factor analysis estimation methods. Front. Educ. 2020, 5, 589965. [Google Scholar] [CrossRef]
- Robitzsch, A. On the bias in confirmatory factor analysis when treating discrete variables as ordinal instead of continuous. Axioms 2022, 11, 162. [Google Scholar] [CrossRef]
- Davidov, E.; Meuleman, B.; Cieciuch, J.; Schmidt, P.; Billiet, J. Measurement equivalence in cross-national research. Annu. Rev. Sociol. 2014, 40, 55–75. [Google Scholar] [CrossRef]
- Millsap, R.E. Statistical Approaches to Measurement Invariance; Routledge: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- VanderWeele, T.J. Constructed measures and causal inference: Towards a new model of measurement for psychosocial constructs. Epidemiology 2022, 33, 141–151. [Google Scholar] [CrossRef]
- Westfall, P.H.; Henning, K.S.; Howell, R.D. The effect of error correlation on interfactor correlation in psychometric measurement. Struct. Equ. Model. 2012, 19, 99–117. [Google Scholar] [CrossRef]
- Funder, D. Misgivings: Some thoughts about “Measurement Invariance”. 2020. Available online: https://bit.ly/3caKdNN (accessed on 31 January 2020).
- Robitzsch, A.; Lüdtke, O. Reflections on analytical choices in the scaling model for test scores in international large-scale assessment studies. PsyArXiv 2021. [Google Scholar] [CrossRef]
- Welzel, C.; Inglehart, R.F. Misconceptions of measurement equivalence: Time for a paradigm shift. Comp. Political Stud. 2016, 49, 1068–1094. [Google Scholar] [CrossRef]
- McDonald, R.P. The theoretical foundations of principal factor analysis, canonical factor analysis, and alpha factor analysis. Brit. J. Math. Stat. Psychol. 1970, 23, 1–21. [Google Scholar] [CrossRef]
- Zinbarg, R.E.; Revelle, W.; Yovel, I.; Li, W. Cronbach’s α, Revelle’s β, and McDonald’s ωH: Their relations with each other and two alternative conceptualizations of reliability. Psychometrika 2005, 70, 123–133. [Google Scholar] [CrossRef]
- Cronbach, L.J. Coefficient alpha and the internal structure of tests. Psychometrika 1951, 16, 297–334. [Google Scholar] [CrossRef]
- Cronbach, L.J.; Schönemann, P.; McKie, D. Alpha coefficients for stratified-parallel tests. Educ. Psychol. Meas. 1965, 25, 291–312. [Google Scholar] [CrossRef]
- Ellis, J.L. A test can have multiple reliabilities. Psychometrika 2021, 86, 869–876. [Google Scholar] [CrossRef]
- Nunnally, J.C.; Bernstein, I.R. Psychometric Theory; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Brennan, R.L. Generalizability theory and classical test theory. Appl. Meas. Educ. 2010, 24, 1–21. [Google Scholar] [CrossRef]
- Cronbach, L.J.; Shavelson, R.J. My current thoughts on coefficient alpha and successor procedures. Educ. Psychol. Meas. 2004, 64, 391–418. [Google Scholar] [CrossRef]
- Tryon, R.C. Reliability and behavior domain validity: Reformulation and historical critique. Psychol. Bull. 1957, 54, 229–249. [Google Scholar] [CrossRef]
- McNeish, D. Thanks coefficient alpha, we’ll take it from here. Psychol. Methods 2018, 23, 412–433. [Google Scholar] [CrossRef]
- Kane, M. The errors of our ways. J. Educ. Meas. 2011, 48, 12–30. [Google Scholar] [CrossRef]
- Carroll, R.J.; Ruppert, D.; Stefanski, L.A.; Crainiceanu, C.M. Measurement Error in Nonlinear Models: A Modern Perspective; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar] [CrossRef]
- Feldt, L.S. Can validity rise when reliability declines? Appl. Meas. Educ. 1997, 10, 377–387. [Google Scholar] [CrossRef]
- Kane, M.T. A sampling model for validity. Appl. Psychol. Meas. 1982, 6, 125–160. [Google Scholar] [CrossRef]
- Heene, M.; Hilbert, S.; Draxler, C.; Ziegler, M.; Bühner, M. Masking misfit in confirmatory factor analysis by increasing unique variances: A cautionary note on the usefulness of cutoff values of fit indices. Psychol. Methods 2011, 16, 319–336. [Google Scholar] [CrossRef]
- Hu, L.t.; Bentler, P.M. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Model. 1999, 6, 1–55. [Google Scholar] [CrossRef]
- McNeish, D.; Wolf, M.G. Dynamic fit index cutoffs for confirmatory factor analysis models. Psychol. Methods 2021. [Google Scholar] [CrossRef]
- Moshagen, M. The model size effect in SEM: Inflated goodness-of-fit statistics are due to the size of the covariance matrix. Struct. Equ. Model. 2012, 19, 86–98. [Google Scholar] [CrossRef]
- Wu, H.; Browne, M.W. Quantifying adventitious error in a covariance structure as a random effect. Psychometrika 2015, 80, 571–600. [Google Scholar] [CrossRef] [PubMed]
- Robitzsch, A.; Dörfler, T.; Pfost, M.; Artelt, C. Die Bedeutung der Itemauswahl und der Modellwahl für die längsschnittliche Erfassung von Kompetenzen [Relevance of item selection and model selection for assessing the development of competencies: The development in reading competence in primary school students]. Z. Entwicklungspsychol. Pädagog. Psychol. 2011, 43, 213–227. [Google Scholar] [CrossRef]
- Robitzsch, A. Is it really more robust? Comparing the robustness of the structural after measurement (SAM) approach to structural equation modeling (SEM) against local model misspecifications with alternative estimation approaches. PsyArXiv 2022. [Google Scholar] [CrossRef]



| Bias | RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | 100 | 250 | 500 | 1000 | 2500 | 100 | 250 | 500 | 1000 | 2500 | ||
| No residual correlations | ||||||||||||
| ML | −0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.21 | 0.12 | 0.09 | 0.06 | 0.04 | 0.01 |
| ULS | 0.01 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.20 | 0.12 | 0.08 | 0.06 | 0.04 | 0.01 |
| RME | 0.01 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.22 | 0.14 | 0.10 | 0.07 | 0.04 | 0.01 |
| LSAM | −0.16 | −0.07 | −0.03 | −0.01 | −0.01 | 0.00 | 0.25 | 0.14 | 0.09 | 0.06 | 0.04 | 0.01 |
| GSAM-ML | −0.16 | −0.07 | −0.03 | −0.01 | −0.01 | 0.00 | 0.25 | 0.14 | 0.09 | 0.06 | 0.04 | 0.01 |
| GSAM-ULS | −0.11 | −0.05 | −0.02 | −0.01 | 0.00 | 0.00 | 0.25 | 0.13 | 0.09 | 0.06 | 0.04 | 0.01 |
| GSAM-RME | −0.12 | −0.05 | −0.02 | −0.01 | 0.00 | 0.00 | 0.26 | 0.15 | 0.11 | 0.07 | 0.04 | 0.01 |
| Geomin | −0.33 | −0.24 | −0.16 | −0.10 | −0.06 | −0.03 | 0.35 | 0.27 | 0.19 | 0.12 | 0.07 | 0.03 |
| Lp | −0.34 | −0.27 | −0.20 | −0.14 | −0.07 | 0.00 | 0.37 | 0.29 | 0.22 | 0.16 | 0.09 | 0.01 |
| Geomin(THR) | −0.32 | −0.24 | −0.16 | −0.10 | −0.06 | −0.03 | 0.34 | 0.26 | 0.19 | 0.12 | 0.07 | 0.03 |
| Lp(THR) | −0.33 | −0.26 | −0.20 | −0.14 | −0.07 | 0.00 | 0.36 | 0.28 | 0.22 | 0.16 | 0.09 | 0.01 |
| Geomin(RME) | −0.11 | −0.07 | −0.04 | −0.01 | 0.00 | 0.00 | 0.26 | 0.17 | 0.11 | 0.07 | 0.04 | 0.01 |
| Lp(RME) | −0.01 | 0.06 | 0.08 | 0.06 | 0.03 | 0.00 | 0.27 | 0.19 | 0.16 | 0.14 | 0.09 | 0.01 |
| Geomin(THR,RME) | −0.10 | −0.07 | −0.05 | −0.02 | 0.00 | 0.00 | 0.27 | 0.17 | 0.11 | 0.07 | 0.04 | 0.01 |
| Lp(THR,RME) | 0.01 | 0.06 | 0.08 | 0.06 | 0.03 | 0.00 | 0.26 | 0.19 | 0.16 | 0.13 | 0.09 | 0.01 |
| One positive residual correlation | ||||||||||||
| ML | 0.05 | 0.06 | 0.07 | 0.07 | 0.07 | 0.07 | 0.21 | 0.14 | 0.11 | 0.09 | 0.08 | 0.07 |
| ULS | 0.07 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.20 | 0.13 | 0.10 | 0.08 | 0.07 | 0.06 |
| RME | 0.06 | 0.05 | 0.04 | 0.02 | 0.01 | 0.00 | 0.22 | 0.15 | 0.11 | 0.07 | 0.04 | 0.01 |
| LSAM | −0.12 | −0.02 | 0.02 | 0.04 | 0.05 | 0.05 | 0.23 | 0.13 | 0.09 | 0.07 | 0.06 | 0.05 |
| GSAM-ML | −0.12 | −0.02 | 0.02 | 0.04 | 0.05 | 0.05 | 0.23 | 0.13 | 0.09 | 0.07 | 0.06 | 0.05 |
| GSAM-ULS | −0.06 | 0.00 | 0.03 | 0.04 | 0.05 | 0.05 | 0.38 | 0.12 | 0.09 | 0.07 | 0.06 | 0.05 |
| GSAM-RME | −0.07 | −0.02 | 0.01 | 0.01 | 0.01 | 0.00 | 0.39 | 0.15 | 0.11 | 0.07 | 0.04 | 0.01 |
| Geomin | −0.32 | −0.26 | −0.20 | −0.15 | −0.10 | −0.02 | 0.34 | 0.28 | 0.22 | 0.18 | 0.13 | 0.03 |
| Lp | −0.33 | −0.28 | −0.24 | −0.19 | −0.14 | −0.02 | 0.36 | 0.30 | 0.26 | 0.22 | 0.17 | 0.04 |
| Geomin(THR) | −0.31 | −0.23 | −0.18 | −0.12 | −0.07 | −0.03 | 0.33 | 0.26 | 0.20 | 0.14 | 0.09 | 0.03 |
| Lp(THR) | −0.32 | −0.26 | −0.22 | −0.16 | −0.09 | 0.00 | 0.35 | 0.29 | 0.24 | 0.18 | 0.12 | 0.01 |
| Geomin(RME) | −0.09 | −0.05 | −0.04 | −0.03 | −0.02 | 0.00 | 0.25 | 0.18 | 0.13 | 0.09 | 0.06 | 0.01 |
| Lp(RME) | −0.01 | 0.04 | 0.05 | 0.05 | 0.03 | 0.00 | 0.25 | 0.19 | 0.15 | 0.12 | 0.07 | 0.02 |
| Geomin(THR,RME) | −0.08 | −0.04 | −0.03 | −0.01 | 0.01 | 0.00 | 0.25 | 0.17 | 0.12 | 0.08 | 0.05 | 0.01 |
| Lp(THR,RME) | 0.02 | 0.06 | 0.07 | 0.05 | 0.03 | 0.00 | 0.25 | 0.19 | 0.15 | 0.12 | 0.07 | 0.01 |
| Two positive residual correlations | ||||||||||||
| ML | 0.10 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.22 | 0.17 | 0.14 | 0.13 | 0.12 | 0.12 |
| ULS | 0.12 | 0.12 | 0.12 | 0.11 | 0.11 | 0.11 | 0.21 | 0.16 | 0.14 | 0.13 | 0.12 | 0.11 |
| RME | 0.09 | 0.08 | 0.05 | 0.03 | 0.01 | 0.00 | 0.22 | 0.16 | 0.12 | 0.08 | 0.04 | 0.01 |
| LSAM | −0.08 | 0.03 | 0.07 | 0.09 | 0.10 | 0.11 | 0.22 | 0.13 | 0.11 | 0.11 | 0.11 | 0.11 |
| GSAM-ML | −0.08 | 0.03 | 0.07 | 0.09 | 0.10 | 0.11 | 0.22 | 0.13 | 0.11 | 0.11 | 0.11 | 0.11 |
| GSAM-ULS | −0.03 | 0.05 | 0.09 | 0.10 | 0.10 | 0.11 | 0.19 | 0.13 | 0.12 | 0.11 | 0.11 | 0.11 |
| GSAM-RME | −0.04 | 0.03 | 0.04 | 0.03 | 0.01 | 0.00 | 0.24 | 0.16 | 0.12 | 0.08 | 0.05 | 0.01 |
| Geomin | −0.32 | −0.27 | −0.24 | −0.24 | −0.23 | −0.27 | 0.34 | 0.29 | 0.26 | 0.25 | 0.25 | 0.28 |
| Lp | −0.33 | −0.29 | −0.27 | −0.27 | −0.27 | −0.30 | 0.36 | 0.31 | 0.29 | 0.29 | 0.28 | 0.31 |
| Geomin(THR) | −0.30 | −0.23 | −0.19 | −0.16 | −0.13 | −0.12 | 0.33 | 0.25 | 0.21 | 0.19 | 0.17 | 0.18 |
| Lp(THR) | −0.32 | −0.26 | −0.23 | −0.21 | −0.18 | −0.16 | 0.35 | 0.29 | 0.25 | 0.23 | 0.21 | 0.22 |
| Geomin(RME) | −0.09 | −0.05 | −0.04 | −0.03 | −0.02 | 0.00 | 0.25 | 0.18 | 0.14 | 0.10 | 0.06 | 0.01 |
| Lp(RME) | −0.01 | 0.04 | 0.05 | 0.04 | 0.03 | 0.01 | 0.24 | 0.19 | 0.16 | 0.12 | 0.07 | 0.01 |
| Geomin(THR,RME) | −0.07 | −0.03 | −0.02 | −0.01 | 0.00 | 0.00 | 0.25 | 0.18 | 0.13 | 0.10 | 0.06 | 0.01 |
| Lp(THR,RME) | 0.02 | 0.07 | 0.07 | 0.06 | 0.03 | 0.02 | 0.24 | 0.19 | 0.16 | 0.12 | 0.07 | 0.07 |
| N | ||||||
|---|---|---|---|---|---|---|
| Method | 100 | 250 | 500 | 1000 | 2500 | |
| ML | 0.211 | 0.123 | 0.085 | 0.059 | 0.037 | 0.006 |
| ULS | 0.198 | 0.119 | 0.084 | 0.058 | 0.037 | 0.006 |
| RME | 0.220 | 0.143 | 0.101 | 0.068 | 0.043 | 0.006 |
| LSAM | 0.194 | 0.125 | 0.086 | 0.058 | 0.037 | 0.006 |
| GSAM-ML | 0.194 | 0.125 | 0.086 | 0.058 | 0.037 | 0.006 |
| GSAM-ULS | 0.225 | 0.119 | 0.084 | 0.058 | 0.037 | 0.006 |
| GSAM-RME | 0.228 | 0.146 | 0.103 | 0.069 | 0.042 | 0.006 |
| Geomin | 0.122 | 0.107 | 0.092 | 0.063 | 0.038 | 0.006 |
| Lp | 0.133 | 0.111 | 0.095 | 0.077 | 0.056 | 0.006 |
| Geomin(THR) | 0.124 | 0.104 | 0.088 | 0.064 | 0.039 | 0.006 |
| Lp(THR) | 0.134 | 0.109 | 0.093 | 0.078 | 0.057 | 0.006 |
| Geomin(RME) | 0.241 | 0.156 | 0.101 | 0.065 | 0.040 | 0.006 |
| Lp(RME) | 0.266 | 0.182 | 0.144 | 0.121 | 0.081 | 0.007 |
| Geomin(THR,RME) | 0.245 | 0.154 | 0.101 | 0.065 | 0.040 | 0.006 |
| Lp(THR,RME) | 0.263 | 0.182 | 0.143 | 0.120 | 0.081 | 0.007 |
| Bias | RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | 100 | 250 | 500 | 1000 | 2500 | 100 | 250 | 500 | 1000 | 2500 | ||
| No residual correlations | ||||||||||||
| ML (UVI) | −0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.21 | 0.12 | 0.08 | 0.06 | 0.04 | 0.01 |
| ML (ULI) | −0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.20 | 0.12 | 0.08 | 0.06 | 0.04 | 0.01 |
| ULS (UVI) | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.19 | 0.12 | 0.08 | 0.06 | 0.04 | 0.01 |
| ULS (ULI) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.19 | 0.12 | 0.08 | 0.06 | 0.04 | 0.01 |
| LSAM (UVI) | −0.16 | −0.07 | −0.03 | −0.02 | −0.01 | 0.00 | 0.25 | 0.15 | 0.09 | 0.06 | 0.04 | 0.01 |
| LSAM (ULI) | −0.14 | −0.07 | −0.03 | −0.02 | −0.01 | 0.00 | 0.23 | 0.14 | 0.09 | 0.06 | 0.04 | 0.01 |
| One positive residual correlation | ||||||||||||
| ML (UVI) | 0.06 | 0.06 | 0.07 | 0.07 | 0.07 | 0.07 | 0.20 | 0.14 | 0.11 | 0.09 | 0.08 | 0.07 |
| ML (ULI) | 0.06 | 0.06 | 0.07 | 0.07 | 0.07 | 0.07 | 0.20 | 0.14 | 0.11 | 0.09 | 0.08 | 0.07 |
| ULS (UVI) | 0.07 | 0.07 | 0.07 | 0.06 | 0.06 | 0.06 | 0.19 | 0.14 | 0.11 | 0.09 | 0.07 | 0.06 |
| ULS (ULI) | 0.07 | 0.07 | 0.07 | 0.06 | 0.06 | 0.06 | 0.19 | 0.14 | 0.11 | 0.09 | 0.07 | 0.06 |
| LSAM (UVI) | −0.12 | −0.02 | 0.03 | 0.04 | 0.05 | 0.05 | 0.23 | 0.14 | 0.09 | 0.07 | 0.06 | 0.05 |
| LSAM (ULI) | −0.09 | −0.02 | 0.03 | 0.04 | 0.05 | 0.05 | 0.21 | 0.13 | 0.09 | 0.07 | 0.06 | 0.05 |
| Two positive residual correlations | ||||||||||||
| ML (UVI) | 0.12 | 0.12 | 0.12 | 0.12 | 0.11 | 0.12 | 0.22 | 0.17 | 0.14 | 0.13 | 0.12 | 0.12 |
| ML (ULI) | 0.12 | 0.12 | 0.12 | 0.12 | 0.11 | 0.12 | 0.22 | 0.17 | 0.14 | 0.13 | 0.12 | 0.12 |
| ULS (UVI) | 0.13 | 0.12 | 0.11 | 0.12 | 0.11 | 0.11 | 0.22 | 0.16 | 0.14 | 0.13 | 0.12 | 0.11 |
| ULS (ULI) | 0.13 | 0.12 | 0.11 | 0.12 | 0.11 | 0.11 | 0.22 | 0.16 | 0.14 | 0.13 | 0.12 | 0.11 |
| LSAM (UVI) | −0.08 | 0.02 | 0.07 | 0.09 | 0.10 | 0.11 | 0.22 | 0.13 | 0.11 | 0.11 | 0.10 | 0.11 |
| LSAM (ULI) | −0.05 | 0.03 | 0.07 | 0.09 | 0.10 | 0.11 | 0.20 | 0.13 | 0.11 | 0.11 | 0.10 | 0.11 |
| 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | |
|---|---|---|---|---|---|
| 0.4 | 0.00 | −0.09 | −0.20 | −0.29 | −0.39 |
| 0.5 | 0.01 | −0.05 | −0.10 | −0.16 | −0.20 |
| 0.6 | 0.00 | −0.02 | −0.04 | −0.07 | −0.09 |
| 0.7 | 0.00 | 0.00 | −0.02 | −0.03 | −0.04 |
| 0.8 | 0.00 | 0.00 | −0.01 | −0.02 | −0.02 |
| Bias | SD | RMSE | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | 100 | 250 | 500 | 1000 | 2500 | 100 | 250 | 500 | 1000 | 2500 | 100 | 250 | 500 | 1000 | 2500 |
| No residual correlations | |||||||||||||||
| ML | −0.02 | −0.01 | 0.00 | 0.00 | 0.00 | 0.21 | 0.13 | 0.08 | 0.06 | 0.04 | 0.21 | 0.13 | 0.08 | 0.06 | 0.04 |
| ML (BBC) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.25 | 0.13 | 0.08 | 0.06 | 0.04 | 0.25 | 0.13 | 0.08 | 0.06 | 0.04 |
| LSAM | −0.16 | −0.07 | −0.03 | −0.01 | 0.00 | 0.19 | 0.12 | 0.08 | 0.06 | 0.04 | 0.25 | 0.14 | 0.09 | 0.06 | 0.04 |
| LSAM (BBC) | −0.08 | 0.00 | 0.01 | 0.00 | 0.00 | 0.27 | 0.15 | 0.09 | 0.06 | 0.04 | 0.28 | 0.15 | 0.09 | 0.06 | 0.04 |
| One positive residual correlation | |||||||||||||||
| ML | 0.06 | 0.06 | 0.07 | 0.07 | 0.07 | 0.21 | 0.13 | 0.08 | 0.06 | 0.04 | 0.22 | 0.14 | 0.11 | 0.09 | 0.08 |
| ML (BBC) | 0.09 | 0.07 | 0.06 | 0.07 | 0.07 | 0.25 | 0.14 | 0.09 | 0.06 | 0.04 | 0.27 | 0.15 | 0.11 | 0.09 | 0.08 |
| LSAM | −0.11 | −0.03 | 0.02 | 0.04 | 0.05 | 0.20 | 0.13 | 0.09 | 0.06 | 0.04 | 0.23 | 0.14 | 0.09 | 0.07 | 0.06 |
| LSAM (BBC) | −0.03 | 0.04 | 0.06 | 0.06 | 0.06 | 0.29 | 0.16 | 0.10 | 0.06 | 0.04 | 0.29 | 0.17 | 0.11 | 0.08 | 0.07 |
| Two positive residual correlations | |||||||||||||||
| ML | 0.10 | 0.11 | 0.12 | 0.11 | 0.12 | 0.20 | 0.13 | 0.08 | 0.06 | 0.04 | 0.22 | 0.17 | 0.14 | 0.13 | 0.12 |
| ML (BBC) | 0.14 | 0.12 | 0.12 | 0.11 | 0.12 | 0.24 | 0.13 | 0.08 | 0.06 | 0.04 | 0.27 | 0.18 | 0.14 | 0.13 | 0.12 |
| LSAM | −0.09 | 0.02 | 0.07 | 0.09 | 0.10 | 0.21 | 0.14 | 0.09 | 0.06 | 0.04 | 0.23 | 0.14 | 0.11 | 0.10 | 0.11 |
| LSAM (BBC) | 0.01 | 0.10 | 0.11 | 0.11 | 0.11 | 0.30 | 0.17 | 0.10 | 0.06 | 0.04 | 0.30 | 0.20 | 0.14 | 0.12 | 0.11 |
| Bias | RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | 100 | 250 | 500 | 1000 | 2500 | 100 | 250 | 500 | 1000 | 2500 | ||
| One positive cross-loading | ||||||||||||
| ML | 0.12 | 0.13 | 0.13 | 0.12 | 0.13 | 0.12 | 0.21 | 0.17 | 0.15 | 0.13 | 0.13 | 0.12 |
| ULS | 0.13 | 0.13 | 0.12 | 0.12 | 0.12 | 0.12 | 0.21 | 0.17 | 0.14 | 0.13 | 0.12 | 0.12 |
| RME | 0.13 | 0.13 | 0.13 | 0.12 | 0.12 | 0.12 | 0.22 | 0.18 | 0.16 | 0.14 | 0.13 | 0.12 |
| LSAM | −0.07 | 0.05 | 0.09 | 0.10 | 0.11 | 0.12 | 0.21 | 0.14 | 0.12 | 0.11 | 0.12 | 0.12 |
| GSAM-ML | −0.07 | 0.05 | 0.09 | 0.10 | 0.11 | 0.12 | 0.21 | 0.14 | 0.12 | 0.11 | 0.12 | 0.12 |
| GSAM-ULS | −0.01 | 0.08 | 0.10 | 0.11 | 0.12 | 0.12 | 0.19 | 0.14 | 0.13 | 0.12 | 0.12 | 0.12 |
| GSAM-RME | −0.03 | 0.06 | 0.08 | 0.08 | 0.05 | 0.01 | 0.22 | 0.16 | 0.13 | 0.11 | 0.08 | 0.01 |
| Geomin | −0.26 | −0.18 | −0.11 | −0.05 | −0.02 | 0.00 | 0.29 | 0.21 | 0.14 | 0.08 | 0.04 | 0.01 |
| Lp | −0.30 | −0.22 | −0.16 | −0.12 | −0.07 | 0.00 | 0.33 | 0.25 | 0.19 | 0.14 | 0.09 | 0.01 |
| Geomin(THR) | −0.26 | −0.18 | −0.11 | −0.06 | −0.02 | 0.00 | 0.29 | 0.21 | 0.14 | 0.09 | 0.04 | 0.01 |
| Lp(THR) | −0.29 | −0.23 | −0.17 | −0.13 | −0.07 | 0.00 | 0.32 | 0.26 | 0.20 | 0.15 | 0.09 | 0.01 |
| Geomin(RME) | −0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.21 | 0.16 | 0.13 | 0.09 | 0.05 | 0.01 |
| Lp(RME) | 0.06 | 0.10 | 0.10 | 0.10 | 0.09 | 0.08 | 0.24 | 0.20 | 0.17 | 0.14 | 0.12 | 0.10 |
| Geomin(THR,RME) | −0.03 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.22 | 0.17 | 0.13 | 0.09 | 0.05 | 0.01 |
| Lp(THR,RME) | 0.07 | 0.10 | 0.10 | 0.10 | 0.09 | 0.08 | 0.23 | 0.20 | 0.17 | 0.15 | 0.12 | 0.10 |
| Two positive cross-loadings | ||||||||||||
| ML | 0.22 | 0.24 | 0.24 | 0.24 | 0.24 | 0.24 | 0.25 | 0.25 | 0.24 | 0.24 | 0.24 | 0.24 |
| ULS | 0.22 | 0.23 | 0.23 | 0.23 | 0.23 | 0.23 | 0.25 | 0.25 | 0.24 | 0.23 | 0.23 | 0.23 |
| RME | 0.22 | 0.23 | 0.24 | 0.24 | 0.25 | 0.22 | 0.26 | 0.26 | 0.25 | 0.25 | 0.25 | 0.22 |
| LSAM | 0.07 | 0.17 | 0.21 | 0.23 | 0.24 | 0.25 | 0.19 | 0.20 | 0.22 | 0.24 | 0.24 | 0.25 |
| GSAM-ML | 0.07 | 0.17 | 0.21 | 0.23 | 0.24 | 0.25 | 0.19 | 0.20 | 0.22 | 0.24 | 0.24 | 0.25 |
| GSAM-ULS | 0.14 | 0.21 | 0.23 | 0.25 | 0.25 | 0.26 | 0.21 | 0.23 | 0.24 | 0.25 | 0.26 | 0.26 |
| GSAM-RME | 0.11 | 0.18 | 0.20 | 0.21 | 0.24 | 0.27 | 0.24 | 0.22 | 0.23 | 0.23 | 0.25 | 0.27 |
| Geomin | −0.21 | −0.14 | −0.07 | −0.02 | 0.02 | 0.03 | 0.24 | 0.18 | 0.13 | 0.09 | 0.05 | 0.03 |
| Lp | −0.25 | −0.18 | −0.13 | −0.10 | −0.07 | 0.00 | 0.28 | 0.22 | 0.17 | 0.13 | 0.09 | 0.01 |
| Geomin(THR) | −0.21 | −0.14 | −0.08 | −0.02 | 0.02 | 0.03 | 0.25 | 0.18 | 0.13 | 0.09 | 0.05 | 0.03 |
| Lp(THR) | −0.25 | −0.19 | −0.14 | −0.10 | −0.07 | 0.00 | 0.29 | 0.22 | 0.18 | 0.13 | 0.09 | 0.01 |
| Geomin(RME) | 0.04 | 0.08 | 0.08 | 0.06 | 0.02 | 0.00 | 0.22 | 0.18 | 0.16 | 0.13 | 0.08 | 0.01 |
| Lp(RME) | 0.12 | 0.17 | 0.18 | 0.19 | 0.19 | 0.18 | 0.22 | 0.22 | 0.21 | 0.21 | 0.20 | 0.20 |
| Geomin(THR,RME) | 0.04 | 0.09 | 0.09 | 0.06 | 0.02 | 0.00 | 0.22 | 0.19 | 0.16 | 0.13 | 0.08 | 0.01 |
| Lp(THR,RME) | 0.13 | 0.17 | 0.17 | 0.19 | 0.18 | 0.18 | 0.23 | 0.23 | 0.21 | 0.21 | 0.20 | 0.20 |
| Bias | RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | 100 | 250 | 500 | 1000 | 2500 | 100 | 250 | 500 | 1000 | 2500 | ||
| ML | 0.16 | 0.17 | 0.17 | 0.17 | 0.17 | 0.17 | 0.23 | 0.20 | 0.19 | 0.18 | 0.17 | 0.17 |
| ULS | 0.17 | 0.16 | 0.17 | 0.16 | 0.17 | 0.16 | 0.23 | 0.19 | 0.18 | 0.17 | 0.17 | 0.16 |
| RME | 0.16 | 0.15 | 0.15 | 0.14 | 0.13 | 0.12 | 0.24 | 0.20 | 0.18 | 0.15 | 0.14 | 0.12 |
| LSAM | −0.02 | 0.09 | 0.13 | 0.14 | 0.16 | 0.16 | 0.20 | 0.15 | 0.15 | 0.16 | 0.16 | 0.16 |
| GSAM-ML | −0.02 | 0.09 | 0.13 | 0.14 | 0.16 | 0.16 | 0.20 | 0.15 | 0.15 | 0.16 | 0.16 | 0.16 |
| GSAM-ULS | 0.03 | 0.11 | 0.14 | 0.15 | 0.16 | 0.17 | 0.19 | 0.16 | 0.16 | 0.16 | 0.17 | 0.17 |
| GSAM-RME | 0.02 | 0.10 | 0.13 | 0.12 | 0.12 | 0.06 | 0.22 | 0.18 | 0.17 | 0.15 | 0.14 | 0.11 |
| Geomin | −0.26 | −0.19 | −0.15 | −0.11 | −0.06 | 0.03 | 0.29 | 0.22 | 0.18 | 0.14 | 0.09 | 0.03 |
| Lp | −0.29 | −0.24 | −0.20 | −0.17 | −0.12 | −0.05 | 0.32 | 0.26 | 0.22 | 0.19 | 0.14 | 0.05 |
| Geomin(THR) | −0.25 | −0.19 | −0.14 | −0.08 | −0.04 | 0.00 | 0.28 | 0.21 | 0.16 | 0.11 | 0.07 | 0.01 |
| Lp(THR) | −0.29 | −0.23 | −0.19 | −0.15 | −0.10 | 0.00 | 0.32 | 0.26 | 0.21 | 0.17 | 0.12 | 0.01 |
| Geomin(RME) | −0.03 | 0.01 | 0.03 | 0.04 | 0.03 | 0.00 | 0.22 | 0.17 | 0.14 | 0.12 | 0.09 | 0.01 |
| Lp(RME) | 0.08 | 0.13 | 0.13 | 0.12 | 0.13 | 0.16 | 0.23 | 0.20 | 0.18 | 0.16 | 0.16 | 0.17 |
| Geomin(THR,RME) | −0.01 | 0.03 | 0.04 | 0.04 | 0.03 | 0.00 | 0.22 | 0.17 | 0.14 | 0.11 | 0.08 | 0.01 |
| Lp(THR,RME) | 0.09 | 0.13 | 0.13 | 0.11 | 0.11 | 0.10 | 0.24 | 0.21 | 0.19 | 0.16 | 0.15 | 0.13 |
| Bias | RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | 100 | 250 | 500 | 1000 | 2500 | 100 | 250 | 500 | 1000 | 2500 | ||
| Correctly specified model (DGM1) | ||||||||||||
| ML | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | 0.09 | 0.06 | 0.05 | 0.03 | 0.00 |
| ULS | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | 0.09 | 0.07 | 0.05 | 0.03 | 0.00 |
| LSAM | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.14 | 0.09 | 0.06 | 0.04 | 0.03 | 0.00 |
| RME | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.16 | 0.10 | 0.07 | 0.05 | 0.03 | 0.00 |
| Cross-Loadings (DGM2) | ||||||||||||
| ML | 0.08 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.20 | 0.16 | 0.13 | 0.12 | 0.10 | 0.09 |
| ULS | 0.11 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.22 | 0.17 | 0.15 | 0.14 | 0.13 | 0.12 |
| LSAM | 0.05 | 0.05 | 0.06 | 0.06 | 0.06 | 0.06 | 0.16 | 0.12 | 0.10 | 0.08 | 0.07 | 0.06 |
| RME | 0.08 | 0.06 | 0.06 | 0.05 | 0.05 | 0.03 | 0.21 | 0.15 | 0.12 | 0.10 | 0.08 | 0.04 |
| Residual correlations (DGM3) | ||||||||||||
| ML | 0.25 | 0.27 | 0.27 | 0.27 | 0.26 | 0.21 | 0.29 | 0.28 | 0.28 | 0.27 | 0.27 | 0.21 |
| ULS | 0.14 | 0.14 | 0.14 | 0.14 | 0.14 | 0.14 | 0.21 | 0.17 | 0.15 | 0.15 | 0.14 | 0.14 |
| LSAM | 0.15 | 0.16 | 0.17 | 0.17 | 0.17 | 0.17 | 0.21 | 0.19 | 0.18 | 0.17 | 0.17 | 0.17 |
| RME | 0.06 | 0.02 | 0.01 | 0.01 | 0.01 | 0.00 | 0.18 | 0.11 | 0.07 | 0.05 | 0.03 | 0.01 |
| Method | 0.1 | 0.2 | 0.3 | 0.4 |
|---|---|---|---|---|
| Correctly specified model (DGM1) | ||||
| ML | 0.00 | 0.00 | 0.00 | 0.00 |
| ULS | 0.00 | 0.00 | 0.00 | 0.00 |
| LSAM | 0.00 | 0.00 | 0.00 | 0.00 |
| RME | 0.00 | 0.00 | 0.00 | 0.00 |
| Cross-Loadings (DGM2) | ||||
| ML | 0.09 | 0.11 | 0.13 | 0.13 |
| ULS | 0.12 | 0.13 | 0.14 | 0.15 |
| LSAM | 0.06 | 0.07 | 0.08 | 0.08 |
| RME | 0.02 | 0.09 | 0.12 | 0.15 |
| Residual correlations (DGM3) | ||||
| ML | 0.20 | 0.20 | 0.18 | 0.16 |
| ULS | 0.14 | 0.13 | 0.12 | 0.10 |
| LSAM | 0.17 | 0.16 | 0.15 | 0.13 |
| RME | 0.00 | 0.00 | 0.00 | 0.00 |
| All Factor Correlations | All Factor Correlations | All Factor Correlations | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.4 | 0.4 | 0 | 0 | 0.4 | 0.4 | 0 | 0 | 0.4 | 0.4 | |
| 0 | 0.4 | 0 | 0.4 | 0 | 0.4 | 0 | 0.4 | 0 | 0.4 | 0 | 0.4 | |
| No bias | 47.4 | 14.5 | 13.3 | 0.0 | 63.0 | 29.6 | 29.6 | 0.0 | 47.4 | 14.1 | 11.5 | 0.0 |
| SAM better | 9.4 | 6.7 | 7.0 | 1.7 | 14.8 | 13.6 | 12.3 | 4.9 | 0.0 | 0.0 | 0.0 | 0.0 |
| SEM better | 4.9 | 5.8 | 11.9 | 3.2 | 0.0 | 0.0 | 0.0 | 0.0 | 13.0 | 13.0 | 24.5 | 3.1 |
| Both biased | 38.3 | 73.0 | 67.8 | 95.0 | 22.2 | 56.8 | 58.0 | 95.1 | 39.6 | 72.9 | 64.1 | 96.9 |
| All Factor Correlations | All Factor Correlations | All Factor Correlations | ||||
|---|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.2 | 0.4 | 0.2 | 0.4 | |
| No bias | 33.3 | 33.3 | 33.3 | 33.3 | 33.3 | 33.3 |
| SAM better | 0.0 | 3.1 | 0.0 | 4.9 | 0.0 | 0.0 |
| SEM better | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Both biased | 66.7 | 63.6 | 66.7 | 61.7 | 66.7 | 66.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robitzsch, A. Comparing the Robustness of the Structural after Measurement (SAM) Approach to Structural Equation Modeling (SEM) against Local Model Misspecifications with Alternative Estimation Approaches. Stats 2022, 5, 631-672. https://doi.org/10.3390/stats5030039
Robitzsch A. Comparing the Robustness of the Structural after Measurement (SAM) Approach to Structural Equation Modeling (SEM) against Local Model Misspecifications with Alternative Estimation Approaches. Stats. 2022; 5(3):631-672. https://doi.org/10.3390/stats5030039
Chicago/Turabian StyleRobitzsch, Alexander. 2022. "Comparing the Robustness of the Structural after Measurement (SAM) Approach to Structural Equation Modeling (SEM) against Local Model Misspecifications with Alternative Estimation Approaches" Stats 5, no. 3: 631-672. https://doi.org/10.3390/stats5030039
APA StyleRobitzsch, A. (2022). Comparing the Robustness of the Structural after Measurement (SAM) Approach to Structural Equation Modeling (SEM) against Local Model Misspecifications with Alternative Estimation Approaches. Stats, 5(3), 631-672. https://doi.org/10.3390/stats5030039






