Design and Prototype Development of a Combined-Function Quadrupole-Sextupole Magnet for the SPS-II Booster Synchrotron
Abstract
1. Introduction
1.1. Original Design of SPS-II Booster
1.2. Combined-Function Quadrupole-Sextupole Magnet (Combined Quadrupole)
2. Requirements and Design Parameters
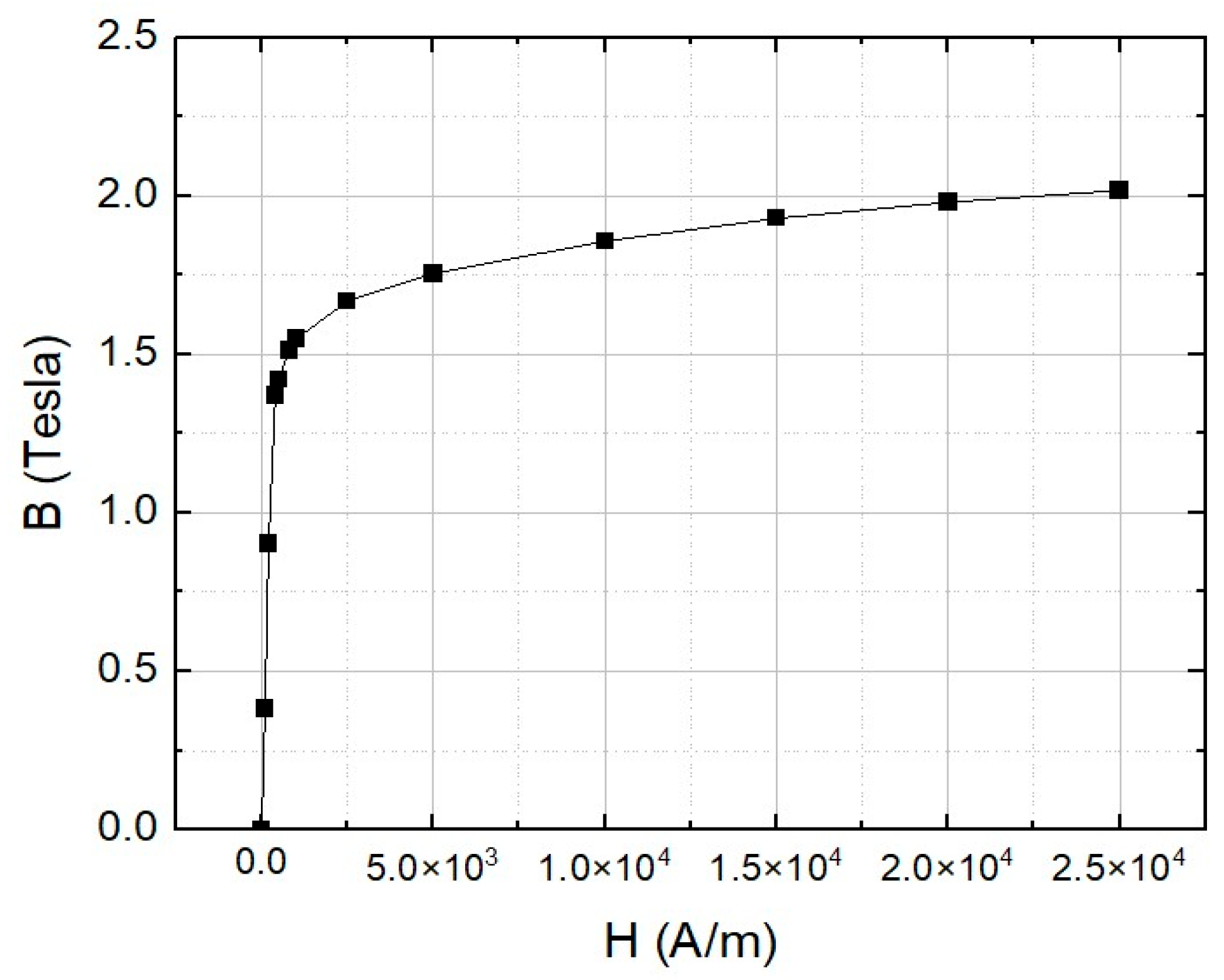
3. Magnet Design and Magnetic Field Simulation
3.1. Magnet Geometry
3.2. Yoke and Coil
3.3. Air Regions Defined in Opera-3D for Magnetic Field Simulation
3.4. Analysis Setting for Magnetic Field Simulation
3.5. Eddy Current Effect
4. Magnet Prototype
4.1. Prototype Manufacturing
4.2. Magnetic Field Measurement System
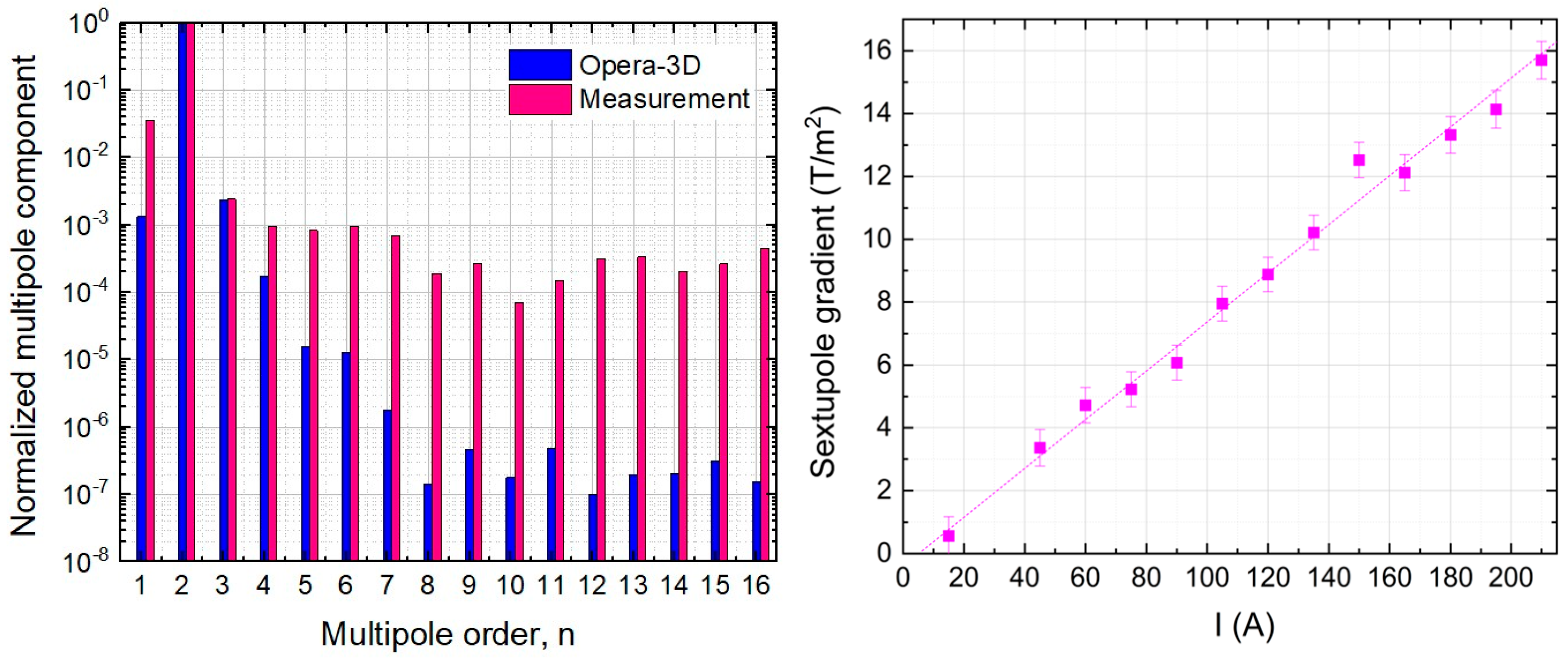
5. Results and Discussion
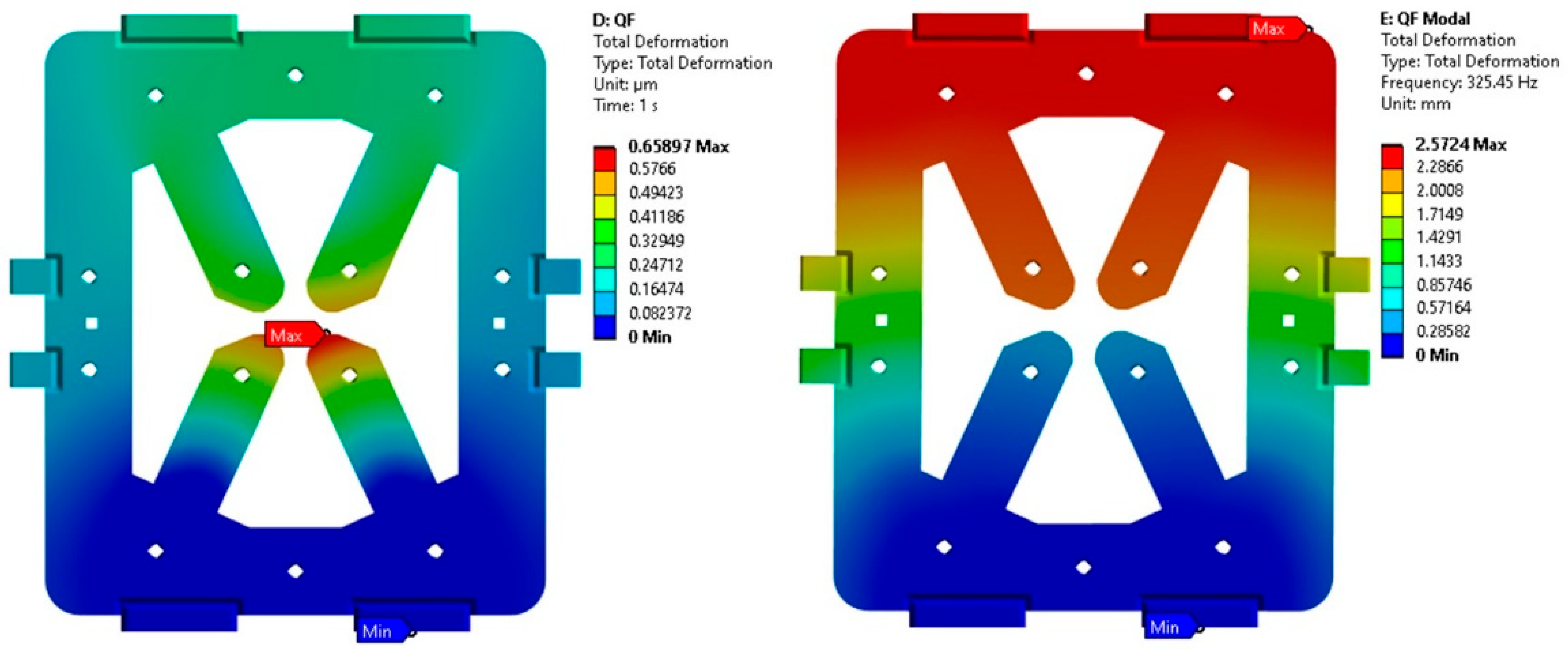
5.1. Mechanical Analysis
5.2. Eddy Effect
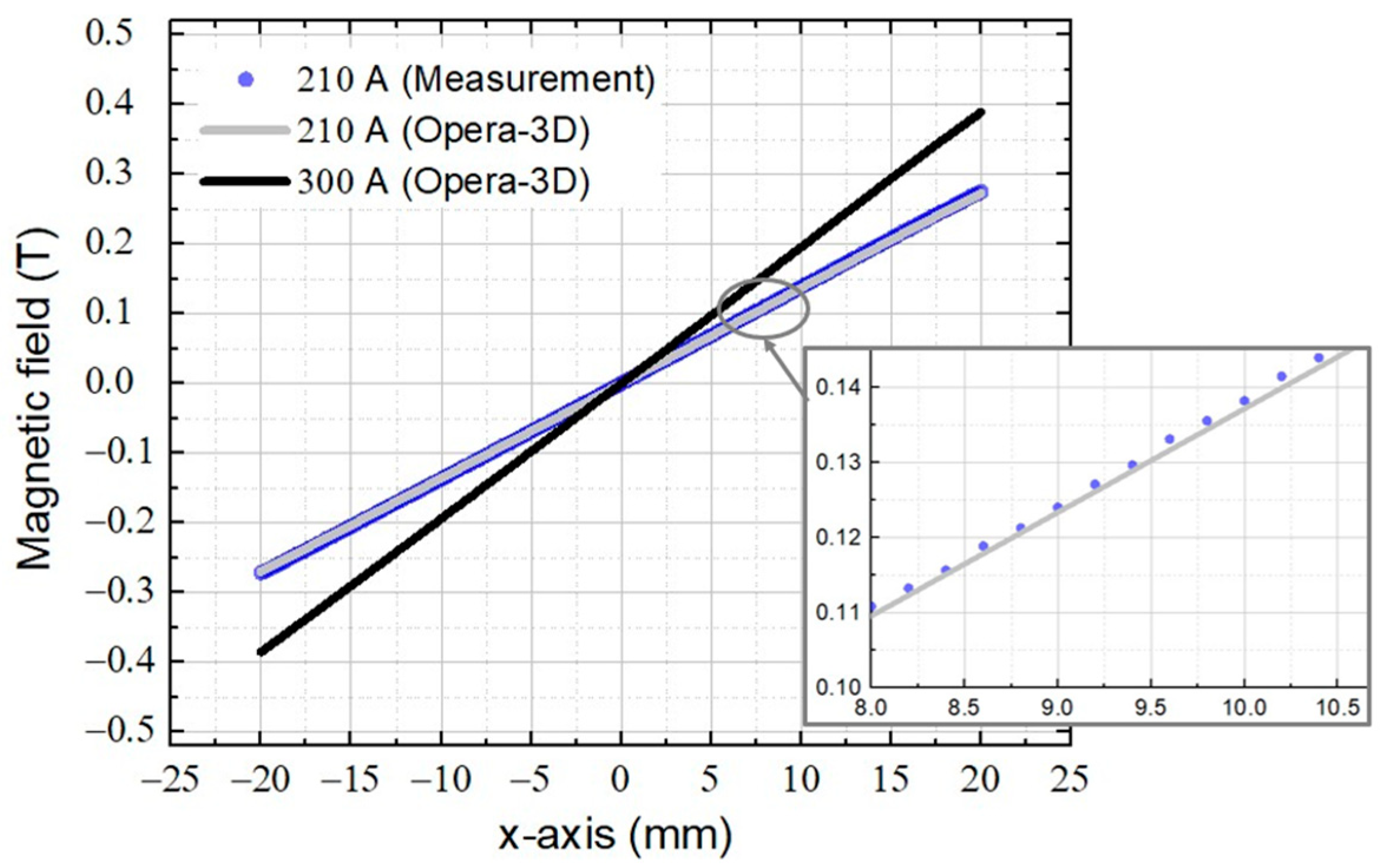
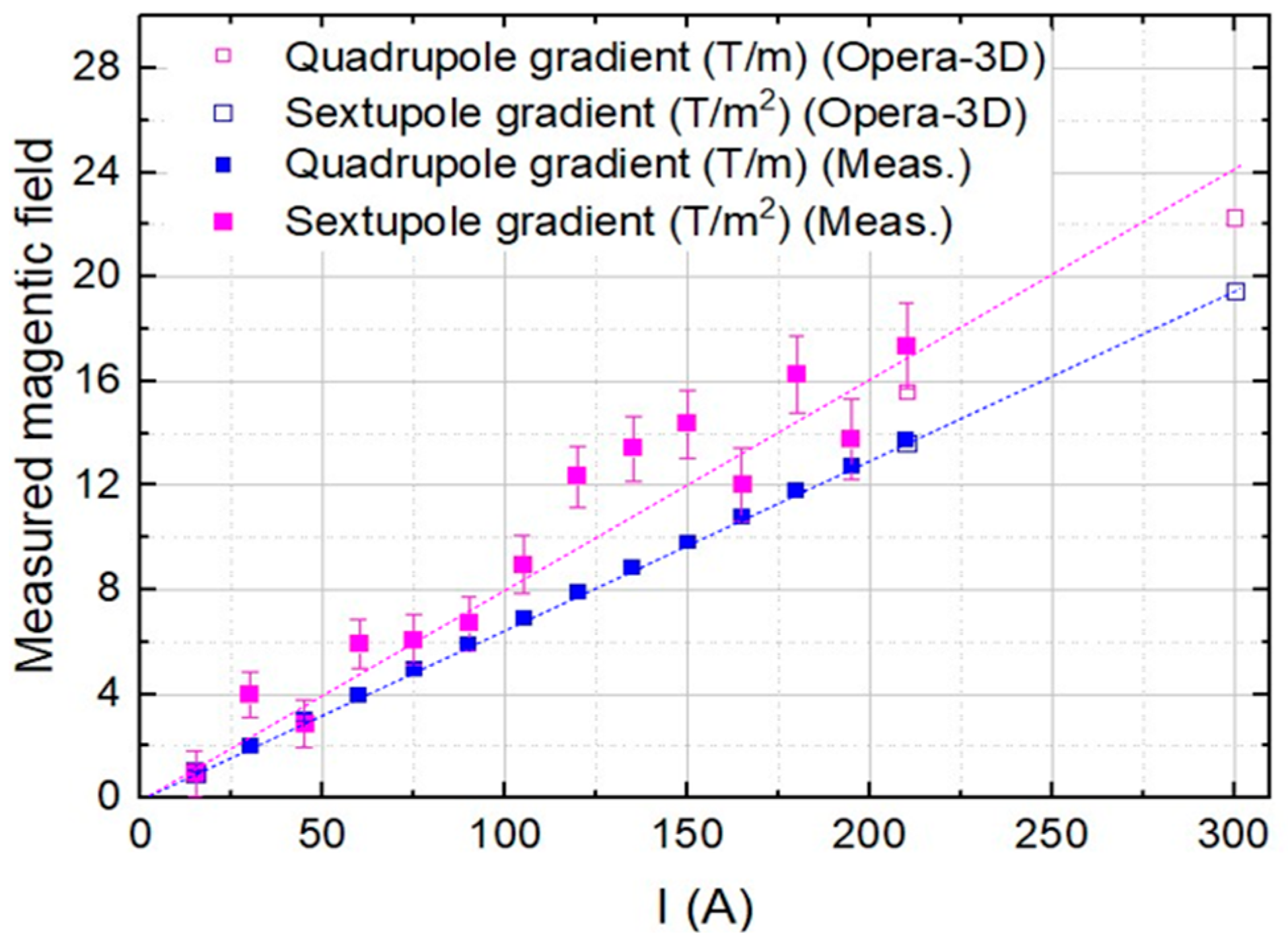
5.3. Magnetic Field of Combined-Function Quadrupole-Sextupole Magnet
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Klysubun, P.; Pulampong, T.; Sudmuang, P. Design and optimization of SPS-II storage ring. In Proceedings of the 8th International Particle Accelerator Conference (IPAC 2017), Copenhagen, Denmark, 14–19 May 2017; pp. 2773–2775. [Google Scholar] [CrossRef]
- Klysubu, P.; Boonsuya, S.; Chanwattana, T.; Jummunt, S.; Juntong, N.; Kwankasem, A.; Phimsen, T.; Photongkam, P.; Prawanta, S.; Pulampong, T.; et al. SPS-II: 4th-generation Synchrotron Light Source in Southeast Asia. In Proceedings of the 13th International Particle Accelerator Conference (IPAC 2022), Bangkok, Thailand, 12–17 June 2022; pp. 764–768. [Google Scholar] [CrossRef]
- Filho, A.H.C.; Rodrigues, A.R.D.; Farias, R.H.A.; Liu, L.R.; Carmo, D.; Nicolodi, C.; Junqueira, T.; Hojvat, C.; Sa, F.M. Commissioning Status of Sirius, the Brazilian 4th Generation Light Source. In Proceedings of the 12th International Particle Accelerator Conference (IPAC 2021), Campinas, Brazil, 24–28 May 2021; pp. 13–18. [Google Scholar] [CrossRef]
- Kuo, C.C.; Chen, C.T.; Chen, J.Y.; Chiu, M.S.; Chou, P.J.; Hsu, K.T.; Liu, Y.C.; Luo, G.H.; Tsai, H.J.; Tseng, F.H. Commissioning of the Taiwan Photon Source. In Proceedings of the IPAC’15, 6th International Particle Accelerator Conference, Richmond, VA, USA, 3–8 May 2015; Paper TUXC3. pp. 1314–1318. [Google Scholar] [CrossRef]
- Willeke, F.J. Commissioning of NSLS-II. In Proceedings of the 6th International Particle Accelerator Conference (IPAC’15), Richmond, VA, USA, 3–8 May 2015; Paper MOYGB3. pp. 15–20. [Google Scholar] [CrossRef]
- Streun, A. SLS 2.0, the Upgrade of the Swiss Light Source. In Proceedings of the 13th International Particle Accelerator Conference (IPAC’22), Bangkok, Thailand, 12–17 June 2022; Paper TUPOST032. pp. 925–928. [Google Scholar] [CrossRef]
- Krainara, S.; Klinkhieo, S.; Klysubun, P.; Pulampong, T.; Sudmuang, P. Conceptual Design of Booster Synchrotron for Siam Photon Source II. In Proceedings of the 12th International Particle Accelerator Conference (IPAC 2021), Campinas, Brazil, 24–28 May 2021; pp. 2795–2797. [Google Scholar]
- Tanabe, J. Iron Dominated Electromagnets: Design, Fabrication, Assembly and Measurements; World Scientific Publishing: Singapore, 2005; pp. 33–286. ISBN 9789813101982. [Google Scholar]
- Tatum, J. Rotation of Axes, Two Dimensions, Physics LibreTexts (Celestial Mechanics), Section 3.6, Updated March 5, 2022; CC BY-NC 4.0. Available online: https://phys.libretexts.org/Bookshelves/Astronomy__Cosmology/Celestial_Mechanics_(Tatum)/03%3A_Plane_and_Spherical_Trigonometry/3.06%3A_Rotation_of_Axes_Two_Dimensions (accessed on 27 June 2025).
- Wiedemann, H. Particle Accelerator Physics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 37–112. ISBN 978-3-540-49043-2. [Google Scholar]
- Dassault Systèmes UK Ltd. Opera-3D, Release 2021, 18R2 Reference Manual; Dassault Systèmes UK Ltd.: Kidlington, UK, 2018; pp. 1–918. [Google Scholar]
- ANSYS®. Academic Research, Release 2022; ANSYS, Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- Peng, Y.M.; Li, J.Y.; Meng, C.; Xu, H.S. Study of the ramping process for HEPS booster. In Proceedings of the 10th International Particle Accelerator Conference (IPAC’19), Melbourne, Australia, 19–24 May 2019; pp. 1521–1523. [Google Scholar] [CrossRef]
- Jummunt, S.; Sunwong, P.; Sudmuang, P.; Phimsen, T.; Klysubun, P. Design Progress of the Booster Synchrotron for Siam Photon Source II. In Proceedings of the 16th International Particle Accelerator Conference (IPAC 2025), Taipei, Taiwan, 1–6 June 2025; pp. 2004–2007. [Google Scholar] [CrossRef]
- Lake Shore Hall Probes. Available online: https://www.lakeshore.com/docs/default-source/product-downloads/catalog/hall-probes_l.pdf?sfvrsn=9e7b957d_6 (accessed on 1 June 2025).
- Kuo, C.Y.; Hwang, C.S.; Chang, C.H. Development of combined function magnets for the Taiwan photon source. In Proceedings of the 23rd Particle Accelerator Conference (PAC 2009), Vancouver, BC, Canada, 4–8 May 2009; pp. 202–204, MO6PFP030. [Google Scholar]
- Sunwong, P.; Prawanta, S.; Jummunt, S.; Numanoy, P.; Leetha, T.; Phimsen, T.; Pruekthaisong, P. Effects of Eddy Current and Permeability of Vacuum Chamber on Magnetic Field in Booster Synchrotron of Siam Photon Source II. J. Phys. Conf. Ser. 2025, 2934, 012013. [Google Scholar] [CrossRef]
- Chen, C.; Yang, C.; Yang, C.; Chen, H.; Huang, J. Integrated Hall probe and stretched wire measurement system for an in-vacuum undulator. In Proceedings of the 15th International Particle Accelerator Conference (IPAC 2025), Nashville, TN, USA, 19–24 May 2024; pp. 1398–1401. [Google Scholar] [CrossRef]
- Le Bec, G.; Chavanne, J.; Pennel, C. Stretched wire measurement of multipole accelerator magnets. Phys. Rev. Accel. Beams 2012, 15, 22401. [Google Scholar] [CrossRef]








| Design Parameters | BD | QF | QD | SF/SD |
|---|---|---|---|---|
| Effective length (m) | 1.5 | 0.25 | 0.2 | 0.2 |
| Number of magnets | 40 | 40 | 16 | 16/16 |
| Dipole field (T) | 1.048 | 0 | 0 | 0 |
| Quadrupole field (T/m) | −2.084 | 19.395 | −0.707 | 45 |
| Sextupole field (T/m2) | −29.995 | 22.327 | 0 | 167.483/−136.389 |
| Good Field Region (GFR) (mm) | ±10 | ±15 | ±15 | ±18 |
| Field homogeneity | 1 × 10−4 | 1 × 10−3 | 5 × 10−4 | 5 × 10−4 |
| Parameters | Value |
|---|---|
| Effective length | 250 mm |
| Physical length | 223.5 mm |
| Current excitation | 4890.38 A-turns |
| Operating current | 300 A |
| Number of turns | 14 turns |
| Conductor size | 7.5 mm × 7.5 mm |
| Bore radius | 23 mm (pole left), 23.153 mm (pole right) |
| Multipole Field | Opera-3D | Hall-Probe Measurement |
|---|---|---|
| B0 (T) | 0.0001 | 0.0001 ± --- |
| B1 (T/m) | 13.6391 | 13.7320 ± 0.008 |
| B2 (T/m2) | 15.6171 | 17.3266 ± 1.647 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jummunt, S.; Sunwong, P.; Prawanta, S.; Leetha, T.; Numanoy, P.; Thiabsi, N.; Sudmuang, P. Design and Prototype Development of a Combined-Function Quadrupole-Sextupole Magnet for the SPS-II Booster Synchrotron. Particles 2025, 8, 77. https://doi.org/10.3390/particles8030077
Jummunt S, Sunwong P, Prawanta S, Leetha T, Numanoy P, Thiabsi N, Sudmuang P. Design and Prototype Development of a Combined-Function Quadrupole-Sextupole Magnet for the SPS-II Booster Synchrotron. Particles. 2025; 8(3):77. https://doi.org/10.3390/particles8030077
Chicago/Turabian StyleJummunt, Siriwan, Prapaiwan Sunwong, Supachai Prawanta, Thongchai Leetha, Pajeeraporn Numanoy, Netchanok Thiabsi, and Porntip Sudmuang. 2025. "Design and Prototype Development of a Combined-Function Quadrupole-Sextupole Magnet for the SPS-II Booster Synchrotron" Particles 8, no. 3: 77. https://doi.org/10.3390/particles8030077
APA StyleJummunt, S., Sunwong, P., Prawanta, S., Leetha, T., Numanoy, P., Thiabsi, N., & Sudmuang, P. (2025). Design and Prototype Development of a Combined-Function Quadrupole-Sextupole Magnet for the SPS-II Booster Synchrotron. Particles, 8(3), 77. https://doi.org/10.3390/particles8030077





