Exploring the Neutron Magic Number in Superheavy Nuclei: Insights into N = 258

Abstract

In the framework of axial symmetric relativistic Hartree–Bogoliubov (RHB) theory and the Skyrme Hartree–Fock–Bogoliubov (HFB) theory, the evolution of shell structure, density distribution, and ground state deformation in superheavy nuclei proximate to $N=258$ are investigated within the relativistic functionals DD-PC1 and DD-ME2, as well as the non-relativistic functional UNEDF0. The results from DD-ME2 and UNEDF0 indicate that $N=258$ is a neutron magic number, whereas DD-PC1 does not anticipate the existence of a bound $N=258$ magic nucleus. Further discussion suggests that the emergence of the magic number $N=258$ is related to the depression of the central density.

1. Introduction

The synthesis of superheavy elements and the exploration of their stability are important research areas in low-energy nuclear physics, which will help us address fundamental questions such as the boundaries of the nuclear chart and the limits of element existence. The heaviest element observed so far has a proton number $Z=118$ [1,2,3], and attempts to synthesize even heavier elements are ongoing [4,5,6,7]. For superheavy nuclei, their stability is primarily determined by shell effects, and self-consistent mean-field models based on various relativistic and non-relativistic energy density functionals [8,9,10,11,12] are powerful tools for studying the shell structure and stability of these nuclei.

Over the past few decades, numerous systematic studies of the superheavy nuclei region have been conducted using EDFs. Early calculations are based on several sets of relativistic and non-relativistic functionals under the assumption of spherical symmetry and have explored the distribution of magic numbers in superheavy nuclei [13,14,15,16]. The predictions of different functionals show some variation, such as proton numbers $Z=114$ or $Z=120$, and neutron numbers $N=172$ and $N=184$. However, most investigations predict the appearance of a spherical shell gap at $N=258$. Ref. [17] reveals the influence of spin–orbit splitting on the formation of the shell gap at $Z=120$ based on relativistic Hartree–Fock–Bogoliubov (RHFB) calculations. Ref. [18] discusses the impact of the evolution of central density in superheavy nuclei on the shell structure, with results showing that the depression of nuclear central density leads to shell gaps at $Z=120$ and $N=172$. In contrast, a flatter density distribution is more favorable for the appearance of the magic number $N=184$. The RHB calculations under the assumption of axial deformation reveal the significant role of deformation in the shell evolution of superheavy nuclei [19]. The results indicate that the shell gap at $N=172$ has a minimal impact on the structure of superheavy nuclei, whereas the shell gap at $N=184$ has a substantial impact. Ref. [20], based on RHB calculations with axial and triaxial deformation, predicts the widespread existence of toroidal energy minima in superheavy nuclei and forecasts the existence of spherical regions of superheavy nuclei. Nevertheless, none of these studies discuss the potential existence of the larger neutron magic number $N=258$.

Recently, Ref. [21] conducted a systematic study on the ground-state and fission properties of actinides and superheavy elements using various relativistic density functionals, revealing a shell gap at $N=258$. Meanwhile, calculations using the PC-PK1 functional [22] within the framework of deformed relativistic Hartree–Bogoliubov in continuum theory [23] have supported 258 as a neutron magic number [24,25,26]. To investigate whether 258 is indeed a neutron magic number, this work explores the shell structure evolution near $N=258$ within the axial RHB and HFB frameworks, based on the relativistic density functionals DD-PC1 [27] and DD-ME2 [28], as well as the non-relativistic density functional UNEDF0 [29].

The article is arranged as follows. In Section 2, the numerical conditions employed in the calculations using the RHB and Skyrme HFB methods are elaborated. The results for the two-neutron shell gaps near $N=258$, the evolution of the spherical shell structure, and the density distributions obtained from calculations based on different density functionals are presented and discussed in Section 3. The Section 4 provides a summary and offers some perspectives.

2. The Details of the Theoretical Calculations

In the calculations performed within the axial RHB framework [30], a separable form of the finite-range Gogny pairing interaction [31] is adopted to avoid uncertainties arising from the choice of the pairing window [32]. Due to the omission of fission, the selection of ground state is restricted to a certain range of quadrupole deformations. Through multiple tests, it is found that truncating the basis to $N_F=20$ fermionic shells and $N_B=20$ bosonic shells already yields satisfactory accuracy.

The calculations based on the UNEDF0 functional are performed within the axial Skyrme HFB framework [33,34]. A density-dependent zero-range force with a mixture of volume and surface characteristics is chosen for the pairing interaction. To avoid pairing collapse near closed shells, the Lipkin-Nogami (LN) method is employed in the calculations [29,35,36]. After extensive testing, the quasiparticle energy cutoff is set to 60 MeV, and the basis is truncated to 26 shells.

3. Results and Discussion

The peak in the two-nucleon gaps represents the sharp change in the two-nucleon separation energy, which can be regarded as a signature of the emergence of magic numbers [16,17]. The two-neutron gap ${\delta }_{2\mathrm{n}}$ is defined as

$${\delta }_{2\mathrm{n}}(Z,N)=S_{2\mathrm{n}}(Z,N)-S_{2\mathrm{n}}(Z,N+2),$$

(1)

where $S_{2\mathrm{n}}(Z,N)$ is the two neutron separation energy for a nucleus with proton number Z and neutron number N. The two-neutron gap ${\delta }_{2\mathrm{n}}$ essentially reflects the rate of change in the binding energy of nuclei along an isotopic chain.

The two-neutron gaps and ground-state deformations obtained from RHB calculations using the DD-PC1 and DD-ME2 functionals and HFB calculations using the UNEDF0 functional are shown in Figure 1. The hollow symbols represent unbound nuclei. The calculations based on the DD-PC1 functional cover the isotopic chains from $Z=96$ to $Z=110$. The results indicate that DD-PC1 does not yield a bound nucleus at $N=258$ within the calculated isotopic chains. Specifically, for the $Z=110$ chain, the drip line is located at $N=256$.

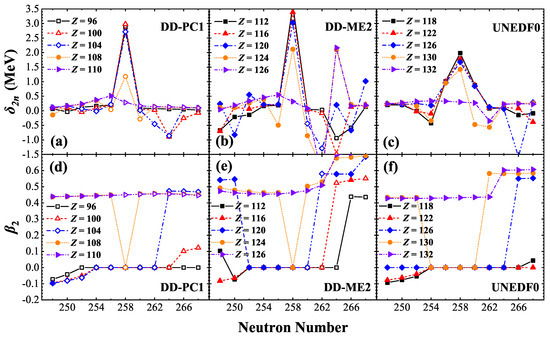
Figure 1. The two-neutron gaps ${\delta }_{2\mathrm{n}}$ (top) and quadrupole deformation ${\beta }_2$ (bottom) at the ground state for several isotopic chains, obtained from RHB calculations based on the DD-PC1 (a,d) and DD-ME2 (b,e) functionals, and from HFB calculations based on the UNEDF0 (c,f) functional. The hollow symbols indicate that the nucleus is unbound.

For the DD-ME2 functional, the calculations span the isotopic chains from $Z=112$ to $Z=126$. In Figure 1b, a strong shell effect is also observed at $N=258$, where the two-neutron shell gap gradually decreases with the increasing proton number. It significantly reduces at $Z=124$, and the peak disappears entirely at $Z=126$. Meanwhile, a prominent peak appears at $N=264$. In Figure 1e, the evolution of the deformation at the ground state shows that the competition between spherical and prolate shapes leads to the disappearance of the shell structure at $Z=126$. On the other hand, for the chains from $Z=112$ to $Z=120$, the nuclei at $N=260$ are unbound. For $Z=120$, the nucleus at $N=264$ becomes bound, likely due to the emergence of a new shell structure at $N=264$, which increases the stability of nearby nuclei.

The results from calculations using the UNEDF0 functional exhibit significant differences compared to those with DD-ME2. As shown in Figure 1c, in the calculations spanning isotopic chains from $Z=118$ to $Z=132$, a broader but lower peak appears near $N=258$, suggesting a weaker shell effect. The shape of the peak changes noticeably at $Z=130$, and it disappears entirely in the $Z=132$ chain. Upon examining the shape evolution in Figure 1f, similar to the case with DD-ME2, the competition between spherical and prolate shapes leads to the disappearance of the shell structure near $N=258$. In Figure 1b,c, instances where the ${\delta }_{2\mathrm{n}}$ becomes negative often correspond to sudden changes in the ground-state shape of the nucleus as illustrated in Figure 1e,f. These shape transitions cause the rate of change in the total energy along the isotopic chain to decrease and then increase with the addition of neutrons, resulting in negative values for the ${\delta }_{2\mathrm{n}}$. Since DD-PC1 produces unbound results, the following discussion will primarily focus on the results from DD-ME2 and UNEDF0.

Based on the DD-ME2 functional, the evolution of the spherical shell structure and density variation near $N=258$ within isotopic chains $Z=124$ and isotonic chains $N=258$ is investigated, with the results presented in Figure 2. In the density distributions shown in Figure 2b,d, the solid lines represent neutron density, while the dash-dot lines represent proton density. As shown in Figure 2a, the spin–orbit splitting of the $1k$ state, along with the approximate restoration of pseudospin symmetry between the three pairs of pseudospin partners ($2h_{9/2}$, $3f_{7/2}$), ($3f_{5/2}$, $4p_{3/2}$) and ($1k_{15/2}$, $2i_{13/2}$) together contribute to the formation of large shell gaps at $N=228$ and $N=258$. In the isotopic chain, as the neutron number increases, the shell gap at $N=258$ gradually decreases. This trend can be explained by the density variations observed in Figure 2b. As the neutron number increases from $N=254$ to $N=258$, the occupancy of the $4p$ orbital causes a sudden rise in neutron density at the center. As the neutron number continues to increase, the $1k_{15/2}$ orbital is occupied, but this only has a small impact on the shape of the potential, particularly on the radial profile at the bottom of the potential. The changes in the potential are reflected in the energy levels, and it can be seen that there are only limited changes in the energy levels near the Fermi surface in the isotopic chain.

Figure 2. The neutron single-particle levels (a) and nucleon density distributions (b) for the spherical states of $Z=124$ isotopes, as well as the neutron single-particle levels (c) and nucleon density distributions (d) for the spherical states of $N=258$ isotones, obtained from RHB calculations based on the DD-ME2 functional. In the density distribution plots, the solid lines represent the neutron density distribution, while the dash-dot lines represent the proton density distribution.

For the isotonic chain $N=258$ as shown in Figure 2c, the increase in proton number leads to a rapid decrease in the shell gap at $N=258$. Observing the density evolution in Figure 2d, it can be observed that as the proton number increases, the occupation of low-j orbitals causes the central proton density to rise. In self-consistent calculations, the change in proton density feeds back to the neutrons through the vector potential, driving the density distributions of proton and neutron to become more similar. In the isotonic chain, this results in a significant change in the shape of the neutron potential. The alterations in the potential are reflected in the neutron energy levels, and it can be seen that as the proton number increases, the shell gap at $N=258$ rapidly decreases. Ref. [37] has comprehensively discussed the physical mechanisms underlying the formation or suppression of the central density depression in nuclei.

To explain the differences observed near $N=258$ with the UNEDF0 functional, Figure 3 presents the two-neutron gaps ${\delta }_{2\mathrm{n}}$ calculated for the $Z=124$ isotopic chain, both with and without the LN method. It can be observed that if the LN method is not employed to account for pairing, the trend of the ${\delta }_{2\mathrm{n}}$ with the UNEDF0 functional near $N=258$ becomes similar to the results from the DD-ME2 functional. Comparing the calculations with and without the LN method, the differences become more pronounced as one approaches $N=258$. A similar result can also be observed in the calculations around $N=184$.

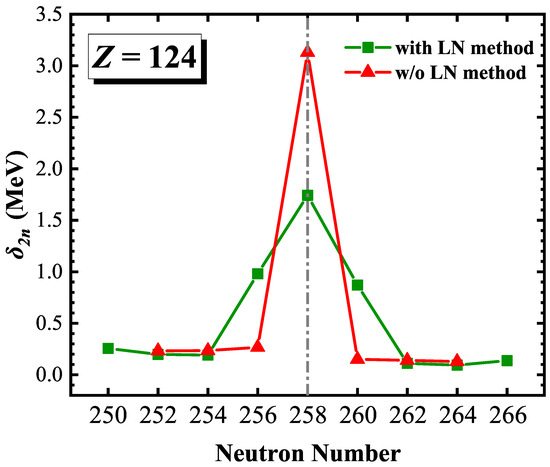
Figure 3. The two-neutron gaps ${\delta }_{2\mathrm{n}}$ for the $Z=124$ isotopic chain obtained from HFB calculations based on the UNEDF0 functional. Green squares indicate the use of the LN method to treat pairing, while red triangles represent calculations without the LN method.

Figure 4 shows the differences in neutron occupancy probabilities near the Fermi surface for the nuclei ${}^{380}124_{256}$ and ${}^{382}124_{258}$ under both the usage and non-usage of the LN method. In the case where the LN method is applied, comparing the results in Figure 4a,b, the neutron occupancy of ${}^{380}124_{256}$ is similar to that of ${}^{382}124_{258}$, with neutrons having a certain occupancy probability above the Fermi surface. Additionally, a significant change in the Fermi energy can be observed, and the shell gap at $N=258$ is noticeably decreased. In contrast, without the LN method, there is a significant difference in neutron occupancy between ${}^{380}124_{256}$ and ${}^{382}124_{258}$. For ${}^{382}124_{258}$, the occupancy probability of levels above the Fermi surface is 0. This difference in occupancy probabilities feeds back into the density distribution, subsequently affecting the energy. The application of the LN method has a substantial impact on the kinetic energy, pairing energy, and volume energy, ultimately leading to smaller energy differences between the isotopes. This also explains why the ${\delta }_{2\mathrm{n}}$ obtained with UNEDF0 in Figure 1c is generally smaller.

Figure 4. The single-neutron level occupation probabilities for ${}^{380}124_{256}$ (a,c) and ${}^{382}124_{258}$ (b,d) obtained from HFB calculations based on the UNEDF0 functional. The top panels use the LN method to treat pairing, while the bottom panels do not. The yellow dash-dot line represents the neutron Fermi energy. The green dashed line corresponds to the BCS formula with an average pairing gap.

Finally, based on the UNEDF0 functional, the evolution of the spherical shell structure and density distribution in the $Z=124$ isotopic chain and the $N=258$ isotonic chain are presented in Figure 5. In the density distributions shown in Figure 5b,d, the solid lines represent neutron density, while the dash-dot lines represent proton density. Figure 5a shows the changes in the spherical shell structure in the $Z=124$ isotopic chain as the neutron number increases. Unlike the results from the DD-ME2 functional, the $1k_{15/2}$ and $2i_{13/2}$ orbitals have exchanged positions, and there is a higher degree of degeneracy between the $3f_{5/2}$ and $4p_{3/2}$, $2h_{9/2}$ and $3f_{7/2}$, as well as between the $1j_{13/2}$ and $2h_{11/2}$. Due to the use of the LN method, the energy level spacing between $4p_{1/2}$ and $2i_{13/2}$ at $N=258$ decreases in the isotopic chain, which is consistent with the results shown in Figure 4. Furthermore, the shell gap at $N=258$ does not decrease with increasing the neutron number but remains stable. Observing the density evolution presented in Figure 5b, as previously mentioned, the neutron and proton density distributions show no significant changes due to the use of the LN method, which corresponds to the stability of the shell structure.

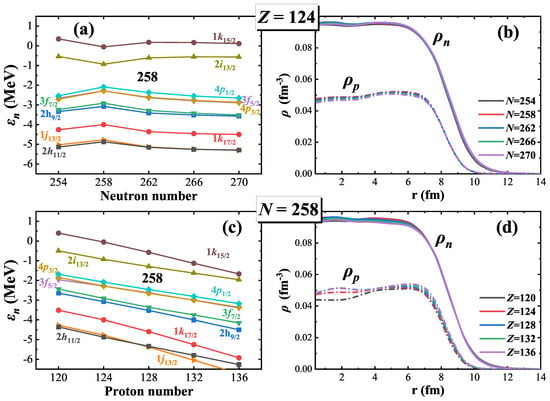
Figure 5. The neutron single-particle levels (a) and nucleon density distributions (b) for the spherical states of $Z=124$ isotopes, as well as the neutron single-particle levels (c) and nucleon density distributions (d) for the spherical states of $N=258$ isotones, obtained from the HFB calculations based on the UNEDF0 functional. In the density distribution plots, the solid lines represent the neutron density distribution, while the dash-dot lines represent the proton density distribution.

For the isotonic chain at $N=258$, Figure 5c shows that as the proton number increases, the neutron shell gap caused by the $4p_{1/2}$ and $2i_{13/2}$ orbitals remains essentially unchanged. However, the energy of the $1k$ orbital drops at a faster rate. It can be anticipated that as the proton number continues to increase, the spherical shell gap at $N=258$ will be determined by the $4p_{1/2}$ and $1k_{15/2}$ orbitals and will gradually decrease.

Figure 5d shows the evolution of the density distribution. As the proton number increases, the central proton density grows, but unlike the results from DD-ME2, this change does not significantly impact the neutron density distribution. However, a slight decrease in neutron density near the surface is still observable, indicating that the density distribution of high-j orbitals is increasingly concentrated toward the center. This is consistent with the evolution of the energy levels.

4. Conclusions

Based on relativistic functionals DD-PC1 and DD-ME2, and the non-relativistic functional UNEDF0, calculations for superheavy nuclei were performed within the axially symmetric RHB and HFB frameworks, respectively. The DD-PC1 functional did not predict a bound magic nucleus at $N=258$, but the results indicated a significant shell gap at this neutron number. Calculations using the DD-ME2 functional yielded a sharp and narrow peak in the two-neutron gap at $N=258$, indicating the presence of a magic number. In contrast, the UNEDF0 functional produced a wider and lower peak for the two-neutron gap.

Further comparison of HFB calculations based on the UNEDF0 functional, with and without the LN method, revealed that the use of the LN method caused the $N=258$ nucleus to have similar single-particle orbital occupations to its neighboring nuclei. This led to similar density distributions and energies across isotopes, resulting in a significantly smaller two-neutron gap compared to the results from DD-ME2.

Due to the competition between spherical and prolate deformations, the neutron magic number $N=258$ disappears at $Z=126$ for DD-ME2 and at $Z=132$ for UNEDF0. By examining the evolution of the spherical shell structure and the nucleon density distribution within isotopic and isotonic chains, it was found that a decreasing central density is more favorable for maintaining the magic number $N=258$. A similar conclusion was observed for $Z=120$ and $N=172$ [18]. For the neutron magic number $N=258$, the results indicate that the central density depression is primarily driven by the proton contribution.

In summary, both the DD-ME2 and UNEDF0 functionals predict that $N=258$ is a neutron magic number, and the emergence of such a shell structure is related to the depression of the central density. However, this does not necessarily imply the existence of a superheavy stability island near $N=258$. Further triaxial deformation calculations are needed to assess whether the nuclei in this region will be reasonably stable against spontaneous fission.