Exploring the Neutron Magic Number in Superheavy Nuclei: Insights into N = 258
Abstract
1. Introduction
2. The Details of the Theoretical Calculations
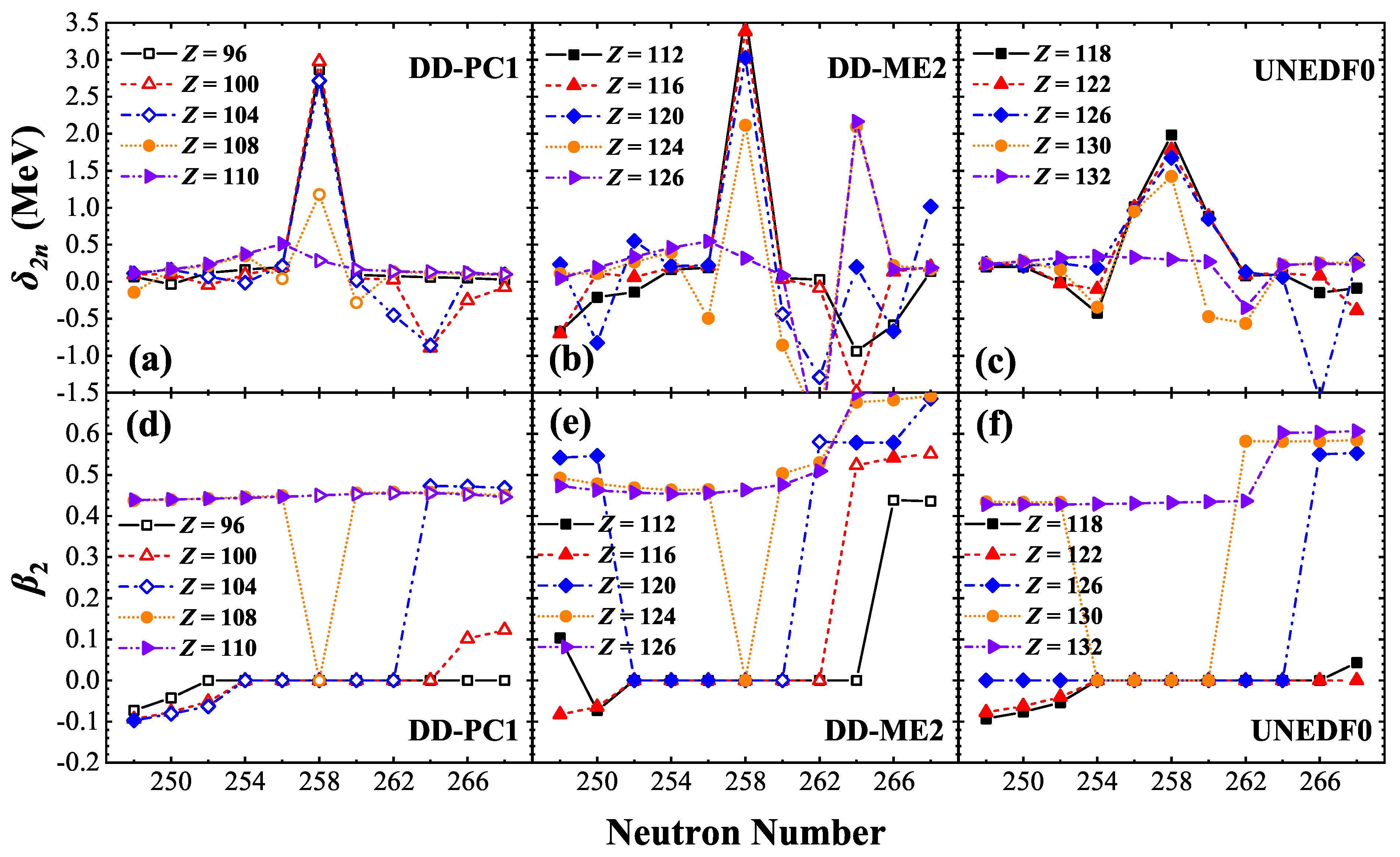
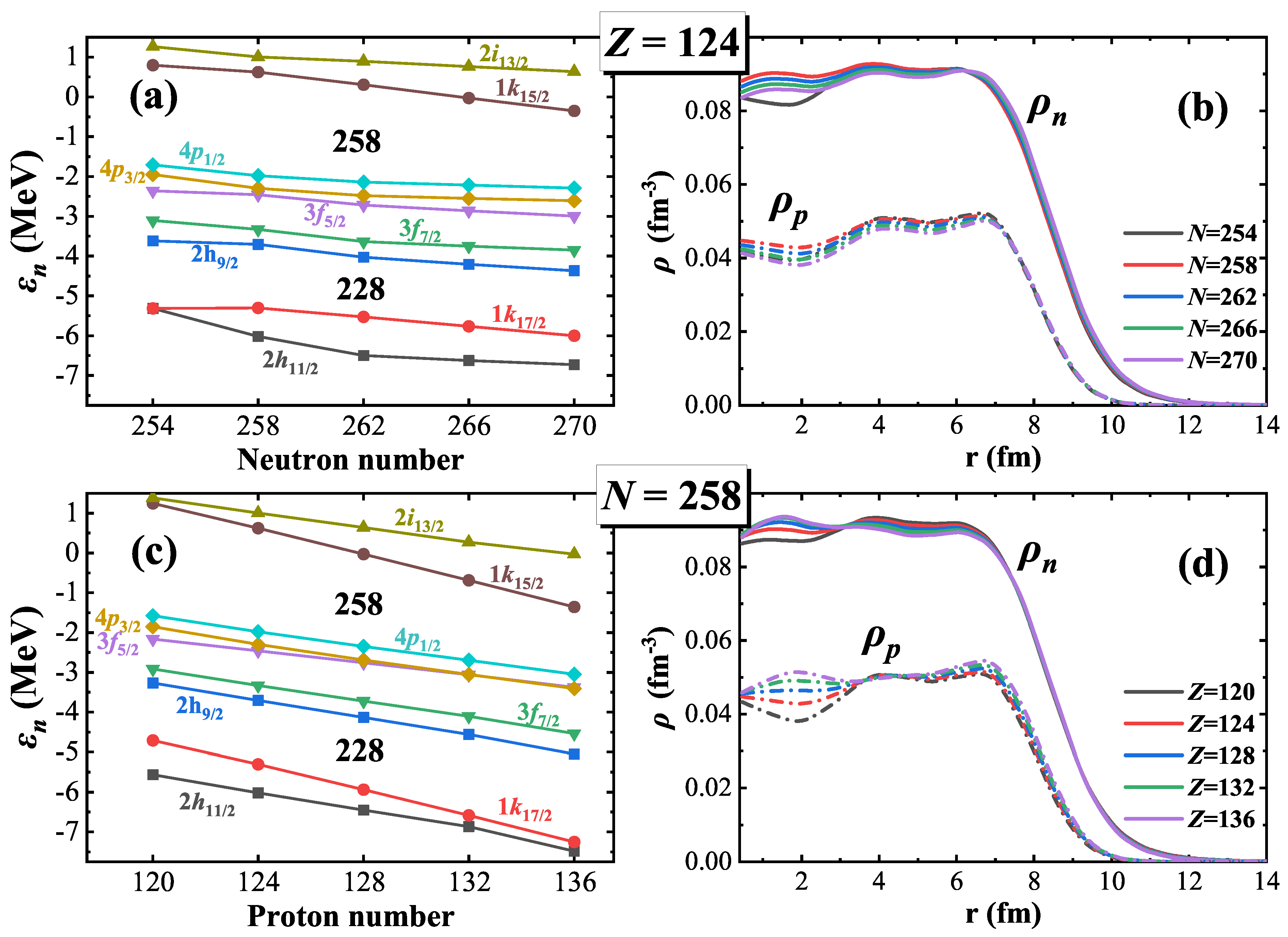
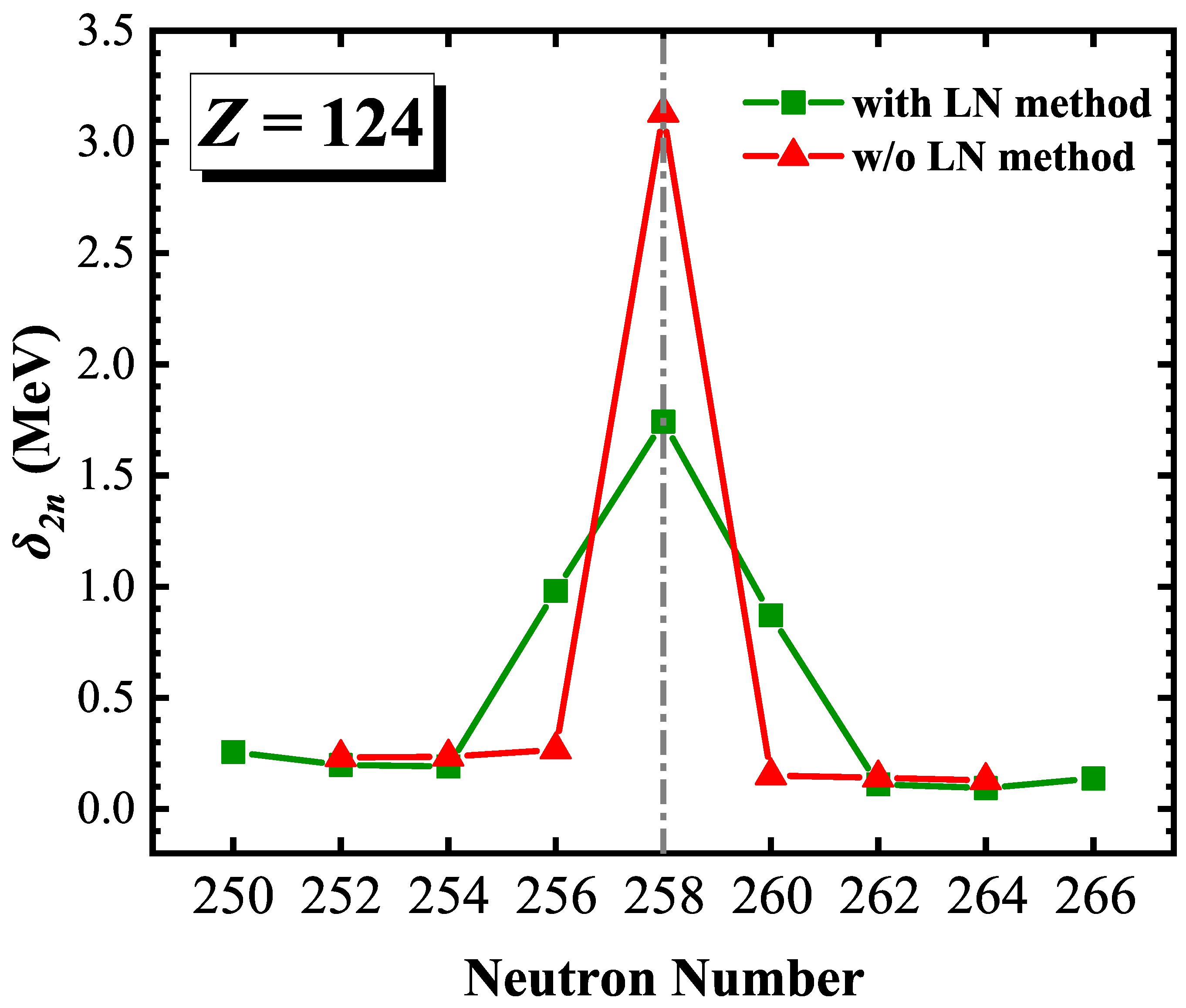
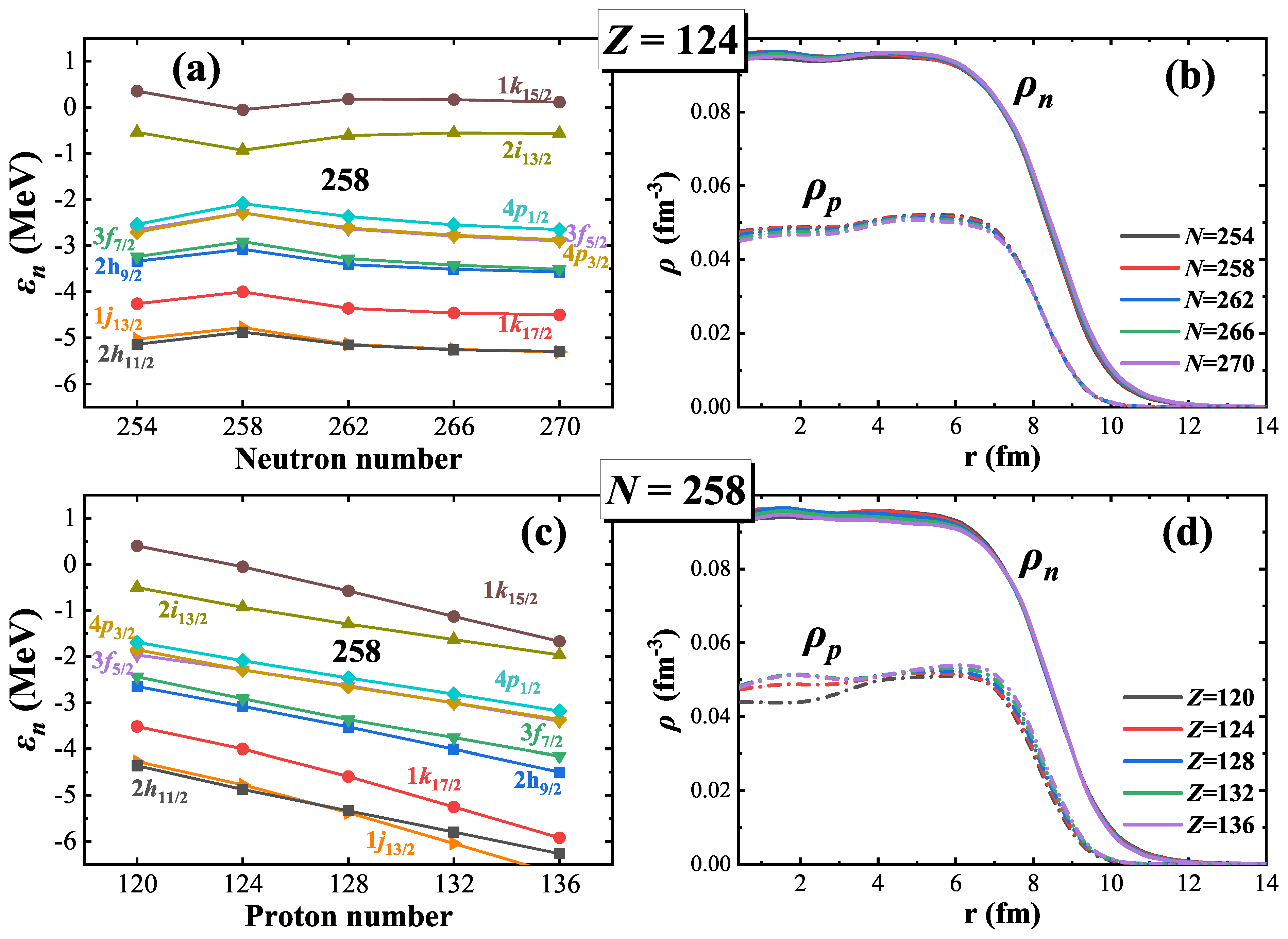
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oganessian, Y.T.; Utyonkov, V.K.; Lobanov, Y.V.; Abdullin, F.S.; Polyakov, A.N.; Sagaidak, R.N.; Shirokovsky, I.V.; Tsyganov, Y.S.; Voinov, A.A.; Gulbekian, G.G.; et al. Synthesis of the isotopes of elements 118 and 116 in the 249Cf and 245Cm+48Ca fusion reactions. Phys. Rev. C 2006, 74, 044602. [Google Scholar] [CrossRef]
- Oganessian, Y.T.; Abdullin, F.S.; Alexander, C.; Binder, J.; Boll, R.A.; Dmitriev, S.N.; Ezold, J.; Felker, K.; Gostic, J.M.; Grzywacz, R.K.; et al. Production and Decay of the Heaviest Nuclei 293,294117 and 294118. Phys. Rev. Lett. 2012, 109, 162501. [Google Scholar] [CrossRef] [PubMed]
- Oganessian, Y.T.; Utyonkov, V.K. Super-heavy element research. Rep. Prog. Phys. 2015, 78, 036301. [Google Scholar] [CrossRef] [PubMed]
- Oganessian, Y.T.; Utyonkov, V.K.; Lobanov, Y.V.; Abdullin, F.S.; Polyakov, A.N.; Sagaidak, R.N.; Shirokovsky, I.V.; Tsyganov, Y.S.; Voinov, A.A.; Mezentsev, A.N.; et al. Attempt to produce element 120 in the 244Pu+58Fe reaction. Phys. Rev. C 2009, 79, 024603. [Google Scholar] [CrossRef]
- Khuyagbaatar, J.; Yakushev, A.; Düllmann, C.E.; Ackermann, D.; Andersson, L.L.; Asai, M.; Block, M.; Boll, R.A.; Brand, H.; Cox, D.M.; et al. Search for elements 119 and 120. Phys. Rev. C 2020, 102, 064602. [Google Scholar] [CrossRef]
- Sakai, H.; Haba, H.; Morimoto, K.; Sakamoto, N. Facility upgrade for superheavy-element research at RIKEN. Eur. Phys. J. A 2022, 58, 238. [Google Scholar] [CrossRef]
- Gan, Z.G.; Huang, W.X.; Zhang, Z.Y.; Zhou, X.H.; Xu, H.S. Results and perspectives for study of heavy and super-heavy nuclei and elements at IMP/CAS. Eur. Phys. J. A 2022, 58, 158. [Google Scholar] [CrossRef]
- Meng, J.; Toki, H.; Zhou, S.G.; Zhang, S.Q.; Long, W.H.; Geng, L.S. Relativistic continuum Hartree Bogoliubov theory for ground-state properties of exotic nuclei. Prog. Part. Nucl. Phys. 2006, 57, 470–563. [Google Scholar] [CrossRef]
- Nikšić, T.; Vretenar, D.; Ring, P. Relativistic nuclear energy density functionals: Mean-field and beyond. Prog. Part. Nucl. Phys. 2011, 66, 519–548. [Google Scholar] [CrossRef]
- Bartel, J.; Quentin, P.; Brack, M.; Guet, C.; Håkansson, H.-B. Towards a better parametrisation of Skyrme-like effective forces: A critical study of the SkM force. Nucl. Phys. A 1982, 386, 79–100. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities Part II. Nuclei far from stabilities. Nucl. Phys. A 1998, 635, 231–256. [Google Scholar] [CrossRef]
- Robledo, L.M.; Rodríguez, T.R.; Rodríguez-Guzmán, R.R. Mean field and beyond description of nuclear structure with the Gogny force: A review. J. Phys. G Nucl. Part. Phys. 2018, 46, 013001. [Google Scholar] [CrossRef]
- Vautherin, D.; Brink, D.M. Hartree-Fock Calculations with Skyrme’s Interaction. I. Spherical Nuclei. Phys. Rev. C 1972, 5, 626–647. [Google Scholar] [CrossRef]
- Rutz, K.; Bender, M.; Bürvenich, T.; Schilling, T.; Reinhard, P.-G.; Maruhn, J.A.; Greiner, W. Superheavy nuclei in self-consistent nuclear calculations. Phys. Rev. C 2008, 56, 238–243. [Google Scholar] [CrossRef]
- Bender, M.; Nazarewicz, W.; Reinhard, P.-G. Shell stabilization of super- and hyperheavy nuclei without magic gaps. Phys. Lett. B 2001, 515, 42–48. [Google Scholar] [CrossRef]
- Zhang, W.; Meng, J.; Zhang, S.Q.; Geng, L.S.; Toki, H. Magic numbers for superheavy nuclei in relativistic continuum Hartree–Bogoliubov theory. Nucl. Phys. A 2005, 753, 106–135. [Google Scholar] [CrossRef]
- Li, J.J.; Long, W.H.; Margueron, J.; Van Giai, N. Superheavy magic structures in the relativistic Hartree–Fock–Bogoliubov approach. Phys. Lett. B 2014, 732, 169–173. [Google Scholar] [CrossRef]
- Afanasjev, A.V.; Frauendorf, S. Central depression in nuclear density and its consequences for the shell structure of superheavy nuclei. Phys. Rev. C 2005, 71, 024308. [Google Scholar] [CrossRef]
- Agbemava, S.E.; Afanasjev, A.V.; Nakatsukasa, T.; Ring, P. Covariant density functional theory: Reexamining the structure of superheavy nuclei. Phys. Rev. C 2015, 92, 054310. [Google Scholar] [CrossRef]
- Afanasjev, A.V.; Agbemava, S.E.; Gyawali, A. Hyperheavy nuclei: Existence and stability. Phys. Lett. B 2018, 782, 533–540. [Google Scholar] [CrossRef]
- Taninah, A.; Agbemava, S.E.; Afanasjev, A.V. Covariant density functional theory input for r-process simulations in actinides and superheavy nuclei: The ground state and fission properties. Phys. Rev. C 2020, 102, 054330. [Google Scholar] [CrossRef]
- Zhao, P.W.; Li, Z.P.; Yao, J.M.; Meng, J. New parametrization for the nuclear covariant energy density functional with a point-coupling interaction. Phys. Rev. C 2010, 82, 054319. [Google Scholar] [CrossRef]
- Li, L.L.; Meng, J.; Ring, P.; Zhao, E.-G.; Zhou, S.-G. Deformed relativistic Hartree-Bogoliubov theory in continuum. Phys. Rev. C 2012, 85, 024312. [Google Scholar] [CrossRef]
- Zhang, K.; Cheoun, M.K.; Choi, Y.B.; Chong, P.S.; Dong, J.; Dong, Z.; Du, X.; Geng, L.; Ha, E.; He, X.T.; et al. Nuclear mass table in deformed relativistic Hartree–Bogoliubov theory in continuum, I: Even–even nuclei. At. Data Nucl. Data Tables 2022, 144, 101488. [Google Scholar] [CrossRef]
- Guo, P.; Cao, X.; Chen, K.; Chen, Z.; Cheoun, M.K.; Choi, Y.B.; Lam, P.C.; Deng, W.; Dong, J.; Du, P.; et al. Nuclear mass table in deformed relativistic Hartree–Bogoliubov theory in continuum, II: Even-Z nuclei. At. Data Nucl. Data Tables 2024, 158, 101661. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Liu, B.R.; Zhang, K.Y.; Yao, J.M. Shell structure and shape transition in odd-Z superheavy nuclei with proton numbers Z = 117, 119: Insights from applying deformed relativistic Hartree-Bogoliubov theory in continuum. Phys. Rev. C 2024, 110, 024302. [Google Scholar] [CrossRef]
- Nikšić, T.; Vretenar, D.; Ring, P. Relativistic nuclear energy density functionals: Adjusting parameters to binding energies. Phys. Rev. C 2008, 78, 034318. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Nikšić, T.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef]
- Kortelainen, M.; Lesinski, T.; Moré, J.; Nazarewicz, W.; Sarich, J.; Schunck, N.; Stoitsov, M.V.; Wild, S. Nuclear energy density optimization. Phys. Rev. C 2010, 82, 024313. [Google Scholar] [CrossRef]
- Nikšić, T.; Paar, N.; Vretenar, D.; Ring, P. DIRHB—A relativistic self-consistent mean-field framework for atomic nuclei. Comput. Phys. Commun. 2014, 185, 1808–1821. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, Z.Y.; Ring, P. A finite range pairing force for density functional theory in superfluid nuclei. Phys. Lett. B 2009, 676, 44–50. [Google Scholar] [CrossRef]
- Karatzikos, S.; Afanasjev, A.V.; Lalazissis, G.A.; Ring, P.T. The fission barriers in Actinides and superheavy nuclei in covariant density functional theory. Phys. Lett. B 2010, 689, 72–81. [Google Scholar] [CrossRef]
- Stoitsov, M.V.; Dobaczewski, J.; Nazarewicz, W.; Ring, P. Axially deformed solution of the Skyrme–Hartree–Fock–Bogolyubov equations using the transformed harmonic oscillator basis. The program HFBTHO (v1.66p). Comput. Phys. Commun. 2005, 167, 43–63. [Google Scholar] [CrossRef]
- Marević, P.; Schunck, N.; Ney, E.M.; Navarro Pérez, R.; Verriere, M.; O’Neal, J. Axially-deformed solution of the Skyrme-Hartree-Fock-Bogoliubov equations using the transformed harmonic oscillator basis (IV) hfbtho (v4.0): A new version of the program. Comput. Phys. Commun. 2022, 276, 108367. [Google Scholar] [CrossRef]
- Reinhard, P.-G.; Nazarewicz, W.; Bender, M.; Maruhn, J.A. Lipkin-Nogami pairing scheme in self-consistent nuclear structure calculations. Phys. Rev. C 1996, 53, 2776–2785. [Google Scholar] [CrossRef]
- Stoitsov, M.V.; Dobaczewski, J.; Nazarewicz, W.; Pittel, S.; Dean, D.J. Systematic study of deformed nuclei at the drip lines and beyond. Phys. Rev. C 2003, 68, 054312. [Google Scholar] [CrossRef]
- Perera, U.C.; Afanasjev, A.V. Bubble nuclei: Single-particle versus Coulomb interaction effects. Phys. Rev. C 2022, 106, 024321. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, P.; Li, J. Exploring the Neutron Magic Number in Superheavy Nuclei: Insights into N = 258. Particles 2024, 7, 1086-1094. https://doi.org/10.3390/particles7040066
Du P, Li J. Exploring the Neutron Magic Number in Superheavy Nuclei: Insights into N = 258. Particles. 2024; 7(4):1086-1094. https://doi.org/10.3390/particles7040066
Chicago/Turabian StyleDu, Pengxiang, and Jian Li. 2024. "Exploring the Neutron Magic Number in Superheavy Nuclei: Insights into N = 258" Particles 7, no. 4: 1086-1094. https://doi.org/10.3390/particles7040066
APA StyleDu, P., & Li, J. (2024). Exploring the Neutron Magic Number in Superheavy Nuclei: Insights into N = 258. Particles, 7(4), 1086-1094. https://doi.org/10.3390/particles7040066






