Magic Number N = 350 Predicted by the Deformed Relativistic Hartree-Bogoliubov Theory in Continuum: Z = 136 Isotopes as an Example

Abstract

The investigation of magic numbers for nuclei in the hyperheavy region $(Z>120)$ is an interesting topic. The neutron magic number $N=350$ is carefully validated by the deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc), via analysing even-even nuclei around $N=350$ of the $Z=136$ isotopes in detail. Nuclei with $Z=136$ and $340\le N\le 360$ are all found to be spherical in their ground states. A big drop of the two-neutron separation energy $S_{2n}$ is observed from $N=350$ to $N=352$ in the isotopic chain of $Z=136$, and a peak of the two-neutron gap ${\delta }_{2n}$ appears at $N=350$. There exists a big shell gap above $N=350$ around the spherical regions of single-neutron levels for nucleus with $(Z=136,N=350)$. These evidences from the DRHBc theory support $N=350$ to be a neutron magic number in the hyperheavy region.

1. Introduction

The investigation of superheavy elements remains one of the most important topics of nuclear physics and chemistry. The element with the largest proton number Z observed so far is Og with $Z=118$ [1]. The limit of the existence of atomic nuclei is a longstanding issue for both experimental and theoretical nuclear physicists, and has important impacts on physics and chemistry. The nuclei with $Z>120$ are usually called hyperheavy nuclei [2]. The studies of hyperheavy nuclei can enhance our understanding of exotic nuclear structures and enable the delving into the limits of charge and mass of atomic nuclei.

Nuclear liquid drop model (LDM) [3] can help us obtain a quick understanding of the hyperheavy nuclei, which suggests the importance of the competition between Coulomb energies and surface effects in the hyperheavy region. However, due to the lack of quantum shell effect, the predictions given by the LDM are pretty rough. Quantum shell effect, which corresponds to a non-uniformity distribution of the individual single-particle energies, is very important for finite nuclear systems. It can produce a significant energy gap in the single-particle energy spectrum near the Fermi level for some nuclei. Such gaps would provide additional binding energies and enhance nuclear stability. These nuclei with additional stability are the so-called “magic nuclei”, and the corresponding proton or neutron numbers are called “magic numbers”. Experimentally, the confirmed neutron magic numbers are $8,20,28,50,82,126$, and the confirmed proton magic numbers are $8,20,28,50,82$.

Due to the additional stability, magic nuclei have drawn a lot of attention [4,5]. Naïvely, if one assumes the potential for nucleons within an atomic nucleus is a harmonic oscillator potential, the obtained magic numbers will be $2,8,20,40,70,112,168,240,...$, which disagree with experiments. If one further takes into account the spin-orbital coupling, the predicted magic numbers are $2,8,20,28,50,82,126,184,258,350,...$, which correctly reproduce the experimental magic numbers for $N\le 126$ and $Z\le 82$. However, due to the limit of experimental information, the large predicted magic numbers, such as 258 and 350, are difficult to be validated in the foreseeable future. For hyperheavy nuclei with $Z>120$, the neutron numbers of which can reach to $N\approx 350$, and it will be interesting to use a microscopic and self-consistent model to theoretically justify the predicted neutron magic number 350.

Nuclear stability is usually described by the binding energy or equivalently nuclear mass. Nuclear mass is important for both nuclear physics [6,7] and astrophysics [8,9,10,11]. Experimentally, the masses of about 2500 nuclear masses have been measured to date [12]. Theoretically, many nuclear models [13,14,15,16,17,18,19,20,21,22,23,24] and machine-learning approaches [25,26,27,28,29,30,31,32,33,34,35,36] are developed to predict nuclear masses. Among these models, the deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc) [37,38] simultaneously treats the deformation degrees of freedom, pairing correlations, and continuum effects properly, which are important for the descriptions of weakly bound exotic nuclei. The DRHBc theory has been successfully applied in studying many nuclear phenomena [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56]. In order to provide a unified and microscopic description for the whole nuclear landscape, the DRHBc Mass Table Collaboration [57] was established, aiming at establishing a nuclear mass table based on the DRHBc theory with the density functional PC-PK1 [58]. The even-even [22] and even-odd [24] parts of the DRHBc mass table have been established recently. The Collaboration is now working on odd-Z nuclei and hyperheavy nuclei with $120<Z\le 136$. Taking this opportunity, one can validate the neutron magic number $N=350$ with the DRHBc theory. In this work, the DRHBc theory is employed to study the even nuclei of $Z=136$ isotopes around $N=350$ to validate the possible neutron magic number $N=350$. To our knowledge, there is currently no literature that employs modern nuclear model to study the neutron magic number $N=350$. In Section 2, the theoretical framework is introduced. The numerical details are introduced in Section 3. The Results and discussions are presented in Section 4. Finally, a summary is given in Section 5.

2. Theoretical Framework

The details of the DRHBc theory with meson-exchange and point-coupling density functionals can be found in Refs. [38,59], respectively. In the following we briefly present its formalism.

Treating self-consistently the mean fields and pairing correlations, the relativistic Hartree Bogoliubov (RHB) equations for the nucleons read [60]

$$\left(\begin{array}{cc}{h}_D-{\lambda }_{\tau }& \Delta \\ -{\Delta }^{*}& -h_D^{*}+{\lambda }_{\tau }\end{array}\right)\left(\begin{array}{c}{U}_k\\ V_k\end{array}\right)=E_k\left(\begin{array}{c}{U}_k\\ V_k\end{array}\right).$$

(1)

To describe properly the possible large spatial extension of exotic nuclei, the RHB equations are solved in a Dirac Woods-Saxon basis, in which the radial wave functions have a proper asymptotic behavior for large r [61]. In Equation (1), ${\lambda }_{\tau }$ is the Fermi energy ($\tau =n/p$ for neutrons or protons), $E_k$ and ${(U_k,V_k)}^{\mathrm{T}}$ the quasiparticle energy and wave function, and $h_D$ the Dirac Hamiltonian,

$$h_D\left(\mathit{r}\right)=\mathit{\alpha }·\mathit{p}+V\left(\mathit{r}\right)+\beta [M+S\left(\mathit{r}\right)],$$

(2)

with the scalar $S\left(\mathit{r}\right)$ and vector $V\left(\mathit{r}\right)$ potentials. The pairing potential $\Delta$ reads

$$\Delta ({\mathit{r}}_1,{\mathit{r}}_2)=V^{\mathrm{pp}}({\mathit{r}}_1,{\mathit{r}}_2)\kappa ({\mathit{r}}_1,{\mathit{r}}_2),$$

(3)

with a density-dependent force of zero range,

$$V^{\mathrm{pp}}({\mathit{r}}_1,{\mathit{r}}_2)=V_0{\displaystyle \frac{1}{2}}(1-P^{\sigma })\delta ({\mathit{r}}_1-{\mathit{r}}_2)\left(1-{\displaystyle \frac{\rho \left({\mathit{r}}_1\right)}{{\rho }_{\mathrm{sat}}}}\right),$$

(4)

and the pairing tensor $\kappa$ [62]. For axially deformed nuclei, the potentials and densities are expanded in terms of the Legendre polynomials,

$$f\left(\mathit{r}\right)=\sum _{\lambda }{f}_{\lambda }\left(r\right)P_{\lambda }(cos\theta ),\lambda =0,2,4,\cdots ,$$

(5)

where $\lambda$ is restricted to be even numbers due to spatial reflection symmetry.

3. Numerical Details

In Equation (4), the pairing strength $V_0=-325$ MeV ${\mathrm{fm}}^3$, the saturation density ${\rho }_{\mathrm{sat}}=0.152$ ${\mathrm{fm}}^{-3}$, and a pairing window of 100 MeV are adopted. The energy cutoff $E_{\mathrm{cut}}^{+}$ = 300 MeV and the angular momentum cutoff $J_{\max }$ = 23/2$\hslash$ are adopted for the Dirac Woods-Saxon basis. In Equation (5), the Legendre expansion is truncated at ${\lambda }_{\max }=10$ [63]. The calculations are carried out with the relativistic density functional PC-PK1 [58]. These numerical details are the same as the calculations of nuclei with $100\le Z\le 120$ in the global DRHBc mass table calculations over the nuclear chart [22,24,59], and have also been examined to be proper for the studies in this work.

4. Results and Discussions

Evolution of the potential energy curves (PECs) of $Z=136$ isotopes with $340\le N\le 360$ is presented in Figure 1. Note that the $Z=136$ element has temporary systematic IUPAC name and symbol as Untrihexium and Uth respectively [64]. One can see the similar behaviours of these PECs, where the total energy increases monotonously with the increasing absolute value of ${\beta }_2$ in the range that $|{\beta }_2|<0.3$, indicating that these nuclei are spherical in their ground states. Note that the cutoff of angular momentum has been examined in Ref. [65], which suggests $J_{max}=31/2\hslash$ in the calculation of the hyperheavy nuclei ($121\le Z\le 136$) with quadruple deformation $|{\beta }_2|>0.3$. The spherical ground states of these nuclei can be interpreted as a clue that $N=350$ (or other adjacent neutron numbers) is a neutron magic number, since atomic nuclei prefer to be spherical around the magic ones. Note that the nuclei that are analyzed in the present work all have spherical ground states, which might lead one to consider $Z=136$ as a potential magic number. However, we have checked the nuclei that are not close to $N=350$ in $Z=136$ isotopic chain, most of which are not spherical ones. We have also checked the single-proton levels around the Fermi level of ⁴⁸⁶Uth, and there is not a significant gap above $Z=136$. Instead, there is a significant gap above $Z=138$, which may suggest 138 to be a proton magic number. However, this is out of the scope of the present paper, which could be an interesting topic for the future work.

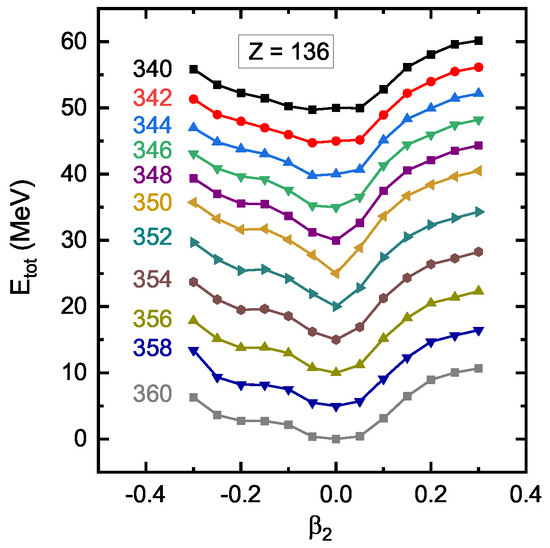
Figure 1. Evolution of the potential energy curves (PECs) of Uth $(Z=136)$ isotopes with $340\le N\le 360$. For clarity reasons, the curves have been scaled to the energy of ${\beta }_2=0$ and have been shifted upward by 5 MeV per decreasing two neutrons.

In order to pin down which neutron number is the magic one, the two-neutron separation energies $S_{2n}$ and Fermi energies ${\lambda }_n$ for these Uth isotopes are presented in Figure 2. One can see that the two-neutron separation energies $S_{2n}$ evolve slowly with the increasing of neutron number from $N=340$ to $N=350$ and from $N=352$ to $N=360$. However, there is a big drop in the $S_{2n}$ from $N=350$ to $N=352$. This indicates that there is a big shell gap at $N=350$, which is a strong evidence for a magic number. There is also a big jump in the Fermi energies ${\lambda }_n$ from $N=350$ to $N=352$, which leads to the same conclusion. Two-neutron gap ${\delta }_{2n}=S_{2n}(N,Z)-S_{2n}(N+2,Z)$ is also a very good signature of magic numbers. As can be clearly seen in Figure 2, a peak of ${\delta }_{2n}$ appears at $N=350$.

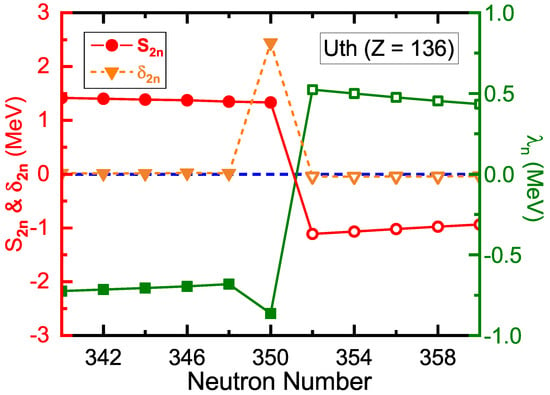
Figure 2. Two-neutron separation energies $S_{2n}$, two-neutron gaps ${\delta }_{2n}$, and Fermi energies ${\lambda }_n$ for the Uth $(Z=136)$ isotopes with $340\le N\le 360$. The bound nuclei predicted by the DRHBc theory are denoted by filled circles, while the unbound nuclei are denoted by empty circles. The blue dashed line displays $S_{2n}=0$, ${\delta }_{2n}=0$, and ${\lambda }_n=0$.

Neutron magic nuclei are typically more stable than their next neutron-rich neighbors, while the neutron-richer nuclei next to the magic nuclei are much more likely to emit extra neutrons outside the shells. One can also see in Figure 2 that the $S_{2n}$ of nuclei $N\ge 352$ are smaller than zero, which means that these nuclei are unstable against neutron emission. The corresponding Fermi energies for these nuclei are larger than 0, which also refers to the unstable characters. Therefore, the neutron drip-line nucleus of Uth isotopic chain locates at $N=350$. Note that the Coulomb repulsion will be very large in superheavy and hyperheavy nuclei, and tends to prevent the nuclear binding. The reason why such a hyperheavy nucleus ⁴⁸⁶Uth still can be bound is due to strong shell effect. The shell effect is a hallmark characteristic in the atomic nucleus as a quantum system, providing extra binding that can overcome Coulomb repulsion and makes the nucleus bound.

In order to confirm the neutron magic number, the single-neutron levels around the Fermi level should be carefully checked. Figure 3 shows the single-neutron levels around the Fermi level of ⁴⁸⁶Uth in the canonical basis obtained from constraint calculations. One can find a big gap above $N=350$ around the spherical regions, i.e., $-0.05<{\beta }_2<0.05$. This strongly supports $N=350$ as a neutron magic number.

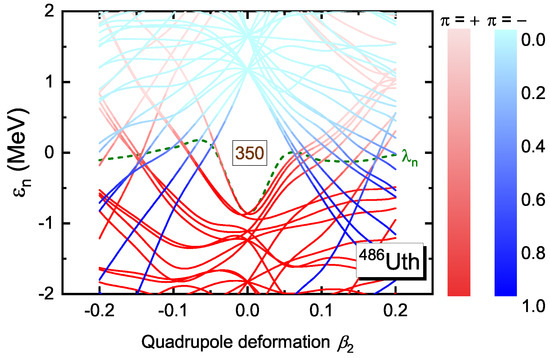
Figure 3. Single-neutron levels around the Fermi level of ⁴⁸⁶Uth in the canonical basis obtained from constraint calculations with the DRHBc theory. The occupation probability of each orbital is represented with different colors. The Fermi level ${\lambda }_n$ is displayed by the green dashed line.

Figure 4 provides single-neutron and single-proton levels around the Fermi levels for the spherical ground state of ⁴⁸⁶Uth, and the corresponding spherical quantum numbers are labeled. As can be seen, the big gap of $N=350$ appears between the level $4{\mathrm{d}}_{3/2}$ and $1{\mathrm{I}}_{17/2}$. In the future works, it would be interesting to check the model dependence of neutron magic number $N=350$, as well as the related levels, among different methods and different functionals employed.

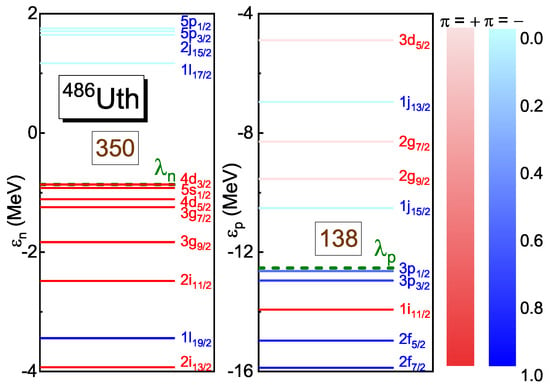
Figure 4. Single-neutron and single-proton levels around the Fermi levels for the spherical ground state of ⁴⁸⁶Uth in the canonical basis obtained with the DRHBc theory. The occupation probability of each orbital is represented with different colors. The Fermi levels ${\lambda }_n,{\lambda }_p$ are displayed by the green dashed lines. The spherical quantum numbers are given for corresponding levels.

5. Summary

The investigation of magic numbers of hyperheavy nuclei is an interesting topic. The neutron number $N=350$ is predicted to be a magic number by the naïve analysis based on harmonic oscillator potential with spin-orbital coupling. In this work, the predicted neutron magic number $N=350$ is validated with the DRHBc theory by studying the Uth ($Z=136$) isotopes around $N=350$. It is found that the Uth isotopes with $340\le N\le 360$ are all spherical in their ground states. A big drop of the $S_{2n}$ appears from $N=350$ to $N=352$, and a peak of ${\delta }_{2n}$ is observed at $N=350$. By taking ⁴⁸⁶Uth as an example, in the single-neutron levels, there exists a big shell gap above $N=350$ around the spherical regions, i.e., $-0.05<{\beta }_2<0.05$. These evidences from DRHBc theory all support $N=350$ to be a neutron magic number in the hyperheavy region.

Note that we presently focus on $Z=136$ isotopic chain as an example, and a more rigorous validation of neutron magic number should be examined also for other isotopic chains. The preliminary results of other isotopic chains in the hyperheavy region from the DRHBc theory also support $N=350$ to be a neutron magic number. A more comprehensive investigation could be carried out in the future to analyze all the results of hyperheavy nuclei. In that case, one could have a more rigorous validation of neutron magic number $N=350$ and also other possible neutron and proton magic numbers in the hyperheavy region. Considering that the present calculations with the DRHBc theory assume nuclei to be axial symmetry and base on the PC-PK1 functional, it would be interesting to investigate the evolution of shell gaps with triaxial deformation or with octupole deformation, to validate whether the triaxial or octupole deformations can challenge the spherical minima of these nuclei. It would also be interesting to check the functional dependence of neutron magic number $N=350$.