Abstract
A review is made of constraints on the nuclear symmetry energy parameters arising from nuclear binding energy measurements, theoretical chiral effective field predictions of neutron matter properties, the unitary gas conjecture, and measurements of neutron skin thicknesses and dipole polarizabilities. While most studies have been confined to the parameters and L, the important roles played by, and constraints on , or, equivalently, the neutron matter incompressibility , are discussed. Strong correlations among , and are found from both nuclear binding energies and neutron matter theory. However, these correlations somewhat differ in the two cases, and those from neutron matter theory have smaller uncertainties. To 68% confidence, it is found from neutron matter theory that MeV, MeV and MeV. Theoretical predictions for neutron skin thickness and dipole polarizability measurements of the neutron-rich nuclei Ca, Sn, and Pb are compared to recent experimental measurements, most notably the CREX and PREX neutron skin experiments from Jefferson Laboratory. By themselves, PREX I+II measurements of Pb and CREX measurement of Ca suggest MeV and MeV, respectively, to 68% confidence. However, we show that nuclear interactions optimally satisfying both measurements imply MeV, nearly the range suggested by either nuclear mass measurements or neutron matter theory, and is also consistent with nuclear dipole polarizability measurements. This small parameter range implies km and , which are consistent with NICER X-ray and LIGO/Virgo gravitational wave observations of neutron stars.
1. Introduction
The nuclear symmetry energy, and its density dependence, as characterized by the traditional symmetry energy parameters and L, has been the focus of much recent activity because it is the most direct link between nuclear physics and nuclear astrophysics [1,2,3]. Both the expected neutrino and gravitational wave signals from gravitational collapse supernovae within our Galaxy are sensitive to the symmetry energy [4,5,6]. The symmetry energy near the baryon density at saturation, fm, determines the radius [7] of a neutron star (NS), which strongly influence the expected gravitational signals from their mergers [8,9]. The symmetry energy also affects the NS crust’s thickness and thermal relaxation time, potentially observable in cooling and accreting [10] NSs and in giant magnetar flares [11,12,13]. The composition of matter at densities above , and the existence of neutrino processes which can rapidly cool NSs, depend on the density dependence of the symmetry energy [14], as do predicted properties of neutron-rich nuclei and reaction rates involved in the astrophysical r-process [15].
Experimental attempts to constrain the nuclear symmetry energy parameters include measurements of nuclear masses, neutron skin thicknesses, nuclear dipole polarizabilities, giant and pygmy dipole resonance energies, flows in heavy-ion collisions, and isobaric analog states. These constraints are influenced by varying degrees of model dependence. In addition, recent advances in neutron matter theory, especially that of systematic expansions involving chiral effective field theory (EFT) [16], also constrain the symmetry energy parameters.
Of considerable interest are the recent parity-violating electron scattering neutron skin experiments of Pb (PREX-I and PREX-II) [17] and Ca [18]. These measure the mean square difference of the neutron and proton radii using a technique which is argued to be the most direct and least model-dependent experiment to date [19]. PREX I+II combined yields fm [17], which implies [20] 68% confidence ranges of MeV and MeV. Both values, and the measured value of itself, are considerably larger than from expectations from neutron matter and nuclear binding energies, and also from previous measurements, although overlapping with them at about the 90% confidence level. This indicates a tension with the current understanding of the equation of state (EOS). For example, these results imply a tidal deformability that lies above the 90% confidence upper limit established for a NS by the LIGO/Virgo observation of the binary NS (BNS) merger GW170817 [21,22]. In contrast, the measurement of the neutron skin of Ca using the same technique [18] is somewhat smaller than the average of earlier experimental measurements and expectations from nuclear binding energies and neutron matter theory.
Ref. [23] performed a Bayesian analysis of the PREX and CREX results. They found that the two experimental results are incompatible with each other at 68% confidence level, but compatible at 90% confidence level. Combining the data, they inferred MeV and MeV at 90% confidence level. They find the combined results predict close to the CREX result, but predict considerably smaller than the PREX result. Ref. [24] also performed a combined analysis, and conclude that a simultaneous accurate description of the skins of Ca and Pb cannot be achieved with their models that accommodate mass, charge radii and experimental dipole polarizabilities.
In this paper, we take a different perspective by discovering the properties of nuclear interactions fit to binding energy and charge radii of large numbers of nuclei that best satisfy both PREX and CREX measurements. We agree with the assessments of both Refs. [23,24] that no conventional nuclear interaction can fit both measurements to 68% confidence level. However, our optimum fit results in ranges of and L that not only have central values larger than those estimated by Ref. [23] but also smaller uncertainties. Our results also agree with results from neutron matter theory while those from Ref. [23] do not. We find similar results when historical measurements of the neutron skins of both nuclei are utilized, instead, suggesting that systematic uncertainties in the measurements are not dominant.
We begin by summarizing nuclear binding energy and theoretical neutron matter constraints on the nuclear symmetry energy parameters and . We show that estimates of symmetry energy parameters from chiral Lagrangian expansions of nuclear matter are more reliably estimated from neutron matter calculations than from both neutron and symmetric matter calculations. We explore systematic uncertainties in parameter estimation stemming from the choice of nuclear interaction model, and note apparent inconsistencies associated with relatively stiff relativistic mean field (RMF) interactions. We show that nuclear models fit to nuclear binding energies that optimally satisfy both CREX and PREX neutron skin measurements confine symmetry parameter values to narrow ranges that are consistent with expectations from neutron matter theory. We also show that they are also consistent with theoretical estimates based on dipole polarizability experiments. We also compare our estimates of symmetry parameters with those estimated from astrophysical observations of neutron stars, especially from gravitational wave observations of GW170817 and Neutron Star Interior Composition ExploreR (NICER) X-ray observations of PSR J0030+0451 [25,26] and PSR J0740+6620 [27,28].
2. The Nuclear Symmetry Energy
The nuclear symmetry energy is defined here to be the difference between the energies of pure neutron matter (PNM), , and isospin symmetric nuclear matter (SNM), , at the baryon density n. Related quantities are the density-dependent coefficients, , of an expansion of the bulk energy per baryon, , in powers of the neutron excess :
A common approximation is to retain only the quadratic term in Equation (1) at every density, even for small proton fractions x, so that . Chiral Lagrangian expansions for PNM, nuclear matter with admixtures of protons, and SNM, indicate that this approximation appears valid [29] for all values of x. For matter with densities below , such as that in nuclei, experimental evidence for higher-than-quadratic contributions is lacking, but this could be partly due to the near-symmetric character of nuclei. It is customary to introduce the volume symmetry energy , symmetry slope , symmetry incompressibility , and symmetry skewness parameters, the coefficients of a Taylor expansion in density around :
where . If only the quadratic term in Equation (1) is retained, we note that . As a result, the energy per baryon and the pressure of PNM at become
where MeV is the bulk binding energy parameter of SNM.
We also introduce the incompressibility and skewness parameters for SNM, and , and for PNM, and , respectively, so that
The corresponding parameters for the symmetry energy are and . MeV has been deduced from giant monopole resonances [30,31], but there is little direct experimental evidence for or .
In this section, we explore correlations involving the symmetry parameters that arise, experimentally, from fitting nuclear binding energies, and, theoretically, from recent neutron matter theory predictions. Neither of these methods can alone predict values of or L to high precision. However, since these correlations are motivated by different considerations, combining them can yield additional restrictions.
2.1. Nuclear Mass Fitting
It is straightforward to understand why a strong correlation between and L from fitting nuclear masses exists by using the simple nuclear liquid drop model, which consists of five main terms,
Here and the individual terms represents the volume, surface, and Coulomb energies, respectively. Additionally, one should consider shell and pairing energies. The terms proportional to represent the symmetry energy of a nucleus:
If the Coulomb energy is ignored, the experimental symmetry energy can be found by taking half the difference of the measured energies of nuclei having the same mass but values of Z and N each differing by two units. This procedure also effectively eliminates shell and pairing effects.
The optimum values of the parameters and can be found by minimizing
with respect to themselves. is the number of measured nuclei, and MeV is a fiducial uncertainty. The result is a confidence ellipse centered at and with uncertainties, angle with respect to the axis, and correlation coefficient
respectively, where is the matrix inverse of . The slope of the confidence ellipse is when is small. Since is linear in and , the symmetric matrix depends only on the measured and , not on or ,
Numerical values were obtained by using the set of 2336 nuclei from Ref. [32] with or . As a result, one finds , , and , which represents a high degree of correlation.
To convert this correlation into one involving and L, it can be noted that originates from an integration of the density-dependent symmetry energy through the nuclear density profile. In the plane-parallel approximation, it can be shown [1] that
The simple approximations and lead to
where . When and , one finds that and . As a result, increases rapidly with L, and the steep correlation translates into a steep correlation, , with a similar correlation coefficient. The liquid droplet model [33], in which the nuclear symmetry energy enters as
provides a much improved fit, and also shows a significant correlation between and L.
This correlation naturally appears when comparing large numbers of non-relativistic Skyrme-like and RMF nuclear interactions which were fitted to nuclear binding energies and, in some cases, additional properties, such as charge radii. Of the 240 Skyrme-like interactions studied by Ref. [34], 45 can be rejected [35] since they have some saturation properties (including ) outside the empirical window or other anomalous behavior. Similarly, of the 256 RMF interactions studied by Ref. [36], 100 can be rejected [35]. The compilation of Ref. [37] contains an additional 206 interactions of both types, of which 169 survive the conditions imposed by Ref. [35], but an additional 58 of these are duplicates from Refs. [34,36]. The properties of confidence ellipses for these three groups of interactions are shown in Table 1.

Table 1.
Symmetry energy parameter correlations.
The UNEDF collaboration [38] determined an correlation in a more precise fashion using a universal energy density functional fit to binding energies and charge radii of selected closed-shell nuclei. The confidence ellipse size depends on the arbitrary value of a fiducial uncertainty parameter . The value MeV yields an approximately equal uncertainty to that of the Skyrme forces in the compilation of Ref. [34], as seen in Figure 1. This is not surprising given the fact that the universal energy density functional of Ref. [38] is non-relativistic. However, the correlation is much tighter than those found from the compilation of Refs. [34,36,37] possibly because the latter forces were not subjected to the same strict calibration involving charge radii. Note that the slope and best-fit parameter values and do not depend on the parameter . Table 1 gives the confidence ellipse specifics.
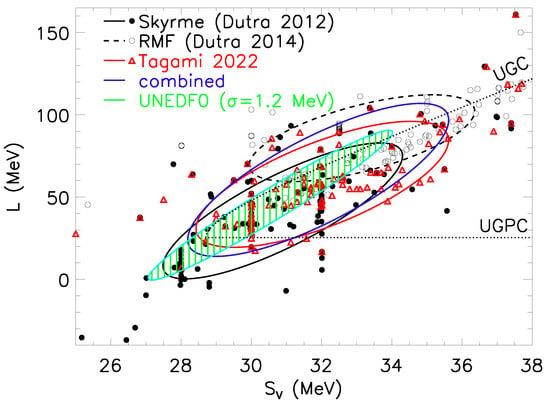
Figure 1.
and L data from individual Skyrme (black filled circles, Ref. [34]), relativistic mean field (RMF, black open circles, Ref. [36]) forces, both interaction types (Tagami 2022, red triangles, Ref. [37]), and all tabulated interactions (combined); corresponding 68.3% confidence ellipses are shown. The green hatched confidence ellipse is taken from the UNEDF collaboration [38] using MeV (see text). The bounds provided by the Unitary Gas Conjecture (UGC, [35]) and the Unitary Gas Pressure Conjecture are shown as dotted curves.
It is also possible to consider correlations involving incompressibilities and skewnesses, It will be seen to be more straightforward to consider and rather than and . Figure 2 displays these correlations for the interactions compiled by Refs. [34,36,37]. Generally, it is seen that and L are more highly correlated than and L for model interactions, especially for Skyrme-like interactions. Although and L are highly correlated for Skyrme-like interactions, they are much less correlated for RMF interactions.

Figure 2.
The same as Figure 1 but for correlations between and L [left panel] and and L [right panel]. The Unitary Gas Pressure Conjecture restricts allowable regions to the right of the dotted lines labelled UGPC.
It is clear there are systematic differences between the behaviors of Skyrme and RMF interactions. In particular, Skyrme forces tend to display higher degrees of parameter correlations than do RMF forces. In addition, mean values of the parameters and are larger, and is smaller, for RMF compared to Skyrme forces. Importantly, these trends raise predicted values of neutron skin thicknesses of neutron-rich nuclei, and, further, raise values of for which increases estimated values of neutron star radii as shown in Section 5. For the compilations of Refs. [34,36], there are two and a half times as many surviving Skyrme interactions as RMF interactions, but for the compilation of Ref. [37], the two types are more equally represented. These relative populations are reflected in their combined correlation.
Other systematic differences exist for symmetric matter parameters as well. For comparison, we display, using the databases of Refs. [34,36], correlations among the symmetric energy parameters , and , or between these symmetric energy parameters and L, in Figure 3 and Figure 4. The parameters cluster in what defines the empirical saturation window, but display themselves display relatively weak correlations. The UNEDF Collaboration [38] also confirmed the lack of significant correlations among and and between those parameters and L or .
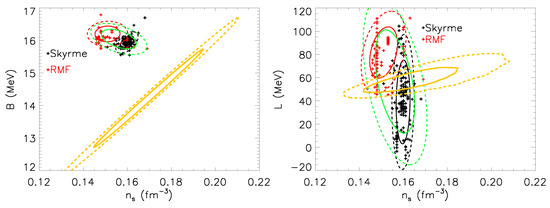
Figure 3.
Correlations among symmetric energy parameters of forces in compilations of Refs. [34,36]. The left and right panels show the and correlations, respectively. Individual interactions are shown by filled circles. 68.3% and 95% confidence ellipses for Skyrme (RMF) interactions are shown by black (red) solid and dashed ellipses, respectively; green ellipses show the confidence ellipses for the combined force models. 68.3% and 95.5% confidence regions determined from EFT calculations of SNM plus PNM (see Section 2.2) are shown by the orange solid and dotted curves, respectively.

Figure 4.
The same as Figure 3 except the left and right panels show the and correlations, respectively.
2.2. Neutron Matter Theory
A major recent advance in the understanding of nuclear matter has been made possible through the development of chiral effective field theory (EFT) [40,41] which provides the only known framework allowing a systematic expansion of nuclear forces at low energies [42,43,44,45] based on the symmetries of quantum chromodynamics, the fundamental theory of the strong interaction. In particular, EFT allows one to derive systematic estimates of uncertainties of thermodynamic quantities [46,47,48,49] for zero-temperature matter for densities up to with two- and three-nucleon interactions at the next-to-next-to-next-to-leading order (N3LO). The energy and pressure of SNM are presented, for example by Ref. [39], as central values and their standard deviations as a function of density. Corresponding values of the energy and pressure of PNM are also given.
Ref. [39] found that the energies and pressures, and the their uncertainties, for PNM and SNM are each significantly correlated, and also significantly correlated with each other. From these calculations, Ref. [39] thereby determined the correlation between and L tabulated in Table 1. It is significantly flatter than from mass fitting, but has very consistent mean values.
These results can be generally reproduced directly using the SNM and PNM results and assuming a high degree of correlation between them. The SNM calculations predict a distribution of saturation densities (defined by the relation , as well as distributions of binding energy (), incompressibility () and skewness () parameters. These distributions are displayed in Figure 3 and Figure 4.
Combining these results with PNM calculations and their distributions of neutron matter energy () and pressures () at the saturation density then yields distributions of and L from and , shown in orange in Figure 5 and tabulated in Table 1. This procedure gives a similar slope and mean parameter values as Ref. [39], but systematically larger standard deviations. The differences may be due to our underestimate of correlations in and between SNM and PNM calculations. The analysis can be extended to higher-order neutron matter parameters. The case of is displayed in orange in Figure 5.
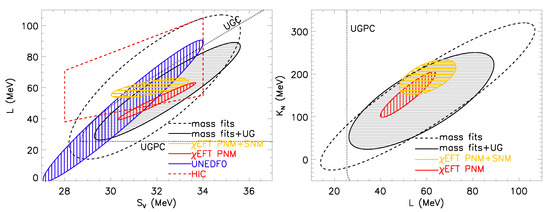
Figure 5.
Black correlation ellipses for (left panel) and (right panel) use model interaction data [34,36,37], with (solid) and without (dashed) application of Unitary Gas Constraints [35] boundaries (dotted). The blue confidence ellipse shows UNEDF [38] results assuming MeV. The red (brown) confidence ellipses are from chiral EFT studies [39] using PNM results with empirical saturation properties (combined PNM+SNM results). The red-dashed quadrilateral are limits determined from elliptic flows in heavy-ion collisions [50].
In contrast to mass fitting, the uncertainties of B and from SNM EFT calculations are extremely large and are also strongly correlated as seen in Figure 3. Most notably, the confidence ellipse does not pass near the empirical saturation window defined by Skyrme or RMF fits to nuclear properties. Other symmetric energy parameters also have large uncertainties and show correlations (Figure 4). Furthermore, the values of are inconsistent with those found from nuclear mass fits.
The failure of EFT calculations of SNM to saturate inside the empirical saturation window, together with inconsistent values of , indicates that PNM calculations are much more reliable than SNM calculations at present. This is not surprising, considering that the latter emerges from a delicate cancellation sensitive to the short- and intermediate-range three-body interactions at next-to-next-to-leading order, in contrast to PNM where these interactions are Pauli-blocked [51].
Therefore, we alternatively infer symmetry energy parameters using only EFT PNM results for the energy and pressure, including their standard deviations, but coupled with and B values randomly chosen from within the empirical saturation window shown in Figure 3. This alternate EFT correlation is displayed in Figure 5 and those involving and L are shown in Figure 5. Interestingly, the correlations so determined have confidence regions with central values consistent with those from mass fitting but with noticeably smaller uncertainties, greater degrees of significance, and also only slightly different slopes. Furthermore, ranges of and values are compatible with those observed from mass fits, neutron skin and dipole polarizability measurements, as well as astrophysical studies, as shown below.
2.3. The Unitary Gas Conjecture
Ref. [35] proposed a constraint on the symmetry parameters arising from the conjecture that the energy of pure neutron matter was greater, at all densities, than that of a unitary gas. A unitary gas is an idealized theoretical collection of fermions interacting only via pairwise s-wave interactions with an infinite scattering length and a vanishing effective range. The average particle separation in such a gas is the only length scale, so the energy of the unitary gas, , is proportional to the Fermi energy,
where is the Fermi wave number at the saturation density, is the neutron mass, the Bertsch parameter, which is experimentally measured [52,53] to be , and MeV. In reality, pure neutron matter at low densities has finite scattering length and range, but both properties lead to larger energies than for a unitary gas. In addition, three-body forces in neutron matter are known to be repulsive, further increasing its energy.
The Unitary Gas Conjecture (UGC) states that at all densities. If it is minimally satisfied at some arbitrary density , in order for it to remain satisfied at higher and lower densities requires [35]
These conditions automatically impose constraints on the parameters and L if the symmetry energy is expanded as in Equation (2). For example, it sets a minimum value where . Further using the correlations shown in Figure 2 to eliminate and , and using mean values for and B, the resulting constraint on and L is displayed in Figure 1 and in subsequent figures. This bound is relatively insensitive to assumed values of and [35]. It is notable that the UGC is obeyed by nearly all EFT results when and empirical values for and B are used (PNM method), but only by about half of EFT results using both and (SNM+PNM method). Similarly, most Skyrme interactions obey the UGC while most RMF forces do not. Even though the exact UGC boundary depends on uncertainties in and the and correlations, it serves as a valuable consistency check. It supports our previous argument that EFT studies of symmetric matter are not presently accurate enough to provide significant constraints, and, further, that RMF forces do not seem to be as well-suited to fitting nuclear properties as are Skyrme forces.
Because the UGC establishes a lower limit to the energy of pure neutron matter, it effectively sets a lower limit to both the radius and tidal deformability of a neutron star as a function of its mass [54], being more restrictive than causality in this regard.
Although the UGC cannot impose corresponding bounds in the or planes, it is possible to propose a corollary Unitary Gas Pressure Conjecture (UGPC), which states that the neutron matter pressure is always greater than the unitary gas pressure for densities larger than . Comparisons shown by Ref. [35] show that this is the case for recent neutron matter calculations and true for PNM chiral EFT studies even considering 90% lower confidence bounds. For , however, it is possible for the unitary gas pressure to be larger than the neutron matter pressure. Using the 90% upper confidence bound suggested by Figure 2 for as a function of L, but ignoring the correlation between and L, the UGPC imposes the bound in the plane shown in Figure 2. All RMF forces obey the UGPC. However, about 30% of the formerly permitted Skyrme forces, those having or , do not satisfy the UGPC.
3. Neutron Skin Thickness Constraints
It has long been known that the neutron skin thicknesses of neutron-rich nuclei, such as Ca and Pb, are highly dependent upon the symmetry parameter L and more weakly dependent upon . For example, the liquid droplet model predicts that the difference between the mean neutron and proton radii is [33]
if Coulomb effects are ignored, where and . The term indicates that the radius difference primarily depends on L, and therefore the symmetry energy slope and the neutron matter pressure at . However, the appearance of the last term in Equation (15) implies that a stronger correlation of exists with the symmetry energy slope at a smaller density than , namely about [55,56] which can be viewed as a sort of average nuclear density. This mimics the situation concerning nuclear binding energies. Ref. [55] showed, in particular, that the neutron skin thickness of Pb, that is, the root-mean-square neutron-proton radius difference , is linearly correlated with the neutron matter pressure (which is proportional to ) most strongly at the density fm:
We will define the symmetry energy slope as
so that . Equation (16) is then equivalent to , an estimate later generalized by several authors as
with and coefficients given in Table 2.

Table 2.
Coefficients for the relation and inferred values of from the error-weighted mean experimental value fm. Also given are two estimated values of from neutron skin measurements of Sn isotopes. 0.01 fm uncertainty introduced for consistency.
We note that evaluated at a subsaturation density can be related to other symmetry energy parameters through its Taylor expansion:
Given the strong correlations between and L, and moderate correlations between and L, displayed for the Skyrme [34] and RMF [36] forces (both displayed in Figure 4),as well as for EFT for PNM using B and from the empirical saturation window, it is not surprising that a strong correlation exists also between and L (Figure 6).When the correlations are combined in Equation (19), they give a confidence ellipse centered at MeV and MeV, with standard deviations MeV and MeV and correlation 0.843. The result MeV from the average Pb and Sn neutron skin thicknesses shown in Table 2) has nearly the same value and uncertainty as those from mass fitting and neutron matter theory shown in Figure 6.Their mean value of about 40 MeV is supported by the results of Refs. [58,59] who argued that a linear correlation also exists for neutron-rich Sn isotopes and derived similar values of near the density from experimental data (Table 2). Collectively, these Pb and Sn studies yield an average value MeV. The implied value MeV is therefore also in remarkable agreement.

Figure 6.
Correlations between (Ltilde) and L for EFT PNM theory (blue), and Skyrme (black) and RMF (red) interactions from Refs. [34,36], respectively. Green ellipses display the combined Skyrme and RMF correlation. Correlation coefficients (r) are shown.
The pseudo-linear correlation between and L implies good linear correlations should exist between with L for both Pb and Sn nuclei. Theoretical modeling, both from mean-field analyses and the dispersive optical model, supports an extension to Ca. Linear relations are indeed validated by examining recent compilations [18,20,37,60,61,62] of neutron skin thicknesses for Pb and Ca using a multitude of both non-relativistic and relativistic interactions. The compilation from Ref. [37] is especially notable in containing results from 206 Skyrme-like and RMF forces, and the other compilations contribute more than 200 additional values. The model estimates from these compilations are displayed in Figure 7 and slopes, intercepts and standard deviations of the linear fits from each reference, as well as their overall means, are provided in Table 3. The mean values of the skin thicknesses from all models shown are nearly the same, fm and fm, but the two correlations have different slopes. Both are within of the respective mean experimental measurements, see Table 4 and Table 5, indicating an overall consistency exists between theory and experiment even though most of the models displayed were not explicitly fit to neutron skin values but rather to binding energy data. In other words, there is no reason to expect that either conventional interactions or modeling lead to large systematic uncertainties with respect to calculations of neutron skin thicknesses.

Figure 7.
Neutron skin thicknesses of Ca (red) and Pb (black) from interactions compiled in Ref. [37] (filled circles) and Refs. [18,60,63,64] (open circles). Means (1 standard deviations) of linear correlations are shown as solid (dashed) lines. The horizontal shaded bands indicate the 1 standard deviation ranges of the averaged experimental results. The dotted black (red) lines indicate the 1 standard deviation range of () from PREX I+II [17] (CREX [18]).

Table 3.
Slopes, intercepts, and standard deviations of linear fits .
Nevertheless, it is worth mentioning that two recent more sophisticated theoretical predictions give divergent views. Relatively small values of neutron skins are implied by coupled cluster ab initio calculations which predict fm [65] and fm [66], which are close to the respective experimental means (Table 4). On the other hand, the nonlocal dispersive optical model predicts that finite-size effects play an important role in enhancing the neutron skin, giving fm [67] and fm [68], both of which are considerably larger than the respective experimental means.
The strong linear correlations existing between model calculations of the neutron skins of these two nuclei with L obviously implies a strong linear correlation exists between the skin thicknesses themselves. Neutron skin data from Ref. [37] alone follows the linear relation
with a very small uncertainty. Including 179 skin calculations using additional Skyrme and RMF forces by Refs. [18,60,63,64], the mean linear relation becomes
which is virtually identical except for having a larger standard deviation reflecting a greater variation in underlying forces (and possibly less strict constraints regarding fitting nuclear masses and charge radii). We note that these references contain a number of the same interactions. These duplicate calculations show variations of as much as 0.01 fm, which should be included as a systematic modeling uncertainty. However, this uncertainty is small enough that it does not affect the results significantly. We also note that Ref. [69] has argued that an accurate determination of is insufficient to constrain because of the significant difference in the surface-to-volume ratio of these two nuclei, a conclusion, however, not supported by our results.
3.1. Neutron Skin Measurements and Correlations
The nuclides Ca and Pb are especially important because they are the only stable neutron-rich, closed-shell, nuclei. Measurements of their neutron skin thicknesses are summarized in Table 4 and Table 5, as well as Figure 8. The error-weighted mean of all tabulated experimental measurements is fm, which is consistent with the average theoretical estimate fm. The mean of historical measurements not including PREX is fm. For Ca, the mean of all measurements is fm, about smaller than the average theoretical estimate fm. The average of historical measurements not including CREX is fm.

Figure 8.
Neutron skin measurements [17,18,70,71,72,73,74,75,76,77,78,79,80,81] with 68% confidence intervals and citations. Horizontal dashed lines denote standard deviations from the weighted means of experiments other than CREX or PREX I+II.

Table 4.
Pb neutron skin measurements and theoretical predictions with uncertainties.
Table 4.
Pb neutron skin measurements and theoretical predictions with uncertainties.
| Pb Experiment | Reference | (fm) |
|---|---|---|
| Coherent production | [77] | |
| Pionic atoms | [73] | |
| Pion scattering | [73] | |
| annihilation | [78,79] | |
| Elastic polarized p scattering | [70] | |
| Elastic polarized p scattering | [80] | |
| Elastic p scattering | [81] | |
| Elastic p scattering | [72] | |
| Parity-violating scattering (PREX I+II) | [17] | |
| Pb experimental weighted mean | ||
| Pygmy dipole resonances | [82] | |
| [83] | ||
| Anti-analog giant dipole resonance | [84] | |
| Symmetry energy Pb | [85] | |
| Dispersive optical model | [86] | |
| Dispersive optical model | [67] | |
| Coupled cluster expansion | [66] | |
| [63,64], this paper | ||
| [62], this paper | ||
| [20,64], this paper | ||
| Pb theoretical weighted mean |

Table 5.
Ca neutron skin measurements and theoretical predictions with uncertainties. * Uncertainty scaled upwards as per Ref. [87].
Table 5.
Ca neutron skin measurements and theoretical predictions with uncertainties. * Uncertainty scaled upwards as per Ref. [87].
| Ca Experiment | Reference | (fm) |
|---|---|---|
| Elastic polarized p scattering | [70] | |
| Elastic p scattering | [76] | |
| Elastic p scattering | [72] | |
| Elastic p scattering | [71] | |
| Pionic atoms | [73] | |
| Pion scattering | [74] | |
| scattering | [75] | |
| Parity-violating scattering (CREX) | [18] | |
| Ca experimental weighted mean | * | |
| Coupled-cluster expansion | [65] | |
| Dispersive optical model | [68] | |
| [63], this paper | ||
| Ca theoretical weighted mean | * |
3.2. Parity-Violating Electron Scattering Measurements
A lot of attention has been paid to the recent PREX [17] and CREX [18] measurements of the neutron skins of Pb and Ca, respectively, using parity-violating electron scattering, which is claimed to have less modeling systematic uncertainty than other experimental methods [19]. Interestingly, the PREX measurement is more than 1 standard deviation higher than the mean value of previous Pb experiments, while the CREX measurement is smaller than the mean of previous Ca experiments, but by less than 1 standard deviation. Fitting the neutron skin thickness from parity-violating scattering of either nuclide alone would give vastly different values for L, about 110 MeV for Pb [20] and 0 MeV for Ca, as can be seen by reference to Figure 9. Even using the mean values of all the experimental results would produce disparate values of L, about 40 MeV and 10 MeV, respectively, although they would lie within a standard deviation of each other. It is important to note that the weighted mean experimental value of decreases by only about 0.007 fm and that of increases by only about 0.003 fm when the PREX and CREX results are excluded. Without compelling reasons to favor measurements of either nuclide, our approach is to instead attempt to simultaneously satisfy experimental information for both nuclides.

Figure 9.
Neutron skin thicknesses of Ca and Pb from interactions compiled in Ref. [37] (filled circles) and Refs. [18,60,63,64] (triangles). Colors indicate L values where known; black triangles indicate points where L values are unspecified. Standard deviations of a linear correlation Equation (21) are shown as dashed lines. The red (blue) confidence ellipses are from PREX I+II [17] and CREX [18] (mean of all experiments); solid (dashed) ellipses are 68% (90%) confidence.
We follow two strategies for satisfaction of joint Ca-Pb measurements. First, one could take the approach that the PREX and CREX experiments qualitatively have fewer systematic uncertainties than other approaches, and only use those measurements. Alternatively, an agnostic approach would be to instead consider the weighted means of all measurements.
As can be seen in Figure 9, the PREX I+II value for is too large and the CREX value for is too small to permit any of the reference interactions from the compilation of Refs. [18,37,60,63,64] from satisfying both of them to within 68% confidence. The situation is different when considering the mean experimental results for Pb and Ca, with 4% of the reference interactions simultaneously satisfying them to 68% confidence.
A much larger number of interactions satisfy skin thickness measurements for both nuclei when considering 90% confidence regions. About 40% of the interactions from Ref. [37] can simultaneously satisfy the UGC, UGPC, PREX I+II and CREX results, and these have 0 MeV MeV. Similarly, about 24% of these interactions simultaneously lie within the 90% confidence region of the averages of all experiments, and also satisfy the UGC and UGPC, and these have 0 MeV MeV.
The associated permitted region in space can be ascertained by weighting those interactions [37] satisfying both unitary gas constraints, and which also have tabulated and values, by their probabilities given by a two-dimensional Gaussian defined by the skin measurements and their uncertainties. Results are shown in Figure 10 and tabulated in Table 1 for both approaches. Interestingly, using CREX+PREX measurements to define the probabilities gives a confidence ellipse in substantial agreement with the PNM EFT result. Using the mean of other skin measurements gives somewhat smaller mean values of and L.

Figure 10.
Symmetry parameters (left panel) and (right panel) jointly satisfying parity-violating experiments to within (exceeding) 90% confidence are shown as red and black filled (black open) circles; filled black circles violate Unitary Gas constraints (dotted boundary). Red (blue) confidence ellipses are for models satisfying Unitary Gas constraints weighted by their two-dimensional Gaussian probability defined by the parity-violating (red) and average (blue) experimental and measurements and uncertainties. The black confidence ellipse shows PNM EFT results.
It is important to note that this internal consistency among neutron skin measurements, mass fitting and neutron matter theory, using either approach, is not particularly sensitive to whether relativistic or non-relativistic interactions are considered, suggesting it is relatively free of associated systematic uncertainties. Partly, this is due to the moderate values of L that are favored, eliminating most RMF interactions in compilations.
We compare to Ref. [88], who combined data from isobaric analog states and the mean of experimental Pb neutron skin measurements (taken to be to fm) to infer to 68% confidence. Additionally, Ref. [61] used experimental values for Pb to infer L/MeV ≲ 77. However, neither of these sources considered the neutron skin of 48
We note an inference of MeV and MeV using a combined analysis of PREX and CREX measurements was recently obtained by Ref. [23]. Their method differs from the present analysis in that they optimized parameters for a Skyrme-like interaction using weak and charge form factors from PREX and CREX rather than inferred skin thicknesses, which are subject to additional theoretical uncertainty, as well as binding, breathing mode and neutron-proton Fermi energies, and charge and diffraction radii. Their estimates are compatible with the present results but have larger uncertainties despite the fact that they are not subject to the additional theoretical uncertainty relating form factors to skin thicknesses.
Another study by Ref. [24] which also considered dipole polarizabilities concluded that no single interaction could satisfy both PREX and CREX interactions to 68% confidence, agreeing with this paper and Ref. [23], but did not attempt to infer a ’best-fit’ interaction.
An analogous analysis for is shown in Figure 10. The confidence regions for both approaches are compatible with that of PNM EFT, although the results using PREX+CREX measurements have nearly the same centroid.
4. Other Nuclear Methods
4.1. Correlations from Nuclear Dipole Polarizabilities
Nuclear measurements involving the giant dipole resonance enable additional constraints on the symmetry energy and can shed light on the somewhat disparate results of recent skin thickness measurements. Measured dipole polarizabilities for the neutron-rich nuclides Ca, Sn and Pb are given in Table 6. Support for the experimental values comes from theoretical calculations of by Ref. [89], who found the linear relations:
with correlation coefficients of 0.82 and 0.96, respectively. These relations predict the values fm, slightly larger than the experimental value, from the measured value of , and fm, slightly smaller than the experimental value, from the measured value of , but both within one standard deviation.

Table 6.
Dipole polarizabilities with uncertainties. values corrected as per Ref. [90].
Ref. [94] determined that the central energy of the giant dipole resonance of Pb and the symmetry energy has its greatest correlation at the density fm, and from the measured value of thereby deduced the symmetry energy at that density to be MeV, which is in agreement with MeV deduced from the masses of closed shell nuclei [55]. Similarly, in a study using 62 non-relativistic and relativistic interactions fitted to ground-state properties of finite nuclei, Ref. [95] deduced that the electric dipole polarizability of Pb has its greatest correlation with the symmetry energy at the density fm, and found the symmetry energy at that density to be MeV (after correcting the measured dipole polarizability as per Ref. [90]). Using the expansion Equation (2), employing empirical correlations to eliminate and , and including uncertainties in , these results imply the two linear relations
respectively. These are in essential agreement with the correlation derived from nuclear mass measurements. The dipole polarizability correlations are also consistent with the relevant confidence regions established from EFT as well as from neutron skin thickness measurements.
Ref. [90] showed the existence of a theoretical correlation between the neutron skin thickness and the electric dipole polarizability, justified by the nuclear droplet model. For Ca, Sn and Pb, these are [89]
We found similar correlations for Pb using calculations of Ref. [62] and Ref. [96], respectively:
Combining relations in Equation (24) with experimental values for the dipole polarizabilities (Table 6) gives the relation
which compares favorably with Equation (21), albeit with larger uncertainties, emphasizing the consistency of polarizability and skin experimental results with theory. The same result is achieved using Equation (25) instead. Equations (24) and (25) also suggest that measurements of and for Ca, Sn or Pb provide constraints on independently of L. The mean experimental data for Ca, Sn ( values are given in Table 7) and Pb yield MeV, MeV, and MeV, respectively, using Equation (24). Equation (25) alternatively yields MeV and MeV for Pb. Collectively, one finds MeV, which, once again, is consistent with mass fitting, EFT and the mean neutron skin results. None of these ranges for are consistent with the PREX measurement by itself.

Table 7.
Sn neutron skin measurements with uncertainties.
4.2. Correlations from Heavy Ion Collisions
Two general problems with extracting symmetry energy parameters from heavy-ion collisions are: (1) matter in these collisions is close to symmetric, with the symmetry energy being perhaps 10% of the total and therefore difficult to ascertain; and (2) the matter has excitation energies of 50-several hundred MeV per baryon (corresponding to 20–50 Mev). This paper has therefore concentrated on probes connected with cold finite nuclei where densities are near and a Taylor expansion is appropriate. Here, some results from analyses of heavy ion experiments are summarized.
It has been proposed [100] to use empirical pressures deduced in cold SNM from hadronic transport model analyses of heavy-ion collisions [101,102]. Data come from studying kaon production [103,104], which provides constraints in the density range from to , and nuclear collective flow [105,106,107,108], which provides constraints from to . Pressures from kaon production (collective flows) have estimated uncertainties of about ––, so such constraints have appreciable errors even before systematic uncertainties, such as from extrapolating from moderate excitation energies to zero temperature, are taken into account. In addition, these estimates are based upon Taylor expansions of the symmetric matter energy like Equation (4), but including a fourth-order (kurtosis Z) term. This introduces additional uncertainty, not only because of questionable validity of such an expansion at high density, but also because the expansion is arbitrarily truncated at fourth order. Although interesting correlations between and are deduced from this analysis, application to PNM and therefore extraction of symmetry energy parameters becomes model dependent.
The symmetry energy might more directly probed in heavy ion collisions through the multiplicity ratio in central collisions [109,110,111] and from isospin diffusion or elliptic flows of neutrons and protons [112,113,114,115]; see Ref. [116] for a summary. Both approaches, however, have given rather conflicting results concerning the stiffness of the symmetry energy, with L ranging from 0 MeV to MeV, indicating a large degree of model dependence in the analyses [50,117,118].
For example, the analysis of Ref. [50], which assumes that the density-dependent symmetry energy has the simple form
where MeV, predicts a band in space which is shown as HIC in Figure 5. For S in Equation (27), a line in the plane with a slope implies that S is best determined at density . In addition, any point in this diagram implies a value
The diagonal sides of the quadrilateral in Figure 4 therefore imply that and . Therefore, this experiment best probes subsaturation densities smaller than do mass fits (), neutron skin thicknesses () or neutron matter theory (). However, the symmetry parameters are rather poorly constrained (possibly because the extrapolation to saturation density is larger in the HIC case), with the quadrilateral having a much larger extent than the regions determined in Figure 10. The analysis of Ref. [117] instead suggests MeV, indicating overall difficulties with this method.
5. Astrophysical Considerations
Astrophysical observations of neutron stars can yield estimates of radii, moments of inertia, and tidal deformabilities. We will consider two of the currently most popular observations: the LIGO/Virgo detection of the neutron star merger GW170817 [21,119] and NICER observations of the rapidly rotating pulsars PSR J0030+0451 [25,26] and PSR J0740+6620 [27,28]. It will be seen that the symmetry parameters ranges suggested by nuclear experiment and theory are consistent with inferences from astrophysical observations of neutron stars.
5.1. Neutron Star Radii
For subsets of forces from Refs. [18,37,60,63,64], the radii of neutron stars ( and and are available (most of the radius information was kindly provided by B. Tsang). Although nuclear interaction models, having been fit to nuclei, describe matter with large proton fractions and ns, one should be wary of making predictions about neutron stars from them. Nevertheless, as shown in Figure 11, there is a clear correlation between L and R1.4. The correlation between PNSM(n) and R1.4 turns out to be greatest at densities in the range 1.5–2ns [48], low enough that interaction models are still reliable. Note, however, that these models should not be used to constrain neutron star maximum masses, which are most sensitive to PNSM for n ≳ 3ns [48].
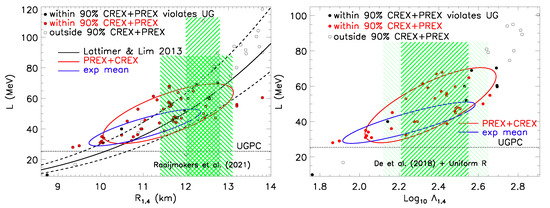
Figure 11.
The same as Figure 10 except showing versus L (left panel) and versus L (right panel) for subsets of forces from Refs. [18,37,60,63,64]. Black solid and dashed curves in the left panel show the correlation and standard deviations derived as in the text. The shaded green bands are 68% and 95% confidence intervals from a joint analysis of GW170817 and PSR J0030+0451 and PSR J0740+6620 by Ref. [120] (left panel) and from GW170817 Bayesian analyses posteriors [21], corrected for priors chosen so as to reflect uniform R priors (right panel).
One can predict a validity range for based on neutron skin measurements in the same way the predictions shown in Figure 9 were made. Weighting the predicted of models satisfying both Unitary Gas constraints by their double Gaussian probabilities in – space, one finds km (and MeV) to 68% confidence using parity-violating neutron skin measurements (Figure 11). In comparison, the weighted average of other experiments yields km (and MeV).
Bayesian analyses combining measurements of tidal deformability (see Section 5.2) from GW170817 and radii from pulse-profile modeling of PSR J0030+0451 and PSR J0740+6620 suggest km to 68% confidence [120]. The 68% and 90% confidence intervals are shown by green shading in the left panel of Figure 11. These astrophysical inferences are in essential agreement with our results using PREX and CREX data, and are about larger then results obtained using other experimental neutron skin data.
It is possible to understand the correlation observed in Figure 11. Since NSM is close to PNM around , there should a high degree of correlation between and L, and therefore between and L. Indeed, a correlation between and , the neutron star matter pressure, around was empirically established some time ago by Ref. [7] and refined by Ref. [121],
It is necessary to convert Equation (29) into one depending directly upon the symmetry parameters by taking into account how NSM differs from PNM. NSM has a finite proton (electron) fraction determined by energy minimization with respect to x at every density, leading to beta-equilibrium. The total energy per baryon of NSM in the quadratic approximation is
where is the energy of PNM, is the density-dependent symmetry energy and x is the proton fraction. The last term is the electron contribution. Beta equilibrium requires , giving
At , one finds
At , Only the L term in a density expansion of S contributes. For a given value of L, a normal distribution of values based on the PNM EFT correlation (Figure 5), i.e.,
can be used to find a corresponding x distribution from Equation (31). Then, Equation (32) gives the distribution and Equation (29) gives the distribution, which is shown with uncertainties in Figure 11 as black lines. The agreement, including uncertainties, with model interactions is remarkable, in spite of the fact that Equation (29) was established using a far smaller number of interactions.
5.2. Tidal Deformabilities and Radii
For GW170817, the most accurately-measured quantity is the chirp mass [119]
where are the masses of the merging stars. Less precisely measured is the radius-sensitive binary tidal deformability of the system,
where is the mass ratio and and are the individual stellar deformabilities. Typical trajectories in the relevant mass range for BNS merger components (judging from galactic BNS [3,122]) have relatively small variations in R for a given EOS. Given the minimum (maximum) neutron star mass is about (), ≤ 1. Ref. [54] found, using piecewise polytropes, that in the absence of significant phase transitions, the average radius satisfies || < 0.5 km for all EOSs in this mass range, and averaged over all EOSs and masses, || has a standard deviation of about 0.1 km. Ref. [54] also determined, to high accuracy, that the dimensionless tidal deformability of individual stars in this mass range obeys the semi-universal (EOS-independent) relation
with a = 0.009 ± 0.002 and β = GM/Rc2. It therefore follows that
where the notation reflects that is measured at a well-defined . The q-dependence in Equation (37) is weak: and . Thus, the fact that q is poorly measured has little consequence, and one finds
Due to radius correlations, the uncertainty in is only half the uncertainty of a itself. Thus, carries significant radius information. To the same accuracy, .
More directly, one can predict , the dimensionless tidal deformability of a neutron star, from neutron skin measurements using the same procedure as used for . Values of for the interactions in the right panel of Figure 11 were provided by B. Tsang. Weighting each by the double Gaussian defined by neutron skin thickness measurements and uncertainties, it is found, to 68% confidence, ( MeV) using the PREX+CREX neutron skin measurements, and ( MeV and) using the average of other skin measurements.
These ranges are consistent with inferences [21] from LIGO/Virgo observations [22,119] of the BNS merger GW170817 (shaded green regions in the right panel of Figure 11). For this comparison, it is useful to convert the observed quantity to . Use of Equation (36) gives
For GW170817, . Ref. [21] calculated the tidal deformability posteriors of the two merging stars from a gravitational wave analysis assuming and causality. They assumed uniform and M priors for the two stars. They found to 68% confidence and to 90% confidence. However, the results are sensitive to the assumed priors. Perhaps it is more realistic to assume uniformity in rather than because has a large dynamic range. This is tantamount to a uniform radius prior. In this case, to 68% confidence, , and to 90% confidence, . Although the predicted means are nearly the same, assuming uniformity in the priors dramatically reduces the upper 68% and 90% confidence bounds, and makes them strikingly similar to those inferred from neutron skin measurements.
6. Conclusions
Compilations containing several hundred theoretical nuclear interactions of both the non-relativistic (Skyrme) or relativistic (RMF) type, which have been fitted to nuclear masses and/or charge radii, show that significant correlations exist among symmetry and neutron energy parameters , L, and . The average values and correlation slopes depend on whether the interactions considered are non-relativistic or relativistic: the relativistic interactions in these compilations tend to have larger values of L and , for example. In both cases, the 68% confidence ellipses for the , and correlations considerably overlap with those predicted by chiral effective field calculations of pure neutron matter, but have different slopes.
Theoretical calculations of neutron skin thicknesses of neutron-rich closed shell nuclei (Ca and Pb) predict strong correlations with L with average uncertainties less than 0.01 fm. The individual weighted means of experimental measurements of these nuclei can be used to predict comparable ranges of L, 0–40 MeV for Ca and 30–60 MeV for Pb, both consistent with the range determined by jointly fitting masses and neutron matter calculations. Without a strong reason to prefer skin measurements of one nucleus over another, simultaneous reconciliation of the weighted means of skin measurements of both nuclei with those from theoretical calculations of forces in the compilations constrains the symmetry parameters MeV and MeV.
Alternatively, one could choose to only employ parity-violating electron scattering results (PREX and CREX), which have been claimed to have smaller systematic uncertainties than other techniques. The two experiments separately predict incompatible ranges of L ( MeV and MeV, respectively), but accepting both measurements to be equally valid suggests MeV and MeV. These alternative approaches in treating neutron skin measurements predict closely overlapping ranges that are consistent with ranges predicted from mass fits and neutron matter theory, and therefore indicate that the PREX and CREX experimental results are consistent with those of other techniques. These estimates are compatible with those calculated by Ref. [23].
Further support for the resulting focus on small ranges of symmetry parameters comes from measurements and theoretical studies of nuclear dipole polarizabilities (). Theory predicts that is linearly correlated to . Measured values of and for Ca, Sn and Pb then imply MeV in good agreement with our result. Further proof that existing measurements of and are compatible comes from the linear relation between and resulting from the theoretical correlation; this linear relation is in remarkable agreement with that predicted by theoretical neutron skin calculations of these nuclei using both relativistic and non-relativistic interactions.
The inferred small ranges of symmetry parameters combining mass fitting, neutron matter theory, and skin thickness and dipole polarizability measurements and theory are robust and do not depend significantly on the type of nuclear interaction considered, despite the systematic differences in predictions of individual quantities arising from a single method alone. Potentially, an improvement of our predictions can be achieved by directly comparing predictions and measurements of the charge and weak form factors of Ca and Pb, as done in Ref. [23]. This would remove the additional uncertainty involved in converting form factors to neutron and proton radii. However, given the compatibility of results from our work with Rev. [23], this additional uncertainty does not appear to be significant. In any case, measurements of form factors or neutron skin thicknesses will have to be performed with much greater precision than at present to improve upon the symmetry parameter constraints from chiral Lagrangian EFT calculations.
For the first time, we extended predictions from neutron skin measurements to include neutron star radii and tidal deformabilities without employing any information from astrophysical observations. Our estimated ranges for and are compatible with recent studies using LIGO/Virgo data from the BNS merger GW170817 and NICER X-ray observations of PSR J0030+0451 and PSR J0740+6620.
Funding
This work was initiated through the NSF-funded Physics Frontier Center Network for Neutrinos, Nuclear Astrophysics, and Symmetries (N3AS) and was supported by the U.S. DOE grant DE-AC02-87ER40317.
Data Availability Statement
Not applicable.
Acknowledgments
Thanks are due to J. Piekarewicz, W. Nazarewicz and B. Tsang for providing data and, together with T. Zhao, C. J. Horowitz and K. Kumar, helpful discussions.
Conflicts of Interest
The author declares no conflict of interest. The funders had no role in the design of the study, the collection, analyses, or interpretation of data, the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| NS | neutron star | BNS | binary neutron stars |
| EOS | equation of state | PSR | pulsar |
| SNM | symmetric nuclear matter | PNM | pure neutron matter |
| EFT | chiral effective field theory | RMF | relativistic mean field |
| UGC | Unitary Gas Conjecture | UGPC | Unitary Gas Pressure Conjecture |
| NICER | Neutron Star Interior Composition ExploreR |
References
- Steiner, A.W.; Prakash, M.; Lattimer, J.M.; Ellis, P. Isospin asymmetry in nuclei and neutron stars. Phys. Rep. 2005, 411, 325. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron star observations: Prognosis for equation of state constraints. Phys. Rep. 2007, 442, 109. [Google Scholar] [CrossRef]
- Lattimer, J.M. Neutron Stars and the Nuclear Matter Equation of State. Annu. Rev. Nucl. Part. Sci. 2021, 71, 433. [Google Scholar] [CrossRef]
- Swesty, F.D.; Lattimer, J.M.; Myra, E.S. The Role of the Equation of State in the “Prompt” Phase of Type II Supernovae. Astrophys. J. 1994, 425, 195. [Google Scholar] [CrossRef]
- Roberts, L.F.; Shen, G.; Cirigliano, V.; Pons, J.A.; Reddy, S.; Woosley, S.E. Protoneutron Star Cooling with Convection: The Effect of the Symmetry Energy. Phys. Rev. Lett. 2012, 108, 061103. [Google Scholar] [CrossRef]
- Morozova, V.; Radice, D.; Burrows, A.S.; Vartanyan, D. The gravitational wave signal from core-collapse supernovae. Astrophys. J. 2018, 861, 10. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron Star Structure and the Equation of State. Astrophys. J. 2001, 550, 426. [Google Scholar] [CrossRef]
- Bauswein, A.; Janka, H.-T. Measuring Neutron-Star Properties via Gravitational Waves from Neutron-Star Mergers. Phys. Rev. Lett. 2012, 108, 011101. [Google Scholar] [CrossRef]
- Lackey, B.D.; Kyutoku, K.; Shibata, M.; Brady, P.R.; Friedman, J.L. Extracting equation of state parameters from black hole-neutron star mergers. I. Nonspinning black holes. Phys. Rev. D 2012, 85, 044061. [Google Scholar] [CrossRef]
- Page, D.; Reddy, S. Thermal and transport properties of the neutron star inner crust. In Neutron Star Crust; Bertulani, C.A., Piekarewicz, J., Eds.; Nova Science Publisheres: New York, NY, USA, 2021. [Google Scholar]
- Hurley, K.; Boggs, S.E.; Smith, D.M.; Duncan, R.C.; Lin, R.; Zoglauer, A.; Krucker, S.; Hurford, G.; Hudson, H.; Wigger, C.; et al. An exceptionally bright flare from SGR 1806–1820 and the origins of short-duration γ-ray bursts. Nature 2005, 434, 1098. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. The giant flare of 1998 August 27 from SGR 1900+ 14. II. Radiative mechanism and physical constraints on the source. Astrophys. J. 2001, 561, 980. [Google Scholar] [CrossRef]
- Samuelsson, L.; Andersson, N. Neutron star asteroseismology. Axial crust oscillations in the Cowling approximation. MNRAS 2007, 374, 256. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Pethick, C.J.; Prakash, M.; Haensel, P. Direct URCA process in neutron stars. Phys. Rev. Lett. 1991, 66, 2701. [Google Scholar] [CrossRef]
- Nikolov, N.; Schunck, N.; Nazarewicz, W.; Bender, M.; Pei, J. Surface symmetry energy of nuclear energy density functionals. Phys. Rev. C 2011, 83, 034305. [Google Scholar] [CrossRef]
- Drischler, C.; Holt, J.W.; Wellenhofer, C. Chiral Effective Field Theory and the High-Density Nuclear Equation of State. Annu. Rev. Nucl. Part. Sci. 2021, 71, 403. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.; Armstrong, D.S.; Averett, T.; Gayoso, C.A.; Barcus, S.; Bellini, V.; Beminiwattha, R.S.; et al. Accurate determination of the neutron skin thickness of 208Pb through parity-violation in electron scattering. Phys. Rev. Lett. 2021, 126, 172502. [Google Scholar] [CrossRef]
- Adhikari, D.; Albatainen, H.; Androic, D.; Anioj, K.A.; Armstrong, D.S.; Averett, T.; Ayerbe Gayoso, C.; Barcus, S.K.; Bellini, V.; Beminiwattha, R.S.; et al. Precision determination of the neutral weak form factor of 48Ca. Phys. Rev. Lett. 2022, 129, 042501. [Google Scholar] [CrossRef]
- Thiel, M.; Sfienti, C.; Piekarewicz, J.; Horowitz, C.J.; Vanderhaeghen, M. Neutron skins of atomic nuclei: Per aspera ad astra. J. Phys. G Nucl. Part. Phys. 2019, 46, 093003. [Google Scholar] [CrossRef]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-2 on the equation of state of neutron-rich matter. Phys. Rev. Lett. 2021, 126, 172503. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal deformabilities and radii of neutron stars from the observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the binary neutron star merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, L.-W. Bayesian inference of the symmetry energy and the neutron skin in 48Ca and 208Pb from CREX and PREX-2. arXiv 2022, arXiv:2207.03328. [Google Scholar]
- Reinhard, P.G.; Roca-Maza, X.; Nazarewicz, W. Combined theoretical analysis of the parity-violating asymmetry for 48Ca and 208Pb. Phys. Rev. Lett. 2022, 129, 232501. [Google Scholar] [CrossRef] [PubMed]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER view of PSR J0030+0451: Millisecond pulsar parameter estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The radius of PSR J0740+6620 from NICER and XMM-Newton data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER view of the massive pulsar PSR J0740+6620 informed by radio timing and XMM-Newton spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Wellenhofer, C.; Holt, J.W.; Kaiser, N. Divergence of the isospin-asymmetry expansion of the nuclear equation of state in many-body perturbation theory. Phys. Rev. C 2016, 93, 055802. [Google Scholar] [CrossRef]
- Agrawal, B.K.; Shlomo, S.; Au, V.K. Nuclear matter incompressibility coefficient in relativistic and nonrelativistic microscopic models. Phys. Rev. C 2003, 68, 031304. [Google Scholar] [CrossRef]
- Todd-Rutel, B.G.; Piekarewicz, J. Neutron-rich nuclei and neutron stars: A new accurately calibrated interaction for the study of neutron-rich matter. Phys. Rev. Lett. 2005, 95, 122501. [Google Scholar] [CrossRef]
- Audi, G.; Wapstra, A.H.; Thibault, C. The Ame2003 atomic mass evaluation: (II). Tables, graphs and references. Nucl. Phys. A 2003, 729, 337. [Google Scholar] [CrossRef]
- Myers, W.D.; Swiatecki, W.J. Average nuclear properties. Ann. Phys. 1969, 55, 395. [Google Scholar]
- Dutra, M.; Loureno, O.; Martins, J.S.S.; Delfino, A.; Stone, J.R.; Stevenson, P.D. Skyrme interaction and nuclear matter constraints. Phys. Rev. 2012, C85, 035201. [Google Scholar] [CrossRef]
- Tews, I.; Lattimer, J.M.; Ohnishi, A.; Kolomeitsev, E.E. Symmetry parameter constraints from a lower bound on neutron-matter energy. Astrophys. J. 2017, 848, 105. [Google Scholar] [CrossRef]
- Dutra, M.; Loureno, O.; Avancini, S.S.; Carlson, B.V.; Delfino, A.; Menezes, D.P.; Providencia, C.; Typel, S.; Stone, J.R. Relativistic mean-field hadronic models under nuclear matter constraints. Phys. Rev. 2014, C90, 055203. [Google Scholar] [CrossRef]
- Tagami, S.; Wakasa, T.; Takechi, M.; Matsui, J.; Yahiro, M. Neutron skin in 48Ca determined from p+48Ca and 48Ca+12C scattering. arXiv 2022, arXiv:2201.08541. [Google Scholar] [CrossRef]
- Kortelainen, M.; Lesinski, T.; Moré, J.; Nazarewicz, W.; Sarich, J.; Schunck, N.; NStoitsov, M.V.; Wild, S. Nuclear energy density optimization. Phys. Rev. C 2010, 82, 024313. [Google Scholar] [CrossRef]
- Drischler, C.; Furnstahl, R.J.; Melendez, J.A.; Phillips, D.R. How well do we know the neutron-matter equation of state at the densities inside neutron stars? A Bayesian approach with correlated uncertainties. Phys. Rev. Lett. 2020, 125, 202702. [Google Scholar] [CrossRef]
- Weinberg, S. Precise relations between the spectra of vector and axial-vector mesons. Phys. Rev. Lett. 1967, 18, 507. [Google Scholar] [CrossRef]
- Weinberg, S. Nonlinear realizations of chiral symmetry. Phys. Rev. 1968, 166, 1568. [Google Scholar] [CrossRef]
- Epelbaum, E.; Hammer, H.-W.; Meissner, U.-G. Modern theory of nuclear forces. Rev. Mod. Phys. 2009, 81, 1773. [Google Scholar] [CrossRef]
- Machleidt, R.; Entem, D. Chiral effective field theory and nuclear forces. Phys. Rep. 2011, 503, 1. [Google Scholar] [CrossRef]
- Hammer, H.-W.; König, S.; van Kolck, U. Nuclear effective field theory: Status and perspectives. Rev. Mod. Phys. 2020, 92, 025004. [Google Scholar] [CrossRef]
- Tews, I.; Davoudi, Z.; Ekström; Holt, J.D.; Lynn, J.E. New Ideas in Constraining Nuclear Forces. J. Phys. G 2020, 47, 103001. [Google Scholar] [CrossRef]
- Drischler, C.; Hebeler, K.; Schwenk, A. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys. Rev. Lett. 2019, 122, 042501. [Google Scholar] [CrossRef]
- Leonhardt, M.; Pospiech, M.; Schallmo, B.; Braun, J.; Drischler, C.; Hebeler, K.; Schwenk, A. Symmetric nuclear matter from the strong interaction. Phys. Rev. Lett. 2020, 125, 142502. [Google Scholar] [CrossRef]
- Drischler, C.; Han, S.; Lattimer, J.M.; Prakash, M.; Reddy, S.; Zhao, T. Limiting masses and radii of neutron stars and their implications. Phys. Rev. C 2021, 103, 045808. [Google Scholar] [CrossRef]
- Drischler, C.; Melendez, J.A.; Furnstahl, R.J.; Phillips, D.R. Quantifying uncertainties and correlations in the nuclear-matter equation of state. Phys. Rev. C 2020, 102, 054315. [Google Scholar] [CrossRef]
- Tsang, M.B.; Zhang, Y.X.; Danielewicz, P.; Famiano, M.; Li, Z.-X.; Lynch, W.G.; Steiner, A.W. Constraints on the density dependence of the symmetry energy. Phys. Rev. Lett. 2009, 102, 122701. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Constraints on Neutron Star Radii Based on Chiral Effective Field Theory Interactions. Phys. Rev. Lett. 2010, 105, 161102. [Google Scholar] [CrossRef]
- Ku, M.J.H.; Sommer, A.T.; Cheui, L.W.; Zwierlein, M.W. Revealing the superfluid lambda transition in the universal thermodynamics of a unitary Fermi gas. Science 2012, 335, 563. [Google Scholar] [CrossRef] [PubMed]
- Zürn, G.; Lompe, T.; Wenz, A.N.; Jochim, S.; Julienne, P.S.; Hutson, J.M. Precise characterization of 6Li Feshbach resonances using trap-sideband-resolved RF spectroscopy of weakly bound molecules. Phys. Rev. Lett. 2013, 110, 135301. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Lattimer, J.M. Tidal deformabilities and neutron star mergers. Phys. Rev. D 2018, 98, 063020. [Google Scholar] [CrossRef]
- Brown, B.A. Neutron radii in nuclei and the neutron equation of state. Phys. Rev. Lett. 2000, 85, 5296. [Google Scholar] [CrossRef] [PubMed]
- Centelles, M.; Roca-Maza, X.; Vinas, X.; Warda, M. Nuclear symmetry energy probed by neutron skin thickness of nuclei. Phys. Rev. Lett. 2009, 102, 122502. [Google Scholar] [CrossRef] [PubMed]
- Typel, S.; Brown, B.A. Neutron radii and the neutron equation of state in relativistic models. Phys. Rev. C 2001, 64, 027302. [Google Scholar] [CrossRef]
- Xu, J.; Xie, W.-J.; Li, B.-A. Bayesian inference of nuclear symmetry energy from measured and imagined neutron skin thickness in 116,118,120,122,124,130,132Sn, 208Pb, and 48Ca. Phys. Rev. C 2020, 102, 044316. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, L.-W. Constraining the symmetry energy at subsaturation densities using isotope binding energy difference and neutron skin thickness. Phys. Lett. B 2013, 726, 234. [Google Scholar] [CrossRef]
- Brown, B.A. Mirror charge radii and the neutron equation of state. Phys. Rev. Lett. 2017, 119, 122502. [Google Scholar] [CrossRef]
- Furnstahl, R.J. Neutron radii in mean-field models. Nucl. Phys. 2002, A706, 85. [Google Scholar] [CrossRef]
- Reinhard, P.-G.; Roca-Maza, X.; Nazarewicz, W. Information content of the parity-violating asymmetry in 208Pb. Phys. Rev. Lett. 2021, 127, 232501. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, C.J.; Kumar, K.S.; Michaels, R. Electroweak measurements of neutron densities in CREX and PREX at JLab, USA. Eur. Phys. J. A 2014, 50, 48. [Google Scholar] [CrossRef]
- Piekarewicz, J.; Agrawal, B.K.; Colò, G.; Nazarewicz, W.; Paar, N.; Reinhard, P.-G.; Roca-Maza, X.; Vretenar, D. Electric dipole polarizability and the neutron skin. Phys. Rev. C 2012, 85, 041302. [Google Scholar] [CrossRef]
- Hagen, G.; Ekström, A.; Forssén, C.; Jansen, G.R.; Nazarewicz, W.; Papenbrock, T.; Wendt, K.A.; Bacca, S.; Barnea, N.; Carlsson, B.; et al. Neutron and weak-charge distributions of the 48Ca nucleus. Nat. Phys. 2016, 12, 186. [Google Scholar]
- Hu, B.; Jiang, W.; Miyagi, T.; Sun, Z.; Ekström, A.; Forssén, C.; Hagen, G.; Holt, J.D.; Papenbrock, T.; Stroberg, S.R.; et al. Ab initio predictions link the neutron skin of 208Pb to nuclear forces. Nature Phys. 2021, 18, 1196. [Google Scholar] [CrossRef]
- Atkinson, M.C.; Mahzoon, M.H.; Keim, M.A.; Bordelon, B.A.; Pruitt, C.D.; Charity, R.J.; Dickhoff, W.H. Dispersive optical model analysis of 208Pb generating a neutron-skin prediction beyond the mean field. Phys. Rev. C 2020, 101, 044303. [Google Scholar] [CrossRef]
- Mahzoon, M.H.; Atkinson, M.C.; Charity, R.J.; Dickhoff, W.H. Precision Determination of the Neutral Weak Form Factor of 48Ca. Phys. Rev. Lett. 2017, 119, 22503. [Google Scholar]
- Reinhard, P.-G.; Piekarewicz, J.; Nazarewicz, W.; Agrawal, B.K.; Paar, N.; Roca-Maza, X. Information content of the weak-charge form factor. Phys. Rev. C 2013, 88, 034325. [Google Scholar] [CrossRef]
- Ray, L. Neutron isotopic density differences deduced from 0.8 GeV polarized proton elastic scattering. Phys. Rev. C 1979, 19, 1855. [Google Scholar] [CrossRef]
- Zenhiro, J.; Sakaguchi, H.; Terashima, S.; Uesaka, T.; Hagen, G.; Itoh, M.; Murakami, T.; Nakatsugawa, Y.; Ohnishi, T.; Sagawa, H.; et al. Direct determination of the neutron skin thicknesses in 40,48Ca from proton elastic scattering at Ep = 295 MeV. arXiv 2018, arXiv:1810.11796. [Google Scholar]
- Clark, B.C.; Kerr, L.J.; Hama, S. Neutron densities from a global analysis of medium-energy proton-nucleus elastic scattering. Phys. Rev. C 2003, 67, 054605. [Google Scholar] [CrossRef]
- Friedman, E. Neutron skins of 208Pb and 48Ca from pionic probes. Nucl. Phys. A 2012, 896, 46. [Google Scholar] [CrossRef]
- Gibbs, W.R.; Dedonduer, J.-P. Neutron radii of the calcium isotopes. Phys. Rev. C 1992, 46, 1825. [Google Scholar] [CrossRef] [PubMed]
- Gils, H.J.; Rebel, H.; Friedman, E. Isotopic and isotonic differences between α particle optical potentials and nuclear densities of 1 nuclei. Phys. Rev. C 1984, 29, 1295. [Google Scholar] [CrossRef]
- Shlomo, S.; Schaeffer, R. The difference between neutron and proton radii in the Ca isotopes. Phys. Lett. B 1979, 83, 5. [Google Scholar] [CrossRef]
- Tarbert, C.M.; Watts, D.P.; Glazier, D.I.; Aguar, P.; Ahrens, J.; Annand, J.R.M.; Arends, H.J.; Beck, R.; Bekrenev, V.; Boillat, B.; et al. Neutron Skin of 208Pb from Coherent Pion Photoproduction. Phys. Rev. Lett. 2014, 112, 242502. [Google Scholar] [CrossRef]
- Brown, B.A.; Shen, G.; Hillhouse, G.C.; Meng, J.; Trzcinska, A. Neutron skin deduced from antiprotonic atom data. Phys. Rev. C 2007, 76, 034305. [Google Scholar] [CrossRef]
- Brown, B.A.; Shen, G.; Hillhouse, G.C.; Meng, J.J.; Trzcinska, A. Neutron density distributions from antiprotonic 208Pb and 209 Bi atoms. Phys. Rev. C 2007, 76, 014311. [Google Scholar]
- Zenhiro, J.; Sakaguchi, H.; Murakami, T.; Yosoi, M.; Yasuda, Y.; Terashima, S.; Iwao, Y.; Takeda, H.; Itoh, M.; Yoshida, H.P.; et al. Neutron density distributions of 204,206,208Pb deduced via proton elastic scattering at Ep = 295 MeV. Phys. Rev. C 2010, 82, 044611. [Google Scholar]
- Starodubnsky, V.E.; Hintz, N.M. Extraction of neutron densities from elastic proton scattering by 206,207,208Pb at 650 MeV. Phys. Rev. C 1994, 49, 2118. [Google Scholar] [CrossRef]
- Klimkiewicz, A.; Paar, N.; Adrich, P.; Fallot, M.; Boretzky, K.; Aumann, T.; Cortina-Gil, D.; Pramanik, U.D.; Elze, T.W.; Emling, H.; et al. Nuclear symmetry energy and neutron skins derived from pygmy dipole resonances. Phys. Rev. C 2007, 76, 051603. [Google Scholar] [CrossRef]
- Chen, L.-W.; Ko, C.; Li, B.-A.; Xu, J. Density slope of the nuclear symmetry energy from the neutron skin thickness of heavy nuclei. Phys. Rev. C 2010, 82, 024321. [Google Scholar] [CrossRef]
- Yasuda, J.; Wakasa, T.; Okamoto, M.; Dozono, M.; Hatanaka, K.; Ichimura, M.; Kuroita, S.; Maeda, Y.; Noro, T.; Sakemi, Y.; et al. Anti-Analog Giant Dipole Resonance and the Neutron Skin in 208Pb. JPS Conf. Proc. 2014, 1, 013036. [Google Scholar]
- Dong, J.; Zuo, W.; Gu, J. Constraints on neutron skin thickness in 208Pb and density-dependent symmetry energy. Phys. Rev. C 2015, 91, 034315. [Google Scholar] [CrossRef]
- Pruitt, C.D.; Charity, R.J.; Sobotka, L.G.; Atkinson, M.C.; Dickhoff, W.H. Systematic Matter and Binding-Energy Distributions from a Dispersive Optical Model Analysis. Phys. Rev. Lett. 2020, 125, 102501. [Google Scholar] [CrossRef]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar]
- Danielewicz, P.; Lee, J. Symmetry energy II: Isobaric analog states. Nucl. Phys. A 2014, 922, 1–70. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Viñas, X.; Centelles, M.; Agrawal, B.K.; Colò, G.; Paar, N.; Piekarewicz, J.; Vretenar, D. Neutron skin thickness from the measured electric dipole polarizability in 68Ni, 120Sn, and 208Pb. Phys. Rev. C 2015, 92, 064304. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Brenna, M.; Colò, G.; Centelles, M.; Viñas, X.; Agrawal, B.K.; Paa, N.; Vretenar, D.; Piekarewicz, J.R. Electric dipole polarizability in 208Pb: Insights from the droplet model. Phys. Rev. C 2013, 88, 024316. [Google Scholar] [CrossRef]
- Tamii, A. Complete Electric Dipole Response and the Neutron Skin in 208Pb. Phys. Rev. Lett. 2011, 107, 062502. [Google Scholar] [CrossRef]
- Hashimoto, T.; Krumbholz, A.M.; Reinhard, P.G.; Tamii, A.; von Neumann-Cosel, P.; Adachi, T.; Aoi, N.; Bertulani, C.A.; Fujita, H.; Fujita, Y.; et al. Dipole polarizability of 120 Sn and nuclear energy density functionals. Phys. Rev. C 2015, 92, 031305. [Google Scholar] [CrossRef]
- Birkhan, J.; Miorelli, M.; Bacca, S.; Bassauer, S.; Bertulani, C.A.; Hagen, G.; Matsubara, H.; von Neumann-Cosel, P.; Papenbrock, T.; Pietralla, N.; et al. Electric Dipole Polarizability of 48Ca and Implications for the Neutron Skin. Phys. Rev. Lett. 2017, 118, 252501. [Google Scholar] [CrossRef]
- Trippa, L.; Coló, G.; Vigezzi, E. Giant dipole resonance as a quantitative constraint on the symmetry energy. Phys. Rev. C 2008, 77, 061304. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, L.-W. Electric dipole polarizability in 208Pb as a probe of the symmetry energy and neutron matter around ρ0/3. Phys. Rev. C 2015, 92, 031301. [Google Scholar] [CrossRef]
- Piekarewicz, J. Implications of PREX-2 on the electric dipole polarizability of neutron rich nuclei. Phys. Rev. C 2021, 104, 024329. [Google Scholar] [CrossRef]
- Terashima, S.; Sakaguchi, H.; Takeda, H.; Ishikawa, T.; Itoh, M.; Kawabata, T.; Murakami, T.; Uchida, M.; Yasuda, Y.; Yosoi, M.; et al. Proton elastic scattering from tin isotopes at 295 MeV and systematic change of neutron density distributions. Phys. Rev. C 2008, 77, 024317. [Google Scholar] [CrossRef]
- Karsznahorkay, A.; Fujiwara, M.; van Aarle, P.; Akimune, H.; Daito, I.; Fujimura, H.; Fujita, Y.; Harakeh, M.N.; Inomata, T.; Jänecke, J.; et al. Excitation of Isovector Spin-Dipole Resonances and Neutron Skin of Nuclei. Phys. Rev. Lett. 1999, 82, 3216. [Google Scholar] [CrossRef]
- Trzcinska, A.; Jastrzȩbski, J.; Lubiński, P.; Hartmann, F.J.; Schmidt, R.; von Egidy, T.; Kłos, B. Neutron Density Distributions Deduced from Antiprotonic Atoms. Phys. Rev. Lett. 2001, 87, 082501. [Google Scholar] [CrossRef]
- Xie, W.-J.; Li, B.-A. Bayesian inference of the incompressibility, skewness and kurtosis of nuclear matter from empirical pressures in relativistic heavy-ion collisions. J. Phys. G Nucl. Part. Phys. 2021, 48, 025110. [Google Scholar] [CrossRef]
- Fuchs, C. Kaon production in heavy ion reactions at intermediate energies. Prog. Part. Nucl. Phys. 2006, 56, 1. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. The Equation of State of Nuclear Matter and Neutron Stars Properties. Science 2002, 298, 1592. [Google Scholar] [CrossRef]
- Laue, F.; Sturm, C.; Böttcher, I.; Dȩbowski, M.; Förster, A.; Grosse, E.; Koczoń, P.; Kohlmeyer, B.; Mang, M.; Naumann, L.; et al. Medium Effects in Kaon and Antikaon Production in Nuclear Collisions at Subthreshold Beam Energies. Phys. Rev. Lett. 1999, 82, 1640. [Google Scholar] [CrossRef]
- Ivanov, E.I.; Stienike, D.L.; Ryabchikov, D.I.; Adams, G.S.; Adams, T.; Bar-Yam, Z.; Bishop, J.M.; Bodyagin, V.A.; Brown, D.S.; Cason, N.M.; et al. Observation of Exotic Meson Production in the Reaction π−p→η′π−p at 18 GeV/c. Phys. Rev. Lett. 2001, 86, 3977–3980. [Google Scholar] [CrossRef]
- Partlan, M.D.; Albergo, S.; Bieser, F.; Brady, F.P.; Caccia, Z.; Cebra, D.; Chacon, A.D.; Chance, J.; Choi, Y.; Costa, S.; et al. Fragment Flow in Au +Au Collisions. Phys. Rev. Lett. 1995, 75, 2100. [Google Scholar] [CrossRef]
- Liu, H.; Ajitanand, N.N.; Alexander, J.; Anderson, M.; Best, D.; Brady, F.P.; Case, T.; Caskey, W.; Cebra, D.; Chance, J.; et al. Sideward Flow in Au+Au Collisions between 2A and 8A GeV. Phys. Rev. Lett. 2000, 84, 5488. [Google Scholar] [CrossRef]
- Pinkenburg, C.; Ajitanand, N.N.; Alexander, J.M.; Anderson, M.; Best, D.; Brady, F.P.; Case, T.; Caskey, W.; Cebra, D.; Chance, J.L.; et al. Elliptic Flow: Transition from Out-of-Plane to In-Plane Emission in Au+Au Collisions. Phys. Rev. Lett. 1999, 83, 1295. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Stachel, J. Dynamics of ultra-relativistic nuclear collisions with heavy beams: An experimental overview. Nucl. Phys. A 1998, 638, 3c. [Google Scholar] [CrossRef]
- Xiao, Z.; Li, B.-A.; Chen, L.-W.; Yong, G.-C.; Zhang, M. Circumstantial Evidence for a Soft Nuclear Symmetry Energy at Suprasaturation Densities. Phys. Rev. Lett. 2009, 102, 062502. [Google Scholar] [CrossRef]
- Feng, Z.-Q.; Jin, G.-M. Probing high-density behavior of symmetry energy from pion emission in heavy-ion collisions. Phys. Lett. B 2010, 683, 140. [Google Scholar] [CrossRef]
- Xie, W.-J.; Su, J.; Zhu, L.; Zhang, F.-S. Symmetry energy and pion production in the Boltzmann-Langevin approach. Phys. Lett. B 2013, 718, 1510. [Google Scholar] [CrossRef]
- Tsang, M.B.; Liu, T.X.; Shi, L.; Danielewicz, P.; Gelbke, C.K.; Liu, X.D.; Lynch, W.G.; Tan, W.P.; Verde, G.; Wagner, A.; et al. Isospin Diffusion and the Nuclear Symmetry Energy in Heavy Ion Reactions. Phys. Rev. Lett. 2004, 92, 062701. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.-X.; Lynch, W.G.; Tsang, M.B.; Liu, X.D.; Shomin, R.; Tan, W.P.; Verde, G.; Wagner, A.; Xi, H.F.; Xu, H.S.; et al. Isospin diffusion observables in heavy-ion reactions. Phys. Rev. C 2007, 76, 034603. [Google Scholar] [CrossRef]
- Famiano, M.A.; Liu, T.; Lynch, W.G.; Mocko, M.; Rogers, A.M.; Tsang, M.B.; Wallace, M.S.; Charity, R.J.; Komarov, S.; Sarantites, D.G.; et al. Neutron and proton transverse emission ratio measurements and the density dependence of the asymmetry term of the nuclear equation of state. Phys. Rev. Lett. 2006, 97, 052701. [Google Scholar] [CrossRef]
- Cozma, M.D.; Leifels, Y.; Trautmann, W.; Li, Q.; Russotto, P. Toward a model-independent constraint of the high-density dependence of the symmetry energy. Phys. Rev. C 2013, 88, 044912. [Google Scholar] [CrossRef]
- Yong, G.-C.; Guo, Y.-F. Probing High-density Symmetry Energy Using Heavy-ion Collisions at Intermediate Energies. Nucl. Phys. Rev. 2020, 37, 136. [Google Scholar]
- Cozma, M.D.; Tsang, M.B. In-medium Δ(1232) potential, pion production in heavy-ion collisions and the symmetry energy. Eur. Phys. J. A 2021, 57, 309. [Google Scholar] [CrossRef]
- Jhang, G.; Estee, J.; Barney, J.; Cerizza, G.; Kaneko, M.; Lee, J.W.; Lynch, W.G.; Isobe, T.; Kurata-Nishimura, M.; Murakami, T.; et al. Symmetry energy investigation with pion production from Sn+Sn systems. Phys. Lett. B 2021, 813, 136016. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, A.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Greif, S.K.; Hebeler, K.; Hinderer, T.; Nissanke, S.; Schwenk, A.; Riley, T.E.; Watts, A.L.; Lattimer, J.M.; Ho, W.C.G. Constraints on the Dense Matter Equation of State and Neutron Star Properties from NICER’s Mass–Radius Estimate of PSR J0740+6620 and Multimessenger Observations. Ap. J. Lett. 2021, 918, L29. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Lim, Y. Constraining the Symmetry Parameters of the Nuclear Interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Lattimer, J.M. The Nuclear Equation of State and Neutron Star Masses. Annu. Rev. Nucl. Part. Sci. 2012, 62, 485. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).