Abstract
This investigation compares the dynamic simulation results of perfect, elastically-supported, axially-functionally-graded (AFG) beams between viscoelastic and elastic models. When modeling and simulating the dynamics of AFG beams, the elastic model is commonly assumed so as to simplify calculations. This investigation shows how the dynamics varies if viscosity is present. The nonlinear continuous/discretized, axial/transverse motion derivation procedure is explained briefly based on Hamilton’s principle for energy/energy-loss, Kelvin–Voigt viscosity, elastic foundation assumption, and exponential functions for material and geometric variations along the axial axis. A comparison between elastic and Kelvin–Voigt viscoelastic AFG beams on an elastic foundation shows that the viscosity influences the asymmetric dynamics of AFG beams; the viscosity effects become more dominant for larger motion amplitudes, for example.
1. Introduction
Structures such as the plates and beams [1,2] of the functionally graded (FG) type are able to resist both mechanical and thermal stresses simultaneously [3,4,5]. Moreover, they require fairly low maintenance for such a high strength to weight ratio. They are made using powder metallurgy, and hence there are no discrete layers (as opposed to conventional composite plates and beams), which fact prevents large stress concentrations and residual stresses, hence a stronger bonding. The class of FG beams with x-axis-varying properties is called axially-functionally-graded (AFG).
Viscosity (internal friction) in structural elements, such as plates and beams, can be dominant, especially when the dynamics is in a nonlinear regime. There are different theoretical schemes proposed to incorporate viscosity; the famous ones are linear standard, Maxwell, and Kelvin–Voigt [6]; the last one is employed in this investigation. In addition to viscosity, nonlinearities play an important role in structural dynamics [7,8,9,10,11,12,13,14]. As opposed to micro/nano structures [15,16,17,18,19,20,21,22,23,24], macro structures display size-independent behaviour.
The cost and weight optimization of AFG beams necessitates the use of nonuniform cross-sections (or varying cross-sections in the axial direction) in many civil and mechanical applications. A tapered shape, via an exponential distribution for the beams’ width, is considered in this paper.
There are papers on the dynamical behavior of AFG beams [25,26,27] based on linear theories. Calim [28] examined the oscillatory response of AFG Timoshenko beams additionally supported by a viscoelastic bed. Sarkar and Ganguli [29] considered fixed-fixed AFG Timoshenko beams and developed a closed-form-solution for oscillations.
Simsek [30] examined the under-force vibrations of an AFG beam excited by a traveling force by obtaining the vibration amplitude as a function of the frequency of the moving force. Hein and Feklistor [31], via analyzing the free vibrations, determined natural frequencies via Haar wavelets. Rajasekaran [32], via the differential quadrature method, calculated the natural frequencies of AFG beams. Huang et al. [33] used the Timoshenko theory and obtained the natural frequencies for different boundary conditions. Extensions to incorporate nonlinearities involve a study by Shaba et al. [34], who investigated the vibrations and buckling instability of AFG beams using the Timoshenko theory; an investigation by Kein [35], who analyzed the bending phenomenon of AFG beams.
This investigation compares the asymmetric dynamic simulation results of elastically-supported AFG beams between viscoelastic and elastic models. Based upon both asymmetric and symmetric modes, the Kelvin–Voigt scheme is used for viscosity. A nonuniform cross-section is considered for the Euler–Bernoulli type beam. The model of the viscoelastic system is nonlinear, and there are axial/transverse couplings. Numerical simulations are conducted based on a continuation-time-integration method.
2. Mathematical Model of Elastically Supported AFG Viscoelastic Beam
The mathematical model of the perfect viscoelastic, elastically-supported AFG beam used in this paper is presented graphically in Figure 1. The displacement has two components of transverse w(x,t) and axial u(x,t). The length, thickness and width are respectively shown by L, h and b; b = b(x) is a function of the axial coordinate to form the tapered shape. An external force F(x)cos(ωt) excites the elastically-supported AFG beam in the transverse direction. The derivation procedures for continuous and discretized equations of motion are briefly explained in Section 2 and Section 3; more-detailed procedures are available in [36] for not additionally supported system in the absence of imperfection for more information.
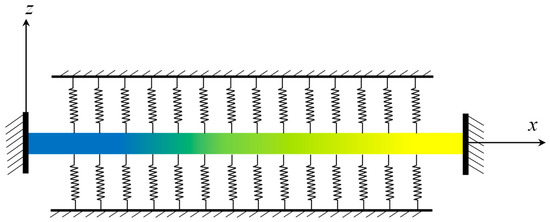
Figure 1.
Schematic of a perfect, elastically-supported, axially-functionally-graded (AFG) viscoelastic beam.
Mechanical properties and the cross-sectional area vary using the following,
where Π is the representative of the viscosity coefficient (η), mass density (ρ), width (b) and Young’s modulus (E) (where all are x-dependent functions), with L and R being the left-end and right-end of the AFG viscoelastic beam, respectively. The elastic foundation has linear/nonlinear stiffness coefficients as KLin and KNon.
Employing the Euler–Bernoulli AFG viscoelastic, elastically-supported beam, the elastic component of the stress forms the following potential energy
The contribution of the Kelvin–Voigt viscous stress is incorporated via its work as
Using Hamilton’s principle for energy/energy-loss, considering Equations (2)–(5), for F(x) = f1, and using
leads to
where the asterisk notation has been dropped for notation simplicity.
3. Perfect Elastically Supported AFG Viscoelastic Beam in a Discretized Form
A weighted residual technique [37,38] is used for the discretization of Equations (5) and (6), using the basis functions of a clamped-clamped linear homogenous beam and the generalized coordinates to be determined numerically. As such
inserting Equation (7) into Equations (5) and (6) and application of Galerkin’s method [39,40,41,42] gives
Retaining both the symmetric as well as asymmetric modes in Equations (8) and (9), in total 20 modes (10 for each motion type), is considered, and a combination of the pseudo-arclength continuation-time-integration method and eigenvalue technique is used for numerical integrations.
4. Numerical Results for Asymmetric Elastic versus Viscoelastic Dynamics including Foundation Effects
The axial nonuniform distribution of the material-properties/cross-section make the dynamical behavior asymmetric. An AFG viscoelastic beam is made by mixing Steel of [νL] equals to 0.29, [ρL] equals to 7800 kg/m3, [EL] equals to 210 GPa and the alumina of [νR] equals to 0.25, [ρR] equals to 3960 kg/m3, [ER] equals to 390 GPa; [L/h] equals to 180, [hR =hL =h] equals to 0.11 m and [bL/h] equals to 2. The properties of the foundation are given separately for each figure.
Figure 2 shows that how the vibration amplitude changes with the excitation frequency for [(ηs)L] = 0.00036, n = 1.5, [(ηs)R] = 0.00130, f1 = 40.0, kLin = 50.0, KNon = 20.0, and bR = 2.5bL. As seen, even though that the boundary conditions are the same at the left and right ends of the beam, the vibration behavior is asymmetric; the peak value of the q2 motion is about 11% q1 motion, highlighting a fairly large contribution. This again emphasizes that a large number of mode basis to be considered to capture these effects; in this study, a 20-mode approximation is considered. As seen, there are two bifurcations at Ω/ω1= 1.3913 and 1.0956 for all the asymmetric and symmetric motions.
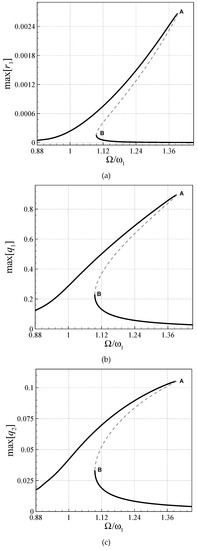
Figure 2.
Frequency responses of perfect elastically supported AFG system based on viscoelasticity; (a) ; (b) ; (c) .
Figure 3 illustrates the relation between different modes of vibrations and the excitation-force amplitude for [(ηs)L] = 0.00036, n = 1.5, [(ηs)R] = 0.00130, kLin = 50.0, kNon = 20.0, [bR] = 2.5bL, and Ω/ω1 = 1.2000. There are two jumps at f1 = 129.5 and 18.1 corresponding to saddle bifurcations. Again, the asymmetric modes display a fairly significant contribution.
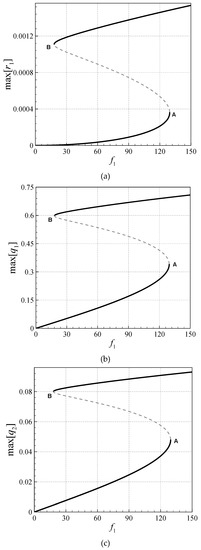
Figure 3.
Force responses of perfect elastically supported AFG system based on viscoelasticity. (a) ; (b) ; (c) .
Figure 4 reveals the effect of viscosity on the nonlinear vibrations of the elastically-supported AFG beam by plotting the frequency diagrams for a system with full linear and nonlinear damping (the system of this paper), with those of a system with just a simple linear viscous damping (with a model damping ratio equals to 0.005). For a complete damping system, [(ηs)L] = 0.00036 and [(ηs)R] = 0.00130 are chosen. For both the systems n = 1.5, bR = 2.5bL, kLin = 50.0, kNon = 20.0 and f1 = 40.0 are selected. For small-amplitude forces, the discrepancy in the vibration amplitude of both cases is fairly small; however, for large enough forcing amplitudes the discrepancy is more visible. It can be concluded that, for both the transverse and axial vibrations, Kelvin–Voigt type viscosity is more important in larger vibration amplitudes.
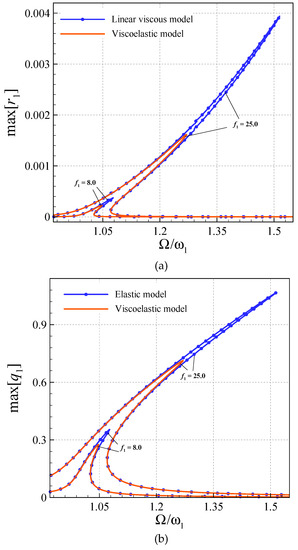
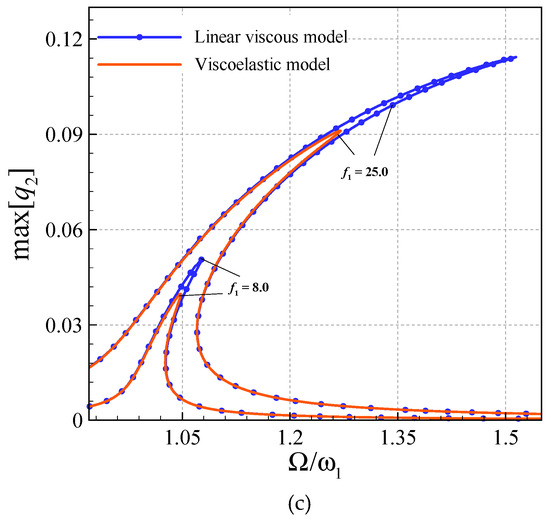
Figure 4.
Frequency responses of perfect elastically supported AFG system based on viscoelasticity. [(ηs)L] = 0.00036 and [(ηs)R] = 0.00130 and linear viscous model (ζ = 0.005). (a) ; (b) ; (c) .
The influences of the gradient index of the material on the frequency curves of the viscoelastic system on an elastic foundation are highlighted in Figure 5 for [(ηs)L] = 0.00036, [(ηs)R] = 0.00130, [bR] = 2.5bL, kLin = 50.0, kNon = 20.0 and f1 = 40.0. As seen, the larger the index is, the smaller the resonant frequency becomes. This is accompanied by an amplitude increase for the first-mode transverse vibrations.
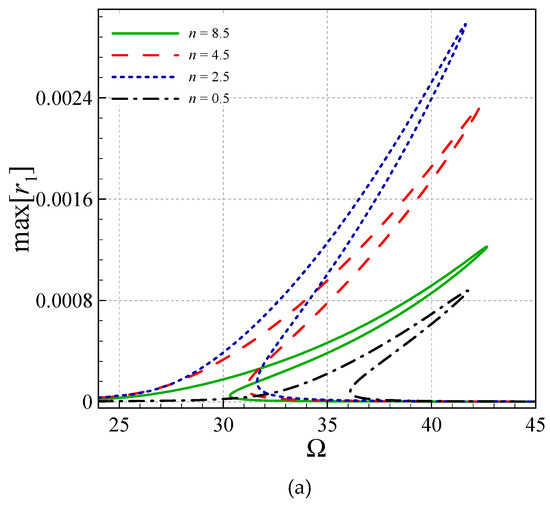
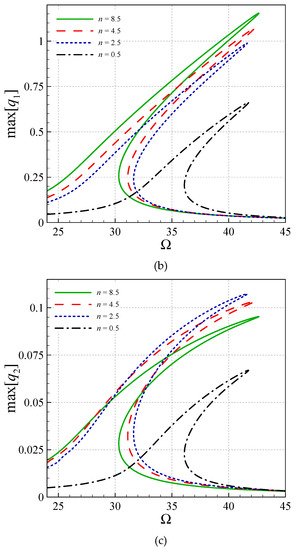
Figure 5.
Frequency responses of a perfect elastically supported AFG system based on viscoelasticity for various n. (a) ; (b) ; (c) .
Illustrated in Figure 6 is the influences of the taper ratio (bR/bL) for n = 1.5, [(ηs)L] = 0.00036, [(ηs)R] = 0.00130, kLin = 50.0, kNon = 20.0 and f1 = 40.0. It can be seen in Figure 6b that the largest symmetric transverse amplitude belongs to a uniform beam, where this is not the case for the asymmetric transverse amplitude. Moreover, for larger taper ratios, the resonance domain shifts to the left, implying a smaller value for the natural frequency of the transverse motions.
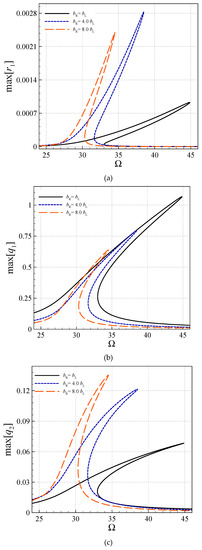
Figure 6.
Frequency responses of perfect elastically supported AFG system based on viscoelasticity for various taper ratios. (a) ; (b) ; (c) .
Shown in Figure 7 is a highlight on the variations occur in frequency diagrams of the elastically-supported AFG beam with different kNon values; n = 1.5, [(ηs)L] = 0.00036, [(ηs)R] = 0.00130, bR = 2.5bL, kLin = 50.0, and f1 = 40.0. As seen, the hardening behavior of the viscoelastic beam tends to become stronger as nonlinear stiffness of the elastic support increases. The maximum peak amplitude of the resonant domain also belongs to larger, nonlinear stiffness for all modes.
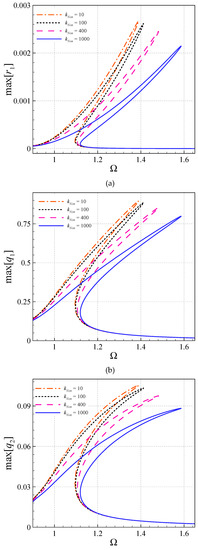
Figure 7.
Frequency responses of a perfect, elastically-supported AFG system based on viscoelasticity for various kNon. (a) ; (b) ; (c) .
5. Conclusions
The viscosity impact on the asymmetric, nonlinear dynamics of perfect, elastically-supported beams of AFG nature with nonuniform cross-sections have been investigated by comparing elasticity versus viscoelasticity. The AFG nature of the structure, as well as the nonuniformity in the width, gave rise to asymmetric coupled nonlinear vibrations for both viscoelastic and elastic AFG (elastically supported) systems, where, in some cases, asymmetric components on the dynamics becomes significant. The necessity of hiring large dimensions, due to asymmetry, was satisfied using a high-dimensional method of solution. It was found that: (i) Even though asymmetric modes are present, the frequency diagrams are hardening for both the translational motions regardless of elasticity or viscoelasticity; (ii) asymmetry in geometry and material distribution causes asymmetric modes to get excited; (iii) the viscosity effects are more dominant at larger forces, highlighting the importance of incorporating a full viscous model using the Kelvin–Voigt scheme; (iv) the gradient index effect is that in increasing, it shifts the resonance regime to the left; (v) for larger values of the taper ratio, the peak amplitude is larger in the fundamental transverse mode; (vi) larger nonlinear elastic foundation stiffness shows stronger hardening behavior and smaller peak amplitudes in all symmetric/asymmetric modes.
Author Contributions
Conceptualization, M.H.G.; methodology, A.G.; software, M.H.G.; validation, A.G., M.H.G., Y.Z.; investigation, A.G., M.H.G., Y.Z.; writing—original draft preparation, A.G., M.H.G.; writing—review and editing, A.G., Y.Z.; supervision, M.H.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no funding.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
Validation of the current study has been obtained by comparing first dimensionless transverse frequency parameter λ = ω0.5 of a pinned-pinned AFG linear elastic beam (simplified model of the current study). As seen in Table A1, frequency parameters for different gradient index (n) and Young’s modulus ratio (Eratio = Eleft/Eright) are in good agreement with [43].

Table A1.
Comparison between simplified model of current study (axially-functionally-graded (AFG) elastic pinned-pinned beam) and [43] for linear regime: first transverse dimensionless frequency parameter (λ = ω0.5) for different gradient indices (n), Young’s modulus ratio (Eleft/Eright), and L/h=100.
Table A1.
Comparison between simplified model of current study (axially-functionally-graded (AFG) elastic pinned-pinned beam) and [43] for linear regime: first transverse dimensionless frequency parameter (λ = ω0.5) for different gradient indices (n), Young’s modulus ratio (Eleft/Eright), and L/h=100.
| Eleft/Eright | n = 0 | n = 0.5 | n = 1 | n = 2 | n = 5 | |
|---|---|---|---|---|---|---|
| 0.25 | Present study | 2.2214 | 2.5834 | 2.7547 | 2.9293 | 3.0850 |
| [43] | 2.2214 | 2.5834 | 2.7546 | 2.9293 | 3.0849 | |
| 1.0 | Present study | 3.1415 | 3.1415 | 3.1415 | 3.1415 | 3.1415 |
| [43] | 3.1415 | 3.1415 | 3.1415 | 3.1415 | 3.1415 | |
| 4.0 | Present study | 4.4428 | 4.1408 | 3.8957 | 3.5812 | 3.2683 |
| [43] | 4.4428 | 4.1408 | 3.8957 | 3.5812 | 3.2684 |
References
- Darabi, M.A.; Kazemirad, S.; Ghayesh, M.H. Free vibrations of beam-mass-spring systems: Analytical analysis with numerical confirmation. Acta Mech. Sin. 2012, 28, 468–481. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M. Post-buckling bifurcations and stability of high-speed axially moving beams. Int. J. Mech. Sci. 2013, 68, 76–91. [Google Scholar] [CrossRef]
- Du, C.; Li, Y.; Jin, X. Nonlinear forced vibration of functionally graded cylindrical thin shells. Thin-Walled Struct. 2014, 78, 26–36. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, A.V.; Pavlov, S.P.; Zhigalov, M.V.; Krysko, V.A. Stability of the size-dependent and functionally graded curvilinear timoshenko beams. ASME J. Comput. Nonlinear Dyn. 2017, 12, 041018. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R.; Sahmani, S. Study of small scale effects on the nonlinear vibration response of functionally graded timoshenko microbeams based on the strain gradient theory. ASME J. Comput. Nonlinear Dyn. 2012, 7, 031009. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Viscoelastic shear deformable microplates: Nonlinear forced resonant characteristics. Mech. Syst. Signal Process. 2019, 118, 742–756. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M. Nonlinear dynamics of an axially moving timoshenko beam with an internal resonance. Nonlinear Dyn. 2013, 73, 39–52. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Kazemirad, S.; Darabi, M.A.; Woo, P. Thermo-mechanical nonlinear vibration analysis of a spring-mass-beam system. Arch. Appl. Mech. 2012, 82, 317–331. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M. Nonlinear vibrations and stability of an axially moving timoshenko beam with an intermediate spring support. Mech. Mach. Theory 2013, 67, 1–16. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Gholipour, A. Dynamics of functionally graded micro-cantilevers. Int. J. Eng. Sci. 2017, 115, 117–130. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear dynamic response of a simply-supported Kelvin-Voigt viscoelastic beam, additionally supported by a nonlinear spring. Nonlinear Anal. Real World Appl. 2012, 13, 1319–1333. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Yourdkhani, M.; Balar, S.; Reid, T. Vibrations and stability of axially traveling laminated beams. Appl. Math. Comput. 2010, 217, 545–556. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Kazemirad, S.; Darabi, M.A. A general solution procedure for vibrations of systems with cubic nonlinearities and nonlinear/time-dependent internal boundary conditions. J. Sound Vib. 2011, 330, 5382–5400. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Kazemirad, S.; Reid, T. Nonlinear vibrations and stability of parametrically exited systems with cubic nonlinearities and internal boundary conditions: A general solution procedure. Appl. Math. Model. 2012, 36, 3299–3311. [Google Scholar] [CrossRef]
- Gholipour, A.; Farokhi, H.; Ghayesh, M.H. In-plane and out-of-plane nonlinear size-dependent dynamics of microplates. Nonlinear Dyn. 2014, 79, 1771–1785. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Gholipour, A.; Hussain, S. Motion characteristics of bilayered extensible timoshenko microbeams. Int. J. Eng. Sci. 2017, 112, 1–17. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Chaotic motion of a parametrically excited microbeam. Int. J. Eng. Sci. 2015, 96, 34–45. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Alici, G. Size-dependent performance of microgyroscopes. Int. J. Eng. Sci. 2016, 100, 99–111. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M.; Farokhi, H. Three-dimensional nonlinear size-dependent behaviour of timoshenko microbeams. Int. J. Eng. Sci. 2013, 71, 1–14. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear dynamics of a microscale beam based on the modified couple stress theory. Compos. Part B Eng. 2013, 50, 318–324. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. In-plane and out-of-plane motion characteristics of microbeams with modal interactions. Compos. Part B Eng. 2014, 60, 423–439. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Nonlinear mechanics of doubly curved shallow microshells. Int. J. Eng. Sci. 2017, 119, 288–304. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Hussain, S. On the nonlinear mechanics of layered microcantilevers. Int. J. Eng. Sci. 2017, 120, 1–14. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear size-dependent behaviour of single-walled carbon nanotubes. Appl. Phys. A. Mater. Sci. Process. 2014, 117, 1393–1399. [Google Scholar] [CrossRef]
- Noori, A.R.; Aslan, T.A.; Temel, B. An efficient approach for in-plane free and forced vibrations of axially functionally graded parabolic arches with nonuniform cross section. Compos. Struct. 2018, 200, 701–710. [Google Scholar] [CrossRef]
- Temel, B.; Noori, A.R. Out-of-plane vibrations of shear-deformable AFG cycloidal beams with variable cross section. Appl. Acoust. 2019, 155, 84–96. [Google Scholar] [CrossRef]
- Lee, J.W.; Lee, J.Y. Contribution rates of normal and shear strain energies to the natural frequencies of functionally graded shear deformation beams. Compos. Part B Eng. 2019, 159, 86–104. [Google Scholar] [CrossRef]
- Calim, F.F. Free and forced vibration analysis of axially functionally graded timoshenko beams on two-parameter viscoelastic foundation. Compos. Part B Eng. 2016, 103, 98–112. [Google Scholar] [CrossRef]
- Sarkar, K.; Ganguli, R. Closed-form solutions for axially functionally graded timoshenko beams having uniform cross-section and fixed–fixed boundary condition. Compos. Part B Eng. 2014, 58, 361–370. [Google Scholar] [CrossRef]
- Şimşek, M.; Kocatürk, T.; Akbaş, Ş. Dynamic behavior of an axially functionally graded beam under action of a moving harmonic load. Compos. Struct. 2012, 94, 2358–2364. [Google Scholar] [CrossRef]
- Hein, H.; Feklistova, L. Free vibrations of non-uniform and axially functionally graded beams using Haar wavelets. Eng. Struct. 2011, 33, 3696–3701. [Google Scholar] [CrossRef]
- Rajasekaran, S. Differential transformation and differential quadrature methods for centrifugally stiffened axially functionally graded tapered beams. Int. J. Mech. Sci. 2013, 74, 15–31. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, L.-E.; Luo, Q.-Z. Free vibration of axially functionally graded timoshenko beams with non-uniform cross-section. Compos. Part B Eng. 2013, 45, 1493–1498. [Google Scholar] [CrossRef]
- Shahba, A.; Attarnejad, R.; Marvi, M.T.; Hajilar, S. Free vibration and stability analysis of axially functionally graded tapered timoshenko beams with classical and non-classical boundary conditions. Compos. Part B Eng. 2011, 42, 801–808. [Google Scholar] [CrossRef]
- Nguyen, D.K. Large displacement response of tapered cantilever beams made of axially functionally graded material. Compos. Part B Eng. 2013, 55, 298–305. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Asymmetric viscoelastic nonlinear vibrations of imperfect AFG beams. Appl. Acoust. 2019, 154, 121–128. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Mechanics of viscoelastic functionally graded microcantilevers. Eur. J. Mech. A/Solids 2019, 73, 492–499. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Dynamical analysis of multilayered cantilevers. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 244–253. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Alici, G. Subcritical parametric dynamics of microbeams. Int. J. Eng. Sci. 2015, 95, 36–48. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear resonant response of imperfect extensible timoshenko microbeams. Int. J. Mech. Mater. Des. 2017, 13, 43–55. [Google Scholar] [CrossRef]
- Kazemirad, S.; Ghayesh, M.H.; Amabili, M. Thermo-mechanical nonlinear dynamics of a buckled axially moving beam. Arch. Appl. Mech. 2013, 83, 25–42. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Subharmonic dynamics of an axially accelerating beam. Arch. Appl. Mech. 2012, 82, 1169–1181. [Google Scholar] [CrossRef]
- Alshorbagy, A.E.; Eltaher, M.; Mahmoud, F. Free vibration characteristics of a functionally graded beam by finite element method. Appl. Math. Model. 2011, 35, 412–425. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).