Abstract
This work proposed a novel model to simultaneously reconstruct temperature distribution and soot volume fraction field for two-dimensional thin-slice flames using the knowledge of monochromatic radiation intensities at two wavelengths using a CCD camera. The deduction process and numerical analysis of the model were described. Effects of wavelength combinations and measurement errors on reconstruction accuracy were considered in detail. Numerical results have proven the model’s accuracy and showed that the temperature and soot volume fraction fields can be reconstructed well even with noisy input data from flame radiation. In addition, a series of experiments were conducted on a mesoscale combustor to obtain the real thin-slice flames for further experimental reconstruction via the model. The experimental results indicated that the proposed model can successfully reconstruct the flame temperature distribution and soot volume fraction field and the main features of thin-slice flames also can be reasonably reproduced.
1. Introduction
With the continuous development of the economy and society, combustion, as a primary type of energy utilization, has been extensively applied in various professions [1,2,3,4]. New technologies and achievements are emerging in various combustion fields. Among them, the development of advanced combustion diagnostics technology has important scientific significance and application value [5,6,7,8,9,10,11].
Temperature and soot volume fraction (SVF) are the key parameters of combustion diagnostics [12]. For a deeper understanding of the combustion process and better control of pollutant emissions, it is necessary to establish reliable and effective methods for the measurement of these parameters with high accuracy. Therefore, an enormous amount of numerical and experimental research based on the inverse radiation problem [13,14,15,16,17,18,19,20] has been devoted to improving optical technologies to determine the distributions of temperature and soot volume fraction in various flame configurations. Arana et al. [21] adopted the full-field light extinction method to measure soot volume fraction distributions in partially premixed laminar co-flow ethylene flames. Zheng et al. [22] proposed a multiwavelength radiation thermometry method employing multispectral imaging technology to measure flame temperature and emissivity. Joo et al. [13] used a CCD camera to obtain the radiation intensity of the methane–air laminar flame boundary. The temperature and soot concentration field in the flame were simultaneously reconstructed and the influence of pressure on soot formation was also analyzed. Liu et al. [23] introduced a nonintrusive measurement technique to simultaneously reconstruct the three-dimensional soot temperature and volume fraction in axisymmetric and nonaxisymmetric flames using a CCD camera.
The aforementioned studies have widely investigated optical diagnostic techniques in three-dimensional axisymmetric and nonaxisymmetric flames. However, in some specific flame conditions such as micro- and meso-scale combustion, the conventional reconstructed model may not be convenient or suitable for these specific flame configurations. Moreover, the flame formed in microconfined space is usually very small and thin, which increases the difficulties of temperature and soot concentration measurement using the traditional contact method. If the traditional thermocouple method is adopted in microcombustion, the temperature field of the flame will be easily disturbed and extinction may happen. Up to now, the simultaneous diagnostic method of temperature and SVF specific to the micro- or meso-scale combustion is still scarce.
In micro- and meso-scale combustion, there are many specific flame structures and configurations. One of them is the impinging diffusion flame, which is formed via the impingement of two streams in a microconfined space [24,25,26]. The flame thickness of this kind of structure is very small, which has been observed in a previous study [26], and can be approximately regarded as a two-dimensional slice shape. In the consideration of the unique characteristics of micro- and meso-scale combustion, it is necessary to develop a corresponding reconstruction model to measure the fields of temperature and soot concentration. Therefore, this study aims to propose a novel reconstruction model specific to the two-dimensional thin-slice flame based on the inverse radiation problem using a CCD camera system. In the present work, the model and numerical analysis are described in Section 2. The numerical results on the model accuracy are given in Section 3. An experimental reconstruction for the practical slice flame is presented in Section 4.
2. Reconstruction Model
2.1. Direct Problem
The direct problem here was to determine the flame radiation intensity with the known distributions of temperature and soot volume fraction. With regard to the two-dimensional thin-slice flame, the cross-section of a flame at a specific height could be simplified as shown in Figure 1.
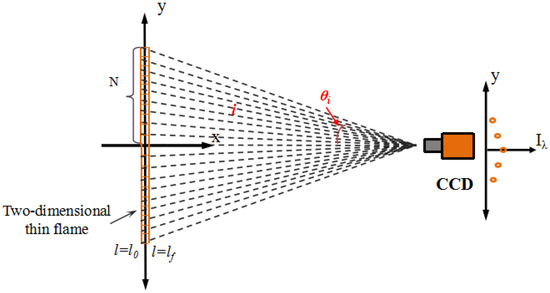
Figure 1.
Reconstruction system based on a single CCD camera for a two-dimensional thin-slice flame.
At the specific spectral range of 400–700 nm, the radiation emissions of soot particles were taken into consideration [27] but the emissions of gaseous compositions such as CO2 and H2O could be neglected [13]. Without the consideration of self-absorption and the scattering effect [28], the radiation emission intensity along rays from the flame to the CCD camera could be expressed as follows:
where Iλ(i) is the monochromatic radiation emission intensity from the flame to the CCD along the ray i, κλ is the local monochromatic absorption coefficient, and Ib,λ is the local monochromatic radiation intensity of the blackbody. The following applies according to Wien’s law [29]:
where T(i) is the local temperature, and C1 and C2 are the first and second radiation constants (C1 = 3.7419 × 10−16 W·m2, and C2 = 1.4388 × 10−2 m·K).
Under this condition, because the flame was very thin, it was reasonable to assume that the radiation intensity emitted from the inside of the flame (at the position between l0 and lf in Figure 1) along the ray i was approximately the same and homogeneous. Therefore, the radiation intensity emission along the ray i could also be simplified as follows:
where sf is the thickness of the flame, and θi is the angle between the CCD optical center and ray i. The field angle between the flame edge and the CCD optical center was 2θ. According to the Rayleigh approximation, the value of local monochromatic absorption coefficient κλ could be calculated via the following equation:
where fv(n) is the local soot volume fraction, and E(m) is a function of the complex refractive index of soot (m = n − ik), which varied with the wavelength. The values of n and k could be selected from Refs. [30,31].
2.2. Inverse Problem
For the inverse problem, the fields of temperature and soot volume fraction were considered unknowns. From this, the unknown parameters above could be deduced from the known received radiation intensity, Iλ, via the CCD camera. From Equation (3), the radiation intensity values at two different wavelengths could be expressed as follows:
By combining Equations (7) and (8), the temperature could be finally calculated using the following equation:
Once the temperature was determined using Equation (9), the local soot volume fraction fv (i) could be quickly obtained by substituting the temperature back into Equation (3) using either λ1 or λ2, as follows:
Therefore, the fields of temperature and soot volume fraction in two-dimensional thin-slice flames could be simultaneously reconstructed according to Equations (3)–(10) with the knowledge of radiation intensities Iλ1 and Iλ2 at two different wavelengths. In the present work, thin-slice flames are defined as flames with a thickness of less than 1mm. Moreover, it should be mentioned that the emissivities of the two wavelengths could be calculated using the present method, but these parameters were considered identical according to the principle of the two-color method [12]. Therefore, this method theoretically has higher accuracy than the two-color method.
3. Numerical Reconstruction Results and Discussion
In this numerical section, the received radiation intensities were calculated using Equations (3) and (4) based on the assumed known input temperature and soot volume fraction distributions via solving the direct problem. Inversely, to validate the modeling and algorithm proposed here, the temperature and soot volume fraction distributions could be reconstructed simultaneously using the measured radiation intensities via solving the inverse problem.
Figure 2 displays the assumed input temperature and soot volume fraction distributions, which were adopted from the actual experimental results of Ref. [32]. The temperature and soot volume fraction usually exhibit opposite trends, which has also been observed in Ref [7]. The field angle (2θ) between the flame edge and the CCD optical center was assumed to be 20°, and the flame thickness was assumed to be 1 mm. It should be mentioned that the symbol “r” represents the different flame widths in the cross-section of the thin-slice flame.
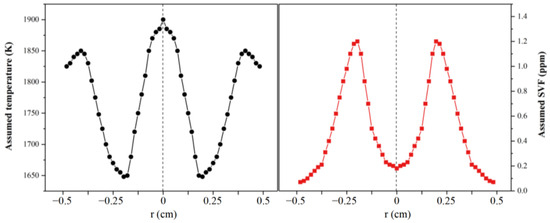
Figure 2.
The input temperature and soot volume fraction distributions.
Due to the disturbance in practice, measurement errors usually exist in the received radiation intensity, Iλ. Therefore, the random error following normal distributions with mean square deviations, σ, was introduced into the radiation intensity, Iλ, for the examination of model accuracy, as shown in the following:
where Iλ,meas and Iλ,exa are the measured radiation intensity with the error and the exact (input) radiation intensity. The average value, μ, was equal to zero and ξ was a variable of a standard normal distribution with a 99% probability in the range of 2.576 < ξ < 2.576.
The signal-to-noise ratio (SNR) was defined in terms of the logarithmic decibel scale [33]. The SNR of the radiation intensity, Iλ, was defined as follows:
Several numerical calculations were performed to examine the accuracy and robustness of the reconstruction model. The local relative errors of temperature (ET) and soot volume fraction (Efv) were defined as follows:
where Trec (i) and Texa (i) represent the local reconstructed and exact temperature distribution, respectively. fvrec (i) and fvexa (i) are the local reconstructed and exact soot volume fraction, respectively.
For a better direct comparison, the mean reconstruction errors of temperature and soot volume fraction are also described as follows:
In the following two cases, the effects of wavelength combinations and measurement errors of radiation intensity, Iλ, were investigated.
3.1. Effects of Wavelength Combinations on Reconstruction Accuracy
The reconstructed results and errors of temperature and soot volume fraction in this model using three different wavelength combinations (700/650 nm, 700/600 nm and 700/550 nm) with a fixed SNR of 50 dB are shown in Figure 3 and Figure 4. In Figure 3, the temperature and soot volume fraction are reconstructed generally using the selected three wavelength combinations, but with different reconstruction effects. As for the wavelength combination of 700/650 nm, the reconstructed curves of temperature and soot volume fraction all had large distortions. However, when using the combination of 700/550 nm, the reconstructed results seemed to be much smoother and closer to the input parameters.
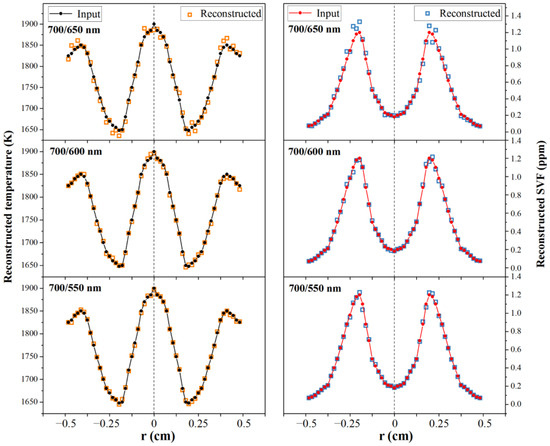
Figure 3.
Effects of wavelength combination on the reconstructed results for temperature (ET) and soot volume fraction (Efv).
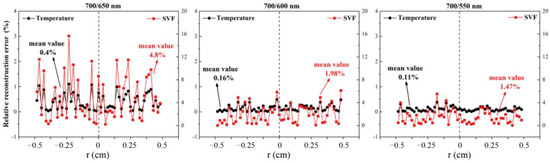
Figure 4.
The reconstructed accuracy for different wavelength combinations.
Combined with the detailed error analysis in Figure 4, it could be observed that when 700 nm and 550 nm were used, the mean and max reconstruction errors of temperature were 0.11% and 0.38%, respectively. Meanwhile, the average and largest soot volume fraction errors were less than 1.47% and 5.52%. However, with regard to the combinations of 700/650 nm and 700/600 nm, the reconstruction accuracy was not relatively satisfied, especially when 700/650 nm was chosen. In this case, the average relative errors of temperature and soot volume fraction increased to 0.4% and 4.80%, and the local maximum errors even reached 1.10% and 15.65%, respectively. The reconstruction effect of the wavelength combination of 700/550 nm was the most convincing among the three selected cases. Therefore, the application of 700/550 nm was used for further examination in the following analysis.
3.2. Effects of Measurement Errors on Reconstruction Accuracy
In the present section, the effects of three different measurement errors on the accuracy of the model are investigated, which were σ = 5.62 × 10−4 (SNR = 65 dB), σ = 3.16 × 10−3 (SNR = 50 dB) and σ = 1 × 10−2 (SNR = 40 dB). As exhibited in Figure 5, the reconstructed temperature and soot volume fraction both had a similar distribution to that of the input temperature and soot volume fraction in general. However, as the SNR declined, the reconstructed curves became obviously rough, indicating a worse reconstruction effect. In the error analysis of Figure 6, for the SNR of 65 dB, the mean and max relative error of the reconstructed temperature was 0.02% and 0.06%, respectively. The mean value of soot volume fraction relative errors was 0.26%, where the largest error was 0.83%. The error distribution of every point was almost consistent. With the decrease in the SNR to 40 dB, the reconstruction errors of mean and max temperature increased to 0.35% and 1.22%, respectively. In addition, the average and largest reconstructed soot volume fraction errors rose up to 4.81% and 16.5%, respectively. The range of error distribution fluctuated violently. In conclusion, a great reconstruction effect could be achieved with the SNR reaching 65 dB. It could also be noted that the relative errors of the reconstructed soot volume fraction were much higher than those of temperature, which indicated that the reduction in the SNR affected the accuracy of the reconstruction results of the soot volume fraction more obviously than it did that of the results of temperature. This was mainly because the reconstruction result of the soot volume fraction depended strongly on the accuracy of the reconstructed temperature. According to Equation (10), when there was a small error in the reconstructed temperature field, the model enlarged this error in the reconstructed soot volume fraction.
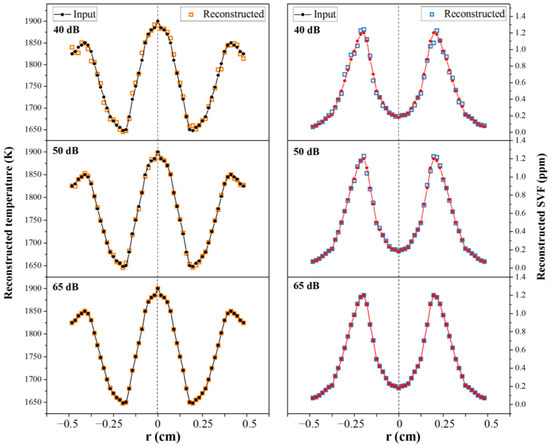
Figure 5.
Effects of measurement errors (SNR) on the reconstruction results and accuracies for temperature (ET) and soot volume fraction (Efv).
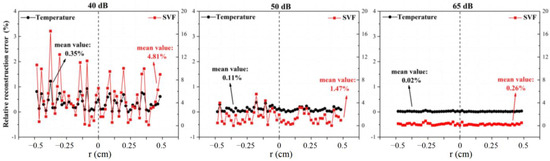
Figure 6.
The reconstructed errors for different SNRs.
4. Experimental Reconstruction Results and Discussion
To evaluate the practical application of the reconstruction model above, a series of experiments were conducted on a ψ-shaped meso-scale combustor. As shown in Figure 7, the fuel stream (ethylene) was ejected from the middle inlet channel of the combustor, and the oxidizer stream (air) was transported via the bilateral inlet channels. The flame formed in this combustor could be approximately regarded as a two-dimensional thin flame, which was successfully applied in Ref. [34]. The front and side views of this kind of flame are presented in Figure 8. According to the practical measurements, the flame thickness was approximately 1 mm, and the max flame width was 6 mm. The distance between the CCD and the flame was 10 cm. Therefore, the field angle (2θ) between the flame edge and the CCD optical center was 3.4° and cosθi could be approximated as 1 for all rays.
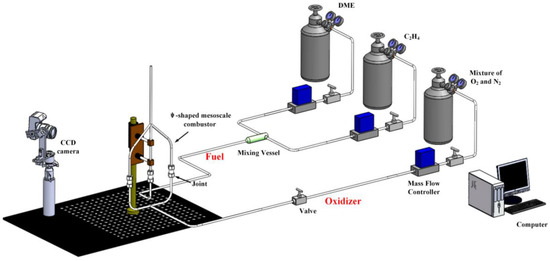
Figure 7.
Schematic diagram of the measurement system.

Figure 8.
The front and side views of the two-dimensional thin-slice flame.
Using the above-mentioned deduction, it could be found that the key step in determining the fields of temperature and soot volume fraction in this model was the accurate measurement of radiation intensities at two wavelengths. The radiation produced by the flame after passing through the optical system was stored in the form of a gray scale. The value of the gray scale read out from the computer had a strong relationship with the radiation intensity emitted by the flame itself. The relationship between the accumulated radiation intensity, Iλ, of a single wavelength and the gray value, Xλ, obtained via the image acquisition system can be expressed as follows [23]:
This specific relationship could be acquired via the calibration of the CCD system. As shown in Figure 9, the calibration procedures were as follows. Firstly, we used the blackbody furnace with a known temperature to calculate the released monochromatic radiation intensity Iλ. Then, we allowed the CCD system to shoot this blackbody furnace to obtain the corresponding gray value, Xλ. Therefore, the correlation between Iλ and Xλ could be ascertained via function fitting. During the calibration process, the exposure time and f-number of the CCD system were set to 1/40 s and f-22, respectively. The practical calibrated images are shown in Figure 10.
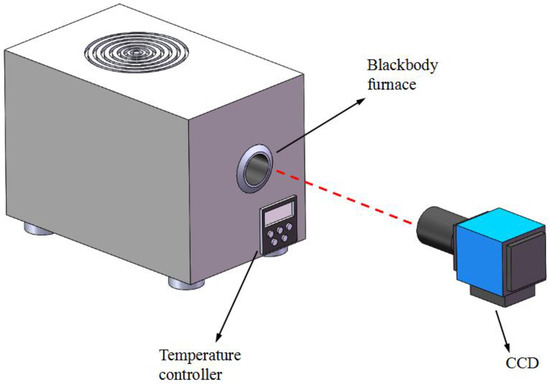
Figure 9.
Calibration system based on blackbody furnace.

Figure 10.
Calibration images of CCD camera.
According to chromatic theory, each pixel of the image generated three digital numbers (R, G, and B) which, respectively, represent the spectral responses of the red, green and blue spectral bands for the CCD camera approximately. In the present work, red (700 nm) and green (546 nm) wavelengths were selected as the measurement temperature band because the previous numerical results indicated that the adjacent wavelength combination (700/550 nm) had a high reconstruction accuracy. The polynomials obtained by fitting the values of Iλ (monochromatic radiation intensity) and Xλ (gray value) with R-squares of 0.9985 and 0.9997 are exhibited in Figure 11. After the calibration, the local monochromatic radiation intensity (Iλ) in the flame at two different wavelengths could be determined.
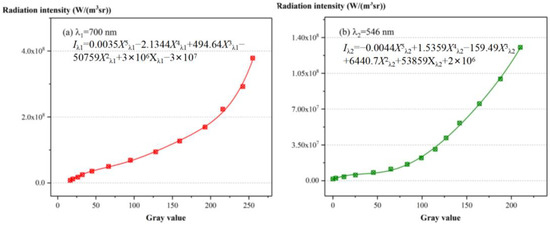
Figure 11.
Fitting results of red and green wavelengths.
To verify the feasibility of the proposed model, two representative experimental conditions were used for experimental reconstruction. It is worth mentioning that only one image was selected for each working condition because the adopted flame was a steady-state flame, and its morphology would not change with the variation in time. Figure 12 exhibits two representative thin-slice flames for the experimental reconstruction. Figure 12a shows the DME/ethylene flame with a DME fuel flow of 40 mL/min and an ethylene flow rate of 60 mL/min. Figure 12b shows the pure ethylene flame with an ethylene flow rate of 100 mL/min. Combined with the calibration results and the model above, the distributions of temperature and soot volume fraction for typical two-dimensional slice flames at two specific heights can be reconstructed, as shown in Figure 13.
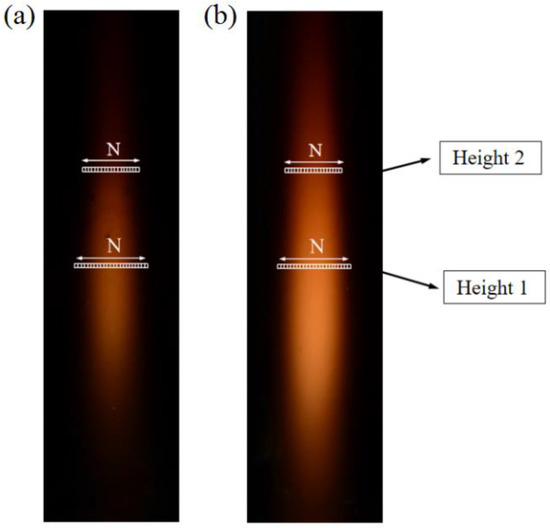
Figure 12.
Two representative thin-slice flames used for the reconstruction of the model: (a) 40%DME/60% ethylene flame, (b) pure ethylene flame.
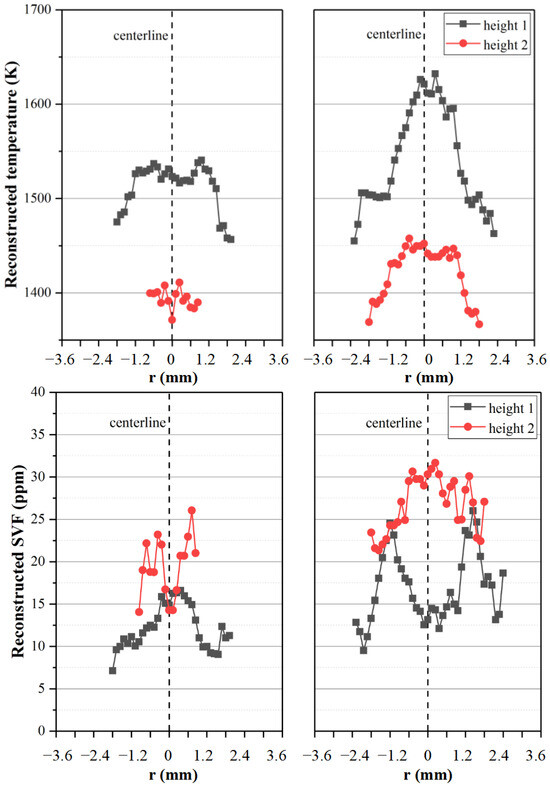
Figure 13.
Experimental reconstruction results of temperature and soot volume fraction in a two-dimensional slice flame at two specific heights.
As shown in Figure 13, the reconstructed flame temperature ranged from 1400 K to 1650 K, and the flame temperature in the central area was generally higher than that on both sides. The reconstructed temperature curve of Figure 12b was relatively smooth, and could reflect the law of temperature distribution at both heights well. However, there were some fluctuations in the reconstructed results of Figure 12a, especially at height 2. This was because the brightness of flame (a) was much lower than that of flame (b). The radiation intensity emitted by the flame was stored in the digital image as gray information. Because the gray value could only be expressed as an integer, the larger the gray value was, the more accurate the radiation intensity and the smaller the reconstruction error. Moreover, the reconstructed temperature and soot volume fraction both had good symmetry. The flame temperature at height 1 was higher than that at height 2, but the soot volume fraction had the opposite distribution trend. This result was generally reasonable and had good agreement with previous experiments [27]. The reconstruction result successfully indicated that the flame with a large DME addition had apparently lower combustion temperatures and soot volume fractions, which was consistent with the practical combustion situation [35]. Through the analysis above, the reconstructed result of the proposed model had good reliability and could reproduce the actual combustion condition.
5. Conclusions
This work proposed a novel model to simultaneously reconstruct the temperature and soot volume fraction field specific to the two-dimensional slice flame using the knowledge of monochromatic radiation intensity at two wavelengths. The numerical analysis and deduction process of the model was described in detail. The effects of wavelength combination (700/650 nm, 700/600 nm, and 700/550 nm) and measurement errors (65 dB, 50 dB, and 40 dB) on reconstruction accuracy were investigated. In addition to the numerical analysis, a series of experiments were also conducted on a meso-scale combustor to obtain a real thin-slice flame for further reconstruction via the new model. Numerical results indicated that the temperature and soot volume fraction field could be reconstructed exactly for both the accurate and noisy input data. The mean reconstruction errors of the temperature and soot volume fraction were 0.11% and 1.47% for 700/550 nm, and were the most accurate among the three selected wavelength combinations. When the SNR was 65 dB, the average errors of the temperature and soot volume fraction could reach 0.02% and 0.26%. Furthermore, the experimental results showed that the temperature and soot volume fraction field could be determined successfully based on a CCD image system. The reconstruction results had high reliability with regard to the actual combustion condition. Furthermore, the model proposed in this work could also be applied to a large-scale two-dimensional thin-slice flame structure. In this study, micro- or meso-scale combustion was only used as an example.
Author Contributions
Conceptualization, M.C. and D.L.; methodology, T.L.; software, Y.C.; validation, M.C., Y.C. and T.L.; formal analysis, M.C.; investigation, M.C. and Y.C.; resources, D.L.; data curation, Y.C.; writing—original draft preparation, M.C.; writing—review and editing, D.L. and T.L.; visualization, M.C.; supervision, D.L. and T.L.; project administration, D.L.; funding acquisition, M.C. and T.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Fundamental Research Funds for the Central Universities (JZ2023HGQB0161, 30922010409).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by the Fundamental Research Funds for the Central Universities (JZ2023HGQB0161, 30922010409).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Meng, X.; de Jong, W.; Kudra, T. A state-of-the-art review of pulse combustion: Principles, modeling, applications and R&D issues. Renew. Sustain. Energy Rev. 2016, 55, 73–114. [Google Scholar]
- Holme, J.A.; Vondráček, J.; Machala, M.; Lagadic-Gossmann, D.; Vogel, C.F.; Le Ferrec, E.; Sparfel, L.; Øvrevik, J. Lung cancer associated with combustion particles and fine particulate matter (PM2.5)—The roles of polycyclic aromatic hydrocarbons (PAHs) and the aryl hydrocarbon receptor (AhR). Biochem. Pharmacol. 2023, 216, 115801. [Google Scholar] [CrossRef] [PubMed]
- Broumand, M.; Albert-Green, S.; Yun, S.; Hong, Z.; Thomson, M.J. Spray combustion of fast pyrolysis bio-oils: Applications, challenges, and potential solutions. Prog. Energy Combust. Sci. 2020, 79, 100834. [Google Scholar] [CrossRef]
- Ardebili, S.M.S.; Solmaz, H.; Ïpci, D.; Calam, A.; Mostafaei, M. A review on higher alcohol of fusel oil as a renewable fuel for internal combustion engines: Applications, challenges, and global potential. Fuel 2020, 279, 118516. [Google Scholar] [CrossRef]
- Li, T.; Geschwindner, C.; Dreizler, A.; Böhm, B. An experimental study of coal particle group combustion in conventional and oxy-fuel atmospheres using multi-parameter optical diagnostics. Proc. Combust. Inst. 2023, 39, 3259–3269. [Google Scholar] [CrossRef]
- Aliramezani, M.; Koch, C.R.; Shahbakhti, M. Modeling, diagnostics, optimization, and control of internal combustion engines via modern machine learning techniques: A review and future directions. Prog. Energy Combust. Sci. 2022, 88, 100967. [Google Scholar] [CrossRef]
- Kiefer, J.; Ewart, P. Laser diagnostics and minor species detection in combustion using resonant four-wave mixing. Prog. Energy Combust. Sci. 2011, 37, 525–564. [Google Scholar] [CrossRef]
- Zheng, S.; Yang, Y.; Li, X.; Liu, H.; Yan, W.; Sui, R.; Lu, Q. Temperature and emissivity measurements from combustion of pine wood, rice husk and fir wood using flame emission spectrum. Fuel Process. Technol. 2020, 204, 106423. [Google Scholar]
- Tornatore, C.; Marchitto, L.; Valentino, G.; Corcione, F.E.; Merola, S.S. Optical diagnostics of the combustion process in a PFI SI boosted engine fueled with butanol-gasoline blend. Energy 2012, 45, 277–287. [Google Scholar] [CrossRef]
- Kerl, J.; Sponfeldner, T.; Beyrau, F. An external Raman laser for combustion diagnostics. Combust Flame 2011, 158, 1905–1907. [Google Scholar] [CrossRef]
- Aldén, M.; Bood, J.; Li, Z.; Richter, M. Visualization and understanding of combustion processes using spatially and temporally resolved laser diagnostic techniques. Proc. Combust. Inst. 2011, 33, 69–97. [Google Scholar] [CrossRef]
- Zhao, H.; Ladommatos, N. Optical diagnostics for soot and temperature measurement in diesel engines. Prog. Energy Combust. Sci. 1998, 24, 221–255. [Google Scholar] [CrossRef]
- Joo, H.I.; Guider, Ö.L. Soot formation and temperature field structure in co-flow laminar methane-air diffusion flames at pressures from 10 to 60 atm. Proc. Combust. Inst. 2009, 32, 769–775. [Google Scholar] [CrossRef]
- Salinero, J.; Gómez-Barea, A.; Tripiana, M.; Leckner, B. Measurement of char surface temperature in a fluidized bed combustor using pyrometry with digital camera. Chem. Eng. J. 2016, 288, 441–450. [Google Scholar] [CrossRef]
- Govender, D.; Liu, H.; Peng, F.; Cai, W.; Worth, N.A. Tomographic reconstruction of an azimuthally forced flame in an annular chamber. Proc. Combust. Inst. 2023, 39, 1367–1375. [Google Scholar] [CrossRef]
- Kailasanathan, R.K.A.; Zhang, J.; Fang, T.; Roberts, W.L. Effects of diluents on soot surface temperature and volume fraction in diluted ethylene diffusion flames at pressure. Combust. Sci. Technol. 2014, 186, 815–828. [Google Scholar] [CrossRef]
- Hottel, H.C.; Broughton, F.P. Determination of True Temperature and Total Radiation from Luminous Gas Flames. Ind. Eng. Chem. Res. 1932, 4, 166–175. [Google Scholar] [CrossRef]
- Park, H.M.; Lee, W.J. An inverse radiation problem of estimating heat-transfer coefficient in participating media. Chem. Eng. Sci. 2002, 57, 2007–2014. [Google Scholar] [CrossRef]
- Draper, T.S.; Zeltner, D.; Tree, D.R.; Xue, Y.; Tsiava, R. Two-dimensional flame temperature and emissivity measurements of pulverized oxy-coal flames. Appl. Energy 2012, 95, 38–44. [Google Scholar] [CrossRef]
- Liu, F.; Thomson, K.A.; Smallwood, G.J. Soot temperature and volume fraction retrieval from spectrally resolved flame emission measurement in laminar axisymmetric coflow diffusion flames: Effect of self-absorption. Combust Flame 2013, 160, 1693–1705. [Google Scholar] [CrossRef]
- Arana, M.; Pontoni, S.; Sen, I.K. Field measurements of soot volume fractions in laminar partially premixed coflow ethylene/air flames. Combust Flame 2004, 138, 362–372. [Google Scholar] [CrossRef]
- Zheng, S.; Cai, W.; Zhao, C.; Li, D.; Zhang, J.; Lu, Q. On the Measurement of Flame Temperature and Emissivity Based on Multispectral Imaging Technique. Measurement 2022, 196, 111272. [Google Scholar] [CrossRef]
- Liu, D.; Huang, Q.X.; Wang, F.; Chi, Y.; Cen, K.F.; Yan, J.H. Simultaneous measurement of three-dimensional soot temperature and volume fraction fields in axisymmetric or asymmetric small unconfined flames with CCD cameras. J. Heat Transf. 2010, 132, 061202. [Google Scholar] [CrossRef]
- Gross, M.L.; Hedman, T.D.; Son, S.F.; Jackson, T.L.; Beckstead, M.W. Coupling micro and meso-scale combustion models of AP/HTPB propellants. Cobust Flame 2013, 160, 982–992. [Google Scholar] [CrossRef]
- Agarwal, S.; Kumar, V.; Shakher, C. Temperature measurement of wick stabilized micro diffusion flame under the influence of magnetic field using digital holographic interferometry. Opt. Lasers Eng. 2018, 102, 161–169. [Google Scholar] [CrossRef]
- Kim, I.; Kim, J.; Choe, Y.; Ryu, K.; Cha, J.; Ri, J. Effect of vane angle on combustion characteristics of premixed H2/air in swirl micro-combustors with straight vane or twisted vane. Appl. Therm. Eng. 2023, 228, 120528. [Google Scholar] [CrossRef]
- Das, D.D.; Cannella, W.J.; McEnally, C.S.; Mueller, C.J.; Pfefferle, L.D. Two-dimensional soot volume fraction measurements in flames doped with large hydrocarbons. Proc. Combust. Inst. 2017, 36, 871–879. [Google Scholar] [CrossRef]
- Anchukaitis, K.J.; Smerdon, J.E. Progress and uncertainties in global and hemispheric temperature reconstructions of the Common Era. Quat. Sci. Rev. 2022, 286, 107537. [Google Scholar] [CrossRef]
- Braga, N.R.F.; Junqueira, O.C. Configuration entropy in the soft wall AdS/QCD model and the Wien law. Phys. Lett. B 2021, 820, 136485. [Google Scholar] [CrossRef]
- Modest, M.F. Radiative Heat Transfer; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Chang, H.-C.; Charalampopoulos, T.T. Determination of the wavelength dependence of refractive indices of flame soot. Proc. R. Soc. A Math. Phys. Eng. Sci. 1990, 430, 577–591. [Google Scholar]
- Zhou, H.-C.; Lou, C.; Lu, J. Recent achievements in measurements of soot volume fraction and temperatures in a coflow diffuse Ethylene-air flame by visible image processing. J. Phys. Conf. Ser. 2009, 147, 012086. [Google Scholar] [CrossRef]
- Thériault, J.-F.; Yu, L.; Stephen, P.; Sheng, Y.; Lin, S.-X. Tunable ultraviolet laser induces high signal-to-noise ratio in intrinsic fluorescence titration for protein- ligand interaction studies. Results Phys. 2023, 44, 106120. [Google Scholar] [CrossRef]
- Chen, M.; Liu, D.; Jiang, B. Soot formation and combustion characteristics in confined mesoscale combustors under conventional and oxy-combustion conditions (O2/N2 and O2/CO2). Fuel 2020, 264, 116808. [Google Scholar] [CrossRef]
- Liu, F.; He, X.; Ma, X.; Zhang, Q.; Thomson, M.; Guo, H.; Smallwood, G.; Shuai, S.; Wang, J. An experimental and numerical study of the effects of dimethyl ether addition to fuel on polycyclic aromatic hydrocarbon and soot formation in laminar coflow ethylene/air diffusion flames. Combust Flame 2011, 158, 547–563. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).