Abstract
This study presents an innovative control strategy for enabling ships to perform automatic U-turns in restricted waters, with a focus on minimizing energy consumption and reducing wear on the steering gear. The strategy integrates a closed-loop gain-shaping algorithm with nonlinear feedback control, applied to a nonlinear motion mathematical model specifically designed for low-speed operations in shallow waters. The simulations, conducted under a Beaufort wind scale conditions up to No. 5 and water depths of 15 m, demonstrate that ships can successfully execute automatic U-turns within a distance three times their length. The incorporation of nonlinear feedback technology significantly reduces energy consumption and steering gear wear, with specific improvements including a reduction in the average rudder angle by up to 18.26%, a reduction in the mean absolute error (MAE) by up to 3.6%, a reduction in the mean integrated absolute (MIA) by up to 13.55%, and a reduction in the mean total variation (MTV) by up to 36.36%. These enhancements not only optimize the control effect but also extend the service life of the steering gear, thereby contributing to more sustainable maritime operations. Theoretical proofs and Matlab-based simulations validate the effectiveness of the controller, highlighting its potential for energy savings and improved navigational efficiency in challenging maritime environments.
1. Introduction
With the continuous growth of global trade, ports, as crucial logistics hubs, play a vital role in ensuring the smooth operation of the entire supply chain. The operation of ships within the port constitutes a crucial aspect of port operations. Effective in-port turning of ships not only enhances the throughput of the port but also reduces the turnaround time of ships in the port, thereby lowering operational costs. Moreover, good heading-keeping ability is indispensable for ensuring the safe and efficient completion of in-port operations. This paper aims to study the in-port turning problem of ships and explore the heading-keeping strategies of ships, and ultimately proposes a control method combining a closed-loop gain-shaping algorithm and a nonlinear feedback algorithm to optimize the in-port operation performance of ships.
The automatic U-turn of ships within port environments is a pivotal aspect of smart ship technology. This technology is proposed with the primary aim of enhancing the efficiency and safety of port operations, including path planning, path following, and course keeping. As ship sizes increase and port traffic intensifies, the necessity for sophisticated automatic turning technologies becomes more pronounced. Traditional ship-turning methods, which rely heavily on crew experience and manual maneuvers, are effective in simple settings and with smaller vessels. However, they face significant limitations in complex port environments, especially with larger ships. Manual operations struggle to accurately control the ship’s movement trajectory and are susceptible to environmental factors such as wind and currents, leading to prolonged turning times and heightened operational risks.
With advancements in control theory, model-based control methods have been increasingly applied to ships, including sliding mode control [1,2], adaptive control [3,4], and fuzzy control [5,6]. For instance, Chen et al. [7] explored the impact of water depth and speed on ship maneuverability and control and proposed an adaptive controller to enhance performance in shallow waters based on extensive experimental studies. The authors of Gao et al. [8] investigated the Boussinesq–Burgers system for shallow water waves, identifying transformations and similarity reductions to aid in understanding wave behavior near ocean beaches, which has implications for ocean engineering fields. The authors of Biagioli et al. [9] presented a modified shallow water equations model incorporating a scalar transport equation, utilizing a finite volume central–upwind scheme and an implicit–explicit Runge–Kutta method for the accurate and efficient simulation of geophysical flows with vertical profiles. The authors of Himaya and Sano [10] examined the combined effects of various loading and wind conditions on a container ship’s course-keeping performance, aiming to improve safe navigation practices by understanding the ship’s response to different environmental and operational scenarios. The authors of Lin et al. [11] introduced a particle swarm optimization (PSO)-based predictive PID-backstepping controller to enhance ship course-keeping performance under varying conditions, demonstrating improved efficiency and stability through simulation tests. The authors of Nguyen et al. [12] utilized computational fluid dynamics simulations to analyze the maneuvering characteristics of a container ship in shallow waters, revealing significant changes in roll and turning diameter compared to deeper waters, with results that align well with experimental data. The authors of Yin et al. [13] presented an integrated framework using enhanced LQR control and adaptive strategies for autonomous ship berthing, validated through simulations under various operating conditions. The authors of Li et al. [14] proposed a fuzzy logic-based human-like decision-making method for ultra-large ship berthing, validated with pilotage data, offering insights for autonomous navigation in port waters. The authors of Xu et al. [15] examined the impact of shallow water on vessel steering models using system identification methods and compared parameter estimation accuracy among different modeling techniques, demonstrating that shallow water significantly impairs ship maneuverability. The authors of Priya et al. [16] presented a mathematical model to analyze the motion of moored ships in harbors, incorporating strategies like porous breakwaters and wave absorbers to mitigate resonance and enhance safety in maritime navigation. The authors of Hu et al. [17] introduced a nonlinear feedback-based controller design that enhances system robustness, reduces energy consumption, and demonstrated significant practical engineering value through simulations with the training ship “Yupeng”. The authors of Rybczak and Lazarowska [18] outlined a method for autonomous ship operation in ports, utilizing the ant colony optimization algorithm for safe trajectory calculation and a combination of trajectory and low-speed controllers to maneuver a very large crude carrier model.
The aforementioned methods have proposed various research and evaluation approaches in the domain of shallow water navigation analysis and ship motion control, showing promising results in simulations and experiments. They face issues related to model complexity and high computational costs. These challenges necessitate more advanced hardware support and meticulous parameter tuning, increasing the difficulty and cost of implementation. Moreover, the increasing complexity of algorithms often relies on accurate models and parameters, making the system difficult to adapt quickly to unknown or changing environments. Building on the aforementioned research, this paper proposes a simple and robust control strategy for the automatic U-turn of ships in the port. By employing the closed-loop gain-shaping algorithm to design the controller and integrating nonlinear feedback techniques for error processing, this approach achieves effective automatic U-turn control for ships within port environments. In addition, the controller was further optimized to reduce the variation of the system output, reduce the wear of the rudder, and extend its service life. Reducing the wear of rudder can ensure that the rudder is in good working condition, preventing the generation of more wear particles. These wear particles can enter the hydraulic and lubrication systems of the ship, causing system contamination and further exacerbating wear. At the same time, reducing rudder motor wear can also lower fuel consumption, reduce noise and vibration, and decrease waste oil emissions. This can reduce the negative impact of the ship on the environment and improve the environmental performance of the ship, embracing the concept of green shipbuilding. The main innovations of this paper include:
- (1)
- third-order Nomoto model, it is rewritten into state–space form; the wind and wave interference models are added in the ship model to design the ship U-turn controller.
- (2)
- Nonlinear feedback technology is used to improve the controller, reducing the energy consumption of ship U-turns with low speed in the port and reducing the wear of the steering gear, which can prolong its service life.
The remaining sections of this paper are arranged as follows: Section 2 introduces the establishment and revision of ship models in low-speed shallow waters, providing reasonable simplifications to complex shallow water models; Section 3 details the design process of the controller presented in this paper; Section 4 demonstrates the stability of the system, proving that system errors can converge within a finite time; Section 5 is the simulation experiment verification section, where Matlab is used for simulation comparison experiments to validate the effectiveness and superiority of the controller; Section 6 summarizes the content of the paper and outlines future research directions.
2. System Design and Implementation
Mathematical Model of Ship Motion with Low Speed in Shallow Water
The motion of a ship in a port involves a movement with low speed and large drift angle, and the disturbance of the wind and waves in the port is relatively increased; the water depth is shallower than that in the general sea, which will lead to an increase in the ship’s resistance and the deterioration of the rudder response. This will lead to some difficulties being encountered in controlling the ship. Since ships are divided into specifications and sizes, they need to be judged according to the ratio of the water depth to the ship’s draft, . At present, there is no clear and unified concept definition for shallow water in the international community. For normal transport ships, water depth is usually divided into four ranges of standard: deep water (), medium water depth (), shallow water (), and very shallow water (). Generally speaking, when the ratio of water depth, h, to draft, d: , is less than 3, the shallow-water effect will occur. In shallow water, the hydrodynamic force and hydrodynamic torque of the ship increase due to an increase in the speed of water around the hull, and the main effect is reflected in the increase in the difficulty of berthing and turning around in port [19].
The automatic U-turn operation of ships is generally only applicable for medium- and small-sized ships under good environmental conditions and wide water areas. For large ships, the automatic U-turn operation is difficult to achieve, and tugs are usually used to assist the turning operation.
The flow scene caused by the movement of ships in shallow waters is significantly different from that in deep waters. Generally speaking, the inertial fluid power acting on the hull—that is, the additional mass and additional moment of inertia of the hull—will increase with the decrease in water depth; the viscous fluid power acting on the hull also has the same situation. The coordinate point is taken at the center of the ship, and the ship motion model is shown as Equation (1):
where m is ship mass; is moment of inertia of and ; is the additional mass and additional moment of inertia of the ship. and N represent the force and moment acting on the ship; the subscripts and R represent the hull, propeller, and rudder, respectively; represents the distance from the coordinate origin to the ship’s center. are the ship’s position coordinates; is the ship’s heading angle; represent the ship’s surge velocity, sway velocity, and yaw rate, respectively.
According to the Inoue model, the force and moment in Equation (1) can be calculated as Equation (2):
where represent the ship’s direct sailing resistance; ; S is the wet area of the hull; is the ship’s total drag coefficient; the coefficients preceding the remaining velocity terms are all hydrodynamic derivatives, which are related to the ship’s own parameters. For specific calculations of hydrodynamic derivatives, see the Appendix A.
In shallow-water conditions, the traditional ship model needs to be modified; the formulas are shown below.
The modification of the drag coefficient for the direct navigation of ships is shown as Equation (3):
where is the ship’s total drag coefficient in deep water; is the ship’s total drag coefficient at a water depth of h; A and B are the experimental coefficients of the ship model.
The modification of the viscous hydrodynamic derivatives is conducted as follows:
where is the hydrodynamic derivative in deep water; is the hydrodynamic derivative at a water depth of h.
The modification of viscous hydrodynamic derivatives is shown as in Equation (5):
where , , and are the additional mass and additional moment of inertia in deep waters.
The modifications of the accompanying coefficient, hydrodynamic derivative to the propeller, and the rudder force are shown as Equations (6) and (7):
is the hull accompaniment coefficient, is the rectification coefficient of the hull and oars in deep water, is the increase coefficient of the hull fluid force caused by steering, and is the central coordinate of the action center of the hull fluid force caused by steering.
In this paper, different from the traditional ship model in the shallow water correction mentioned above, the third-order Nomoto model is converted into state–space form to facilitate the addition of environmental interference. Ship speed and water depth in the port and the ship draft are associated with the parameters of the ship motion model to describe the ship’s low-speed movement in shallow water. Simulation experiments show that the model in this paper is simple and has certain accuracy.
Ship motion in port needs to consider water depth, ship speed, the external nonlinear force, as well as the interference of wind and wave. By processing the parameters of the Nomoto model, the relationship between the model and water depth and ship speed can be obtained, while the state–space form of the second-order Nomoto model is inconvenient for adding the interference of the nonlinear force and external interference. Compared to higher-order and nonlinear models, the third-order model has a relatively simple structure, with parameters that are easy to identify and adjust, facilitating controller design and system analysis. At the same time, it can accurately reflect the motion characteristics of ships in shallow-water restricted areas, meeting the basic requirements for model accuracy in research. The third-order Nomoto model has been widely applied and verified in the field of ship maneuverability research, accumulating extensive experience and data. Research findings based on this model are highly reliable and credible, meaning that they can be easily accepted and applied in the industry. Therefore, this paper selected the third-order Nomoto model for the simulation experiments, and the third-order Nomoto model is adopted as Equation (8):
where is called the ship-turning ability index, which is the static gain from to . The larger the is, the better the ship’s turning ability will be. , , and are called the ship turning lag indices; the smaller and are, the larger will be, and the better the ship’s following ability will be. Small and mean that the transient motion decays to stable rotation quickly, while a large mainly increases the angular acceleration of initial rotation [20].
In order to add nonlinear force and wind and wave interference, the form of transfer function must be transformed into three degrees of freedom for the state–space model [21]. Using the symbolic toolbox in Matlab, the third-order Nomoto model can be transformed into a three-degrees-of-freedom state–space model. The transformed model parameter matrices A, B, and C are shown as Equation (9).
Remark 1.
When transforming the third-order Nomoto model into a state–space model, certain assumptions are typically made to simplify the model and make it more suitable for control design and analysis:
- (1)
- Higher-order nonlinear hydrodynamic effects in the model, such as wave-making resistance and the nonlinear variation of viscous resistance, are neglected. These higher-order terms have a relatively minor impact on ship motion under small-angle and low-speed conditions, and can be reasonably ignored to simplify the model.
- (2)
- It is assumed that the maneuvering parameters of the ship (such as K0, T1, T2, and T3) remain constant during the operation. These parameters mainly depend on the ship’s design and underwater shape, and can be considered constants over short periods, thereby simplifying the dynamic characteristics of the model.
- (3)
- It is assumed that dynamic disturbances change relatively slowly and can be treated as quasi-static processes. This allows the use of static gains in control design to compensate for these disturbances.
However, this form of model is different from the standard form; it cannot add the interference items in directly. In order to convert it into the standard form, according to Hankel’s norm and balance realization definition, the transformation matrix can be obtained using Equation (10).
The transformed , , and are, respectively, shown as Equation (11):
Furthermore, is shown as Equation (12):
According to the state–space model, ship plane motion is shown as Equation (13):
After being converted into the standard form, it is convenient to add the nonlinear force and environment interference to Equation (13). In this paper, the wind and wave model used can be referenced in [22].
The relationship between ship parameters , and in Equation (8) and water depth are shown in Table 1; is the ratio of water depth to ship draft.

Table 1.
Parameters under different water depths.
According to Table 1, it can be seen that there is an imaginary part. These values are related to the ship’s operational parameters in the context of a frequency–domain analysis. Specifically, they represent the complex gains of the system at different frequencies, which are essential for understanding the dynamic response of the ship. However, the existence of the imaginary part does not affect the calculation; this is because, when calculating the linear interpolation, the values of and in each water depth can be obtained according to the data in the table; then, use the linear interpolation method can be used, which can avoid imaginary parts.
Remark 2.
The parameters in Table 1 are dimensionless. The ship maneuverability indices and can be obtained in a dimensionless form using the following formula: , . Here, V is the ship speed and L is the length between the perpendiculars of the ship; h is the water depth and d is the ship draft.
Remark 3.

According to Table 1 and Table 2, the values of , , , and , corresponding to each water depth, can be obtained by linear interpolation in Matlab. According to the parameters and of the Nomoto model, has a linear relationship with V, and has an inverse linear relationship with V. The mathematical relations are shown as Equation (14):

Table 2.
Relevant parameters of “Mariner”.
Therefore, the time constant , is the design speed.
Remark 4.
In Remarks 1 and 2, the ship maneuverability index is connected with the water depth and ship speed, respectively, which shows that the model is suitable for describing the ship’s motion at low speeds in shallow waters.
3. Nonlinear Controller Design
3.1. Design of Controller for U-Turn Operation in Port
The ship U-turn operation in the port can be divided into two parts. One is the feed-forward link of large angle turning, which can improve the sensitivity of the system and speed up the response of the system [23]. In the process of a ship’s U-turn, in order to improve the response speed, the feed-forward control link is necessary. When the ship turns at a large angle without feed-forward control, the system response time will be quite long, which is very unfavorable for ship’s that need to make a U-turn in an emergency. Therefore, with the selection and judgment function of the switch, the ship steering angle is divided into seven zones: 0°–5°, 5°–15°, 15°–30°, 30°–50°, 50°–90°, 90°–130°, 130°–180°. The small angle range in each zone can take all the angle situations into account. The parameters of the feed-forward response link for the seven zones are as follows: , where s is the Laplacian operator. According to different turning angles, the corresponding interval can achieve a good control effect. The feed-forward controller is shown in Figure 1.
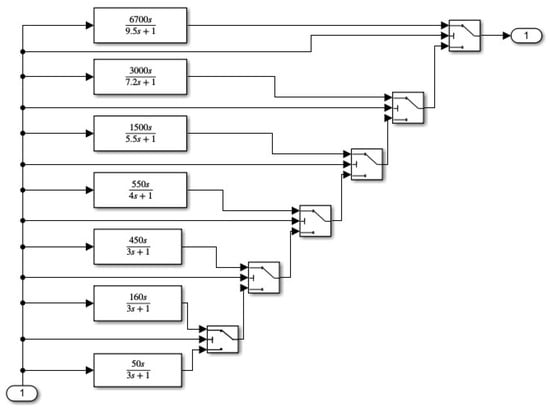
Figure 1.
Block diagram of feed-forward controller.
The other part mainly adopts a simple and direct robust form of control based on the closed-loop gain-shaping algorithm (CGSA) [24]. It is an engineering algorithm based on the results of the hybrid sensitivity control algorithm of robust control and the closed-loop shaping algorithm. For controller design using the closed-loop gain-shaping algorithm, the third-order model needs to be transformed into a second-order, deeply strict model, as shown in Equation (15):
and are the ship manipulative indices: see in Table 1.
The bandwidth frequency of the closed-loop system is assumed to be , according to the second-order CGSA. Thus, Equation (16) can be obtained:
Since a ship is a kind of vehicle with a large inertia and it has long adjustment time, the improved simple robust control algorithm presented in [25] is adopted, and a constant, , is added to the proportional coefficient, which improves the dynamic performance of the system.
Therefore, the final control law is shown as Equation (17):
and are the ship manipulative indices; = 4 s, which makes the system bandwidth frequency less than the high-frequency wave disturbance () and fully suppresses the influence of wave interference. The introduction of a constant can improve the response speed of the closed-loop system, speed up the process of U-turn, reduce the turning time, and make the turning area meet the limited requirements.
Remark 5.
CGSA obtains the controller parameters directly based on the system characteristics through a frequency domain analysis, omitting the parameter-tuning process of traditional PID controllers. Its control law is similar to that of a PD controller, without introducing an integral term. Although the integral term can provide some resistance to external disturbances, it is also prone to integral saturation and slow system response. In applications where rapid control is required, the closed-loop gain-shaping algorithm is more easily applicable.
3.2. Nonlinear Feedback Improvement
Nonlinear feedback technology is an improvement of the existing linear feedback technology [26]. The system block diagram of nonlinear feedback technology is shown as Figure 2. It uses the nonlinear function of error to replace the error in the original system as the input of the controller, which simplifies the system structure and reduces the difficulty of controller design. The essence of nonlinear feedback technology is that the controller is driven by the function of the error and use smaller control output to achieve the same or better control effect without changes to the control law. In a ship motion control system, it is helpful to use a smaller rudder angle to achieve a better control effect.
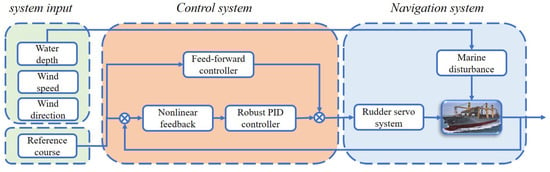
Figure 2.
System block diagram of nonlinear feedback technology.
Remark 6.
The processing formula for error signals in Figure 2 is: . It is different from the common block diagram operation mode , because a better block diagram drawing method is not found; it is temporarily replaced by the common block diagram drawing.
4. Proof of System Stability
After many comparative experiments, this paper uses the arctangent function to improve the performance of the controller. The controller has a simple structure and is widely used in various engineering control applications; its parameters are easy to adjust. Therefore, this paper uses the robust controller obtained through the CGSA to control a ship’s automatic U-turn in a port. After many simulation experiments, the control effect is satisfied when .
- (1)
- Impact on the stability of the system: it can be seen that the function has the n-th order derivative at the origin point; through Taylor expansion, it can be obtained that . Therefore, ; after the introduction of nonlinear feedback, the system control law changes from K to , which is equivalent to adding a coefficient on the basis of the original controller. Moreover, the structure of the system has not changed and does not affect the closed-loop stability of the system [27]. In order to further prove the stability of the system, the Routh criterion is used in this paper.The expression of the second-order Nomoto model of the ship is shown as Equation (18):Write the characteristic function of the system as Equation (19) and make a Routh table:According to Equation (18), the Routh table of the characteristic function can be written. It can be known that, in the first column of the Routh table, , , and are all positive numbers. According to the Routh stability criterion, the numbers in the first column of the Routh table are all positive numbers, which can prove that the system is stable.
- (2)
- Influence on the stabilization value of the system: Take the step signal, , as the input signal; according to the final value theorem of Laplace transform, the heading angle of the steady state output of the system is shown as Equation (20):
- (3)
- Impact on the dynamic performance of the system: according to the closed-loop gain-shaping algorithm, the open-loop frequency characteristics () of the system need to meet the requirements of high gain at low-frequency and low gain at high-frequency. Furthermore, the introduction of a nonlinear feedback link has little impact on the dynamic performance of the system.
- (4)
- The transfer function of the rudder angle from the input of the system to the output is shown as Equation (21):
It can be seen that the introduction of nonlinear function makes the denominator change more significantly than the numerator, so the introduction of a nonlinear feedback link does not affect the original control effect of the controller, and the same control effect can be achieved with less energy.
Remark 7.
In this part, we choose arctangent function to realize nonlinear feedback. Some reasons for this choice are presented here:
- (1)
- The arctangent function possesses smooth nonlinear characteristics, which can provide different control gains within different error ranges. This characteristic allows the arctangent function to effectively balance speed and stability during the ship’s in-port turning process.
- (2)
- In some nonlinear feedback algorithms, singular points may occur, leading to the failure of control signals. The characteristics of the arctangent function can effectively avoid such situations.
- (3)
- The nonlinear feedback algorithm using the arctangent function can effectively reduce energy consumption during the control process, reducing the energy consumption of the actuators. This is of great significance for meeting the energy-saving requirements in practical engineering applications.
Remark 8.
In the simulation experiments, we found that the selection of parameters also has a certain impact on the control effect. If and are too large ( or ), it will lead to deviations in the control results and cause overshooting. If and are too small ( or ), then the expected control effect will not be achieved. Therefore, it is necessary to choose appropriate parameter values to optimize the controller.
5. Matlab Simulation and Result Analysis
According to the controller design and ship model established above, Matlab is used to simulate the ship automatic U-turn in port. Both wind direction and wind speed are measured by absolute wind direction, , and absolute wind speed, ; the north wind direction is and the east wind direction is ; the absolute wind speed is the vector sum of the relative wind speed and the ship speed. Generally, the water environment in the port is not too harsh. In this paper, the wind level in the port is set below the Beaufort wind scale of No. 5, the water depth is set as 15 m, and the parameter of the nonlinear feedback link is .
This paper takes the ship “Mariner” as an example for discussion, and its relevant parameters are shown in Table 2.
In addition, this paper quotes MIA, MAE, MTV, and some other indexes to quantitatively analyze the control effect of the controller. MAE is used to measure the deviation between the design ship course and the actual ship course; MIA is used to quantitatively analyze the energy consumption during ship navigation; MTV is used to measure the smoothness of the rudder angle output curve. MIA, MAE, and MTV are calculated as Equations (22)–(24):
After many simulation experiments, it can be concluded that, when the wind level is below the Beaufort wind scale of No. 5 and the water depth is more than 15 m, the ship can complete an automatic U-turn in restricted waters under the control of the proposed controller. When the wind level is higher than the Beaufort wind scale of No. 6, the ship can achieve an automatic U-turn under certain environmental conditions. Due to the large rudder angle being maintained for a long time, the roll motion of the ship increases, which affects the safety of navigation. Due to the shallow-water effect, it is also not recommended to carry out an automatic U-turn operation in a water area with a water depth of less than 15 m during actual navigation. Some simulation results and analyses are given below. The simulation time is set at 600 s, the simulation experiment is carried in simulink of Matlab, the differential equation is solved by using ode45 solver, and the sample time is set as 1 s.
In the following simulation results, we compared the control effect of three kinds of control methods: Zhang et al. (proposed in [28]), NF+CGSA (proposed in this paper), and the traditional PID control method. The decline ratio is the comparative result of the first two control methods.
- (1)
- Beaufort wind scale of No. 4, =
It can be seen from the data in Figure 3, Figure 4 and Figure 5 and Table 3 that, when the wind level in port is at a Beaufort wind scale of No.4, the water depth is 15 m, and the wind direction is = , the ship can complete an automatic U-turn in the port. After adding the nonlinear feedback link, the turning range of the ship is reduced by 3.00%, the average rudder angle is reduced by 0.21%, and MIA, MAE, and MTV are reduced by 4.01%, 3.15%, and 36.36%, respectively. It can be seen that the existence of a nonlinear feedback link reduces the change in the rudder angle and the energy consumption of navigation.
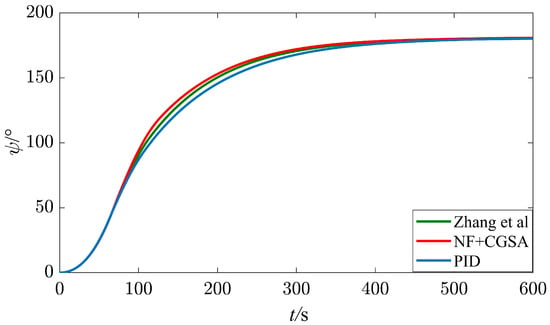
Figure 3.
Heading angle under a Beaufort wind scale of No. 4, = [28].
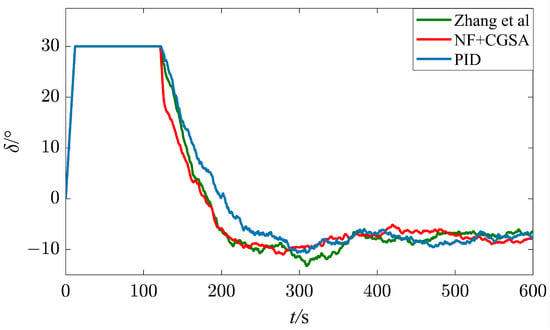
Figure 4.
Rudder angle under a Beaufort wind scale of No. 4, = [28].
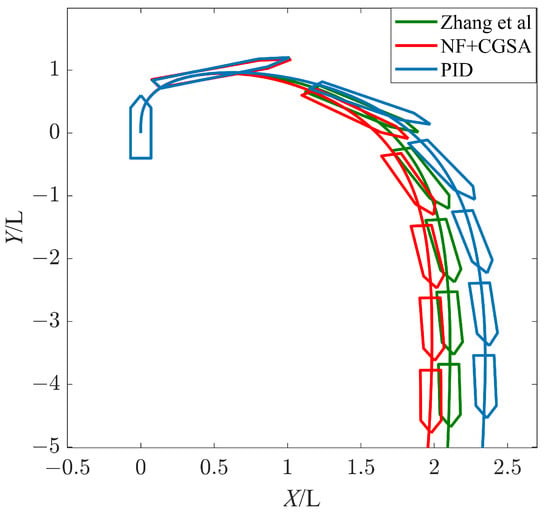
Figure 5.
Ship trajectory of U-turn under a Beaufort wind scale of No. 4, = [28].

Table 3.
Comparison of parameters of automatic U-turn in port at a water depth of 15 m.
- (2)
- Beaufort wind scale of No. 4, =
It can be seen from Figure 6, Figure 7 and Figure 8 and Table 4 that, when the wind level is at a Beaufort wind scale of No. 4, the water depth is 15 m, and the wind angle is = , the ship can complete a U-turn in a port within 10 min. After the nonlinear feedback link is added, the turning range of the ship is reduced by 5.40%, the average rudder angle is reduced by 3.24%, and the MIA, MAE, and MTV are reduced by 1.25%, 2.83%, and 33.33%, respectively. It can be seen that, after the introduction of nonlinear feedback, the energy output of the whole system is reduced, and the rudder angle output is smoother.
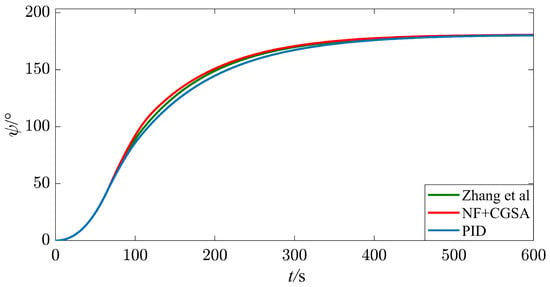
Figure 6.
Heading angle under a Beaufort wind scale of No.4, = [28].
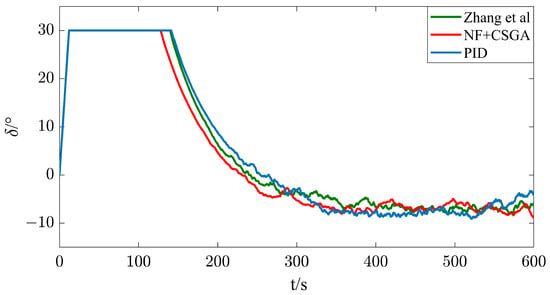
Figure 7.
Rudder angle under a Beaufort wind scale of No. 4, = [28].
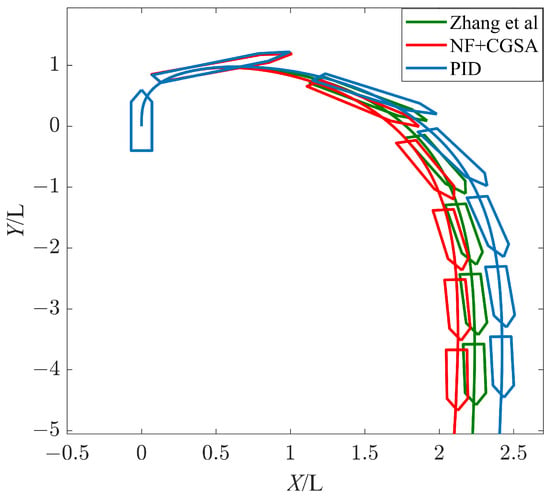
Figure 8.
Ship trajectory of U-turn under a Beaufort wind scale of No. 4, = [28].

Table 4.
Comparison of parameters of automatic U-turn in port at a water depth of 15 m.
- (3)
- Beaufort wind scale of No. 5,
It can be seen from Figure 9, Figure 10 and Figure 11 and Table 5 that, under the condition of a Beaufort wind scale of No. 5, a wind direction of 45°, a water depth of 15 m, and moving with slow speed (4.5 kn), the ship can complete an automatic U-turn in a restricted water area. After adding a nonlinear feedback link, the control output curve has no overshoot, the turning range is reduced by 1.58%, the average rudder angle is reduced by 18.26%, and the three parameters of MIA, MAE, and MTV are reduced by 13.55%, 1.89%, and 25.00%, respectively. It can be seen that the turning range of the ship is reduced, which means the risk of ship collision is reduced, the time of large rudder angle is reduced, and the rudder angle output curve is smoother, which reduces the wear of the rudder and prolongs its service life.
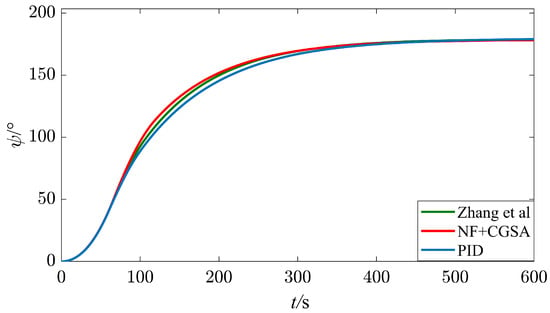
Figure 9.
Heading angle under a Beaufort wind scale of No. 5, [28].
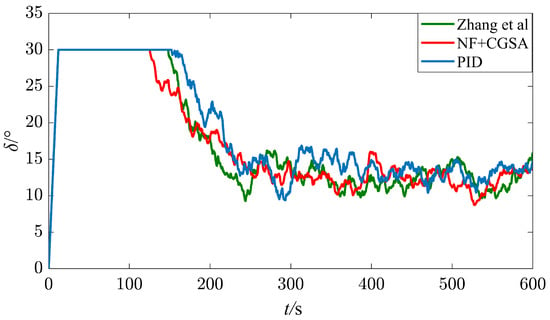
Figure 10.
Rudder angle under a Beaufort wind scale of No. 5, [28].
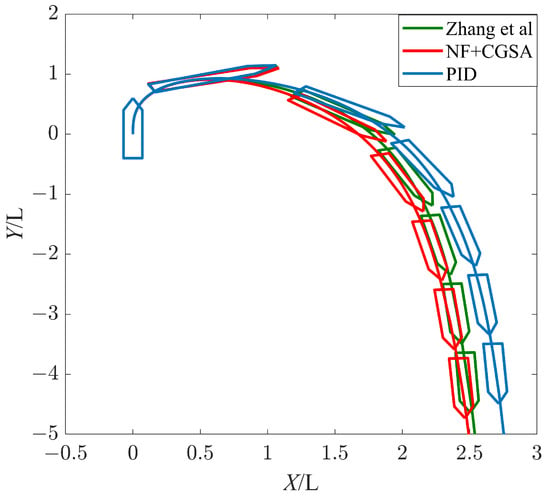
Figure 11.
Ship trajectory under a Beaufort wind scale of No. 5, [28].

Table 5.
Comparison of parameters of automatic U-turn in port at a water depth of 15 m.
- (4)
- Beaufort wind scale of No. 5, =
It can be seen from Figure 12, Figure 13 and Figure 14 and Table 6 that, when the wind direction angle is 135°, the ship can automatically complete U-turn in a restricted water area. With or without nonlinear feedback link, the time to reach the given course is roughly the same; however, with a nonlinear feedback link, the turning range of the ship is reduced by 5.11%, the average rudder angle is reduced by 3.88%, and the three indexes of MIA, MAE, and MTV are reduced by 2.43%, 3.60%, and 22.22%, respectively; this shows that the deviation between the course and the actual course is reduced, the energy consumption is reduced, and the rudder angle output curve is smoother.
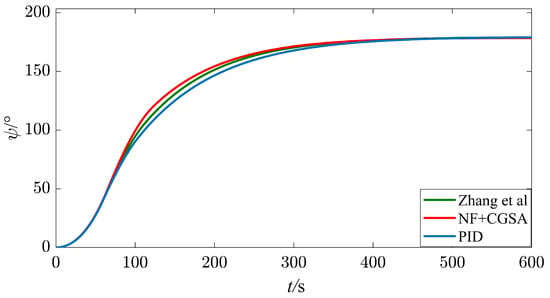
Figure 12.
Heading angle under a Beaufort wind scale of No. 5, = [28].
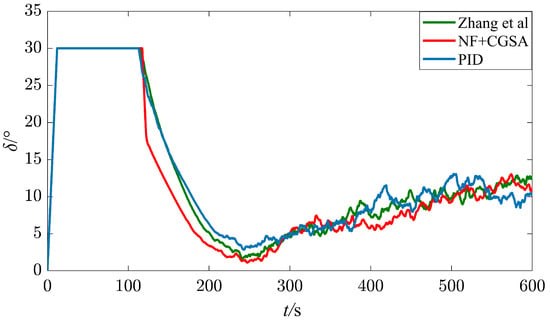
Figure 13.
Rudder angle under a Beaufort wind scale of No. 5, = [28].
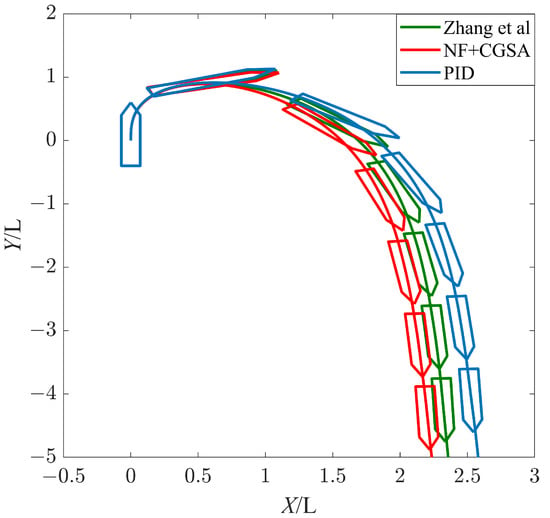
Figure 14.
Ship trajectory under a Beaufort wind scale of No. 5, = [28].

Table 6.
Comparison of parameters of automatic U-turn in port at a water depth of 15 m.
Remark 9.
It should be noted that the third-order Nomoto model, while widely used, simplifies complex ship dynamics and assumes constant maneuvering parameters. This may not accurately represent real-world conditions, particularly in dynamic environments or with varying ship configurations. To obtain a more accurate description of ship motion, further modeling based on actual ship data identification and similar operations is required.
6. Conclusions
From the perspective of the control effect, the simulation results and relevant data presented above demonstrate that the CGSA algorithm is effective for the automatic U-turn control of ships in restricted waters. The introduction of nonlinear feedback does not compromise the controller’s performance. The figures show that, under favorable port conditions, a ship can complete the automatic U-turn operation in a restricted water area within 10 min, with the duration of large rudder angles controlled to approximately 1–3 min. After incorporating the nonlinear feedback link into the original control system, both the time spent at large rudder angles and the range of the U-turn are reduced to some extent, and the average rudder angle of the ship is also decreased throughout the turning process. Therefore, the theoretical proof and simulation experiments conducted above confirm that the introduction of a nonlinear feedback link in the control system can achieve the same control effect with less energy input, ensure the smooth output of various variables, reduce the wear of the steering gear, extend its service life, and effectively realize energy savings during navigation. The reduction in energy consumption not only lowers operational costs but also aligns with the initiatives to decarbonize the shipping industry; it holds significant engineering implications for the motion control of large vessels that are challenging to maneuver and respond slowly. Our findings directly contribute to the goals of green shipbuilding and operational efficiency. Based on the current achievements, future research will integrate advanced intelligent control algorithms to further optimize the study of ship motion control in port areas; furthermore, we will improve the current model, taking into account the nonlinear and inertial characteristics of ships under harsh environmental conditions, and conduct research using more accurate models.
Author Contributions
Conceptualization, S.G. and X.Z.; methodology, S.G.; software, S.G.; validation, S.G. and X.Z.; formal analysis, S.G.; investigation, S.G.; resources, S.G.; data curation, S.G.; writing—original draft preparation, S.G.; writing—review and editing, S.G. and X.Z.; visualization, S.G.; supervision, X.Z.; project administration, X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by the National Science Foundation of China (Grant No. 52171291), Dalian Innovation Team Support Plan in the Key Research Field (Grant No. 2020RT08), Doctoral Research Initial Fund Project of Liaoning Province (No. 2021-BS-078), Dalian Maritime University University-level Team “Open Ranking” Project (No. 3132023502), the University 111 Project of China (Grant No. B08046), and International cooperation training program for innovative talents of Chinese Scholarships Council (Grant No. CSC [2022] 2260).
Data Availability Statement
The data are contained within the article.
Acknowledgments
The authors are grateful to each reviewer for their valuable comments and suggestions which improved the quality of this article. The authors would like to thank anonymous reviewers for their valuable comments which improved the quality of this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Calculation of Hydrodynamic Derivatives
The dimensionless calculation formulas for hydrodynamic derivatives are given in Equation (A1):
References
- Deng, F.; Yang, H.; Ding, Q.; Li, B. Discrete-Time Integral Fast Terminal Sliding Mode Predictive Control for Dynamic Positioning Ships With Lumped Uncertainties and Input Constraints. Int. J. Robust Nonlinear Control. 2024. [Google Scholar] [CrossRef]
- Liu, S.; Song, J.; Zhang, L.; Tan, Y. Adaptive Finite-Time Backstepping Integral Sliding Mode Control of Three-Degree-of-Freedom Stabilized System for Ship Propulsion-Assisted Sail Based on the Inverse System Method. J. Mar. Sci. Eng. 2024, 12, 348. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Sui, B. Robust Fixed-Time Adaptive Fault-Tolerant Control for Dynamic Positioning of Ships with Thruster Faults. Appl. Sci. 2024, 14, 5738. [Google Scholar] [CrossRef]
- Li, P.; Bai, W.; Zhang, W.; Zhao, Y. ADP-based adaptive control of ship course tracking system with prescribed performance. Proc. Inst. Mech. Eng. Part J. Syst. Control. Eng. 2024. [Google Scholar] [CrossRef]
- Han, B.; Duan, Z.; Peng, Z.; Chen, Y. A Ship Path Tracking Control Method Using a Fuzzy Control Integrated Line-of-Sight Guidance Law. J. Mar. Sci. Eng. 2024, 12, 586. [Google Scholar] [CrossRef]
- Ning, J.; Ma, Y.; Li, T.; Chen, C.P.; Tong, S. Event-triggered based trajectory tracking control of under-actuated unmanned surface vehicle with state and input quantization. IEEE Trans. Intell. Veh. 2023. [Google Scholar] [CrossRef]
- Chen, C.; Delefortrie, G.; Lataire, E. Effects of water depth and speed on ship motion control from medium deep to very shallow water. Ocean. Eng. 2021, 231, 109102. [Google Scholar] [CrossRef]
- Gao, X.Y.; Guo, Y.J.; Shan, W.R. Beholding the shallow water waves near an ocean beach or in a lake via a Boussinesq-Burgers system. Chaos Solitons Fractals 2021, 147, 110875. [Google Scholar] [CrossRef]
- Biagioli, E.; De’ Michieli Vitturi, M.; Di Benedetto, F. Modified shallow water model for viscous fluids and positivity preserving numerical approximation. Appl. Math. Model. 2021, 94, 482–505. [Google Scholar] [CrossRef]
- Himaya, A.N.; Sano, M. Course-Keeping Performance of a Container Ship with Various Draft and Trim Conditions under Wind Disturbance. J. Mar. Sci. Eng. 2023, 11, 1052. [Google Scholar] [CrossRef]
- Lin, B.; Zheng, M.; Han, B.; Chu, X.; Zhang, M.; Zhou, H.; Ding, S.; Wu, H.; Zhang, K. PSO-Based Predictive PID-Backstepping Controller Design for the Course-Keeping of Ships. J. Mar. Sci. Eng. 2024, 12, 202. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Phan, T.L.; Le, T.H.; Mai, T.L.; Yoon, H.K. Four-DOF Maneuvering Motion of a Container Ship in Shallow Water Based on CFD Approach. J. Mar. Sci. Eng. 2024, 12, 981. [Google Scholar] [CrossRef]
- Yin, J.; Chen, G.; Yang, S.; Huang, Z.; Suo, Y. Ship Autonomous Berthing Strategy Based on Improved Linear-Quadratic Regulator. J. Mar. Sci. Eng. 2024, 12, 1245. [Google Scholar] [CrossRef]
- Li, Y.; Song, G.; Yip, T.L.; Yeo, G.T. Fuzzy Logic-Based Decision-Making Method for Ultra-Large Ship Berthing Using Pilotage Data. J. Mar. Sci. Eng. 2024, 12, 717. [Google Scholar] [CrossRef]
- Xu, H.; Hinostroza, M.A.; Wang, Z.; Guedes Soares, C. Experimental investigation of shallow water effect on vessel steering model using system identification method. Ocean. Eng. 2020, 199, 106940. [Google Scholar] [CrossRef]
- Priya, P.; Kumar, P.; Gulshan; Rajni. Mathematical Modeling of Moored Ship Motion in Arbitrary Harbor utilizing the Porous Breakwater. China Ocean. Eng. 2023, 37, 738–752. [Google Scholar] [CrossRef]
- Hu, Y.; Su, W.; Zhang, Q.; Zhang, Y.; Wang, C. A Nonlinear Power Feedback Improvement of the Ship Course-Keeping Controller. Math. Probl. Eng. 2022, 2022, 1–8. [Google Scholar] [CrossRef]
- Rybczak, M.; Lazarowska, A. Safe Control of an Autonomous Ship in a Port Based on Ant Colony Optimization and Linear Matrix Inequalities. Electronics 2024, 13, 3525. [Google Scholar] [CrossRef]
- Liu, C. Analysis on the influence of shallow water on ship maneuvering in harbor. Ship Supplies Mark. 2022, 30, 1–3. [Google Scholar] [CrossRef]
- Sutulo, S.; Soares, C.G. Nomoto-type manoeuvring mathematical models and their applicability to simulation tasks. Ocean. Eng. 2024, 304, 117639. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, W.; Guo, C. Course keeping for ships entering and leaving port at low speeds. J. Traffic Transp. Eng. 2005, 4, 77–81. [Google Scholar]
- Li, Z.; Bu, R. Trajectory tracking of under-actuated ships based on optimal sliding mode control with state observer. Ocean. Eng. 2021, 233, 109186. [Google Scholar] [CrossRef]
- Xu, S.; Li, B.; Wang, X.; Wang, L. A novel real-time estimate method of wave drift force for wave feed-forward in dynamic positioning system. Ships Offshore Struct. 2016, 11, 747–756. [Google Scholar] [CrossRef]
- Peng, X.; Jia, S.; Yu, Y. A novel control method based on fuzzy optimization algorithm of ship lateral motion control. In Proceedings of the 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 31 May–2 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4551–4554. [Google Scholar]
- Budak, G.; Beji, S. Controlled course-keeping simulations of a ship under external disturbances. Ocean. Eng. 2020, 218, 108126. [Google Scholar] [CrossRef]
- Liang, L.; Cheng, Q.; Li, J.; Le, Z.; Cai, P.; Jiang, Y. Design of the roll and heel reduction controller on ship’s turning motion. Ocean. Eng. 2023, 284, 115093. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, M.; Hu, Y.; Zhu, G. Error-driven-based adaptive nonlinear feedback control of course-keeping for ships. J. Mar. Sci. Technol. 2021, 26, 357–367. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, G. Simple and robust control of ship turning maneuvers in harbor. Chin. Navig. 2014, 37, 31–34. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).