Internet Traffic Prediction with Distributed Multi-Agent Learning

Abstract

Internet traffic prediction has been considered a research topic and the basis for intelligent network management and planning, e.g., elastic network service provision and content delivery optimization. Various methods have been proposed in the literature for Internet traffic prediction, including statistical, machine learning and deep learning methods. However, most of the existing approaches are trained and deployed in a centralized approach, without considering the realistic scenario in which multiple parties are concerned about the prediction process and the prediction model can be trained in a distributed approach. In this study, a distributed multi-agent learning framework is proposed to fill the research gap and predict Internet traffic in a distributed approach, in which each agent trains a base prediction model and the individual models are further aggregated with the cooperative interaction process. In the numerical experiments, two sophisticated deep learning models are chosen as the base prediction model, namely, long short-term memory (LSTM) and gated recurrent unit (GRU). The numerical experiments demonstrate that the GRU model trained with five agents achieves state-of-the-art performance on a real-world Internet traffic dataset collected in a campus backbone network in terms of root mean square error (RMSE) and mean absolute error (MAE).

1. Introduction

Internet traffic has grown considerably in the past few years, with the development of new networking paradigms, including 5G/6G, the Internet of Things and the Industrial Internet, and new Internet applications, including live streaming, video sharing and virtual reality. A precise prediction for Internet traffic has been proposed as an important research topic in the past few years as the basis for intelligent network management and planning, e.g., elastic network service provision and content delivery optimization. Different approaches have been proposed for achieving satisfactory traffic prediction performance, which can be categorized into statistical, machine learning and deep learning types.

Statistical models mainly include autoregressive integrated moving average (ARIMA) and vector autoregression (VAR) when the Internet traffic prediction problem is modeled as a univariate or multivariate time series problem. These statistical models have the advantages of low computational cost and high interpretability. However, their prediction performance is not as competitive as that of machine learning and deep learning models [1]. Machine learning models mainly include support vector machine and decision tree-based models, e.g., random forest and AdaBoost, and have both a medium computation cost and a medium prediction performance. More recently, deep learning models including various neural network structures have been proven more effective for prediction problems [2,3,4,5]. With a flexible structure, deep learning can be used in different problem formats, e.g., recurrent neural networks for time series-format prediction [6,7], convolutional neural networks for grid-based prediction [8,9] and graph neural networks for graph-format prediction [10,11].

However, most of the existing studies for Internet traffic prediction focus on the centralized approach, in which the prediction models are trained and deployed in a centralized server, neglecting the case that multiple parties are concerned about the prediction process and want to be involved in the training process in a distributed approach. In reality, multiple parties would be interested in the prediction result of Internet traffic usages. For example, for the campus backbone network considered in this paper, the involved parties include the university network management department, the Internet service provider and the Internet content provider. All these parties behave as an intelligent agent with their own computation and communication facilities that can be leveraged in the traffic prediction task. On the other hand, distributed multi-agent learning has been proven more efficient than training a deep learning model on a single agent [12]. However, few previous discussed whether better performance can be achieved with such settings in the problem of Internet traffic prediction.

To the best of our knowledge, this paper presents a pioneer work which predicts Internet traffic with a distributed multi-agent learning approach when Internet traffic prediction is modeled as a supervised learning problem. For this paper, the research motivation is to validate the marginal benefit of the distributed multi-agent learning approach over traditional centralized learning and initiate the research direction of a potential further performance improvement in follow-up studies. Two recurrent neural networks, namely, long short-term memory (LSTM) [13] and gated recurrent unit (GRU) [14], are adopted as the base prediction model and compared on a real-world Internet traffic dataset. The numerical experiments show that the GRU-based distributed multi-agent learning approach achieves state-of-the-art performance, outperforming both the LSTM-based multi-agent learning approach and the centralized learning approach in a previous study [15].

The contributions of this paper are summarized as follows:

• To the best of our knowledge, this paper presents a pioneer work which predicts Internet traffic with a distributed multi-agent learning approach when Internet traffic prediction is modeled as a supervised learning problem and the base prediction models are trained cooperatively among different agents.
• An effective interaction process is used for coordinating the different agents in the distributed training step, which can be modeled and analyzed as an irreducible aperiodic Markov chain with a finite state, and the convergence property of the interaction process is proved.
• The effectiveness of the proposed approach is validated with a real-world Internet traffic dataset collected at the State University of Ceará for half a year from 16 January 2019 to 15 July 2019, and the five-agent GRU-based distributed multi-agent learning scheme achieves state-of-the-art performance with the smallest prediction errors and outperforms several sophisticated deep learning models in terms of root mean square error (RMSE) and mean absolute error (MAE).

The remainder of this paper is organized as follows. In Section 2, different types of prediction models are further discussed. In Section 3, a real-world Internet traffic dataset is introduced and the prediction problem is defined. In Section 4, the distributed multi-agent learning approach as well as the LSTM and GRU models are introduced. In Section 5, numerical experiments are conducted with the traffic dataset and the results are analyzed. In Section 6, the conclusion and future research directions are discussed.

2. Related Work

In this section, a brief introduction for the different types of prediction models is given, including statistical, machine learning and deep learning models. More comprehensive discussions can be found in recent relevant surveys [16,17,18].

2.1. Statistical Prediction Models

Statistical models are featured by their explicit mathematical formulas based on a set of statistical assumptions for the data generation or distribution patterns. Their prediction performance can be analyzed and quantified in theory. Some representative statistical prediction models include ARIMA and Holt–Winters (HW) models. Other models include the simple exponential smoothing model, which is used for cellular traffic prediction [19], and the particle filtering method, which is used for 5G traffic demand prediction [20]. However, statistical prediction models are less common in recent years for network traffic prediction problems, because their prediction performance is worse than machine learning and deep learning models.

2.2. Machine Learning-Based Prediction Models

Machine learning models are applied for network traffic prediction because of their strong learning ability for mapping historical network traffic data to future situations in a supervised learning approach. With the accumulation of network traffic datasets and the growth of computation capacities, machine learning models are becoming popular in the computer network domain, not only for traffic prediction but also for a wider range of applications, e.g., traffic classification, routing and intrusion detection [21].

Compared with deep learning models represented by deep neural networks, the machine learning models discussed in this subsection are those with shallow structures, e.g., decision trees and random forests. These tree-based machine learning models represent better interpretability and less overfitting severity compared with neural networks and are still used in network traffic prediction tasks, e.g., Gaussian process regression has been adopted for network traffic prediction in different network scenarios [22,23,24]

Besides, different machine learning models can be used jointly, e.g., random forest (RF) and LightGBM are used together for mobile network traffic prediction when RF is used for feature filtering and LightGBM is used to make predictions [25]. Machine learning models can also be used together with statistical models for further performance improvement, e.g., the combination of soft clustering and traditional time series models [26].

2.3. Deep Learning-Based Prediction Models

As a subset of machine learning models, deep learning models are becoming the mainstream solutions for network traffic prediction problems in various scenarios due to their superior performance. Deep learning-based prediction models can be roughly divided into different categories based on the neuron connection method in neural networks, i.e., recurrent neural networks, convolutional neural networks and graph neural networks.

Recurrent neural networks (RNNs) have been proposed for handling long sequence data, e.g., natural languages and time series, by adding the recurrent connection and memory mechanism. LSTM and GRU are two representative RNN variants and solve the problem of vanishing gradients faced by the original RNN structure. They have been adopted in network traffic problems with both univariate and multivariate time series forecasting problem formulations [7,27,28].

When considering network traffic prediction problems in a regular grid, convolutional neural networks (CNNs) can be used by taking traffic data in different grids as image pixel values [29,30,31]. The attention mechanism [32] can be further incorporated into CNNs for a better prediction performance [33]. For example, the attention mechanism is combined with ConvLSTM for capturing long-term spatial-temporal dependency for cellular traffic prediction and helps to achieve accurate prediction under hourly and daily time scales [34]. Based on the Transformer network, a spatial-temporal downsampling neural network model is further proposed for citywide mobile traffic prediction [35].

More recently, graph neural networks (GNNs) have been proposed as the new frontier of artificial intelligence research, and the input data are formulated as graphs [36]. GNNs have been successfully applied in communication networks, with a wide range of applications including network traffic prediction [37,38,39]. To further improve the performance of the GNN-based prediction model in large-scale traffic prediction, transfer learning is introduced for knowledge reuse and computation reduction in cellular traffic prediction [40].

While there are various network traffic prediction models in the literature, most of them are considered in a centralized approach. Thus, the main research motivation of this paper is to fill in the research gap that the distributed multi-agent learning approach has not been considered in the Internet traffic prediction problem before, in the cooperative way more specifically. Two main research questions arise in this paper, i.e., would the interaction among different agents converge in the long run, and could the distributed multi-distributed learning approach outperform the traditional centralized learning approach? From our research, both questions are answered in the affirmative.

3. Dataset and Problem

In this paper, we use an open real-world dataset [41] to validate the proposed distributed multi-agent learning approach and compare it with the centralized learning baseline. The dataset contains the Internet traffic data collected in a university campus backbone network located in the State University of Ceará for half a year from 16 January 2019 to 15 July 2019, with a sampling time period of one hour. The mean, maximum, and minimum bandwidth usage values are recorded. Figure 1 shows the Internet traffic data in the first three weeks of the data collection time period. For clarity, the mean, maximum, and minimum values are plotted in three subfigures. Both a weekly pattern and a daily pattern on weekdays are observed from Figure 1. The stationarity of this specific Internet traffic time series has also been validated with the Dickey-Fuller test, and the rationality of using the mean, maximum, and minimum usage values as input has also been justified with the cointegration test [15].

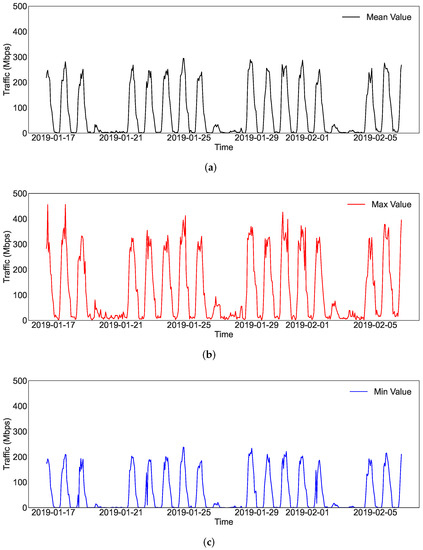
Figure 1. The Internet traffic data in the first three weeks. (a) Mean values; (b) Maximum values; (c) Minimum Values.

Following previous studies [15], the Internet traffic prediction problem is modeled as a supervised learning problem, in which the mean traffic value in the future is the short-term prediction target and the historical traffic data (containing the mean, maximum, and minimum usage values) in the historical time window are the input features. We consider the single-step prediction problem in this study, in which the mean traffic value in the next hour is chosen as the prediction target. To compare with existing centralized learning results, we choose 24 h as the historical time window size and leave the exploration for multi-step predictions as well as the influence of varying historical time window sizes in our future studies.

In this study, we take a step further and consider Internet traffic prediction using supervised learning and distributed multi-agent learning approach. The problem is to design an effective cooperation and aggregation process in which the historical traffic data are used by different agents as the base prediction model input and a final result is aggregated from the predictions of different agents as the output. Different from the centralized learning approach in which only one prediction model is trained in a central server, the learning approach for the base prediction models is distributed among different agents with their own facilities.

4. Methodology

In this paper, a distributed multi-agent learning approach is proposed for Internet traffic prediction, as shown in Figure 2. An interaction process is added into the individual training process so that the base prediction models are trained in a cooperative approach among the agents and an aggregated prediction is used as the final output, e.g., an average value. In this study, the base prediction model is considered a deep learning model with multiple layers and the described interaction is conducted at a layer-to-layer level for agents so that the prediction model can be cooperatively trained.

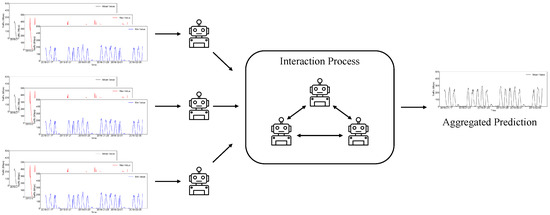
Figure 2. The general process of the proposed distributed multi-agent learning approach.

Mathematically, the influence between different agents in the interaction process is modeled as an adjacency matrix W with row sum 1. Denote that there are m agents and the agent set is I. Each agent trains a base prediction model with L layers. Denote $f_i^{(\ell )}$ as the mapping function for layer ℓ of agent i, to extract information from the input historical data. The distributed multi-agent learning in a single iteration is formulated as follows:

$$f_i^{(\ell +1)}=\sum _{i=1}^m{w}_{ij}{f}_j^{(\ell )}$$

(1)

where $w_{ij}$ is an element of W, which is usually a positive value between 0 and 1. $w_{ij}$ reflects the interaction degree among agent i and agent j. The above process can be iterated n times, and the convergence of the distributed multi-agent learning approach can be guaranteed when n is large enough [12]. The interaction among different agents is modeled as an irreducible aperiodic Markov chain with a finite state, in which a single stationary distribution $\{{\pi }_j,j\in I\}$ exists. Theoretically, when n goes to ∞, the influence among agents converges to the stationary distribution, i.e., ${lim}_{n\to \infty }{w}_{ij}^{\left(n\right)}={\pi }_j,j\in I$. This observation answers our first research question that the interaction among different agents would converge in the long run in our proposed approach.

In the proposed approach, all the agents adopt the homogeneous base prediction model, e.g., LSTM or GRU, so that the computation requirement is the same and fair for different agents who want to be involved. An asynchronous communication requirement among the involved agents is also assumed in the proposed approach, so that the mappings can be exchanged and aggregated. It would be interesting to extend our study from the homogeneous and synchronous case to the heterogeneous or asynchronous cases when different agents have different computation and communication resources. For example, deep learning models with a higher computational burden can be trained on a computation-rich agent.

Two deep learning models are adopted in this paper, namely, LSTM and GRU. Based on the gate mechanism, LSTM is proposed to learn the long dependency relationship from the input sequence while mitigating the problem of vanishing gradients. GRU is a simplified variant of LSTM with only two gates, instead of three gates as LSTM, as shown in Figure 3. More specifically, denote t as the time point, $x_t$ as the input, $h_t$ as the output value, and $c_t$ as the cell state. The three gates used in an LSTM cell can be denoted as follows. The forget gate is as follows:

$$f_t=\sigma (W_{xf}{x}_t+W_{hf}{h}_{t-1}+W_{cf}{c}_{t-1}+b_f)$$

(2)

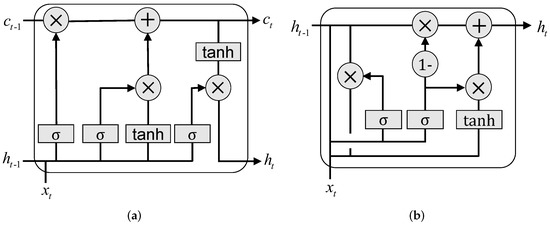
Figure 3. The LSTM and GRU cells. (a) LSTM; (b) GRU.

The input gate is as follows:

$$c_t=f_t\ast c_{t-1}+\sigma (W_{xi}{x}_t+W_{hi}{h}_{t-1}+W_{ci}{c}_{t-1}+b_i)\ast tanh(W_{xc}{x}_t+W_{hc}{h}_{t-1}+b_c)$$

(3)

And the output gate is as follows:

$$h_t=\sigma (W_{xo}{x}_t+W_{ho}{h}_{t-1}+W_{co}{c}_t+b_o)\ast tanh\left(c_t\right)$$

(4)

where $W_{\ast }$ and $b_{\ast }$ are learnable parameters, $\sigma (\ast )$ is the sigmoid activation function and $tanh(\ast )$ is the tanh activation function.

The two gates used in a GRU cell can be denoted similarly. The update gate is as follows:

$$z_t=\sigma (W_{xz}{x}_t+W_{hz}{h}_{t-1}+b_z)$$

(5)

And the output gate is as follows:

$$h_t=(1-z_t)\ast h_{t-1}+z_t\ast tanh(W_{xo}{x}_t+W_{ho}\sigma (W_{xr}{x}_t+W_{hr}{h}_{t-1}+b_r)\ast h_{t-1}+b_o)$$

(6)

Two widely used evaluation metrics are adopted in this paper, namely, RMSE and MAE. Given the true values $\mathbf{y}$ and the predictions $\widehat{\mathbf{y}}$, RMSE is defined as

$$\mathrm{RMSE}(\mathbf{y},\widehat{\mathbf{y}})=\sqrt{\frac{1}{N}\sum _{i=1}^N{(y_i-{\widehat{y}}_i)}^2}$$

(7)

and MAE is defined as

$$\mathrm{MAE}(\mathbf{y},\widehat{\mathbf{y}})=\frac{1}{N}\sum _{i=1}^N|y_i-{\widehat{y}}_i|$$

(8)

where N is the test subset size and the evaluation is conducted on the test subset.

5. Experiment and Analysis

The Internet traffic dataset is divided into training and test subsets at a ratio of 5:1. The deep learning models are implemented with Python and TensorFlow, with three recurrent layers and 20 neurons in each recurrent layer. Adam is used as the optimizer with an adaptive learning rate starting from 0.01 and mean square error (MSE) is used as the loss function. The batch size is 128 and each model is trained for 200 epochs. For each agent number, ten runs are conducted separately. The weight matrix W for different agent numbers from the previous study [12] is used in this paper:

$$W_2=\left[\begin{array}{cc}0.9& 0.1\\ 0.15& 0.85\end{array}\right]$$

(9)

$$W_3=\left[\begin{array}{ccc}0.9& 0.05& 0.05\\ 0.1& 0.8& 0.1\\ 0.025& 0.025& 0.95\end{array}\right]$$

(10)

$$W_4=\left[\begin{array}{cccc}0.8& 0.025& 0.025& 0.1\\ 0.05& 0.85& 0.025& 0.075\\ 0.025& 0.025& 0.9& 0.05\\ 0.05& 0.1& 0.1& 0.75\end{array}\right]$$

(11)

$$W_5=\left[\begin{array}{ccccc}0.8& 0.05& 0.05& 0.05& 0.05\\ 0.05& 0.85& 0.025& 0.025& 0.05\\ 0.025& 0.025& 0.85& 0.05& 0.05\\ 0.05& 0.1& 0.05& 0.7& 0.1\\ 0.04& 0.11& 0.05& 0.05& 0.75\end{array}\right]$$

(12)

The evaluation results with different agent numbers for the LSTM and GRU models are shown in Figure 4, which are box and whisker plots for ten separate runs. With the increase in agent numbers, both LSTM and GRU demonstrate better performance with decreased RMSE and MAE values. GRU maintains a better performance than LSTM in Figure 4. While adding more agents into training might bring a further potential performance improvement, the marginal improvement becomes increasingly smaller. In addition, it becomes more difficult to coordinate more agents in practice. Thus, an agent number up to 5 is used in this paper. Since the research motivation of this paper is to validate the superiority of the distributed multi-agent learning approach over traditional centralized learning, we leave the exploration of using more agents in the follow-up studies.

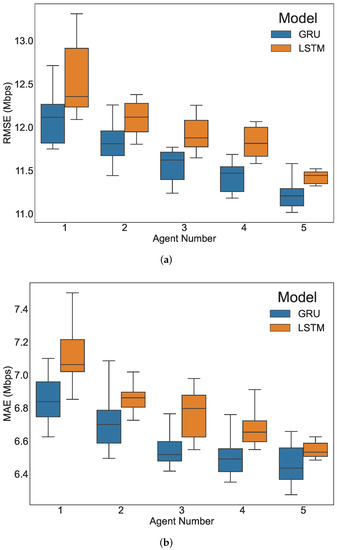
Figure 4. The evaluation results with different agent numbers. (a) RMSE; (b) MAE.

The mean RMSE and MAE results are further listed in Table 1 for LSTM and GRU models trained with different agent numbers. The baselines for comparison are those sophisticated deep learning models from previous studies, including Time Series Transformer (TST) [42], Multilayer Perceptron (MLP) [43], Temporal Convolutional Networks (TCN) [44], Fully Convolutional Network (FCN) [45], Residual Neural Network (ResNet) [45], and InceptionTime [46] in the traditional centralized learning approach. Among these baseline methods, the previous best prediction result is obtained with InceptionTime. While LSTM or GRU trained with a single agent is not competitive with InceptionTime, an improved performance is obtained by adding and involving more agents. Only three agents are enough for defeating InceptionTime when GRU is the base prediction model in individual agents, as indicated in Table 1. A new state-of-the-art performance in the literature is achieved for the considered Internet traffic data by GRU-based distributed multi-agent learning trained with five agents, as shown in bold in Table 1. The results in Table 1 answer our second research question that the proposed distributed multi-distributed learning approach manages to outperform the traditional centralized learning approach and would be worthy a further investigation in the future studies for similar problems.

Table 1. The experimental results.

Model	Agent Number	RMSE (Mbps)	MAE (Mbps)
TST [42]	N/A	16.28	9.71
MLP [43]	N/A	14.81	8.51
TCN [44]	N/A	13.39	9.31
FCN [45]	N/A	12.79	8.10
ResNet [45]	N/A	11.68	7.16
InceptionTime [46]	N/A	11.65	7.07
LSTM	1	12.57	7.10
	2	12.11	6.86
	3	11.93	6.77
	4	11.83	6.69
	5	11.43	6.54
GRU	1	12.11	6.84
	2	11.84	6.71
	3	11.56	6.55
	4	11.42	6.50
	5	11.22	6.45

Figure 5 further shows the comparison between true and predicted results for the first week in the test set. For clarity, only a single run with five agents is plotted for LSTM or GRU. From Figure 5, the predictions from both models present a similar pattern with the true values. However, LSTM generates larger predicted values when the true values are small, e.g., from 22 June 2019 to 23 June 2019, which results in a larger error than GRU. In other words, the GRU-based scheme is more stable, with less extreme predicted values than LSTM and a better overall prediction performance.

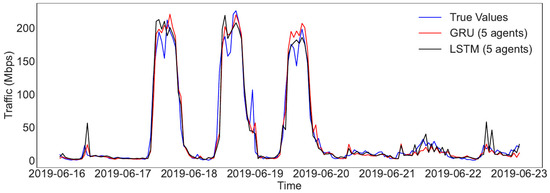
Figure 5. The comparison between true and predicted results for the first week in the test set.

6. Conclusions

The Internet traffic prediction problem is considered in this paper when multiple parties are involved, and a distributed multi-agent learning approach is proposed as the solution for the first time. In the proposed approach, an effective interaction process is used for coordinating the different agents in the distributed training step and the aggregated prediction from different agents is the final result. The interaction process is modeled and analyzed as an irreducible aperiodic Markov chain with a finite state, and its convergence is proven to be guaranteed. Numerical experiments are further conducted with LSTM or GRU as the prediction model, based on a real-world Internet traffic dataset collected at the State University of Ceará for half a year from 16 January 2019 to 15 July 2019. Compared with sophisticated deep learning baseline models trained in the centralized learning approach, the five-agent GRU-based distributed multi-agent learning scheme achieves a new state-of-the-art result, with RMSE of 11.22 Mbps and MAE of 6.45 Mbps for the considered dataset in the literature.

For further research directions, the distributed multi-agent learning approach can be extended to more complex prediction problem scenarios, e.g., grid-format and graph-format prediction problems with more varied neural network structures in a distributed way [47]. Another research direction which can be further explored is that the time-varying or learnable weight matrix in the interaction network can be further explored, instead of using the empirical predefined values.