Abstract
An increase in temperature typically leads to a decrease in the interfacial tension of a water/oil interface. The addition of surfactants to the system can complicate the situation significantly, i.e., the interfacial tension can increase or decrease with an increasing temperature. For most concentrations of the two studied surfactants, the cationic tetradecyl trimethyl ammonium bromide (TTAB) and the nonionic tridecyl dimethyl phosphine oxide (C13DMPO), the measured interfacial tension of the aqueous mixed surfactant solutions against hexane increases when the temperature decreases between 30 °C and 20 °C. However, with a further temperature decrease between 20 °C and 15 °C, the reverse effect has also been observed at some concentrations, i.e., a decrease of interfacial tension. Additionally, the corresponding dilational interfacial visco-elasticity shows some discrepant temperature effects, depending on the bulk concentration and oscillation frequency. The experiments have been performed with a capillary pressure tensiometer under the conditions of micro-gravity. The reason for the positive and negative interfacial tension and visco-elasticity gradients, respectively, within certain ranges of the temperature, concentration and mixing ratios, are discussed on the basis of all available parameters, such as the solubility and partitioning of the surfactants in the two liquid phases and the oscillation frequency.
1. Introduction
Fundamental knowledge on the adsorption of surfactants at water/oil interfaces is of eminent importance for many technological processes, such as oil recovery [1], food processing [2] and the production of pharmaceutics and cosmetics [3]. In many cases, surfactant mixtures, rather than single surfactants, are required in order to set up efficient production technologies. The key system parameters for a given water/oil system are the surface activity and bulk concentrations of the used surfactants, their mixing ratio and the temperature [4]. While the impact of surfactant bulk concentrations and the mixing ratio on the adsorbed amounts is rather easy to explain via the Gibbs fundamental equation [5], the effect of temperature can be quite complicated.
In the literature, there are quite a number of studies on the temperature dependence of surfactant adsorption layers at the water/air interface; however, only very few investigations deal with water/oil interfaces. Typically, the increase in T should result in an increased molar area and consequently in less adsorbed molecules at the interface. This should lead to a decrease in interfacial tension, according to the Gibbs equation. For example, Girifalco and Good discussed this effect in [6] for liquid–solid interfaces. For typical surfactants adsorbed at solution–air interfaces, the impacts of the temperature are quite regular, i.e., with an increasing temperature, the surface tension decreases systematically, as was demonstrated by Chen et al. for n-dodecyl polyoxyethylene glycol monoether with three different oxyethlyene chain lengths of 4, 6 and 8 [7]. In contrast, the critical micelle concentration CMC of the studied non-ionic surfactants passes through a minimum in temperature dependence, explained by contributions of enthalpy and entropy to the micellization process, which is balanced at about 50 °C. Das and Das studied the adsorption layers of alkyl trimethyl ammonium bromides (hexadeyl, tetradecyl and dodecyl) at the solution–air interface at temperatures between 25 °C and 50 °C, and they also explained their results on the micellization process in terms of enthalpy–entropy compensation effects without peculiarities [8]. For ionic liquids, the thermodynamics of micelle formation was investigated at temperatures between 5 °C and 55 °C in [9]. The corresponding surface tension isotherms did not show any unexpected temperature effects. For some water–oil systems, however, an opposite trend for interfacial tension changes was observed, i.e., with an increasing temperature, the interfacial tension increased instead of decreasing [10,11]. For mixed surfactant solutions, the temperature dependence of the interfacial tension is much more complex, as discussed by El-Batanoney et al. in [12]. Although investigations on this topic have been published recently [13,14], including Molecular Dynamics simulations [15], many questions could not be answered so far.
Therefore, more measurements on model surfactant solutions at water/oil interfaces are required in order to get some important basic insights into the interfacial behavior. To this end, microgravity conditions are of great importance as they allow for the simplification not only of the experimental measurement conditions but also of the development of new theories for a quantitative description of the interfacial layer behavior [16,17]. More details on the surface/interfacial tension measurements in space can be found, in particular, in ref. [18].
The specific aim of this study is to present an experimental contribution and illustrate the temperature dependence of the interfacial tension and linear dilational viscoelasticity as measured under microgravity conditions with oil drops in aqueous surfactant solutions, subjected to small-amplitude area oscillations. As an oil phase, pure n-hexane was chosen here. The aqueous matrix contained successively injected amounts of the surfactants C13DMPO at a fixed TTAB concentration and of TTAB at a fixed C13DMPO concentration. In these surfactant mixed solutions, the ionic surfactant TTAB is soluble only in the aqueous phase, whereas the non-ionic surfactant C13DMPO is present in both adjacent liquids, according to the corresponding equilibrium partitioning.
2. Materials and Methods
All measurements were performed under microgravity conditions aboard the International Space Station (ISS) by an especially designed instrument, denoted as FASTER (Facility for Adsorption and Surface Tension Research, manufactured by Leonardo S.p.A (formerly Selex-Galileo), Campi Bisenzio, Firenze, Italy). The advantages of microgravity experiments are the possibility of using perfectly spherical shapes of the interface for sufficiently large droplets and the absence of natural convection that usually influences the mass transfer processes in the studied solutions. The instrument is designed as a capillary pressure tensiometer, where the Laplace pressure drop across a curved interface is accurately measured as a function of time by using precise pressure transducers. In this study, a pure n-hexane drop was formed inside an aqueous surfactant solution. The drop was formed at the capillary tip connecting two closed cells filled with the respective liquids. A precise piezo-actuator allows automatic variation of the drop dimensions (radius of curvature and interfacial area) according to a pre-established timeline. The variation of the interfacial area initiates the relaxation of the interfacial tension, which can be monitored by measuring the Laplace pressure.
The aqueous matrix was a mixture of two surfactants, the non-ionic tridecyl dimethyl phosphine oxide (C13DMPO), (CAS 186953-53-7, purchased from Gamma-Service, Berlin, Germany) and the cationic tetradecyl trimethyl ammonium bromide (TTAB), (CAS 1119-97-7, purchased from Sigma-Aldrich, St. Louis, MO, USA), dissolved in pure MilliQ water. The surfactants were injected step-by-step by using two syringes, working according to a pre-established sequence. The sequence included measurements with increasing C13DMPO concentrations c1 = 4.0 × 10−7, 8.0 × 10−7, 4.0 × 10−6, 8.0 × 10−6 and 2.2 × 10−5 mol/dm3 at a fixed TTAB concentration of c2 = 4.5 × 10−5 mol/dm3, continued by measurements with increasing TTAB concentrations c2 = 4.5 × 10−5, 2.2 × 10−4, 4.5 × 10−4, 2.2 × 10−3 and 4.5 × 10−3 mol/dm3 at a fixed C13DMPO concentration of c1 = 2.2 × 10−5 mol/dm3.
The selection of the above-mentioned surfactants was motivated by the acquisition of new experimental observations for a typical non-ionic surfactant, soluble in both adjacent liquid phases, in mixture with a typical cationic surfactant. Specifically, C13DMPO was selected due to knowledge gained on it as a single component in previous experimental and theoretical studies [19,20]. TTAB was chosen because of the large knowledge on it as an individual component [21] and because of its favorable Kraft temperature, which is below the available temperature range of the experimental tools. Information about the purity of the two used surfactants is given elsewhere [16].
To obtain information about the interfacial dilational viscoelasticity behavior, harmonic oscillations of the drop interfacial area were generated with eight different frequencies (0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.5 and 1.0 Hz, with 12 cycles for each frequency) and three different relative area amplitudes (5%, 10% and 20%). All oscillation experiments were started after 2500 s equilibration time. Additionally, continuously-growing drop experiments were performed for the in-flight pressure sensor calibration adjustment and in-flight CCD-camera calibration, which granted an overall reliability of the obtained results [22]. The measurements were done for three different temperatures (T = 15 °C, 20 °C and 30 °C). The work of the pressure sensors (model PDCR-4000, manufactured by GE Druck, Billerica, MA, USA), piezo-actuator (model P-843.40, manufactured by Physik Instrumente GmbH & Co. KG, Karlsruhe, Germany), CCD-camera (model KP-F120F, manufactured by Hitachi Denshi America Ltd., Woodbury, NY, USA) and the other equipment was carefully synchronized.
The data collected from all devices were telemetered according to a pre-established protocol. The obtained equilibrium interfacial tension values were affected by a variable accuracy (i.e., up to ±0.6 mN m−1), due to occasional push–pull disturbances for the drop caused by the instrumental set parameters. In contrast, the accuracy of the interfacial-viscoelasticity values was much better (i.e., up to ±0.4 mN m−1) because of the simultaneous appearance of the disturbances of interfacial tension and the corresponding interfacial area. Additional information about the instrument and measurement procedures can be found in [16,22].
3. Theoretical Backgrounds
3.1. Interfacial Tension Measurements
The surfactants dissolved in the aqueous matrix (C13DMPO and TTAB) adsorb at the n-hexane/water interface and form a mixed interfacial layer. The resulting interfacial tension is a function of partial surfactant adsorptions (surface concentrations). When the limiting adsorptions (i.e., surface excesses) of two surfactants are not very different, Γ1∞ ≈ Γ2∞, the interfacial tension can be approximately described by Equation (1) [16,23]:
where γ0 is the interfacial tension of the pure hexane/water interface (about 51.1 mN/m [19,21]), Γ1 and Γ2 are the surfactant adsorptions, and are their molar areas in a densely packed state, and is the average molar area. Under equilibrium conditions, the surfactant adsorptions are functions of their bulk concentrations:
where are the surfactant concentrations in the aqueous matrix (phase α), and are their equilibrium adsorption constants. Here and below, the lower indices j = 1, 2 are related to the two surfactants, whereas the upper indices α and β are related to the two contacting liquids (water and hexane, respectively). The model, represented by Equations (1) and (2), is one of the simplest models, as it neglects the interactions between the adsorbed molecules, the possible aggregation or reorientation of the adsorbed molecules, and other effects [24].
When two immiscible liquids are in contact, the surfactant molecules can redistribute between them. Under equilibrium conditions, the surfactants’ partitioning can be described by the distribution (partition) coefficients, which are the ratios of the surfactant concentrations in the two bulk phases:
In the considered case here, the ionic surfactant TTAB is practically not soluble in the oil (n-hexane) phase, i.e., its distribution coefficient can be assumed to be zero. However, the non-ionic surfactant C13DMPO is soluble in both liquid phases. In particular, it is more soluble in n-hexane, and the respective distribution coefficient is about 30 [20,25].
The latter fact can lead to a small uncertainty in the C13DMPO concentration due to this high solubility in hexane. However, the hexane drop is very small compared to the volume of water in the matrix cell (about 68.2 cm3), and therefore the amount of C13DMPO transferred into the hexane drop is negligibly small. However, the surfactant can diffuse through the capillary (the valve is open during the experiment) to the hexane reservoir (5.6 cm3). The change in the C13DMPO concentration due to this effect should also be relatively small, because the surfactants are injected in continuously increasing amounts and the oscillations are performed shortly after the injections. Therefore, the uncertainty in the C13DMPO concentration should be insignificant [16].
3.2. Interfacial Dilational Viscoelasticity Modulus
The interface response to an imposed dilational area perturbation, ΔA(t), is the variation of the measured interfacial tension, Δγ(t). For small-amplitude area perturbations, ΔA(t) << A0, the response of the interface can be characterized by the interfacial dilational viscoelastic modulus:
where F represents the Fourier transform operator of the respective time functions, ω is the variable in the frequency domain (i.e., the angular frequency), and A0 is the initial interfacial area. From the definition Equation (4), one can see that the interfacial viscoelastic modulus is a complex function of frequency, which can be represented as:
where εr and εi are the real and imaginary parts, respectively, and and φ are the modulus and phase of the complex viscoelasticity ε*(iω). In the simplest case of harmonic oscillations, the modulus is the ratio of the amplitudes of interfacial tension and relative interfacial area oscillations, whereas the phase φ is the phase shift of interfacial tension with respect to area oscillations.
In the linear approximation, the interfacial dilational viscoelastic modulus, defined by Equation (4), does not depend on the amplitude and the particular shape of the imposed area perturbations as a function of time. Thus, it can be considered as a constitutive property of the interfacial layer [26,27]. Note that the interfacial layer is not an autonomous phase, and that, therefore, the interfacial dilational viscoelastic modulus can depend on the properties of the two contiguous bulk phases [28]. It characterizes the magnitude and the time-scale of the interface response to the external perturbations. This response depends on the time-scale of the relaxation processes within the interfacial system, such as the diffusional exchange of the molecules between the interface and the adjacent liquid bulk phases, the change of structure and morphology of the interfacial layer, the change of orientation and/or conformation of the molecules within the interfacial layer, and/or chemical reactions between the components.
The interpretation of the measured modulus and phase shift φ(ω) versus frequency dependencies can give access to information about molecular processes occurring in the interfacial system. Accordingly, a number of theoretical models have been developed for the interfacial dilational viscoelasticity modulus in various practical systems [27,29,30,31]. Particularly worth mentioning are the models for surfactant, polymer, surfactant/polymer or surfactant/protein mixed adsorption layers at the air/water surface [23,32,33,34,35,36]. In previous work [16,17], these models were generalized to the case of a mixture of two surfactants at flat oil/water interfaces and the case of one surfactant at curved oil/water interfaces (i.e., oil-in-water or water-in-oil drops). In the system considered here, both effects (the presence of two surfactants and the curved interface) occur simultaneously, and the respective combined model was presented recently in [37]. According to this model, the interfacial dilational viscoelasticity of a drop interface with a macroscopic (or mesoscopic) radius r0 can be described by Equation (6):
where , (j = 1, 2), and are the partial elasticities [23], are the partial derivatives of the adsorptions and by the surfactants’ concentrations and , Γ01 and Γ02 are the equilibrium adsorptions, , , and and are the diffusion coefficients of the surfactants in the outer phase α and inner phase β, respectively. In particular cases, i.e., when either one surfactant is present or a flat interface exists, Equation (6) is reduced to the models discussed in [16,17].
Equation (6) is derived with the assumption of a diffusion limited adsorption mechanism for the two surfactants dissolved in two adjacent liquids. This, particularly, is relevant to microgravity conditions, where surfactant diffusion to/from the interface is not complicated by convection in the bulk. The microgravity conditions also provide a constant value of the curvature radius over the interface for sufficiently large drops and for large density differences between the two liquids.
In our recent work [38], the fractional Maxwell model (FMM), mathematically based on fractional-derivative tools [39,40,41], was adopted to quantify the observed behavior of the linear interfacial dilational viscoelasticity. It has been shown that the single-element fractional Maxwell model allows the description of the modulus and phase angle of the complex viscoelasticity for a single surfactant system but is not adequate for the case of binary surfactant mixtures. The generalization of this model for systems containing two surfactants is underway.
4. Results and Discussion
4.1. Temperature Dependence of Interfacial Tension
The interfacial tensions measured at three temperatures, T = 15 °C, 20 °C and 30 °C, and different surfactant concentrations are shown in Figure 1 and Figure 2. The values presented in these figures are the mean-level values of interfacial tension oscillations measured at each particular frequency. As those, under ideal experimental conditions, they should not depend on frequency as soon as the surfactants’ concentrations and the temperatures are fixed. However, because of random disturbances inherent in the intermittent piezo push–pull action (or other disturbances), they slightly vary with the frequency. Nevertheless, in most cases the measured interfacial tensions remain almost constant (within about ±0.5 mN/m).
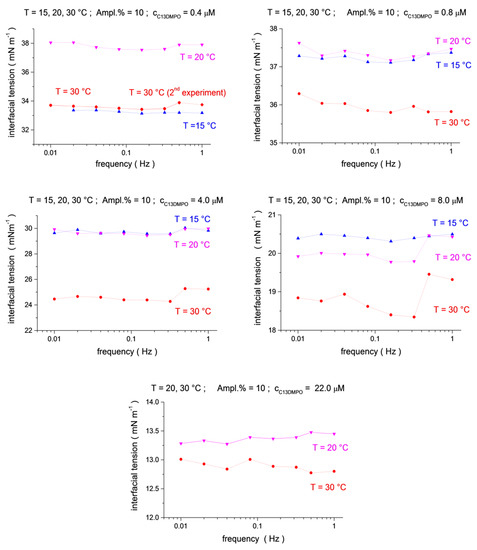
Figure 1.
Temperature dependence (blue up triangles T = 15 °C, magenta down triangles T = 20 °C, red circles T = 30 °C) for the mean-level values of interfacial tension oscillations as a function of frequency (f = 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.5 and 1.0 Hz) at C13DMPO concentrations of c1 = 4.0 × 10−7, 8.0 × 10−7, 4.0 × 10−6, 8.0 × 10−6 and 2.2 × 10−5 mol/dm3, and at a fixed TTAB concentration c2 = 4.5 × 10−5 mol/dm3.
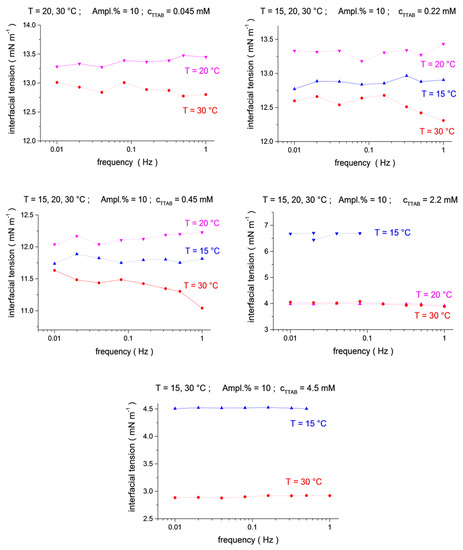
Figure 2.
Temperature dependence (blue up triangles T = 15 °C, magenta down triangles T = 20 °C, red circles T = 30 °C) for the mean-level values of interfacial tension oscillations as a function of frequency (f = 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.5 and 1.0 Hz) at TTAB concentrations of c2 = 4.5 × 10−5, 2.2 × 10−4, 4.5 × 10−4, 2.2 × 10−3 and 4.5 × 10−3 mol/dm3, at a fixed C13DMPO concentration of c1 = 2.2 × 10−5 mol/dm3.
The results presented in Figure 1 and Figure 2 are obtained for drop oscillations with a relative drop area amplitude of about 10%. The results for the amplitudes of 5% and 20% are very similar (more results can be found in the Supplementary Materials, Figures S1 and S2). This indicates an acceptable linearity condition of the interfacial tension responses. Perfect harmonic oscillations of the drop area and an interfacial tension in a wide range of amplitudes of the relative area variations (up to 20%) are advantages of the microgravity environment.
The interfacial tensions generally decrease with increasing surfactant concentrations, except for the two smallest concentrations of C13DMPO in Figure 1. This can be the consequence of incomplete mixing of the solution in the matrix cell after surfactant injections, or of small nitrogen bubbles trapped in the main valve, which might be present at the initial stage of the experiment [16].
The analysis of the temperature dependences shows that the interfacial tensions for the largest temperature, 30 °C, are systematically below those for 15 °C and 20 °C (Figure 1 and Figure 2, see also 3D presentation in the Supplementary Materials, Figures S3–S5), in agreement with the usual behavior, i.e., the interfacial tension decreases with an increasing temperature. However, the interfacial tensions for 15 °C and 20 °C do not always show this regularity. In particular, the interfacial tensions for 15 °C are below those for 20 °C for a C13DMPO concentration of 0.4 μm in Figure 1 and for TTAB concentrations of 0.22 mM and 0.45 mM in Figure 2. In the last two cases, the difference between the results for 15 °C and 20 °C is rather small, of about 0.5 mN/m or less. Such a difference is of the same magnitude as the apparent variation of the interfacial tensions with the frequency for fixed surfactant concentrations and temperatures (as discussed above) or with the oscillation amplitude (see the Supporting Information). Thus, the inverse temperature dependences in these two cases can be a consequence of some disturbances of the measurements. For the C13DMPO concentration of 0.4 μm in Figure 1, the difference is larger; however, the results can be affected in this case, probably by incomplete mixing or the effect of small nitrogen bubbles, as discussed above. Therefore, this case cannot be considered as experimental evidence of the inverse temperature dependences either. Unfortunately, the conditions of space experiments do not give the possibility for repeat measurements. Separate accurate experiments should be performed to check the obtained results.
It should be noted that, in the literature, an interfacial tension increase with the temperature is sometimes reported for liquid/liquid systems containing species (surfactants, nano-particles, impurities) capable of adsorbing at the interface [10,42,43,44,45,46,47,48]. A non-monotonic variation of the equilibrium surface tension at the air/liquid interface with an increasing temperature was also observed for aqueous solutions of fatty alcohols [49,50,51]. This effect was later confirmed by specially designed experiments under microgravity conditions [52,53,54]. A particular consequence of such a non-monotonic variation of the surface tension with the temperature is the specific behavior of “self-rewetting fluids” [55,56,57,58].
A thermodynamic analysis shows that in multicomponent systems the derivative of interfacial tension with respect to the temperature may be of any sign [59]. However, the molecular mechanisms leading to the increase of interfacial tension with temperature can be different for each particular case and are not always obvious. This can be, in particular, surface or bulk rearrangements [46,49], surfactant aggregation in either of the contacting liquids [10,44], a temperature effect on the surfactants’ solubility (and, therefore, on their partition coefficients) [45] or the modification of molecular interactions between the components at the interface [43,47,48]. These factors can influence the form of the equation of state of the adsorption layer and the adsorption isotherms, Equations (1) and (2), or the parameters in these equations. Furthermore, variations of the partition coefficients can result in changes of surfactant bulk concentrations and adsorptions. All these mechanisms have not been sufficiently studied so far. For the case considered here, the situation appears to be more complicated because the system includes two surfactants, which can behave differently. Moreover, one of them is ionic, and therefore charge effects can also come into play.
4.2. Temperature Dependence of Viscoelastic Modulus
The viscoelastic modulus versus frequency dependencies for three temperatures are shown in Figure 3 and Figure 4 (see also 3D presentation in the Supplementary Materials, Figures S3–S5). One can see that the effect of the temperature depends on the surfactants’ concentration. For small concentrations, the modulus shows a clear tendency of decreasing with an increasing temperature (for the two smallest C13DMPO concentrations of 4.0 × 10−7 and 8.0 × 10−7 mol/dm3, and for the smallest TTAB concentration of 4.5 × 10−5 mol/dm3 in Figure 3). However, at higher C13DMPO concentrations (Figure 3) and higher TTAB concentrations (Figure 4), the tendency changes to the opposite—the modulus increases with temperature. The exception to this is the highest TTAB concentration of 4.5 × 10−3 mol/dm3 in Figure 4, where the modulus for 15 °C is again larger than for 30 °C. However, the concentration of 4.5 × 10−3 mol/dm3 is above the CMC for aqueous TTAB solutions (about 3.5 × 10−3 mol/dm3 [60]), so that the mechanisms of the interfacial layer relaxation can be different in this case compared to the lower concentrations. It should also be noted that the magnitude of the modulus is very small in this case (less than 2 mN/m).
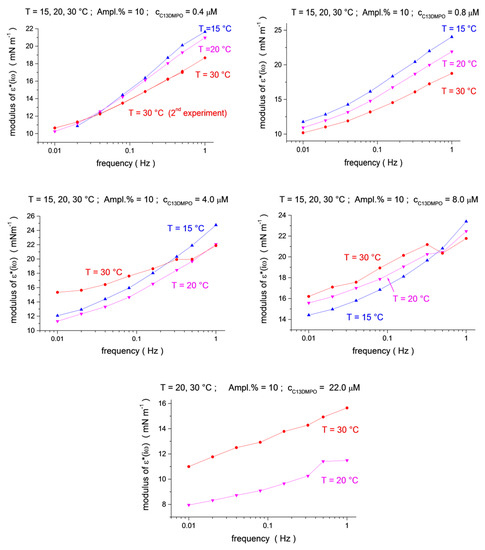
Figure 3.
Temperature dependence (blue up triangles T = 15 °C, magenta down triangles T = 20 °C, red circles T = 30 °C) for the ε*(iω) modulus as a function of frequency (f = 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.5 and 1.0 Hz) at C13DMPO concentrations of c1 = 4.0 × 10−7, 8.0 × 10−7, 4.0 × 10−6, 8.0 × 10−6 and 2.2 × 10−5 mol/dm3, at a fixed TTAB concentration of c2 = 4.5 × 10−5 mol/dm3.
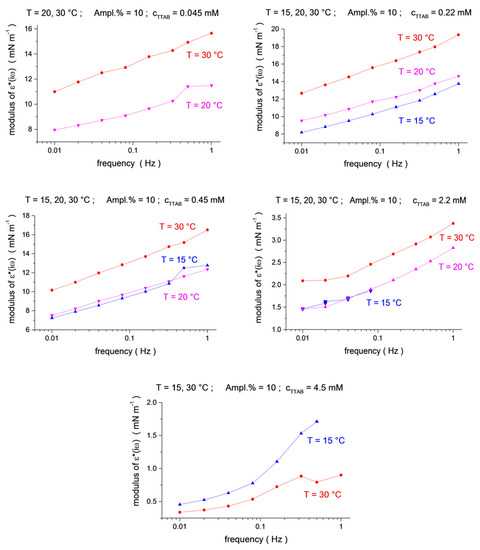
Figure 4.
Temperature dependence (blue up triangles T = 15 °C, magenta down triangles T = 20 °C, red circles T = 30 °C) for the ε*(iω) modulus as a function of frequency (f = 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.5 and 1.0 Hz) at TTAB concentrations of c2 = 4.5 × 10−5, 2.2 × 10−4, 4.5 × 10−4, 2.2 × 10−3 and 4.5 × 10−3 mol/dm3, at a fixed C13DMPO concentration of c1 = 2.2 × 10−5 mol/dm3.
Thus, similar to the interfacial tension, the viscoelastic modulus does not exhibit a clear general trend with respect to temperature changes. The variation of the viscoelastic modulus with the temperature can be different depending on the surfactant concentrations and, sometimes, frequencies. Moreover, the viscoelastic modulus behaves differently compared to the interfacial tension, although it definitely depends on it.
Regarding Equation (6), we can see that it includes a number of parameters, which can be divided into two groups. The first group are the parameters that depend only on the equilibrium properties of the adsorption layer and solutions. These are the two partial elasticities, E01 and E02, the four partial derivatives of the adsorptions with respect to the concentrations, , the two partition coefficients K1 and K2, and the two equilibrium adsorptions Γ01 and Γ02. The partial elasticities and the derivatives of the adsorptions with respect to the concentrations can be obtained from the equation of state of the adsorption layer and the adsorption isotherms, such as Equations (1) and (2) or other similar equations. It is clear that, for fixed surfactant concentrations, all these parameters should depend on the temperature, as the respective equations do. However, it is difficult to predict the exact form of this dependence. The partition coefficients and equilibrium adsorptions also vary with the temperature. The second group of parameters are the kinetic coefficients, such as the diffusion coefficients of the surfactants in the two liquid phases, and , or other kinetic coefficients (if the relaxation of the adsorption layer is not purely diffusion controlled). These kinetic coefficients also strongly depend on the temperature itself and on the liquid’s viscosity (the diffusion coefficients, according to the Stokes–Einstein equation). They can also be influenced by the height of the activation barriers (according to the Arrhenius equation), which is affected by the temperature.
Generally, the effect of the diffusion coefficients is that the dependences of the viscoelastic modulus versus frequency should be shifted along the frequency axis. However, in the present case the effect of the diffusion coefficients overlaps with the effect of the partition coefficients and the parameters aji, which can also lead to complicated shape deformations of these dependences.
This consideration shows that the analysis of temperature dependencies of the viscoelastic modulus is not trivial, as there are so many parameters that can influence the results in a way that is not always predictable. It is clear, however, that the starting point should be the analysis of the temperature dependencies of the equilibrium interfacial tensions for the individual and mixed surfactants solutions. Then, the analysis of the dynamic properties of the interfacial layers will also be much simpler.
5. Conclusions
In this study, the interfacial characteristics (interfacial tension and dilational viscoelastic modulus) of the n-hexane/water interface were measured for mixed solutions of the non-ionic surfactant C13DMPO and cationic surfactant TTAB. The aim was to determine the temperature effect on the interfacial properties in multi-component liquid systems. This study was part of a wider study performed aboard the International Space Station (ISS) [16,22]. The measurements were done with a special designed instrument. It allows the generation of oscillations of a pure n-hexane drop in aqueous matrix solutions. The interfacial tension relaxation served as a response to the drop area oscillations. The microgravity environment allowed for perfect harmonic oscillations of all the system characteristics with sufficiently high amplitudes (up to 20% of the relative area variations), avoiding natural convection in the solution and drop deformations due to gravity.
The experimental data show that the interfacial tensions at all the concentrations appear in a substantially equilibrium steady (when the mean-level values of the interfacial tension do not change during the oscillations) or quasi-steady (when the mean-level values only change very slowly due to a possible slow redistribution of the surfactants) state. Occasional disturbances are sometimes observed (produced, most probably, by other equipment working in the neighbourhood on the space station). This means that the transient surfactant transfer to or through the interface is, due to its possible slow redistribution in the system, negligibly small compared to the surfactant transfer induced by the drop oscillations. The repetition of the oscillation sequences at different amplitudes can serve as a confirmation of reproducibility of the experimental results and of an acceptable linearity condition of the interfacial tension responses. The measurement method is the well-established capillary pressure method, validated by inflight optical and pressure calibration.
In the temperature interval between 20 °C and 30 °C, the interfacial tension exhibits the usually observed behavior, i.e., it decreases with an increasing temperature. Between 15 °C and 20 °C, at some specific concentrations, the temperature effect on the interfacial tension causes an inverted gradient behavior, instead of the decreasing interfacial tension with an increasing temperature that is typical for pure-liquids. However, these particular results are not sufficient to conclude whether the inverted gradient behavior is really observed in the system that is considered here, as this effect is not sufficiently large and is observed only for few concentrations. Thus, additional accurate experiments should confirm or disprove these results.
Unfortunately, the temperature dependencies of the isotherm parameters and partition coefficients of surfactants in liquid–liquid systems are not yet systematically studied, and even respective data for individual TTAB and C13DMPO in the water/hexane system are not available for comparison. Therefore, the modelling of the temperature dependencies is not possible. However, in this case, experimental data on the temperature dependencies becomes especially valuable, because they can be useful for many practical applications and can be the starting point for further studies in this area.
The temperature effect on the viscoelastic modulus manifests distinguished gradient effects as a function of concentration and frequency, different from the corresponding interfacial tension. The viscoelastic modulus decreases with an increasing temperature for small surfactant concentrations and increases for higher concentrations. The origin of such a behavior of the modulus is not clear. The viscoelastic modulus depends on too many temperature-dependent parameters related to the equilibrium and kinetic properties of the two considered surfactants, capable of dissolving in the two contacting liquids and of adsorbing at the interface. This fact complicates the analysis of temperature effects in the system. The observed phenomenology suggests that one perform new experimental studies on the temperature dependence of the interactions between the components of the mixed adsorption layers and the adjacent liquid phases.
Supplementary Materials
The following are available online at https://www.mdpi.com/2504-5377/4/3/27/s1, Figure S1: Temperature (blue T = 15 °C, magenta T = 20 °C, red T = 30 °C) and amplitude (squares—Ampl. 5% up triangles—Ampl. 10%, down triangles—Ampl. 20%) dependences for the mean-level values of interfacial tension oscillations as a function of frequency (f = 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.5 and 1.0 Hz) at C13DMPO concentrations of c1 = 4.0 × 10−7, 8.0 × 10−7, 4.0 × 10−6, 8.0 × 10−6 and 2.2 × 10−5 mol/dm3, and at a fixed TTAB concentration c2 = 4.5 × 10−5 mol/dm3. Figure S2: Temperature (blue T = 15 °C, magenta T = 20 °C, red T = 30 °C) and amplitude (squares—Ampl. 5%, up triangles—Ampl. 10%, down triangles—Ampl. 20%) dependences for the mean-level values of interfacial tension oscillations as a function of frequency (f = 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.5 and 1.0 Hz) at TTAB concentrations of c2 = 4.5 × 10−5, 2.2 × 10−4, 4.5 × 10−4, 2.2 × 10−3 and 4.5 × 10−3 mol/dm3, at a fixed C13DMPO concentration of c1 = 2.2 × 10−5 mol/dm3. Figure S3: Temperature dependence (cyan surface T = 20 °C, red surface T = 30 °C) for the mean-level values of interfacial tension oscillations upper panel) and for the ε*(iω) modulus (lower panel) as a function of frequency (f = 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.5 and 1.0 Hz) and as a function of concentration, in the concentration sequence for C13DMPO (at concentrations of 4.0 × 10−7, 8.0 × 10−7, 4.0 × 10−6, 8.0 × 10−6 and 2.2 × 10−5 mol/dm3 at a fixed TTAB concentration of 4.5 × 10−5 mol/dm3), and of TTAB (at concentrations of 4.5 × 10−5, 2.2 × 10−4, 4.5 × 10−4 and 2.2 × 10−3 mol/dm3 at a fixed C13DMPO concentration of 2.2 × 10−5 mol/dm3). Graph rotation: Horizontal view = 45°; Vertical view = 15°. Figure S4: Same as Figure S3. Graph rotation: Horizontal view = 120°; Vertical view = 15°. Figure S5: Same as Figure S3. Graph rotation: Horizontal view = 240°; Vertical view = 15°.
Author Contributions
V.I.K., G.L., A.G.B., M.F., J.K., L.L., R.M., O.Y.M., B.A.N., F.R., E.S. (Eva Santini) and E.S. (Emanuel Schneck) planned the work and designed the experiments; M.F., J.K., G.L., L.L., and R.M. conducted the microgravity experiments; V.I.K. and G.L. performed the elaboration of the telemetered data; V.I.K., G.L., and R.M. interpreted and discussed the data; V.I.K., G.L., and R.M. wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
European Space Agency MAP Projects “Soft Matter Dynamics”, “Emulsion Dynamics and Droplet Interfaces - EDDI”, “Fundamental and Applied Studies in Emulsion Stability - FASES”. European Space Agency Project “Particle Stabilized Emulsions - PASTA’’ (AO-2009-0813) (and the corresponding grants by the Italian Space Agency ASI n. 2013-028-R.O).
Acknowledgments
We are grateful to Piero Pandolfini for his contribution in the elaboration of the telemetered data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Iglauer, S.; Favretto, S.; Spinosa, G.; Schena, G.; Blunt, M.J. X-ray tomography measurements of power-law cluster size distributions in sandstones. Phys. Rev. E 2010, 82, 056315. [Google Scholar] [CrossRef] [PubMed]
- Fredrick, E.; Walstra, P.; Dewettinck, K. Factors governing partial coalescence in oil-in-water emulsions. Adv. Colloid Interface Sci. 2010, 153, 30–42. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, L.M.; Kobayakawa, T.G.; Zanette, D.; Chaimovich, H.; Cuccovia, I.M. Effects of micelles and vesicles on the oximolysis of p-nitrophenyl diphenyl phosphate: A model system for surfactant-based skin-defensive formulations against organophosphates. J. Pharm. Sci. 2009, 98, 1040–1052. [Google Scholar] [CrossRef] [PubMed]
- Al-Sahhaf, T.; Elkamel, A.; Suttar Ahmed, A.; Knan, A.R. The influence of temperature, pressure, salinity, and surfactant concentration on the interfacial tension of the n-octane-water system. Chem. Eng. Comm. 2005, 192, 667–684. [Google Scholar] [CrossRef]
- He, Y.; Yazhgur, P.; Salonen, A.; Langevin, D. Adsorption–desorption kinetics of surfactants at liquid surfaces. Adv. Colloid Interf. Sci. 2015, 222, 377–384. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Good, R.J. A theory for the estimation of surface and interfacial energies. Derivation and application to interfacial tension. J. Phys. Chem. 1957, 61, 904–909. [Google Scholar] [CrossRef]
- Chen, L.J.; Lin, S.Y.; Huang, C.C.; Chen, E.M. Temperature dependence of critical micelle concentration of polyoxyethylenated non-ionic surfactants. Colloids Surf. A 1998, 135, 175–181. [Google Scholar] [CrossRef]
- Das, C.; Das, B. Thermodynamic and Interfacial Adsorption Studies on the Micellar Solutions of Alkyltrimethylammonium Bromides in Ethylene Glycol (1) + Water (2) Mixed Solvent Media. J. Chem. Eng. Data 2009, 54, 559–565. [Google Scholar] [CrossRef]
- Geng, F.; Liu, J.; Zheng, L.; Yu, L.; Li, Z.; Li, G.; Tung, C. Micelle Formation of Long-Chain Imidazolium Ionic Liquids in Aqueous Solution Measured by Isothermal Titration Microcalorimetry. J. Chem. Eng. Data 2010, 55, 147–151. [Google Scholar] [CrossRef]
- Aveyard, R.; Binks, B.P.; Chen, J.; Esquena, J.; Fletcher, P.D.I.; Buscall, R.; Davies, S. Surface and Colloid Chemistry of Systems Containing Pure Sugar Surfactant. Langmuir 1998, 14, 4699–4709. [Google Scholar] [CrossRef]
- Aoudia, M.; Al-Shibli, M.N.; Al-Kasimi, L.H.; Al-Maamari, R.; Al-Bemani, A. Novel surfactants for ultralow interfacial tension in a wide range of surfactant concentration and temperature. J. Surfactant Deterg. 2006, 9, 287–293. [Google Scholar] [CrossRef]
- El-Batanoney, M.; Abdel-Moghny, T.; Ramzi, M. The effect of mixed surfactants on enhancing oil recovery. J. Surfactant Deterg. 1999, 2, 201–205. [Google Scholar] [CrossRef]
- Fu, D.; Gao, X.R.; Huang, B.; Wang, J.; Sun, Y.; Zhang, W.J.; Kan, K.; Zhang, X.C.; Xie, Y.; Sui, X. Micellization, surface activities and thermodynamics study of pyridinium-based ionic liquid surfactants in aqueous solution. RSC Adv. 2019, 9, 28799–28807. [Google Scholar] [CrossRef]
- Szymczyk, K.; Szaniawska, M.; Krawczyk, J. Temperature Effect on the Adsorption and Volumetric Properties of Aqueous Solutions of Kolliphor®ELP. Molecules 2020, 25, 743. [Google Scholar] [CrossRef] [PubMed]
- Ivanova, A.A.; Cheremisin, A.N.; Barifcani, A.; Iglauer, S.; Phan, C. Molecular insights in the temperature effect on adsorption of cationic surfactants at liquid/liquid interfaces. J. Mol. Liq. 2020, 299, 112104. [Google Scholar] [CrossRef]
- Loglio, G.; Kovalchuk, V.I.; Bykov, A.G.; Ferrari, M.; Krägel, J.; Liggieri, L.; Miller, R.; Noskov, B.A.; Pandolfini, P.; Ravera, F.; et al. Dynamic properties of mixed cationic/nonionic adsorbed layers at the n-hexane/water interface: Capillary pressure experiments under low gravity conditions. Colloids Interfaces 2018, 2, 53. [Google Scholar] [CrossRef]
- Kovalchuk, V.I.; Aksenenko, E.V.; Makievski, A.V.; Fainerman, V.B.; Miller, R. Dilational interfacial rheology of tridecyl dimethyl phosphine oxide adsorption layers at the water/hexane interface. J. Colloid Interf. Sci. 2019, 539, 30–37. [Google Scholar] [CrossRef]
- Passerone, A. Twenty Years of Surface Tension Measurements in Space. Microgravity Sci. Technol. 2011, 23, 101–111. [Google Scholar] [CrossRef]
- Ferrari, M.; Liggieri, L.; Ravera, F.; Amodio, C.; Miller, R. Adsorption kinetics of alkyl phosphine oxides at the water/hexane interface 1. Pendant drop experiments. J. Colloid Interface Sci. 1997, 186, 40–45. [Google Scholar] [CrossRef]
- Liggieri, L.; Ravera, F.; Ferrari, M.; Passerone, A.; Miller, R. Adsorption Kinetics of alkyl phosphine oxides at water/hexane interface 2. Theory of the adsorption with transport across the interface in finite systems. J. Colloid Interface Sci. 1997, 186, 46–52. [Google Scholar] [CrossRef]
- Mucic, N.; Kovalchuk, N.M.; Pradines, V.; Javadi, A.; Aksenenko, E.V.; Krägel, J.; Miller, R. Dynamic properties of CnTAB adsorption layers at the water/oil interface. Colloids Surf. A 2014, 441, 825–830. [Google Scholar] [CrossRef]
- Pandolfini, P.; Loglio, G.; Ravera, F.; Liggieri, L.; Kovalchuk, V.I.; Javadi, A.; Karbaschi, M.; Krägel, J.; Miller, R.; Noskov, B.A.; et al. Dynamic properties of Span-80 adsorbed layers at paraffin–oil/water interface: Capillary pressure experiments under low gravity conditions. Colloids Surf. A Phys. Eng. Asp. 2017, 532, 228–243. [Google Scholar] [CrossRef]
- Joos, P. Dynamic Surface Phenomena; VSP: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Fainerman, V.B.; Miller, R.; Aksenenko, E.V.; Makievski, A.V. Equilibrium Adsorption Properties of Single and Mixed Surfactant Solutions. In Surfactants Chemistry, Interfacial Properties, Applications, Studies in Interface Science; Fainerman, V.B., Möbius, D., Miller, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 13, chapter 3. [Google Scholar]
- Fainerman, V.B.; Sharipova, A.A.; Aidarova, S.B.; Kovalchuk, V.I.; Aksenenko, E.V.; Makievski, A.V.; Miller, R. Direct determination of the distribution coefficient of tridecyl dimethyl phosphine oxide between water and hexane. Colloids Interfaces 2018, 2, 28. [Google Scholar] [CrossRef]
- Loglio, G.; Tesei, U.; Cini, R. Spectral Data of Surface Viscoelastic Modulus Acquired via Digital Fourier Transformation. J. Colloid Interface Sci. 1979, 71, 316–320. [Google Scholar] [CrossRef]
- Miller, R.; Liggieri, L. Interfacial Rheology, 1st ed.; CRC Press: Boca Raton, FL, USA, 2009; Volume 1, pp. 1–37. [Google Scholar]
- Defay, R.; Prigogine, I.; Sanfeld, A. Surface thermodynamics. J. Colloid Interface Sci. 1977, 58, 498–510. [Google Scholar] [CrossRef]
- Noskov, B.A.; Loglio, G. Dynamic surface elasticity of surfactant solutions. Colloids Surf. A 1998, 143, 167–183. [Google Scholar] [CrossRef]
- Ivanov, I.B.; Danov, K.D.; Ananthapadmanabhan, K.P.; Lips, A. Interfacial rheology of adsorbed layers with surface reaction: On the origin of the dilatational surface viscosity. Adv. Colloid Interface Sci. 2005, 114, 61–92. [Google Scholar] [CrossRef]
- Ravera, F.; Ferrari, M.; Liggieri, L. Modelling of dilational visco-elasticity of adsorbed layers with multiple kinetic processes. Colloids Surf. A 2006, 282, 210–216. [Google Scholar] [CrossRef]
- Jiang, Q.; Valentini, J.E.; Chiew, Y.C. Theoretical models for dynamic dilational surface properties of binary surfactant mixtures. J. Colloid Interface Sci. 1995, 174, 268–271. [Google Scholar] [CrossRef]
- Noskov, B.A. Dynamic surface elasticity of polymer solutions. Colloid Polym. Sci. 1995, 273, 263–270. [Google Scholar] [CrossRef]
- Aksenenko, E.V.; Kovalchuk, V.I.; Fainerman, V.B.; Miller, R. Surface dilational rheology of mixed adsorption layers at liquid interfaces. Adv. Colloid Interface Sci. 2006, 122, 57–66. [Google Scholar] [CrossRef] [PubMed]
- Aksenenko, E.V.; Kovalchuk, V.I.; Fainerman, V.B.; Miller, R. Surface dilational rheology of mixed surfactants layers at liquid interface. J. Phys. Chem. C 2007, 111, 14713–14719. [Google Scholar] [CrossRef]
- Liu, F.; Darjani, S.; Akhmetkhanova, N.; Maldarelli, C.; Banerjee, S.; Pauchard, V. Mixture Effect on the Dilatation Rheology of Asphaltenes-Laden Interfaces. Langmuir 2017, 33, 1927–1942. [Google Scholar] [CrossRef] [PubMed]
- Bykov, A.G.; Ferrari, M.; Kovalchuk, V.I.; Krägel, J.; Liggieri, L.; Loglio, G.; Makievski, A.V.; Miller, R.; Milyaeva, O.Y.; Noskov, B.A.; et al. The surface dilational viscoelasticity of a curved oil-water interface with two surfactants soluble in both the oil and water phase. In Proceedings of the 8th Bubble and Drop Conference (B&D 2019), Sofia, Bulgaria, 24–28 June 2019. [Google Scholar]
- Loglio, G.; Kovalchuk, V.I.; Bykov, A.G.; Ferrari, M.; Krägel, J.; Liggieri, L.; Miller, R.; Noskov, B.A.; Pandolfini, P.; Ravera, F.; et al. Interfacial Dilational Viscoelasticity of Adsorption Layers at the Hydrocarbon/Water Interface: The Fractional Maxwell Model. Colloids Interfaces 2019, 3, 66. [Google Scholar] [CrossRef]
- Costa, M.F.P.; Ribeiro, C. Generalized fractional Maxwell model: Parameter estimation of a viscoelastic material. AIP Conf. Proc. 2012, 1479, 790–793. [Google Scholar] [CrossRef]
- Stankiewicz, A. Fractional Maxwell model of viscoelastic biological materials. BIO Web Conf. 2018, 10, 02032. [Google Scholar] [CrossRef]
- Povstenko, Y. Essentials of fractional calculus. In Fractional Thermoelasticity; Springer International Publishing: Basel, Switzerland, 2015; Volume 219. [Google Scholar] [CrossRef]
- Lutton, E.S.; Stauffer, C.E.; Martin, J.B.; Fehl, A.J. Solid and liquid monomolecular film at oil/H2O interfaces. J. Colloid Interface Sci. 1969, 30, 283–290. [Google Scholar] [CrossRef]
- Ataev, G.M. Anomalous Temperature Dependence of Interfacial Tension in Water–Hydrocarbon Mixtures. Russ. J. Phys. Chem. 2007, 81, 2094–2095. [Google Scholar] [CrossRef]
- Ye, Z.; Zhang, F.; Han, L.; Luo, P.; Yang, J.; Chen, H. The effect of temperature on the interfacial tension between crude oil and gemini surfactant solution. Colloids Surf. A 2008, 322, 138–141. [Google Scholar] [CrossRef]
- Miquilena, A.; Coll, V.; Borges, A.; Melendez, J.; Zeppieri, S. Influence of Drop Growth Rate and Size on the Interfacial Tension of Triton X-100 Solutions as a Function of Pressure and Temperature. Int. J. Thermophys. 2010, 31, 2416–2424. [Google Scholar] [CrossRef]
- Ferdous, S.; Ioannidis, M.A.; Henneke, D.E. Effects of temperature, pH, and ionic strength on the adsorption of nanoparticles at liquid–liquid interfaces. J. Nanopart. Res. 2012, 14, 850. [Google Scholar] [CrossRef]
- Hyde, A.; Horiguchi, M.; Minamishima, N.; Asakuma, Y.; Phan, C. Effects of microwave irradiation on the decane-water interface in the presence of Triton X-100. Colloids Surf. A 2017, 524, 178–184. [Google Scholar] [CrossRef]
- Shibata, Y.; Hyde, A.; Asakuma, Y.; Phan, C. Thermal response of a non-ionic surfactant layer at the water/oil interface during microwave heating. Colloids Surf. A 2018, 556, 127–133. [Google Scholar] [CrossRef]
- Vochten, R.; Petre, G. Study of the heat of reversible adsorption at the air-solution interface. II. Experimental determination of the heat of reversible adsorption of some alcohols. J. Colloid Interface Sci. 1973, 42, 320–327. [Google Scholar] [CrossRef]
- Petre, G.; Azouni, M.A. Experimental evidence for the minimum of surface tension with temperature at aqueous alcohol solution air interfaces. J. Colloid Interface Sci. 1984, 98, 261–263. [Google Scholar] [CrossRef]
- Slavtchev, S.G.; Miladinova, S.P. Thermocapillary flow in a liquid layer at minimum in surface tension. Acta Mech. 1998, 127, 209–224. [Google Scholar] [CrossRef]
- Legros, J.C.; Limbourg-Fontaine, M.C.; Petre, G. Influence of a surface tension minimum as a function of temperature on the Marangoni convection. Acta Astronaut. 1984, 11, 143–147. [Google Scholar] [CrossRef]
- Limbourg-Fontaine, M.C.; Petre, G.; Legros, J.C. Thermocapillary movements under at a minimum of surface tension. Naturwissenschaften 1986, 73, 360–362. [Google Scholar] [CrossRef]
- Savino, R.; Cecere, A.; Vaerenbergh, S.V.; Abe, Y.; Pizzirusso, G.; Tzevelecos, W.; Mojahed, M.; Galand, Q. Some experimental progresses in the study of the self-rewetting fluids for the SELENE experiment to be carried in the Thermal Platform 1 hardware. Acta Astronaut. 2013, 89, 179–188. [Google Scholar] [CrossRef]
- Savino, R.; Cecere, A.; Paola, R.D. Surface tension driven flow in wickless heat pipes with self-rewetting fluids. Int. J. Heat Fluid Flow 2009, 30, 380–388. [Google Scholar] [CrossRef]
- Karapetsas, G.; Sahu, K.C.; Sefiane, K.; Matar, O.K. Thermocapillary-Driven Motion of a Sessile Drop: Effect of Non-Monotonic Dependence of Surface Tension on Temperature. Langmuir 2014, 30, 4310–4321. [Google Scholar] [CrossRef]
- Tripathi, M.K.; Sahu, K.C.; Karapetsas, G.; Sefiane, K.; Matar, O.K. Non-isothermal bubble rise: Non-monotonic dependence of surface tension on temperature. J. Fluid Mech. 2015, 763, 82–108. [Google Scholar] [CrossRef]
- Balla, M.; Tripathi, M.K.; Sahu, K.C.; Karapetsas, G.; Matar, O.K. Non-isothermal bubble rise dynamics in a self-rewetting fluid: Three-dimensional effects. J. Fluid Mech. 2019, 858, 689–713. [Google Scholar] [CrossRef]
- Rusanov, A.I.; Prokhorov, V.A. Interfacial tensiometry. In Studies in Interface Science; Elsevier: Amsterdam, The Netherlands, 1996; Volume 3, Chapter 1. [Google Scholar]
- Bergeron, V. Disjoining Pressures and Film Stability of Alkyltrimethylammonium Bromide Foam Films. Langmuir 1997, 13, 3474–3482. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).