Diff-KNN: Residual Correction of Baseline Wind Predictions in Urban Settings

Abstract

Accurate prediction of urban wind flow is essential for urban planning and environmental assessment. Classical computational fluid dynamics (CFD) methods are computationally expensive, while machine learning approaches often lack explainability and generalizability. To address the limitations of both approaches, we propose Diff-KNN, a hybrid method that combines Coarse-Scale CFD simulations with a K-Nearest Neighbors (KNN) model trained on the residuals between coarse- and fine-scale CFD results. Diff-KNN reduces velocity prediction errors by up to 83.5% compared to Pure-KNN and 56.6% compared to coarse CFD alone. Tested on the AIJE urban dataset, Diff-KNN effectively corrects flow inaccuracies near buildings and within narrow street canyons, where traditional methods struggle. This study demonstrates how residual learning can bridge physics-based and data-driven modeling for accurate and interpretable fine-scale urban wind prediction.

1. Introduction

Accurate prediction of wind velocity in complex urban environments is crucial for applications spanning pollutant dispersion, pedestrian comfort, renewable-energy siting, and safety planning. Classical computational fluid dynamics (CFD) methods, while capable of high fidelity, often entail heavy meshing and long runtimes that limit coverage in space, time, or boundary-condition variability. To mitigate this, the community has advanced surrogate and reduced-order approaches that learn structure from data or encode physics efficiently.

Urban-flow surrogates span complementary families: NIROMs for fast reconstruction [1,2,3], hybrid meso→micro regressors [4], GANs for real-time image-to-field translation [5,6], operator-learning (e.g., FNO) that learns PDE solution maps [7], and physics-informed GNNs on unstructured meshes [8]. A pure k-Nearest Neighbors approach has been used in [9]. These approaches provide order-of-magnitude speed-ups with strong in-domain accuracy but face limits in generalization, interpretability, and training overhead. Table 1 summarizes typical speed-up, accuracy, pros, and limitations across these families and adds a residual-correction entry for urban dispersion [10]. In that work, coupling a fast physics proxy with learned residual corrections enabled millisecond inference while improving accuracy and transfer across cities. We adopt this residual paradigm for urban wind: retaining a physics-consistent coarse CFD baseline and learning local corrections on fine–coarse residuals with KNN to create a lightweight, interpretable, and deployable surrogate (Diff-KNN) that targets under-resolved canyon recirculation and shear layers.

Table 1. Summary of urban-flow surrogate families with typical speed-ups, accuracy, pros, and limitations; includes a residual-correction line for dispersion and our Diff-KNN.

Approach	Ref.	Speed-Up (Typ.)	Accuracy (Typ.)	Pros	Limitations
NIROM (autoencoders + regressors)	[1,2]	$226\times$–$800\times$	$R^2(u,v)\approx 0.9$, $R^2\left(w\right)$ lower	Fast inference; good horizontal fidelity	Data curation; GPU training; vertical velocity weaker
Hybrid CFD–NN (MLP/DNN downscaling)	[4]	High	$R^2\approx 0.74$–$0.94$ (in/out-of-domain)	Leverages morphology; good accuracy	Generalization limits; data-hungry
GAN surrogates (pix2pix/cycleGAN)	[5]	$120\times$–$240\times$	$R^2$ up to $0.86$–$0.93$	Real-time; multi-target feasible	Task-specific datasets; domain adaptation
Operator learning (FNO)	[7]	∼25×	Low one-step error; increases over long rollout	Learns solution operators; accurate short horizon	Compute-intensive training; rollout drift
Physics-informed GNNs (unstructured)	[8]	$10\times$–$100\times$	Good vs. RANS baselines	Physics constraints; mesh-aware	Complex training/engineering
kNN	[9]	High	Reasonable vs. RANS baselines	Consideration of urban morphology; low amount of training data required	Covers mainly local effects
Hybrid residual correction (dispersion)	[10]	Milliseconds/query	>2× MSE improvement vs. Gaussian	Iterative residuals; very fast	Needs base physics + corrections
Diff-KNN (this work)	—	Adds $O\left(0.19\mathrm{ms}/\mathrm{pt}\right)$ over precomputed coarse field	RMSE decrease vs. coarse CFD and Pure-KNN	Physics-guided residuals; no GPU; robust vs. Pure-KNN	Dependent on coarse baseline; scope limited to AIJE in this study

Complementing these case studies, a recent field review synthesizes trends and open challenges for AI-accelerated CFD in the built environment [11]. It reports “computational time gains of several orders of magnitude” for direct surrogates and ROMs in specific scenarios, but emphasizes persistent gaps in generalizability, interpretability, scalability (global vs. local modeling), and the pre-deployment cost of data generation and training. The review explicitly advocates (i) stronger physics integration and hybridization with numerical solvers, (ii) local modeling strategies to enable scalability to large 3D domains, (iii) transfer learning to reduce data needs, and (iv) standardized benchmarks to ensure fair comparisons. We adopt these recommendations by designing a lightweight hybrid residual surrogate, operating locally in feature space, and evaluating robustness across directional and morphological variations.

Against this backdrop, there is a need for lightweight, data-efficient, and easily deployable surrogates that (i) leverage available physics, (ii) improve accuracy over fast coarse solvers, and (iii) remain robust when test geometries or boundary conditions deviate from the training set. Coarse physics-informed baselines like coarse CFD provide fast, stable predictions by down-sampling meshes or truncating solver iterations, but they can miss fine-scale urban variability. Purely data-driven regressors (e.g., KNN) are rapid and mesh-free, yet degrade sharply outside the convex hull of the training data.

To address these limitations, we introduce Diff-KNN, a hybrid residual framework that learns to correct the systematic error of coarse CFD relative to the fine CFD ground truth. Rather than predicting wind velocity from scratch, Diff-KNN first computes the fast coarse CFD baseline and then trains a local KNN regressor on residuals (fine–coarse). This preserves the Navier–Stokes-consistent structure from coarse CFD while using inexpensive, non-parametric learning to capture local fine-scale discrepancies. In line with [11], our approach is hybrid, physics-guided, and local (scalable), and, paralleling [10], it focuses learning capacity on corrections rather than the full solution, enabling practical speed–accuracy trade-offs.

Our contributions are as follows:

• A head-to-head comparison of three surrogates—coarse CFD, Pure-KNN, and Diff-KNN—against a fine CFD ground truth, situated within the recent NIROM, GAN, operator-learning, and physics-informed GNN literature [1,2,4,5,7,8], and aligned with review guidance on hybridization and local modeling [11].
• A quantitative speed–accuracy trade-off analysis, showing that residual learning with Diff-KNN closes a substantial fraction of the coarse CFD–fine CFD gap at negligible training cost and with favorable robustness outside the training distribution.

In summary, Diff-KNN complements recent high-capacity surrogates by offering a pragmatic, physics-guided, and low-overhead error-correction layer for coarse CFD, improving fidelity toward fine CFD without the training burden of deep networks.

2. Simulation Setup

2.1. Case AIJE Computational Volume Setup

In this paper, our focus is on a particular real-world urban site, which is the benchmark case E from the Architectural Institute of Japan [12]. The building complex is situated in Niigata city, Japan, and mainly consists of two-story, low-rise buildings on flat terrain at $z=0$ m with the exception of a single high-rise building (height, $H=$ 60 m) and two mid-rise buildings with a height of 18 m. The geometry of the district is shown in Figure 1. This geometry has been used for a series of wind tunnel experiments investigating the wind flow from varying wind directions and velocity measurements at 80 points at a height of 2 m are provided.

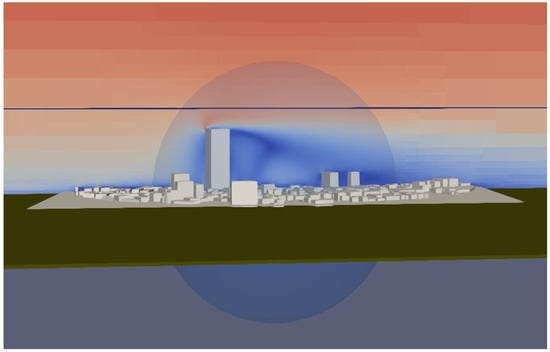
Figure 1. AIJE case: filtering steps and wind velocity visualization for training data preparation. A truncation sphere is centered at the coordinate (499.5 m, 499.5 m, 0 m) to isolate the region of interest. A truncation plane is defined at a height of $z=80$ m to limit the vertical extent of the data.

2.2. Specification Summary of the Two Grids Used in This Study

The wind simulations shown in this study are conducted using the Immersed Boundary Octree Flow solver, FCC IBOFlow (version 1.39.3.0; Fraunhofer–Chalmers Research Centre (FCC), Gothenburg, Sweden) [13]. The solver has been validated for urban wind simulations, e.g., in [14], and has previously been used for simulation-based optimization, e.g., in [15], and for training machine learning-based surrogate models in [16].

The solver, simulation setup, and results for the AIJE case used in this study have been described in detail in [17] and thus it only follows a summary.

Assuming an incompressible, isothermal flow, the Reynolds-Averaged Navier–Stokes equations are solved along with the $k-g$ shear-stress transport (SST) turbulence model [18], an immersed boundary variant of the $k-\omega$ SST turbulence model.

The geometry for the CFD model is created based on the CAD files provided by the AIJ Database (Available at https://www.aij.or.jp/jpn/publish/cfdguide/index_e.htm; accessed on 20 October 2025). A box-shaped computational domain with dimensions 1600 m × 1000 m × 360 m was used. A west wind direction was chosen for this study as it is among the predominant ones, as shown by AIJ [12]. The inlet boundary is defined as a velocity inlet with profiles for velocity and the turbulent properties taken as described by AIJ [12]. A zero-pressure Dirichlet boundary condition is assigned to the outlet, while the top and side walls are modeled with symmetry boundary conditions. The building walls and the ground are represented by a no-slip wall boundary condition with a sand-grain height of 0.72 m prescribed to the ground. A single wind direction and velocity using the experimental wind velocity profile have been used for this study.

Two different meshes, a fine-scale and a coarse-scale mesh, have been used for the following analysis. The domain is discretized using a base grid with a total of six refinement levels around the buildings, all with a ratio of 1:2. The number of refinement levels and their positioning is the same for both grids; the differentiating factor is the base grid size which is refined with a factor of 1.5. The simulations were performed on 16 CPUs making use of an A40 Nvidia GPU. Detailed information about the two grids and the corresponding simulation run time is presented in Table 2.

Table 2. Specification summary of the two grids used in this study.

Grid	Minimum Grid Size [m]	Total Number of Cells	Simulation Run Time per 1000 Iterations [h]
Coarse	0.42	$8\times {10}^6$	2.5
Fine	0.28	$21\times {10}^6$	6

3. Surrogate Models

To enhance the efficiency of wind behavior predictions compared to fine-scale CFD simulations, we evaluated three distinct surrogate models. The first model utilizes a Coarse-Scale CFD simulation, which offers a rapid approximation of the fine simulation, significantly reducing computational time. This approach was benchmarked against a straightforward K-Nearest Neighbors (KNN) model, known for its simplicity in both construction and evaluation.

The primary aim of this study, however, was to integrate physical prior knowledge with machine learning techniques. To achieve this, we developed a KNN model trained on the discrepancies between coarse and fine simulations, effectively creating an error correction model. This model, when combined with coarse simulations, facilitates more accurate and efficient predictions of wind effects, aligning with our objective to optimize predictive performance in urban wind analysis.

3.1. CFD Result Preprocessing

For the subsequent analysis of the CFD simulation results, the following data-processing steps were taken:

(1)

Spherical truncation

• Radius: 125 m;
• Center: (499.5 m, 499.5 m, 0 m);
• Purpose: Focus on the urban core and discard areas prone to be influenced by boundary effects.

(2)

Vertical range filter

• Keep: $0\le z\le 80$ m;
• Remove: cells with $z<0$ m or $z>80$ m;
• Purpose: Exclude regions largely undisturbed by buildings, reducing data volume without losing key turbulence–structure interactions.

(3)

Building-interior mask

• Action: Exclude cells whose centers lie inside the solid building mesh;
• Purpose: Retain only fluid cells around and above structures for training and validation.

Combined, these filters yield a compact yet representative computational volume that captures the flow phenomena in the city core while eliminating irrelevant or non-fluid cells, improving both accuracy and efficiency for all surrogate models.

3.2. Coarse-Scale CFD

Coarse-Scale CFD serves as our baseline physics-informed surrogate. By down-sampling the finite-volume mesh (e.g., reducing cell counts by a factor of x–y in each dimension) or limiting solver iterations, we obtain a faster evaluation whose runtime is typically 10×–50× lower than the full-resolution simulation. Although this coarse model solves the Navier–Stokes equations, it smooths out fine-scale flow features near building edges and in narrow channels, leading to systematic under- or over-predictions of local wind speeds.

3.3. Pure-KNN

Pure-KNN is a fully data-driven surrogate that learns a direct mapping from input features to fine-scale CFD outputs. We assemble a training set of tuples

$$(x_i,v_i^{\mathrm{fine}}),$$

(1)

where $x_i$ comprises geometric features (building heights, distances-to-ground, and building-distance components) and, optionally, coarse CFD velocities. At inference, Pure-KNN locates the k-Nearest Neighbors in feature space and predicts

$${\widehat{v}}^{\mathrm{pure}}={\displaystyle \frac{1}{k}}\sum _{j\in \mathcal{N}\left(i\right)}{v}_j^{\mathrm{fine}}.$$

(2)

while mesh-free and straightforward, Pure-KNN degrades sharply when test points lie outside the convex hull of the training set—common in novel urban geometries—resulting in large extrapolation errors.

3.4. Diff-KNN

Diff-KNN combines the strengths of physics-based and data-driven surrogates by learning only the residual between coarse and fine CFD outputs. It proceeds in three steps:

• Coarse Prediction: Compute the fast, down-sampled CFD solution $v_i^{\mathrm{coarse}}$.
• Residual Training: Form the training targets

  $$r_i=v_i^{\mathrm{fine}}-v_i^{\mathrm{coarse}},$$

  (3)

  and train a KNN regressor on $\left\{(x_i,r_i)\right\}$ to predict $\widehat{r}$.
• Correction and Surrogate Output: For a new point, compute

  $${\widehat{v}}^{\mathrm{diff}}=v^{\mathrm{coarse}}+\widehat{r}.$$

  (4)

By focusing on the systematic error of coarse CFD, Diff-KNN preserves the underlying physics- and mesh-based structure while using local interpolation to capture fine-scale discrepancies. This residual framework yields both lower RMSEs and better out-of-distribution robustness compared to Pure-KNN or coarse CFD alone.

4. Training Process

The training process utilized the filtered dataset described in Section 2.1. This dataset was curated to capture the complexities of urban wind flow, incorporating both geometric and fluid dynamic features as outlined in Table 3.

Table 3. Feature composition for KNN models.

Feature Type	Features Included
Base Features	ClosestBuildingHeight, DistanceToGround,
	DistanceToClosestBuilding (x, y, z components)
Velocity Components	VelocityFluid coarse (x, y, z components)

The dataset was partitioned into training and testing subsets using a standard 80–20 split to ensure comprehensive training and robust validation. A pipeline was established, employing a MinMax scaler for feature normalization followed by a K-Nearest Neighbors (KNN) regressor. The KNN model was configured with the hyperparameters specified in Table 4, chosen based on preliminary experiments to optimize accuracy.

Table 4. Hyperparameters for KNN training.

Hyperparameter	Value
Number of Neighbors	14
Weighting Scheme	Distance-based
Train-Test Split	80–20
Feature Scaler	MinMax Scaler

Table 5 delineates the input and output features for the Pure-KNN and Diff-KNN models. The model was trained to predict wind flow characteristics, with performance evaluated using metrics such as Mean Squared Error (MSE) and R-squared score.

Table 5. Input and output features for KNN models.

Model	Input Features	Output Features
Pure-KNN	Base Features	VelocityFluid fine (x, y, z components)
Diff-KNN	Base Features,	Residuals between coarse and fine velocities
	Velocity Components

Regarding computational setup and training cost, all KNN experiments were executed on a single workstation (Intel Core i7-1370P, 14C/20T; 32 GB RAM; Intel Iris Xe; SSD). On this machine, fitting (feature scaling and KD/Ball-tree index build) required 33.94 s for Pure-KNN and 65.88 s for Diff-KNN. Despite the doubled fit time for Diff-KNN, the absolute training overhead remains below two minutes and does not require a GPU. On the held-out split, training quality improved from MSE = 0.297 and $R^2=0.588$ (Pure-KNN) to MSE = 0.00941 and $R^2=0.728$ (Diff-KNN), consistent with the accuracy gains reported in Section 6.

5. Performance Measures Overview

In this section, we outline the nature and purpose of the plots used to evaluate and compare the performance of the AIJE-trained KNN model against the coarse CFD model at ground-level heights (0.0–2.0 m). These plots provide insight into the effectiveness of the models in predicting wind flow characteristics in urban environments.

5.1. Model Comparison at Height 0.0–2.0 m

The first plot, Model comparison at height 0.0–2.0 m, visually contrasts the performance of the KNN and coarse CFD models. For each spatial point $p\in {\mathbb{R}}^3$, the color is determined by the following equation:

$$\mathrm{Color}\left(p\right)=\left\{\begin{array}{cc}\mathrm{Orange},\hfill & \mathrm{if}\Delta V_{\mathrm{CFD}}\left(p\right)>\Delta V_{\mathrm{KNN}}\left(p\right)\hfill \\ \mathrm{Blue},\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(5)

where $\Delta V$ represents the absolute velocity difference between the predicted and actual values. This visualization helps identify spatial patterns in model performance, highlighting areas where each model excels.

5.2. Absolute Improvement at Height 0.0–2.0 m

The second plot, Absolute improvement at height 0.0–2.0 m, illustrates the absolute improvements in predictions made by each model. The improvement at each point $p\in {\mathbb{R}}^3$ is calculated as follows:

$$\mathrm{Improvement}\left(p\right)=\Delta V_{\mathrm{CFD}}\left(p\right)-\Delta V_{\mathrm{KNN}}\left(p\right)$$

(6)

Regions where KNN outperforms coarse CFD are shown in red, while blue denotes areas where coarse CFD performs better. This plot is crucial for understanding the magnitude and spatial distribution of performance enhancements.

5.3. Model Performance Distribution

The third plot, Which model performs better?, provides a quantitative summary of the number of data points where each model performs better. This bar chart shows the proportion of points where KNN outperforms coarse CFD and vice versa, offering a clear view of the overall effectiveness of each model.

5.4. Cumulative Absolute Improvements

The fourth plot, Cumulative absolute improvements, aggregates the total improvements in velocity predictions. The cumulative gain is calculated as follows:

$$\mathrm{Cumulative}\mathrm{Improvement}=\sum _{p}w\left(p\right)·\left|\mathrm{Improvement}\left(p\right)\right|$$

(7)

where $w\left(p\right)$ represents the weight assigned to each point based on its spatial characteristics. This plot provides insight into the overall performance benefits of using KNN over coarse CFD.

5.5. Absolute Velocity Difference

The fifth and sixth plots, Absolute Velocity Difference (KNN) at 0.0–2.0 m and Absolute Velocity Difference (CFD) at 0.0–2.0 m, display the absolute velocity differences at each point $p\in {\mathbb{R}}^3$ given by the following equations:

$$\Delta V_{\mathrm{KNN}}\left(p\right)=\left|V_{\text{true\_fine}}\left(p\right)-V_{\text{pred\_fine}}\left(p\right)\right|$$

(8)

$$\Delta V_{\mathrm{CFD}}\left(p\right)=\left|V_{\text{true\_fine}}\left(p\right)-V_{\text{true\_coarse}}\left(p\right)\right|$$

(9)

These plots highlight the error magnitudes in velocity predictions, with specific attention to how each model handles complex street canyon environments.

5.6. Cumulative Absolute Velocity Errors

Finally, the seventh plot, Cumulative absolute velocity errors, presents the total cumulative errors for both models. The cumulative error is calculated as follows:

$$\mathrm{Cumulative}\mathrm{Error}=\sum _{p}w\left(p\right)·\left|V_{\mathrm{predicted}}\left(p\right)-V_{\mathrm{actual}}\left(p\right)\right|$$

(10)

This plot provides a comprehensive view of the overall error magnitude, illustrating the aggregate performance differences between KNN and fine CFD.

5.7. Relative Improvement Along y-Axis Bins

The eighth plot, Relative Improvement along y-axis bins, provides a detailed analysis of the relative improvements of the KNN and coarse CFD models across different spatial bins along the y-axis of the city area. The bins are equidistantly chosen with the centers as bin representatives. The relative improvement for each bin is calculated using the cumulative absolute improvements normalized by the sum of weights for each model:

$$\mathrm{Relative}\mathrm{Improvement}\left(\mathrm{bin}\right)={\displaystyle \frac{\mathrm{Cumulative}\mathrm{Improvement}\left(\mathrm{bin}\right)}{{\sum }_{p\in \mathrm{bin}}w\left(p\right)}}$$

(11)

This formula provides a normalized measure of improvement, allowing for a fair comparison across different spatial bins. This visualization helps in identifying the spatial variability in model performance, highlighting areas where each model shows significant improvement or degradation in predictive accuracy. The fluctuations in the lines indicate varying levels of performance across different spatial regions, providing insights into the spatial robustness and sensitivity of each model.

Note that the weighting scheme $w\left(p\right)$ from Section 5.4 is identical across all models and is solely determined by spatial representativeness: points with more distant neighbors cover a larger portion of the domain and therefore receive a higher weight, while points in densely sampled regions are assigned a smaller weight. This ensures that for example the relative improvement plots in Figure 2 and Figure 3 are directly comparable.

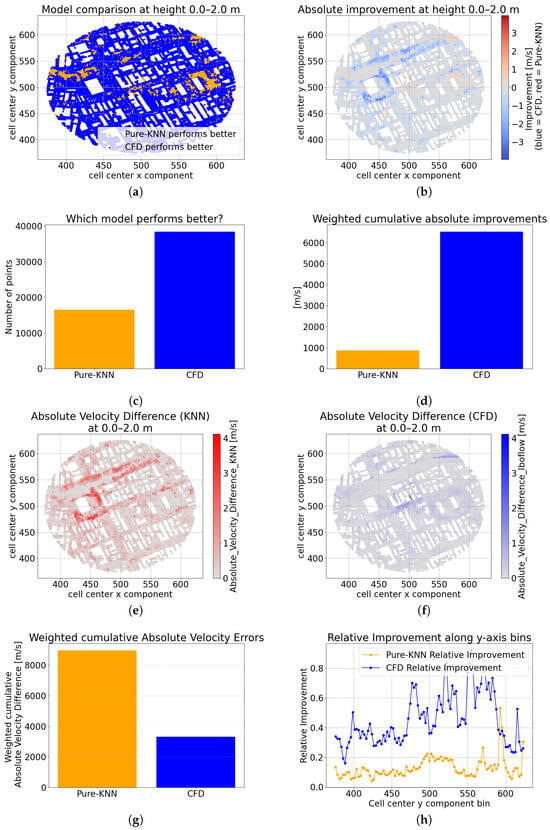
Figure 2. Performance comparison between Pure-KNN and CFD models at height 0.0–2.0 m. (a) Model comparison showing regions of better performance; (b) absolute improvement in velocity prediction; (c) model performance in contrast; (d) weighted cumulative absolute improvements; (e) absolute velocity difference for Pure-KNN; (f) absolute velocity difference for CFD; (g) weighted cumulative absolute velocity errors; (h) relative improvement along y-axis bins.

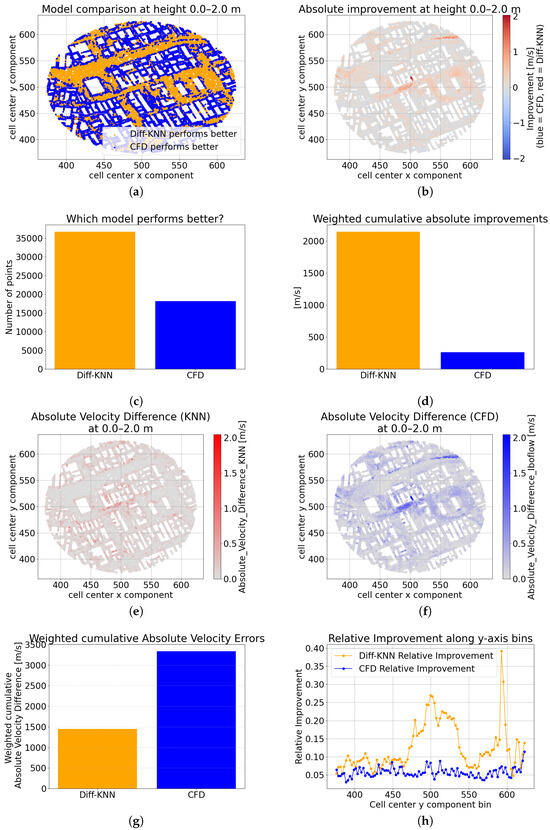
Figure 3. Performance comparison between Diff-KNN and CFD models at height 0.0–2.0 m. (a) Model regions where Diff-KNN (orange) or CFD (blue) performs better; (b) absolute improvement (CFD error minus Diff-KNN error); (c) count of points where each model outperforms the other; (d) weighted cumulative absolute improvements in error; (e) raw absolute velocity error for Diff-KNN; (f) raw absolute velocity error for CFD; (g) weighted cumulative absolute velocity errors for each model; (h) relative improvement binned along y-axis.

6. Results

In this section, we present the results of our comparative analysis between the Pure-KNN, Coarse-Scale CFD, and Diff-KNN models at ground-level heights of 0.0–2.0 m. The Root Mean Square Error (RMSE) metrics for each model are summarized in Table 6.

Table 6. Performance metrics comparison of different models. Component-wise metrics (x,y,z).

Surrogate	Metric	x	y	z
Pure-KNN	RMSE	0.7687	0.4919	0.2439
	MAE	0.4597	0.2875	0.1361
	R2	0.8576	0.3168	0.5910
	NME	0.0534	0.0326	0.0164
Coarse-Scale CFD	RMSE	0.2918	0.1636	0.1120
	MAE	0.1611	0.0992	0.0649
	R2	0.9795	0.9244	0.9137
	NME	0.0187	0.0113	0.0078
Diff-KNN	RMSE	0.1267	0.0908	0.0627
	MAE	0.0648	0.0462	0.0291
	R2	0.9961	0.9769	0.9729
	NME	0.0075	0.0052	0.0036

The RMSE values indicate that the Diff-KNN model consistently outperforms both the Pure-KNN and Coarse-Scale CFD models across all spatial dimensions, exhibiting the lowest error rates. This trend is further supported by the MAE, where Diff-KNN achieves errors of (0.0648, 0.0462, and 0.0291), compared to (0.4597, 0.2875, and 0.1361) for Pure-KNN and (0.1611, 0.0992, and 0.0649) for Coarse-Scale CFD, reinforcing its precision in capturing local flow variations. Additionally, Diff-KNN demonstrates superior explanatory power, with R² values of (0.9961, 0.9769, and 0.9729), significantly exceeding those of Pure-KNN (0.8576, 0.3168, and 0.5910) and even surpassing the Coarse-Scale CFD baseline (0.9795, 0.9244, and 0.9137). The normalized mean error (NME) results—(0.0075, 0.0052, and 0.0036)—highlight its robustness, as these values are an order of magnitude lower than those of Pure-KNN and substantially better than Coarse-Scale CFD. Together, these metrics confirm that Diff-KNN not only reduces absolute errors but also maintains high fidelity to true wind patterns, especially in complex urban geometries. This suggests that Diff-KNN provides the most accurate and reliable predictions for wind flow in urban environments, particularly at ground-level heights where fine-scale resolution is critical.

Regarding runtime and prediction effort, we benchmarked inference with ≈3.73 × 10⁵ query points. Pure-KNN completed in 31.226 s, i.e., 0.0836 ms per query (≈12,000 queries/s). Diff-KNN required 70.834 s, i.e., 0.190 ms per query (≈5260 queries/s), about 2.27× slower. The added latency stems from neighbor search in a higher-dimensional feature space and a larger index. These timings exclude the one-off coarse-CFD solve. In our workflow the coarse field is precomputed once per boundary condition and then reused, so the incremental cost of Diff-KNN is 0 (minutes) per field and typically dominated by the coarse-CFD runtime (see Table 2).

6.1. AIJE at 0.0–2.0 m (Pure-KNN vs. CFD)

Figure 2 highlights how Pure-KNN is superior where coarse CFD cannot resolve the physics correctly. In panel (a) (Figure 2a), the orange points mostly overlap the hotspots in the CFD error field (see Figure 2f), where $\Delta V_{\mathrm{CFD}}$ reaches its maximum. The magnitude of these local gains is made clear in panel (b) (Figure 2b), where red shading peaks at over 2 m/s improvement in tight canyon geometries. Nevertheless, panel (c) (Figure 2c) shows that CFD still outperforms Pure-KNN at roughly two-thirds of the grid points, reflecting its robustness in broad, homogeneous flow regions.

Despite its ability to correct the largest local errors of coarse CFD, Pure-KNN still performs far worse overall. This is most evident in Figure 2d, where the blue bar (CFD) towers above the orange bar (Pure-KNN), underscoring that Pure-KNN’s isolated wins at high-error points cannot compensate for its much larger aggregate error.

Panels (e) and (f) (Figure 2e,f) show the raw absolute velocity errors for each model at 0.0–2.0 m. In Figure 2e, Pure-KNN’s errors (red) are tightly clustered along building façades and narrow gaps, indicating its strength in open areas but persistent difficulties near sharp geometry. By contrast, Figure 2f reveals that the largest errors of coarse CFD (blue) occur primarily in sheltered courtyards and enclosed alcoves—zones where the coarse solver under-resolves recirculation. Together, these complementary error patterns underscore the potential of a residual Diff-KNN correction to leverage each model’s relative advantages.

Panel (g) (Figure 2g) underlines the dominance of CFD: the blue bar, which represents its weighted cumulative absolute error, is substantially lower than the orange bar for Pure-KNN. In panel (h) (Figure 2h), the CFD (blue) curve lies above the Pure-KNN (orange) curve in nearly every y-axis bin, indicating that CFD consistently outperforms the KNN correction in almost every slice.

Together, these panels demonstrate that Pure-KNN provides targeted corrections to the coarse CFD solution at critical urban flow features, laying the groundwork for our hybrid Diff-KNN approach presented in Section 3.4.

6.2. AIJE at 0.0–2.0 m (Diff-KNN vs. CFD)

Figure 3 confirms the power of our hybrid approach: by training the KNN model on the CFD residual, Diff-KNN (yellow) delivers superior predictions across virtually all broad, open-street regions, while coarse CFD (blue) only outperforms in the tightest pockets immediately adjacent to building walls. These continuous swaths of yellow illustrate that the residual correction seamlessly fills in the fine-scale flow features missing from the coarse CFD simulation, and the sparse blue fringe along façades highlights the few remaining zones where coarse CFD captures the underlying physics sufficiently well.

Panel (b) (Figure 3b) shows the magnitude of these corrections: intense red regions—peaking above 2 m/s—stretch continuously through the central street canyons, confirming that Diff-KNN delivers its largest gains precisely where coarse CFD errors were highest.

The win-count histogram in panel (c) (Figure 3c) quantifies this advantage: Diff-KNN outperforms CFD at roughly 67% of the grid points, again highlighting its consistent superiority.

Panel (d) (Figure 3d) aggregates these pointwise gains into a weighted cumulative improvement. The orange bar towers over the blue, showing that Diff-KNN recovers more than an order of magnitude more error (≈2200 m/s) compared to the coarse baseline’s modest gains (≈250 m/s).

Panels (e) and (f) (Figure 3e,f) plot the raw absolute errors. Diff-KNN residuals, rarely exceeding 1 m/s corrected errors, remain uniformly low, even in complex intersections, whereas coarse CFD errors spike in sheltered courtyards and behind obstacles.

Finally, panel (g) (Figure 3g) shows that Diff-KNN cuts the total weighted absolute error by more than half relative to coarse CFD, and panel (h) (Figure 3h) demonstrates that this advantage persists in every y-axis bin.

Together, these panels confirm that Diff-KNN not only patches CFD worst local errors but also achieves a uniform, domain-wide improvement, validating the efficacy of our residual learning framework.

7. Discussion

The KNN models utilized in this study can be further refined through the adoption of more complex constructions, such as LightGBM or XGBoost models, which were explored during this research. However, these advanced models did not yield significant improvements in predictive performance. To emphasize the primary contribution of this work—the integration of coarse evaluation with tree-based models—we opted to maintain a straightforward comparison using KNN models.

Additionally, we observed that the removal of outliers can significantly enhance model performance. Despite this improvement, transitioning to more complex models does not directly correlate with enhanced prediction quality. This limitation is primarily attributed to out-of-distribution values, suggesting that the current dataset may not fully capture the variability and complexity of unseen urban structures.

A key challenge we encountered is the inherent ambiguity in defining “coarse” and “fine” CFD simulations. Mesh resolution is not standardized across studies, and what is considered “coarse” in one setup may qualify as “fine” in another. As a result, the magnitude of the residuals—and consequently the effectiveness of any hybrid correction—can vary substantially. For example, a moderately refined coarse mesh may already capture most building-edge effects, leaving little room for correction, whereas a more aggressively down-sampled mesh may introduce systematic errors that dominate the correction process. This variability underscores the importance of clearly reporting grid specifications and runtime trade-offs when comparing surrogate approaches. Without such transparency, performance gains attributed to a hybrid model may instead reflect differences in the chosen resolution baseline.

To address these challenges and improve model transferability, it is essential to expand the dataset to include a broader range of urban geometries and potentially incorporate additional features. This approach will not only enhance the model’s robustness but also its ability to generalize across diverse and complex urban environments.

7.1. Generalization and Transferability

In this study, training and evaluation were restricted to AIJ case E in Niigata under a west wind. We did not perform cross-site validation on different urban morphologies. Thus, robustness claims are limited to this testbed. To strengthen external validity, future work may (i) test additional AIJ benchmark morphologies (e.g., Cases A–D), (ii) evaluate multiple wind directions to assess directional robustness, and (iii) enrich the local descriptor set beyond the current inputs (local building-height context within a radius (e.g., mean, variance, and gradient), street-axis alignment with inflow (angle between local canyon orientation and wind), etc.). Context features may improve residual predictability near edges and in canyons while keeping the surrogate lightweight. Also, careful feature scaling and distance-weighting and out-of-distribution checks in feature space to fall back to the coarse baseline when appropriate can be considered for improved robustness.

7.2. Practical Impact and Deployment

Diff-KNN consisting of a Coarse-CFD + residual-learning surrogate model accelerates scenario testing and design optimization by replacing fine-CFD evaluations. Each new geometry requires one coarse-CFD simulation being the runtime bottleneck where the residual learning surrogate model only adds ∼0.19 ms per query and is negligible.

The runtime difference between coarse and fine simulations thus defines the speed-up and is dependent on the actual mesh layout. For the chosen AIJE setup (Table 2), this difference in the two meshes, while still moderate, already allows more evaluations. It should be noted that we did not study a minimum resolution that would yield a maximum speedup for the tested setting, and hence for settings where fine simulations are substantially slower than coarse simulations, optimization loops become even faster; however, real-time estimates cannot be reached with the suggested approach.

8. Conclusions

The comparative analysis revealed that the Diff-KNN model consistently outperformed both the Pure-KNN and the Coarse-Scale CFD models across all spatial dimensions, exhibiting the lowest error rates. This suggests that Diff-KNN provides the most accurate predictions for wind flow in urban environments, particularly at ground-level heights.

The visualizations and performance metrics underscored the effectiveness of the Diff-KNN model in correcting the largest local errors of coarse CFD and achieving a uniform, domain-wide improvement. The hybrid approach of Diff-KNN leverages the strengths of both physics-based and data-driven methods, offering a robust solution for urban wind flow predictions.

In summary, while KNN models are valued for their simplicity and mesh-free nature, they face significant challenges with extrapolation errors, particularly in novel urban geometries that extend beyond the convex hull of the training set. This transferability issue is a critical area for future research, as it is essential for developing models that can generalize effectively across diverse and previously unseen urban configurations. Addressing these challenges will further refine the integration of physical and data-driven approaches, thereby advancing the field of urban wind flow prediction.