Federated Learning for Soil Moisture Prediction: Benchmarking Lightweight CNNs and Robustness in Distributed Agricultural IoT Networks

Abstract

Federated learning (FL) provides a privacy-preserving approach for training machine learning models across distributed datasets; however, its deployment in environmental monitoring remains underexplored. This paper uses the WHIN dataset, comprising 144 weather stations across Indiana, to establish a benchmark for FL in soil moisture prediction. The work presents three primary contributions: the design of lightweight CNNs optimized for edge deployment, a comprehensive robustness assessment of FL under non-IID and adversarial conditions, and the development of a large-scale, reproducible agricultural FL benchmark using the WHIN network. The paper designs and evaluates lightweight (∼0.8 k parameters) and heavy (∼9.4 k parameters) convolutional neural networks (CNNs) under both centralized and federated settings, supported by ablation studies on feature importance and model architecture. Results show that lightweight CNNs achieve near-heavy CNN performance (MAE = 7.8 cbar vs. 7.6 cbar) while reducing computation and communication overhead. Beyond accuracy, this work systematically benchmarks robustness under adversarial and non-IID conditions, providing new insights for deploying federated models in agricultural IoT.

1. Introduction

Global climate modeling, flood forecasting, drought monitoring, and agricultural yield are all influenced mainly by soil moisture [1]. Accurate estimation of soil moisture supports climate initiatives, improves irrigation management, and reduces water losses [1]. However, although in situ sensors provide high precision, they remain expensive to deploy at scale and offer limited spatial coverage [2]. Therefore, recent advances in machine learning (ML) and remote sensing have enabled data-driven soil moisture forecasting by combining diverse data sources, such as satellite imagery, weather station measurements, and environmental records [2].

At both field and regional scales, integrating soil, crop, and weather data has improved prediction accuracy. For example, combining soil and weather variables improved local soil moisture prediction in the Red River Valley [3]. Similarly, the multimodal MIS-ME framework, which merged weather and imagery data, achieved a mean absolute percentage error (MAPE) of approximately 10.14%, outperforming unimodal baselines [4]. In Egypt, an IoT-based irrigation system was implemented that combined soil moisture sensors and weather forecasts to improve water management [5].

A wide range of ML and deep learning architectures have been applied to soil moisture prediction, including multimodal fusion models that integrate heterogeneous variables [2,3,4,6,7], long short-term memory (LSTM) networks that capture temporal dynamics [6], and convolutional neural networks (CNNs) that extract spatial features from environmental data [8]. Earlier ML-based IoT systems have been developed to monitor soil and environmental parameters, integrating sensor networks with predictive algorithms for crop and fertilizer recommendations [9]. More recently, transformer-based models have shown competitive results for soil and weather time-series forecasting [10]. Physics-informed deep learning methods [2] and knowledge-guided frameworks that couple Sentinel-1 SAR with physical backscatter models [11] also improved generalization under noisy data. Other studies employed active learning [12] to optimize sensor placement and multiscale deep learning [13] to combine satellite and in situ data, achieving regional correlations of $R\approx 0.90$.

Despite these advancements, most existing models rely on centralized data collection, which is often impractical for distributed agricultural networks due to privacy, ownership, and bandwidth constraints [6,8,9,10,14,15]. Centralized frameworks, such as MIS-ME [4] and multiscale deep learning models [13], achieved strong predictive performance (MAPE = 10.14%, RMSE = 0.034 m³/m³), yet they required data aggregation on a central server. Similarly, physics-informed and knowledge-guided models [2,11] have improved robustness under certain physical or sensing constraints; however, they were still developed and validated in centralized settings. None of these studies systematically evaluated performance under federated or heterogeneous (non-IID) conditions.

Federated learning (FL) offers a decentralized alternative that enables model training across multiple clients without exchanging raw data. Early studies in agriculture showed FL’s potential for communication-efficient optimization [16,17], IoT-based environmental monitoring [18], and crop yield prediction [19]. However, its application to soil moisture prediction is underexplored.  Previous research has primarily focused on algorithmic enhancements rather than evaluating the application of federated sensor networks for soil moisture prediction [7]. 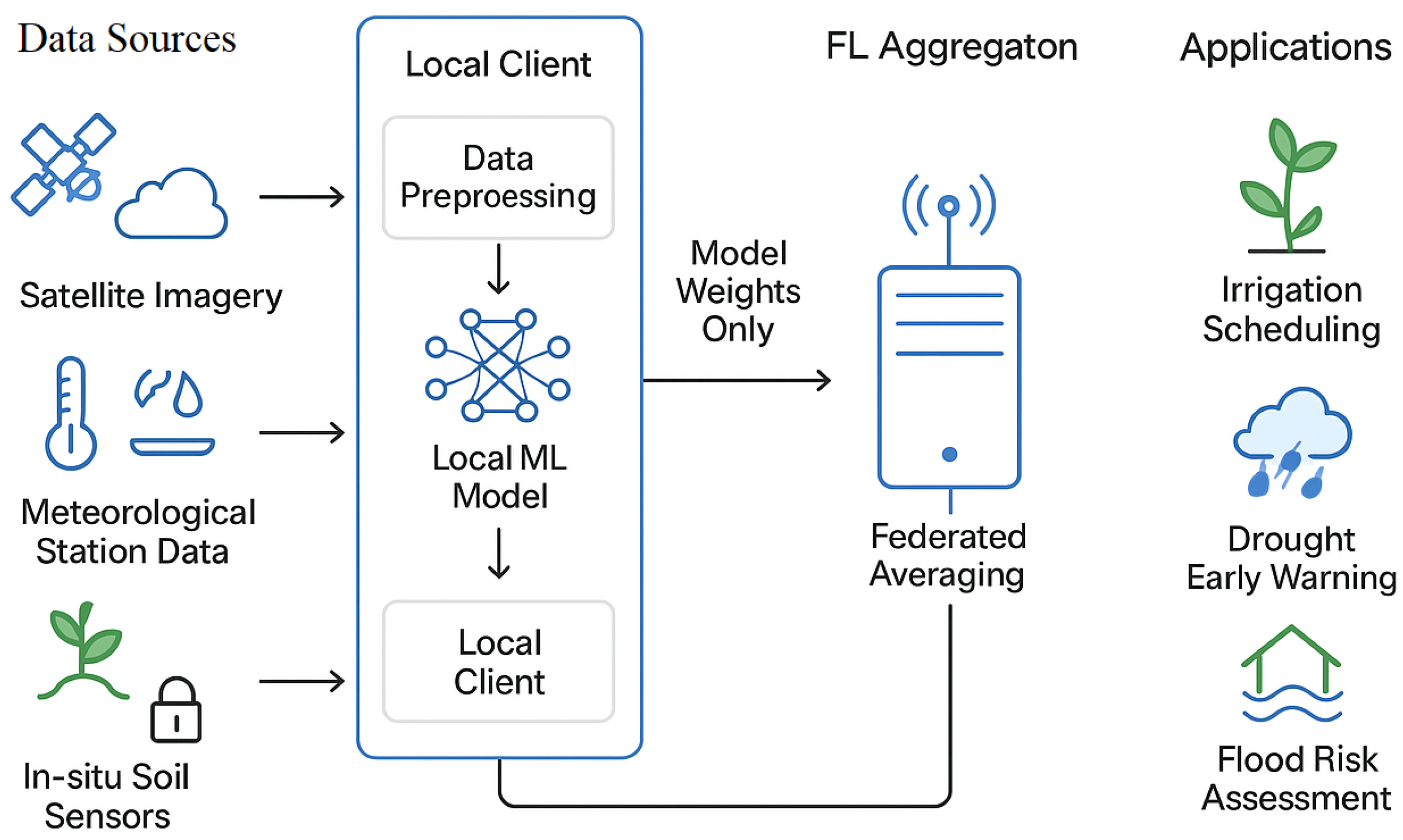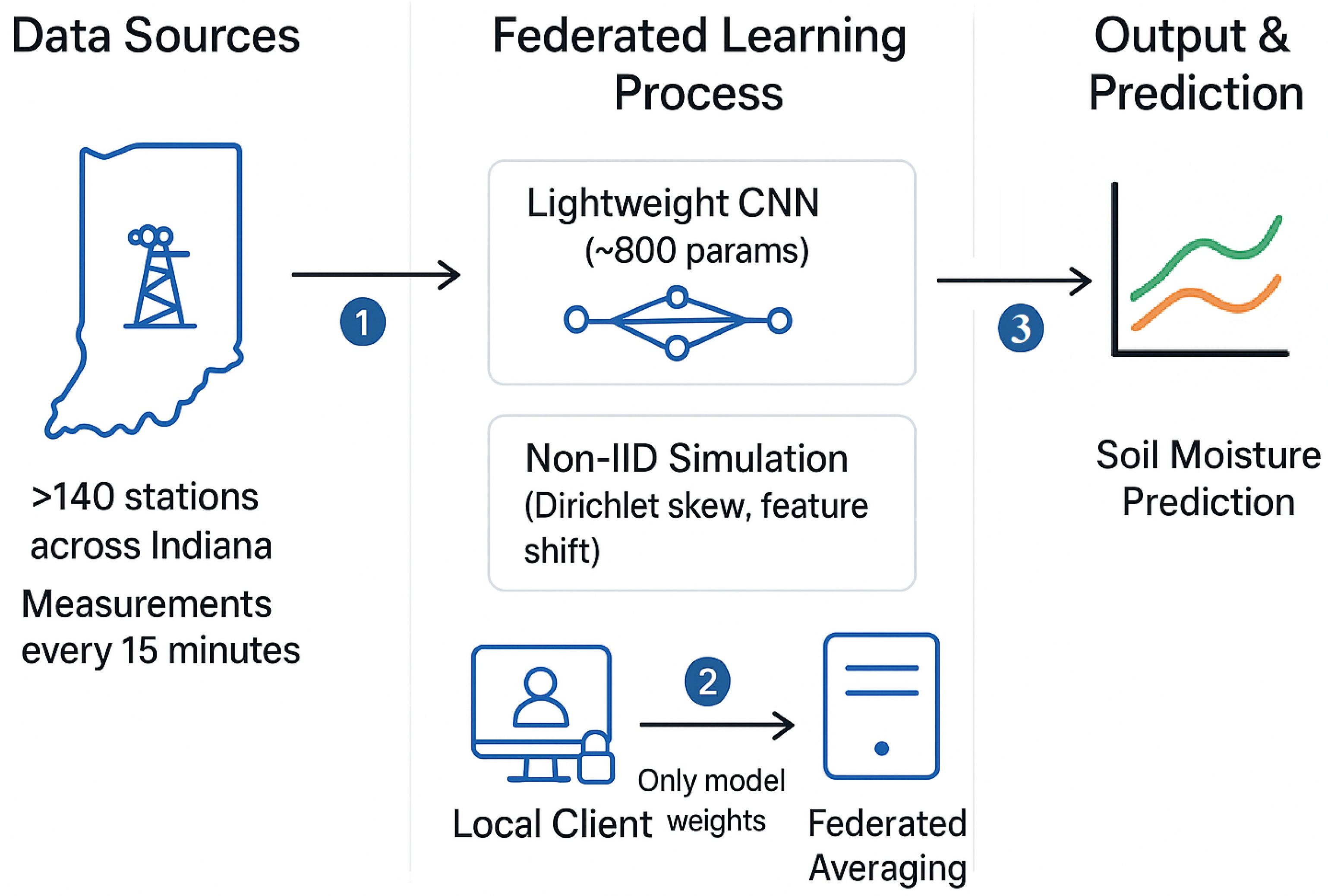Figure 1 shows the conceptual framework of federated learning applied to soil moisture prediction. In this setup, multi-source environmental data such as satellite imagery, meteorological records, and in situ sensor measurements are processed locally at each weather station. Only model updates (not raw data) are exchanged using federated averaging, enabling privacy-preserving model training. While such a framework could support broader applications, such as irrigation scheduling, drought monitoring, and flood risk assessment, this study focuses explicitly on soil moisture prediction using distributed weather-station data.

This work represents a systematic benchmark of FL for soil moisture prediction in a large-scale IoT environment. It includes robustness evaluation under non-IID and adversarial conditions, a lightweight CNN architecture with approximately 0.8 k parameters optimized for resource-constrained edge devices [20], and a large-scale, reproducible benchmark built on the WHIN sensor network. Experimental results show an efficiency–robustness trade-off, where the lightweight CNN achieved performance comparable to heavier models (approximately 9.4 k parameters) while reducing computational and communication costs. Therefore, the results show that lightweight FL models can achieve high predictive accuracy while remaining practical for real-world IoT deployment.

The rest of this paper is organized as follows: Section 2 describes the dataset specifications and preprocessing steps. Section 3 introduces the baseline federated learning models. Section 4 discusses ablation studies and model selection. Section 5 compares the performance of centralized and federated models. Section 6 evaluates robustness under non-IID conditions. Section 7 presents the final discussion, and Section 8 concludes the paper, outlining future work.

2. Dataset Specifications and Preprocessing

The dataset used in this study is provided by the Wabash Heartland Innovation Network (WHIN), a digital agriculture Living Laboratory spanning 10 counties in north-central Indiana [21]. WHIN’s sensor network gathers structured, real-time data from over 160 weather stations across its deployment area, making it one of the most densely deployed agricultural weather networks in the US [21]. Geographically, the WHIN network covers approximately 39° to 42° N latitude and −87°to −86° W longitude. The WHIN dataset is freely available to researchers, students, and educators under open-access licensing terms [21]. This dataset comprises measurements from 144 weather stations for May 2020, and is available in both CSV and JSON formats. It can also be accessed programmatically through the WHIN API for automated data retrieval and analysis.

Each weather station records 24 environmental variables every 15 min [21], including air temperature, humidity, barometric pressure, rainfall, solar radiation, wind direction and speed, and soil temperature and moisture at four depths (1–4 inches). In this study, soil moisture at a depth of 4 inches (soil_moist_4) is selected as the target variable because it reflects conditions in the root zone that are significant and difficult to measure accurately [22]. Soil moisture (soil_moist_4) is measured in centibars (cbar), which represent soil water tension. Higher cbar values indicate drier soil, while lower values correspond to wetter conditions. The observed range of 0–200 cbar is consistent with the calibration of WHIN’s field sensors for typical agricultural soils.

To identify the most relevant input features for (soil_moist_4), all variables from each station are aggregated, non-numeric identifiers are removed, and the other soil moisture depth levels are excluded. Feature importance is then estimated locally at each station using a Random Forest surrogate model with permutation importance, a technique known for its robustness to nonlinear relationships and reduced risk of overfitting. The averaged importance scores across all stations are summarized in

Table 1. Feature importance across 144 WHIN stations.

Feature	Importance Score
soil_temp_4	0.5185
pressure_in_hg	0.1651
soil_temp_3	0.1037
humidity	0.0645
soil_temp_2	0.0330
soil_temp_1	0.0236
temp_low	0.0184
wind_direction_degrees	0.0132
wind_gust_speed_mph	0.0130
temp	0.0118
temp_high	0.0110
wind_speed_mph	0.0104
wind_gust_direction_degrees	0.0060
solar_radiation	0.0027
solar_radiation_high	0.0021
rain	0.0016
rain_inches_last_hour	0.0015

. A higher importance value indicates a greater influence of that feature on soil moisture prediction, and the importance scores for all features sum to 1.

To prepare the data for model training, each local dataset is divided chronologically into 70% training, 10% validation, and 20% test subsets, ensuring that future timestamps are never used during training. To standardize feature ranges across clients, Min–Max normalization is applied separately for each station, while missing values are imputed using the median. For reproducibility, the same data splits are used across all experiments.

3. Baseline Federated Learning Models

This study evaluates the predictive capability of FL for soil moisture estimation using three baseline models of increasing architectural complexity: Linear Regression (LR), Multilayer Perceptron (MLP), and a lightweight convolutional neural network (CNN). This enables a fair comparison between a traditional regression approach, a simple neural network, and a deep convolutional model under identical FL settings.

The LR model serves as a simple non-deep learning baseline. The MLP architecture comprises two hidden layers with 64 and 32 neurons, respectively, each using ReLU activations, which provides a good trade-off between performance and computational efficiency. The lightweight CNN is designed for low-resource environments and includes a single one-dimensional convolutional layer (kernel size = 1) with ReLU activations, followed by adaptive average pooling and a fully connected regression output. A dropout rate of 0.2 helps prevent overfitting. Depending on the number of hidden channels (8–64), the CNN has between 0.7 k and 3.2 k parameters, making it suitable for deployment on edge devices [20].

Federated training follows the FedAvg algorithm, where a central server aggregates model updates from multiple clients to build a shared global model. To efficiently configure FedAvg, a sensitivity analysis is performed by varying the number of local epochs (2–5) and the client sampling ratio (20–40%). The analysis shows that the mean MAE fluctuation remains below 2%, confirming stable convergence across configurations. Based on these findings, the setup uses 40 clients (approximately 28% of the 144 total) per round and three local epochs to balance predictive accuracy and communication efficiency. Each client trains locally using the Adam optimizer (learning rate = 0.001, batch size = 32), and client updates are weighted according to their sample counts. For reproducibility, deterministic random seeds (seed = 42 + client_ID) are applied to each client.

After establishing a stable training configuration, the models are statistically compared to determine whether their performance differences are meaningful or due to random variation. The paired Wilcoxon signed-rank test compares MAE values across the 144 weather stations. The test produces the signed-rank statistic (W) and standardized Z-value, which indicates how far the observed difference deviates from the null hypothesis in standard deviation units. The effect size ($r=Z/\sqrt{N}$), where $N=144$, quantifies the magnitude of improvement beyond random noise. According to [23,24], r values of 0.1, 0.3, and 0.5 correspond to small, medium, and large effects, respectively; therefore, the values between 0.62 and 0.74 observed in

Table 2. Wilcoxon signed-rank test results comparing model performance across 144 stations.

Comparison	Wilcoxon Statistic (W)	Z-Value	p-Value	Effect Size (r)
LR vs. CNN	1545.00	−8.88	<$1\times {10}^{-6}$	0.74
LR vs. MLP	1263.00	−8.17	<$1\times {10}^{-6}$	0.68
CNN vs. MLP	2093.00	−7.44	<$1\times {10}^{-6}$	0.62

represent practically meaningful improvements.

Furthermore, to ensure that the results are not dependent on a single training run, each experiment is repeated five times with different random seeds. Random number generators are initialized deterministically to ensure reproducibility. Results are reported as mean ± standard deviation (SD), where smaller SD values indicate more consistent performance. Additionally, 95% confidence intervals ($C{I}_{95}=1.96\times \sigma /\sqrt{n}$, with $n=5$) are computed; narrower intervals indicate greater reliability and stability of the model’s performance.

As shown in

Table 3. Federated model performance over five independent runs.

Model	MAE (cbar) ± SD	RMSE (cbar) ± SD	95% CI MAE (cbar)
Linear Regression (LR)	$12.03\pm 0.41$	$22.45\pm 0.56$	$\pm 0.36$
Multilayer Perceptron (MLP)	$9.68\pm 0.38$	$21.95\pm 0.49$	$\pm 0.33$
Lightweight CNN (FL)	$8.07\pm 0.26$∗	$22.01\pm 0.31$∗	$\pm 0.23$
Heavy CNN (FL)	$7.59\pm 0.28$∗	$21.82\pm 0.33$∗	$\pm 0.25$

^∗ Statistically significant improvement over MLP and LR ($p<1\times {10}^{-6}$); Wilcoxon signed-rank test.

, both federated CNN variants outperform the MLP and LR baselines in soil moisture prediction. The lightweight CNN achieves an MAE of 8.07 ± 0.26 cbar, outperforming the MLP (9.68 ± 0.38 cbar) and LR (12.03 ± 0.41 cbar) models. The heavy CNN achieves the best accuracy (7.59 ± 0.28 cbar), but at a higher computational cost. The narrow confidence intervals across CNN variants confirm stable, reproducible performance, indicating that FedAvg aggregation maintains predictive accuracy and robustness under decentralized WHIN network conditions.

4. Ablation Studies and Model Selection

Building on the baseline FL experiments, which demonstrate that both lightweight and heavy CNN models outperform LR and MLP in soil moisture prediction, we are now investigating how input features and architectural design influence predictive performance. The baseline results indicate that even minor modifications in architecture or feature representation can significantly impact performance. This observation underscores the need for a systematic ablation analysis to identify optimal configurations for effective FL deployment.

4.1. Feature Ablation

The effect of feature selection on model performance is evaluated using Random Forest permutation importance: features are ranked, and models are trained with 1–17 features in order of importance. All MAE and RMSE values are reported in centibars (cbar) for consistency.

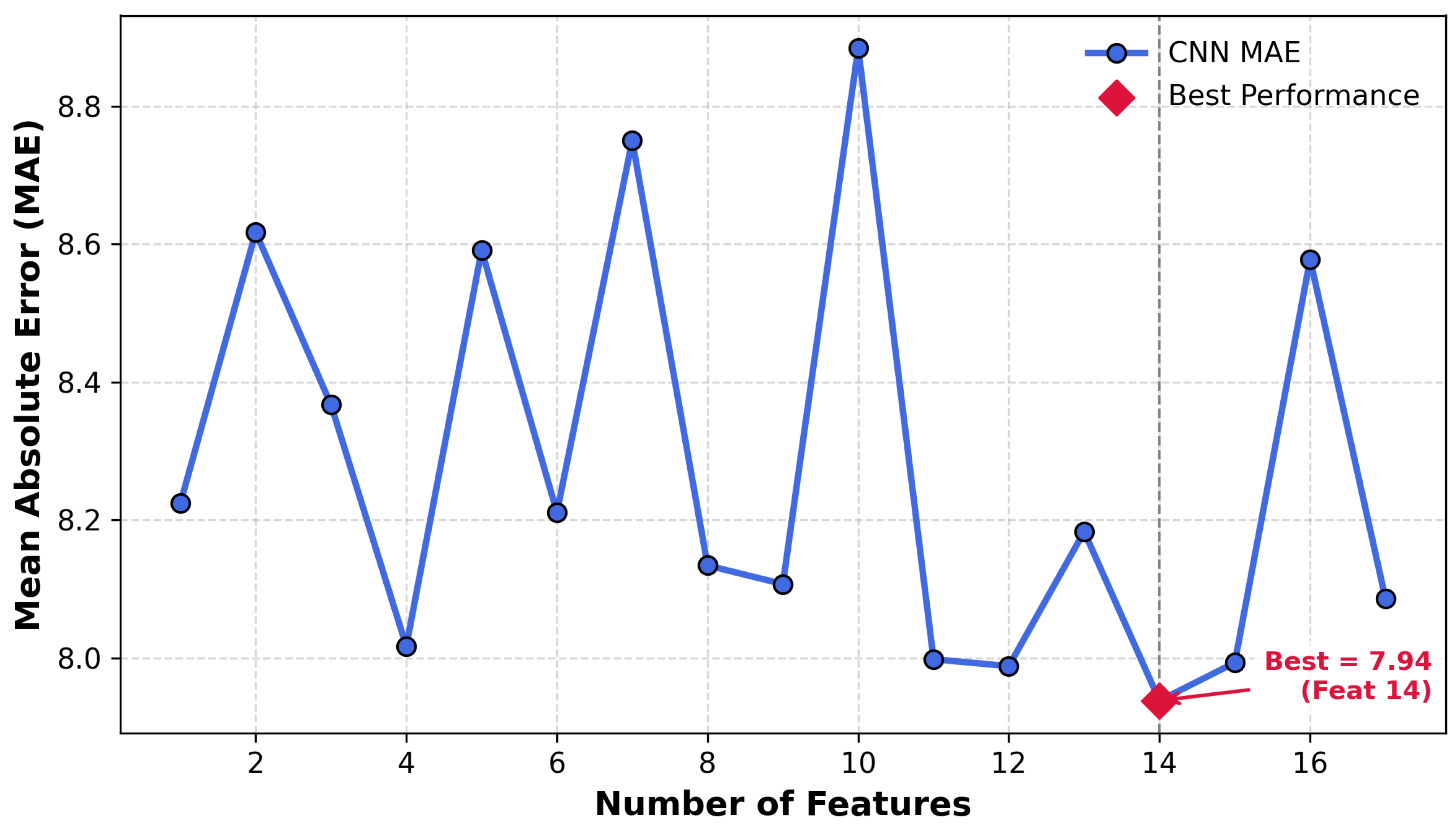
As shown in

Table 4. Federated CNN performance with a varying number of features (MAE and RMSE in cbar).

Num. Features	MAE	RMSE
1	8.224	21.978
2	8.617	21.850
3	8.367	21.897
4	8.017	22.034
5	8.591	21.835
6	8.211	21.927
7	8.750	21.840
8	8.134	21.957
9	8.107	21.942
10	8.884	21.805
11	7.998	22.036
12	7.988	22.049
13	8.183	21.930
14	7.938	22.022
15	7.993	21.975
16	8.578	21.771
17	8.086	21.906

and Figure 2, predictive accuracy improves as more features are included, particularly between 10 and 15 features. Beyond 15 features, performance gains plateau, suggesting diminishing returns and indicating that 14–15 features capture the most informative data for soil moisture prediction. RMSE values remain stable across feature counts, indicating that the model consistently captures the data’s underlying patterns.

4.2. Architecture Ablation

Once a nearly optimal feature subset has been identified, the impact of CNN architectural choices, including the number of convolutional layers (1 to 3) and the number of hidden channels (8 to 64), on predictive performance is assessed. All models are trained under identical FL settings to isolate the effect of the architecture.

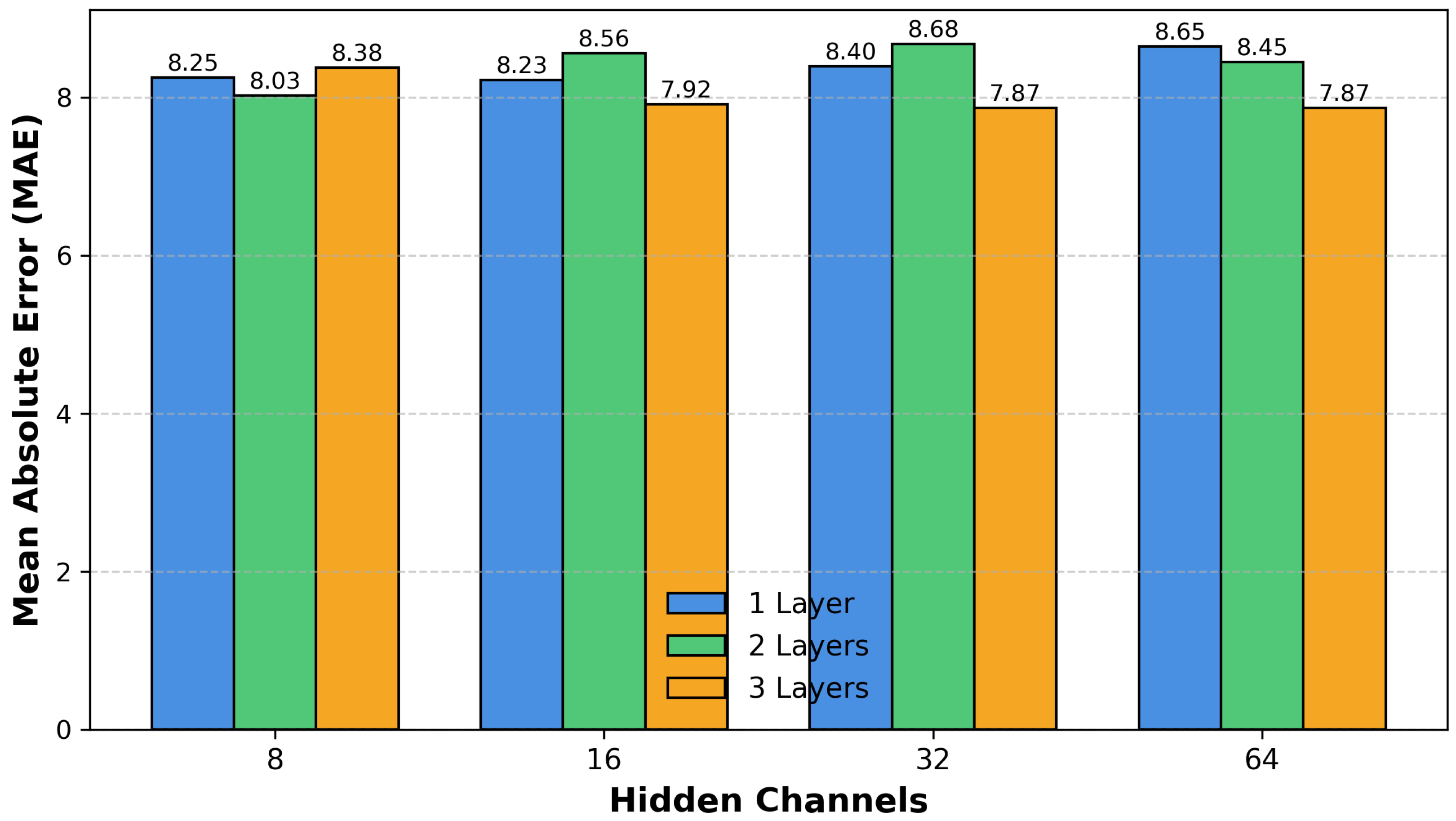
The results in

Table 5. Federated CNN performance with varying hidden channels and convolutional layers (MAE and RMSE in cbar).

Hidden Channels	Conv. Layers	MAE	RMSE
8	1	8.252	22.527
8	2	8.030	21.922
8	3	8.378	22.873
16	1	8.226	22.457
16	2	8.564	23.381
16	3	7.920	21.621
32	1	8.400	22.932
32	2	8.684	23.707
32	3	7.869	21.481
64	1	8.650	23.614
64	2	8.449	23.065
64	3	7.873	21.492

and Figure 3 show that increasing hidden channels generally improves performance, while adding a third convolutional layer provides moderate gains over two-layer models. Therefore, deeper and wider architectures capture more complex relationships without overfitting, consistent with the improvements observed in the baseline heavy CNN. Together, depth and width adjustments enable the model to explore the distributed data fully.

4.3. Combined Ablation Study

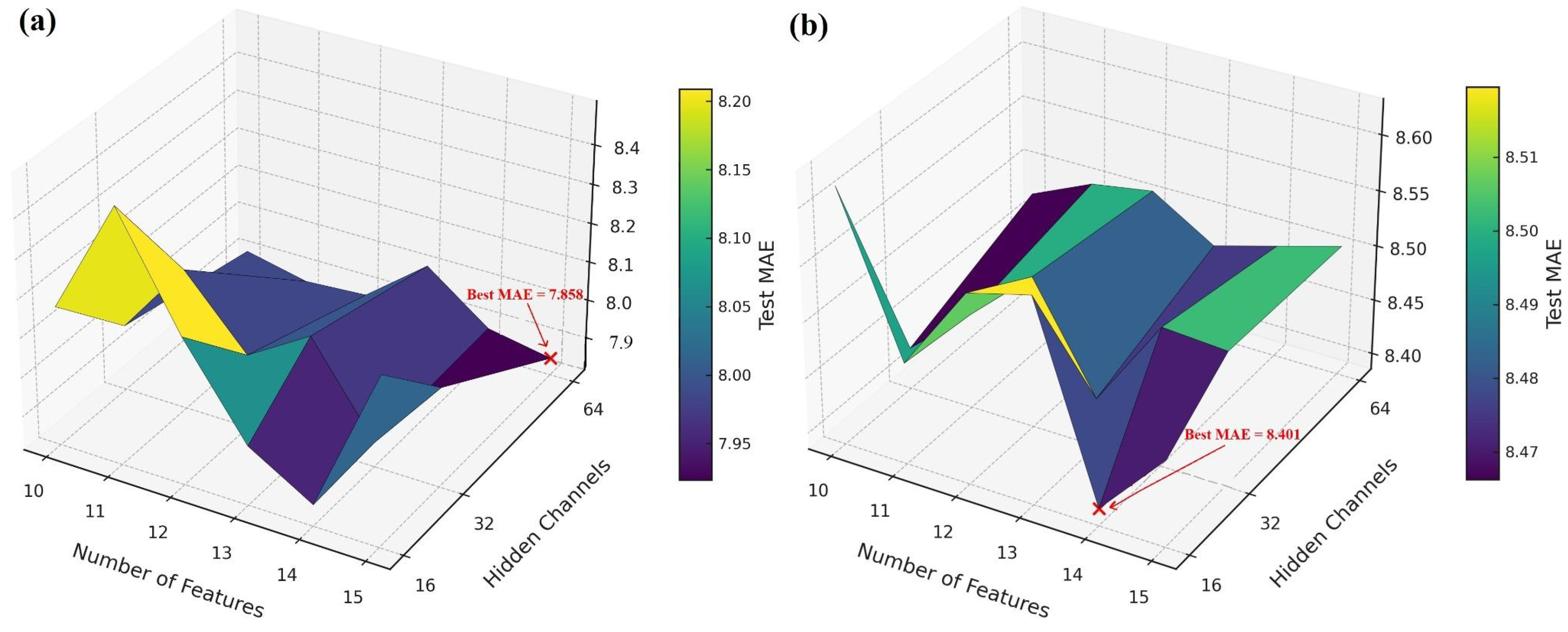
Finally, a combined ablation is performed to identify the configuration that optimizes both feature selection and architecture collectively. Models are trained with 2–3 convolutional layers, 16–64 hidden channels, and 10–15 input features (the ranges previously identified as most effective). Efficient training under federated averaging is ensured through early stopping based on validation MAE.

Figure 4 shows that deeper networks and larger feature sets generally achieve lower MAE.

Table 6. Model performance with a varying number of features, hidden channels, and convolutional layers (MAE in cbar).

Num. Features	Hidden Channels	Conv. Layers	Test MAE
10	16	2	8.635
10	16	3	8.170
10	32	2	7.956
10	32	3	7.982
10	64	2	8.294
10	64	3	7.910
11	16	2	8.484
11	16	3	8.466
11	32	2	8.094
11	32	3	8.175
11	64	2	8.456
11	64	3	7.874
12	16	2	8.011
12	16	3	8.191
12	32	2	8.960
12	32	3	8.003
12	64	2	8.365
12	64	3	7.884
13	16	2	8.114
13	16	3	7.966
13	32	2	8.270
13	32	3	8.101
13	64	2	7.922
13	64	3	8.009
14	16	2	8.192
14	16	3	7.869
14	32	2	8.301
14	32	3	7.877
14	64	2	8.026
14	64	3	7.889
15	16	2	7.960
15	16	3	8.246
15	32	2	8.020
15	32	3	8.069
15	64	2	8.088
15	64	3	7.858

confirms that the heavy CNN (64 channels, three layers, 15 features) achieves the lowest MAE (7.86 cbar), while a lightweight CNN (16 channels, three layers, 14 features) reaches nearly the same performance (7.87 cbar) with fewer parameters.

5. Centralized vs. Federated Performance

Building on the ablation studies, which identified near-optimal feature sets and CNN architectures, we next compare the performance of federated and centralized training configurations. Both the lightweight and heavy CNN models are evaluated under identical preprocessing and training settings, allowing for a fair assessment of how distributed learning affects predictive accuracy.

Table 7. Performance comparison of lightweight and heavy CNNs under centralized and federated settings (MAE and RMSE in cbar; mean ± standard deviation and 95% CI across five runs).

Setting	Params	MAE (Mean ± Std)	RMSE (Mean ± Std)	95% CI (MAE)
Centralized, Light CNN	∼0.8 k	$7.25\pm 0.07$	$21.3\pm 0.2$	$\pm 0.06$
Centralized, Heavy CNN	∼9.4 k	$6.95\pm 0.06$	$20.8\pm 0.2$	$\pm 0.05$
Federated, Light CNN	∼0.8 k	$7.80\pm 0.09$	$22.0\pm 0.2$	$\pm 0.08$
Federated, Heavy CNN	∼9.4 k	$7.60\pm 0.10$	$21.8\pm 0.2$	$\pm 0.09$

and Figure 5 summarize the results, showing that centralized training achieves slightly lower MAE and RMSE values, as it benefits from direct access to the full dataset during optimization. However, federated learning achieves a slight increase of ∼0.5 cbar in MAE, showing that the FedAvg aggregation maintains strong predictive performance even under distributed, heterogeneous data conditions.

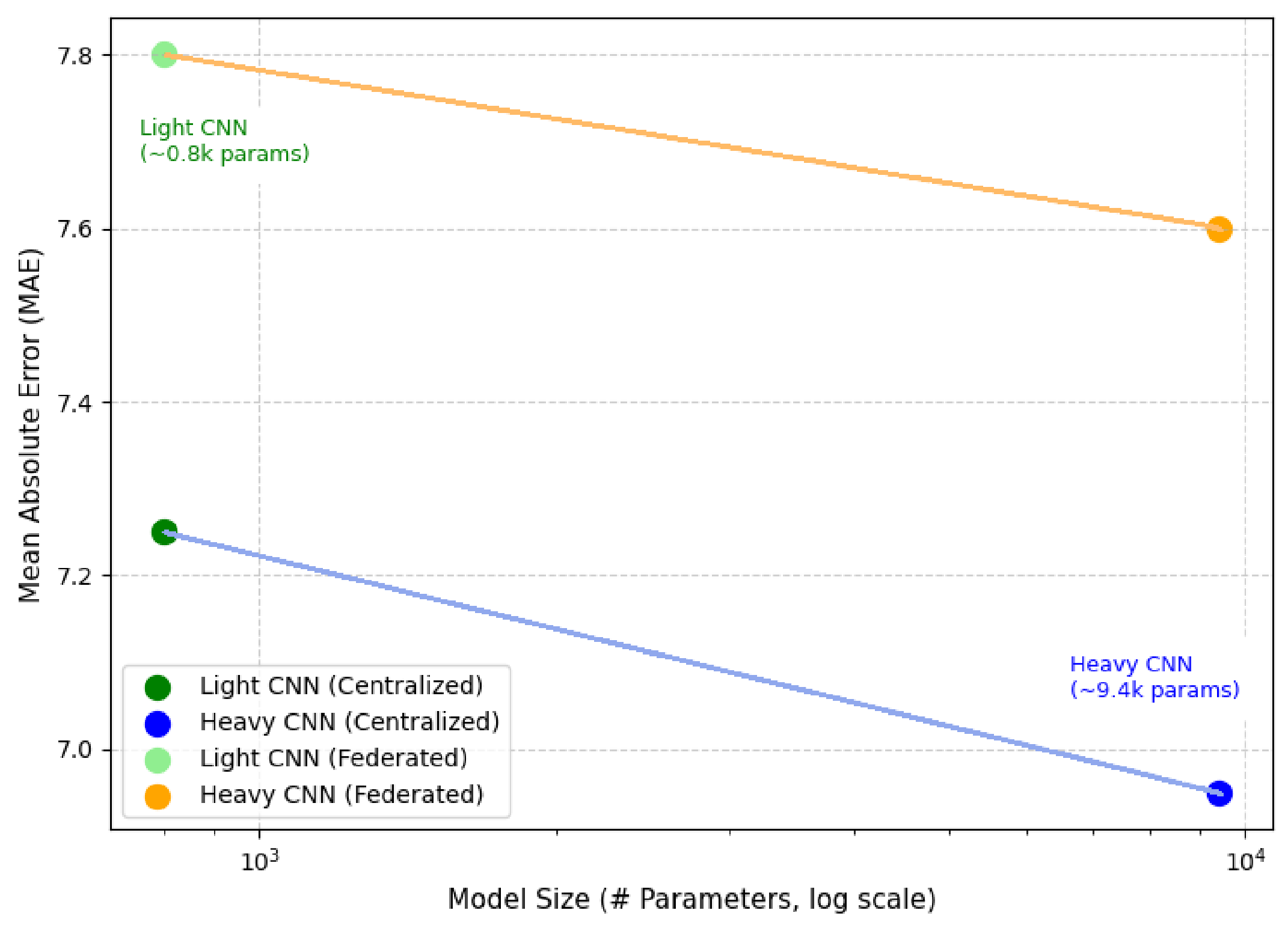
Notably, the lightweight CNN achieves competitive accuracy compared to the heavy CNN while requiring nearly ten times fewer parameters (0.8 k vs. 9.4 k). This reduction in model size makes it highly suitable for edge deployment, where resource constraints and communication efficiency are critical. The heavy CNN provides marginal gains in accuracy but at a higher computational cost, showing the trade-off between model complexity and practical deployment considerations.

Given these findings, the lightweight CNN is selected for subsequent robustness experiments and stress tests under non-IID data distributions, ensuring that the model is both accurate and deployable in real-world WHIN network environments.

6. Robustness Evaluation Under Non-IID Conditions

Building on the baseline and ablation studies, the efficiency of the selected lightweight CNN is evaluated in heterogeneous and adverse deployment scenarios. While previous experiments identified an optimal configuration (14 input features, 16 hidden channels, three convolutional layers, ∼0.8 k parameters) that achieves near-optimal accuracy (MAE = 7.87 cbar), it is still critical to verify whether this architecture maintains performance under non-IID data distributions and robustness perturbations, which are common in real-world IoT deployments.

Therefore, we designed a robustness evaluation pipeline, shown in Figure 6, that simulates two types of non-IID scenarios (Dirichlet distribution skew and feature shift) at multiple severity levels. Three classes of robustness perturbations are introduced: label noise, input noise, and Byzantine failures, applied at varying intensities. Specifically, the perturbations are simulated as follows:

• Label noise: 10–30% of local samples have randomly flipped soil moisture labels.
• Input noise: Gaussian noise $\mathcal{N}(0,{\sigma }^2)$ with $\sigma \in$ 0.01, 0.05, and 0.1 is added to normalized features.
• Byzantine attacks: A subset of clients (5–20%) replaced local model updates with random gradients scaled to match the ${\mathsf{\ell }}_2$ norm of valid updates.

To systematically model heterogeneous client distributions, Dirichlet sampling with concentration parameter $\alpha$ is applied. Low $\alpha$ (0.1) creates highly unbalanced local datasets, while higher $\alpha$ (1.0) approximates near-IID conditions. Across all configurations, the model maintains stable MAE and RMSE under moderate non-IID and up to 20% label corruption, with only minor degradation. Performance decreases at intermediate heterogeneity ($\alpha =0.5$) are attributed to moderate client drift, where label imbalance and feature skew slow down local convergence before FedAvg aggregation stabilizes the global model.

Table 8. Federated learning experiment results for various non-IID and robustness configurations: Dirichlet severity 0.1 (MAE and RMSE in cbar).

Non_Iid_TYPE	Severity	Robust._TYPE	Robust._SEV.	Avg MAE	Std MAE	Avg RMSE	Std RMSE	Avg Rounds
Dirichlet	0.1	byzantine	0.050	14.538	10.952	34.431	34.614	60.000
Dirichlet	0.1	byzantine	0.100	15.566	11.044	35.536	33.987	60.000
Dirichlet	0.1	byzantine	0.200	16.049	10.936	35.947	33.697	60.000
Dirichlet	0.1	input_noise	0.010	14.199	10.257	33.485	33.764	42.500
Dirichlet	0.1	input_noise	0.050	14.197	10.255	33.496	33.778	42.500
Dirichlet	0.1	input_noise	0.100	14.202	10.259	33.509	33.790	42.500
Dirichlet	0.1	label_noise	0.050	14.198	10.265	33.477	33.763	43.000
Dirichlet	0.1	label_noise	0.100	14.193	10.282	33.481	33.773	43.000
Dirichlet	0.1	label_noise	0.200	14.197	10.305	33.482	33.782	43.000

,

Table 9. Federated learning experiment results for various non-IID and robustness configurations: Dirichlet severity 0.5 and 1.0 (MAE and RMSE in cbar).

Non_Iid_TYPE	Severity	Robust._TYPE	Robust._SEV.	Avg MAE	Std MAE	Avg RMSE	Std RMSE	Avg Rounds
Dirichlet	0.5	byzantine	0.050	16.808	2.750	41.927	4.981	25.500
Dirichlet	0.5	byzantine	0.100	16.824	2.763	41.934	4.987	25.500
Dirichlet	0.5	byzantine	0.200	16.899	2.707	41.972	4.957	21.500
Dirichlet	0.5	input_noise	0.010	14.134	2.326	39.414	4.461	57.000
Dirichlet	0.5	input_noise	0.050	14.137	2.325	39.413	4.465	57.000
Dirichlet	0.5	input_noise	0.100	14.153	2.345	39.395	4.456	57.000
Dirichlet	0.5	label_noise	0.050	14.137	2.328	39.415	4.457	57.000
Dirichlet	0.5	label_noise	0.100	14.140	2.335	39.413	4.446	57.000
Dirichlet	0.5	label_noise	0.200	14.144	2.342	39.417	4.433	57.000
Dirichlet	1.0	byzantine	0.050	10.361	1.528	19.959	9.026	40.000
Dirichlet	1.0	byzantine	0.100	10.385	1.495	19.979	8.998	35.000
Dirichlet	1.0	byzantine	0.200	10.613	1.791	20.106	9.156	19.000
Dirichlet	1.0	input_noise	0.010	8.272	1.848	18.091	9.700	60.000
Dirichlet	1.0	input_noise	0.050	8.270	1.845	18.088	9.696	60.000
Dirichlet	1.0	input_noise	0.100	8.264	1.842	18.077	9.695	60.000
Dirichlet	1.0	label_noise	0.050	8.273	1.848	18.092	9.701	60.000
Dirichlet	1.0	label_noise	0.100	8.275	1.847	18.096	9.698	60.000
Dirichlet	1.0	label_noise	0.200	8.274	1.850	18.093	9.702	60.000

and

Table 10. Federated learning experiment results for various non-IID and robustness configurations: feature-shift experiments (MAE and RMSE in cbar).

Non_Iid_TYPE	Severity	Robust._TYPE	Robust._SEV.	Avg MAE	Std MAE	Avg RMSE	Std RMSE	Avg Rounds
feature_shift	(0.02, 0.02)	byzantine	0.050	8.060	0.089	22.429	0.460	18.500
feature_shift	(0.02, 0.02)	byzantine	0.100	8.092	0.118	22.184	0.096	16.500
feature_shift	(0.02, 0.02)	byzantine	0.200	8.912	0.569	23.400	0.536	11.000
feature_shift	(0.02, 0.02)	input_noise	0.010	7.987	0.050	22.259	0.177	32.000
feature_shift	(0.02, 0.02)	input_noise	0.050	7.986	0.026	22.231	0.234	39.500
feature_shift	(0.02, 0.02)	input_noise	0.100	7.983	0.058	22.393	0.393	48.000
feature_shift	(0.02, 0.02)	label_noise	0.050	8.010	0.005	22.249	0.259	22.000
feature_shift	(0.02, 0.02)	label_noise	0.100	8.026	0.001	22.232	0.255	26.000
feature_shift	(0.02, 0.02)	label_noise	0.200	8.024	0.013	22.247	0.284	22.000
feature_shift	(0.05, 0.05)	byzantine	0.050	8.068	0.103	22.456	0.458	18.500
feature_shift	(0.05, 0.05)	byzantine	0.100	8.104	0.124	22.191	0.084	16.500
feature_shift	(0.05, 0.05)	byzantine	0.200	8.964	0.508	23.444	0.482	11.500
feature_shift	(0.05, 0.05)	input_noise	0.010	8.036	0.037	22.211	0.201	26.000
feature_shift	(0.05, 0.05)	input_noise	0.050	8.012	0.021	22.258	0.252	26.000
feature_shift	(0.05, 0.05)	input_noise	0.100	7.996	0.047	22.378	0.420	48.000
feature_shift	(0.05, 0.05)	label_noise	0.050	8.033	0.021	22.228	0.237	26.000
feature_shift	(0.05, 0.05)	label_noise	0.100	8.036	0.018	22.232	0.253	26.000
feature_shift	(0.05, 0.05)	label_noise	0.200	8.026	0.002	22.252	0.280	22.000
feature_shift	(0.1, 0.1)	byzantine	0.050	8.050	0.037	22.401	0.365	27.000
feature_shift	(0.1, 0.1)	byzantine	0.100	8.121	0.117	22.212	0.085	16.500
feature_shift	(0.1, 0.1)	byzantine	0.200	8.986	0.503	23.465	0.471	11.500
feature_shift	(0.1, 0.1)	input_noise	0.010	8.094	0.097	22.185	0.173	19.000
feature_shift	(0.1, 0.1)	input_noise	0.050	8.033	0.021	22.261	0.280	22.000
feature_shift	(0.1, 0.1)	input_noise	0.100	8.063	0.072	22.197	0.183	22.500
feature_shift	(0.1, 0.1)	label_noise	0.050	8.051	0.016	22.256	0.291	22.000
feature_shift	(0.1, 0.1)	label_noise	0.100	8.108	0.097	22.174	0.175	19.000
feature_shift	(0.1, 0.1)	label_noise	0.200	8.046	0.003	22.270	0.313	22.000

report detailed results across varying non-IID and robustness settings, while Figure 7 summarizes the aggregated MAE and RMSE trends.

Under mild non-IID and low-noise conditions ($\alpha =1.0$, $\sigma =0.01$), the lightweight CNN achieves an average MAE of 8.27 cbar. As the severity of non-IID skew or Byzantine participation increases, both MAE and RMSE rise predictably, but no catastrophic failures occur. This indicates that the lightweight architecture maintains convergence stability and robustness, even when facing challenging conditions.

7. Discussion

Table 11. Comparison of related work on soil moisture prediction using machine learning approaches.

Study	Dataset/Source	ML Approach	Learning Setup	Results	Key Advantage/Limitation
[3]	Red River Valley (soil, crop, weather)	ML regression models	Centralized	${\mathrm{R}}^2$ = 0.72 (soil + crop + weather)	Improved accuracy by integrating multiple inputs
[4]	Weather + imagery data	Multimodal DL fusion (MIS-ME)	Centralized	MAPE ≈ 10.14%	Strong multimodal fusion; centralized only
[5]	Egypt (soil sensors + forecasts)	IoT + ML irrigation system	Edge/Centralized	Improved irrigation efficiency (qualitative)	IoT integration; lacks quantitative metrics
[10]	Soil + weather time-series	Transformer foundation models	Centralized	MAE = 0.031, RMSE = 0.042	High accuracy; computationally heavy
[2]	Field observations	Physics-informed DL	Centralized	$\mathrm{RMSE}\approx 3.73\times {10}^{-3}{\mathrm{m}}^3/{\mathrm{m}}^3$	Robust generalization; no distributed setup
[11]	Sentinel-1 SAR + in situ validation	Knowledge-guided DL	Centralized	R ≈ 0.64; Uncertainty ↓ 0.02	Handles vegetation effects; centralized only
[12]	In situ sensors (field scale)	Physics-constrained DL + active learning	Centralized/Active	Relative error reduced by  42–52% vs random sensor placement	Data-efficient; lacks robustness testing
[13]	Satellite + in situ (U.S.)	Multiscale DL	Centralized	R = 0.90; RMSE = 0.034	Large-scale validation; high computation
This work	WHIN sensor network (140+ stations)	Lightweight (0.8 k) and heavy (9.4 k) CNNs + ablations	Federated and Centralized	MAE = 7.80 (FL), 7.25 (centralized)	First FL benchmark; robust to non-IID, noise, Byzantine clients

provides a comparative overview of soil moisture prediction studies using machine learning. Most previous works relied on centralized setups and often used satellite or field-scale datasets, while none employed the WHIN sensor network. This study establishes the first quantitative federated baselines on WHIN, contributing to distributed soil moisture modeling.

Compared with previous centralized models [2,10,13], which achieved low RMSE values using complex architectures such as transformers or physics-informed deep learning, the proposed lightweight CNN offers a substantially smaller model footprint (0.8 k parameters) with comparable predictive capability. Despite its simplicity, it achieves near-centralized accuracy (MAE = 7.80 for FL vs. 7.25 centralized) and demonstrates efficiency–accuracy balance, as illustrated in Figure 8. This supports the feasibility of deploying compact models on edge and IoT devices without sacrificing performance.

While multimodal or knowledge-guided approaches [4,11] enhance interpretability and performance under specific conditions, they remain limited to centralized frameworks that require unified access to data. In contrast, the proposed federated setup ensures data privacy and scalability across distributed stations, aligning with the real-world constraints of agricultural sensing. Moreover, previous IoT-based systems [5] lacked quantitative evaluation metrics, whereas the present study provides concrete benchmarks based on real sensor data.

An additional strength of this work lies in its robustness evaluation. Previous studies ignored the effects of non-IID distributions, sensor noise, or Byzantine failure conditions that frequently occur in field-deployed networks. The proposed FL framework maintained stable performance under these perturbations, showing minimal degradation across robustness tests. This confirms that the model generalizes well to heterogeneous and imperfect sensing environments.

Overall, the results indicate that lightweight CNNs, when integrated into a federated learning framework, can deliver competitive performance in soil moisture prediction while ensuring data privacy and computational efficiency.

8. Conclusions and Future Work

This work presented the first FL benchmark for soil moisture prediction using the WHIN dataset (144 weather stations). Lightweight (0.8 k) and heavy (9.4 k) CNNs were evaluated under centralized and federated setups, including robustness to noise, non-IID data, and Byzantine failures. Lightweight CNNs nearly performed as well as large CNN models, while being over 10 times smaller, offering strong trade-offs in efficiency and communication. FL achieved near-centralized performance while preserving data privacy and remaining robust under adverse conditions, proving its suitability for distributed agricultural sensing. Notably, all baselines were evaluated under reproducible settings, providing a reliable benchmark for future research. Future work will explore communication-efficient FL (such as compression, partial participation), enhanced robustness (such as differential privacy, resilient aggregation), and deployment on live WHIN infrastructure. Extending to multi-season, multi-region data will further validate generalizability. This work demonstrates that FL with compact models is both effective and practical for scalable, privacy-aware agricultural monitoring.