Abstract
The present work aims to quantify the influence of uncertainties in the ply orientation of multi-layered bio-inspired helicoidal laminated composite conical, hemispherical, and toroidal shells under thermal conditions. Any change in the ply orientation affects the free vibration behavior of the laminates. The present investigation focuses on the different levels of uncertainties in the ply orientation on the free vibration behavior of the shell. Moreover, the study also focuses on the sensitivity of the uncertainties in ply orientations on the free vibration behavior of the shells, which is also quantified. To quantify the stochastic free vibration behavior of the shells, the Gaussian process regression (GPR) machine learning algorithm-based surrogate model is developed to predict the frequencies of the shells. The surrogate is created in the framework of higher-order shear deformation theory. The uncertainties in the ply orientations are introduced using bootstrapping. The present results are compared with the stochastic frequencies obtained using Monte Carlo simulations (MCS) to determine the model’s accuracy. The study highlights the influence of the temperature, type of shell, and end conditions on the stochastic free vibration behavior of bio-inspired laminated shells.
1. Introduction
The availability of extensive research on analyzing the behavior of laminated composite structures highlights their importance in constructing various engineering structures such as aircraft, automobiles, defense structures, thin-walled structures, etc. [1,2]. Laminated composites are layered structures in which all the layers are bonded together using resin. Each layer is made up of orthotropic material [3]. Thus, the effective stiffness or strength of the laminated composite structure can be altered by changing the orientation or thickness of the layers within the laminate. This property of laminates is termed tailor-ability [4,5].
The orientation of the layer within the laminate widely affects the behavior of the structure [6]. With the help of the first-order perturbation technique, Tripathi et al. [7] predicted uncertainty in the free vibration behavior of laminated conical shells. With the help of the D-optimal design approach, Dey et al. [8] studied the influence of uncertainties in material properties and ply orientation on the free vibration behavior of laminated conical shells. The bottom-up surrogate approach for studying the influence of uncertainties on the free vibration behavior of laminates was proposed by Dey et al. [9]. Using a first-order shear deformation theory-based Kriging surrogate model was proposed by Mukhopadhyay et al. [10] They predicted the influence of noise on the free vibration behavior of shallow laminated composite shells. Dey et al. [11] predicted the stochastic free vibration response of laminated shallow doubly curved shells using the Kriging surrogate model. With the help of the discrete singular convolution method, Seçgin and Kara [12] predicted the influence of randomness in the properties of the laminates on their free vibration behavior. Using a reproducing kernel particle method in aid of meshless solutions, Wang et al. [13] studied the influence of randomness in material properties on the vibration behavior of carbon fiber-reinforced plates. In aid of Flügge’s theory for orthotropic shells, Huo et al. [14] proposed a discrete analytical method for quantifying the influence of randomness on the free vibration behavior of thin orthotropic cylindrical shells. Employing first-order shear deformation theory along with the pseudo-excitation method, Zuo et al. [15] predicted the free vibration behavior of conical–cylindrical shell structure under random thermal conditions. Considering stochasticity in the thermal gradient, Parviz and Fakoor [16] predicted its effect on the free vibration behavior of laminated structures. Chen et al. [17] studied the stochastic vibration behavior of laminates using the Kriging model. Hakula et al. [18] considered uncertainties in various properties of joined cylindrical shells subjected to free vibration conditions.
Singh et al. [19] predicted stochasticity in the free vibration behavior of laminates containing material uncertainty using the Monte Carlo simulations. The influence of uncertainties in material properties on the free vibration behavior of conical laminated shells was carried out by Lal et al. [20] using a higher-order shear deformation theory-based first-order perturbation technique. A similar methodology was adopted by Parhi and Singh [21] for predicting the influence of uncertainties in the free vibration behavior of spherical and cylindrical shells under thermal conditions. Pseudo-excitation method-based analytical solutions were proposed by Chen et al. [22] for studying the stochastic free vibration behavior of thin cylindrical shells. Singh et al. [23] studied the influence of randomness in material properties on the free vibration behavior of laminated cylindrical shells. Employing higher-order shear deformation theory along with Monte Carlo simulations, Garg and Li [24] predicted the influence of uncertainties in ply angle on the free vibration behavior of helicoidal laminated composite cylindrical shells. Huo et al. [25] considered uncertainties in the geometrical and material properties of laminated shells and predicted their influence on the deformation studies of laminates. Belarbi et al. [26] employed Monte Carlo to quantify the stochasticity in the free vibration behavior of functionally graded beams.
Amongst the studies available in the literature on the stochastic free vibration behavior of laminates, ply orientation is found to be one of the most important properties affecting their behavior. To exploit the strength of the laminates up to their peak, researchers and scientists tried to mock up the layer orientation as observed in several living organisms, such as the dactyl club of mantis shrimp, scales of fishes, nacre, etc. [27]. The layup configuration found in biological beings is similar to a helix in appearance and is commonly called a helicoid lamination scheme [28]. In a helicoidal or Bouligand lamination scheme, each new layer is rotated by a specific angle concerning the previous layer, thus giving rise to the overall circular staircase-like structure. The helicoidal laminates in living beings increase their toughness and energy absorption [29,30]. Recently, researchers carried out free vibration [31,32], bending [33,34], and buckling [35,36,37,38,39] analysis of bio-inspired helicoidal laminated composite structures with various helicoidal layup schemes. By changing the helicoidal layup scheme, the behavior and mode shape of the laminate are found to be affected.
To estimate the distribution of sample statistics and generate random sampling or resampling of the data, bootstrapping is amongst the most preferred statistical methods [40]. Compared to parametric methods, such as ANOVA, no assumption is required by bootstrapping and it does not involve complex mathematical formulations [41]. Monte Carlo simulation generates samples based on the probability model and thus depends on the accuracy of the model developed [42]. From the review work on the stochasticity of the free vibration behavior of laminates, Kriging and first-order perturbation techniques are amongst the most widely used techniques for uncertainty quantification and statistical interference [43]. However, Kriging required special assumptions during its application, i.e., assumptions involved for the specific distribution of the data [44]. Also, the Kriging model necessitates fitting a variogram, which, in turn, is a complex and time-consuming exercise [45]. Considering the first-order perturbation technique, the bootstrap can handle non-linear data effectively and efficiently and can be applied to any statistical model [46,47]. The straightforwardness, effectiveness with small sample size, and lack of complex statistics are some of the other advantages of bootstrapping compared to the Kriging and first-order perturbation techniques [48,49,50]. The present work proposes the use of bootstrapping along with the Gaussian Process Regression (GPR) machine learning algorithm [51] for studying the influence of the uncertainties in the orientation of angle of layers for 20- and 28-layered bio-inspired helicoidal clamped laminated composite cylindrical, hemispherical, and toroid shells. The layup schemes adopted during the present study are presented in Table 1. For generating random samples, bootstrapping is used. The dataset for training the GPR model is obtained using higher-order shear deformation theory. For randomly generated uncertain samples, a trained GPR surrogate is used to predict the frequencies of the shells. The methodology adopted during the present study is presented in Figure 1. The present results are compared with the results obtained using the Monte Carlo simulations. The proposed methodology can effectively predict the stochastic behavior of the laminated shells without a large dataset, thus incorporating the benefits of both bootstrapping and GPR.

Table 1.
Orientation of layers in bio-inspired helicoidal laminated composite panels.
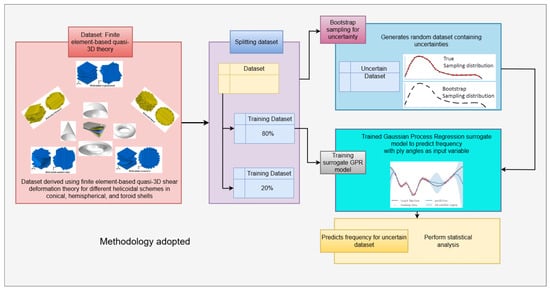
Figure 1.
The methodology adopted during the present study for generating randomized ply orientations following helicoidal schemes for quantifying stochastic free vibration behavior of bio-inspired helicoidal laminated composite shells using bootstrap-assisted GPR algorithm figure.
2. Mathematical Formulation
2.1. Quasi-3D Theory
The generalized displacement field for laminated composite shell structures using quasi-3D shear deformation theory can be stated as [52,53]
where the mid-plane displacements are denoted by , , and along X-, Y-, and-axes, respectively. The shear deformations of the mid-plane are denoted by , , and . The shape function governs the distribution of strains across the thickness of the shell. In the present study, parabolic function is employed, which is expressed as [54]
The Green–Lagrange non-linear strain-displacement relationships can be stated as
The strain matrix is the sum of linear and nonlinear strain matrices as
Using generalized strain-displacement relationship, the linear strain vector can be expressed as
where, and is the matrix containing terms related to thickness coordinates of the shell. In terms of nodal degrees of freedom, the can be re-stated as
In the similar manner, the nonlinear strain vector can be expressed as
where, , which can be re-stated as , where is the vector containing degrees of freedom .
The stress–strain relationship can be expressed as
where, and are the stress and strain vectors, respectively, and is the transformed rigidity matrix.
Nine-noded isoparametric finite element with eight degrees of freedom per node is considered. Considering the penalty parameter , the Lagrange equation of motion can be expressed as
where and are the strain and kinetic energies of the shell, respectively, which can be computed as
Substituting the Equation (9) in Equation (8), we can get the governing equation as
where is the global linear stiffness matrix, represents the artificial constraint stiffness matrix, , , and . The temperature-dependent material properties were adopted while evaluating the stiffness matrices.
2.2. Gaussian Process Regression
For a collection of a finite set of random variables having input–output pairs and possessing Gaussian distribution as , the general form of the model built by GPR can be stated as
where represents the covariance function and denotes the kernel function which governs the smoothness of the GPR function. The mean function for the GP model is expressed as . For a normalized dataset , the mean function equals to zero, then the Gaussian and covariance can be stated as
and
For predicting the output for any unseen dataset , the mean function can be expressed as . The joint distribution of and can be expressed as
For regression distribution over , the output can be expressed as
GPR can handle complex relationships in data without assuming a specific mathematical formula for how the data is related. It can work with different types of data distributions and is especially helpful when dealing with data that is not linear and has a lot of noise. The output data has the noise as and is identically distributed and independent with covariance that can be expressed as . Thus, the predicted value can be stated as
Thus, the final predictive equation can be expressed as
2.3. Bootstrapping
A statistical method of resampling that allows estimation of sampling distribution of statistics by replacing the same from original data. Let the original sample be
For generating large number of bootstrap samples , each bootstrap sample can be stated as
This data is then fed to a trained GPR surrogate to predict the frequency of the bio-inspired laminated composite shells.
3. Results and Discussion
This section presents the results for the stochastic free vibration behavior of clamped bio-inspired laminated composite conical, hemispherical, and toroid shells with uncertainties in ply orientation for 20- and 28-layered shells. The material properties are taken as temperature-dependent are presented in Table 2. The wide dependence and variation of ply angles can be observed from the same.

Table 2.
Temperature-dependent material properties adopted during the present study (G13 = G12, G23 = 0.5 × G12, ν12 = 0.3, ρ = 1627 kg/m3, α1 = −0.3 × 10−6/K, and α2 = 28.1 × 10−6/K) [55].
3.1. Validation Study
No study is available in the literature regarding the free vibration analysis of bio-inspired helicoidal laminated composite shells. The present results are first validated with the higher-order zigzag theory-based results for natural frequencies of helicoidal laminated composite plates under thermal conditions published by Paruthi et al. [31]. For the same, the cross [0°/90°/6°/84°/12°/78°/…/78°/12°/84°/6°/90°/0°] and double [0°/6°/12°/18°/…/84°/90°]s helicoidal laminated composite plate is considered with clamped at all edges (a/h = 5). The present results (Table 3) are found to be in good agreement with the results published by Paruthi et al. [31].

Table 3.
Validation study.
After validating the present model, the stochasticity in the natural frequencies of the bio-inspired helicoidal laminated composite shells due to uncertainties in the ply orientation is predicted. For generating the dataset, different geometric parameters, such as the height and radius of the conical shells, the radius of the hemispherical shell, and the inner and outer radius of toroidal shells, along with their different thickness, are adopted for having generalized stochastic behavior of the shells.
3.2. Influence of Uncertainties in Ply Orientation on the Free Vibration Behavior of Bio-Inspired Helicoidal Laminated Composite Conical Shells
In this section, the influence of uncertainties in ply orientation for 20- and 28-layered clamped bio-inspired helicoidal laminated composite conical shells is carried out using the proposed methodology. The present results are compared with the stochastic results obtained using Monte Carlo simulations (MCS) with 10,000 samples. The results for the statistics of stochastic non-dimensional natural frequency are reported in Table 4 and Table 5 for 20- and 28-layered shells, respectively, for different levels of noise and temperature (T). The results obtained using the present methodology with only 700 samples are the results obtained using MCS. Also, the time taken by the present methodology is much less when compared to the time taken by the MCS. Increasing the noise level, the mean of the simulated outputs decreases for the 20-layered shell and increases for the 28-layered shell. This indicates the non-linear relationship between ply orientation and frequency. At lower noise levels and near room temperature (T = 300 K), the value of skewness is close to zero, which indicates the even distribution of the frequencies around the mean value. This is also supplemented by the probability distribution curves as given in Figure 2 and Figure 3 for 20- and 28-layered shells, respectively. However, negative skewness is observed for the shell made up of 28 layers, which indicates that the tail on the left side is longer and fatter on the right side (Figure 3). Positive skewness may indicate potential high risks. Therefore, the 20-layered shells are more sensitive to the uncertainties in ply angles compared to the 28-layered shells.

Table 4.
Statistical data for uncertainties in ply angles for 20-layered bio-inspired clamped helicoidal laminated composite conical shells were obtained using the present methodology (700 samples) and MCS simulations (10,000 samples).

Table 5.
Statistical data for uncertainties in ply angles for 28-layered bio-inspired clamped helicoidal laminated composite conical shells were obtained using the present methodology (700 samples) and MCS simulations (10,000 samples).
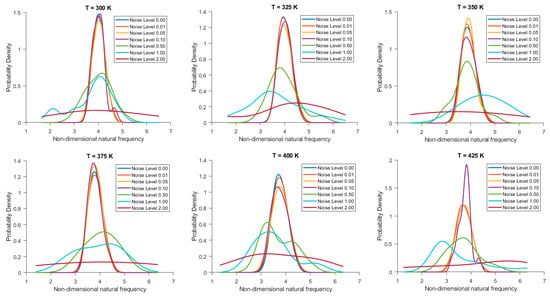
Figure 2.
Probability density function of non-dimensional natural frequency for clamped 20-layered bio-inspired helicoidal laminated composite conical shells under thermal conditions for different levels of noise in ply orientation.
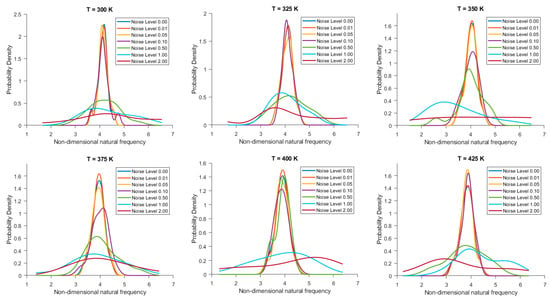
Figure 3.
The probability density function of non-dimensional natural frequency for clamped 28-layered bio-inspired helicoidal laminated composite conical shells under thermal conditions for different levels of noise in ply orientation.
From the probability density functions (PDF) of the non-dimensional natural frequency for clamped 20-layered bio-inspired helicoidal laminated composite conical shells under different thermal conditions and varying noise levels in ply orientation as reported in Figure 2, it has been observed that across all temperatures, the trend is consistent. The PDF is narrowest and highest at noise level 0.00, indicating low uncertainty. As noise levels increase, the distribution broadens and flattens, indicating increased uncertainty in the non-dimensional natural frequency. At higher noise levels, there is a noticeable skewness in the distribution, indicating that the noise is not symmetrically distributed. Figure 3 depicts the PDF for 28-layered shells. Both sets show increased uncertainty with higher noise, but the 28-layered shells seem to maintain a slightly narrower distribution, suggesting better stability and lower variability. However, the effect of temperature on the spread and mean shift is consistent across both sets of data.
The importance scores/sensitivities for different plies vary significantly with temperature changes and are presented in Figure 4 and Figure 5 for 20- and 28-layered shells, respectively. For instance, at lower temperatures (300 K and 325 K), certain plies such as ply10 in the 20-layered and ply 17 in the 28-layered shell show higher importance scores (Figure 4). As the temperature increases to 400 K and 425 K, the importance scores for specific plies (e.g., ply 10, ply 17) become even more pronounced in the 20-layered shell, whereas the pattern is more evenly distributed among various plies in the 28-layered shell. Higher noise levels (1.00 and 2.00) consistently show higher importance scores compared to lower noise levels (0.01, 0.05, 0.10). For both shell types, the zero-noise level (Noise Level 0.00) generally shows the lowest importance scores across all plies, indicating that noise introduces variability and sensitivity in the ply orientations. In 20-layered shells, specific plies (e.g., ply 10, ply 12, ply 17) exhibit high sensitivity across all temperatures and noise levels, suggesting these plies play a critical role in the vibration behavior. In 28-layered shells, the importance scores are more distributed, but certain plies (e.g., ply 10, ply 17, ply 26) still show significant sensitivity, indicating critical plies but with a more distributed influence compared to the 20-layered shells.
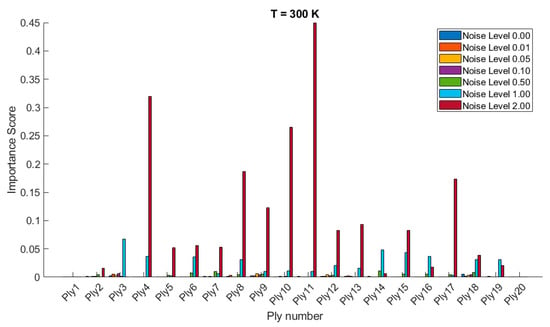
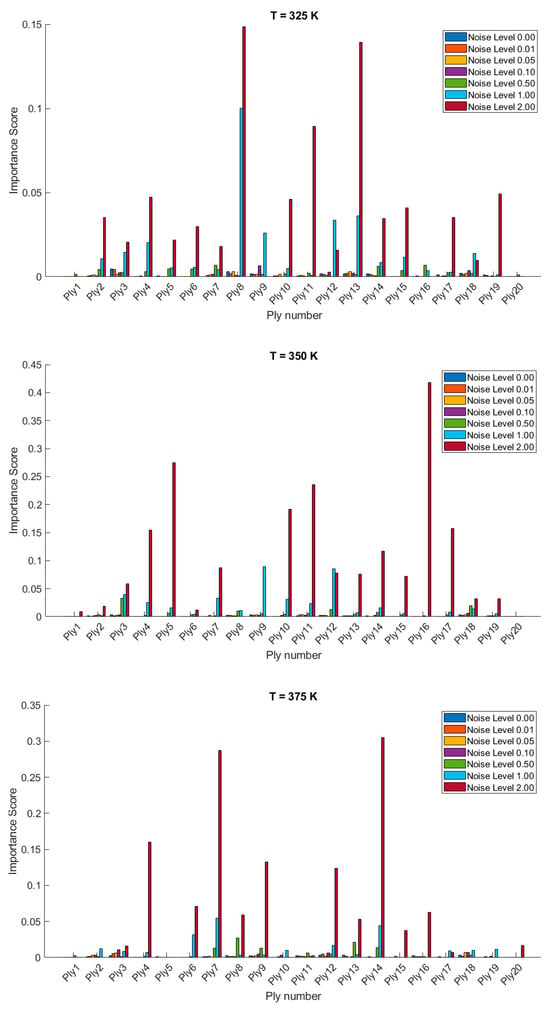
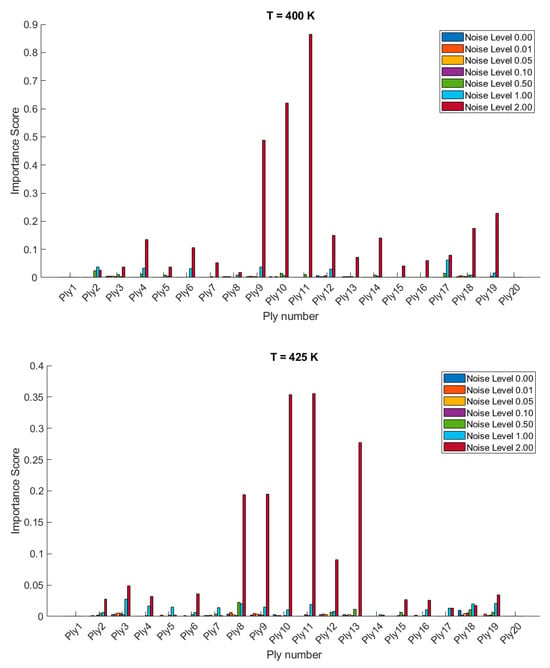
Figure 4.
Variable importance or sensitivity of orientation of each ply on the stochastic free vibration behavior of 20-layered clamped bio-inspired helicoidal laminated composite conical shells.
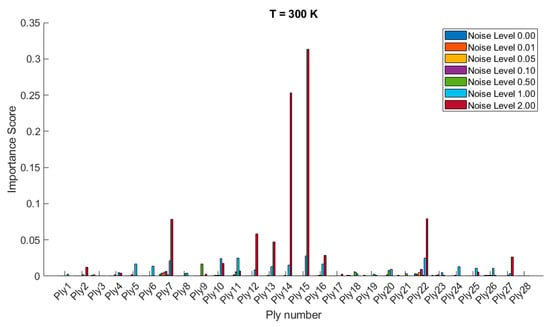
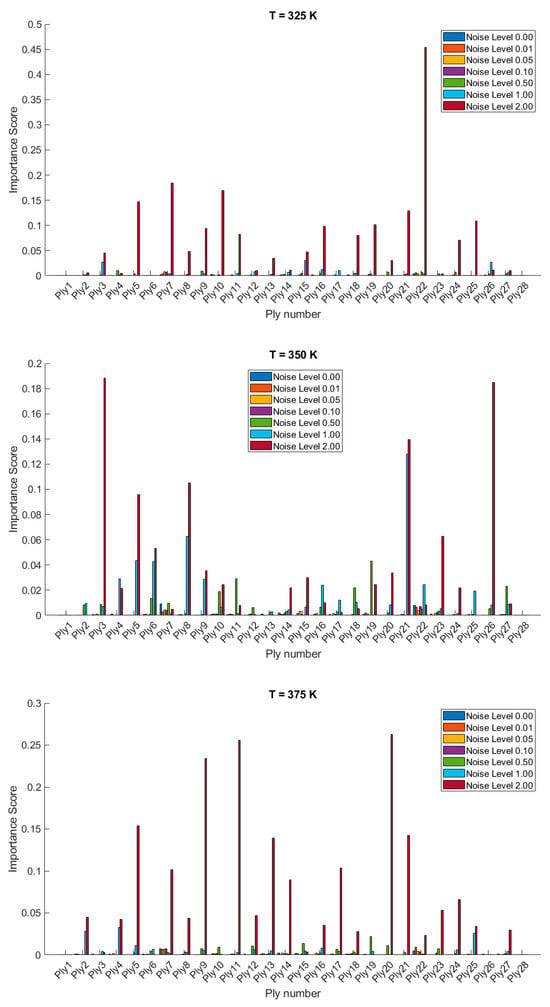
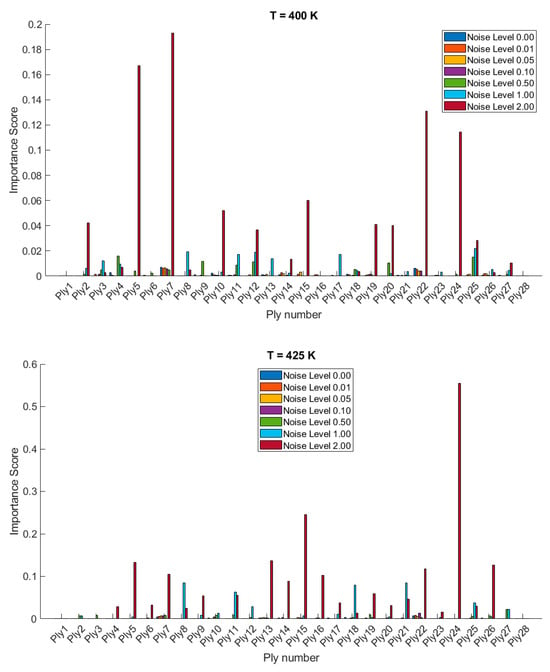
Figure 5.
Variable importance or sensitivity of orientation of each ply on the stochastic free vibration behavior of 28-layered clamped bio-inspired helicoidal laminated composite conical shells.
3.3. Influence of Uncertainties in Ply Orientation on the Free Vibration Behavior of Bio-Inspired Helicoidal Laminated Composite Hemispherical Shells
This section presents the influence of the uncertainties in the ply angle for clamped bio-inspired helicoidal laminated composite hemispherical shells under thermal conditions with different levels of noise. The results for the same are presented in Table 6 and Table 7 for shells made of 20- and 28-layers, respectively. With an increase in noise level, both the mean and standard deviation generally increase for both 20- and 28-layered configurations. The computational time required for the MCS method is significantly higher compared to the present methodology. Figure 6 and Figure 7 illustrate the PDFs of the non-dimensional natural frequency for clamped bio-inspired helicoidal laminated composite hemispherical shells under different thermal conditions and noise levels in ply orientation with 20- and 28-layers, respectively. In both the 20-layered and 28-layered configurations, the PDFs show that the natural frequency distribution broadens and flattens with increasing noise levels, indicating increased variability. Both configurations show that as noise levels increase, the distributions broaden and flatten, indicating greater variability in natural frequencies. The 28-layered shells consistently exhibit slightly higher and narrower peaks at lower noise levels compared to the 20-layered shells, suggesting less variability in their natural frequencies under low-noise conditions. Across all temperatures, the trend of increasing noise leading to broader distributions is observed, with higher noise levels causing more significant shifts and spreading in the peak frequency. This pattern highlights the substantial impact of noise on the vibrational characteristics of these composite shells, increasing uncertainty in their natural frequencies.

Table 6.
Statistical data obtained for uncertainties in ply angles for 20-layered bio-inspired clamped helicoidal laminated composite hemispherical shells were obtained using the present methodology (700 samples) and MCS simulations (10,000 samples).

Table 7.
Statistical data obtained for uncertainties in ply angles for 28-layered bio-inspired clamped helicoidal laminated composite hemispherical shells were obtained using the present methodology (700 samples) and MCS simulations (10,000 samples).
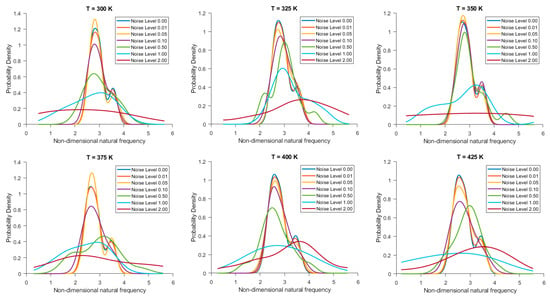
Figure 6.
Probability density function of non-dimensional natural frequency for clamped 20-layered bio-inspired helicoidal laminated composite hemispherical shells under thermal conditions for different levels of noise in ply orientation.
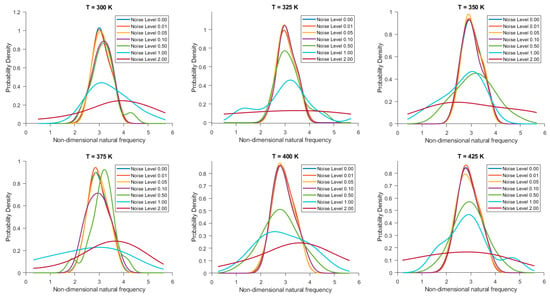
Figure 7.
Probability density function of non-dimensional natural frequency for clamped 28-layered bio-inspired helicoidal laminated composite hemispherical shells under thermal conditions for different levels of noise in ply orientation.
Figure 8 and Figure 9 show the variable importance or sensitivity of the orientation of each ply on the stochastic free vibration behavior of 20- and 28-layered clamped bio-inspired helicoidal laminated composite hemispherical shells at various temperatures (300 K, 325 K, 350 K, 375 K, 400 K, 425 K) and different noise levels (0.00, 0.01, 0.05, 0.10, 0.50, 1.00, 2.00). As the temperature increases from 300 K to 425 K, there is a noticeable increase in the importance scores for certain plies, particularly under higher noise levels. The sensitivity of certain plies (e.g., ply 3, ply 8, ply 12, ply 20 in the 20-layered configuration) tends to increase significantly at higher temperatures and higher noise levels. For the 28-layered configuration, plies such as ply 7, ply 12, ply 18, and ply 25 show significant sensitivity changes at higher temperatures and noise levels. Higher noise levels (1.00 and 2.00) consistently result in higher importance scores across many plies, indicating that noise has a strong impact on the sensitivity of ply orientation. At lower noise levels (0.00, 0.01, 0.05), the importance scores are generally lower, suggesting a more stable system with less sensitivity to ply orientation changes. Noise levels of 0.50 and above significantly amplify the importance scores, highlighting the system’s increased sensitivity to perturbations in ply orientation. The 20-layered configuration shows distinct peaks in importance scores for specific plies, especially under high-noise and high-temperature conditions. The 28-layered configuration exhibits a more distributed sensitivity pattern, with several plies showing notable importance scores under similar conditions. Certain plies in the 28-layered configuration exhibit high sensitivity at moderate noise levels (e.g., ply 7, ply 12, ply 18), which might indicate critical structural roles or positions within the composite structure.
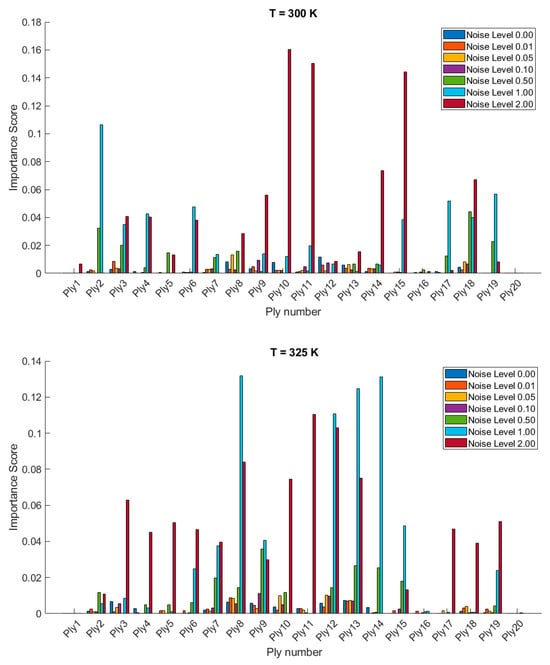
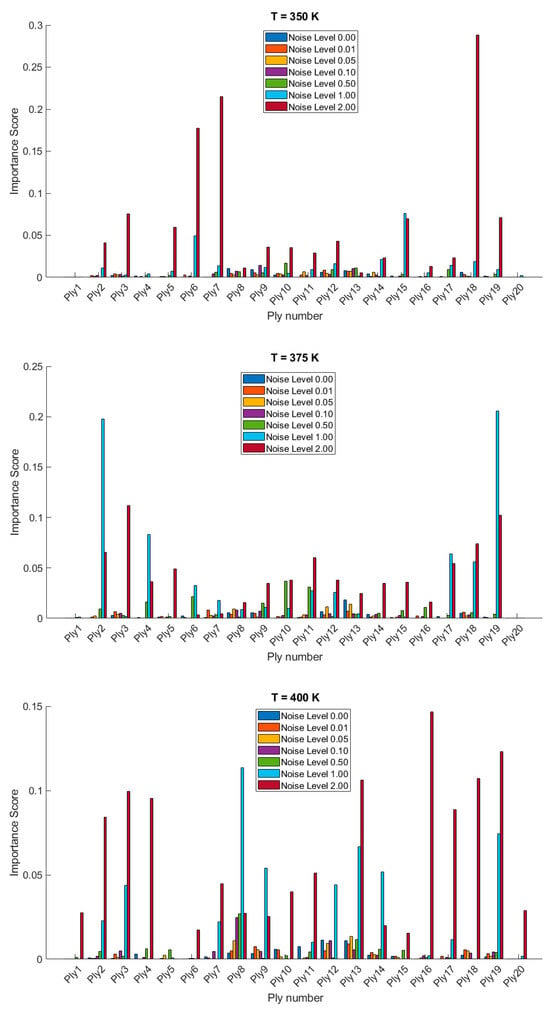
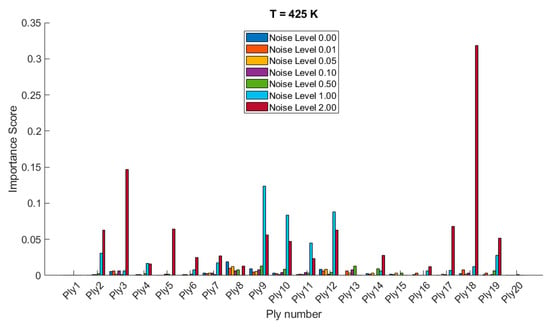
Figure 8.
Variable importance or sensitivity of orientation of each ply on the stochastic free vibration behavior of 20-layered clamped bio-inspired helicoidal laminated composite hemispherical shells.
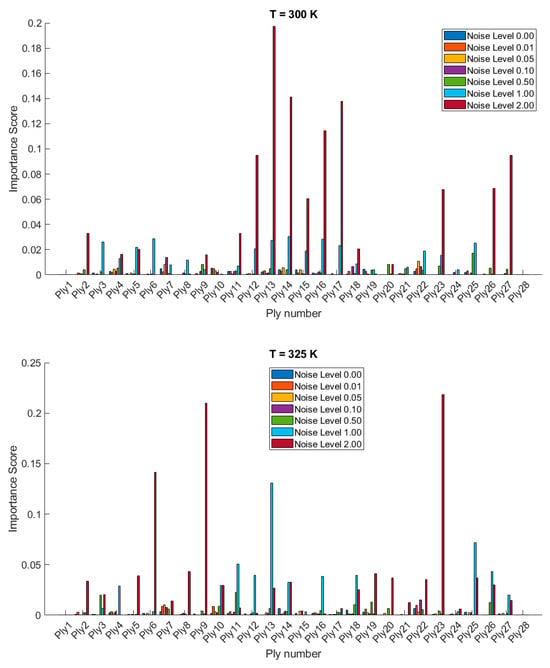
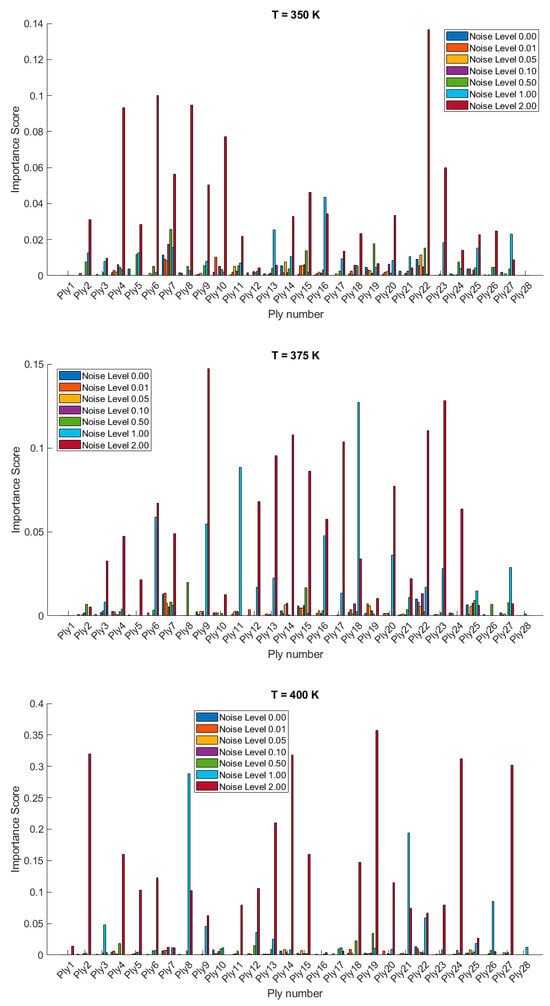
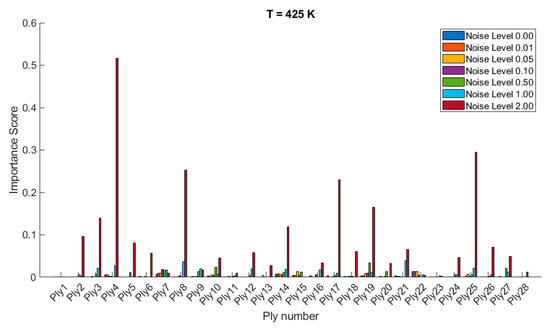
Figure 9.
Variable importance or sensitivity of orientation of each ply on the stochastic free vibration behavior of 28-layered clamped bio-inspired helicoidal laminated composite hemispherical shells.
3.4. Influence of Uncertainties in Ply Orientation on Free Vibration Behavior of Bio-Inspired Helicoidal Laminated Composite Toroid Shells
Under this section, a study of the influence of uncertainties in ply orientation on free vibration behavior of bio-inspired helicoidal laminated composite toroid shells is carried out. The statistics of non-dimensional natural frequencies are presented in Table 8 and Table 9 for 20- and 28-layered shells, respectively. The mean values are generally consistent between the present methodology and MCS, with standard deviations slightly higher in MCS. The time taken for MCS is significantly higher than for the present methodology. The mean values for 28-layered shells are generally higher than those for 20-layered shells, with differences also observed in standard deviations, kurtosis, and skewness. Overall, both methodologies provide similar mean values, but MCS is more computationally intensive. Figure 10 and Figure 11 present the PDFs for 20- and 28-layered clamped bio-inspired helicoidal laminated composite toroid shells, respectively, for different levels of noise and temperature conditions. In both figures, the probability density functions exhibit a peak around a non-dimensional natural frequency of approximately 2, with the peak height varying depending on the noise level. As the noise level increases, the peak tends to broaden and decrease in height, indicating a wider distribution of natural frequencies. However, the 28-layered composite shell (Figure 11) generally shows higher peak probability densities compared to the 20-layered composite shell (Figure 10), suggesting a more concentrated distribution of natural frequencies. Additionally, the 28-layered shell exhibits a higher sensitivity to noise, with more pronounced changes in the probability density functions as the noise level increases. This comparison highlights the influence of the number of layers on the dynamic behavior of the composite shells under thermal and noise conditions. Figure 12 shows the sensitivity of the uncertainty in ply angles on the free vibration behavior of toroid shells. For 20-layered shells, it has been observed that the inner layers are found to affect the free vibration behavior of the shell compared to the outer layers. In case of 28-layered shells, the outer layers are found to affect the free vibration behavior of shells containing uncertainties in the ply orientations (Figure 13).

Table 8.
Statistical data obtained for uncertainties in ply angles for 20-layered bio-inspired clamped helicoidal laminated composite toroidal shells were obtained using the present methodology (700 samples) and MCS simulations (10,000 samples).

Table 9.
Statistical data obtained for uncertainties in ply angles for 28-layered bio-inspired clamped helicoidal laminated composite toroidal shells were obtained using the present methodology (700 samples) and MCS simulations (10,000 samples).
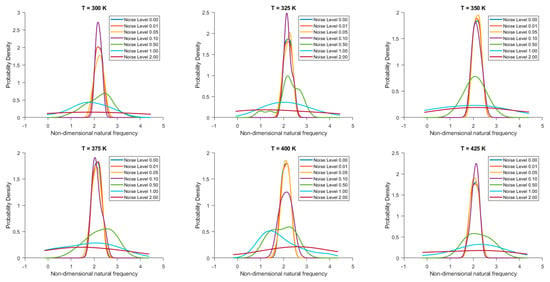
Figure 10.
Probability density function of non-dimensional natural frequency for clamped 20-layered bio-inspired helicoidal laminated composite toroidal shells under thermal conditions for different levels of noise in ply orientation.
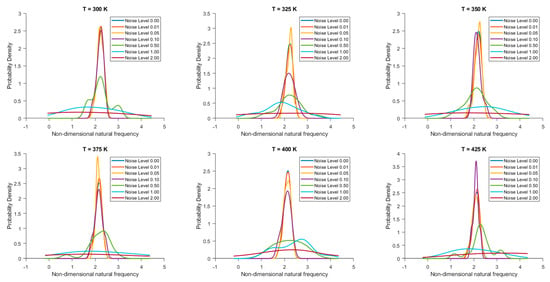
Figure 11.
Probability density function of non-dimensional natural frequency for clamped 28-layered bio-inspired helicoidal laminated composite toroidal shells under thermal conditions for different levels of noise in ply orientation.
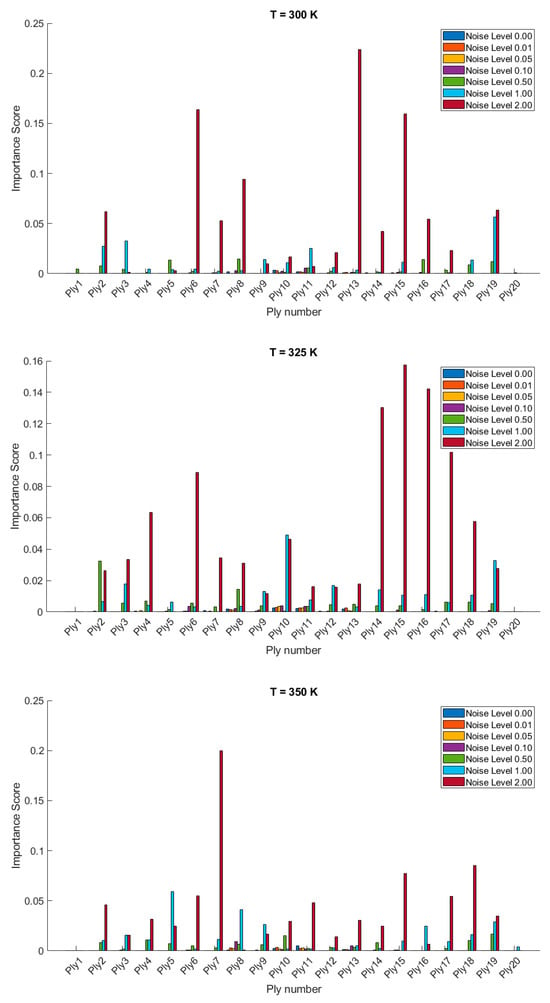
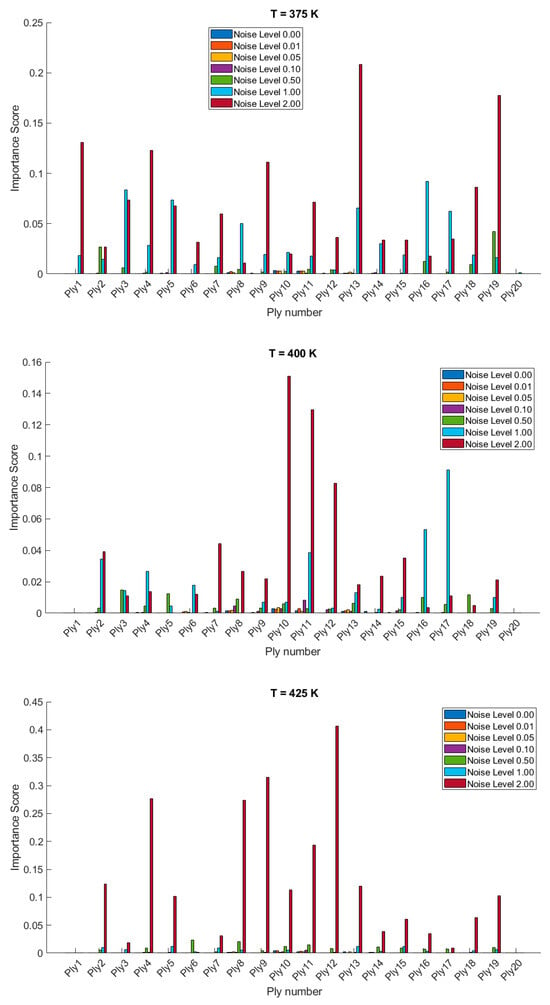
Figure 12.
Variable importance or sensitivity of orientation of each ply on the stochastic free vibration behavior of 20-layered clamped bio-inspired helicoidal laminated composite toroidal shells.
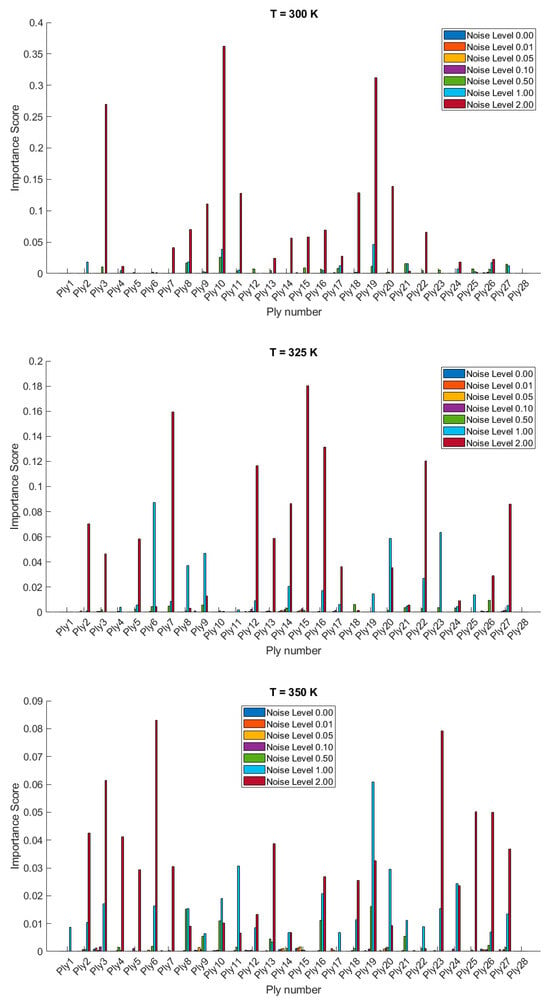
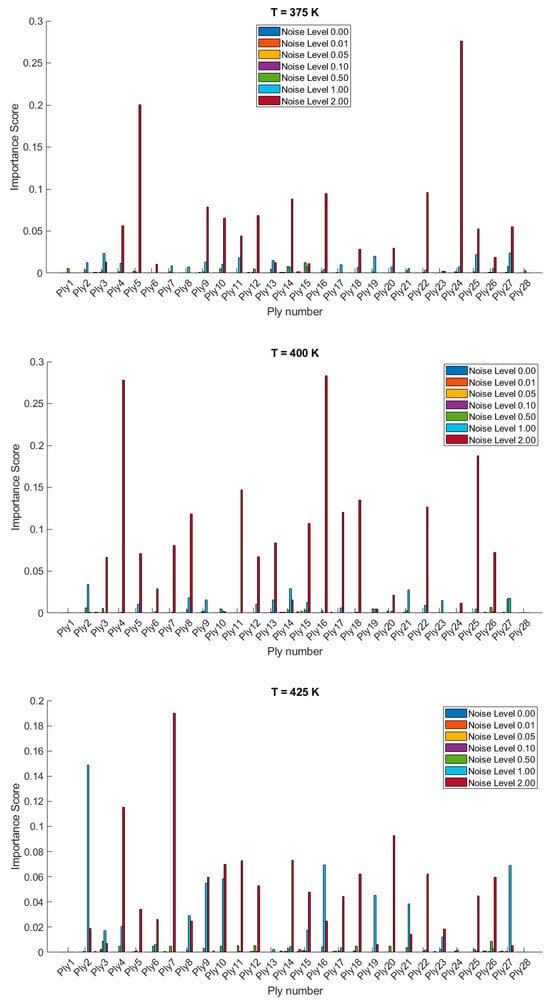
Figure 13.
Variable importance or sensitivity of orientation of each ply on the stochastic free vibration behavior of 28-layered clamped bio-inspired helicoidal laminated composite toroidal shells.
4. Conclusions
The present work proposed the use of a bootstrap-based Gaussian Process Regression machine learning algorithm for predicting the influence of uncertainties in the ply angle on the free vibration behavior of bio-inspired clamped helicoidal laminated composite conical, hemispherical, and toroid shells. For training the surrogate model, quasi-3D shear deformation theory in the framework of the finite element method is used. The following important points are noted from the present study:
- The proposed methodology is found to be computationally efficient compared to the conventional Monte Carlo simulation model, as the present methodology requires very little random data.
- Uncertainty in ply angles widely governs the free vibration behavior of conical, hemispherical, and toroid bio-inspired clamped laminated composite shells.
- Higher temperatures and noise levels tend to increase the sensitivity of the ply orientations, indicating that the structural behavior of these composite shells is more affected by perturbations under such conditions.
- The distribution of sensitivity across plies varies between the 20- and 28-layered configurations, reflecting the complexity and interactions within the composite structure.
- Both 20-layered and 28-layered clamped bio-inspired helicoidal laminated composite conical shells show increased uncertainty with higher noise levels. The 28-layered shells maintain slightly better stability and lower variability in their natural frequency measurements.
- Specific plies within all three configurations exhibit higher sensitivity, suggesting critical layers that might require more precise control or monitoring in practical applications.
Author Contributions
Conceptualization, A.G., L.L., M.-O.B., W.Z. and R.R.; methodology, A.G. and L.L.; software, A.G., R.R. and M.-O.B.; validation, A.G., W.Z. and R.R.; formal analysis, A.G., L.L. and M.-O.B.; investigation, A.G., L.L., M.-O.B., W.Z. and R.R.; data curation, A.G. and R.R.; writing—original draft preparation, A.G., M.-O.B. and R.R.; writing—review and editing, L.L. and W.Z.; visualization, A.G., L.L. and M.-O.B.; supervision, L.L. and W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by the National Natural Science Foundation of China (Grant No. 52175095) and the Young Top-notch Talent Cultivation Program of Hubei Province of China.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yu, J.; Wu, J.; Wang, X.; Li, Y. Drop Tests and Numerical Analyses of Composite Beams with Corrugated Web. J. Compos. Sci. 2024, 8, 438. [Google Scholar] [CrossRef]
- Sharma, A.; Joshi, S.C. A Study of the Interply Strengthening of CF/PA6 Composites Using Micro-Size Core-Shell Particles. J. Compos. Sci. 2024, 8, 447. [Google Scholar] [CrossRef]
- Garg, A.; Chalak, H.D. A Review on Analysis of Laminated Composite and Sandwich Structures under Hygrothermal Conditions. Thin Walled Struct. 2019, 142, 205–226. [Google Scholar] [CrossRef]
- Haruna, S.I.; Ibrahim, Y.E.; Umar, I.K. Machine Learning Approach for Prediction and Reliability Analysis of Failure Strength of U-Shaped Concrete Samples Joined with UHPC and PUC Composites. J. Compos. Sci. 2025, 9, 23. [Google Scholar] [CrossRef]
- Haggui, M.; Jendli, Z.; El Mahi, A.; Akrout, A.; Haddar, M. Damage Analysis in Flax/Elium Composite Using Linear and Nonlinear Resonance Techniques. J. Vib. Eng. Technol. 2024, 12, 2811–2827. [Google Scholar] [CrossRef]
- Ni, B.; Wang, X.; Lv, T.; Wang, L.; Li, Z. Non-Probabilistic Thermo-Elastic Reliability-Based Topology Optimization (NTE-RBTO) of Composite Laminates with Interval Uncertainties. Eng. Comput. 2022, 38, 5713–5732. [Google Scholar] [CrossRef]
- Tripathi, V.; Singh, B.N.; Shukla, K.K. Free Vibration of Laminated Composite Conical Shells with Random Material Properties. Compos. Struct. 2007, 81, 96–104. [Google Scholar] [CrossRef]
- Dey, S.; Mukhopadhyay, T.; Khodaparast, H.H.; Adhikari, S. Stochastic Natural Frequency of Composite Conical Shells. Acta Mech. 2015, 226, 2537–2553. [Google Scholar] [CrossRef]
- Dey, S.; Mukhopadhyay, T.; Spickenheuer, A.; Adhikari, S.; Heinrich, G. Bottom up Surrogate Based Approach for Stochastic Frequency Response Analysis of Laminated Composite Plates. Compos. Struct. 2016, 140, 712–727. [Google Scholar] [CrossRef][Green Version]
- Mukhopadhyay, T.; Naskar, S.; Dey, S.; Adhikari, S. On Quantifying the Effect of Noise in Surrogate Based Stochastic Free Vibration Analysis of Laminated Composite Shallow Shells. Compos. Struct. 2016, 140, 798–805. [Google Scholar] [CrossRef]
- Dey, S.; Mukhopadhyay, T.; Adhikari, S. Stochastic Free Vibration Analyses of Composite Shallow Doubly Curved Shells—A Kriging Model Approach. Compos. Part B Eng. 2015, 70, 99–112. [Google Scholar] [CrossRef]
- Seçgin, A.; Kara, M. Stochastic Vibration Analyses of Laminated Composite Plates via a Statistical Moments-Based Methodology. J. Vib. Eng. Technol. 2019, 7, 73–82. [Google Scholar] [CrossRef]
- Wang, J.F.; Yang, J.P.; Lai, S.K.; Zhang, W. Stochastic Meshless Method for Nonlinear Vibration Analysis of Composite Plate Reinforced with Carbon Fibers. Aerosp. Sci. Technol. 2020, 105, 105919. [Google Scholar] [CrossRef]
- Huo, H.; Zhou, Z.; Chen, G.; Yang, D. Exact Benchmark Solutions of Random Vibration Responses for Thin-Walled Orthotropic Cylindrical Shells. Int. J. Mech. Sci. 2021, 207, 106644. [Google Scholar] [CrossRef]
- Zuo, P.; Shi, X.; Huang, Z.; Luo, J.; Ge, R. Random Vibration Analysis of Composite Laminated Conical–Cylindrical Cabin Structures of Air Vehicles Considering Thermal Load. Structures 2023, 55, 626–637. [Google Scholar] [CrossRef]
- Parviz, H.; Fakoor, M. Stochastic Free Vibration of Composite Plates with Temperature-Dependent Properties under Spatially Varying Stochastic High Thermal Gradient. Mech. Based Des. Struct. Mach. 2023, 51, 5878–5901. [Google Scholar] [CrossRef]
- Chen, Y.; Zhong, R.; Wang, Q.; Chen, L.; Qin, B. Uncertain Stochastic Vibration Characteristic Analysis of Composite Laminated Rectangular Plate Based on Improved Kriging Model. Compos. Struct. 2024, 340, 118180. [Google Scholar] [CrossRef]
- Hakula, H.; Kaarnioja, V.; Laaksonen, M. Cylindrical Shell with Junctions: Uncertainty Quantification of Free Vibration and Frequency Response Analysis. Shock Vib. 2018, 2018, 5817940. [Google Scholar] [CrossRef]
- Singh, B.N.; Bisht, A.K.S.; Pandit, M.K.; Shukla, K.K. Nonlinear Free Vibration Analysis of Composite Plates with Material Uncertainties: A Monte Carlo Simulation Approach. J. Sound Vib. 2009, 324, 126–138. [Google Scholar] [CrossRef]
- Lal, A.; Choski, P.; Singh, B.N. Stochastic Nonlinear Free Vibration Analysis of Piezolaminated Composite Conical Shell Panel Subjected to Thermoelectromechanical Loading with Random Material Properties. J. Appl. Mech. 2012, 79, 061008. [Google Scholar] [CrossRef]
- Parhi, A.; Singh, B.N. Stochastic Response of Laminated Composite Shell Panel in Hygrothermal Environment. Mech. Based Des. Struct. Mach. 2014, 42, 454–482. [Google Scholar] [CrossRef]
- Chen, G.; Huo, H.; Zhan, S.; Yang, D. Analytical Stochastic Responses of Thin Cylindrical Shells under Various Stationary Excitations. Int. J. Mech. Sci. 2021, 190, 106048. [Google Scholar] [CrossRef]
- Singh, B.; Yadav, D.; Iyengar, N.G. Free Vibration of Composite Cylindrical Panels with Random Material Properties. Compos. Struct. 2002, 58, 435–442. [Google Scholar] [CrossRef]
- Garg, A.; Li, L. Data-Driven Uncertainty Quantification and Sensitivity Studies in Free Vibration Behavior of Bio-Inspired Helicoidal Laminated Composite Cylindrical Shells. Mech. Adv. Mater. Struct. 2024, 2355369. [Google Scholar] [CrossRef]
- Huo, H.; Yu, T.; Zhao, J.; Chen, G.; Yang, D. A Novel Uncertainty Quantification Method for Determining Deformations and Reliabilities of Stochastic Laminated Composite Plates with Geometric Nonlinearity. Comput. Methods Appl. Mech. Eng. 2024, 420, 116731. [Google Scholar] [CrossRef]
- Belarbi, M.-O.; Khechai, A.; Houari, M.S.A.; Bessaim, A.; Hirane, H.; Garg, A. Free Vibration Behavior of Sandwich FGM Beams: Parametric and Uncertainty Analysis. J. Vib. Eng. Technol. 2024, 12 (Suppl. S1), 883–905. [Google Scholar] [CrossRef]
- Rawat, P.; Zhu, D.; Rahman, M.Z.; Barthelat, F. Structural and Mechanical Properties of Fish Scales for the Bio-Inspired Design of Flexible Body Armors: A Review. Acta Biomater. 2021, 121, 41–67. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Shukla, N.K.; Belarbi, M.-O.; Abbas, M.; Garg, A.; Li, L.; Bhutto, J.; Bhatia, A. Bio-Inspired Nacre and Helicoidal Composites: From Structure to Mechanical Applications. Thin Walled Struct. 2023, 192, 111146. [Google Scholar] [CrossRef]
- Yin, B.B.; Sun, W.K.; Zhang, X.Y.; Liew, K.M. Deciphering Structural Biological Materials: Viewing from the Mechanics Perspective and Their Prospects. Compos. Part B Eng. 2022, 245, 110213. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, J.; Yu, T.X. Dynamic Behaviors of Bio-Inspired Structures: Design, Mechanisms, and Models. Eng. Struct. 2022, 265, 114490. [Google Scholar] [CrossRef]
- Saurabh, S.; Kiran, R.; Singh, D.; Vaish, R.; Chauhan, V.S. A Comprehensive Investigation on Nonlinear Vibration and Bending Characteristics of Bio-Inspired Helicoidal Laminated Composite Structures. Appl. Math. Mech. 2025, 46, 81–100. [Google Scholar] [CrossRef]
- Garg, A.; Belarbi, M.-O.; Li, L.; Sharma, N.; Gupta, A.; Chalak, H.D. Free Vibration Analysis of Bio-Inspired Helicoid Laminated Composite Plates. J. Strain Anal. Eng. Des. 2023, 58, 538–548. [Google Scholar] [CrossRef]
- Lu, T.; Shen, H.-S.; Wang, H.; Chen, X.; Feng, M. Optimization Design and Nonlinear Bending of Bio-Inspired Helicoidal Composite Laminated Plates. Materials 2023, 16, 4550. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, S.; Mohamed, N.; Eltaher, M.A. Bending, Buckling and Linear Vibration of Bio-Inspired Composite Plates. Ocean Eng. 2022, 259, 111851. [Google Scholar] [CrossRef]
- Malekinejad, H.; Carbas, R.J.C.; Akhavan-Safar, A.; Marques, E.A.S.; Ferreira, M.; da Silva, L.F.M. Bio-Inspired Helicoidal Composite Structure Featuring Graded Variable Ply Pitch under Transverse Tensile Loading. J. Compos. Sci. 2024, 8, 228. [Google Scholar] [CrossRef]
- Singh, A.; Garg, A.; Sahu, V. Stability and Mode Shape Analysis of Doubly- and Cross-Helicoidal Laminated Sandwich Plates Inspired from Dactyl’s Club. Mech. Adv. Mater. Struct. 2023, 31, 8764–8780. [Google Scholar] [CrossRef]
- Almitani, K.H.; Mohamed, N.; Alazwari, M.A.; Mohamed, S.A.; Eltaher, M.A. Exact Solution of Nonlinear Behaviors of Imperfect Bioinspired Helicoidal Composite Beams Resting on Elastic Foundations. Mathematics 2022, 10, 887. [Google Scholar] [CrossRef]
- Khotjanta, P.; Aimmanee, S. Optimal Interply Angle of Bio-Inspired Composite Curved Panels with Helicoidal Fiber Architecture. Compos. Struct. 2024, 343, 118269. [Google Scholar] [CrossRef]
- Mohamed, S.A.; Mohamed, N.; Eltaher, M.A. Snap-through Instability of Helicoidal Composite Imperfect Beams Surrounded by Nonlinear Elastic Foundation. Ocean Eng. 2022, 263, 112171. [Google Scholar] [CrossRef]
- Esmaeili, M.; Osanloo, M.; Rashidinejad, F.; Aghajani Bazzazi, A.; Taji, M. Multiple Regression, ANN and ANFIS Models for Prediction of Backbreak in the Open Pit Blasting. Eng. Comput. 2014, 30, 549–558. [Google Scholar] [CrossRef]
- Gardner, B.J.; Gransberg, D.D.; Rueda, J.A. Stochastic Conceptual Cost Estimating of Highway Projects to Communicate Uncertainty Using Bootstrap Sampling. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2017, 3, 05016002. [Google Scholar] [CrossRef]
- Gollapalli, M.; Rahman, A.; Kudos, S.A.; Foula, M.S.; Alkhalifa, A.M.; Albisher, H.M.; Al-Hariri, M.T.; Mohammad, N. Appendicitis Diagnosis: Ensemble Machine Learning and Explainable Artificial Intelligence-Based Comprehensive Approach. Big Data Cogn. Comput. 2024, 8, 108. [Google Scholar] [CrossRef]
- Ibarra Kwick, J.M.; Hernández-Uribe, Ó.; Cárdenas-Robledo, L.A.; Luque-Morales, R.A. Extended Reality Applications for CNC Machine Training: A Systematic Review. Multimodal Technol. Interact. 2024, 8, 80. [Google Scholar] [CrossRef]
- Linero-Ramos, R.; Parra-Rodríguez, C.; Espinosa-Valdez, A.; Gómez-Rojas, J.; Gongora, M. Assessment of Dataset Scalability for Classification of Black Sigatoka in Banana Crops Using UAV-Based Multispectral Images and Deep Learning Techniques. Drones 2024, 8, 503. [Google Scholar] [CrossRef]
- Balderas, L.; Lastra, M.; Benítez, J.M. An Efficient Green AI Approach to Time Series Forecasting Based on Deep Learning. Big Data Cogn. Comput. 2024, 8, 120. [Google Scholar] [CrossRef]
- Banker, R.; Natarajan, R.; Zhang, D. Two-Stage Estimation of the Impact of Contextual Variables in Stochastic Frontier Production Function Models Using Data Envelopment Analysis: Second Stage OLS versus Bootstrap Approaches. Eur. J. Oper. Res. 2019, 278, 368–384. [Google Scholar] [CrossRef]
- Cao, J.; Hao, Y.X.; Zhang, W.; Liu, L.T.; Yang, S.W.; Cao, Y.T. Bi-Stability and Vibration of Asymmetric and Antisymmetric Laminates with Four Points Simply Supported at Arbitrary Location. J. Vib. Eng. Technol. 2023, 11, 1679–1695. [Google Scholar] [CrossRef]
- Cheng, C.; Yang, B.; Wang, X.; Lee, I. Uncertainty-oriented Thermoelastic Topology Optimization with Stress Constraint. Int. J. Numer. Methods Eng. 2024, 125, e7441. [Google Scholar] [CrossRef]
- Jiang, X.; Mahadevan, S. Bayesian Hierarchical Uncertainty Quantification by Structural Equation Modeling. Int. J. Numer. Methods Eng. 2009, 80, 717–737. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, H.; Zheng, J.; Zhang, Y.; Li, E.; He, Z.C. Robust Topology Optimization with Interval Field Model: On the Spatially Varied Non-Probabilistic Uncertainty of Material Property, Loading and Geometry. Eng. Comput. 2024, 40, 1093–1109. [Google Scholar] [CrossRef]
- Angiulli, G.; Calcagno, S.; La Foresta, F.; Versaci, M. Concrete Compressive Strength Prediction Using Combined Non-Destructive Methods: A Calibration Procedure Using Preexisting Conversion Models Based on Gaussian Process Regression. J. Compos. Sci. 2024, 8, 300. [Google Scholar] [CrossRef]
- Lore, S.; Deshpande, A.S.; Singh, B.N. Nonlinear Free Vibration Analysis of Functionally Graded Plates and Shell Panels Using Quasi-3D Higher Order Shear Deformation Theory. Mech. Adv. Mater. Struct. 2024, 31, 453–469. [Google Scholar] [CrossRef]
- Sokołowski, D.; Kamiński, M. Computational homogenization of carbon/polymer composites with stochastic interface defects. Compos. Struct. 2018, 183, 434–449. [Google Scholar] [CrossRef]
- Garg, A.; Mukhopadhyay, T.; Chalak, H.D.; Belarbi, M.-O.; Li, L.; Sahoo, R. Multiscale Bending and Free Vibration Analyses of Functionally Graded Graphene Platelet/Fiber Composite Beams. Steel Compos. Struct. 2022, 44, 707–720. [Google Scholar] [CrossRef]
- Ram, K.S.S.; Sinha, P.K. Hygrothermal Effects on the Free Vibration of Laminated Composite Plates. J. Sound Vib. 1992, 158, 133–148. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).